密克定理在解圆共点和点共圆问题中的应用_刘小满
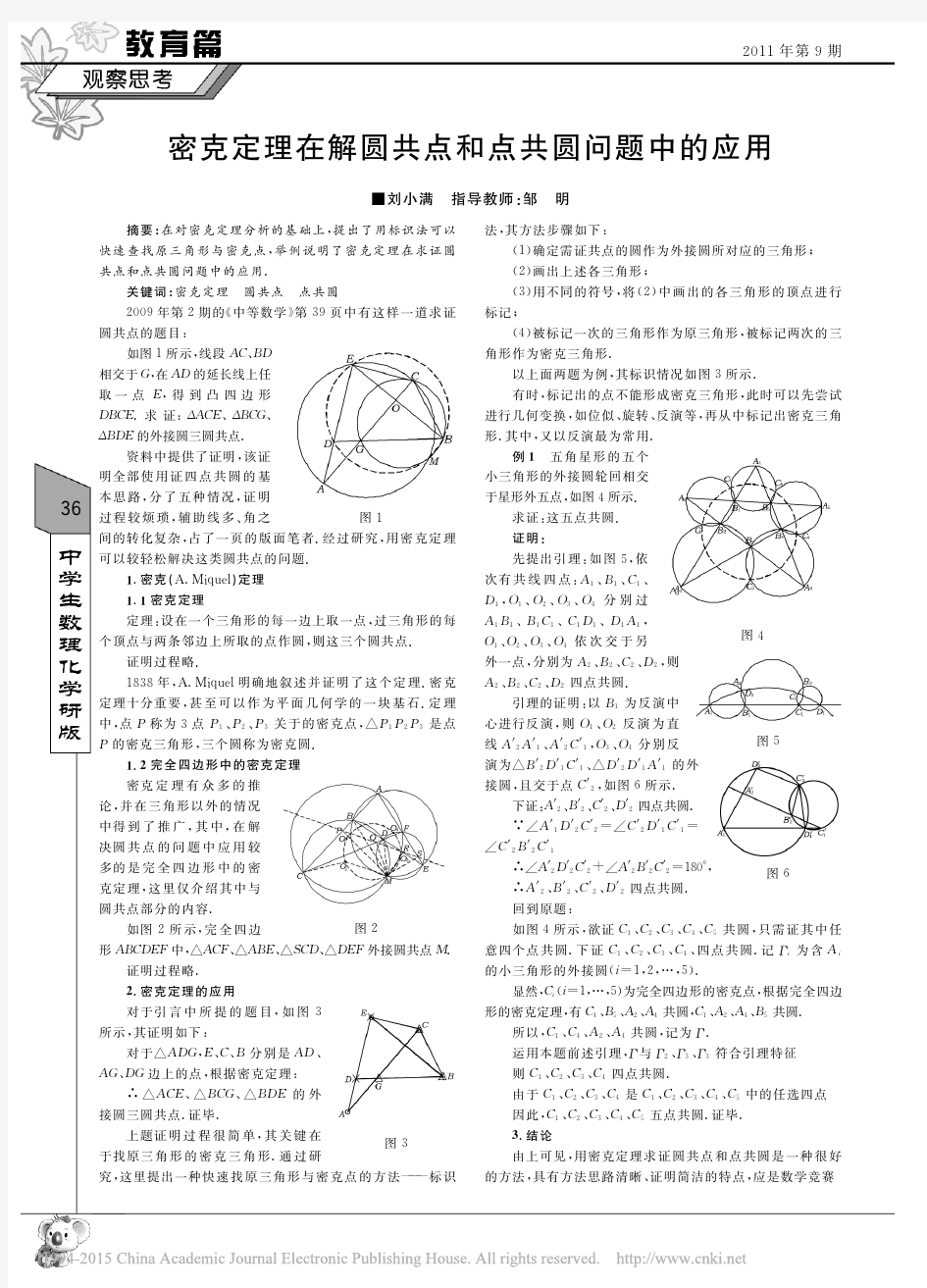

圆幂定理
圆幂定理 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。或:经过圆内一点引两条弦,各弦被这点所分成的两段的积相等。 定理 圆内的两条相交弦,被交点分成的两条线段长的积相等。(经过圆内一点引两条弦,各弦被这点所分成的两段的积相等) 几何语言:若弦AB、CD交于点P则PA·PB=PC·PD(相交弦定理) 概述 相交弦定理为圆幂定理之一,其他两条定理为: 切割线定理 割线定理 2证明 证明:连结AC,BD 由圆周角定理的推论,得∠A=∠D,∠C=∠B。(圆周角推论2: 同(等)弧所对圆周角相等.)∴△PAC∽△PDB ∴PA∶PD=PC∶PB,PA·PB=PC·PD 注:其逆定理可作为证明圆的内接四边形的方法. P点若选在圆内任意一点更具一般性。其逆定理也可用于证明四点共圆。 P 不是圆心 3比较
切割线定理 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。是圆幂定理的一种。 切割线定理示意图 几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT2=PA·PB(切割线定理) 推论: 从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等 几何语言: ∵PT是⊙O切线,PBA,PDC是⊙O的割线 ∴PD·PC=PA·PB(切割线定理推论)(割线定理) 由上可知:PT2=PA·PB=PC·PD 2证明 切割线定理证明: 设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT2=PA·PB
证明:连接AT, BT ∵∠PTB=∠PAT(弦切角定理 ) 切割线定理的证明 ∠APT=∠APT(公共角) ∴△PBT∽△PTA(两角对应相等,两三角形相似) 则PB:PT=PT:AP 即:PT2=PB·PA 3比较 相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们的推论统称为圆幂定理。一般用于求直线段长度。 割线定理:指的是从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等, 1定义 文字表达:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。 数学语言:从圆外一点L引两条割线与圆分别交于A.B.C.D 则有LA·LB=LC·LD=LT^2。如下图所示。(LT为切线)
《1.3.1圆幂定理》教学案3
《1.3.1圆幂定理》教学案 【教学目标】 1.使学生理解相交弦定理、切割线定理及其推论间的相互关系,并能综合运用它们解 决有关问题; 2.从运动的观点来统一认识圆幂定理.对学生进行事物之间是相互联系和运动变化的 观点的教育. 【教学重难点】 重点:相交弦定理、切割线定理及其推论之间的关系以及应用; 难点:灵活运用圆幂定理解题. 【教学过程】 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等. 或:经过圆内一点引两条弦,各弦被这点所分成的两段的积相等. 定理 圆内的两条相交弦,被交点分成的两条线段长的积相等.(经过圆内一点引两条弦,各弦被这点所分成的两段的积相等) 几何语言:若弦AB、CD交于点P则P A·PB=PC·P D(相交弦定理) 2证明 证明:连结AC,BD 由圆周角定理的推论,得∠A=∠D,∠C=∠B.(圆 周角推论2: 同(等)弧所对圆周角相等.) ∴△P AC∽△PDB ∴P A∶PD=PC∶PB,P A·PB=PC·PD 注:其逆定理可作为证明圆的内接四边形的方法. P点若选在圆内任意一点更具一般性.其逆定理也可用于证明四点共圆. 3比较 相交弦定理、切割线定理以及他们的推论统称为圆幂定理.一般用于求线段长度. 4相交弦定理推论 定理 如果弦与直径垂直相交,那么弦的一半是它所分直径所成的两条线段的比例中项. 说明几何语言:若AB是直径,CD垂直AB于点P,则=P A·PB(相交弦定理推论)
切割线定理 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.是圆幂定理的一种. 切割线定理示意图 几何语言:∵PT切⊙O于点T,PBA是⊙O的割线∴PT2=P A·PB(切割线定理) 推论: 从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等几何语言: ∵PT是⊙O切线,PBA,PDC是⊙O的割线 ∴PD·PC=P A·PB(切割线定理推论)(割线定理) 由上可知:PT2=P A·PB=PC·PD 2证明 切割线定理证明: 设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT2=P A·PB 证明:连接AT,BT ∵∠PTB=∠P AT(弦切角定理 ) 切割线定理的证明 ∠APT=∠APT(公共角) ∴△PBT∽△PTA(两角对应相等,两三角形相似) 则PB:PT=PT:AP 即:PT2=PB·P A
初三下册数学圆知识点定理总结
1.垂径定理及推论: 如图:有五个元素,“知二可推三”;需记忆其中四个定理, 即“垂径定理”“中径定理”“弧径定理”“中垂定理”. 几何表达式举例: ∵ CD过圆心 ∵CD⊥AB 2.平行线夹弧定理: 圆的两条平行弦所夹的弧相等. 几何表达式举例: 3.“角、弦、弧、距”定理:(同圆或等圆中) “等角对等弦”;“等弦对等角”; “等角对等弧”;“等弧对等角”; “等弧对等弦”;“等弦对等(优,劣)弧”; “等弦对等弦心距”;“等弦心距对等弦”. 几何表达式举例: (1) ∵∠AOB=∠COD ∴ AB = CD (2) ∵ AB = CD ∴∠AOB=∠COD 4.圆周角定理及推论: (1)圆周角的度数等于它所对的弧的度数的一半; (2)一条弧所对的圆周角等于它所对的圆心角的一半;(如图) (3)“等弧对等角”“等角对等弧”; (4)“直径对直角”“直角对直径”;(如图) (5)如三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(如 图) (1)(2)(3)(4) 几何表达式举例: (1)∵∠ACB=∠AOB ∴…………… (2)∵ AB是直径 ∴∠ACB=90° (3)∵∠ACB=90° ∴ AB是直径 (4)∵ CD=AD=BD ∴ΔABC是RtΔ 5.圆内接四边形性质定理: 圆内接四边形的对角互补,并且任何一个外 角都等于它的内对角. 几何表达式举例: ∵ ABCD是圆内接四边形 ∴∠CDE =∠ABC ∠C+∠A =180° 6.切线的判定与性质定理: 如图:有三个元素,“知二可推一”;需记忆其中四个定理. (1)经过半径的外端并且垂直于这条 半径的直线是圆的切线; (2)圆的切线垂直于经过切点的半径; ※(3)经过圆心且垂直于切线的直线必经过切点; ※(4)经过切点且垂直于切线的直线必经过圆心. 几何表达式举例: (1)∵OC是半径∵OC⊥AB ∴AB是切线 (2)∵OC是半径 ∵AB是切线 ∴OC⊥AB (3)…………… 7.切线长定理: 从圆外一点引圆的两条切线, 它们的切线长相等;圆心和这一 点的连线平分两条切线的夹角. 几何表达式举例: ∵ PA、PB是切线 ∴ PA=PB ∵PO过圆心 ∴∠APO =∠BPO 8.弦切角定理及其推论: 几何表达式举例:
初中数学中被删掉的有用知识圆幂定理及其应用
圆幂定理及其应用 教学目标 1.使学生理解相交弦定理、切割线定理及其推论间的相互关系,并能综合运用它们解决有关问题; 2.通过对例题的分析,提高学生分析问题和解决问题的能力,并领悟添加辅助线的方法; 3.从运动的观点来统一认识圆幂定理.对学生进行事物之间是相互联系和运动变化的 观点的教育. 教学重点和难点 相交弦定理、切割线定理及其推论之间的关系以及应用是重点;灵活运用圆幂定理解题是难点. 教学过程设计 一、从学生原有的认知结构提出问题 1.根据图7-162(1)、(2)、(3),让学生结合图形,说出相交弦定理、切割线定理、割线定理的内容. 2.然后提出问题.相交弦定理、切割线定理及其推论这三者之间是否有联系? 提出问题让学生思考,在学生回答的基础上,教师用电脑或投影演示图形的变化过程,从相交弦定理出发,用运动的观点来统一认识定理. (1)如图7-163,⊙O的两条弦AB,CD相交于点P,则PA·PB=PC·PD.这便是我们学过的相交弦定理.对于这个定理有两个特例: 一是如果圆内的两条弦交于圆心O,则有PA=PB=PC=PD=圆的半径R,此时AB,CD 是直径,相交弦定理当然成立.(如图7-164)
二是当P点逐渐远离圆心O,运动到圆上时,点P和B,D重合,这时PB=PD=O,仍然有PA·PB=PC·PD=O,相交弦定理仍然成立.(图7-165) (2)点P继续运动,运动到圆外时,两弦的延长线交于圆外 一点P,成为两条割线,则有PA·PB=PC·PD,这就是我们学过 的切割线定理的推论(割线定理).(图7-166) (3)在图7-166中,如果将割线PDC按箭头所示方向绕P点 旋转,使C,D两点在圆上逐渐靠 近,以至合为一点C,割线PCD变成切线PC.这时有PA·PB=PC·PD =PC2,这就是我们学过的切割线定理.(图7-167) (4)如果割线PAB也绕P点向外旋转的话,也会成为一条切线PA.这时应有PA2=PB2,可 得PA=PB,这就是我们学过的切线长定理.(图7-168) 至此,通过点的运动及线的运动变化,我们发现,相交弦定理、切割线定理及其推论和切线长定理之间有着密切的联系. 3.启发学生理解定理的实质. 经过一定点P作圆的弦或割线或切线,如图7-169. 观察图7-169,可以得出:(设⊙O半径为R) 在图(1)中,PA·PB=PC·PD=PE·PF =(R-OP)(R+OP) =R2-OP2; 在图(2)中,PA·PB=PT2=OP2-OT2 =OP2-R2 在图(3)中,PA·PB=PC·PD=PT2 =OP2-R2. 教师指出,由于PA·PB均等于|OP2-R2|,为一常数,叫做点P关于⊙O的幂,所以相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理. 二、例题分析(采用师生共同探索、讲练结合的方式进行) 例1 如图7-170,两个以O为圆心的同心圆,AB切大圆于B,AC切小圆于C,交大圆
圆幂定理及其应用
[文件] sxc3jja0008.doc [科目] 数学 [年级] 初三 [章节] [关键词] 圆/圆幂定理/应用 [标题] 圆幂定理及其应用 [内容] 教学目标 1.使学生理解相交弦定理、切割线定理及其推论间的相互关系,并能综合运用它们解 决有关问题; 2.通过对例题的分析,提高学生分析问题和解决问题的能力,并领悟添加辅助线的方 法; 3.从运动的观点来统一认识圆幂定理.对学生进行事物之间是相互联系和运动变化的 观点的教育. 教学重点和难点 相交弦定理、切割线定理及其推论之间的关系以及应用是重点;灵活运用圆幂定理解题是难点. 教学过程设计 一、从学生原有的认知结构提出问题 1.根据图7-162(1)、(2)、(3),让学生结合图形,说出相交弦定理、切割线定理、割线定理的内容. 2.然后提出问题.相交弦定理、切割线定理及其推论这三者之间是否有联系? 提出问题让学生思考,在学生回答的基础上,教师用电脑或投影演示图形的变化过程, 从相交弦定理出发,用运动的观点来统一认识定理. (1)如图7-163,⊙O的两条弦AB,CD相交于点P,则PA·PB=PC·PD.这便是我们学过的相交弦定理.对于这个定理有两个特例: 一是如果圆内的两条弦交于圆心O,则有PA=PB=PC=PD=圆的半径R,此时AB,CD是直径,相交弦定理当然成立.(如图7-164)
二是当P点逐渐远离圆心O,运动到圆上时,点P和B,D重合,这时PB=PD=O,仍然有PA·PB=PC·PD=O,相交弦定理仍然成立.(图7-165) (2)点P继续运动,运动到圆外时,两弦的延长线交于圆外一 点P,成为两条割线,则有PA·PB=PC·PD,这就是我们学过的 切割线定理的推论(割线定理).(图7-166) (3)在图7-166中,如果将割线PDC按箭头所示方向绕P点旋 转,使C,D两点在圆上逐渐靠 近,以至合为一点C,割线PCD变成切线PC.这时有PA·PB=PC·PD =PC2,这就是我们学过的切割线定理.(图7-167) (4)如果割线PAB也绕P点向外旋转的话,也会成为一条切线PA.这时应有PA2=PB2,可得PA=PB,这就是我们学过的切线长定理.(图7-168) 至此,通过点的运动及线的运动变化,我们发现,相交弦定理、切割线定理及其推论和 切线长定理之间有着密切的联系. 3.启发学生理解定理的实质. 经过一定点P作圆的弦或割线或切线,如图7-169. 观察图7-169,可以得出:(设⊙O半径为R) 在图(1)中,PA·PB=PC·PD=PE·PF =(R-OP)(R+OP) =R2-OP2;
初三圆知识点及定理
《圆》知识点及定理 一、圆的概念 集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合; 2、圆的外部:可以看作是到定点的距离大于定长的点的集合; 3、圆的内部:可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念: 1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆; (补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线); 3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线; 4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线; 5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。 二、点与圆的位置关系 1、点在圆内?d r ?点A在圆外; 三、直线与圆的位置关系 1、直线与圆相离?d r >?无交点; 2、直线与圆相切?d r =?有一个交点; 3、直线与圆相交?d r +; 外切(图2)?有一个交点?d R r =+; 相交(图3)?有两个交点?R r d R r -<<+; 内切(图4)?有一个交点?d R r =-; 内含(图5)?无交点?d R r <-; 五、垂径定理 垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。 推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 以上共4个定理,简称2推3 定理:此定理中共5个结论中,只要知道其中2 个即可推出其它3个结论,即: ①AB是直径②AB CD ⊥③CE DE =④弧BC=弧BD ⑤弧AC= 弧AD 中任意2个条件推出其他3个结论。 推论2:圆的两条平行弦所夹的弧相等。 即:在⊙O中,∵AB∥CD ∴弧AC=弧BD 六、圆心角定理 圆心角定理:同圆或等圆中,相等的圆心角所对的弦相 等,所对的弧相等,弦心距相等。此定理也称1推3定理, 即上述四个结论中, A 图4 图5 D
圆的性质(垂径定理)
一.选择题(共12小题) 1.(2014?毕节地区)如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是() 2.(2014?舟山)如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=8,则AB的长为() 3.(2014?凉山州)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC 的长为() .cm cm C cm或cm cm或cm 4.(2014?兰州)如图,CD是⊙O的直径,弦AB⊥CD于E,连接BC、BD,下列结论中不一定正确的是() =C 5.(2014?北京)如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为() 6.(2014?泸州)如图,在平面直角坐标系中,⊙P的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是() C 7.(2014?赤峰)如图,AB是⊙O的直径,C,D是⊙O上两点,CD⊥AB.若∠DAB=65°,则∠BOC=() 8.(2014?齐齐哈尔)如图,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数等于()
9.(2014?宜昌)如图,点A,B,C,D都在⊙O上,AC,BD相交于点E,则∠ABD=() 10.(2014?山西)如图,⊙O是△ABC的外接圆,连接OA、OB,∠OBA=50°,则∠C的度数为() 11.(2014?长春)如图,在⊙O中,AB是直径,BC是弦,点P是上任意一点.若AB=5,BC=3,则AP的长不可能为() 12.(2014?重庆)如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是() 二.解答题(共18小题) 13.(2014?黄石)如图,A、B是圆O上的两点,∠AOB=120°,C是弧AB的中点. (1)求证:AB平分∠OAC; (2)延长OA至P,使得OA=AP,连接PC,若圆O的半径R=1,求PC的长. 14.(2014?佛山)如图,⊙O的直径为10cm,弦AB=8cm,P是弦AB上的一个动点,求OP的长度范围.
埃伦费斯特定理
埃伦费斯特定理[编辑] 量子力学里,埃伦费斯特定理(Ehrenfest theorem)表明,量子算符的期望值对于时间的导数,跟这量子算符与哈密顿算符的对易算符,两者之间的关系,以方程表达为[1] ; 其中,是某个量子算符,是它的期望值,是哈密顿算符,是时间,是约化普朗克常数。 埃伦费斯特定理是因物理学家保罗·埃伦费斯特命名。在量子力学的海森堡绘景里,埃伦费斯特定理非常显而易见;取海森堡方程的期望值,就可以得到埃伦费斯特定理。埃伦费斯特定理与哈密顿力学的刘维尔定理密切相关;刘维尔定理使用的泊松括号,对应于埃伦费斯特 定理的对易算符。实际上,从根据经验法则,将对易算符换为泊松括号乘以,再取趋向于0 的极限,含有对易算符的量子定理就可以改变为含有泊松括号的经典定理。 为,则算符的期望值对于时间的导数为 表明哈密顿算符与时间 。 。 , 。
将这三个方程代入的方程,则可得到 。 所以,埃伦费斯特定理成立: 。 使用埃伦费斯特定理,可以简易地证明,假若一个物理系统的哈密顿量显性地不含时间,则这系统是保守系统。 从埃伦费斯特定理,可以计算任何算符的期望值对于时间的导数。特别而言,速度的期望值和加速度的期望值。知道这些资料,就可以分析量子系统的运动行为。 保守的哈密顿量[编辑] 思考哈密顿算符: 。 假若,哈密顿量显性地不含时间,,则 , 哈密顿量是个常数 为的粒子,移动于一维空间.其 ; 其中,为位置,是,
。 由于,位置的期望值对于时间的导数等于速度的期望值: 。 这样,可以得到动量的期望值。 动量的期望值对于时间的导数[编辑] 应用埃伦费斯特定理, 。 由于与自己互相交换,所以,。又在坐标空间里,动量算符不含时间:。所以, 。 将泊松括号展开, 。 。 在量子力学里,动量的期望值对于时间的导数,等于作用力的期望值。
圆幂定理及其证明#(优选.)
圆幂的定义 假设平面上有一圆O,其半径为R,有一点P在圆O外,则OP^2-R^2即为P点到圆O的幂; 若P点在圆内,则圆幂为R^2-OP^2; 综上所述,圆幂为|OP^2-R^2|。 圆幂恒大于或等于零。 圆幂的由来 过任意在圆O外的一点P引一条直线L1与一条过圆心的直线L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D。则PA·PB=PC·PD。若圆半径为r,则PC·PD=(PO-r)·(PO+r)=PO^2-r^2=|PO^2-r^2| (要加绝对值,原因见下)为定值。这个值称为点P到圆O的幂。(事实上所有的过P点与圆相交的直线都满足这个值) 若点P在圆内,类似可得定值为r^2-PO^2=|PO^2-r^2| 故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差,而过这一点引任意直线交圆于A、B,那么PA·PB等于圆幂的绝对值。 圆幂定理 定理内容 过任意不在圆上的一点P引两条直线L1、L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D(可重合),则有 。[1] 圆幂定理的所有情况 考虑经过P点与圆心O的直线,设PO交⊙O与M、N,R为圆的半径,则有
圆幂定理的证明 图Ⅰ:相交弦定理。如图,AB、CD为圆O的两条任意弦。相交于点P,连接AB、BD,由于∠B与∠D同为弧AC所对的圆周角,因此由圆周角定理知:∠B=∠D,同理∠A=∠C,所以 。所以有: ,即: 图Ⅱ:割线定理。如图,连接AD、BC。可知∠B=∠D,又因为∠P为公共角,所以有 ,同上证得 图Ⅲ:切割线定理。如图,连接AC、AD。∠PAC为切线PA与弦AC组成的弦切角,因此有∠PAC=∠D,又因为∠P为公共角,所以有 易证
热力学·统计物理期末考试卷讲解学习
贵州大学2010—2011学年第二学期考试试卷 B 热力学与统计物理 注意事项: 1. 请考生按要求在试卷装订线内填写姓名、学号和年级专业。 2. 请仔细阅读各种题目的回答要求,在规定的位置填写答案。 3. 不要在试卷上乱写乱画,不要在装订线内填写无关的内容。 4. 满分100分,考试时间为120分钟。 一、选择题(共18分,每小题3分) 1. 下列关于状态函数的定义正确的是( )。 A .系统的吉布斯函数是:pV TS U G +-= B .系统的自由能是:TS U F += C .系统的焓是:pV U H -= D .系统的熵函数是:T Q S = 2. 以T 、p 为独立变量,特征函数为( )。 A .内能; B .焓; C .自由能; D .吉布斯函数。 3. 下列说法中正确的是( )。 A .不可能把热量从高温物体传给低温物体而不引起其他变化; B .功不可能全部转化为热而不引起其他变化; C .不可能制造一部机器,在循环过程中把一重物升高而同时使一热库冷却; D .可以从一热源吸收热量使它全部变成有用的功而不产生其他影响。 4. 要使一般气体满足经典极限条件,下面措施可行的是( )。 A .减小气体分子数密度; B .降低温度; C .选用分子质量小的气体分子; D .减小分子之间的距离。
5. 下列说法中正确的是( )。 A .由费米子组成的费米系统,粒子分布不受泡利不相容原理约束; B .由玻色子组成的玻色系统,粒子分布遵从泡利不相容原理; C .系统宏观物理量是相应微观量的统计平均值; D .系统各个可能的微观运动状态出现的概率是不相等的。 6. 正则分布是具有确定的( )的系统的分布函数。 A .内能、体积、温度; B .体积、粒子数、温度; C .内能、体积、粒子数; D .以上都不对。 二、填空题(共20分,每空2分) 1. 对于理想气体,在温度不变时,内能随体积的变化关系为=??? ????T V U 。 2. 在S 、V 不变的情形下,稳定平衡态的U 。 3. 在可逆准静态绝热过程中,孤立系统的熵变ΔS = 。 4. 连续相变的特点是 。 5. 在等温等压条件下,单相化学反应 0=∑i i i A ν 达到化学平衡的条件为 。 6. 在满足经典极限条件1>>α e 时,玻色系统、费米系统以及玻耳兹曼系统的微观状态数满 足关系 。 7. 玻色-爱因斯坦凝聚现象是指 。 8. 在低温下,如果计及电子和离子振动的话,金属的定容热容量可表为 。 9. 按费米分布,处在能量为s ε的量子态s 上的平均粒子数为=s f 。 10.刘维尔定理表明,如果随着一个代表点沿正则方程所确定的轨道在相空间中运动,其邻域的 是不随时间改变的常数。
《1.3.1圆幂定理》教学案1
《1.3.1圆幂定理》教学案 教学目标 1.知识与技能:(1)理解相交弦定理及其推论,并初步会运用它们进行有关的简单证明和计算;(2)学会作两条已知线段的比例中项; 2.过程与方法:师生互动,生生互动,共同探究新知; 3.情感、态度、价值观:通过推论的推导,向学生渗透由一般到特殊的思想方法.教学重、难点 重点:正确理解相交弦定理及其推论 难点:相交弦定理及其推论的熟练运用 教学过程 前面讨论了与圆有关的角之间的关系.下面我们讨论与圆有关的线段的关系及其度量问题.下面沿用从特殊到一般地思路,讨论与圆的相交弦有关的问题. 探究1如图2-20,AB是⊙O的直径,CD⊥AB.AB与CD相交于P,线段P A、PB、PC、P D之间有什么关系? ?=?(老师引导学生完成推导过程) . PA PB PC PD 探究2将图2-20中的AB向上(或向下)平移,使AB不再是直径(图2-21),探究1的结论还成立吗? 连接AD、BC,请同学们自己给出证明. 探究3如果CD与AB不垂直,如图2-22,CD、AB是圆内的任意两条相交弦,探究1的结论还成立吗? 事实上,AB、CD是圆内的任意相交弦时,探究1仍然成立,而证方法不变.请同学们自己给出证明. 由上诉探究和论证,我们有 1.相交弦定理圆内的两条相交弦,被交点分成的两条线段长的积相等. 探究4在图2-24中,使割线PB绕P运动到切线的位置(图2-25),线段P A(或PB)、PC、P D之间有什么关系? 2. =?(老师引导学生完成推导过程) PA PC PD
由上诉探究和论证,我们有 3.切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项. 探究5下面对相交弦定理和切割弦定理作进一步分析: 由切割线定理和相交弦定理不难看出,不论点P在圆内或圆外,通过圆的任一条割线交圆于A,B两点,只要点P的位置确定了,则P A? PB都是定值. 设定植为k,则: 当点P在圆外时,如图,由切割线定理,可得 k = P A? PB = PT2= PO2- r2( r表示⊙O的半径 ) 当点P在圆内时,如图,过点P作AB垂直于OP,则: k = P A? PB = P A2= r2 - PO2( r表示⊙O的半径 ) 当点P在圆上时,显然k=0. 由上,我们可以得到: 圆幂定理: 已知⊙(O,r),通过一定点的任意一条割线交圆于A,B两点,则: 当点P在圆外时,k= PO2- r2; 当点P在圆内时,k= r2- PO2; 当点P在⊙O上时,k= 0. 我们称定值k为点P对⊙O的“幂” 【自主检测】 1. 圆内两弦相交,一弦长8cm且被交点平分,另一弦被交点分为1:4,则另一弦长为_ ____. 2. 已知:⊙O和不在⊙O上的一点P,过P的直线交⊙O于A、B两点,若P A·PB=24,OP=5,则⊙O的半径长为_______. 3 . 若P A为⊙O的切线,A为切点,PBC割线交⊙O于B、C,若BC=20,P A=P C的长为_______. 4. AB、CD是⊙O切线,AB∥CD,⊙O的切线EF和AB、CD分别交于E、F,则∠EOF =______.
有关初中圆的定理
1.圆是以圆心为对称中心的中心对称图形;围绕圆心旋转任意一个角度α,都能够与原来的重合. 2.顶点在圆心的角叫做圆心角.圆心到弦的距离叫做弦心距.? 圆幂定理(相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理) ??切线长定理??垂径定理 圆周角定理? 弦切角定理 四圆定理 3.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等. ? 4.在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等. ? 5.把整个圆周等分成360份,每一份弧是1°的弧.圆
心角的度数和它所对的弧的度数相等. ?6.圆是中心对称图形,即圆绕其对称中心(圆心)旋转180°后能够与原来图形重合,这一性质不难理解.圆和其他中心对称图形不同,它还具有旋转不变性,即围绕圆心旋转任意一个角度,都能够与原来的图形重合. ? 7.垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧 8.(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧? (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧 (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧??9.圆的两条平行弦所夹的弧相等? 10.(1)一条弧所对的圆周角等于它所对的圆心角的一半. (2)同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等. ??(3)半圆(或直径)所
对的圆周角是直角;90°的圆周角所对的弦是直径.?(4)如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形. ? 11.(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.? (2)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧. ??(3)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. (4)弦的垂直平分线经过圆心,并且平分弦所对的两条弦. ?(5)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧. ?(6)圆的两条平行弦所夹的弧度数相等. ?12.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.??垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.? 13.平分弦(不是直径)的直径垂直与弦,并且平分弦所对的两条弧. 14.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等,所对的弦的弦心距也相等.
圆的定义、垂径定理、圆心角、圆周角练习
圆的定义、垂径定理、圆心角、圆周角练习 1.如下图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数 是50o,则∠C的度数是() A)50o B)40o C)30o D)25o 第1题图第2题图 2.如上图,两正方形彼此相邻,且大正方形内接于半圆,若小正方形的面积为 16cm2,则该半圆的半径为(). A)(45) + cm B) 9 cm C)45cm D)62cm 3.⊙O中,M为的中点,则下列结论正确的是( ) A.AB>2AM B.AB=2AM C.AB<2AM D.AB与2AM的大小不能确定 4.如上图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3), M是第三象限内OB上一点,BMO ∠=120,则⊙C的半径为() A. 6 B. 5 C 3 D. 32 5.如下图,P为⊙O的弦AB上的点,PA=6,PB=2,⊙O的半径为5,则OP=______. 第5题图第6题图第7题图
6.如上图,扇形的半径是cm 2,圆心角是? 40,点C为弧AB的中点,点P在直线OB上,则PC PA+的最小值为cm 7.如图,在半径为5的⊙O中,弦AB=6,点C是优弧AB上一点(不与 A、B重合), 则cos C的值为 . 8.圆的一条弦长等于它的半径,求这条弦所对的圆周角的度数 为: . 9.已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠E=18°, 求∠C及∠AOC的度数. 10.已知:如图,AB是⊙O的直径,弦CD交AB于E点,BE=1,AE=5,∠AEC=30°,求CD的长. 11.如图,AB为⊙O的弦,C、D为弦AB上两点,且OC=OD ,延长OC、OD分别交⊙O于E、F, 证明:AE=BF.
代数学基本定理
代数学基本定理:任何复系数一元n次多项式方程在复数域上至少有一根(n≥1),由此推出,n次复系数多项式方程在复数域内有且只有n个根(重根按重数计算).代数基本定理在代数乃至整个数学中起着基础作用。据说,关于代数学基本定理的证明,现有200多种证法。 代数学基本定理说明,任何复系数一元n次多项式方程在复数域上至少有一根。 由此推出,n次复系数多项式方程在复数域内有且只有n个根(重根按重数计算)。 有时这个定理表述为:任何一个非零的一元n次复系数多项式,都正好有n个复数根。这似乎是一个更强的命题,但实际上是“至少有一个根”的直接结果,因为不断把多项式除以它的线性因子,即可从有一个根推出有n个根。 尽管这个定理被命名为“代数基本定理”,但它还没有纯粹的代数证明,许多数学家都相信这种证明不存在[1] 。另外,它也不是最基本的代数定理;因为在那个时候,代数基本上就是关于解实系数或复系数多项式方程,所以才被命名为代数基本定理。 2证明历史 代数基本定理在代数乃至整个数学中起着基础作用。据说,关于代数学基本定理的证明,现有200多种证法。迄今为止,该定理尚无纯代数方法的证明。大数学家J.P. 塞尔曾经指出:代数基本定理的所有证明本质上都是拓扑的。美国数学家John Willard Milnor在数学名著《从微分观点看拓扑》一书中给了一个几何直观的证明,但是其中用到了和临界点测度有关的sard定理。复变函数论中,对代数基本定理的证明是相当优美的,其中用到了很多经典的复变函数的理论结果。 该定理的第一个证明是法国数学家达朗贝尔给出的,但证明不完整。接着,欧拉也给出了一个证明,但也有缺陷,拉格朗日于1772年又重新证明了该定理,后经高斯分析,证明仍然很不严格的。 代数基本定理的第一个严格证明通常认为是高斯给出的(1799年在哥廷根大学的博士论文),基本思想如下: 设为n次实系数多项式,记,考虑方根: 即与 这里与分别表示oxy坐标平面上的两条曲线C1、C2,于是通过对曲线作定性的研究,他证明了这两条曲线必有一个交点,从而得出,即,因此z0便是方程的一个根,这个论证具有高度的创造性,但从现代的标准看依然是不严格的,因为他依靠了曲线的图形,证明它们必然相交,而这些图形是比较复杂,正中隐含了很多需要验证的拓扑结论等等。 高斯后来又给出了另外三个证法,其中第四个证法是他71岁公布的,并且在这个证明中他允许多项式的系数是复数。 3证明方法 所有的证明都包含了一些数学分析,至少是实数或复数函数的连续性概念。有些证明也用到了可微函数,甚至是解析函数。 定理的某些证明仅仅证明了任何实系数多项式都有复数根。这足以推出定理的一般形式,这是因为,给定复系数多项式p(z),以下的多项式 就是一个实系数多项式,如果z是q(z)的根,那么z或它的共轭复数就是p(z)的根。 许多非代数证明都用到了“增长引理”:当|z|足够大时,首系数为1的n次多项式函数p(z)的表现如同z。一个更确切的表述是:存在某个正实数R,使得当|z| > R时,就有: 复分析证明
密克定理是几何学中关于相交圆的定理
密克定理是几何学中关于相交圆的定理。1838年,叙述并证明了数条相关定理。许多有用的定理 可由其推出。 1. 定理陈述 设三个圆C i ,C 2,C 3交于一点0,而M,N,P ,分别是C i 和 C 2, C 2和C 3, C 3和C i 的另一交点。设A 为C i 的点,直线MA 交C 2于B,直线PA 交C 3于C 。那么B,N,C 这三点共线 逆定理:如果△ ABC 是三角形,M,N,P 三点分别在边 AB,BC,CA 上,那么三角形△ APM ^BMN ^CNP 的外接圆交于一点Q 完全四线形定理:如果ABCDE 是,那么三角形△ EAD A EBC,A FAB △ FDC 的外接圆交于一点0,称为密克点。 四圆定理:设C i ,C 2, C 3,C 4为四个圆,A i 和B i 是C i 和C 2的交点,A 2和B 2是C 2和C 3的交点,A 3和 B 3是 C 3,C 4的交点,A 4和B 4是C i 和C 2的交点。那么A i , A 2, A 3, A 4四点共圆当且仅当 B i , B 2, B 3, B 4四点共圆。 五圆定理:设ABCD 为任意,五点,F,G,H,I J 分别是 EA 和BC, AB 和CD, BC 和ED,CD 和EA ,DE 和AB 的交点,那么三角形△ ABF A BCG ^CDH ^DEI. △ EAJ 的外接圆的五个不在五边形上的交点共圆,而且穿过这些交点的圆也穿过五个外接圆的圆心。 逆定理:设C i ,C 2, C3GC 5五个圆的圆心都在圆上C ,相邻的圆交于C 上,那么把它们不在C 上 的交点与比邻同样的点连起来,所成的五条直线相交于这五个圆上。 葛尔刚点:△ ABC 的内切圆分别切边 AB 、BC CA 于F 、D E,贝U AD BE 、CF 三线共点,此 点即为葛尔刚点 三圆定 理:
九年级上学期圆的定义及垂径定理
【圆的认识】第11份 1、弦和直径:连接圆上任意叫做弦,其中经过圆心的弦叫做,是圆中最长的弦。 2、有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧。其中正确的有 3、下列四个命题:①经过任意三点可以作一个圆;②三角形的外心在三角形的内部;③等腰三角形的外心必在底边的中线上;④菱形一定有外接圆,圆心是对角线的交点。其中假命题有 4、若OP的半径为13,圆心P的坐标为(5, 12 ), 则平面直角坐标系的原点O与OP的位置关系是( ) A.在⊙P内B.在⊙P上C.在⊙P外D.无法确定 5、圆上各点到圆心的距离都等于 , 到圆心距离等于半径的点都在 . 6、一个点到定圆上最近点的距离为4,最远点的距离为9,则此圆的半径是__________. 7、如图,AB, CD为⊙O的两条直径,E, F分别为OA, OB的中点,求证:四边形CEDF是平行四边形. 8、⊙0的半径为13cm,圆心O到直线l的距离d=OD=5cm.在直线l上有三点P,Q,R,且PD = 12cm, QD<12cm, RD>12cm,则点P在,点Q在,点R在 . 9、如图,点A,D,G,M在半圆上,四边形ABOC, DEOF,HMNO均为矩形,BC=a,EF=b, NH=C,则a,b,c有什么关系? 10、⊙0的半径为2,点P到圆心的距离OP=m, 且m使关于二的方程2x2-22x+m-1=0有实根,试确定点P 的位置. 11、如图,点P的坐标为(4,0),圆P的半径为5,且圆P与x轴交于点A,B,与y轴交于点 C,D, 试求出点A , B,C,D的坐标.12、下列说法正确的是( ) A.一个点可以确定一条直线 B.两个点可以确定两条直线 C.三个点可以确定一个圆 D.不在同一直线上的三点确定一个圆 13、直角三角形两直角边长分别为3和l,那么它的外接圆的直径是( ) 14、下图是一个圆形轮子的一部分,请你用直尺和圆规把它补完整. 15、_______ 三角形的外心在它的内部,_______三角形的外心在它的外部;直角三角形的外心在 ______________. 16、下列命题正确的个数有( ) ①矩形的四个顶点在同一个圆上;②梯形的四个顶点在同一个圆上; ③菱形的四边中点在同一个圆上;④平行四边形的四边中点在同一个圆上. A. 1个 B. 2个 C. 3个 D. 4个 17、在Rt△ABC中,AB=6 , BC=8,那么这个三角形的外接圆直径是() A. 5 B.10 C.5 或4 D. 10或8 18、已知等腰三角形ABC中,AB=AC,O是ABC ?的外接圆,若O的半径是4,120 BOC ∠=,求AB的长. 19、如图所示,平原上有三个村庄A、B、C,现计划打一口水井p,使水井到三个村庄的距离相等。 (1)在图中画出水井p的位置; (2)若再建一个工厂D,使工厂D到水井的距离等于水井到三个村庄的距离,且工厂D到A、C两个村庄的距离相等,工厂D应建在何处?请画出其位置. .A
专题13相似三角形定理与圆幂定理
专题十三相似三角形定理与圆幂定理 本专题主要复习相似三角形的进一步认识、圆的进一步的认识.通过本专题的复习,了解平行线等分线段定理和平行截割定理;掌握相似三角形的判定定理及性质定理;理解直角三角形射影定理.理解圆周角定理及其推论;掌握圆的切线的判定定理及性质定理;理解弦切角定理及其推论.掌握相交弦定理、割线定理、切割线定理;理解圆内接四边形的性质定理与判定定理.【知识要点】 1.相似三角形概念 相似三角形:对应角相等,对应边成比例的两个三角形是相似三角形. 相似比:相似三角形对应边的比. 2.相似三角形的判定 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似(简叙为:两角对应相等两三角形相似). 如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似(简叙为:两边对应成比例且夹角相等,两个三角形相似). 如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似(简叙为:三边对应成比例,两个三角形相似). 3.直角三角形相似的判定定理 直角三角形被斜边上的高分成两个直角三角形和原三角形相似. 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. 4.相似三角形的性质 相似三角形对应角相等,对应边成比例. 相似三角形对应高的比,对应中线的比和对应角平分线的比都等于相似比.
相似三角形周长的比等于相似比. 相似三角形的面积比等于相似比的平方. 5.相关结论 平行于三角形一边的直线截其他两边,截得的三角形与原三角形的对应边成比例. 三角形的内角平分线分对边成两段的长度比等于夹角两边长度的比. 经过梯形一腰中点而平行于底边的直线平分另一腰. 梯形的中位线平行于两底,并且等于两底和的一半. 若一条直线截三角形的两边(或其延长线)所得对应线段成比例,则此直线与三角形的第三边平行. 6.弦切角定理 弦切角定义:切线与弦所夹的角. 弦切角的度数等于它所夹的弧的圆心角的度数的一半. 7.圆内接四边形的性质 圆的内接四边形的对角互补,并且任意一个外角等于它的内对角. 8.圆幂定理 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等. 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项. 割线定理:从圆外一点P引两条割线与圆分别交于A、B、C、D则有PA·PB=PC·PD.【复习要求】 1.了解平行线等分线段定理和平行截割定理;掌握相似三角形的判定定理及性质定理;理解直角三角形射影定理. 2.理解圆周角定理及其推论;掌握圆的切线的判定定理及性质定理;理解弦切角定理及其推
圆幂定理(垂直弦定理)偏难
【例题求解】 【例1】 如图,PT 切⊙O 于点T ,PA 交⊙O 于A 、B 两点,且与直径CT 交于点D ,CD=2,AD=3,BD=6,则PB= . (市中考题) 思路点拨 综合运用圆幂定理、勾股定理求PB 长. 注:比例线段是几之中一个重要问题,比例线段的学习是一个由一般到特殊、不断深化的过程,大致经历了四个阶段: (1)平行线分线段对应成比例; (2)相似三角形对应边成比例; (3)直角三角形中的比例线段可以用积的形式简捷地表示出来; (4)圆中的比例线段通过圆幂定理明快地反映出来. 【例2】 如图,在平行四边形ABCD 中,过A 、B 、C 三点的圆交AD 于点E ,且与CD 相切,若AB=4,BE=5,则DE 的长为( ) A .3 B .4 C . 415 D .5 16 (全国初中数学联赛题) 思路点拨 连AC ,CE ,由条件可得多等线段,为切割线定理的运用创设条件.
注:圆中线段的算,常常需要综合相似三角形、直角三角形、圆幂定理等知识,通过代数化获解,加强对图形的分解,注重信息的重组与整合是解圆中线段计算问题的关键. 【例3】如图,△ABC接于⊙O,AB是∠O的直径,PA是过A点的直线,∠PAC=∠B. (1)求证:PA是⊙O的切线; (2)如果弦CD交AB于E,CD的延长线交PA于F,AC=8,CE:ED=6:5,,AE:BE=2:3,求AB的长和∠ECB的正切值. (北京市海淀区中考题) 思路点拨直径、切线对应着与圆相关的丰富知识.(1)问的证明为切割线定理的运用创造了条件;引入参数x、k处理(2)问中的比例式,把相应线段用是的代数式表示,并寻找x与k的关系,建立x或k的程. 【例4】如图,P是平行四边形AB的边AB的延长线上一点,DP与AC、BC分别交于点E、E,EG是过B、F、P三点圆的切线,G为切点,求证:EG=DE (省竞赛题) 思路点拨由切割线定理得EG2=EF·EP,要证明EG=D E,只需证明DE2=EF·EP,这样通过圆幂定理把线段相等问题的证明转化为线段等积式的证明. 注:圆中的多问题,若图形中有适用圆幂定理的条件,则能化解问题的难度,而圆中线段等积式是转化问题的桥梁. 需要注意的是,圆幂定理的运用不仅局限于计算及比例线段的证明,可拓展到平面几各种类型的问题
