2016_2017学年高中数学第1章三角函数1.2.1任意角的三角函数学案

1.2.1 任意角的三角函数

1．理解三角函数的定义，会使用定义求三角函数值．(重点、易错点) 2．会判断给定角的三角函数值的符号．(重点)

3．会利用三角函数线比较两个同名三角函数值的大小及表示角的范围．(难点)

[基础2初探]

教材整理1 任意角三角函数的定义

阅读教材P 11～P 12第一自然段的有关内容，完成下列问题．

在平面直角坐标系中，设α的终边上任意一点P 的坐标是(x ，y )，它与原点的距离是

r (r ＝x 2＋y 2>0)，那么

sin α

若角α的终边经过点P ?

????2

2

，－22，则

sin α＝________；cos α＝________；tan α＝________. 【解析】 由题意可知 |OP |＝

? ????22－02＋? ?

?

??－22－02＝1，

∴sin α＝－221＝－2

2；

cos α＝221＝2

2；

tan α＝－22

22＝－1.

【答案】 －

22 22

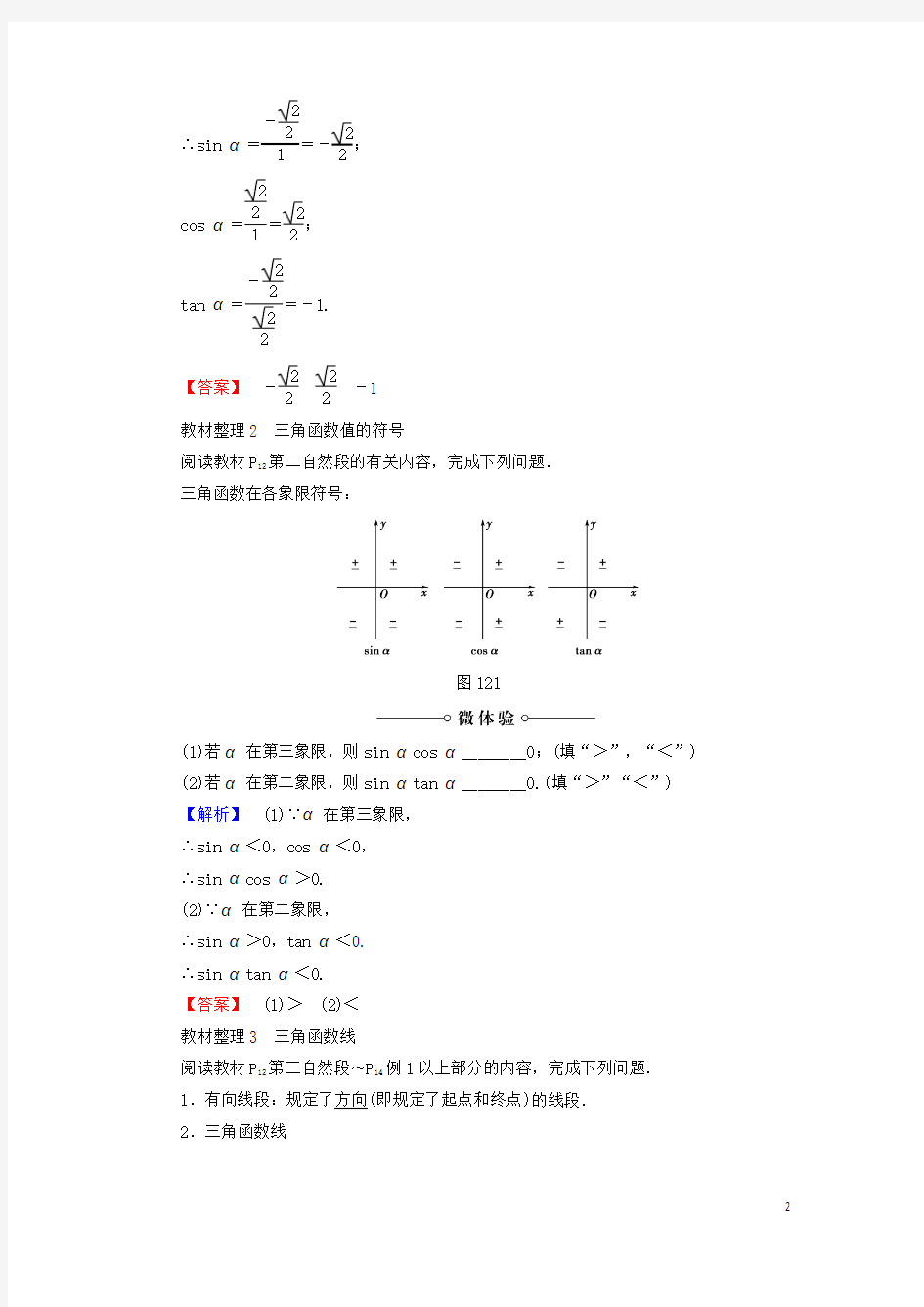
－1 教材整理2 三角函数值的符号

阅读教材P 12第二自然段的有关内容，完成下列问题． 三角函数在各象限符号：

图1-2-1

(1)若α在第三象限，则sin αcos α________0；(填“＞”，“＜”) (2)若α在第二象限，则sin αtan α________0.(填“＞”“＜”) 【解析】 (1)∵α在第三象限， ∴sin α＜0，cos α＜0， ∴sin αcos α＞0. (2)∵α在第二象限， ∴sin α＞0，tan α＜0. ∴sin αtan α＜0. 【答案】 (1)＞ (2)＜ 教材整理3 三角函数线

阅读教材P 12第三自然段～P 14例1以上部分的内容，完成下列问题． 1．有向线段：规定了方向(即规定了起点和终点)的线段． 2．三角函数线

判断(正确的打“√”，错误的打“3”)

(1)α一定时，单位圆的正弦线一定．( )

(2)在单位圆中，有相同正弦线的角必相等．( )

(3)α与α＋π有相同的正切线．( )

【解析】结合三角函数线可知(1)(3)正确，(2)错误．

【答案】(1)√(2)3(3)√

[质疑2手记]

预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：

疑问1：

解惑：

疑问2：

解惑：

疑问3：

解惑：

[小组合作型]

α，cos α，tan α的值．

【精彩点拨】以α的终边分别在第二、四象限为依据，分别取特殊点求sin α，cos α，tan α的值．

【自主解答】当α的终边在第二象限时，在α终边上取一点P(－1,2)，则r＝ －1 2＋22＝5，

所以sin α＝

2

5＝255，cos α＝－15

＝－55，tan α＝2－1＝－2.

当α的终边在第四象限时， 在α终边上取一点P ′(1，－2)， 则r ＝12

＋ －2 2

＝5，

所以sin α＝－25＝－255，cos α＝15＝55

，tan α＝－2

1＝－2.

1．已知角α的终边在直线上的问题，常分两类情况分别计算sin α，cos α，tan α的值．

2．当角α的终边上点的坐标以参数形式给出时，要根据问题的实际情况对参数进行分类讨论．

[再练一题]

1．已知角α的终边上有一点P (－3a,4a )(a ≠0)，求2sin α＋cos α的值.

【导学号：06460006】

【解】 ∵x ＝－3a ，y ＝4a ， ∴r ＝ －3a 2

＋ 4a 2

＝5|a |. 当a ＞0时，r ＝5a ，角α为第二象限角，

∴sin α＝y r ＝4a 5a ＝4

5

，

cos α＝x r ＝

－3a 5a ＝－3

5

，

∴2sin α＋cos α＝2345－3

5

＝1.

当a ＜0时，r ＝－5a ，角α为第四象限角， ∴sin α＝y r ＝4a －5a ＝－4

5

，

cos α＝x r ＝

－3a －5a ＝3

5

，

∴2sin α＋cos α＝23? ????－45＋3

5

＝－1.

判断下列各式的符号：

(1)α是第四象限角，sin α2tan α；

(2)sin 32cos 42tan ? ??

??－

23π4.

【精彩点拨】 先确定各角所在象限，再判定各个三角函数值符号，然后判定三角函数式的符号．

【自主解答】 (1)∵α是第四象限角， ∴sin α<0，tan α<0， ∴sin α2tan α>0. (2) ∵π2<3<π，π<4<3π

2，

∴sin 3>0，cos 4<0. 又∵－23π4＝－6π＋π

4

，

∴tan ?

????－23π4>0，

∴sin 32cos 42tan ? ??

??－

23π4

<0.

对于已知角α，判断α的相应三角函数值的符号问题，常依据三角函数的定义，或利用口诀“一全正、二正弦、三正切、四余弦”来处理

.

[再练一题]

2．确定下列式子的符号：

(1)tan 108°2cos 305°；(2)cos 5π62tan

11π

6

sin

2π3；

(3)tan 120°2sin 269°.

【解】 (1)∵108°是第二象限角，∴tan 108°＜0. ∵305°是第四象限角，∴cos 305°＞0. 从而tan 108°2cos 305°＜0.

(2)∵5π6是第二象限角，11π6是第四象限角，2π3

是第二象限角，

∴cos 5π6＜0，tan 11π6＜0，sin 2π3＞0.

从而cos 5π62tan

11π6

sin

2π3

＞0.

(3)∵120°是第二象限角，∴tan 120°＜0， ∵269°是第三象限角，∴sin 269°＜0. 从而tan 120°sin 269°＞0.

[探究共研型]

探究1 在单位圆中，满足sin α＝2

的正弦线有几条？试在图中明确．

图1-2-2

【提示】 两条，如图所示，MP 1与NP 2都等于1

2

.

探究2 满足sin α≥1

2的角的范围是多少？试在上述单位圆中给予明确．

【提示】 如图中阴影部分所示，所求角α的取值范围为α???

2k

π＋

π6≤α≤2k π

＋5π

6

，k ∈Z .

求函数f (x )＝1－2cos x ＋ln ? ??

??

sin x －22的定义域． 【精彩点拨】 借助单位圆解不等式组

?

????

1－2cos x ≥0sin x －22＞0便可．

【自主解答】 由题意，自变量x 应满足不等式组

?

????

1－2cos x ≥0，

sin x －22＞0，即???

??

cos x ≤1

2，sin x ＞2

2

.

则不等式组的解的集合如图(阴影部分)所示，

∴??????

???

?x ?

??

2k π＋π3≤x ＜2k π＋3

4π，k ∈Z

.

求三角函数定义域时，一般应转化为求不等式 组 的解的问题.利用数轴或三角函数线是解三角不等式常用的方法.解多个三角不等式时，先在单位圆中作出使每个不等式成立的角的范围，再取公共部分.

[再练一题]

3．在单位圆中画出适合下列条件的角α的终边的范围，并由此写出角α的集合： (1)sin α≥

32；(2)cos α≤－12

. 【解】 (1)作直线y ＝

3

2

交单位圆于A ，B 两点，连接OA ，OB ，则OA 与OB 围成的区域(图①阴影部分)即为角α

的终边的范围，故满足条件的角α

的集合为

?

?????

???

?α?

??

2k π＋π3π≤α≤2k π＋2π3π，k ∈Z .

(2)作直线x ＝－1

2交单位圆于C 、D 两点，连接OC 、OD ，则OC 与OD 围成的区域(图②阴

影部分)即为角α

终边的范围，故满足条件的角α

的集合为

?

?????

???

?α?

??

2k π＋23π≤α≤2k π＋43π，k ∈Z . [构建2体系]

1．若角α的终边经过点P (－2,2)，则sin θ＝________. 【解析】 由题意可知，OP ＝ －2 2

＋22

＝8， ∴sin θ＝

28＝2

2

. 【答案】

22

2．若sin α＜0，tan α＞0，则α为第________象限角．

【解析】 由sin α＜0可知α的终边落在第三、四象限及y 轴的负半轴上． 由tan α＞0可知α的终边落在第一、三象限内． 故同时满足sin α＜0，tan α＞0的角α为第三象限角． 【答案】 三

3．角α的终边经过点P (－b,4)且cos α＝－3

5

，则b 的值为________.

【导学号：06460007】

【解析】 由三角函数的定义可知 －b

b 2＋16＝－35，

∴?????

b ＞0，b 2

b 2

＋16＝9

25

，解得b ＝3.

【答案】 3

4．利用三角函数线比较下列各组数的大小(用“＞”或“＜”连接)： (1)sin 2π3________sin 4π5；

(2)cos 2π3________cos 4π

5

；

(3)tan 2π3________tan 4π

5

.

【解析】 借助单位圆中的三角函数线易得sin 2π3＞sin 4π5；cos 2π3＞cos 4π

5；

tan 2π3＜tan 4π

5

.

【答案】 (1)＞ (2)＞ (3)＜

5．已知角α的终边在直线3x ＋4y ＝0上，求sin α，cos α，tan α的值． 【解】 ∵角α的终边在直线3x ＋4y ＝0上，∴在角α的终边上任取一点P (4t ，－

3t )(t ≠0)，则x ＝4t ，y ＝－3t ，r ＝x 2＋y 2＝ 4t 2＋ －3t 2

＝5|t |，

当t ＞0时，r ＝5t ，sin α＝y r ＝－3t 5t ＝－35，cos α＝x r ＝4t 5t ＝45，tan α＝y x ＝－3t

4t

＝

－34

. 当t ＜0时，r ＝－5t ，sin α＝y r ＝－3t －5t ＝35，cos α＝x r ＝4t －5t ＝－45，tan α＝y x ＝

－3t

4t

＝－34

.

综上可知，sin α＝－35，cos α＝45，tan α＝－3

4

；

或sin α＝35，cos α＝－45，tan α＝－3

4

.

我还有这些不足：

(1) (2)

我的课下提升方案： (1) (2)

学业分层测评(三) 任意角的三角函数

(建议用时：45分钟)

[学业达标]

一、填空题

1．已知sin α＝35，cos α＝－4

5

，则角α终边在第________象限．

【解析】 由sin α＝35＞0得，角α的终边在第一或第二象限；由cos α＝－4

5＜0

得，角α的终边在第二或第三象限，故角α的终边在第二象限．

【答案】 二

2．若角α的终边落在y ＝－x 上，则tan α的值为________． 【解析】 设P (a ，－a )是角α上任意一点， 若a >0，P 点在第四象限，tan α＝－a

a ＝－1，

若a <0，P 点在第二象限，tan α＝－a

a

＝－1. 【答案】 －1

3．有三个结论：①π6与5π6的正弦线相等；②π3与4π3的正切线相等；③π4与5π

4的余弦

线相等．其中正确的是________．

【解析】 在单位圆中画出相应角的正弦线、正切线，余弦线，分析可知①正确，②正确，③错误．

【答案】 ①②

4．在△ABC 中，若sin A 2cos B 2tan C ＜0，则△ABC 是________三角形． 【解析】 ∵A ，B ，C 是△ABC 的内角，∴sin A ＞0. ∵sin A 2cos B 2tan C ＜0，∴cos B 2tan C ＜0， ∴cos B 和tan C 中必有一个小于0，

即B ，C 中必有一个钝角，故△ABC 是钝角三角形． 【答案】 钝角

5．(20162扬州高一检测)如果α的终边过点P (2sin 30°，－2cos 30°)，则sin α的值等于________．

【解析】 ∵P (1，－3)，∴r ＝12

＋ －3 2

＝2， ∴sin α＝－32. 【答案】 －

32

6．(20162南通高一检测)在(0,2π)内，使sin α＞cos α成立的α的取值范围是________．

【解析】 如图所示，当α∈? ????π4，5π4时，恒有MP ＞OM ，而当

α∈? ????0，π4∪? ??

??5π4，2π时，则是MP ＜OM .

【答案】 ?

????π4

，5π4

7．若α为第二象限角，则

|sin α|sin α－cos α

|cos α|

＝________.

【解析】 由已知sin α>0，cos α<0， ∴

|sin α|sin α－cos α|cos α|＝sin αsin α－cos α

－cos α

＝1＋1＝2.

【答案】 2

8．(20162无锡高一检测)已知角α的终边经过点(3a －9，a ＋2)，且sin α＞0，cos α≤0，则α的取值范围是________．

【解析】 因为cos α≤0，sin α＞0，所以角α的终边在第二象限或y 轴非负半轴上．

因为α的终边过点(3a －9，a ＋2)，

所以{ 3a －9≤0， a ＋2＞0，所以－2＜a ≤3. 【答案】 (－2,3] 二、解答题

9．判断下列各式的符号： (1)sin 340°cos 265°；

(2)sin cos θ cos sin θ (θ为第二象限角). 【导学号：06460008】 【解】 (1)∵340°是第四象限角，265°是第三象限角， ∴sin 340°＜0，cos 265°＜0， ∴sin 340°cos 265°＞0. (2)∵θ为第二象限角，

∴0＜sin θ＜1＜π2，－π

2＜－1＜cos θ＜0，

∴sin(cos θ)＜0，cos(sin θ)＞0， ∴

sin cos θ

cos sin θ

＜0.

10．已知1|sin α|＝－1

sin α，且lg cos α有意义．

(1)试判断角α所在的象限；

(2)若角α的终边上一点M ? ??

??35，m ，且|OM |＝1(O 为坐标原点)，求m 的值及sin α的值．

【解】 (1)由1|sin α|＝－1

sin α可知sin α＜0，

∴α是第三或第四象限角或终边在y 轴的负半轴上的角． 由lg cos α有意义可知cos α＞0，

∴α是第一或第四象限角或终边在x 轴的正半轴上的角． 综上可知角α是第四象限的角．

(2)∵|OM |＝1，∴? ??

??352＋m 2

＝1，

解得m ＝±4

5

.

又α是第四象限角，故m ＜0，从而m ＝－4

5.

由正弦函数的定义可知 sin α＝y r ＝m |OM |＝－451＝－4

5

.

[能力提升]

1．(20162南京高一检测)若α为第四象限角，则下列函数值一定是负值的是

________．(填序号)

①sin α2；②cos α2；③tan α

2

；④cos 2α.

【解析】 由α为第四象限角，得2k π＋3π2＜α＜2k π＋2π(k ∈Z )，故k π＋3π

4＜

α

2

＜k π＋π(k ∈Z )． 当k ＝2n (n ∈Z )时，α2∈? ????2n π＋3π4，2n π＋π， 此时，α

2

是第二象限角；

当k ＝2n ＋1(n ∈Z )时，α2∈? ????2n π＋7π4，2n π＋2π，此时，α2是第四象限角． 故无论α2落在第二还是第四象限，tan α

2＜0恒成立．

又4k π＋3π＜2α＜4k π＋4π，(k ∈Z )． 故cos 2α有可能为正也有可能为负．

【答案】 ③

2．若角α的终边与直线y ＝3x 重合，且sin α<0，又P (m ，n )是角α终边上一点，且|OP |＝10，则m －n 等于________．

【解析】 由题意得{ n ＝3m ＜0， m 2

＋n 2

＝10，

∴?

??

??

m ＝－1，n ＝－3，∴m －n ＝2.

【答案】 2

3．点P 从(1,0)出发，沿单位圆x 2＋y 2

＝1逆时针方向运动23π弧长到达点Q ，则点Q

的坐标为________．

【解析】 设Q (cos α，sin α)，由2π3＝α21可知α＝2π

3，

所以Q ? ????cos 2π3，sin 2π3，即Q ? ????－12，32.

【答案】 ? ??

??－1

2，32

4．已知：cos α＜0，tan α＜0. (1)求角α的集合；

(2)试判断角α

2

是第几象限角；

(3)试判断sin α2，cos α2，tan α

2

的符号．

【解】 (1)因为cos α＜0，所以角α的终边位于第二或第三象限或x 轴负半轴上．因为tan α＜0，所以角α的终边位于第二或第四象限，所以角α的终边只能位于第二象限．故角α的集合为

?

???

??

????α?

??

π2＋2k π＜α＜π＋2k π，k ∈Z . (2)因为π

2＋2k π＜α＜π＋2k π(k ∈Z )，

所以π4＋k π＜α2＜π

2＋k π(k ∈Z )．

当k ＝2n (n ∈Z )时，

π4＋2n π＜α2＜π

2＋2n π(n ∈Z )． 所以α

2

是第一象限角；

当k ＝2n ＋1(n ∈Z )，

5π4＋2n π＜α2＜3π

2＋2n π(n ∈Z )， 所以α

2是第三象限角．

(3)当α

2

为第一象限角时，

sin α2＞0，cos α2＞0，tan α

2＞0.

当α

2

为第三象限角时， sin α2＜0，cos α2＜0，tan α

2＞0.