拉普拉斯变换及其逆变换表

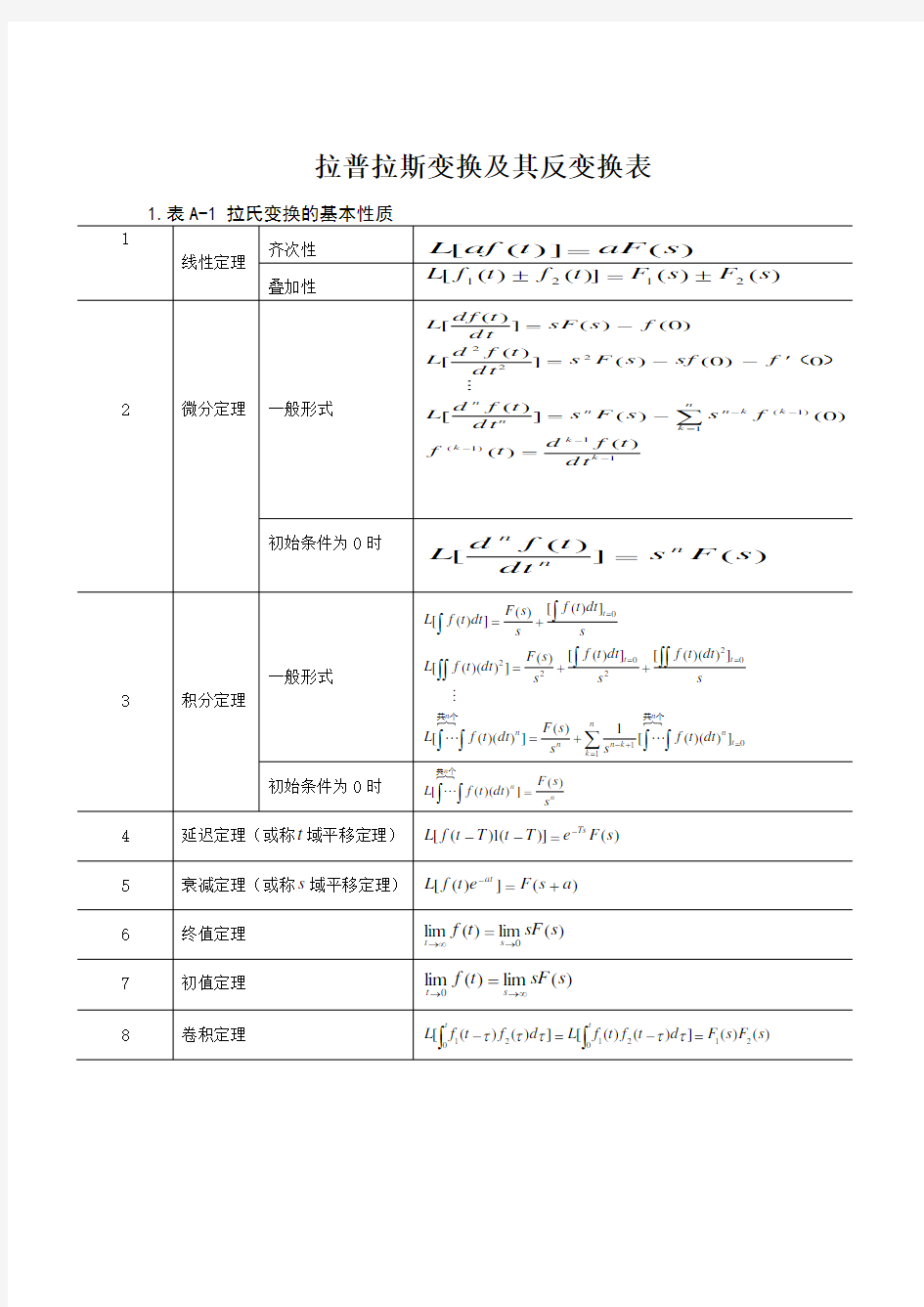
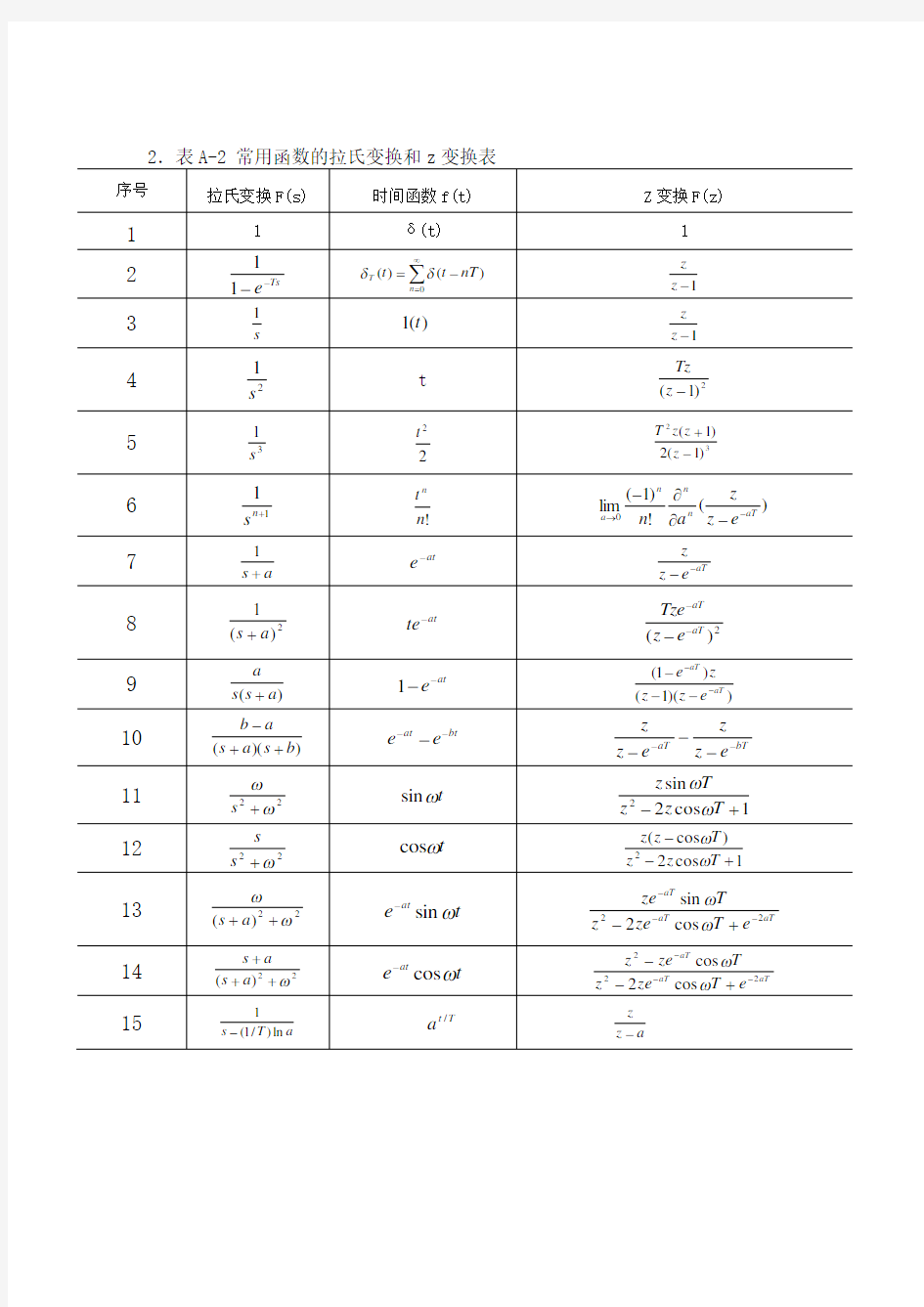
拉普拉斯变换及其反变换表

3． 用查表法进行拉氏反变换

用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。设)(s F 是s 的有理真分式

1

1

n 1

n n

n

1

1

m 1

m m

m

a

s a s a s a b s b s b s b )s (A )s (B )s (F ++++++++=

=---- （m n >）

式中系数n

1

n 1

a ,a ,...,a ,a

-，m

1

m 1

b ,b ,b ,b - 都是实常数；n m ,是正整数。按

代数定理可将)(s F 展开为部分分式。分以下两种情况讨论。 ① 0)(=s A 无重根

这时，F(s)可展开为n 个简单的部分分式之和的形式。

∑

=-=-++-++-+-=n

1

i i

i

n

n

i

i

2

2

1

1

s

s c

s s c s s c s s c s s c )s (F 式中，Sn 2S 1S ，，， 是特征方程A(s)＝0的根。i c 为待定常数，称为F(s)在i s 处的留数，可按下式计算： )s (F )s s (lim c i

s s i

i

-=→

或

i

s s i

)

s (A )

s (B c

='=

式中，)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质，从式（F-1）可求得原函数

[]t s n 1i i n 1

i i i

11i e c s s c L )s (F L )t (f -==--∑∑=??????-==

② 0)(=s A 有重根

设0)(=s A 有r 重根1s ，F(s)可写为

())

s s ()s s ()s s ()

s (B s F n

1

r r 1

---=

+

=

n

n

i

i

1

r 1

r 1

1

1

r 1

1

r r 1

r

s

s c

s s c s s c )s s (c )s s (c )s s (c -+

+-++-+-++-+-++-- 式中，1s 为F(s)的r 重根，1+r s ，…, n s 为F(s)的n-r 个单根；

其中，1+r c ，…, n c 仍按式(F-2)或(F-3)计算，r c ，1-r c ，…, 1c 则按下式计算：

)s (F )s s (lim c r

1

s s r

1

-=→

)]s (F )s s ([ds

d

lim c r

1

s s 1

r 1

-=→-

)s (F )s s (ds

d lim !j 1c r

1

)

j ()

j (s s j

r 1

-=→-

)s (F )s s (ds

d

lim )!1r (1c r

1

)

1r ()

1r (s s 1

1

--=--→

原函数)(t f 为 [])()(1s F L t f -=

??

?

???-+

+-++-+-++-+-=++---n

n

i

i

1

r 1

r 1

1

1

r 1

1

r r

1

r

1

s s c

s s c s s c )s s (c )

s s (c )s s (c L t

s n

1

r i i

t

s 1

2

2

r 1

r 1

r r

1e c e c t c t )!2r (c t )!1r (c ∑+=---+??

????+++-+-= （F-6）