习题答案PLC编程及应用(第4版)课件

3章习题答案
1.填空
1)输出指令(对应于梯形图中的线圈)不能用于过程映像输入寄存器。
2)SM 0.1 在首次扫描时为ON,SM0.0一直为ON 。
3)每一位BCD码用_4_位二进制数来表示,其取值范围为二进制数2#0000_~2#_1001_。
4)二进制数2#0100 0001 1000 0101对应的十六进制数是_16#4185_,对应的十进制数是_16773_,绝对值与它相同的负数的补码是2#_1011 1110 0111 1011_。
5)BCD码2#0100 0001 1000 0101对应的十进制数是_4185_。
6)接通延时定时器TON的使能(IN)输入电路接通时开始定时,当前值大于等于预设值时其定时器位变为ON ,梯形图中其常开触点接通,常闭触点断开。
7)接通延时定时器TON的使能输入电路断开时被复位,复位后梯形图中其常开触点断开,常闭触点接通,当前值等于0 。
8)有记忆接通延时定时器TONR的使能输入电路接通时开始定时,使能输入电路断开时,当前值保持不变。使能输入电路再次接通时继续定时。必须用复位指令来复位TONR。
9)断开延时定时器TOF的使能输入电路接通时,定时器位立即变为ON ,当前值被清零。使能输入电路断开时,当前值从0开始增大。当前值等于预设值时,输出位变为OFF ,梯形图中其常开触点断开,常闭触点接通,当前值保持不变。
10)若加计数器的计数输入电路CU 由断开变为接通、复位输入电路R 断开,计数器的当前值加1。当前值大于等于预设值PV时,梯形图中其常开触点接通,常闭触点断开。复位输入电路接通时,计数器被复位,复位后其常开触点断开,常闭触点接通,当前值为0 。
3.-91
4.16#
5.无符号数。
6.VB20和VB21,VB20
7.VW20和VW22,VB20~VB23,VW22,VB20
8.十进制小数
9.字符的个数
10.32
12.4个,8、16、32位
13.程序组织单元,主程序、子程序、中断程序
14.AIW2
15.VB100的地址,地址指针VD120所指的存储单元中的数
16.在程序中修改操作数的地址,用于间接寻址。
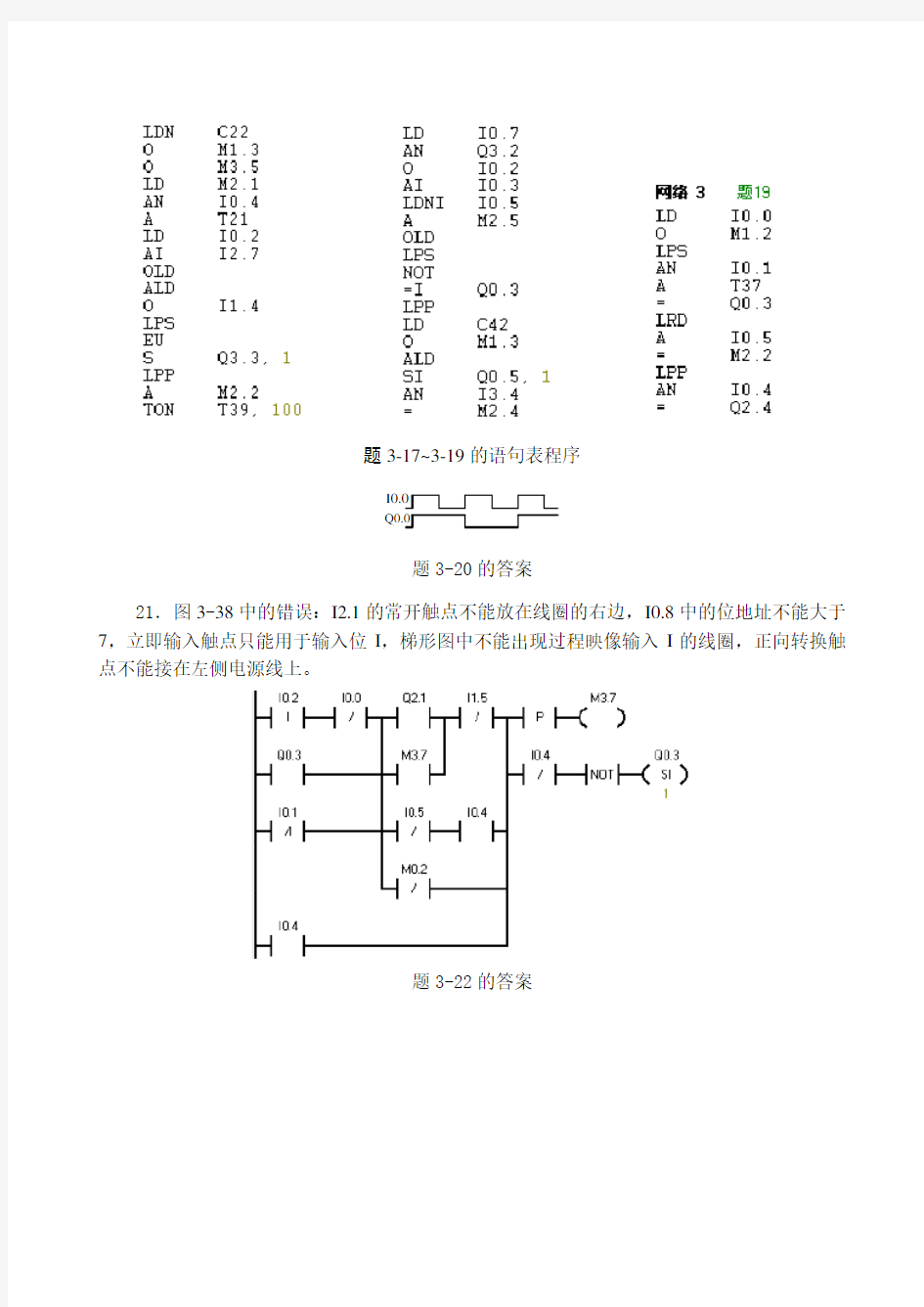
题3-17~3-19的语句表程序
I0.0
Q0.0
题3-20的答案
21.图3-38中的错误:I2.1的常开触点不能放在线圈的右边,I0.8中的位地址不能大于7,立即输入触点只能用于输入位I,梯形图中不能出现过程映像输入I的线圈,正向转换触点不能接在左侧电源线上。
题3-22的答案
题3-23的答案
题3-24的答案
题3-25的答案
题3-27的答案
4章习题答案
1.填空
1)如果方框指令的EN输入端有能流且执行时无错误,则ENO输出端有能流输出。2)字符串比较指令的比较条件只有== 和<> 。
3)主程序调用的子程序最多嵌套_8_层,中断程序调用的子程序_不能_嵌套。
4)VB0的值为2#1011 0110,循环右移2位然后左移4位为2# 1101 0000 。
5)读取实时时钟指令TODR读取的日期和时间的数制为BCD码。
6)执行“JMP 2”指令的条件满足时,将不执行该指令和LBL 2 指令之间的指令。7)主程序和中断程序的变量表中只有临时变量。
8)S7-200 SMART有6个高速计数器,可以设置13种不同的工作模式。
9)HSC0的模式3的时钟脉冲为I0.0,用I0.1控制方向。
2.在MW4小于等于1247时,令M0.1为ON并保持,反之将M0.1复位为OFF。LDW<= MW4, 1247
S M0.1, 1
LDW> MW4, 1247
R M0.1, 1
3.编写程序,在I0.0的上升沿将VW10~VW58清零。
LD I0.0
EU
FILL 0, VW10, 25
5.编写程序,将VW0中以0.01Hz为单位的0~99.99Hz的整数格式的频率值,转换为4位BCD码,送给QW0,通过4片译码芯片和七段显示器显示频率值(见图3-6)。
LD SM0.0
MOVW VW0, QW0
IBCD QW0
6.用I0.0控制接在QB0上的8个彩灯是否移位,每1s移1位。用I0.1控制左移或右移,首次扫描时将彩灯的初始值设置为十六进制数16#0E(仅Q0.1~Q0.3为ON),设计出梯形图程序。
7.用I1.0控制接在QB0上的8个彩灯是否移位,每1s移1位。用IB0设置彩灯的初始值,在I1.1的上升沿将IB0的值传送到QB0,设计出梯形图程序。
8.用实时时钟指令设计控制路灯的程序,20:00时开灯,06:00时关灯。
LD SM0.0
TODR VB0 // 读实时钟,小时值在VB3
LDB>= VB3, 16#20 // 20点~0点(日期、时间值用BCD码表示)
OB< VB3, 16#06 // 0点~6点
= Q0.0 // 点亮路灯
9.用实时时钟指令设计控制路灯的程序,在5月1日~10月31日的20:00开灯,06:00关灯;在11月1日~下一年4月30号的19:00开灯,7:00关灯。
LD SM0.0
TODR VB0 // 读实时钟,小时值在VB3,月日在VW1
LDW>= VW1, 16#1031
OW< VW1, 16#0501
= M0.0 //冬季ON
LDB>= VB3, 16#20 // 20点~6点开灯
OB< VB3, 16#06
AN M0.0 //夏季
LDB>= VB3, 16#19 // 19点~7点开灯
OB< VB3, 16#07
A M0.0 //冬季
OLD
= Q0.1
10.半径(<10000的整数)在VW10中,取圆周率为3.1416。编写程序,用浮点数运算指令计算圆周长,运算结果四舍五入转换为整数后,存放在VW20中。
LD SM0.0
ITD VW10, AC1 // 整数转换为双整数
DTR AC1, AC1 // 双整数转换为实数
*R 3.1416, AC1 // 乘以3.1416
ROUND AC1, AC1 // 乘积四舍五入转换为双整数
MOVW AC1, VW20 // 低16位送VW20
第11题编写语句表程序,实现运算VW2–VW4 = VW6。
LD I0.2
MOVW VW2, VW6
-I VW4, VW6
12.AIW2中A/D转换得到的数值0~32000正比于温度值0~1200 C。在I0.0的上升沿,将AIW2的值转换为对应的温度值存放在VW10中,设计出梯形图程序。
公式: T = 1200*N/32000
LD I0.3
MOVW AIW2, AC0
AENO
MUL 1200, AC0
AENO
/D 27648, AC0
AENO
MOVW AC0, VW10
13.以0.1度为单位的整数格式的角度值在VW0中,在I0.0的上升沿,求出该角度的正弦值,运算结果转换为以6
10 为单位的双整数,存放在VD2中,设计出程序。
LD I0.0
EU
LPS
ITD VW0, AC0
AENO
DTR AC0, AC0
AENO
/R 10.0, AC0
LRD
*R 0.01745329, AC0
AENO
SIN AC0, AC0
LPP
*R 1000000.0, AC0
AENO
ROUND AC0, VD2
16.编写程序,用字节逻辑运算指令,将VB0的高4位置为2#1001,低4位不变。
LD V0.4
MOVB VB0, LB0
AENO
ANDB 16#0F, LB0
AENO
MOVB LB0, VB0
ORB 16#90, VB0
17.编写程序,前后两个扫描周期VW4的值不变将M0.2复位,反之将M0.2置位。
LD I0.4
MOVW VW4, AC0
AENO
XORW VW6, AC0
AENO
LPS
AW= AC0, 0
R M0.2, 1
LRD
AW<> AC0, 0
S M0.2, 1
LPP
MOVW VW4, VW6
18.设计循环程序,求VD20开始连续存放的5个浮点数的平均值。
19.在I0.0的上升沿,用循环程序求VW100~VW108的累加和。为了防止溢出,将被累加的整数转换为双整数后再累加。用VD10保存累加和。
20.编写程序,求出VW10~VW28中最大的数,存放在VW30中。
21.用子程序调用编写图5-3中两条运输带的控制程序,分别设置自动程序和手动程序,用I0.4作自动/手动切换开关。手动时用I0.0和I0.1对应的按钮分别点动控制两条运输带。
主程序自动程序手动程序22.设计程序,用子程序求圆的面积,输入参数为直径(小于32767的整数),输出量为圆的面积(双整数)。在I0.0的上升沿调用该子程序,直径为10000mm,运算结果存放在VD10
中。
主程序子程序
23.用定时中断,每1s将VW8的值加1,在I0.0的上升沿禁止该定时中断,在I0.2的
上升沿重新启用该定时中断。设计出主程序和中断子程序。
主程序
定时中断程序
24.第一次扫描时将VB0清零,用定时中断0,每100ms 将VB0加1,VB0等于100时关闭定时中断,并将Q0.0立即置1。设计出主程序和中断子程序。
主程序
定时中断程序
5章习题答案
40T37Q 0.0Q 0.0T37
I0.0Q 0.1
Q 0.1
I0.1T37I0.1Q 0.1T37
Q 0.1
70
T37
Q 0.0Q 0.0
T37
I0.0
IN PT TO N 100ms
IN PT TO N 100ms
题3的答案 题4的答案 题5的答案
夹紧松开
快进快退
题6的答案题7的答案题9的答案题8的答案:初始步应为双线框;最上面的转换旁边没有转换条件;步M0.2和M0.0之间无转换;转换I0.0与最上面的转换之间没有步,最上面的水平有向连线应放在最上面的转换之下。输入I0.5不能作为动作;一般用输入、定时器和计数器的触点和它们的逻辑组合作转换条件,不用输出位(Q)作转换条件;步M0.3的后面没有转换和步,系统运行到步M0.3时会“死机”。
5s
题10的答案题11的答案
题12的答案
林初中2017届中考数学压轴题专项汇编:专题20简单的四点共圆(附答案)
专题20 简单的四点共圆 破解策略 如果同一平面内的四个点在同一个圆上,则称之为四个点共圆·一般简称为”四点共圆”.四点共圆常用的判定方法有: 1.若四个点到一个定点的距离相等,则这四个点共圆. 如图,若OA=OB=OC=OD,则A,B,C,D四点在以点O为圆心、OA为半径的 圆上. D 【答案】(1)略;(2)AB,CD相交成90°时,MN取最大值,最大值是2. 【提示】(1)如图,连结OP,取其中点O',显然点M,N在以OP为直径的⊙O'上,连结NO'并延长,交⊙O'于点Q,连结QM,则∠QMN=90°,QN=OP=2,而∠MQN=180°-∠BOC=60°,所以可求得MN的长为定值. (2)由(1)知,四边形PMON内接于⊙O',且直径OP=2,而MN为⊙O'的一条弦,故MN为⊙O'的直径时,其长取最大值,最大值为2,此时∠MON=90°. 2.若一个四边形的一组对角互补,则这个四边形的四个顶点共圆. 如图,在四边形ABCD中,若∠A+∠C=180°(或∠B+∠D=180°)则A,B,C,D四点在同一个圆上.
D 【答案】(1)略;(2)AD ;(3)AD=DE·tanα. 【提示】(1)证A,D,B,E四点共圆,从而∠AED=∠ABD=45°,所以AD=DE. (2)同(1),可得A,D,B,E四点共圆,∠AED=∠ABD=30°,所以AD DE =tan30°, 即AD= 3 DE. 3.若一个四边形的外角等于它的内对角,则这个四边形的四个顶点共圆. 如图,在四边形ABCD中,∠CDE为外角,若∠B=∠CDE,则A,B,C,D四点在同一个圆上. 【答案】略 4.若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线段的两个端点共圆. 如图,点A,D在线段BC的同侧,若∠A=∠D,则A,B,C,D四点在同一个圆上.
九年级数学四点共圆例题讲解
九年级数学四点共圆例题讲解 知识点、重点、难点 四点共圆就是圆得基本内容,它广泛应用于解与圆有关得问题.与圆有关得问题变化多,解法灵活,综合性强,题型广泛,因而历来就是数学竞赛得热点内容。 在解题中,如果图形中蕴含着某四点在同一个圆上,或根据需要作出辅助圆使四点共圆,利用圆得有关性质定理,则会使复杂问题变得简单,从而使问题得到解决。因此,掌握四点共圆得方法很重要。 判定四点共圆最基本得方法就是圆得定义:如果A、B、C、D四个点到定点O得距离相等,即OA=OB=OC =OD,那么A、B、C、D四点共圆. 由此,我们立即可以得出 1、如果两个直角三角形具有公共斜边,那么这两个直角三角形得四个顶点共圆。 将上述判定推广到一般情况,得: 2、如果四边形得对角互补,那么这个四边形得四个顶点共圆。 3、如果四边形得外角等于它得内对角,那么这个四边形得四个顶点共圆。 4、如果两个三角形有公共底边,且在公共底边同侧又有相等得顶角,那么这两个三角形得四个顶点共圆。 运用这些判定四点共圆得方法,立即可以推出: 正方形、矩形、等腰梯形得四个顶点共圆。 其实,在与圆有关得定理中,一些定理得逆定理也就是成立得,它们为我们提供了另一些证明四点共圆得方法.这就就是: 1、相交弦定理得逆定理:若两线段AB与CD相交于E,且AE·EB=CE·ED,则A、B、C、D四点共圆。 2.割线定理得逆定理:若相交于点P得两线段PB、PD上各有一点A、C,且PA·PB =PC·PD,则A、B、 C、D四点共圆。 3、托勒密定理得逆定理:若四边形ABCD中,AB·CD+BC·DA= AC·BD,则ABCD就是圆内接四边形。 另外,证多点共圆往往就是以四点共圆为基础实现得一般可先证其中四点共圆,然后证其余各点均在这个圆上,或者证其中某些点个个共圆,然后判断这些圆实际就是同一个圆。 例题精讲 例1:如图,P为△ABC内一点,D、E、F分别在BC、CA、AB上。已知P、D、C、E四点共圆,P、E、A、F 四点共圆,求证:B、D、P、F四点共圆。 证明连PD、PE、PF.由于P、D、C、F四点共圆,所以∠BDP = ∠PEC.又由于A、E、P、F四点共圆,所以∠PEC =∠AFP.于就是∠BDP= ∠AFP,故B、D、P、F四点共圆。 例2:设凸四边形ABCD得对角线AC、BD互相垂直,垂足为E,证明:点E关于AB、BC、CD、DA得对称点共圆。 为1 2 ,此变换把E关于AB、BC、 证明以E为相似中心作相似变换,相似比 CD、DA得对称点变为E在AB、BC、CD、DA上得射影P、Q、R、S(如图)、只需证明PQRS就是圆内接四边形。 由于四边形ESAP、EPBQ、EQCR及ERDS都就是圆内接四边形(每个四边形都有一组对角为直角),由E、P、B、Q共圆有∠EPQ = ∠EBQ、由E、Q、C、R共圆有∠ERQ=∠ECQ,于就是∠EPQ+∠ERQ = ∠EBQ+∠ECQ=90°、同理可得∠EPS +∠ERS =90°、从而有∠SPQ+∠QRS =180°,故PQRS就是圆内接四边形。 例3:梯形ABCD得两条对角线相交于点K,分别以梯形得两腰为直径各作一圆,点K位于这两个圆之外,证明:由点K向这两个圆所作得切线长度相等。 证明如图,设梯形ABCD得两腰为AB与CD,并设AC、BD与相应二圆得第二个交点分别为M、N、由于∠AMB、∠CND就是半圆上得圆周角,所以∠AM B=∠CND = 90°.从而∠BMC =∠BNC=90°,故B、M、N、C四点共圆,因此∠MNK=∠ACB.又∠ACB =∠KAD,所以∠MNK =∠KAD、于就是M、N、D、A四点共圆,因此KM·KA = KN·KD、由切割线定理得K向两已知圆所引得切线相等。 例4:如图,A、B为半圆O上得任意两点,AC、BD垂直于直径EF,BH⊥OA,求证:DH=AC、证法一在BD上取一点A',使A'D = AC,则ACDA'就是矩形。连结A'H、AB、OB、由于BD⊥EF、BH⊥OA,所以∠BDO =∠B HO=90°、于就是D、B, H、O四点共圆,所以∠HOB =∠HDB、由于∠AHB =∠AA'B = 90°,所以A、H、A'、B四点共圆。故∠DA'H=∠OAB,因此∠DHA'=∠OBA、而OA = OB,所以∠OBA=∠OAB,于就是∠DHA'=∠D A'H、所以DH=DA',故DH =
四点共圆(习题)
圆内接四边形与四点共圆 思路一:用圆的定义:到某定点的距离相等的所有点共圆。→若连在四边形的三边的中垂线相交于一点,那么这个四边形的四个顶点共圆。(这三边的中垂线的交点就是圆心)。 产生原因:圆的定义:圆可以看作是到定点的距离等于定长的点的集合。 基本模型: AO=BO=CO=DO ? A、B、C、D四点共圆(O为圆心) 思路二:从被证共圆的四点中选出三点作一个圆,然后证另一个点也在这个圆上,即可证明这四点共圆。→要证多点共圆,一般也可以根据题目条件先证四点共圆,再证其他点也在这个圆上。 思路三:运用有关性质和定理: ①对角互补,四点共圆:对角互补的四边形的四个顶点共圆。 产生原因:圆内接四边形的对角互补。 基本模型: ∠ + = 180 B)? A、B、C、D四点共圆 ∠D 180 = ∠ + ∠D A(或0 ②张角相等,四点共圆:线段同侧两点与这条线段两个端点连线的夹角相等,则这两个点和线段的两个端点共四个点共圆。 产生原因:在同圆或等圆中,同弧所对的圆周角相等。 方法指导:把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角(即:张角)相等(同弧所对的圆周角相等),从而即可肯定这四点共圆。
∠? A、B、C、D四点共圆 = CAB∠ CDB ③同斜边的两个直角三角形的四个顶点共圆,其斜边为圆的直径。 产生原因:直径所对的圆周角是直角。 ∠D = C? A、B、C、D四点共圆 = ∠ 90 ④外角等于内对角,四点共圆:有一个外角等于其内对角的四边形的四个顶点共圆。产生原因:圆内接四边形的外角等于内对角。 基本模型: ∠? A、B、C、D四点共圆 = ECD∠ B
四点共圆例题及答案
证明四点共圆的基本方法 证明四点共圆有下述一些基本方法: 方法1 从被证共圆的四点中先选出三点作一圆,然后证另一点也在这个圆上,若能证明这一点,即可肯定这四点共圆. 方法2 把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等,从而即可肯定这四点共圆.(若能证明其两顶角为直角,即可肯定这四个点共圆,且斜边上两点连线为该圆直径。) 方法3 把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆. 方法4 把被证共圆的四点两两连成相交的两条线段,若能证明它们各自被交点分成的两线段之积相等,即可肯定这四点共圆;或把被证共圆的四点两两连结并延长相交的两线段,若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积,即可肯定这四点也共圆.(根据托勒密定理的逆定理) 方法5 证被证共圆的点到某一定点的距离都相等,从而确定它们共圆. 上述五种基本方法中的每一种的根据,就是产生四点共圆的一种原因,因此当要求证四点共圆的问题时,首先就要根据命题的条件,并结合图形的特点,在这五种基本方法中选择一种证法,给予证明. 例1 如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H 四点共圆. 证明菱形ABCD的对角线AC和 BD相交于点O,连接OE、OF、OG、OH. ∵AC和BD 互相垂直, ∴在Rt△AOB、Rt△BOC、Rt△COD、 Rt△DOA中,E、F、G、H,分别是AB、 BC、CD、DA的中点,
即E、F、G、H四点共圆. (2)若四边形的两个对角互补(或一个外角等于它的内对角),则四点共圆. 例2 如图,在△ABC中,AD⊥BC,DE⊥AB,DF⊥AC. 求证:B、E、F、C四点共圆. 证明∵DE⊥AB,DF⊥AC, ∴∠AED+∠AFD=180°, 即A、E、D、F四点共圆, ∠AEF=∠ADF. 又∵AD⊥BC,∠ADF+∠CDF=90°, ∠CDF+∠FCD=90°, ∠ADF=∠FCD. ∴∠AEF=∠FCD, ∠BEF+∠FCB=180°, 即B、E、F、C四点共圆. (3)若两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,那么这两个三角形有公共的外接圆. 【例1】在圆内接四边形ABCD中,∠A-∠C=12°,且∠A∶∠B=2∶3.求∠A、∠B、∠C、∠D的度数. 解∵四边形ABCD内接于圆,
最新九年级数学四点共圆例题讲解
精品文档 九年级数学四点共圆例题讲解 知识点、重点、难点 四点共圆是圆的基本内容,它广泛应用于解与圆有关的问题.与圆有关的问题变化多,解法灵活,综合性强,题型广泛,因而历来是数学竞赛的热点内容。 在解题中,如果图形中蕴含着某四点在同一个圆上,或根据需要作出辅助圆使四点共圆,利用圆的有关性质定理,则会使复杂问题变得简单,从而使问题得到解决。因此,掌握四点共圆的方法很重要。 、、、===OCOB四个点到定点DO 判定四点共圆最基本的方法是圆的定义:如果A的距离相等,即BOAC、、、D四点共圆.,那么ACB OD 由此,我们立即可以得出 1.如果两个直角三角形具有公共斜边,那么这两个直角三角形的四个顶点共圆。 将上述判定推广到一般情况,得: 2.如果四边形的对角互补,那么这个四边形的四个顶点共圆。 3.如果四边形的外角等于它的内对角,那么这个四边形的四个顶点共圆。 4.如果两个三角形有公共底边,且在公共底边同侧又有相等的顶角,那么这两个三角形的四个顶点共圆。 运用这些判定四点共圆的方法,立即可以推出: 正方形、矩形、等腰梯形的四个顶点共圆。 其实,在与圆有关的定理中,一些定理的逆定理也是成立的,它们为我们提供了另一些证明四点共圆的方法.这就是: 、、、D四点共圆。B =CE·ED,则AC· 1.相交弦定理的逆定理:若两线段AB和CD相交 于E,且AEEB、、、BPD,则APA,且·PB =PC 2.割线定理的逆定理:若相交于点P的两线段PB·PD上各有一点A、C 、D四点共圆。C 3.托勒密定理的逆定理:若四边形ABCD中,AB·CD+BC·DA= AC·BD,则ABCD是圆内接四边形。 另外,证多点共圆往往是以四点共圆为基础实现的一般可先证其中四点共圆,然后证其余各点均在这个圆上,或者证其中某些点个个共圆,然后判断这些圆实际是同一个圆。 例题精讲 、、、、、、、、、、F四点共圆,上。已知PPDAC1例:如图,P为△ABC内一点,DEEF分别在BCECAAB、、、
四点共圆例题及答案
四点共圆的应用 例1 如图1,已知P 为⊙O 外一点,PA 切⊙O 于A ,PB 切⊙O 于B ,OP 交AB 于E . 求证:∠APC =∠BPD . 例2 如图2,从⊙O 外一点P 引切线PA 、PB 和割线PDC ,从A 点作弦AE 平行于DC ,连结BE 交DC 于F ,求证:FC =FD . 例3 如图3,在△ABC 中,AB=AC ,AD ⊥BC ,∠B 的两条三等分线交AD 于E 、G ,交AC 于F 、H .求证:EH ∥GC . P P
例4 如图4,⊿ABC 为等边三角形,D 、E 分别为BC 、AC 边上的点,且BD=31BC,CE=3 1 AC,AD 与 BE 相交于P 点。求证:CP ⊥AD 例5 如图5,AB 为半圆直径,P 为半圆上一点,PC ⊥AB 于C ,以AC 为直径的圆交PA 于D ,以 BC 为直径的圆交PB 于E ,求证:DE 是这两圆的公切线. 例6 AB 、CD 为⊙O 中两条平行的弦,过B 点的切线交CD 的延长线于G ,弦PA 、PB 分别交CD 于E 、F .求证:FG FD CF EF
例7 ABCD 为圆内接四边形,一组对边AB 和DC 延长交于P 点,另一组对边AD 和BC 延长交于Q 点,从P 、Q 引这圆的两条切线,切点分别是E 、F , (如图 7)求证:PQ 2=QF 2+PE 2. 例8 如图8,△ABC 的高AD 的延长线交外接圆于H ,以AD 为直径作圆和AB 、AC 分别交于E 、F 点,EF 交 AD 于 G ,若 AG=16cm ,AH=25cm ,求 AD 的长. 例9 如图9,D 为△ABC 外接圆上任意一点,E 、F 、G 为D 点到三边垂线的垂足,求证:E 、F 、G 三点在一条直线上. 例10 如图10,H 为△ABC 的垂心,H 1、H 2、 H 3为H 点关于各边的对称点,求证:A 、B 、 C 、H 1、H 2、H 3六点共圆. 2 B
四点共圆练习题
C F E A H B N M C A B 四点共圆练习题 1. 如图,ABC ?三边上的高交于H ,H 不于任一顶点重合,则以A 、B 、C 、D 、E 、F 、H 中某四个点可以确定的圆共有多少个? 2. 在梯形ABCD 中,AB ‖DC ,DC AB >,K 、M 分别在AD 、BC 上,CBK DAM ∠=∠,求证:CKB DMA ∠=∠ 3. 正方形ABCD 的中心为O ,面积为2 1989cm ,P 为正方形内一点,?=∠45OPB , 14:5:=PB PA ,求PB 。 4.如图8,△ABC 的高AD 的延长线交外接圆于H ,以AD 为直径作圆和AB 、AC 分别交于E 、F 点,EF 交 AD 于 G ,若 AG=16cm ,AH=25cm ,求 AD 的长. 5. 如图,在平行四边形ABCD 中,BC AM ⊥于M ,CD AN ⊥于N ,若13=AB ,5=BM ,9=MC ,求MN 的长度 6.如图所示,棱形ABCD 的对角线AC,BD 相交于点O,四条边AB,BC,CD,DA 的中点为E,F,G ,H. 求证:E,F,G ,H 四点共圆 7. 如图2,从⊙O 外一点P 引切线PA 、PB 和割线PDC ,从A 点作弦AE 平行于DC ,连结 BE 交DC 于F ,求证:FC =FD . B C M K D A C B O P D A F E D A B O C
8.在△ABC中,AB=AC,AD⊥BC,∠B的两条三等分线交AD于E、G,交AC于F、H.求证:EH∥GC. 9.如图,△ABC为等边三角形,D,E分别为BC,AC边上的点,且BD=1 3 BC,CE= 1 3 AC ,AD与BE 相交于点P,求证:CP⊥AD 10.锐角△ABC中,BD,CE分别是AC,AB边上的高线,EM⊥BD于M,DN⊥CE于N.求证:MN//BC. 11.在△ABC中,,B C ∠∠的平分线相交于T, ,B C ∠∠的外角平分线相交于P.求证: () 1 2 BPC ABC ACB ∠=∠+∠ 12.如图所示,如果五边形ABCDE中,. ABC ADE AEC ADB ∠=∠∠=∠ 且求证:BAC DAE ∠=∠. 13.四边形ABCD内接于圆,通过M和N分别表示直线AB和CD,BC与AD的交点,设 1 B是已 知圆同过点B、M、N三点的圆的异于B的交点,求证:直线 1 B D平分线段MN.
四点共圆练习题
作业16 1、锐角ABC ?的三条高AD 、BE 、CF 交于H ,在A 、B 、C 、D 、E 、F 、H 七个点中.能组成四点共圆的组数是( ) A 、4组 B 、5组 C 、6组 D 、7组 2、已知点)02(,A ,)53(,B ,直线l 过点B 与y 轴交于点)0(c ,C ,若 O 、A 、B 、C 四点共圆,则c 的值为( ) A 、 522 B 、5 28 C 、17 D 、无法求出 3.如图, AB 是⊙O 的直径, 弦CD ⊥AB, P 是弧CAD 上一点(不与C 、D 重合) . (1) 求证:∠CPD =∠COB ; (2) 若点P 在劣弧CD 上(不与C 、D 重合), ∠CPD 与∠COB 的数量关系是否发生变化?若不变, 请画图并证明;若变化, 请写出新的关系式并画图证明. 4、如图,在平行四边形ABCD 中,BAD ∠为钝角,且BC AE ⊥,CD AF ⊥. (1)求证:A 、E 、C 、F 四点共圆; (2)设线段BD 与(1 )中的圆交于M 、N .求证:ND BM =. 5、如图所示, I 为ABC ?的内心,求证:BIC ?的外心O 与A 、B 、C 四点共圆. B
B A 6.如图, ⊙O 的内接△ABC 的外角∠AC B 的平分线交⊙O 于E, EF ⊥BD 于F. (1) 探索EO 与AB 的位置关系, 并予以证明; (2) 当△AB C 的形状发生改变时, AC CF BF +的值是否发生改变?若不变, 请求出该值;若改变, 请求出其变化范围. 7.如图,已知AB 是⊙O 的直径,D 是弧AB 上一点,C 是弧AD 的中点,AD 、BC 相交于E ,CF ⊥AB ,F 为垂足,CF 交AD 于G ,求证:CG=EG. 8、如图,已知ABC ?中的两条角平分线AD 和CE 相交于H ,?=∠60B ,F 在AC 上,且AF AE =. (1)证明:B ,D ,H ,E 四点共圆; (2)证明:CE 平分DEF ∠. B
四点共圆练习题word版本
作业16 1、锐角ABC的三条高AD、BE、 CF交于H,在A、B、C、D、 E、F、H七个点中?能组成四点共圆的组数是( ) A、4组 B 、5组 C 、6组 D 7组 2、已知点A(2 ,0),B(3,5),直线I过点B与y轴交于点C(0 , c),若 O、A、B、C四点共圆,贝U c的值为( ) 3. 如图,AB是OO的直径,弦CDLAB, P是弧CAD±一点(不与C D重合). (1) 求证:/ CP亠/ COB (2) 若点P在劣弧CD上(不与C D重合),/ CPD与Z COB的数量关系是否发生变化?若不变,请画图并证明;若变化,请写出新的关系式并画图证明? (1)求证:A、E、C、F四点共圆; (2)设线段BD与(1)中的圆交于M、N .求证:BM ND . 5、如图所示,I为ABC的内心,求证: 圆?BIC的外心O与A、B、C四点共 A、22 5 28 5 C 、17 D 、无法求出 4、如图,在平行四边形ABCD 中, BAD为钝角,且AE BC,AF CD.
6. 如图,O0的内接△ ABC的外角/ ACB勺平分线交O 0于E, EF丄 BD于F. (1)探索E0与AB的位置关系,并予以证明; ⑵当厶ABC的形状发生改变时,BF CF的值是否发生改变?AC 若不变,请求出该值;若改变,请求出其变化范围. 7. 如图,已知AB是。0的直径,D是弧AB上一点,C是弧AD的中 点,AD BC 相交于E, CF丄AB F为垂足,CF交AD于G 求证:CG=EG. 8、如图,已知ABC中的两条角平分线AD和CE相交于H , B 60,F在 AC 上,且AE AF . (1)证明:B,D,H,E四点共圆;(2)证明:CE平分DEF . F C A
中考数学专题复习 四点共圆模型 含答案
共圆模型 模型1共端点,等线段模型 如图①,出现“共端点,等线段”时,可利用圆定义构造辅助圆. 如图②,若OA=OB=OC,则A、B、C三点在以O为圆心,OA为半径的圆上. 如图③,常见结论有:∠ACB=1 2 ∠AOB,∠BAC= 1 2 ∠BOC. 模型分析 ∵OA=OB=OC. ∴A、B、C三点到点O的距离相等. ∴A、B、C三点在以O为圆心,OA为半径的圆上.∵∠ACB是?AB的圆周角,∠AOB是?AB的圆心角, ∴∠ACB=1 2 ∠AOB. 同理可证∠BAC=1 2 ∠BOC. (1)若有共端点的三条线段,可考虑构造辅助圆. (2)构造辅助圆是方便利用圆的性质快速解决角度问题. 模型实例 如图,△ABC和△ACD都是等腰三角形,AB=AC,AC=AD,连接BD. 求证:∠1+∠2=90°. 证明 证法一:如图①, ∵AB=AC=AD.∴B、C、D在以A为圆心,AB为半径的⊙A上.∴∠ABC=∠2. 在△BAC中,∵∠BAC+∠ABC+∠2=180°,∴2∠1+2∠2=180°.∴∠1+∠2=90°. 证法二:如图②, ∵AB=AC=AD.∴∠BAC=2∠1.∵AB=AC, ∴B、C、D在以A为圆心,AB为半径的⊙O上. 延长BA与圆A相交于E,连接CE. ∴∠E=∠1.(同弧所对的圆周角相等.) ∵AE=AC,∴∠E=∠ACE. ∵BE为⊙A的直径,∴∠BCE=90°. ∴∠2+∠ACE=90°.∴∠1+∠2=90°. 小猿热搜 1.如图,△ABC为等腰三角形,AB=AC,在△ABC的外侧作直线AP,点B与点D关于AP轴对称,连接BD、CD,CD与AP交于点E.求证:∠1=∠2. 证明 ∵A、D关于AP轴对称,∴AP是BD的垂直平分线. ∴AD=AB,ED=EB.又∵AB=AC. ∴C、B、D在以A为圆心,AB为半径的圆上. ∵ED=EB,∴∠EDB=∠EBD.∴∠2=2∠EDB.又∵∠1=2∠CDB.∴∠1=∠2. 2.己知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b,求BD的长. 解答 以A为圆心,以a为半径作圆,延长BA交⊙A于E点,连接ED.
四点共圆例题及答案汇编
例1 如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H 四点共圆. 证明菱形ABCD的对角线AC和BD相交于点O,连接OE、OF、OG、OH. ∵AC和BD 互相垂直, ∴在Rt△AOB、Rt△BOC、Rt△COD、Rt△DOA中,E、F、G、H,分别是AB、BC、CD、DA的中点, 即E、F、G、H四点共圆. (2)若四边形的两个对角互补(或一个外角等于它的内对角),则四点共圆. 例2 如图,在△ABC中,AD⊥BC,DE⊥AB,DF⊥AC. 求证:B、E、F、C四点共圆. 证明∵DE⊥AB,DF⊥AC, ∴∠AED+∠AFD=180°, 即A、E、D、F四点共圆,
∠AEF=∠ADF. 又∵AD⊥BC,∠ADF+∠CDF=90°, ∠CDF+∠FCD=90°, ∠ADF=∠FCD. ∴∠AEF=∠FCD, ∠BEF+∠FCB=180°, 即B、E、F、C四点共圆. (3)若两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,那么这两个三角形有公共的外接圆. 证明在△ABC中,BD、CE是AC、AB边上的高. ∴∠BEC=∠BDC=90°,且E、D在BC的同侧, ∴E、B、C、D四点共圆. ∠AED=∠ACB,∠A=∠A, ∴△AED∽△ACB.
上述三种方法是证“四点共圆”的基本方法,至于证第四点在前三点(不在同一直线上)所确定的圆上就不叙述了. 【例1】在圆内接四边形ABCD中,∠A-∠C=12°,且∠A∶∠B=2∶3.求∠A、∠B、∠C、∠D的度数. 解∵四边形ABCD内接于圆, ∴∠A+∠C=180°. ∵∠A-∠C=12°, ∴∠A=96°,∠C=84°. ∵∠A∶∠B=2∶3, ∠D=180°-144°=36°. 利用圆内接四边形对角互补可以解决圆中有关角的计算问题. 【例2】已知:如图1所示,四边形ABCD内接于圆,CE∥BD交AB 的延长线于E.求证:AD·BE=BC·DC. 证明:连结AC. ∵CE∥BD,
四点共圆问题
第四讲 四点共圆问题 “四点共圆”问题在数学竞赛中经常出现,这类问题一般有两种形式:一是以“四点共圆”作为证题的目的,二是以“四点共圆”作为解题的手段,为解决其他问题铺平道路. 1 “四点共圆”作为证题目的 例1.给出锐角△ABC ,以AB 为直径的圆与AB 边的高CC ′及其延长线交于M , N .以AC 为直径的圆与AC 边的高BB ′及其延长线将于P ,Q .求证:M ,N ,P ,Q 四点共圆. 分析:设PQ ,MN 交于K 点,连接AP ,AM . 欲证M ,N ,P ,Q 四点共圆,须证 MK ·KN =PK ·KQ , 即证(MC ′-KC ′)(MC ′+KC ′) =(PB ′-KB ′)·(PB ′+KB ′) 或MC ′2-KC ′2=PB ′2-KB ′2 . ① 不难证明 AP =AM ,从而有 AB ′2+PB ′2=AC ′2+MC ′2. 故 MC ′2-PB ′2=AB ′2-AC ′2 =(AK 2-KB ′2)-(AK 2-KC ′2) =KC ′2-KB ′2. ② 由②即得①,命题得证. 例2.A 、B 、C 三点共线,O 点在直线外, O 1,O 2,O 3分别为△OAB ,△OBC , △OCA 的外心.求证:O ,O 1,O 2, O 3四点共圆. 分析:作出图中各辅助线.易证O 1O 2垂直平分OB ,O 1O 3垂直平分OA .观察△OBC 及其外接圆,立得∠OO 2O 1=2 1 ∠OO 2B =∠OCB .观察△OCA 及其外接圆, 立得∠OO 3O 1=2 1 ∠OO 3A =∠OCA . 由∠OO 2O 1=∠OO 3O 1?O ,O 1,O 2,O 3共圆. 利用对角互补,也可证明O ,O 1,O 2,O 3四点共圆,请同学自证. 2 以“四点共圆”作为解题手段 这种情况不仅题目多,而且结论变幻莫测,可大体上归纳为如下几个方面. (1)证角相等 例3.在梯形ABCD 中,AB ∥DC ,AB >CD ,K ,M 分别在AD ,BC 上,∠DAM =∠CBK . 求证:∠DMA =∠CKB . 分析:易知A ,B ,M ,K 四点共圆.连接KM , 有∠DAB =∠CMK .∵∠DAB +∠ADC =180°, ∴∠CMK +∠KDC =180°. 故C ,D ,K ,M 四点共圆?∠CMD =∠DKC . A B C K M N P Q B ′C ′A B C O O O O 1 23 ? ?A B C D K M ··
四点共圆问题
四点共圆问题 “四点共圆”问题在数学竞赛中经常出现,这类问题一般有两种形式:一是以“四点共圆”作为证题的目的,二是以“四点共圆”作为解题的手段,为解决其他问题铺平道路.判定“四点共圆”的方法,用得最多的是统编教材《几何》二册所介绍的两种(即P 89定理和P 93例3),由这两种基本方法推导出来的其他判别方法也可相机采用. 1 “四点共圆”作为证题目的 例1.给出锐角△ABC ,以AB 为直径的圆与AB 边的高CC ′及其 延长线交于M ,N.以AC 为直径的圆与AC 边的高BB ′及其延长线将于P ,Q.求证:M ,N ,P ,Q 四点共圆. (第19届美国数学奥林匹克) 分析:设PQ ,MN 交于K 点,连接AP ,AM. 欲证M ,N ,P ,Q 四点共圆,须证 MK ·KN =PK ·KQ , 即证(MC ′-KC ′)(MC ′+KC ′) =(PB ′-KB ′)·(PB ′+KB ′) 或MC ′2-KC ′2=PB ′2-KB ′2 . ① 不难证明 AP =AM ,从而有 AB ′2+PB ′2=AC ′2+MC ′2. 故 MC ′2-PB ′2=AB ′2-AC ′2 =(AK 2-KB ′2)-(AK 2-KC ′2) =KC ′2-KB ′2. ② 由②即得①,命题得证. 例2.A 、B 、C 三点共线,O 点在直线外, O 1,O 2,O 3分别为△OAB ,△OBC , △OCA 的外心.求证:O ,O 1,O 2, O 3四点共圆. (第27届莫斯科数学奥林匹克) 分析:作出图中各辅助线.易证O 1O 2垂直平分OB ,O 1O 3垂直平分 OA.观察△OBC 及其外接圆,立得∠OO 2O 1=21 ∠OO 2B=∠OCB. 观察△OCA 及其外接圆,立得∠OO 3O 1=2 1 ∠OO 3A =∠OCA. 由∠OO 2O 1=∠OO 3O 1 O ,O 1,O 2,O 3共圆. A B C K M N P Q B ′C ′A B C O O O O 1 23 ? ?
【高中数学竞赛】四点共圆专题详解
四点共圆 四点共圆的定义 四点共圆的定义:如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。 证明四点共圆有下述一些基本方法: 【方法1】从被证共圆的四点中先选出三点作一圆,然后证另一点也在这个圆上,若能证明这一点,即可肯定这四点共圆.或利用圆的定义,证各点均与某一定点等距。 【方法2 】如果各点都在某两点所在直线同侧,且各点对这两点的张角相等,则这些点共圆.(若能证明其两张角为直角,即可肯定这四个点共圆,且斜边上两点连线为该圆直径。)【方法3 】把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆. 【方法4】把被证共圆的四点两两连成相交的两条线段,若能证明它们各自被交点分成的两线段之积相等,即可肯定这四点共圆;或把被证共圆的四点两两连结并延长相交的两线段,若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线 段之积,即可肯定这四点也共圆.即利用相交弦、切割线、割线定理的逆定理证四点共圆。【方法5】证被证共圆的点到某一定点的距离都相等,从而确定它们共圆. 【方法6】根据托勒密定理的逆定理,在四边形ABCD中,若AC*BD=AB*CD+AD*BC,那么A,B,C,D四点共圆。或根据西姆松定理的逆定理证四点共圆。 【方法7】证明五点或五点以上的点共圆,可以分别证各四点共圆,且四点中有三点相同。
【方法8】证连结各点所得凸多边形与某一圆内接凸多边形相似。 上述六种基本方法中的每一种的根据,就是产生四点共圆的一种原因,因此当要求证四点共圆的问题时,首先就要根据命题的条件,并结合图形的特点,在这8种基本方法中选择一种证法,给予证明. 一.某些知识的补充 1.已知:ABCD共圆,AB中点为E、CD中点为F,EF中点为G,过E点分别作AD、BC的垂线,垂足为H、I求证:GH=GI 首先可这样转化图形:作E点关于AD、BC边的轴对称点S、T,显然I、H分别是ES、ET中点。由中位线,可将原题转化为证:FS=FT。再延长AD、BC相交于P点。由A、B、C、D是圆内接四边形。知△PCD∽△PAB,而PF、PE分别是这两个三角形的对应中线,故∠DPF=∠BPE;这就表明E和F是∠APB内的两个“等角点”(即指满足左、右两角相等)。 下面是等角点的一个常用性质(Poncelet定理): “设E、F是∠APB内的两点,满足∠APF=∠BPE。作E关于PA、PB的轴对称点S、T。求证:FS =FT。”
巧用四点共圆证题
巧用四点共圆证题 圆有许多重要的性质,如果同学们在把这些性质学好的基础上,能巧妙地应用这些性 例1. 是切点,CB 证明:联结AB CD 是圆O 1 ∴∠=∠BCD 同理∠=BDC ∠+∠BCD 而∠=∠CBD ∴∠+∠ BAC 即∠+∠=?FAE EBF 180 ∴F A E B 、、、四点共圆 ∴?=DE DA 例2. 已知:如图角形,联结BE 、CD 证明: ?ABD ∴∠=∠DAB ∴∠+∠DAB 即∠=∠DAC DA BA DAC BAE SAS =∴?,??() ∴∠=∠∠=∠1234, ∠=∠∠121,和∠2在AF 的同侧, ∴A 、D 、B 、F 四点共圆
∴∠=∠DBA DFA (同弧所对的圆周角相等) 同理∠=∠ECA EFA ∠=∠∴∠=∠DBA ECA DFA EFA 即AF 平分∠DFE 例3. 已知: 交AE 于点B , 求证:AC 2= 证明:过点D 过点B 作BN ⊥ CF AF ⊥, ∴M 、C 、F 、D ∴?=?AD AF AM AC (1) 同理B 、E 、C 、N 四点共圆 ∴?=?AB AE AN AC (2) 又因为??ADM CBN ?,四边形ABCD 为平行四边形,所以AM=CN (1)+(2)得 AB AE AD AF AN AC AM AC ?+?=?+? =+=+=AC AN AM AC AN CN AC ()()2 即AC AB AE AD AF 2 =?=? 说明:以上三例,都是利用了四点共圆,再根据圆的有关性质来达到证题目的的。 证明四点共圆有下述一些基本方法 证明四点共圆有下述一些基本方法: 方法 1 从被证共圆的四点中先选出三点作一圆,然后证另一点也在这个圆上,若能证明这一点,即可肯定这四点共圆. 方法 2 把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等,从而即可肯定这四点共圆. (若能证明其两顶角为直角,即可肯定这四个点共圆,且斜边上两点连线为该圆直径。) 方法 3 把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆. 方法 4 把被证共圆的四点两两连成相交的两条线段,若能证明它们各自被交点分成的两线段之积相等,即可肯定这四点共圆;或把被证共圆的四点两两连结并延长
四点共圆问题 (数学竞赛)
P 四点共圆问题 四点共圆是平面几何证题中一个十分有利的工具,四点共圆这类问题一般有以下两种形式: (1) 证明某四点共圆或者以四点共圆为基础证明若干点共圆; (2) 通过某四点共圆得到一些重要结论,进而解决问题 下面给出与四点共圆有关的一些基本知识 (1) 若干个点与某定点的距离相等,则这些点在一个圆上; (2) 在若干个点中有两点,其他点对这两点所成线段的视角均为直角,则这些点共圆; (3) 若四点连成的四边形对角互补或有一外角等于它的内对角,则这四点共圆; (4) 若点C 、D 在线段AB 的同侧,且ACB ADB ∠=∠,则A B C D 、、、四点共圆; (5) 若线段AB CD 、交于E 点,且AE EB CE ED = ,则A B C D 、、、四点共圆; (6) 若相交线段PA PB 、上各有一点C D 、,且PA PC PB PD = ,则A B C D 、、、四点共圆。 四点共圆问题不但是平面几何中的重要问题,而且是直线形和圆之间度量关系或者位置关系相互转化的媒介。 例1、已知PQRS 是圆内接四边形,0 90PSR ∠=,过点Q 作PR PS 、的垂线,垂足分别为点H K 、求证:HK 平分QS 例2、给定锐角ABC ,以AB 为直径的圆与边AB 上的高线' CC 及其延长线交于点M N 、,以AC 为直径的圆与AC 上的高线' BB 及其延长线交于点P Q 、。证明:M P N Q 、、、四点共圆。 例3、在等腰ABC 中,P 为底边BC 上任意一点,过点P 做两腰的平行线分别与AB AC 、交于点 Q R 、,又点'P 是点P 关于直线QR 的对称点。求证:点'P 在ABC 分析:
四点共圆例题及答案
四点共圆的应用 知识点: (1)如果四个点与一定点距离相等,那么这四个点共圆. (2)如果一个四边形的一组对角互补,那么这个四边形的四个顶点共圆. (3)如果一个四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆. (4)如果两个直角三角形有公共的斜边,那么这两个三角形的四个顶点共圆(因为四个顶点与斜边中点距离相等). 四点共圆在平面几何证明中应用广泛,熟悉这种应用对于开阔证题思路,提高解题能力都是十分有益的. 一用于证明两角相等 例1 如图1,已知P为⊙O外一点,PA切⊙O于A,PB切⊙O于B,OP交AB于E.求证:∠APC=∠BPD. 证明连结OA,OC,OD.由射影定理,得AE2=PE·EO,又AE=BE,则AE·BE=PE·EO……(1);由相交弦定理,得AE·BE=CE·DE……(2);由(1)、(2)得CE·ED=PE·EO,∴ P、C、O、D四点共圆,则∠1=∠2,∠3=∠4,又∠2=∠4.∴∠1=∠3,易证∠APC=∠BPD(∠4=∠EDO). 二用于证明两条线段相筹 例2 如图2,从⊙O外一点P引切线PA、PB和割线PDC,从A点作弦AE平行于DC,连结BE交DC于F,求证:FC=FD.
证明连结AD、AF、EC、AB.∵PA切⊙O于A,则∠1=∠2.∵AE∥CD,则∠2=∠4.∴∠1=∠4,∴P、A、F、B四点共圆.∴∠5=∠6,而∠5=∠2=∠3,∴∠3=∠6.∵AE∥CD,∴EC=AD,且∠ECF=∠ADF,∴△EFC≌△AFD,∴FC=FD. 三用于证明两直线平行 例3 如图3,在△ABC中,AB=AC,AD⊥BC,∠B的两条三等分线交AD于E、G,交AC于F、H.求证:EH∥GC. 证明连结EC.在△ABE和△ACE中,∵AE=AE,AB=AC,∠BAE=∠CAE,∴△AEB≌AEC,∴∠5=∠1=∠2,∴B、C、H、E四点共圆,∴∠6=∠3.在△GEB和△GEC中,∵GE=GE,∠BEG=∠CEG,EB=EC,∴△GEB ≌△GEC,∴∠4=∠2=∠3,∴∠4=∠6.∴EH∥GC.
四点共圆练习试题
四点共圆 判定定理1:若两个直角三角形共斜边,则四个顶点共圆,且直角三角形的斜边为圆的直径. 判定定理2:共底边的两个三角形顶角相等,且在底边的同侧,则四个顶点共圆. 判定定理3:对于凸四边形ABCD ,若对角互补,则A 、B 、C 、D 四点共圆. 判定定理4:相交弦定理的逆定理:对于凸四边形ABCD 其对角线AC 、BD 交于P , 若PA ·PC=PB ·PD ,则A 、B 、C 、D 四点共圆。 判定定理5:割线定理的逆定理:对于凸四边形ABCD 两边AB 、DC 的延长线相交于P , 若PB ·PA=PC ·PD ,则A 、B 、C 、D 四点共圆。 1:如图,在圆内接四边形ABCD 中,∠A=60°,∠B=90°,AB=2,CD=1,求BC 的长 2:如图,正方形ABCD 的面积为5,E 、F 分别为CD 、DA 的中点,BE 、CF 相交于P , 求AP 的长 3:如图,四边形ABCD 内接于⊙O ,CB=CD=4,AC 与BD 相交于E ,AE=6,线段BE 和DE 的长都是正整 F
数,求BD 的长 4:如图,OQ ⊥AB ,O 为△ABC 外接圆的圆心,F 为直线OQ 与AB 的交点,BC 与OQ 交于P 点,A 、C 、 Q 三点共线,求证:OA 2 =OP·OQ 5:如图,P 是⊙O 外一点,PA 与⊙O 切于点A ,PBC 是⊙O 的割线,AD ⊥PO 于D , 求证:PB :BD=PC :CD 6:如图,直线AB 、AC 与⊙O 分别相切于B 、C 两点,P 为圆上一点,P 到AB 、AC 的距离分别为6cm 、 4cm ,求P 到BC 的距离 A
