根号1-30近似值 11-30平方数 (可直接打印)

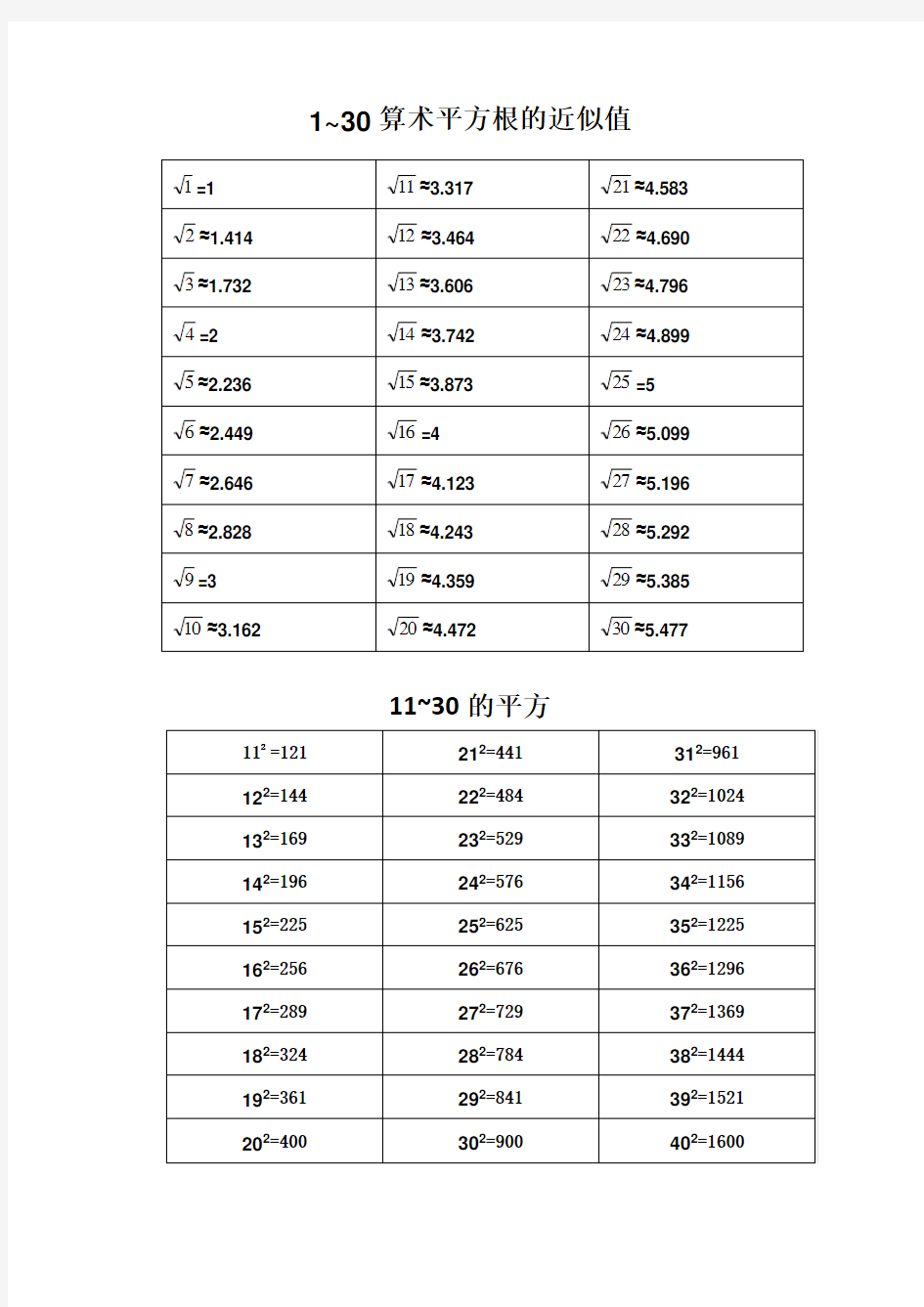
1~30算术平方根的近似值

1=1 11≈3.317 21≈4.583

2≈1.414 12≈3.464 22≈4.690

3≈1.732 13≈3.606 23≈4.796

4=2 14≈3.742 24≈4.899

5≈2.236 15≈3.873 25=5

6≈2.449 16=4 26≈5.099

7≈2.646 17≈4.123 27≈5.196

8≈2.828 18≈4.243 28≈5.292

9=3 19≈4.359 29≈5.385

10≈3.162 20≈4.472 30≈5.477

11~30的平方

112 =121212=441312=961

122=144222=484322=1024

132=169232=529332=1089

142=196242=576342=1156

152=225252=625352=1225

162=256262=676362=1296

172=289272=729372=1369

182=324282=784382=1444

192=361292=841392=1521

202=400302=900402=1600

无理数典型练习题(菁优网)

无理数无理数无理数无理数

无理数无理数无理数无理数一．选择题（共5小题） 1．（2013?安顺）下列各数中，3.14159，，0.131131113…，﹣π，，，无理数的个数有（）和和D 与 5．（2006?梧州）在﹣7.5，，4，，﹣π，，中，无理数的个数是（）二．填空题（共5小题） 6．（2011?淄博）写出一个大于3且小于4的无理数_________． 7．（2010?建邺区一模）写出﹣1和2之间的一个无理数：_________． 8．（2012?大丰市模拟）在数据﹣π，，中无理数的个数是_________个．9．（2010?泰安）1，2，3…，100这100个自然数的算术平方根和立方根中，无理数的个数有_________个．10．在，﹣（+5），，0，π，，0.303003000中，无理数是_________．三．解答题（共2小题） 11．在：，，0，3.14，﹣，﹣，7.151551…（每相邻两个“1”之间依次多一个“5”）中，整数集合{…}，分数集合{…}，无理数集合{…}．

12．下列数中：①﹣|﹣3|，②﹣0.3，③﹣，④，⑤，⑥，⑦0，⑧﹣，⑨1.2020020002…（每两个2之间依次多一个0）（请填序号）无理数是_________，整数是_________．负分数是_________．

无理数无理数无理数无理数参考答案与试题解析一．选择题（共5小题） 1．（2013?安顺）下列各数中，3.14159，，0.131131113…，﹣π，，，无理数的个数有（）和和D 解：其中此题考查了无理数的概念，注意其中的与与、在这三个代数式中， 4．（1997?广西）下面说法中，正确的是（）

怎样证明根号2是一个无理数

怎样证明2是一个无理数 2是一个非常著名的无理数，第一个发现并坚持这个结果的希帕索斯因此付出了生命的代价——后世的数学史家所说的“第一次数学危机”盖源于此.风暴过去后，唤醒的却是数学家们对数的重新认识，实数的概念开始确立，在此意义上讲，2的发现是人们对真理的追求、探索以致明朗的一个极好例证. 换一个角度来看这个数，我们可以把它看作一根“晾衣绳”，上面挂着许多有趣的方法，值得你仔细玩味.我们准备从不同的角度来证明2是一个无理数，从而体会这一点. 证法1：尾数证明法.假设2是一个有理数，即2可以表示为一个分数的形式2=b a .其中(a,b )=1，且a 与b 都是正整数.则222b a =.由于完全平方数2b 的尾数只能是0、1、4、5、6、9中的一个，因此22b 的尾数只能是0、2、8中的一个.因为222b a =，所以2a 与22b 的尾数都是0，因此2b 的尾数只能是0或5，因此a 与b 有公因数5，与(a,b )=1矛盾！因此2是无理数. 这个证法可以证明被开方数的尾数是2、3、7、8的平方根都是无理数. 证法2：奇偶分析法.假设2=b a .其中(a, b )=1，且a 与b 都是正整数.则222b a =.可知a 是偶数，设a =2 c ,则2224b c =，222c b =，可知b 也是偶数，因此a 、b 都是偶数，这与(a,b )=1矛盾！因此2是无理数. 希帕索斯就是用这种方法证明了2不是有理数，动摇了毕达哥拉斯学派的“万物皆数(任何数都可表示成整数之比)”的数学信仰，使毕达哥拉斯学派为之大为恐慌，希帕索斯因此葬身海底. 证法3：仿上，得到222b a =，易见b >1，否则b=1，则2=a 是一个整数,这是不行的.222b a =改写成a a b ?= 22.因为b >1，因此b 有素因子p ，因此p 整除2 a 或a ，总之，p 整除a ，因此p 同时整除a 与 b ，这与(a,b )=1矛盾. 证法4：仿上，得到222b a =，等式变形为))((222b a b a b a b -+=-=，因为b >1，因此存在素因子p ，p 整除a+b 或a-b 之一，则同时整除a+b 与a-b ，因此p 整除a ，因此p 是a 、b 的公因数，与(a,b )=1矛盾. 证法5：利用代数基本定理，如果不考虑素因子的顺序，任何一个正整数都可以唯一地写成素数幂的积的形式，因此m r m r r p p p a 2121=，n s n s s q q q b 2121=，其中m p p ,,1 与n q q ,,1 都是素数，m r r ,,1 与n s s ,1都是正整数，因此m r m r r p p p 2222121 =2n s n s s q q q 2222121 ，素数2在等式左边是偶数次幂，但在右边是奇数次幂，矛盾，因此2是无理数.

求实数a的值或取值范围专题练习

专题练习求实数a 的值或取值范围 1．已知全集U ＝{2,3，a 2－a －1}，A ＝{2,3}，若?U A ＝{1}，则实数a 的值是________． 2．设集合A ＝{x |x ＋m ≥0}，B ＝{x |－2＜x ＜4}，全集U ＝R ，且(?U A )∩B ＝?，求实数m 的取值范围为________． 3．已知全集U ＝R ，A ＝{x |－4≤x ＜2}，B ＝{x |－1＜x ≤3}，P ＝{x |x ≤0或x ≥5 2 }，求A ∩B ， (?U B )∪P ，(A ∩B )∩(?U P )． 4．已知集合A ＝{x |x 2＋ax ＋12b ＝0}和B ＝{x |x 2－ax ＋b ＝0}，满足B ∩(?U A )＝{2}，A ∩(?U B )＝{4}，U ＝R ，求实数a ，b 的值． 5．已知集合A ＝{x |2a －2

9. 已知方程02 =++c bx x 有两个不相等的实根x 1， x 2. 设C ＝{x 1， x 2}， A ＝{1，3， 5，7，9}， B ＝{1，4，7，10}，若C B C C A =Φ= ,，试求b ， c 的值。 10. 设集合}121|{},52|{-≤≤+=≤≤-=m x m x B x x A ，（1）若Φ=B A ，求m 的范围；（2）若A B A = ，求m 的范围。 10. 已知A ＝{0，1}， B ＝{x|x ?A}，用列举法表示集合B ，并指出集合A 与B 的关系。 11. 设集合M ＝,24},17|{=≤a x x 则（） A. M a ∈ B. M a ? C. a ＝ M D. a > M 12. 有下列命题：①}{Φ是空集 ② 若N b N a ∈∈,，则2≥+b a ③ 集合 }012|{2 =+-x x x 有两个元素 ④ 集合 },100 | {Z x N x x B ∈∈=为无限集，其中正确命题的个数是（） A. 0 B. 1 C. 2 D. 3 13. 下列集合中，表示同一集合的是（） A. M ＝{（3，2）} ， N ＝{（2，3）} B. M ＝{3，2} ， N ＝{（2，3）} C. M ＝{（x ，y ）|x ＋y ＝1}， N ＝{y|x ＋y ＝1} D.M ＝{1，2}， N ＝{2，1} 14. 设集合}1 2,4{},1,3,2{2 2+-+=+=a a a N a M ，若}2{=N M ，则a 的取值集合是（） A. } 21 ,2,3{- B. {－3} C. } 21 ,3{- D. {－3，2} 15. 设集合A ＝ {x| 1 < x < 2}， B ＝ {x| x < a}，且B A ?，则实数a 的范围是（） A. 2≥a B. 2>a C. 1≤a D. 1>a 16. 设x ，y ∈R ，A ＝{（x ，y ）|y ＝x}， B ＝}1| ),{(=x y y x ，则集合A ，B 的关系是（） A. A B B. B A C. A ＝B D. A ?B 17. 已知M ＝{x|y ＝x 2－1} ， N ＝{y|y ＝x 2－1}，那么M ∩N ＝（）

无理数的常见形式

无理数的常见形式，科学计数法无理数概念：无理数即无限不循环小数。明确无理数的存在无理数来自实践，无理数并不“无理”，也不是人们臆想出来的，它是实实在在存在的，例如：（1）一个直角三角形，两条直角边长分别为1和2，由勾股定理知，它的斜边长为；（2）任何一个圆，它的周长和直径之比为一常数等等；像这样的数，在我们周围的生活中，不是只有少数几个，而是像有理数一样有无限个。概念剖析：无限不循环小数叫无理数，这说明无理数是具有两个基本特征的小数：一是小数位数是无限的；二是不循环的。这对初学者来说有一定难度，因此，我们必须掌握它的表现形式。无理数的常见形式：在初中阶段，无理数表现形式主要有以下几种： 1. 无限不循环的小数，如0.1010010001……（两个1之间依次多一个0） 2. 含的数，如：，，等。 3. 开方开不尽而得到的数，如，等。 4. 某些三角函数值：如，等。无理数与有理数的区别：1、把有理数和无理数都写成小数形式时，有理数能写成整数、小数或无限循环小数，比如4=4.0，4/5=0.8，1/3=0.33333……。而无理数只能写成无限不循环小数，比如√2=1.414213562…………。根据这一点,人们把无理数定义为无限不循环小数； 2、无理数不能写成两整数之比。错误辨析： 1. 无限小数都是无理数； 2. 无理数包括正无理数、负无理数和零； 3.带根号的数是无理数； 4. 无理数是用根号形式表示的数； 5.无理数是开方开不尽的数； 6. 两个无理数的和、差、积、商仍是无理数； 7.无理数与有理数的乘积是无理数； 8. 有些无理数是分数； 9. 无理数比有理数少；10. 一个无理数的平方一定是有理数。综上，学习无理数应把握住无理数的三个特征：（1）无理数是小数；（2）无理数是无限小数；（3）无理数是不循环小数。判断一个数是否是无理数对照这三个特征一个不能少。另外，还应注意无理数的几种常见的表示形式，才是弄清无理数概念的关键。

无理数练习题

【知识要点】 1．无理数：定义：无限不循环小数叫做无理数，如π=3.1415926 1.414213= ，－1.010010001…，都是无理数。注意： ①既是无限小数，又是不循环小数，这两点必须同时满足； ②无限不循环小数与有限小数、无限循环小数的本质区别是：前者不能化成分数，而后两者都可以化成分数； 2．实数：有理数和无理数统称为实数。 ????????????????????????? 正有理数有理数零有限小数或无限循环小数负有理数实数正无理数无理数无限不循环小数负无理数 3．实数的几个有关概念： ①相反数：a 与－a 互为相反数，0的相反数是0。a+b=0?a 、b 互为相反数。 ②倒数：若0a ≠，则1a 称为a 的倒数，0没有倒数。1ab a =?、b 互为倒数。 ③绝对值：一个正实数的绝对值是它本身，一个负实数的绝对值是它的相反数，0的绝对值是0。即()()()0000a a a a a a >??==??-

④无理数乘以有理数是无理数； ⑤无理数除以有理数是无理数； ⑥有理数除以无理数是无理数。 A ．0个 B ．2个 C ．4个 D ．6个 4．判断（正确的打“√”，错误的打“×”） ①带根号的数是无理数；（）（） ③绝对值最小的实数是0；（） ④平方等于3 （） ⑤有理数、无理数统称为实数；（） ⑥1的平方根与1的立方根相等；（） ⑦无理数与有理数的和为无理数；（） ⑧无理数中没有最小的数，也没有最大的数。（） 5．a ） A ．有理数 B ．正无理数 C ．正实数 D ．正有理数 6．下列四个命题中，正确的是（） A ．倒数等于本身的数只有1 B ．绝对值等于本身的数只有0 C ．相反数等于本身的数只有0 D ．算术平方根等于本身的数只有1 7．下列说法不正确的是（） A ．有限小数和无限循环小数都能化成分数 B ．整数可以看成是分母为1的分数 C ．有理数都可以化为分数 D ．无理数是开方开不尽的数 8．代数式 21a +y ，()21a -中一定是正数的有（） A ．1个 B ．2个 C ．3个 D ．4个 9 ） A ．m 是完全平方数 B ．m 是负有理数 C ．m 是一个完全平方数的相反数 D ．m 是一个负整数 10．已知a 为有理数，b 为无理数，则a+b 为（） A ．整数 B ．分数 C ．有理数 D ．无理数 11 215 的大小关系是（） A 215< B ．215<<215<<215<< 12的相反数之和的倒数的平方为。 13、设a 、b 互为相反数，但不为0;c 、d 互为倒数;m 的倒数等于它本身，化简111c m m m d a b ??÷++- ???的结果是。

《无理数》习题

《无理数》习题一、选择题 1、正三角形的边长为4，高h ( ) A ．是整数 B ．是分数 C ．是有理数 D ．不是有理数 2、如果一个圆的半径是2，那么该圆的周长是( ) A ．一个有理数 B ．一个无理数 C ．一个分数 D ．一个整数 4、下列说法正确的是( ) A ．分数是无理数 B ．无限小数是无理数 C ．不能写成分数形式的数是无理数 D ．不能在数轴上表示的数是无理数 5、在实数3.14，25，3.3333，0.412?? ，0.10110111011110…，π，中，有( )个无理数？ A ．2个 B ．3个 C ．4个 D ．5个 6、下列说法中，正确的是( ) A ．带根号的数是无理数 B ．无理数都是开不尽方的数 C ．无限小数都是无理数 D ．无限不循环小数是无理数 7、下列命题中，正确的个数是( ) ①两个有理数的和是有理数； ②两个无理数的和是无理数； ③两个无理数的积是无理数； ④无理数乘以有理数是无理数； ⑤无理数除以有理数是无理数； ⑥有理数除以无理数是无理数. A ．0个 B ．2个 C ．4个 D ．6个 8、a 一定是( ) A ．有理数 B ．正无理数 C ．正实数 D ．正有理数 9、下列四个命题中，正确的是( )

A ．倒数等于本身的数只有1 B ．绝对值等于本身的数只有0 C ．相反数等于本身的数只有0 D ．算术平方根等于本身的数只有1 10、下列说法不正确的是( ) A ．有限小数和无限循环小数都能化成分数 B ．整数可以看成是分母为1的分数 C ．有理数都可以化为分数 D ．无理数是开方开不尽的数二、填空题 1、整数包括，分数包括 . 2、把两个边长为1的小正方形，用剪拼的方法可以得到一个大正方形，则大正方形的面积是，边长a 满足 . 3、如图1，是由9个边长为1的小正方形拼成的，则图中标明字母的线段中，和是有理数的线段，和不是有理数的线段. 4、如图2为一个底面为正方形，侧面为四个全等三角形围成的的几何体(其中高与底面边长相等)，若它的体积为7，试问它的棱长是整数吗-------------------，是分数吗，借助计算器求它精确到0.001的值为 .(该几何体的体积V =1/3a 2h ，a 边长，h 为高) 5、若a 、b 都是无理数，且a +b =2，则a ，b 的值可以是和．(填上一组满足条件的值即可) 6的相反数之和的倒数的平方为 . 7、设a 、b 互为相反数，但不为0；c 、d 互为倒数；m 的倒数等于它本身，化简111c m m m d a b ??÷++- ??? 的结果是 . 8、大于的负整数是 . 9、试比较下列各组数的大小； ①_______② ，1π-，310-

带根号的数未必是无理数

带根号的数未必是无理数鹿泉市获鹿镇第三中学崔怀平在新教材七年级数学下册第十章第三节讲到：“很多数的平方根和立方根都是无限不循环小数。”接着引出定义：“无限不循环小数又叫无理数。”例如： 2，3，是无理数，π=3.14159265......,也是无理数。时间一长，有的学生把无理数和带根号的数混淆起来，误认为带根号的数就是无理数。其实带根号的数不一定是无理数，无理数也不一定都是带根号的数得来的。无理数的定义是：“无限不循环小数叫无理数”。最本质特征是无限不循环。我们知道，开方开不尽的数，开方后可以得到无限不循环小数，既无理数。但是无限不循环小数不一定非得由开方得来，例如圆周率=3.14159265．．．．．．，它不是开放得来的，它是圆的周长除以直径得到的，它是一个比值。还有自然对数的底数e=2.718……也是无理数；它是通过求极限的方法得到的。还有我们也可以有意识地构造一些无理数，如：0.101001000…..，（构成的规律是1后面0的个数逐次增加一个），显然这个数是无限不循环的小数，也是一个无理数。就是说无理数并不都是开方开不尽而得来，还有其他方式可以形成无理数。另一方面，虽然很多带根号的数都是无理数，例如：2、45、33等，但不是带根号的数就一定是无理数。例如：35 2++35 2-，从感觉上看，这个数很像无理数，但是他确实是一个有理数。现在证明一下：设x= 35 2++35 2- 两边3次方得：3x= 3 3 35 2 5 2? ? ? ? ?- + + = 3 35 2? ? ? ? ?++3? ? ? ? ? ?+ ? 2 35 235 2-+3? + ?35 2 2 35 2? ? ? ? ?-+

实数,无理数常见形式

精锐教育学科教师辅导讲义学员编号：xxxxx 年级：xx 课时数：xx 学员姓名：xxxx 辅导科目：数学学科教师：xx 授课类型C(数的开方) C （实数及其运算）T （实数应用）授课日期及时段Xxxx年x月x日xxxx---xxxx 教学内容一、专题讲解平方根定义：一般地，如果一个数的平方等于a，那么这个数叫做a的平方根，或叫a的二次方根。特点：一个正数有正负两个平方根，它们互为相反数，0的平方根是0，负数没有平方根。表示方法：一个整数a的正的平方根表示为“a”或“2a”，其中a叫做被开方数;“2”中的2叫做根的指数（一般可省略不写）；“a”或“2a”读作“二次根号a”或“根号a”；正数a的负的平方根表示为“－a”或“－2a”；正数a的平方根为±a，读作“正负根号a”我们把a的正的平方根a称为a的算术平方根。开平方运算定义：求一个非负数a的平方根的运算叫做开平方，其中数a叫做被开方数；平方运算与开平方运算是互为逆运算的关系平方根（或算术平方根）的几个公式：式子±a有意义的条件为a≥0； a表示a的算术平方根，a是非负数，即a≥0； ()2a =a（a≥0），()2a-=a（a≥0）；2a=a=a，a≥0或；－a，a﹤0

例题：1、使式子2 52 x x --有意义的x 的取值范围是。 2. 使等式2()x x --=成立的x 的值（） A 、是正数 B 、是负数 C 、是0 D 、不能确定 3.81的平方根是（） A ．9 B ．9± C ．3 D ．3± 非负性： A ．非负数：若a ≥0，则称a 为非负数，初中阶段有三种非负数：a ，a ，2 a B ．若几个非负数的和为0 ，在这几个非负数均为0. 例题：1. 已知231(1)0,a b a b ++-=+=则。 2. 已知实数211,,a-b 20,24c a b c b c c c ab +++-+=满足则的算术平方根是。 3.△ABC 的三边长为a 、b 、c ，a 和b 满足21440a b b -+-+=，求c 的取值范围。立方根定义：如果一个数x 的立方等于a ，即3 x =a ，那么就称这个数x 为a 的立方根或三次方根。表示法：a 的立方根表示为3a ，其中a 为被开方数，“3”中的3为根指数（根指数3不能省略）；3a 读作“三次根号a ”或“a 的立方根”。性质：任意数都有立方根，任意一个数都有唯一的立方根。正数有一个正的立方根；负数有一个负的立方根；0的立方根仍为0. 有关立方根的补充说明和公式 1）在3a 中，被开方数a 可为正数，负数，0；且3a 的正负与a 一致 2）3a -=－3a ； 3）() 3 3 a =3 3a =a 4）开立方运算：求一个数a 的立方根的运算叫做开立方运算。（开立方运算与立方运算是互为逆运算

经典证明：几乎所有有理数都是无理数的无理数次方

一个无理数的无理数次方是否有可能是一个有理数？这是一个非常经典的老问题了。答案是肯定的，证明方法非常巧妙：考虑根号 2 的根号 2 次方。如果这个数是有理数，问题就已经解决了。如果这个数是无理数，那么就有：我们同样会得到一个无理数的无理数次方是有理数的例子。这是一个典型的非构造性证明的例子：我们证明了无理数的无理数次方有可能等于有理数，但却并没有给出一个确凿的例子。毕竟我们也不知道，真实情况究竟是上述推理中的哪一种。那么，真实情况究竟是上述推理中的哪一种呢？Gelfond-Schneider 定理告诉我们，假设α 和β 都是代数数，如果α 不等于0 和1 ，并且β 不是有理数，那么α 的β 次方一定是超越数。根据这一定理我们可以立即看出，根号 2 的根号 2 次方真的是一个无理数，实际情况应该是上述推理中的后者。那么，是否存在一个无理数a ，使得a 的a 次方是有理数呢？最近，Stan Dolan 证明了这样一个结论：事实上，几乎所有(1, ∞) 里的有理数都是某个无理数a 的 a 次方。注意到当x 大于1 时，函数f(x) = x x是连续单调递增的，因而对于所有(1, ∞) 里的有理数r ，一定存在唯一的a ，使得a a = r 。不妨假设a 是一个有理数，它的最简分数形式是n / m 。如果m = 1 ，那么我们会有平凡解n n = r 。下面我们证明，m 是不可能大于 1 的，否则会产生矛盾。假设有理数r 的最简分数形式是c / b ，于是我们有： (n / m)n / m = c / b 或者说： n n · b m = m n · c m 注意到，m n是n n · b m的约数。然而，m 和n 是互质的，m n与n n没有公共因子，因而m n一定是b m的约数。同理，b m是m n · c m的约数，但由于b

根号2是无理数的8种证明

1 2是无理数的8种证明南京师大附中江宁分校叶军 2是一个非常著名的无理数，第一个发现并坚持这个结果的希帕索斯因此付出了生命的代价——后世的数学史家所说的“第一次数学危机”盖源于此.“危机”过去后，唤醒的却是数学家们对数的重新认识，实数的概念开始确立，在此意义上讲，2的发现是人们对真理的追求、探索以致明朗的一个极好见证. 换一个角度来看这个数，我们可以把它看作一根“晾衣绳”，上面悬挂着许多有趣的方法，从中可以窥见数学的趣味.我们准备从不同的角度来证明2是一个无理数，以体会这一点. 证法1：尾数证明法.假设2是一个有理数，即2可以表示为一个分数的形式2=b a .其中(a,b )=1，且a 与b 都是正整数.则222b a =.由于完全平方数2b 的尾数只能是0、1、4、5、6、9中的一个，因此22b 的尾数只能是0、2、8中的一个.因为222b a =，所以2a 与22b 的尾数都是0，因此2b 的尾数只能是0或5，因此a 与b 有公因数5，与(a,b )=1矛盾！因此2是无理数. 这个证法可以证明被开方数的尾数是2、3、7、8的平方根都是无理数. 证法2：奇偶分析法.假设2=b a .其中(a,b )=1，且a 与b 都是正整数.则222b a =.可知a 是偶数，设a =2c ,则2224b c =，222c b =，可知b 也是偶数，因此a 、b 都是偶数，这与(a,b )=1矛盾！因此2是无理数. 希帕索斯就是用这种方法证明了2不是有理数，动摇了毕达哥拉斯学派的“万物皆数(任何数都可表示成整数之比)”的数学信仰，使毕达哥拉斯学派为之大为恐慌，希帕索斯因此葬身海底. 证法3：仿上，得到222b a =，易见b >1，否则b=1，则2=a 是一个整数,这是不行的.222b a =改写成a a b ?=22.因为b >1，因此b 有素因子p ，因此p 整除2a

无理数与实数(基础)

学习目标 1. 了解无理数和实数的意义； 2. 了解有理数的概念、运算法则在实数范围内仍适用 . 要点梳理要点一、有理数与无理数有限小数和无限循环小数都称为有理数.无限不循环小数叫无理数. 要点诠释：（1）无理数的特征：无理数的小数部分位数无限.无理数的小数部分不循环，不能表示成分数的形式. （2）常见的无理数有三种形式：①含类.②看似循环而实质不循环的数，如：1.313113111…….③带有根号的数，但根号下的数字开方开不尽，如. 要点二、实数有理数和无理数统称为实数.有理数和无理数组成了一个新的数集——实数集，实数集通常用字母R表示. 1.实数的分类按定义分：实数按与0的大小关系分：实数 2.实数与数轴上的点一一对应. 数轴上的任何一个点都对应一个实数，反之任何一个实数都能

类型一、实数概念出下列各数中的有理数和无理数：【思路点拨】对实数进行分类时，应先对某些数进行计算或化简，然后根据它的最后结果进行分类，不能仅看到根号表示的数就认为是无理数.π是无理数，化简后含π的代数式也是无理数. 【答案与解析】有理数有无理数有…… 【总结升华】有限小数和无限循环小数都称为有理数.无限不循环小数叫无理数. 常见的无理数有三种形式：①含类.②看似循环而实质不循环的数，如：0.1010010001…….③带有根号的数，但根号下的数字开方开不尽，如，，，. 【变式】下列说法错误的是（） ①无限小数一定是无理数；②无理数一定是无限小数； ③带根号的数一定是无理数；④不带根号的数一定是有理数. A．①②③ B. ②③④ C. ①③④ D. ①②④

(完整word版)证明根号2为无理数的方法

试证明2是无理数. 证明：易知2是方程022=-x 的一个根，设它有有理根,a b 即)0(2≠=a a b 先证明一个引理：若整系数方程： 0...02211=+++++--a ax x a x a x a n n n n )0(0≠?a a n 有有理根p q 0(≠pq 且q p ,互质)，则有： p a n ，q a 0. 证明：把p q x =代入原方程，得： 0...02211=++??? ? ??++???? ??+???? ??--a p q a p q a p q a p q a n n n n ，两边同乘n p ，得: .00...0122211== +++++----n n n n n n n n p p a aqp p q a p q a q a 那么，由于0≠p ，所以一定有0p ，那么一定有： ....0122211n n n n n n n p a aqp p q a p q a q a p +++++---- 由于n p p p ,...,,2都满足被p 整除，那么有：n n q a p ，又因1),(=q p ，所以有： .n a p 同理，由于0≠q ，所以一定有0q ，那么一定有： ....0122211n n n n n n n p a aqp p q a p q a q a q +++++---- 由于n q q q ,...,,2都满足被q 整除，那么有：n p a q 0，又因1),(=q p ，所以有： q a 0. 回到原命题，由于0)2(1≠-?，1)2,1(=-，所以方程022=-x 的有理根 a b 满足： 1a ，2-b .22,1±=?±=±=?a b b a 经检验，2±都不是方程022=-x 的根，那么022=-x 无有理根，即2为无理数. ...D E Q

证明根号2是无理数的八种方法

怎样证明是一个无理数 2 2 是一个非常著名的无理数，第一个发现并坚持这个结果的希帕索斯因此付出了生命的代价——后世的数学史家所说的“第一次数学危机”盖源于此.风暴过去后，唤醒的却是数学家们对数的重新认识，实数的概念开始确立，在此意义上讲， 2 的发现是人们对真理的追求、探索以致明朗的一个极好例证. 换一个角度来看这个数，我们可以把它看作一根 “晾衣绳”，上面挂着许多有趣的方法，值得你仔细玩味.我们准备从不同的角度来证明 2 是一个无理数，从而体会这一点. a 证法 1：尾数证明法.假设 2 是一个有理数，即 2 可以表示为一个分数的形式 2 = . b 其中(a ,b )=1，且 a 与 b 都是正整数.则 2 .由于完全平方数的尾数只能是 0、1、4、5、 a 2 b 2 b 2 6、9 中的一个，因此 2 的尾数只能是 0、2、8 中的一个.因为 2 ，所以与2 的尾 b 2 a 2 b 2 a 2 b 2 数都是 0，因此的尾数只能是 0 或 5，因此 a 与 b 有公因数 5，与(a ,b)=1 矛盾！因此 2 是 b 2 无理数. 这个证法可以证明被开方数的尾数是 2、3、7、8 的平方根都是无理数. a 证法 2：奇偶分析法.假设 2 = .其中(a , b )=1，且 a 与 b 都是正整数.则 2 .可知 a a 2 b 2 b 是偶数，设 a=2 c ,则 4 2 ， 2 ，可知 b 也是偶数，因此 a 、b 都是偶数，这与(a,b )=1 c 2 b 2 b 2 c 2 矛盾！因此 2 是无理数. 希帕索斯就是用这种方法证明了 2 不是有理数，动摇了毕达哥拉斯学派的“万物皆数(任何数都可表示成整数之比)”的数学信仰，使毕达哥拉斯学派为之大为恐慌，希帕索斯因此葬身海底. 证法 3：仿上，得到 2 ，易见 b>1，否则 b=1，则 2 =a 是一个整数,这是不行的. a 2 b 2 a a 改写成 2 .因为 b>1，因此 b 有素因子 p ，因此 p 整除或 a ，总之，p 整除 a ， a 2 2b 2 b a 2 2 因此 p 同时整除 a 与 b ，这与(a ,b )=1 矛盾. 证法 4：仿上，得到 2 ，等式变形为b a b (a b )(a b) ，因为 b>1，因此 a 2 b 2 2 2 2 ，存在素因子 p p 整除 a+b 或 a-b 之一，则同时整除 a+b 与 a-b ，因此 p 整除 a ，因此 p 是 a 、 b 的公因数，与(a ,b )=1 矛盾. 证法 5：利用代数基本定理，如果不考虑素因子的顺序，任何一个正整数都可以唯一地写成素数幂的积的形式，因此 a p p p ，b q q q ，其中 , , 与 , , p p q q r r r m s s s 1 2 1 2 n 1 2 m 1 2 n 1 1 m n

北师大版八年级上册无理数复习

【无理数】 √2=1.414 √3=1.732 √5=2.236 √7=2.645 （熟记） 1. 定义：无限不循环小数的小数叫做无理数；注：它必须满足“无限”以及“不循环” 这两个条件。 2. 常见无理数的几种类型：（1）特殊意义的数，如：圆周率π以及含有π的一些数，如：2-π，3π等；（2）特殊结构的数（看似循环而实则不循环）：如：2.010 010 001 000 01…（两个1 之间依次多1个0）等。（3）无理数与有理数的和/差结果都是无理数。如：2-π是无理数（4）无理数乘/除以一个不为0的有理数结果是无理数。如2π, （5）开方开不尽的数，如:39,5,2等；应当要注意的是：带根号的数不一定是无理数，如：9等；无理数也不一定带根号，如：π） 3.有理数与无理数的区别：（1）有理数指的是有限小数和无限循环小数，而无理数则是无限不循环小数；（2）所有的有理数都能写成分数的形式（整数可以看成是分母为1的分数），而无理数则不能写成分数形式。例：（1）下列各数：①3.141、②0.33333……、③75-、④π、⑤252.±、⑥3 2-、⑦0.3030003000003……（相邻两个3之间0的个数逐次增加2）、其中是有理数的有＿＿＿＿；是无理数的有＿＿＿。（填序号）（2）有五个数:0.125125…,0.1010010001…,-π,4,32其中无理数有 ( )个拓展中考在线： 1.下列各数中：－1,23,3.14,－π,3,0,2,27, 2 5,－0.2020020002……(相邻两个2之间0的个数逐次加1).其中，是有理数的是_____________，是无理数的是_______________.在上面的有理数中，分数有____________，整数有______________. 2.x 2=8，则x______分数，______整数，______有理数．（填“是”或“不是”） 3.面积为3的正方形的边长______有理数；面积为4的正方形的边长______有理数．（填“是”或“不是”） 4.一个高为2米，宽为1米的大门，对角线大约是______米（精确到0.01）. 5.下列数中是无理数的是（）. A.0.12??32 B.2π C ．0 D ．7 22

人教版七年级下知识点试题精选-关于无理数

七年级下册关于无理数一．选择题（共20小题） 1．下列四个数中，无理数是（） A．3.14 B．0.33030030003… C．0.3333… D． 2．下列各式化简结果为无理数的是（） A．B．（﹣1）0C．D． 3．下列说法正确的个数是（） ①无理数是实数； ②无理数是带根号的数； ③无理数是无限不循环的小数； ④无理数有有限个小数． A．1个 B．2个 C．3个 D．4个 4．以下七个数中：①﹣；②0.305；③；④﹣0.102030405…；⑤；⑥； ⑦．其中是无理数的是（） A．①③⑦B．①④⑥C．②⑤⑥D．④⑤⑥ 5．在下列各数中是无理数的有（） ﹣0.333…，，，，﹣π，2.010010001，4.0123456…（小数部分由相继的正整数组成）． A．2个 B．3个 C．4个 D．5个 6．在实数，0，，﹣3.14，π+3，2.313113111…中无理数有（）A．1个 B．2个 C．3个 D．4个 7．下列实数中无理数是（） A．0 B．πC．D．﹣ 8．实数，0，﹣，0.1010010001…（相邻两个1之间依次多一个0），其中无理数有（）

A．1个 B．2个 C．3个 D．4个 9．下列各数：中无理数的个数有（）A．1个 B．2个 C．3个 D．4个 10．下列实数是无理数的是（） A．﹣1 B．0 C．πD． 11．在实数﹣，0.，，π，中，无理数的个数是（） A．1 B．2 C．3 D．4 12．在下列各数中是无理数的有（） ﹣0.333…，，，3π，3.141 5，2.010 101…（相邻两个1之间有1个0）．A．2个 B．3个 C．4个 D．5个 13．下列实数：，π，，3.14159，0，，，2.020020002…（相邻两个2之间0的个数逐次加1），其中是无理数的有（） A．1个 B．2个 C．3个 D．4个 14．在，，，，，0.202 002 000 2…中，无理数的个数有（）A．6个 B．5个 C．4个 D．3个 15．在实数4.，π，，|﹣3|，，﹣中，无理数有（） A．1个 B．2个 C．3个 D．4个 16．下列数中，0.4583，3.，3.14，，，，0.373373337…是无理数的有（） A．2个 B．3个 C．4个 D．5个 17．对与实数，﹣π，，3.1415，0.333…，2.010101…（相邻两个1之间0的个数逐个加1），其中无理数的个数是（） A．3个 B．4个 C．5个 D．6个 18．在﹣，，0，，﹣0.3，，3.1415，2.010101…（相邻两个1之间有1个0）中，无理数有（） A．1个 B．2个 C．3个 D．4个

无理数与实数(基础)知识讲解

无理数与实数（基础）责编：杜少波【学习目标】 1. 了解无理数和实数的意义； 2. 了解有理数的概念、运算法则在实数范围内仍适用 . 【要点梳理】要点一、有理数与无理数有限小数和无限循环小数都称为有理数.无限不循环小数叫无理数. 要点诠释：（1）无理数的特征：无理数的小数部分位数无限.无理数的小数部分不循环，不能表示成分数的形式. （2）常见的无理数有三种形式：①含π类.②看似循环而实质不循环的数，如：1.313113111…….③带有根号的数，但根号下的数字开方开不尽，要点二、实数有理数和无理数统称为实数.有理数和无理数组成了一个新的数集——实数集，实数集通常用字母R 表示. 1.实数的分类按定义分：实数????????????????????????? 正有理数有理数零有限小数或无限循环小数负有理数正无理数无理数无限不循环小数负无理数按与0的大小关系分：实数0??????????????? 正有理数正数正无理数负有理数负数负无理数 2.实数与数轴上的点一一对应. 数轴上的任何一个点都对应一个实数，反之任何一个实数都能在数轴上找到一个点与之对应. 要点三、实数大小的比较对于数轴上的任意两个点，右边的点所表示的实数总是比左边的点表示的实数大. 正实数大于0，负实数小于0，两个负数，绝对值大的反而小. 要点四、实数的运算有理数中关于相反数和绝对值的意义同样适合于实数. 当数从有理数扩充到实数以后，实数之间不仅可以进行加、减、乘、除（除数不为0）、乘方运算，而且正数及0可以进行开平方运算，任意一个实数可以进行开立方运算.在进行

实数的运算时，有理数的运算法则及运算性质等同样适用. 【典型例题】类型一、实数概念 1、指出下列各数中的有理数和无理数： 332222,,,9,8,9,0,,12,55,0.1010010001 (73) π--- 【思路点拨】对实数进行分类时，应先对某些数进行计算或化简，然后根据它的最后结果进行分类，不能仅看到根号表示的数就认为是无理数.π是无理数，化简后含π的代数式也是无理数. 【答案与解析】有理数有3222,9,8,0,,73-- 无理数有32,,9,12,55,0.1010010001π-…… 【总结升华】有限小数和无限循环小数都称为有理数.无限不循环小数叫无理数. 常见的无理数有三种形式：①含π类.②看似循环而实质不循环的数，如：0.1010010001……. ③带有根号的数，但根号下的数字开方开不尽，如55，39，2，12-. 举一反三：【高清课堂： 389318 实数复习，巩固练习3】【变式】下列说法错误的是（） ①无限小数一定是无理数； ②无理数一定是无限小数； ③带根号的数一定是无理数；④不带根号的数一定是有理数. A ．①②③ B. ②③④ C. ①③④ D. ①②④ 【答案】C ；类型二、实数大小的比较 2、（2014秋?新华区校级期中）比较和1的大小．【答案与解析】解：∵＜＜，即2＜＜3， ∴1＜﹣1＜2， ∴＜1．【总结升华】此题主要考查了实数比较大小，得出 ﹣1的取值范围是解题关键．举一反三：【变式】比较大小 ___ 3.14π--754__23 33232 90－ 3___10- |43___(7)--- 【答案】＜；＞；＜；＜；＜；＞；＜.

平方根和无理数

经典例题类型一．有关概念的识别 1．下面几个数：0.23 ，1.010010001…，，3π，，，其中，无理数的个数有（） A 、1 B 、2 C 、3 D 、4 2. 下列说法中 ①无限小数都是无理数 ②无理数都是无限小数 ③-2是4的平方根 ④带根号的数都是无理数。其中正确的说法有（） A ．3个 B. 2个 C. 1个 D. 0个 3．在（两个“1”之间依次多1个“0”）中，无理数的个数有（） A ．3个 B. 4个 C. 5个 D. 6个 4．一个正数x 的两个平方根分别是a+2和a-4，则a=_____，x=_____。 5. 把下列各数填入相应的集合内:－7, 0.32, 31,46, 0, 8,2 1,3216,－2π. ①有理数集合: { …};②无理数集合: { …}; 6下列说法正确的是（） A ．有理数只是有限小数 B ．无理数是无限小数 C ．无限小数是无理数 D ．是分数 7 下列说法中 ①无限小数都是无理数 ②无理数都是无限小数 ③-2是4的平方根 ④带根号的数都是无理数。其中正确的说法有（） A ．3个 B. 2个 C. 1个 D. 0个 8、在实数3.14，25 ，3.33330.412?? ，0.10110111011110…，π，中，有（）个无理数？ A ．2个 B ．3个 C ．4个 D ．5个 9、下列说法中，正确的是（） A ．带根号的数是无理数 B ．无理数都是开不尽方的数 C ．无限小数都是无理数 D ．无限不循环小数是无理数 10．下列命题中，正确的个数是（）

①两个有理数的和是有理数； ②两个无理数的和是无理数； ③两个无理数的积是无理数； ④无理数乘以有理数是无理数； ⑤无理数除以有理数是无理数； ⑥有理数除以无理数是无理数。 A ．0个 B ．2个 C ．4个 D ．6个 11．判断（正确的打“√”，错误的打“×”） ①带根号的数是无理数；（）（） ③绝对值最小的实数是0；（） ④平方等于3（） ⑦无理数与有理数的和为无理数；（） ⑧无理数中没有最小的数，也没有最大的数。（） 12下面几个数：0.23 ，1.010010001…，，3π，，，其中，无理数的个数有（） A 、1 B 、2 C 、3 D 、4 13．求下列各数的平方根。 ⑴ 169 ⑵ 0.0256 ⑶ 24125 ⑷ ()22- 14．下列各式中无意义的是（） A ．7- B ．7 C.7- D ．()27-- 15.41的平方根是（） A ．161 B ．81 C ．21 D ．2 1± 16. 如果某数的一个平方根是-6，那么这个数为________． 17.如果正数m 的平方根为1x +和3x -，则m 的值是．三求下列各式中的（1）（2）

无理数练习题1

【实数知识要点】 1．无理数：定义：无限不循环小数叫做无理数。如π=3.1415926 …， 1.414213= ，－1.010010001…，都是无理数。注意：①既是无限小数，又是不循环小数，这两点必须同时满足； ②无限不循环小数与有限小数、无限循环小数的本质区别是：前者不能化成分数，而后两者都可以化成分数； ③凡是整数的开不尽的方根都是无理数，如 2．实数：有理数和无理数统称为实数。 ????????? ?????? ? ????????? 正有理数有理数零有限小数或无限循环小数负有理数实数正无理数无理数无限不循环小数负无理数 3．实数的几个有关概念： ①相反数：a 与－a 互为相反数，0的相反数是0。a+b=0?a 、b 互为相反数。 ②倒数：若0a ≠，则 1 a 称为a 的倒数，0没有倒数。1ab a =?、b 互为倒数。 ③绝对值：一个正实数的绝对值是它本身，一个负实数的绝对值是它的相反数，0的绝对值是0。即()()() 0000a a a a a a >?? ==?? -

3．下列命题中，正确的个数是（） ①两个有理数的和是有理数；②两个无理数的和是无理数；③两个无理数的积是无理数； ④无理数乘以有理数是无理数；⑤无理数除以有理数是无理数；⑥有理数除以无理数是无理数。 A．0个 B．2个 C．4个 D．6个 4．判断（正确的打“√”，错误的打“×”） ①带根号的数是无理数；（）（） ③绝对值最小的实数是0；（）④平方等于3（） ⑤有理数、无理数统称为实数；（）⑥1的平方根与1的立方根相等；（） ⑦无理数与有理数的和为无理数；（）⑧无理数中没有最小的数，也没有最大的数。（） 5．a） A．有理数 B．正无理数 C．正实数 D．正有理数 6．下列四个命题中，正确的是（） A．倒数等于本身的数只有1 B．绝对值等于本身的数只有0 C．相反数等于本身的数只有0 D．算术平方根等于本身的数只有1 7．下列说法不正确的是（） A．有限小数和无限循环小数都能化成分数 B．整数可以看成是分母为1的分数 C．有理数都可以化为分数 D．无理数是开方开不尽的数 8．代数式21 a+，y，()21 a-中一定是正数的有（） A．1个 B．2个 C．3个 D．4个 9．） A．m是完全平方数 B．m是负有理数 C．m是一个完全平方数的相反数 D．m是一个负整数 10．已知a为有理数，b为无理数，则a+b为（） A．整数 B．分数 C．有理数 D．无理数 11． 2 1 5 的大小关系是（） A． 2 1 5 << B． 2 1 5 << 2 1 5 < 2 1 5 < 12、。