移动加权平均法例题
移动加权平均法例题
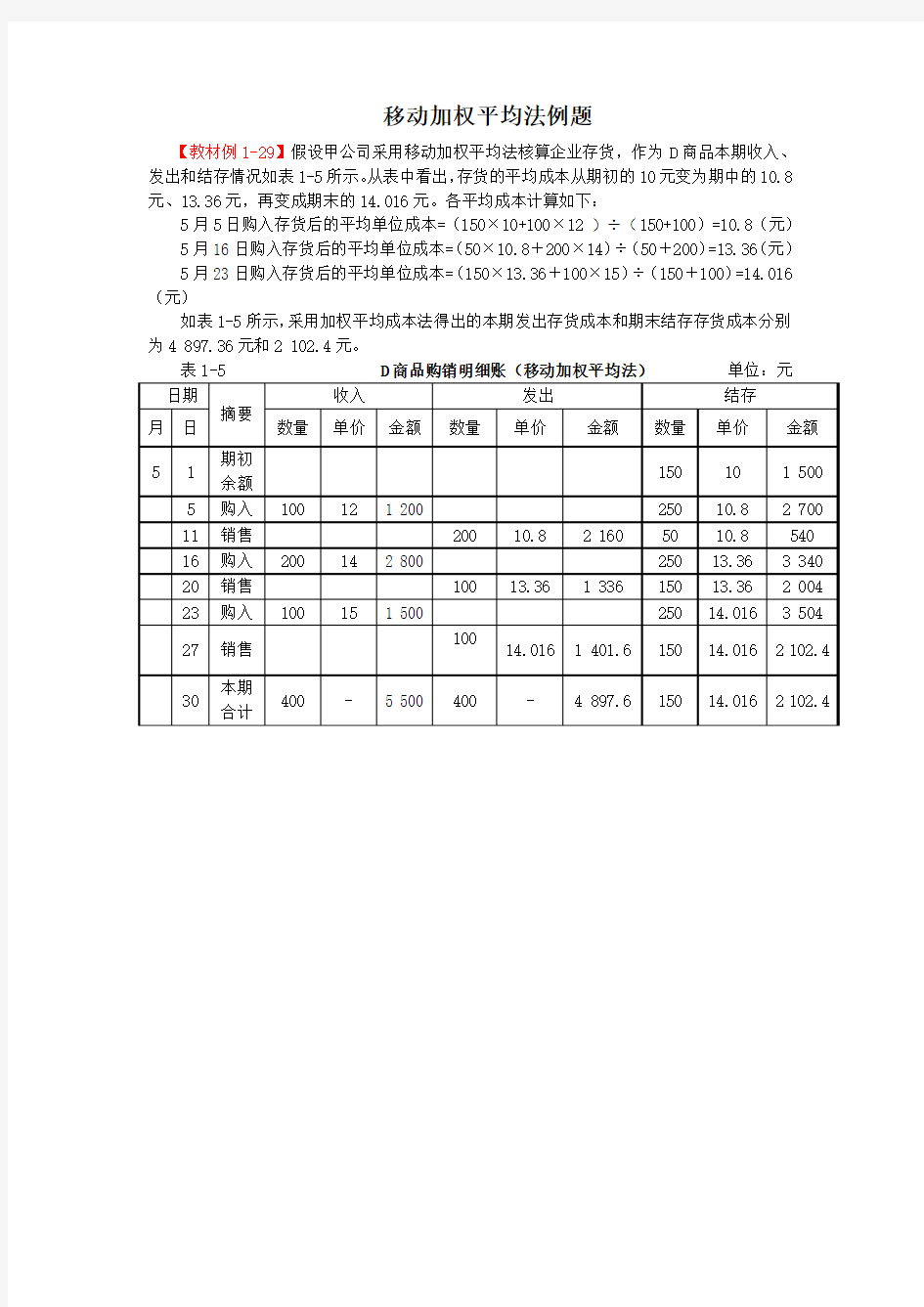
【教材例1-29】假设甲公司采用移动加权平均法核算企业存货,作为D商品本期收入、发出和结存情况如表1-5所示。从表中看出,存货的平均成本从期初的10元变为期中的10.8元、13.36元,再变成期末的14.016元。各平均成本计算如下:
5月5日购入存货后的平均单位成本=(150×10+100×12 )÷(150+100)=10.8(元)5月16日购入存货后的平均单位成本=(50×10.8+200×14)÷(50+200)=13.36(元)5月23日购入存货后的平均单位成本=(150×13.36+100×15)÷(150+100)=14.016(元)
如表1-5所示,采用加权平均成本法得出的本期发出存货成本和期末结存存货成本分别为4 897.36元和2 102.4元。
第章时间序列预测习题答案
第10章时间序列预测
从时间序列图可以看出,国家财政用于农业的支出额大体上呈指数上升趋势。(2)年平均增长率为: 。 (3)。 下表是1981年—2000年我国油彩油菜籽单位面积产量数据(单位:kg / hm2)年份单位面积产量年份单位面积产量 1981 1451 1991 1215 1982 1372 1992 1281 1983 1168 1993 1309 1984 1232 1994 1296 1985 1245 1995 1416 1986 1200 1996 1367 1987 1260 1997 1479 1988 1020 1998 1272 1989 1095 1999 1469
1990 1260 2000 1519 (1)绘制时间序列图描述其形态。 (2)用5期移动平均法预测2001年的单位面积产量。 (3)采用指数平滑法,分别用平滑系数a=和a=预测2001年的单位面积产量,分析预测误差,说明用哪一个平滑系数预测更合适? 详细答案: (1)时间序列图如下: (2)2001年的预测值为: | (3)由Excel输出的指数平滑预测值如下表: 年份单位面积产量 指数平滑预测 a=误差平方 指数平滑预测 a= 误差平方 19811451 19821372
19831168 19841232 19851245 19861200 19871260 19881020 19891095 19901260 19911215 19921281 19931309 19941296 19951416 19961367 19971479 19981272 19991469 20001519 合计———2001年a=时的预测值为: a=时的预测值为:
移动平均法简单应用
移动平均法 移动平均法是一种简单平滑预测技术,它的基本思想是:根据时间序列资料、逐项推移,依次计算包含一定项数的序时平均值,以反映长期趋势的方法。因此,当时间序列的数值由于受周期变动和随机波动的影响,起伏较大,不易显示出事件的发展趋势时,使用移动平均法可以消除这些因素的影响,显示出事件的发展方向与趋势(即趋势线),然后依趋势线分析预测序列的长期趋势。 1. 移动平均法的基本理论①简单移动平均法 设有一时间序列,则按数据点的顺序逐点推移求出N个数的平均数,即可得到一次移动平均数: 式中为第t周期的一次移动平均数;为第t周期的观测值;N为移动平均的项数,即求每一移动平均数使用的观察值的个数。 这个公式表明当t向前移动一个时期,就增加一个新近数据,去掉一个远期数据,得到一个新的平均数。由于它不断地“吐故纳新”,逐期向前移动,所以称为移动平均法。 由于移动平均可以平滑数据,消除周期变动和不规则变动的影响,使得长期趋势显示出来,因而可以用于预测。其预测公式为: 即以第t周期的一次移动平均数作为第t+1周期的预测值。 ②趋势移动平均法当时间序列没有明显的趋势变动时,使用一次移动平均就能够准确地反映实际情况,直接用第t周期的一次移动平均数就可预测第t+1周期之值。但当时间序列出现线性变动趋势时,用一次移动平均数来预测就会出现滞后偏差。因此,需要进行修正,修正的方法是在一次移动平均的基础上再做二次移动平均,利用移动平均滞后偏差的规律找出曲线的发展方向和发展趋势,然后才建立直线趋势的预测模型。故称为趋势移动平均法。 设一次移动平均数为,则二次移动平均数的计算公式为: 再设时间序列从某时期开始具有直线趋势,且认为未来时期亦按此直线趋势变化,则可设此直线趋势预测模型为: 式中t为当前时期数;T为由当前0时期数t到预测期的时期数,即t以后模型外推 的时间;为第t+T期的预测值;为截距;为斜率。,又称为平滑系数。
3移动平均法
第二节移动平均法 移动平均法是根据时间序列资料,逐项推移,依次计算包含二定项数的序时平均数,以反映长期趋势的方法。当时间序列的数值由于受周期变动和不规则变动的影响,起伏较大,不易显示出发展趋势时,可用移动平均法,消除这些因素的影响,分析,预测序列的长期趋势。 移动平均法有简单移动平均法,加权移动平均法,趋势移动平均法,分别介绍如下: 一简单移动平均法 设时间序列为Y1,Y2,……YT……;简单移动平均法公式为: 式中:Mt为t期移动平均数;N为移动平均数的项数. 这公式表明:当T向前移动一个时期,就增加一个新近数据,去掉一个远期数据,得到一个新的平均数. ∴t-1+ M t=M t-1 这是它的递堆公式。当N较大时,利用递堆公式可以大大减少计算量。 由于移动平均可以平滑数据,消除周期变动和不规则变动的影响使长期趋势显示出来,因而可以用于预测: 预测公式为:y t+1=M t 即以第t期移动平均数作为第t+1期的预测值。 例1:某市汽车配件销售公司,某年1月至12月的化油器销量如表4-1所示。试用简单移动平均法,预测下年1月的销售量。 解:分别取N=3和N=5按列预公式 y t = y t+1= 计算3个月和5个月移动平均预测值,其结果如表: y t-y t-N y t-y t-N ^ ^ y t+y t-1+y t-2 3 y t+y t-1+y t-2+y t-3+y t-4 ^ 5
1002003004005006001 2 3 4 5 6 7 8 9101112 实际销售量3个月移动平均预测值 5个月移动平均预测值 由图可以看出,实际销售量的随机波动比较大,经过移动平均法计算以后,随即波动显著减小,即消除随机干扰。而且求取平均值所用的月数越多,即N 越大,修匀的程度也越大,波动也越小。但是,在这种情况下,对实际销售量真实的变化趋势反应也越迟钝。 反之,如果N 取的越小,对销售量真实变化趋势反应越灵敏,但修匀性越差,从而把随机干扰作为趋势反映出来。 因此,N 的选择甚为重要,N 应取多大,应根据具体情况作出抉择,当N 等于周期变动的周期时,则可消除周期变动影响。 在实用上,一个有效的方法是:取几个N 值进行试算,比较它们的平均预测误差,从中选择最优的。 如:在本例中,要确定化油器销售量预测,究竟是取3合适还是取5合适,可通过计算这两个预测公式的均方误差MSE ,选择MSE 较小的那个N 。
移动加权平均法.doc
移动加权平均法:移动加权平均法下库存商品的成本价格根据每次收入类单据自动加权平均;其计算方法是以各次收入数量和金额与各次收入前的数量和金额为基础,计算出移动加权平均单价。 其计算公式如下: 移动加权平均单价= (本次收入前结存商品金额+本次收入商品金额)/(本次收入前结存商品数量+本次收入商品数量 ) 移动加权平均法计算出来的商品成本比较均衡和准确,但计算起来的工作量大,一般适用于经营品种不多、或者前后购进商品的单价相差幅度较大的商品流通类企业。 以下以一个简单的例子来说明: 例1:货品A,期初结存数量10,加权价10,金额为100,发生业务如下: 销售11;采购10,采购价格11; 成本计算过程如下: 销售时,成本金额为11*10=110;销售后结存数量:-1;加权价:10;结存金额:-10;
采购后,结存单价位:(-10+10*11)/(-1+10)=11.111111 一、月末一次加权平均法 加权平均法也叫全月一次加权平均法,指以本月收入全部存货数量加月初存货数量作为权数,去除本月收入全部存货成本加月初存货成本的和,计算出存货的加权平均单位成本,从而确定存货的发出成本和库存成本的方法。计算公式如下: 加权平均单价=(本月收入全部存货成本+月初存货成本)/ (本月收入全部存货数量加+月初存货数量) 本月发出存货成本=本月发出存货数量×加权平均单价 月末结存存货成本=月末库存存货数量×加权平均单价 二、移动加权平均法。 移动平均法亦称移动加权平均法,指本次收货的成本加原有库存的成本,除以本次收货数量加原有存货数量,据以计算加权平均单价,并对发出存货进行计价的一种方法。移动平均法与加权平均法的计算原理基
加权平均法(月末一次加权平均)和移动平均法
(月末一次)加权平均的计算方法 本月有300件产品,单价为2万元/件,6号出售100件,12号购入300件,单价为2.2万元/件,15号出售200件,请问使用加权平均法的月末成本为多少? 加权平均单价:(300*2)+(300*2.2)/(300+300)=2.1(万元) 发出产品的成本:(100+200)*2.1=630(万元) 期末结存成本:(300*2)+(300*2.2)-630=630(万元) 区别: (月末一次)加权平均法是指在期末计算存货的平均单位成本时,用期初存货数量和本期各批收入的数量作为权数来确定存货的平均单位成本,从而计算出期末存货和已销存货成本的一种计价方法。这种方法只需在期末计算一次加权平均单价,比较简单。 移动加权平均法是指在每次收到存货以后,以各批收入数量与各批收入前得结存数量为权数,为存货计算出新的加权平均单位成本的一种方法。每次进货后,都要重新计算一次加权平均单位成本。 本批销售或耗用存货成本=本批销售或耗用存货数量*本批存货移动加权平均单位成本; 加权平均法与移动平均法有什么区别? 两种方法都是实际成本法。 ●(月末一次)加权平均法是指某段时间内的加权。适用于价格变化不大或要求不是特别 精确的成本核算。核算起来比较简单,省时省力。 ●移动加权是指按照上一日结存来加权的。适用于价格变化大或要求精确核算的成本核算。 核算比较费时。 公式: 移动加权平均单位成本=(结存存货成本+本批进货成本)/(结存存货数量+本批进货数量) a.移动加权平均单价=(上次结存数量×上次结存单价+本次入库数量×本次入库单价)÷(上次结存数量+本次入库数量) b.本期(月末一次)加权平均单价=(上期结存数量×上期结存单价+∑本期入库数量×本期入库单价)÷(上期结存数量+∑本期入库数量)
移动平均法案例
移动平均法。该方法是根据时间数列的各期数值作出非直线长期趋势线的一种比 较简单的方法,连续地求其平均值,再计算相邻两期平均值的变动趋势,然后计算平均发展趋势,进行预测。例 某公司1997年1~12月销售额的统计资料如表7-1所示,用移动平均法预测1998年1月的销售额。 第一步,计算相邻五个月的销售额平均数(按多少期计算平均数,要根据具体情况而定,期数少,则反映波动比较灵敏,但预测误差大;期数多,则反映波动平滑,预测较为精确)。如1~5月销售额的平均值为: 8.355 41 343734331=++++= X 依次类推:求出,,...,,,8432X X X X 并填入表中。 第二步,计算相邻两个平均值的差,该差称为平均值的变动趋势,如1X 与2X 之差为: 38—35.8=2.2依此类推,计算变动趋势值,填入表中。 第三步,计算相邻四期变化趋势之平均值,称为四期平均发展趋势,如前四期变动趋势的平均值为:(2.2+3.2+1.8+2.6)÷4=2.45依此类推,将数字填人表中。 第四步,预测1998年1月的销售额,最后5个月的平均月销售额为49万元,加上最后一期平均发展趋势1.5万元,所以1998年1月的预测值为: 49+3ⅹ1.5=53.5(万元) (其中3ⅹ1.5,是因为预测期距平均月销售额为3个月,所以需要乘以3)。 季节性波动分析。当产品的市场需求呈明显的季节性波动时,用平均法进行销售 预测就不能正确地反映销售量的波动。要用计算季节指数的办法来预测季节性波动。 例 某地区涤棉府绸三年内各个季节的市场销售量如表6.2所示。 从表6.2中很明显地可以看出,涤棉府绸的销售量淡季与旺季相差近一倍左右。如果简单地用移动平均来预测某一个季节的市场需要,就不符合实际情况,这就可以用季节指数进行预测。其计算方法如下:
加权平均 和 移动平均法
加权平均 统计学名词. “统计初步”这部分内容中,平均数是一个非常重要而又有广泛用途的概念,在日常生活中,我们经常会听到这样一些名词:平均气温、平均降雨量、平均产量、人均年收入等;而平均分数、平均年龄、平均身高等名词更为同学们所熟悉.一般来说,平均数反映了一组数据的一般水平,利用平均数,可以从横向和纵向两个方面对事物进行分析比较,从而得出结论.例如,要想比较同一年级的两个班同学学习成绩,如果用每个班的总成绩进行比较,会由于班级人数不同,而使比较失去真正意义.但是如果用平均分数去比较,就可以把各班的平均水平呈现出来.从纵向的角度来看,可以对同一个事物在不同的时间内的情况利用平均数反映出来,例如,通过两个不同时间人均年收入来比较人们生活水平、经济发展等状况. 但是,当一组数据中的某些数重复出现几次时,那么它们的平均数的表示形式发生了一定的变化.例如,某人射击十次,其中二次射中10环,三次射中8环,四次射中7环,一次射中9环,那么他平均射中的环数为: (10 *2+8*3+7*4+9*1)/10 = 8.1 这里,7,8,9,10这四个数是射击者射中的几个不同环数,但它们出现的频数不同,分别为4,3,l,2,数据的频数越大,表明它对整组数据的平均数影响越大,实际上,频数起着权衡数据的作用,称之为权数或权重,上面的平均数称为加权平均数,不难看出,各个数据的权重之和恰为10. 在加权平均数中,除了一组数据中某一个数的频数称为权重外,权重还有更广泛的含义. 在评估某个同学一学期的学生成绩时,一般不只看他期末的一次成绩,而是将平时测验、期中考试等成绩综合起来考虑,比如说,一同学两次单元测验的成绩分别为88,90,期中的考试成绩为92,而期末的考试成绩为85,如果简单地计算这四个成绩的平均数,即将平时测验与期中、期末考试成绩同等看待,就忽视了期末考试的重要性.鉴于这种考虑,我们往往将这四个成绩分配以不同的权重。 由于10%+10%+30%+50%=1,即各个权重之和为1,所以求加权平均数的式子中分母为1.下面的例子是未知权重的情况: 股票A,1000股,价格10; 股票B,2000股,价格15; 算数平均 = (10 + 15) / 2 = 12.5; 加权平均 = (10 x 1000 + 15 x 2000) / (1000 + 2000) = 13.33 其实,在每一个数的权数相同的情况下,加权平均值就等于算数平均值。 此外在一些体育比赛项目中,也要用到权重的思想.比如在跳水比赛中,每个运动员除完成规定动作外,还要完成一定数量的自选动作,而自选动作的难度是不同的,两位选手由于所选动作的难度系数不
第六章_时间数列练习题及解答
《时间序列》练习题及解答 一、单项选择题 从下列各题所给的4个备选答案中选出1个正确答案,并将其编号(A、B、C、D)填入题干后面的括号内。 1、构成时间数列的两个基本要素是()。 A、主词和宾词 B、变量和次数 C、时间和指标数值 D、时间和次数 2、最基本的时间数列是()。 A、时点数列 B、绝对数数列 C、相对数数列 D、平均数数列 3、时间数列中,各项指标数值可以相加的是()。 A、相对数数列 B、时期数列 C、平均数数列 D、时点数列 4、时间数列中的发展水平()。 A、只能是总量指标 B、只能是相对指标 C、只能是平均指标 D、上述三种指标均可以 5、对时间数列进行动态分析的基础指标是()。 A、发展水平 B、平均发展水平 C、发展速度 D、平均发展速度 6、由间断时点数列计算序时平均数,其假定条件是研究现象在相邻两个时点之间的变动为()。 A、连续的 B、间断的 C、稳定的 D、均匀的 7、序时平均数与一般平均数的共同点是()。 A、两者均是反映同一总体的一般水平 B、都是反映现象的一般水平 C、两者均可消除现象波动的影响 D、共同反映同质总体在不同时间上的一般水平 8、时间序列最基本的速度指标是()。 A、发展速度 B、平均发展速度 C、增长速度 D、平均增长速度 9、根据采用的对比基期不同,发展速度有()。 A、环比发展速度与定基发展速度 B、环比发展速度与累积发展速度 C、逐期发展速度与累积发展速度 D、累积发展速度与定基发展速度 10、如果时间序列逐期增长量大体相等,则宜配合()。 A、直线模型 B、抛物线模型 C、曲线模型 D、指数曲线模型 A、100%124%104% 108.6% 3 ++ = B、 506278 108.6% 506278 100%124%104% ++ = ++
市场调查与预测习题答案
市场调研预测及决策练习题答案 一、移动平均类 1.已知某厂山地自行车各年销量Y(万辆),算出一次指数平滑值如表。请计算二次指数平滑值,并用公式T b a Y t t T t +=+预测2004、2005年的销量。 (α=0.3)。 ))](1/([,2)2()1()2()1(t t t t t t S S b S S a --=-=αα 答案:
2.某商场某品牌家电产品1998-2007年销售额资料如下表所示,当平滑系数α1=0.2,α2=0.8时,试用一次指数平滑法预测该商场该商品2008年销售额为多少万元? 答案:
3、某商店近10周的食盐销售量如下表:试分别用3周和5周为移动期使用移动平均法预测第11周的食盐销售量。 答案:
4、下表为某公司2006年出口商品月销售额, (1)列出二次移动平均法计算表。(N=3,移动平均值取1位小数) (3)预测该企业2007年1月、2月、3月销售额。 答案:
5、某电视机厂销量平稳,连续多年运用一次指数平滑法对该厂电视机销量进行了预测,对2005年的销量预测值为130万台,而当年实际销售量为150万台,请据此预测2006年该厂电视机的销售量(平滑常数α为0.3)。 答案: 6、企业近年产品销售额如下表,请用一次移动平均法确定2002年销售额预测值。(要 求n=3和n=5,并计算它们的平均绝对误差,以确定最后的预测值) 某企业近年产品销售额单位:万元 答案:
7.某洗衣机厂近年洗衣机销售量如下表,当n=4时,用二次移动平均法预测2003年销售量 表4-1 某企业近年产品销售额单位:万台 答案:
移动平均法简单应用
. 移动平均法 移动平均法是一种简单平滑预测技术,它的基本思想是:根据时间序列资料、逐项推移,依次计算包含一定项数的序时平均值,以反映长期趋势的方法。因此,当时间序列的数值由于受周期变动和随机波动的影响,起伏较大,不易显示出事件的发展趋势时,使用移动平均法可以消除这些因素的影响,显示出事件的发展方向与趋势(即趋势线),然后依趋势线分析预测序列的长期趋势。 1. 移动平均法的基本理论①简单移动平均法 设有一时间序列,则按数据点的顺序逐点推移求出N个数的平均数,即可得到一次移动平均数: 为第t周期的一次移动平均数;为第式中t周期的观测值;N为移动平均的项数, 即求每一移动平均数使用的观察值的个数。 这个公式表明当t向前移动一个时期,就增加一个新近数据,去掉一个远期数据,得到一个新的平均数。由于它不断地“吐故纳新”,逐期向前移动,所以称为移动平均法。 由于移动平均可以平滑数据,消除周期变动和不规则变动的影响,使得长期趋势显示出来,因而可以用于预测。其预测公式为: 即以第t周期的一次移动平均数作为第t+1周期的预测值。 ②趋势移动平均法当时间序列没有明显的趋势变动时,使用一次移动平均就能够准确地反映实际情况,直接用第t周期的一次移动平均数就可预测第t+1周期之值。但当时间序列出现线性变动趋势时,用一次移动平均数来预测就会出现滞后偏差。因此,需要进行修正,修正的方法是在一次移动平均的基础上再做二次移动平均,利用移动平均滞后偏差的规律找出曲线的发展方向和发展趋势,然后才建立直线趋势的预测模型。故称为趋势移动平均法。 设一次移动平均数为,则二次移动平均数的计算公式为:
从某时期开始具有直线趋势,且认为未来时期亦按此直再设时间序列 线趋势变化,则可设此直线趋势预测模型为: 式中t为当前时期数;T为由当前0时期数t到预测期的时期数,即t以后模型外推的时 间;为第t+T期的预测值;为截距;为斜率。,又称为平滑系数。 文档资料Word . 的计算公式为:根据移动平均值可得截距和斜率 的选择十分关键,它取决于预测目标和实际在实际应用移动平均法时,移动平均项数N 数据的变化规律。 2. 应用举例年该商场的年销售额。1998年的年销售额如下表所示,试预测1999已知某商场1978~ 销售额销售额年份年份 76 1989 32 1978 73 1979 41 1990 48 1980 79 1991 1992 53 1981 84
移动加权平均法详解_多批次入库的成本计算
移动加权平均法 公式:(原成本x 原库存+ 新成本x 新入数量)÷总库存数(新+原)= 新成本例:退热贴单位:张销售规格8元/张 场景1:原库存为零、原成本与入库成本相同 原库存:0张原成本:5元/张 入库:10张入库成本:5元/张 总库存:0+10=10 新成本:(5x0 + 5x10) / 10 = 5元/张 场景2:原库存为零、原成本与入库成本不相同 原库存:0张原成本:8元/张 入库:10张入库成本:5元/张 总库存:0+10=10 新成本:(8x0 + 5x10) / 10 = 5元/张 场景3:原库存大于入库数量、原成本与入库成本相同 原库存:30张原成本:5元/张 入库:20张入库成本:5元/张 总库存:30+20=50 新成本:(5x30 + 5x20) / 50 = 5元/张 场景4:原库存小于入库数量、原成本与入库成本相同 原库存:20张原成本:5元/张 入库:30张入库成本:5元/张 总库存:20+30=50 新成本:(5x20 + 5x30) / 50 = 5元/张 场景5:原库存大于入库数量、原成本大于入库成本 原库存:30张原成本:8元/张 入库:20张入库成本:5元/张 总库存:30+20=50 新成本:(8x30 + 5x20) / 50 = 6.8元/张 场景6:原库存大于入库数量、原成本小于入库成本 原库存:30张原成本:5元/张 入库:20张入库成本:8元/张 总库存:30+20=50 新成本:(5x30 + 8x20) / 50 = 6.2元/张
场景7:原库存小于入库数量、原成本大于入库成本 原库存:20张原成本:8元/张 入库:30张入库成本:5元/张 总库存:20+30=50 新成本:(8x20 + 5x30) / 50 = 6.2元/张场景8:原库存小于入库数量、原成本小于入库成本 原库存:20张原成本:5元/张 入库:30张入库成本:8元/张 总库存:20+30=50 新成本:(5x20 + 8x30) / 50 = 6.8元/张 说明: 原成本:上次入库时的单品成本 原库存:上次入库时的单品库存 新成本:本次入库后的单品成本 总库存:本次入库后的单品库存
第七章 时间序列分析习题
第七章时间序列分析习题 一、填空题 1.时间序列有两个组成要素:一是,二是。 2.在一个时间序列中,最早出现的数值称为,最晚出现的数值称为。 3.时间序列可以分为时间序列、时间序列和时间序列三种。其中是最基本的序列。 4.绝对数时间序列可以分为和两种,其中,序列中不同时间的数值相加有实际意义的是序列,不同时间的数值相加没有实际意义的是序列。 5.已知某油田1995年的原油总产量为200万吨,2000年的原油总产量是459万吨,则“九五”计划期间该油田原油总产量年平均增长速度的算式为。 6.发展速度由于采用的基期不同,分为和两种,它们之间的关系可以表达为。 7.设i=1,2,3,…,n,a i为第i个时期经济水平,则a i/a0是发展速度,a i/a i-1是发展速度。 8.计算平均发展速度的常用方法有方程式法和. 9.某产品产量1995年比1990年增长了105%,2000年比1990年增长了306.8%,则该产品2000年比1995增长速度的算式是。 10.如果移动时间长度适当,采用移动平均法能有效地消除循环变动和。 11.时间序列的波动可分解为长期趋势变动、、循环变动和不规则变动。 12.用最小二乘法测定长期趋势,采用的标准方程组是。 二、单项选择题 1.时间序列与变量数列( ) A都是根据时间顺序排列的B都是根据变量值大小排列的 C前者是根据时间顺序排列的,后者是根据变量值大小排列的 D前者是根据变量值大小排列的,后者是根据时间顺序排列的 2.时间序列中,数值大小与时间长短有直接关系的是( ) A平均数时间序列B时期序列C时点序列D相对数时间序列 3.发展速度属于( ) A比例相对数B比较相对数C动态相对数D强度相对数 4.计算发展速度的分母是( ) A报告期水平B基期水平C实际水平D计划水平 则该车间上半年的平均人数约为( ) A 296人 B 292人 C 295 人 D 300人 6.某地区某年9月末的人口数为150万人,10月末的人口数为150.2万人,该地区10月的人口平均数为( ) A150万人B150.2万人C150.1万人D无法确定 7.由一个9项的时间序列可以计算的环比发展速度( ) A有8个B有9个C有10个D有7个 8.采用几何平均法计算平均发展速度的依据是( )
移动加权平均法
移动加权平均法:移动加权平均法下库存商品的成本价 格根据每次收入类单据自动加权平均;其计算方法是以各次收入数量和金额与各次收入前的数量和金额为基础,计算出移动加权平均单价。 其计算公式如下: 移动加权平均单价=(本次收入前结存商品金额+本次收入商品金额)/(本次收入 前结存商品数量+本次收入商品数量) 移动加权平均法计算出来的商品成本比较 均衡和准确,但计算起来的工作量大,一般适用于经营品种不多、或者前后购进商品的单价相差幅度较大的商品流通类企业。 以下以一个简单的例子来说明:例1:货品A,期初结存数量10,加权价10,金额为100,发生业务如下:销售11;采购 10,采购价格11; 成本计算过程如下:销售时,成本金额为11*10=110 ;销售后结存数量:-1 ;加权价:10;结存金额:-10 ;
采购后,结存单价位:(-10+10*11 )/(- 1+10 )=11.111111 一、月末一次加权平均法 加权平均法也叫全月一次加权平均法, 指以本月收入全部存货数量加月初存货数 量作为权数,去除本月收入全部存货成本加月初存货成本的和,计算出存货的加权平均单位成本,从而确定存货的发出成本和库存成本的方法。计算公式如下: 加权平均单价=(本月收入全部存货成本+月初存货成本)/ (本月收入全部存货数量加 +月初存货数量) 本月发出存货成本=本月发出存货数量X加 权平均单价 月末结存存货成本=月末库存存货数量X加 权平均单价 二、移动加权平均法。 移动平均法亦称移动加权平均法,指本次收货的成本加原有库存的成本,除以本次收货数量加原有存货数量,据以计算加权平均单价,并对发出存货进行计价的一种方法。移动平均法与加权平均法的计算原理基
2014初级会计职称《初级会计实务》学习提高:移动加权平均法
2014初级会计职称《初级会计实务》学习提高:移动加权平均法移动加权平均法 注:每购入一次货物就需从新计算一次成本 第一批收货后的平均单位成本 =(150×10+100×12)/(150+100)=10.8 第一批发货的存货成本=200×10.8=2160 当时结存的存货成本=50×10.8=540 第二批收货后的平均单位成本 =(50×10.8+200×14)/(50+200)=13.36 第二批发货的存货成本=100X 13.36=1 336 当时结存的存货成本=150X10.36=2 004 定义:指以每次进货的成本加上原有库存存货的成本,除以每次进货数量加上原有库存存货的数量,据以计算加权平均单位成本,作为在下次进货前计算各次发出存货成本依据的一种方法。 存货单位成本 =(原有库存的成本+本次进货的成本)/(原有存货数量+本次进货数量) 本次发出存货的成本 =本次发出存货的数量×本次发货前存货的单位成本 本月月末库存存货成本 =月末库存存货的数量×本月月末存货单位成本 【多选题】下列税金中,应计入存货成本的有()。 A、由受托方代收代缴的委托加工直接用于对外销售的商品负担的消费税
B、由受托方代收代缴的委托加工继续用于生产应纳消费税的商品负担的消费税 C、进口原材料交纳的进口关税 D、小规模纳税人购买原材料交纳的增值税 【正确答案】 ACD 【答案解析】由受托方代收代缴的委托加工直接用于对外销售的商品负担的消费税计入委托加工物资的成本;由受托方代收代缴的委托加工继续用于生产应纳消费税的商品负担的消费税应记入“应交税费——应交消费税”科目的借方;进口原材料交纳的进口关税应计入原材料成本;小规模纳税人购买原材料交纳的增值税不能抵扣,应该计入原材料成本。
统计学时间数列习题及答案
第十章时间数列分析和预测 一、填空题 1.同一现象在不同时间的相继____________排列而成的序列称为 _______________。 2.时间序列在__________重复出现的____________称为季节波动。 3.时间序列在___________呈现出来的某种持续_______________称长期趋势。 4.增长率是时间序列中_________观察值与基期观察值______减1 后的结果。 5.由于比较的基期不同,增长率可分为_____________和______________。 6.复合型序列是指含有___________季节性和___________的序列。 7.某企业2005年的利润额比2000年增长45%,2004年2000年增长30%,则2005年比2004年增长_______;2004年至2000年平均增长率__________。 8.指数平滑法是对过去的观察值__________进行预测的一种方法。 9.如果时间序列中各期的逐期增减量大致相等,则趋势近似于 _____________;各期环比值大体相等,则趋势近似于___________。 10.测定季节波动的方法主要有____________和_____________。 二、单项选择题 1.用图形描述时间序列,其时间一般绘制在()
A. 纵轴上 B. 横轴上 C. 左端 D. 右端 2.求解()趋势参数方法是先做对数变换,将其化为直线模型,然后用最小二乘法求出模型参数 A. 三次曲线 B. 指数曲线 C. 一次直线 D. 二次曲线 3.对运用几个模型分别对时间序列进行拟合后,()最小的模型即位最好的拟合曲线模型 A. 判定系数 B. 相关系数 C. 标准误差 D.D—W值 4.当数据的随机波动较大时,选用的移动间隔长度K应该() A. 较大
移动平均法
移动平均法 ② 移动平均法 通过对时间数列相邻各项求平均数作为趋势值或预测值的平滑或预测方法,称为移动平均法。它具体可分为简单移动平均法和加权移动平均法。 a.简单移动平均法 简单移动平均法是将最近的K期数据加以平均,作为移动中项的趋势测定值。 设移动时期项数为k,则第t期的移动平均值为: 注意:当k取奇数或偶数的不同形式时,处理方法有区别。对于k取奇数时,可直接运用公式(3·21)即可;当k取偶数时,要在第一次对原数列作移动平均后,对所得新数列再做一次相邻两项的移动平均,这样才能完成中心化。 例13:下表是1991-2000年我国的原煤产量数据,计算移动项数k=3,k=4时的反映趋势变动的新数列。 表3-16 我国1991-2000年原煤产量数据 年份19911992199319941995 产量(亿吨)10.8711.1611.5012.4013.61年份19961997199819992000 产量(亿吨)13.9713.3712.5010.459.98 解:k=3时,移动项数为奇数,根据公式(3·21)得到
依此类推,最终结果汇集在表3-17中 当k=4时,移动项数为偶数,要移动两次,第一次移动运用公式(3·21)得到: 依此类推可得到表中第四列k=4时的第一次移动平均。这时求出的移动平均数还不能作为趋势值,因为他们代表的时期不明确。因此要计算二次移动平均值来代表第三期的长期趋势,即进行中心化。 第二步,对k=4时的第一次移动平均的结果(第四列)进行中心化处理。 依此类推得到表3-17的第五列。 从表3-17的计算结果看,我国的原煤产量经历了先高后低的发展态势。 b.加权移动平均法 加权移动平均法是对各期指标值进行加权后计算移动平均数。在使用加权移动平均法时,一般计算奇数项加权移动数,各期权数以二项展开式为计算基础,使得中项时期指标值的权数最大,两
移动平均法
实验二 :移动平均法在 Excel 中的实现 一、实验过程描述 1. 录入实验数据 打开 EXCLE 程序,录入题目数据, A 列为月份, B 列为销售额。录入后如下图所示: 2. 移动平均法的计算 M t y t y t 1 y t N 1 ; y t 1 M t ; 根据移动平均法的公式: N 误差: 2 y ? /项数 y 在 EXCEL 中进行如下操作: (1)三年移动平均法的计算 C 列存放三年移动平均法求出的数值, D 列存放三年移动平均法的误差, 由 于是三年移动平均,所以从第四年开始才有预测值,在 C5 单元格中输入移动平 均法的公式“ =SUM(B2:B4)/3 ”,在 D5 单元格中输入误差公式 “=(B5-C5)*(B5-C5) ”, 如下图所示:
将这两列分别下拉,向下复制计算出各个月份的预测值和误差,如下图所示; (2)五年移动平均法的计算 E 列存放五年移动平均法求出的数值, F 列存放五年移动平均法的误差,由于是五年移动平均,所以从第六年开始才有预测值,在E7 单元格中输入移动平均法的公式“ =AVERAGE(B2:B6) ”,在 F7 单元格中输入误差公式“=(B7- E7)^2 ”,如下图所示:
将这两列分别下拉,向下复制计算出各个月份的预测值和误差,如下图所示;( 3)比较两种计算方法的误差
根据误差公式:y y 2分别在 D13和 F13 单元格中求出三年、 ?, 五年移动平均法的平均误差。在D13 单元格中输入”=AVERAGE(D5:D12) ”,在F13 中输入“ =AVERAGE(F7:F12) ”,如下图所示: 由于平均误差 3005.833,<6385.667,因此五项移动平均比三项移动平均好。 3.绘出移动平均法的图形: 点击工具菜单中的插入——图表,选择折线图中的数据点折线图,如下所示:
移动平均法
实验二 :移动平均法在Excel 中的实现 一、实验过程描述 1. 录入实验数据 打开EXCLE 程序,录入题目数据,A 列为月份,B 列为销售额。录入后如下图所示: 2.移动平均法的计算 根据移动平均法的公式: N y y y M 1 N t 1t t t +--+++= ;t 1t M y =+ ; 误差:()项数/?2 y y ∑- 在EXCEL 中进行如下操作: (1)三年移动平均法的计算 C 列存放三年移动平均法求出的数值, D 列存放三年移动平均法的误差,由于是三年移动平均,所以从第四年开始才有预测值,在C5单元格中输入移动平均法的公式“=SUM(B2:B4)/3”,在D5单元格中输入误差公式“=(B5-C5)*(B5-C5)”,如下图所示:
将这两列分别下拉,向下复制计算出各个月份的预测值和误差,如下图所示; (2)五年移动平均法的计算 E列存放五年移动平均法求出的数值,F列存放五年移动平均法的误差,由于是五年移动平均,所以从第六年开始才有预测值,在E7单元格中输入移动平均法的公式“=A VERAGE(B2:B6)”,在F7单元格中输入误差公式“=(B7-E7)^2”,如下图所示:
将这两列分别下拉,向下复制计算出各个月份的预测值和误差,如下图所示; (3)比较两种计算方法的误差
根据误差公式:()项数/?2 y y ∑-, 分别在D13和F13单元格中求出三年、 五年移动平均法的平均误差。在D13单元格中输入”=A VERAGE(D5:D12)”,在 F13中输入“=A VERAGE(F7:F12)”,如下图所示: 由于平均误差3005.833,<6385.667,因此五项移动平均比三项移动平均好。 3.绘出移动平均法的图形: 点击工具菜单中的插入——图表,选择折线图中的数据点折线图,如下所示:
(完整版)应用时间序列分析习题答案解析
第二章习题答案 2.1 (1)非平稳 (2)0.0173 0.700 0.412 0.148 -0.079 -0.258 -0.376 (3)典型的具有单调趋势的时间序列样本自相关图 2.2 (1)非平稳,时序图如下 (2)-(3)样本自相关系数及自相关图如下:典型的同时具有周期和趋势序列的样本自相关图
2.3 (1)自相关系数为:0.2023 0.013 0.042 -0.043 -0.179 -0.251 -0.094 0.0248 -0.068 -0.072 0.014 0.109 0.217 0.316 0.0070 -0.025 0.075 -0.141 -0.204 -0.245 0.066 0.0062 -0.139 -0.034 0.206 -0.010 0.080 0.118 (2)平稳序列 (3)白噪声序列 2.4 ,序列 LB=4.83,LB统计量对应的分位点为0.9634,P值为0.0363。显著性水平=0.05 不能视为纯随机序列。 2.5 (1)时序图与样本自相关图如下
(2) 非平稳 (3)非纯随机 2.6 (1)平稳,非纯随机序列(拟合模型参考:ARMA(1,2)) (2)差分序列平稳,非纯随机 第三章习题答案 3.1 解:1()0.7()()t t t E x E x E ε-=?+ 0)()7.01(=-t x E 0)(=t x E t t x ε=-)B 7.01( t t t B B B x εε)7.07.01()7.01(221Λ+++=-=- 229608.149 .011 )(εεσσ=-= t x Var 49.00212==ρφρ 022=φ 3.2 解:对于AR (2)模型: ?? ?=+=+==+=+=-3.05 .02110211212112011φρφρφρφρρφφρφρφρ 解得:???==15/115 /72 1φφ 3.3 解:根据该AR(2)模型的形式,易得:0)(=t x E 原模型可变为:t t t t x x x ε+-=--2115.08.0 2212122 ) 1)(1)(1(1)(σφφφφφφ-+--+-= t x Var 2) 15.08.01)(15.08.01)(15.01() 15.01(σ+++--+= =1.98232σ ?????=+==+==-=2209.04066.06957.0)1/(122130 2112211ρφρφρρφρφρφφρ ?? ???=-====015.06957.033222111φφφρφ
SAP标准成本法和移动加权平均法
[摘要]本文简单介绍了ERP环境下采购核算的两种方法:标准成本法和移动加权平均法。同时还介绍了新环境下对存货采购的控制。 关键字:存货计价,信息化,ERP,SAP 存货作为企业的一种资产,在企业资产中占有相当比重,有的企业甚至在其流动资金中占了70~80%的比率。合理选择存货的计价方法对企业的财务状况、经营成果和现金流量会产生不同的影响。因此,企业对存货的管理成为企业管理中非常重要的工作重心之一。随着经济的快速发展,企业对存货的管理手段也在不断加强,技术也越来越先进。党的十六大报告中也指出:信息化是我国加快实现工业化和现代化的必然选择。坚持以信息化带动工业化,以工业化促进信息化,走出一条科技含量高、经济效益好、资源消耗低、环境污染少、人力资源优势得到充分发挥的新型工业化路子。很多大型的企业随着企业的不断发展,也逐渐从手工或小型的物资或库存管理信息系统(MIS)转向集成的企业信息化来管理企业。 ERP(Enterprise Resource Planning,企业资源计划/规划)是集成了企业采购、库存、生产制造、销售、财务成本、人力资源、资产、质量、资金、项目投资管理等在内的企业管理信息系统。与传统的存货管理和财务软件核算上,ERP环境下存货的管理出现了一些新的变化,这种变化不仅对于企业对存货的管理是重要的,另一方面对于会计师审计存货也是具有重要意义的。ERP系统的重要特点之一就是高度的集成性和数据的共享。在高度集成的ERP环境下,大多数和库存相关的财务核算都是由系统在业务发生时自动产生的,而不再需要财务单独计帐完成。 由于ERP环境下的存货管理出现了这些新的特点,因此有必要弄清楚ERP系统中的物流及资金流的情况以加强存货管理控制。ERP系统中的存货计价一般都支持计划/标准价、移动平均价、先进先出法和后进先出法等。这里主要介绍ERP系统中最典型也时最常使用的两种计价方法:标准成本和移动平均价。本文将以ERP软
移动平均法案例
表 单位:万元 第一步,计算相邻五个月的销售额平均数(按多少期计算平均数,要根据具体情况而定,期数少,则反映波动比较灵敏,但预测误差大;期数多,则反映波动平滑,预测较为精确)。如1~5月销售额的平均值为: 8.355 41 343734331=++++= X 依次类推:求出,,...,,,8432X X X X 并填入表中。 第二步,计算相邻两个平均值的差,该差称为平均值的变动趋势,如1X 与2X 之差为: 38—=依此类推,计算变动趋势值,填入表中。 第三步,计算相邻四期变化趋势之平均值,称为四期平均发展趋势,如前四期变动趋势的平均值为:+++÷4=依此类推,将数字填人表中。 第四步,预测1998年1月的销售额,最后5个月的平均月销售额为49万元,加上最后一期平均发展趋势万元,所以1998年1月的预测值为: 49+3ⅹ=(万元)
(其中3ⅹ,是因为预测期距平均月销售额为3个月,所以需要乘以3)。 季节性波动分析。当产品的市场需求呈明显的季节性波动时,用平均法进行销售 预测就不能正确地反映销售量的波动。要用计算季节指数的办法来预测季节性波动。 例 某地区涤棉府绸三年内各个季节的市场销售量如表所示。 从表中很明显地可以看出,涤棉府绸的销售量淡季与旺季相差近一倍左右。如果简单地用移动平均来预测某一个季节的市场需要,就不符合实际情况,这就可以用季节指数进行预测。其计算方法如下: 表 单位:万米 某年各季节平均需要量=当年市场销售量/4 某季市场需求量=某季节的市场销售量/当年各季度平均销售量ⅹ100% 如1996年春季的季度指数为:11271.79%%1004 624 =?÷ 以此类推,计算各年各季的季节指数,然后计算各季的平均季节指数,亦分别列入表中。 利用季节指数就可以对某季节的市场需要量进行预测,现预计1999年全年市场对涤棉府绸需要量是720万米,各个季节的市场需要量可以用上述季节指数进行预测。 平均季节指数年需求量 某季度预测需求量?= 4 )(128%7141 7201999万米年春季:=?? )(198%11041 7201999万米年夏季:=?? )(248%1384 1 7201999万米年秋季:=??
