初中平面几何训练题(较难)

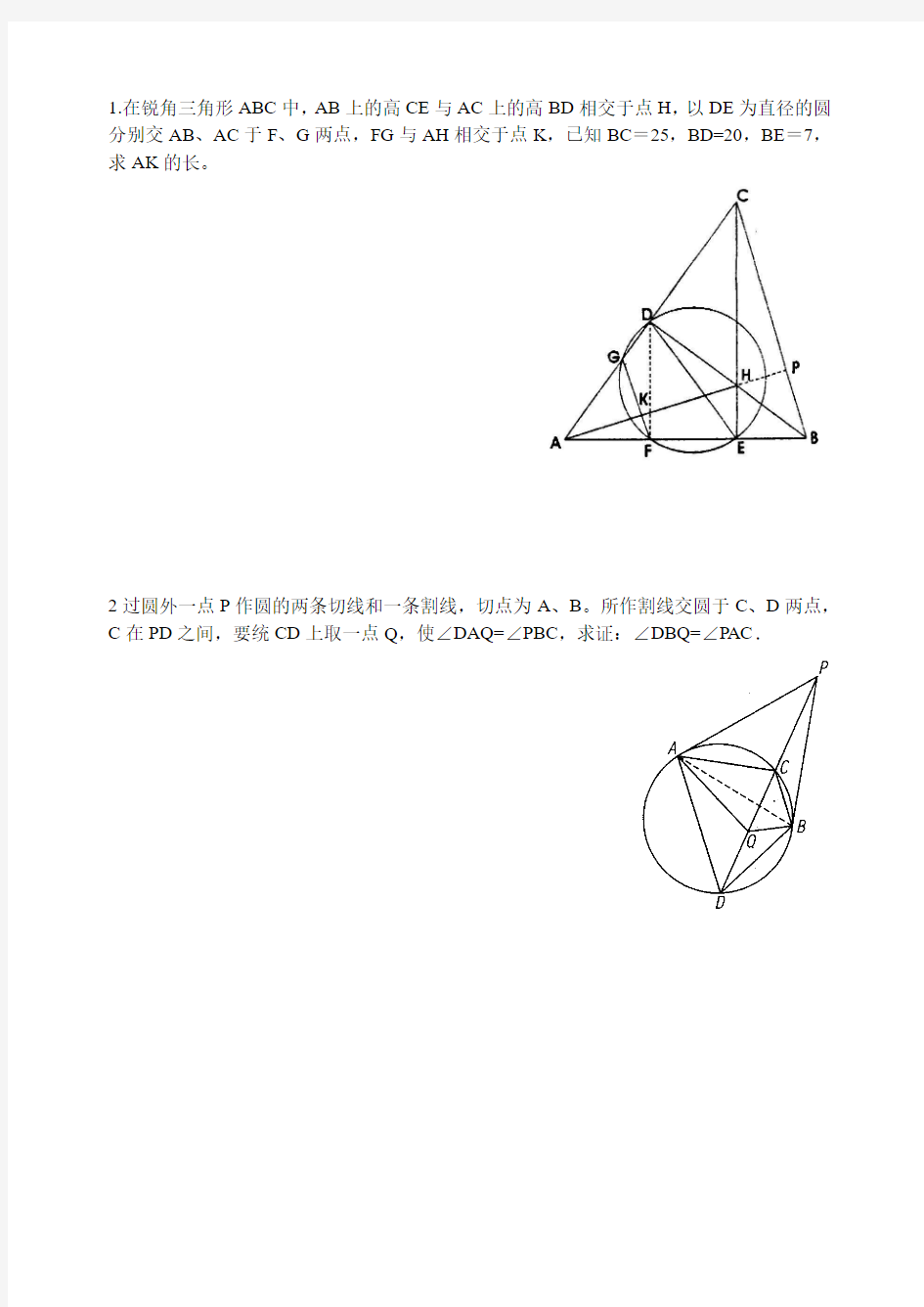
1.在锐角三角形ABC中，AB上的高CE与AC上的高BD相交于点H，以DE为直径的圆分别交AB、AC于F、G两点，FG与AH相交于点K，已知BC＝25，BD=20，BE＝7，求AK的长。

2过圆外一点P作圆的两条切线和一条割线，切点为A、B。所作割线交圆于C、D两点，C在PD之间，要统CD上取一点Q，使∠DAQ=∠PBC，求证：∠DBQ=∠PAC．

3.是外心。

，点，＝中，如图，在O AC AB A ABC >?∠?60、

点，点交于、两条高M H CF BE 的值。

，求

上，且满足、分别在线段OH

MH CN BM HF BH N +=

4.、、为外心，三条高中，如图，BE AD O ABC ? ，交于点和，直线交于点M AB ED H CF

;)2(;,)1(MN OH DE OC DF OB N AC FD ⊥⊥⊥。求证：交于点和

的面积相等；

与点，证明四边形的外接圆于交，延长是垂足、，作，满足、边上有两点的在锐角如图ABC AMDN D ABC AE N M AC

FN AB FM CAF BAE F E BC ABC ??⊥⊥∠=∠?)(,,.5

EAC

GAC G BC DF F AC BE E CD BAD AC ABCD ∠=∠∠，求证：于交延长，相交于与，上取一点，在平分中，对角线如图，在四边形.6

三点共线；

、、的充分必要条件是两点，求证：、内切于分别与圆、圆两点，且圆、相交于和圆相等的圆如图，已知两个半径不T N S MN OM T S O O O N M O O 2121.7

参考答案

PB PC PBD PCB AD

PA PC PAD PCA DQ AB AD BC AD

AB BC ABC ADQ CAB PBC DAQ ABC ADQ ABC ADQ AB =

???=∴

????=??=???∴∠=∠=∠∠=∠??得：同理：由又由切割线关系可知：从而有

中，与，在证：如图：连结,

PAC

ABC DBQ ABD CBQ ABD CBQ BAD

BCQ BC

BC DQ AB AD ABD CBQ DQ CQ CD DQ DQ AB CD AB CD

AB AD BC BD AC ABCD DQ AB AD BC BD AC BD

AD AC PB

PA ∠=∠=∠∴∠=∠∴???∴∠=∠??=?=??=??=?+??=?=??=∴

=,2

2＝＝中：与在于是：的托勒密定理有：关于圆内接四边形又又

3,330sin 120sin 30,120,,1201801202=+?==+=+∴=∴==?=?=

???=∠=∠?=∠=∠∴=∠=∠???∴==∠=∠∴∴∠=∠∴?=∠-?=∠?=∠?=∠=OH

MH OH KH KM MH NH MH NH

KM CH BK CN BM OH

KH OH

KH OKH OHK OKH BOC KOH OH

OK COH BOK COH

BOK CH BK OC OB OCH

OBH O H C B BHC

BOC A BHC A BOC OK OC OB CH BK BE 故

又则有：观察又四点共圆。、、、可知：由三角形的垂心的性质可知：由三角形的外心的性质、、，连结上取解：如图在

OB BAC

BOC OBC BAC

BDF F D C A ⊥∴∠-?=∠-?=∠∠=∠∴90)180(2

)1( 又四点共圆；、、、证：

OH NH NO MH MO OM ON MH NH OD OM CD CM DE

OC OD ON BD BN DF

OB AC BA CD BD BC

DA AH AB NH NB NA

BE AH AC MH MC MA

CF DE OC ⊥∴-=--=--

-=-∴⊥-=-∴⊥-=-∴⊥-=-∴⊥-=-∴⊥⊥2222222222222222222222222222,)2(得：

由同理

5．

ADB ACF DAB CAF MN AD S AD

MN CAF AFN BAE AMN AFN

AMN N F M A AC FN AB FM BD MN AMDN ∠=∠∠=∠?=

∴⊥?=∠+∠=∠+∠∴∠=∠∴∴⊥⊥,2

90 即：四点共圆、、、，、证明：如图，连结 MN ABC AF AF BAC MN N F M A AF AF AD AC AB AD

AB AF ABD AFC =∠?=∠∴?=??=?

???∴sin sin 四点的圆的直径

、、、是过又

AMDN

ABC AMDN

ABC S S S MN AD BAC AF AD BAC AC AB S =∴=?=∠??=∠??=

∴??21

sin 21

6．

EAC

GAC JAC IAC ACJ ACI ACJ DAC BAC ACI AD

CJ AB CI CJ

CI CJ AD AD AB AB CI CJ AD EC DE AB CI GB CG J AE AD C I AG AB C EC

DE AD AB GB CG AD

HD BH BAD AH BC

HD BH GB CG BCD H AC BD ∠=∠∴∠=∠∴???∴∠=∠-=∠-=∠∴==??∴=

==??=∠=???ππ//,//:1,1

1 又从而则：的延长线于的平行线交作，过点的延长线于的平行线交作过点故：定理，可得的平分线，由角平分线是因为用塞瓦定理，有：，对于交证明：如图，连结

7．

1221212121,,O O N O M O N O NT SN OT OS r OT OS T O O S O O r r r O O O 、、、、、、连结且三点共线，

、、三点共线，、、由条件可知，、、的半径分别为，圆，圆证明：如图，设圆==

12121212211212222111121212121211112222121121221210))(())()(()

)()((,2

,,,,//,,)(//,//,//,,)(212121r r r r r r r r r r S a p r r p r p p a p r r p r p p S r

a p r a OM O MO O r M O r r O O r r O O r M O a

OM S S OM O O MN O O MN OM MN

OM MN O O OM O O S S OM O MO O MO r N O OO MO r N O OO NO OO OT

N O OS N O NS O T NT O S NT O T NS O S NT O SN O T S T N S MO

O MO O OM O MO O OM O MO O +=∴≠=---=-+--=

-+--=+=

+??=-=-===∴⊥⊥⊥∴⊥∴=∴???∴======∴∴∴∠=∠∠=∠∴∠=∠∠=∠∴??∠∠??????有，又已知化简可得：式，有：由三角形面积的海伦公记的周长都等于与可知由于＝设有若必要性又为平行四边形

四边形均为等腰三角形，与又，＝三点共线，则、、设充分性

NS O S NO O NS O S NT O T NT O SN O T NT O S NS O NO OO N O r r r O O N O r r r O O ∠+∠=∠+∠∴∠=∠∠=∠∴??∠+∠=?=∠+∠∴==-===-=22112211221112222112,180,,均为等腰三角形与又为平行四边形

故

三点共线

、、T N S S SNO NT O NO O NS O NT

O NS O T

S T

NO O T NT O ∴?=∠+∠=∠+∠+∠∴∠=∠∴∠=∠∴∠+∠=∠+∠=18022221121211

答案：

人教七数上册几何图形初步专题训练.doc

2.（2015?甘孜州）如图所示的几何体，从正面看的平面图形是（A ） 3.（2015-通辽）如图，由几个相同的小正方体搭成的一个几何体 , < D ） 5.下面的图形'是由A 、B 、C 、D 中的哪个图旋转形成的（A ）第四章《几何图形初步》章末专题训练类型1:立体图形的三种视图及展开图 1.（2015-黄石）下列四个立体图形中'从左面看为长方形的是（B ） S ? A 3 ①正方体 ②球 ③国锥 ④国柱 A.①③ B.①④ C.②③ D.③④ B C. B. 4?在下面的图形中是正方体的展开图的是（B ） B. C.

6.（2015-茂名）如囹是一个正方体的平面展开图，折盏成正方体后与“建”字所在面相对的面的字是（C ） A-创 B.教 C.强 D.市 7.如图，在平整的地面上，有若干个完全相同的棱长为10cm 的小正方体堆成一个几何体. （1）这个几何体由10个小正方体组成. （2）如果在这个几何体的表面喷上黄色的赧，则在所有的小正方体中，有1个正方体只有一个面是黄色，有2个正方体只有两个面是黄色，有3个正方体只有三个 <3）这个几何体喷糠的面积为3200 cm2. 8.（2015-随州）如图是一个长方体的三视图（单位：cm）,根据图中数据计算这个长方体的体积是24 cm3. 9.以长为24皿，赏为10cm的长方形的一边所在直线为旋转轴，旋转一周形成一个圆柱.贝U这个圆柱的底面半径是24或10 cm. 10.（2015-牡丹江）由一些大小相同的小正方体搭成的几何体的主视图和俯视图，如图所示，则搭成该几何体的小正方体最多是7个. 主视图俯视图类型2：线段的和、差、倍、分的计算 1?如图，点C为线段局的中点'点D为线段AC的中点、已知AB=8,则BD= （ C ）

初中几何经典例题及解题技巧精编版

初中几何证明技巧及经典试题证明两线段相等 1.两全等三角形中对应边相等。 2.同一三角形中等角对等边。 3.等腰三角形顶角的平分线或底边的高平分底边。 4.平行四边形的对边或对角线被交点分成的两段相等。 5.直角三角形斜边的中点到三顶点距离相等。 6.线段垂直平分线上任意一点到线段两段距离相等。 7.角平分线上任一点到角的两边距离相等。 8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。 *9.同圆（或等圆）中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。 *10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。 11.两前项（或两后项）相等的比例式中的两后项（或两前项）相等。 *12.两圆的内（外）公切线的长相等。 13.等于同一线段的两条线段相等。证明两个角相等 1.两全等三角形的对应角相等。 2.同一三角形中等边对等角。 3.等腰三角形中，底边上的中线（或高）平分顶角。 4.两条平行线的同位角、内错角或平行四边形的对角相等。 5.同角（或等角）的余角（或补角）相等。 *6.同圆（或圆）中，等弦（或弧）所对的圆心角相等，圆周角相等，弦切角等于它所夹的弧对的圆周角。*7.圆外一点引圆的两条切线，圆心和这一点的连线平分两条切线的夹角。 8.相似三角形的对应角相等。 *9.圆的内接四边形的外角等于内对角。 10.等于同一角的两个角相等。证明两条直线互相垂直 1.等腰三角形的顶角平分线或底边的中线垂直于底边。 2.三角形中一边的中线若等于这边一半，则这一边所对的角是直角。 3.在一个三角形中，若有两个角互余，则第三个角是直角。 4.邻补角的平分线互相垂直。 5.一条直线垂直于平行线中的一条，则必垂直于另一条。 6.两条直线相交成直角则两直线垂直。 7.利用到一线段两端的距离相等的点在线段的垂直平分线上。 8.利用勾股定理的逆定理。 9.利用菱形的对角线互相垂直。 *10.在圆中平分弦（或弧）的直径垂直于弦。 *11.利用半圆上的圆周角是直角。证明两直线平行 1.垂直于同一直线的各直线平行。 2.同位角相等，内错角相等或同旁内角互补的两直线平行。 3.平行四边形的对边平行。 4.三角形的中位线平行于第三边。 5.梯形的中位线平行于两底。 6.平行于同一直线的两直线平行。 7.一条直线截三角形的两边（或延长线）所得的线段对应成比例，则这条直线平行于第三边。

对一道课本试题的变式

对一道课本习题的变式、推广与思考波利亚指出：“拿一个有意义又不复杂的题目去帮助学生发掘问题的各个方面，使得通过这个题目就好像通过一道门户，把学生引入一个完整的领域。” 题目：已知ABC ?两个顶点()()0,6,0,6B A -，边BC AC ,所在直线的斜率之积等于9 4-，求顶点C 的轨迹方程。（北师大版数学选修2-1第三章§1椭圆习题3-1A 组第8题）一、动手实践，掌握方法解析：设()y x C ,，则直线BC AC ,的斜率分别是()6,66 ,621-≠≠-= +=x x x y k x y k ，根据题意，9 4 21- =?k k ，所以 9 4 362 2-=-x y ，化简，得()6,6116362 2 -≠≠=+x x y x 所以顶点C 的轨迹是椭圆，去掉左右顶点。评析：（1）典型的用直接法求动点的轨迹方程，注意6,6-≠≠x x ，一方面它保证了直线BC AC ,的斜率的存在性，另一方面符合C 为ABC ?的一个顶点，C B A ,,不能共线。（2）题目的几何条件包括“两个定点、一个动点、一个定值，两条直线的斜率，一个等量关系”。（3）轨迹是椭圆，去掉左右顶点。二、引进参数，化静为动变式1、已知两个定点()()()00,,0, a a B a A -，动点C 满足直线BC AC ,的斜率之积等于()0≠m m ，试讨论动点C 的轨迹。分析：首先确定动点C 的轨迹方程，然后依据方程判定它的轨迹。解析：设()y x C ,，则直线BC AC ,的斜率分别是 a x y k a x y k -=+= 21,，()a x + - ≠，根据题意，m k k =?2 1 ，所以m a x y =-2 22，化简，得动点C 的轨迹方程122 22=-ma y a x ，所以 1、当0 m 时，动点C 的轨迹是焦点在x 轴上的双曲线，去掉它的两个顶点； 2、当0 m 时（1）若1-=m ，则动点C 的轨迹方程为2 2 2 a y x =+，所以它的轨迹是圆心在原点，半径为a 的圆，去掉与x 轴的两个交点；（2）当01 m -时，2 2ma a - ，所以动点C 的轨迹是焦点在x 轴上的椭圆，去掉左右顶点；（3）当1- m 时，2 2ma a - ，所以动点C 的轨迹是焦点在 y 轴上的椭圆去掉左右顶点。评析：引进参数，化静为动，培养学生分类讨论的数学思想，发展学生的数学思维能力。注意到变式1并没有改变题目中的几何关系，但是参数值及它的的符号决定了轨迹的不同形式——圆、椭圆、双曲线，这也从一个侧面说明三种曲线之间有着内在的联系，可以想象当参数m 由()+∞→≠→-→∞-001变化时，动点 c 的轨迹由焦点在y 轴上的椭圆，变为圆，再变为焦点在x 轴上椭圆，然后蜕变为焦点在x 轴上的双曲线，

初中数学经典几何题及答案解析

第 1 页共 14 页 4e d c 经典难题（一） 1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二） 2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二） 3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、 CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二） 4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ． A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A N F E C D M B

第 2 页共 14 页 P C G F B Q A D E 经典难题（二） 1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二） 2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二） 3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二） 4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形 CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二）经典难题（三） 1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二） · A D H E M C B O · G A O D B E C Q P N M · O Q P B D E C N M · A A F D E C B

初中数学几何图形初步经典测试题及答案解析

初中数学几何图形初步经典测试题及答案解析一、选择题 1．如图是由若干个大小相同的小正方体堆砌而成的几何体，那么其三种视图中面积最小的是（） A ．主视图 B ．俯视图 C ．左视图 D ．一样大【答案】C 【解析】如图，该几何体主视图是由5个小正方形组成，左视图是由3个小正方形组成，俯视图是由5个小正方形组成，故三种视图面积最小的是左视图，故选C ． 2．如图，一个正六棱柱的表面展开后恰好放入一个矩形内，把其中一部分图形挪动了位置，发现矩形的长留出5cm ，宽留出1,cm 则该六棱柱的侧面积是（） A ．210824(3) cm - B ．(2 108123cm - C ．(2 54243cm - D ．(2 54123cm - 【答案】A 【解析】【分析】设正六棱柱的底面边长为acm ，高为hcm ，分别表示出挪动前后所在矩形的长与宽，由题意列出方程求出a ＝2，h ＝9?36ah 求解．【详解】解：设正六棱柱的底面边长为acm ，高为hcm ，

如图，正六边形边长AB ＝acm 时，由正六边形的性质可知∠BAD ＝30°， ∴BD ＝ 12a cm ，AD ＝32 a cm ， ∴AC ＝2AD ＝3a cm ， ∴挪动前所在矩形的长为（2h ＋23a ）cm ，宽为（4a ＋ 1 2 a ）cm ，挪动后所在矩形的长为（h ＋2a ＋3a ）cm ，宽为4acm ，由题意得：（2h ＋23a ）?（h ＋2a ＋3a ）＝5，（4a ＋1 2 a ）?4a ＝1， ∴a ＝2，h ＝9?23， ∴该六棱柱的侧面积是6ah ＝6×2×（9?23）＝210824(3) cm -；故选：A ．【点睛】本题考查了几何体的展开图，正六棱柱的性质，含30度角的直角三角形的性质；能够求出正六棱柱的高与底面边长是解题的关键． 3．将一副三角板如下图放置，使点A 落在DE 上，若BC DE P ，则AFC ∠的度数为（） A ．90° B ．75° C ．105° D ．120° 【答案】B 【解析】【分析】根据平行线的性质可得30E BCE ==?∠∠，再根据三角形外角的性质即可求解AFC ∠的度数．【详解】

七年级数学几何图形初步专题练习(word版

一、初一数学几何模型部分解答题压轴题精选（难） 1．将一副三角板放在同一平面内，使直角顶点重合于点O （1）如图①，若∠AOB=155°，求∠AOD、∠BOC、∠DOC的度数. （2）如图①，你发现∠AOD与∠BOC的大小有何关系？∠AOB与∠DOC有何关系？直接写出你发现的结论. （3）如图②，当△AOC与△BOD没有重合部分时，（2）中你发现的结论是否还仍然成立，请说明理由. 【答案】（1）解：∵ 而同理： ∴ ∴ （2）解：∠AOD与∠BOC的大小关系为：∠AOB与∠DOC存在的数量关系为：（3）解：仍然成立. 理由如下：∵ 又∵ ∴

【解析】【分析】（1）先计算出再根据（2）根据(1)中得出的度数直接写出结论即可.（3）根据即可得到利用周角定义得∠AOB+∠COD+∠AOC+∠BOD=360°，而∠AOC=∠BOD=90°，即可得到∠AOB+∠DOC=180°． 2．在△ABC中，∠ACB=2∠B，如图①，当∠C=90°，AD为∠BAC的角平分线时，在AB上截取AE=AC，连接DE，易证AB=AC+CD。（1）如图②，当∠C≠90°，AD为∠BAC的角平分线时，线段AB、AC、CD又有怎样的数量关系?请写出你的猜想并证明；（2）如图③，当AD为△ABC的外角平分线时，线段AB、AC、CD又有怎样的数量关系?请写出你的猜想，并对你的猜想给予证明。【答案】（1）解：猜想：AB=AC+CD．证明：如图②，在AB上截取AE=AC，连接DE， ∵AD为∠BAC的角平分线时， ∴∠BAD=∠CAD， ∵AD=AD， ∴△ADE≌△ADC（SAS）， ∴∠AED=∠C，ED=CD， ∵∠ACB=2∠B， ∴∠AED=2∠B， ∵∠AED=∠B+∠EDB， ∴∠B=∠EDB， ∴EB=ED， ∴EB=CD， ∴AB=AE+DE=AC+CD.

初中数学几何证明题解题方法--

————————————————————————————————作者：————————————————————————————————日期：

浅谈初中数学几何证明题解题方法内容摘要：几何证明题的一般结构由已知条件和求证目标组成。做几何证明题的一般步骤：审题，寻找证明的思路，书写证明过程关键词：几何证明条件结论 .执因索果执果索因辅助线初中学生正处于自觉形象思维向逻辑思维的过度阶段，几何证明，是学生逻辑思维的起步。这种思维方式学生刚接触，会遇到一些困难。许多学生在几何证明这里“跌倒了”，丧失了信心，以至于几何越学越糟。为此，我根据自己几年的数学教学实践，就初中数学中几何证明题的一般结构，解题思路进行初步探讨。学好几何证明，起步要稳，要求学生在学习几何时要扎扎实实，一步一个脚印，在掌握好几何基础知识的同时，还要培养学生的逻辑思维能力。一、几何证明题的一般结构初中几何证明题的一般结构由已知条件和求证目标两部分（即前提和结论）组成。已知条件是几何证明的前提，指题目中用文字和符号直接给出的明确条件，也包括所给图形中暗含的条件。求证指题目要求的经过推理最终得出的结论。已知条件是题目既定成立的、毋庸置疑而且必然正确的。求证是几何证明题的最终目标，就是根据题目给出的已知条件，利用数学中的公理、定理、性质，用合理的推理形式推导出的最后结果，而且只能出现在证明过程的最后。例如：如图，在△ABC 和△DCB 中，AB = DC ，AC = DB ，AC 与DB 交于点M ．求证：△ABC ≌△DCB ；已知条件：文字给出的有：△ABC 和△DCB ，AB = DC ，AC = DB ，AC 与DB 交于点M 图形给出的有：BC=CB,∠BMA 与∠CMD 是对顶角等等求证目标是：△ABC ≌△DCB 注意，已知条件除了上面列出的，就没有其它的了，不可随意出现AM=DM ,BN=CN 等等二、做几何证明题的一般步骤（一）、审题审题就是读题，这一步是解决几何证明题的关键，非常重要。许多学生读几何证明题时讲快，常常忽略了题目中蕴含的重要信息。和读其它类型的题有所不同，读几何证明题要求 B A M N

如何对几何习题拓展变式

如何对几何习题拓展变式 “变式”原为心理学上的名词，其含义是变换材料的出现形式。在教学中的所谓变式，即是指对数学概念、定义、定理、公式，以及问题背景不同角度、不同层次、不同情形、不同背景的变化，使其面目不一，而本质特征不变。在数学教学中，可以充分利用变式，有意识地把教学过程施行为数学思维活动的过程，充分调动和展示学生的思维过程，让学生积极、主动地参与教学的全过程，培养学生独立分析和解决问题的能力，以及大胆创新、勇于探索的精神，从而真正把学生能力的培养落到实处。通过变式练习，可以使学生在全面、深刻的理解和掌握知识的同时，思维品质也获得良好的发展。通过变式教学，使一题多用，多题重组，常给人以新鲜感，能唤起学生的好奇心和求知欲，因而能产生主动参与的动力，保持其参与教学过程的兴趣和热情。通过变式训练，可以帮助学生提出问题、分析问题、解决问题，搞清问题的内涵和外延，提高数学能力。 “变式训练”的实质是根据学生的心理特点在设计问题的过程中，创设认知和技能的最近发展区，诱发学生通过探索、求异的思维活动，发展能力。对习题的变式可以从以下几种不同的角度进行：一、一题多解、一题多变、一题多思、多题一法…… 1、一题多解，培养思维的发散性一题多解实际上是解题或证明定理、公式的变式，因为它的实质是以不同的论证方式反映条件和结论问的同一必然的本质联系，运用这种变式教学，可以引导学生对同一材料，从不同角度、从不同方位、用各种途径、多种方法思考问题，探求不同的解答方案，这样，既可暴露学生解题的思维过程，增加教学透明度，

又能够拓广学生思路，使学生熟练掌握知识的内在联系，使思维向多方向发展，培养思维的发散性。这方面的例子很多，尤其是几何证明题。例如：已知：点O是等边△ABC内一点, OA=4，OB=5，OC=3 求∠AOC的度数。练习：把此题适当变式: 在△ABC中，AB=AC，∠BAC=90° OA=4，OB=6，OC=2 求∠AOC的度数。变式2：如图,点O是等边△ABC内一点,∠AOB=110°, ∠BOC=135° 试问:(1)以OA、OB、OC为边能否构成一个三角形?若能,请求出三角形各内角的度数;若不能,请说明理由. (2)如果∠AOB的大小保持不变,那么当∠BOC等于多少度时, 以OA、OB、OC为边的三角形是一个直角三角形? 2、一题多变，培养思维的灵活性一题多变是题目结构的变式，是指变换题目的条件或结论，或者变换题目的 B C A B C O A B C O

初中数学经典几何题及答案

4e d c 经典难题（一） 1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二） 2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二） 3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、 CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二） 4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ． A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A N F E C D M B

P C G F B Q A D E 经典难题（二） 1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝AO ．（初二） 2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二） 3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二） 4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形 CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二）经典难题（三） 1、如图，四边形ABCD 为正方形，DE ∥AC ，AE ＝AC ，AE 与CD 相交于F ．求证：CE ＝CF ．（初二） · A D H E M C B O · G A O D B E C Q P N M · O Q P B D E C N M · A A F D E C B

初中几何题解题技巧(带例题)

初中几何题解题技巧 (带例题) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN

初中几何题解题技巧在小学阶段，我们学过许多关于几何图形面积计算的知识。在计算几何图形面积时，除了能正确运用面积计算公式外，还需要掌握一定的解题技巧。一、割补法割补法是指将一些不规则的、分散的几何图形经过分割、移补，拼成一个规则的几何图形，从而求出面积的方法。例1如图1，已知正方形的边长是6厘米，求阴影部分的面积。分析与解：如图2所示，连接正方形的对角线，可以将阴影I分割成I1和I2两部分，然后将阴影I1移至空白I1′处，将阴影I2移至空白I2′处，这样阴影部分就拼成了一个等腰直角三角形。要求阴影部分的面积，只要求出这个等腰直角三角形的面积即可，列式为：6×6÷2＝18（平方厘米）。练一练1：如图3，已知AB＝BC＝4厘米，求阴影部分的面积。二、平移法平移法是指把一些不规则的几何图形沿水平或垂直方向移动，拼成一个规则的几何图形，从而求出面积的方法。例2如图4，已知长方形的长是12厘米，宽是6厘米，求阴影部分的面积。分析与解：如图5所示，连结长方形两条长的中点，把阴影部分分成左右两部分，然后把左边的阴影部分向右平移至空白处，这样阴影部分就转化成了一个边长为6厘米的正方形。要求阴影部分的面积，只要求出这个正方形的面积，列式为：6×6＝36（平方厘米）。练一练2：如图6，求阴影部分的面积（单位：分米）。三、旋转法旋转法是指把一些几何图形绕某一点沿顺时针（或逆时针）方向转动一定的角度，使分散的、不规则的几何图形合并成一个规则的几何图形，从而求出面积的方法。例3如图7，已知ABC是等腰直角三角形，斜边AB＝20厘米，D是AB的中点，扇形DAE和DBF都是圆的，求阴影部分的面积。分析与解：如图8所示，把扇形DBF绕D点沿顺时针方向旋转180°后，扇形DBF与扇形DAE就合并成了一个半径为10厘米的半圆，两个空白三角形也合并成了一个直角边为10厘米的等腰直角三角形，要求阴影部分的面积，只要用半圆的面积减去空白部分的面积即可，列式为：3.14×（20÷2）2÷2－（20÷2）2÷2＝107（平方厘米）。练一练3：如图9，在直角三角形ABC中有一个正方形BDEF，E点正好落在直角三角形的斜边AC上，已知AE＝8厘米，EC＝12厘米，求图中阴影部分的面积。

中考数学复习指导：一道几何旋转变换题的变式训练

一道几何旋转变换题的变式训练如图，分别以△ABC的边AB、AC为一边向外作正方形AEDB和正方形ACFG，连结CE、BG。求证：BG=CE 变式一：条件不变、增加探究结论（2）观察图形猜想CE与BG之间的位置关系，并证明你的猜想。（3）图中哪个三角形是由哪个三角形变换得到？请说出是怎样的变换？变式二：图形旋转，探究原结论（4）正方形AEDB绕点A逆时针方向旋转，使AE与AG重合时，如图（1）上述两个结论是否成立？（5）继续旋转到如图（2）位置，上述两个结论是否成立？

变式三：图形旋转，探究新结论（6）如图（2），连结DF ，求CE :BG :DF 的值. 变式四：添加条件，探索新结论如图，AB ＝11，AC ＝7，连结EG ，求2 2 BC EG +的值变式五：改变图形，探究原结论把“正方形AEDB 和正方形ACFG ”改为“矩形AEDB 、ACFG （长宽不等）”且AG AC AE AB =，线段CE 、BG 有怎样的关系呢？

如图，分别以△ABC 的边AB 、AC 为一边向外作正三角形ABD 和正三角形ACE ，连结CD 、BE 。（1）求证：BE =DC （2）求直线CD 与直线BE 的所夹锐角变式七：根据结论，探究条件如图，在△ABC 中，分别以AB ,AC ,BC 为边在BC 的同侧作等边三角形ABD ,ACE ,BCF （1）求证：四边形DAEF 是平行四边形；（2）探究下列问题 ①当△ABC 满足什么条件时，四边形DAEF 是矩形？ ②当△ABC 满足什么条件时，四边形DAEF 是菱形？ ③当△ABC 满足什么条件时，以D ,A ,E ,F 为顶点的四边形不存在？

初中数学经典几何题(附答案)

初中数学经典几何题（附答案）经典难题（一） 1、已知：如图，O 是半圆的圆心，C 、E 是圆上的两点，CD ⊥AB ，EF ⊥AB ，EG ⊥CO ．求证：CD ＝GF ．（初二） 2、已知：如图，P 是正方形ABCD 内点，∠PAD ＝∠PDA ＝150．求证：△PBC 是正三角形．（初二） A P C D B A F G C E B O D

3、如图，已知四边形ABCD 、A 1B 1C 1D 1都是正方形，A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点．求证：四边形A 2B 2C 2D 2是正方形．（初二） 4、已知：如图，在四边形ABCD 中，AD ＝BC ，M 、 N 分别是AB 、CD 的中点，AD 、BC 的延长线交MN 于E 、F ．求证：∠DEN ＝∠F ． D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A N F E C D M B

经典难题（二） 1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且OM ⊥BC 于M ．（1）求证：AH ＝2OM ；（2）若∠BAC ＝600，求证：AH ＝ 2、设MN 是圆O 外一直线，过O 作OA ⊥MN 于A ，自A 引圆的两条直线，交圆于B 、C 及D 、E ，直线EB 及CD 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二） · A D H E M C B O · G A O D B E C Q P N M

P C G F B Q A D E 3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题：设MN 是圆O 的弦，过MN 的中点A 任作两弦BC 、DE ，设CD 、EB 分别交MN 于P 、Q ．求证：AP ＝AQ ．（初二） 4、如图，分别以△ABC 的AC 和BC 为一边，在△ABC 的外侧作正方形ACDE 和正方形CBFG ，点P 是EF 的中点．求证：点P 到边AB 的距离等于AB 的一半．（初二） · O Q P B D E C N M · A

几何图形初步专项训练

几何图形初步专项训练一、选择题 1．如图，在Rt ABC V 中，90ACB ∠=?，3tan 4B = ，CD 为AB 边上的中线，CE 平分ACB ∠，则AE AD 的值（） A ．35 B ．34 C ．45 D ．67 【答案】D 【解析】【分析】根据角平分线定理可得AE ：BE ＝AC ：BC ＝3:4，进而求得AE ＝37 AB ，再由点D 为AB 中点得AD ＝ 12AB ，进而可求得AE AD 的值．【详解】解：∵CE 平分ACB ∠， ∴点E 到ACB ∠的两边距离相等，设点E 到ACB ∠的两边距离位h ，则S △ACE ＝12AC·h ，S △BCE ＝12 BC·h ， ∴S △ACE ：S △BCE ＝ 12AC·h ：12 BC·h ＝AC ：BC ，又∵S △ACE ：S △BCE ＝AE ：BE ， ∴AE ：BE ＝AC ：BC ， ∵在Rt ABC V 中，90ACB ∠=?，3tan 4B = ， ∴AC ：BC ＝3:4， ∴AE ：BE ＝3:4 ∴AE ＝37 AB ， ∵CD 为AB 边上的中线， ∴AD ＝12 AB ，

∴3 6717 2 AB AE AD AB ==，故选：D ．【点睛】本题主要考查了角平分线定理的应用及三角函数的应用，通过面积比证得AE ：BE ＝AC ：BC 是解决本题的关键． 2．一副直角三角板如图放置，其中∠C =∠DFE =90°，∠A =45°，∠E =60°，点F 在CB 的延长线上．若DE ∥CF ，则∠BDF 等于（） A ．30° B ．25° C ．18° D ．15° 【答案】D 【解析】【分析】根据三角形内角和定理可得45ABC ∠=?和30EDF ∠=?，再根据平行线的性质可得45EDB ABC ==?∠∠，再根据BDF EDB EDF =-∠∠∠，即可求出BDF ∠的度数．【详解】 ∵∠C =90°，∠A =45° ∴18045ABC A C =?--=?∠∠∠ ∵//DE CF ∴45EDB ABC ==?∠∠ ∵∠DFE =90°，∠E =60° ∴18030EDF E DFE =?--=?∠∠∠ ∴15BDF EDB EDF =-=?∠∠∠ 故答案为：D ．【点睛】本题考查了三角板的角度问题，掌握三角形内角和定理、平行线的性质是解题的关键． 3．如图为一直棱柱，其底面是三边长为5、12、13的直角三角形．若下列选项中的图形均由三个矩形与两个直角三角形组合而成，且其中一个为如图的直棱柱的展开图，则根据图形中标示的边长与直角记号判断，此展开图为何？（）

一道解析几何题的研究与思考

一道解析几何题的研究与思考发表时间：2019-07-19T11:45:05.693Z 来源：《中国教师》2019年9月刊作者：李开成 [导读] 解题的正确思路得出后，选择合理的解题方法才能使“思路”迅速、简捷. 训练解题方法的多样化，并从中评选出最佳方案，是提高解题速度、能力的有效方式. 平时应加强一题多解，一题多变的训练。我以一道典型的解析几何题为例，对其进行解法研究和变式思考。李开成浦江职业技术学校 322200 【摘要】解题的正确思路得出后，选择合理的解题方法才能使“思路”迅速、简捷. 训练解题方法的多样化，并从中评选出最佳方案，是提高解题速度、能力的有效方式. 平时应加强一题多解，一题多变的训练。我以一道典型的解析几何题为例，对其进行解法研究和变式思考。【关键词】思维品质；一题多解；一题多变中图分类号：G652.2 文献标识码：A 文章编号：ISSN1672-2051（2019）09-188-02 数学教学大纲在教学目的中提出，数学教学要“注意培养学生良好的思维品质”。怎样更好地实现这个目标呢？我在教学中发现，采用一题多解和一题多变的教学方式是比较有效的途径。所谓一题多解就是对同一问题从不同角度去分析、寻找不同的解题途径。通过一题多解可以沟通各种知识的内在联系，使已学知识形成系统，同时，学生也学会从不同角度去观察思考问题，遇到问题时，能多向联想、随机应变，提高学生的应变能力和思维能力。所谓一题多变，就是不断变换所提供的材料或问题呈现的形式，使事物的非本质特征时隐时现，而事物的本质特征却保持不变。通过变式练习，可以使学生在全面、深刻的理解和掌握知识的同时，思维品质也获得良好的发展。下面我以一个典型的解析几何题为例，对其进行解法研究和变式思考。题目：在椭圆上求一点，使它与两焦点的连线互相垂直。解法1（向量法）设点，由题设知为. ∵，即（1）又点P在椭圆上，∴（2）联立（1）、（2），解得点P的坐标为（3，±4），（－3，±4）. 解法2（交轨法）设点， ∵，∴P点在以F1F2为直径的圆上，即，以下同解法1. 解法3（应用斜率）设， ∴，∴，即.以下同解法1. 解法4（应用焦半径公式）设，∵，则，. ∵，∴， ∴.以下同解法1. 解法5（面积法）设点，则.由椭圆定义知，∴ =180，又，∴， ∴. ∴，，以下同解法1. 解法6（几何法）如图，以坐标原点O为圆心，以|F1F2|为直径画圆与椭圆交于A、B、C、D四点，由直径所对的圆周角是直角可知：当点P位于A、B、C、D四点时，∠F1PF2为直角，以下同解法2. 比较上述六中解法，笔者认为第六种解法最直观，简洁，易懂，让学生能够很清楚地看到点P在什么位置时是直角，锐角，或者钝角,在下面的变式题目中也有很好的启示作用。对本题的思考还没有结束，接着我们对它尝试着做如下的变式训练：变式1：椭圆的两个焦点是F1、F2，，点P为它上面一动点，当∠F1PF2为钝角时，点P的横坐标的取值范围是___________。分析：受原题的启发，无论是钝角还是锐角，都是以直角为参照，该题解法很多，但以几何法最为简洁。当点P位于椭圆上弧AB或弧CD上时，∠F1PF2为钝角；锐角的情况不言而喻，易求点P横坐标的取值范围是。变式2：双曲线的两个焦点为F1、F2，点P在双曲线上，且PF1⊥PF2，则点P到x轴的距离为_____________。分析：该题将原题中的椭圆改为双曲线，而点到x轴的距离等于点的纵坐标的绝对值，以|F1F2|为直径作圆与双曲线的交点（即点P）的坐标，易求点P的纵坐标为，故所求距离为。变式3：已知椭圆的左、右焦点分别为F1、F2，点P在椭圆上，若P、F1、F2为直角三角形的三个顶点，则点P到x轴的距离为（） A. B.3 C. D. 分析：该题是将原题中∠为直角改为△为直角三角形，题中没确定哪个角为直角，从而使该题更具有开放性，当∠=90°时，只要找以|F1F2|为直径的圆与椭圆的交点纵坐标，显然以|F1F2|为直径的圆的方程与椭圆无交点，故此种情况无解；当∠=90°或∠=90°时，易求点P到x轴的距离为，故选D。变式4：已知F1、F2是椭圆C：的两焦点，在C上满足PF1⊥PF2的点P的个数为_____。分析：该题只将求点的坐标改为判断点的个数，但解法是相同的，只是求以|F1F2|为直径的圆与椭圆的交点个数，显然以|F1F2|为直径的圆方程为，与椭圆C：相切于椭圆短轴端点，故点P的个数为2个。变式5：设椭圆的两个焦点是F1（－c，0），F2（c，0），c>0，且椭圆上存在点P，使得PF1与PF2垂直，求实数m的取值范围。分析：显然该题在椭圆中引入参数，将求点的坐标改为“求参数的取值范围”的热点问题，解法是相同的，要使椭圆上存在点使

初中数学经典几何题及答案经典

经典难题（一）仁已知：如图，0是半圆的圆心，C. E是圆上的两点，CD丄AB, EF丄AB, EG丄CO. 求证：CD=GF?（初二） 2、已知：如图，P是正方形ABCD内点，ZPAD=ZPDA=15°. 求证： APBC是正三角形.（初二） 3、如图，已知四边形ABCD、AiBiQDi都是正方形,毗、B2. DDj 的中点. 求证：四边形A2B2C2D2是正方形.（初二） 4、已知：如图，在四边形ABCD中.AD=BC, M、N分别是AB. CD的中点，AD、BC的延长线交MN于E、F. 求证：ZDEN=ZF.

经典难题（二）仁已知：AABC中，H为垂心（各边髙线的交点），0为外心，且0M丄BC于M. （1）求证：AH=20M；（2）若ZBAC = 60°,求证：AH=A0?（初二） 2、设MN是圆0外一直线，过0作0A丄MN于A,自A引圆的两条直线，交圆于B、C及 D、E,直线EB及CD分别交MN于P、Q. 求证：AP=AQ?（初二） 3、如果上题把直线MN 由圆外平移至圆内，则由此可得以下命题: G N A

4、如图，分别以ZkABC的AC和BC为一边?在AABC的外侧作正方形ACDE和正方形CBFG, 点P是EF的中点?

仁如图，四边形ABCD为正方形，DE〃AC, AE=AC, AE与CD相交于F?求证：CE=CF.（初二） 2、如图，四边形ABCD为正方形，DE〃AC,且CE=CA,直线EC交DA延长线于F?求证： AE=AF.（初二）亠 3、设P是正方形A BCD-边BC上的任一点，PF丄AP, CF平分ZDCE. 求证：PA = PF?（初二） 4、如图，PC切圆0于C, AC为圆的直径，PEF为圆的割线，AE、AF与直线P0相交于B、 D.求证：AB = DC, BC=AD?（初三） A C

初中几何题思考方式和解题思路总结,先思后解超简单!

初中几何题思考方式和解题思路总结，先思后解超简单！很多几何证明题的思路往往是填加辅助线，分析已知、求证与图形，探索证明。证明题要掌握三种思考方式 ●正向思维对于一般简单的题目，我们正向思考，轻而易举可以做出，这里就不详细讲述了。 ●逆向思维顾名思义，就是从相反的方向思考问题。在初中数学中，逆向思维是非常重要的思维方式，在证明题中体现的更加明显。同学们认真读完一道题的题干后，不知道从何入手，建议你从结论出发。例如：可以有这样的思考过程：要证明某两条边相等，那么结合图形可以看出，只要证出某两个三角形相等即可；要证三角形全等，结合所给的条件，看还缺少什么条件需要证明，证明这个条件又需要怎样做辅助线，这样思考下去。这样我们就找到了解题的思路，然后把过程正着写出来就可以了。 ●正逆结合对于从结论很难分析出思路的题目，可以结合结论和已知条件认真的分析。初中数学中，一般所给的已知条件都是解题过程中要用到的，所以可以从已知条件中寻找思路，比如给我们三角形某边中点，我们就要想到是否要连出中位线，或者是否要用到中点倍长法。

给我们梯形，我们就要想到是否要做高，或平移腰，或平移对角线，或补形等等。正逆结合，战无不胜。要掌握初中数学几何证明题技巧，熟练运用和记忆如下原理是关键。下面归类一下，多做练习，熟能生巧，遇到几何证明题能想到采用哪一类型原理来解决问题。证明题要用到哪些原理 ●证明两线段相等 1.两全等三角形中对应边相等。 2.同一三角形中等角对等边。 3.等腰三角形顶角的平分线或底边的高平分底边。 4.平行四边形的对边或对角线被交点分成的两段相等。 5.直角三角形斜边的中点到三顶点距离相等。 6.线段垂直平分线上任意一点到线段两段距离相等。 7.角平分线上任一点到角的两边距离相等。 8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。 9.同圆（或等圆）中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。 10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。 11.两前项（或两后项）相等的比例式中的两后项（或两前项）相等。 12.两圆的内（外）公切线的长相等。 13.等于同一线段的两条线段相等。 ●证明两个角相等 1.两全等三角形的对应角相等。

初中数学变式习题的设计

数学变式习题的设计习题是训练学生的思维材料，是教师将自己的思想、方法以及分析问题和解决问题的技能技巧施达于学生的载体。要想不被千变万化的表象所迷惑，抓住本质的东西，变式教学是一种有效的办法。通常可以利用习题变式训练学生的思维，使学生在多变的问题中受到磨练，举一反三，加深理解。如将练习中的条件或结论做等价性变换，变更练习的形式或内容，形成新的练习变式，可有助于学生对问题理解的逐步深化。下面本人结合理论学习和数学课堂教学的实践，谈谈在数学教学中如何进行变式训练培养学生的思维能力。一、利用变式来改变题目的条件或结论，培养学生转化、推理、归纳、探索的思维能力。（一）、一题多问，通过变式培养学生的创新意识和探究、概括能力牛顿说过：“没有大胆的猜想就做不出伟大的发现。”中学生的想象力丰富，因此，可以通过例题所提供的结构特点，鼓励、引导学生大胆地猜想，以培养学生的创造性思维和发散思维。例题1．如图（1）已知△ABC中，∠BAC的平分线与边BC和外接圆分别相交于点D和E.求证：△ABD∽△AEC 此题是很简单的证明题，将图形变式，添加切线BF，则可变为： [变式训练]1. 如图（2）已知△ABC中，∠BAC的平分线与边BC和外接圆分别相交于点D和E.过B作⊙O的切线交CE延长线与F点. 求证：CE:BC=BF:CF 本题需证△BEF∽△CBF,若将条件进一步发展，延长AD交BF于N，则有： 2. 如图（3）已知△ABC中，∠BAC的平分线与边BC和外接圆分别相交于点D和 E.过B作⊙O的切线交CE延长线于F点,交AE延长线于N点. 求证：BN·DE=BD·EN 本题需证BE平分∠FBC和△ABD∽△CDE，并借助中间比推证，若再将F为BF、CE交点改为F是由C点作切线BN垂线的垂足，则又变为： 3. 如图（4）已知△ABC中，∠BAC的平分线与边BC和外接圆分别相交于点D和 E.过B作⊙O的切线交AE延长线于N点,作EF⊥BN. 求证：BN·DE=BD·EN