2.1矩阵的概念及其运算(精)

矩阵行列式的概念与运算
知识点总结: 一、矩阵的概念与运算 1、 矩阵1112 132122 23a a a a a a ?? ??? 中的行向量是()111213a a a a =r ,()2122 23b a a a =r ; 2、 如:1112131112111221222321222122,,c c c a a b b A B C c c c a a b b ?? ???? === ? ? ??????? ,那么 11111212111221212222212233,333a b a b a a A B A a b a b a a ++???? +== ? ? ++????, 1111122111121222 111312232111222121122222 21132223a c a c a c a c a c a c AC a c a c a c a c a c a c +++?? = ?+++?? 矩阵加法满足交换律和结合律,即如果,,A B C 是同阶的矩阵,那么有: ,()()A B B A A B C A B C +=+++=++。 同理如果矩阵,A B 是两个同阶矩阵,那么将它们对应位置上的元素相减所得到的矩阵C 叫做矩阵A 与B 的差,记作C A B =-。 实数与矩阵的乘法满足分配律:即()a A B aA aB +=+。 矩阵对乘法满足:()A B C AB AC +=+,()B C A BA CA +=+,()()()a AB aA B A aB == ()()AB C A BC = 3、 矩阵乘法不满足交换率,如111 11 11 122222222.a b c d c d a b a b c d c d a b ????????≠ ??? ??????????? 矩阵乘法能进行的条件是左边的矩阵A 的列数与右边矩阵B 的行数相等,而且矩阵的乘法不满足交换率,不满足消去律。 二、行列式概念及运算 1.用记号 2 2 11b a b a 表示算式1221b a b a -,即 2 2 11b a b a =1221b a b a -,其中 2 2 11b a b a 叫做二阶行列 式;算式1221b a b a -叫做二阶行列式的展开式;其计算结果叫做行列式的值;2121,,,b b a a 都叫做行列式的元素.利用对角线 2 2 11b a b a 可把二阶行式写成它的展开式,这种方法叫做二阶行列式 展开的对角线法则;即在展开时用主对角线元素的乘积减去副对角线元素的乘积. 2.二元一次方程组的解 二元一次方程组???=+=+222 1 11c y b x a c y b x a (其中2121,,,b b a a 不全为零);记 2 211b a b a 叫做方程组的系数
矩阵的定义及其运算规则
矩阵的定义及其运算规则 1、矩阵的定义 一般而言,所谓矩阵就是由一组数的全体,在括号()内排列成m行n 列(横的称行,纵的称列)的一个数表,并称它为m×n阵。 矩阵通常是用大写字母 A 、B …来表示。例如一个m 行n 列的矩阵可以简记为: ,或 。即: (2-3) 我们称(2-3)式中的为矩阵A的元素,a的第一个注脚字母,表示矩阵的行数,第二个注脚字母j(j=1,2,…,n)表示矩阵的列数。 当m=n时,则称为n阶方阵,并用表示。当矩阵(a ij)的元素仅有一行或一列时,则称它为行矩阵或列矩阵。设两个矩阵,有相同的行数和相同的列数,而且它们的对应元素一一相等,即,则称该两矩阵相等,记为A=B。 2、三角形矩阵 由i=j的元素组成的对角线为主对角线,构成这个主对角线的元素称为主对角线元素。 如果在方阵中主对角线一侧的元素全为零,而另外一侧的元素不为零或不全为零,则该矩阵叫做三角形矩阵。例如,以下矩阵都是三角形矩阵: ,,,。 3、单位矩阵与零矩阵 在方阵中,如果只有的元素不等于零,而其他元素全为零,如: 则称为对角矩阵,可记为。如果在对角矩阵中所有的彼此
都相等且均为1,如:,则称为单位矩阵。单位矩阵常用E来表示,即: 当矩阵中所有的元素都等于零时,叫做零矩阵,并用符号“0”来表示。 4、矩阵的加法 矩阵A=(a ij)m×n和B=(b ij)m×n相加时,必须要有相同的行数和列数。如以C=(c ij)表示矩阵A及B的和,则有: m ×n 式中:。即矩阵C的元素等于矩阵A和B的对应元素之和。 由上述定义可知,矩阵的加法具有下列性质(设A、B、C都是m×n矩阵): (1)交换律:A+B=B+A (2)结合律:(A+B)+C=A+(B+C) 5、数与矩阵的乘法 我们定义用k右乘矩阵A或左乘矩阵A,其积均等于矩阵中的所有元素都乘上k之后所得的矩阵。如: 由上述定义可知,数与矩阵相乘具有下列性质:设A、B都是m×n矩阵,k、h为任意常数,则: (1)k(A+B)=kA+kB (2)(k+h)A=kA+hA (3)k(hA)=khA
矩阵的运算及其运算规则
矩阵基本运算及应用 201700060牛晨晖 在数学中,矩阵是一个按照长方阵列排列的复数或实数集合。矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。在电力系统方面,矩阵知识已有广泛深入的应用,本文将在介绍矩阵基本运算和运算规则的基础上,简要介绍其在电力系统新能源领域建模方面的应用情况,并展望随机矩阵理论等相关知识与人工智能电力系统的紧密结合。 1矩阵的运算及其运算规则 1.1矩阵的加法与减法 1.1.1运算规则 设矩阵,, 则
简言之,两个矩阵相加减,即它们相同位置的元素相加减! 注意:只有对于两个行数、列数分别相等的矩阵(即同型矩阵),加减法运算才有意义,即加减运算是可行的. 1.1.2运算性质 满足交换律和结合律 交换律; 结合律. 1.2矩阵与数的乘法 1.2.1运算规则 数乘矩阵A,就是将数乘矩阵A中的每一个元素,记为或. 特别地,称称为的负矩阵. 1.2.2运算性质 满足结合律和分配律 结合律:(λμ)A=λ(μA);(λ+μ)A =λA+μA. 分配律:λ(A+B)=λA+λB.
已知两个矩阵 满足矩阵方程,求未知矩阵. 解由已知条件知 1.3矩阵与矩阵的乘法 1.3.1运算规则 设,,则A与B的乘积是这样一个矩阵: (1) 行数与(左矩阵)A相同,列数与(右矩阵)B相同,即 . (2) C的第行第列的元素由A的第行元素与B的第列元素对应相乘,再取乘积之和.
第一讲 矩阵的概念、运算
第一讲 Ⅰ 授课题目(章节): §2.1 矩阵的概念; §2.2 矩阵的计算 Ⅱ 教学目的与要求: 理解矩阵概念; 掌握矩阵的线性运算、乘法、转置及其运算规律。 Ⅲ 教学重点与难点: 矩阵的乘法 Ⅳ 讲授内容: §2.1 矩阵 定义2.1 由n m ?个数),,2,,1;,,2,1(n j m a ij =排成的m 行n 列的数表 mn m m n n a a a a a a a a a 21222 21112 11 称为m 行n 列矩阵,简称n m ?矩阵.为表示它是一个整体,总是加一个括弧,并用大写黑体字母表示它,记作 ??????? ??=?mn m m n n n m a a a a a a a a a A 212222111211 两个矩阵B A ,,如果都是m 行n 列的,称它们是同型矩阵。否则,称它们是不同型的。 n 行n 列的矩阵n n A ?称为n 阶矩阵(或n 阶方阵) ,简记为n A 。 只有一行的矩阵)(21n a a a A =称为行矩阵,又称行向量.只有一列的矩阵 ?????? ? ??=n b b b B 21 称为列矩阵,又称列向量. 定义2.2 如果)()(ij ij b B a A ==与是同型矩阵,并且它的对应元素相等 ,即
),,2,1;,,2,1(,n j m i b a ij ij === 那么就称矩阵A 与B 相等,记作B A =. 元素都是零的m 行n 列矩阵称为零矩阵,记作n m O ?,简记为O .不同型的零矩阵是 不同的. ??????? ??=100010001 n I 称为n 阶单位矩阵,简记作I .这个矩阵的特点是:从左上角到右下角的直线(叫做主对角线)上的元素都是1,其它元素都是0. §2.2 矩阵的运算 1. 矩阵的加法 定义2.3 设有两个n m ?矩阵)(),(ij ij b B a A ==,那么矩阵A 与B 的和记作A +B , 规定为 n m ij ij b a B A ?+=+)( 设矩阵)(),(ij ij a A a A -=-=记,A -称为矩阵A 的负矩阵.显然有 0)(=-+A A . 规定矩阵的减法为)(B A B A -+=-. 2. 数与矩阵相乘: 定义2.4 数λ与矩阵)(ij a A =的乘积记作A λ,规定为n m ij a A ?=)(λλ 数乘矩阵满足下列运算规律(设B A ,为同型矩阵,μλ,为数): )(i )()(A A μλλμ= )(ii A A A μλμλ+=+)( )(iii B A B A λλλ+=+)( 3. 矩阵与矩阵相乘: 定义 2.5 设)(ij a A =是一个s m ?矩阵,)(ij b B =是一个n s ?矩阵,那么规定矩阵
矩阵的各种运算详解
一、矩阵的线性运算 定义1 设有两个矩阵和,矩阵与的和记作, 规定为 注:只有两个矩阵是同型矩阵时,才能进行矩阵的加法运算. 两个同型矩阵的和,即为两个矩阵对应位置元素相加得到的矩阵. 设矩阵记 , 称为矩阵的负矩阵, 显然有 . 由此规定矩阵的减法为 . 定义2 数与矩阵A的乘积记作或, 规定为 数与矩阵的乘积运算称为数乘运算. 矩阵的加法与矩阵的数乘两种运算统称为矩阵的线性运算. 它满足下列运算规律: 设都是同型矩阵,是常数,则 (1) (2) ; (3) (4) (5) (6) (7) (8) 注:在数学中,把满足上述八条规律的运算称为线性运算. 二、矩阵的相乘 定义3设 矩阵与矩阵的乘积记作, 规定为
其中,( 记号常读作左乘或右乘. 注: 只有当左边矩阵的列数等于右边矩阵的行数时, 两个矩阵才能进行乘法运算. 若,则矩阵的元素即为矩阵的第行元素与矩阵的第列对应元素乘积的和. 即 . 矩阵的乘法满足下列运算规律(假定运算都是可行的): (1) (2) (3) (4) 注: 矩阵的乘法一般不满足交换律, 即 例如, 设则 而 于是且 从上例还可看出: 两个非零矩阵相乘, 可能是零矩阵, 故不能从必然推出 或 此外, 矩阵乘法一般也不满足消去律,即不能从必然推出例如, 设 则 但 定义4如果两矩阵相乘, 有 则称矩阵A与矩阵B可交换.简称A与B可换. 注:对于单位矩阵, 容易证明 或简写成 可见单位矩阵在矩阵的乘法中的作用类似于数1. 更进一步我们有
命题1设是一个n阶矩阵,则是一个数量矩阵的充分必要条件是与任何n阶矩阵可换。 命题2设均为n阶矩阵,则下列命题等价:
MATLAB实验二 矩阵基本运算(一)答案
实验一 矩阵基本运算(一) (1)设A 和B 是两个同维同大小的矩阵,问: 1)A*B 和A.*B 的值是否相等? ????? ?? =763514432A ???? ? ??=94 525 313 4B A=[2 3 4;4 1 5;3 6 7]; B=[4 3 1;3 5 2;5 4 9]; A*B, A.*B ans = 37 37 44 44 37 51 65 67 78 ans = 8 9 4 12 5 10 15 24 63 2)A./B 和B.\A 的值是否相等? A=[2 3 4;4 1 5;3 6 7]; B=[4 3 1;3 5 2;5 4 9]; A./B, B./A
ans = 0.5000 1.0000 4.0000 1.3333 0.2000 2.5000 0.6000 1.5000 0.7778 ans = 2.0000 1.0000 0.2500 0.7500 5.0000 0.4000 1.6667 0.6667 1.2857 3)A/B和B\A的值是否相等? A=[2 3 4;4 1 5;3 6 7]; B=[4 3 1;3 5 2;5 4 9]; A/B, B/A ans = -0.3452 0.5119 0.3690 0.7857 -0.7857 0.6429 -0.9762 1.3095 0.5952 ans = 110.0000 -15.0000 -52.0000
92.0000 -13.0000 -43.0000 -22.0000 4.0000 11.0000 4)A/B和B\A所代表的数学含义是什么? 解: A/B是B*A的逆矩阵 B\A是B*A的逆矩阵 (2)写出完成下列操作的命令。 1)将矩阵A第2—5行中第1,3,5列元素赋给矩阵B。 A=[0.9501 0.4565 0.9218 0.4103 0.1389 0.0153 0.2311 0.0185 0.7382 0.8936 0.2028 0.7468 0.6068 0.8214 0.1763 0.0579 0.1987 0.4451 0.4860 0.4447 0.4057 0.3529 0.6038 0.9318 0.8913 0.6154 0.9355 0.8132 0.2722 0.4660 0.7621 0.7919 0.9169 0.0099 0.1988 0.4186] B=A(2:5,[1,3,5]) A = 0.9501 0.4565 0.9218 0.4103 0.1389 0.0153 0.2311 0.0185 0.7382 0.8936 0.2028 0.7468 0.6068 0.8214 0.1763 0.0579 0.1987 0.4451 0.4860 0.4447 0.4057 0.3529 0.6038 0.9318 0.8913 0.6154 0.9355 0.8132 0.2722 0.4660 0.7621 0.7919 0.9169 0.0099 0.1988 0.4186 B = 0.2311 0.7382 0.2028 0.6068 0.1763 0.1987 0.4860 0.4057 0.6038 0.8913 0.9355 0.2722 2)删除矩阵A的第7号元素。 A=rand(6,6); >> A(7)=[inf] A = 0.8385 Inf 0.1730 0.1365 0.2844 0.5155
矩阵的概念和运算
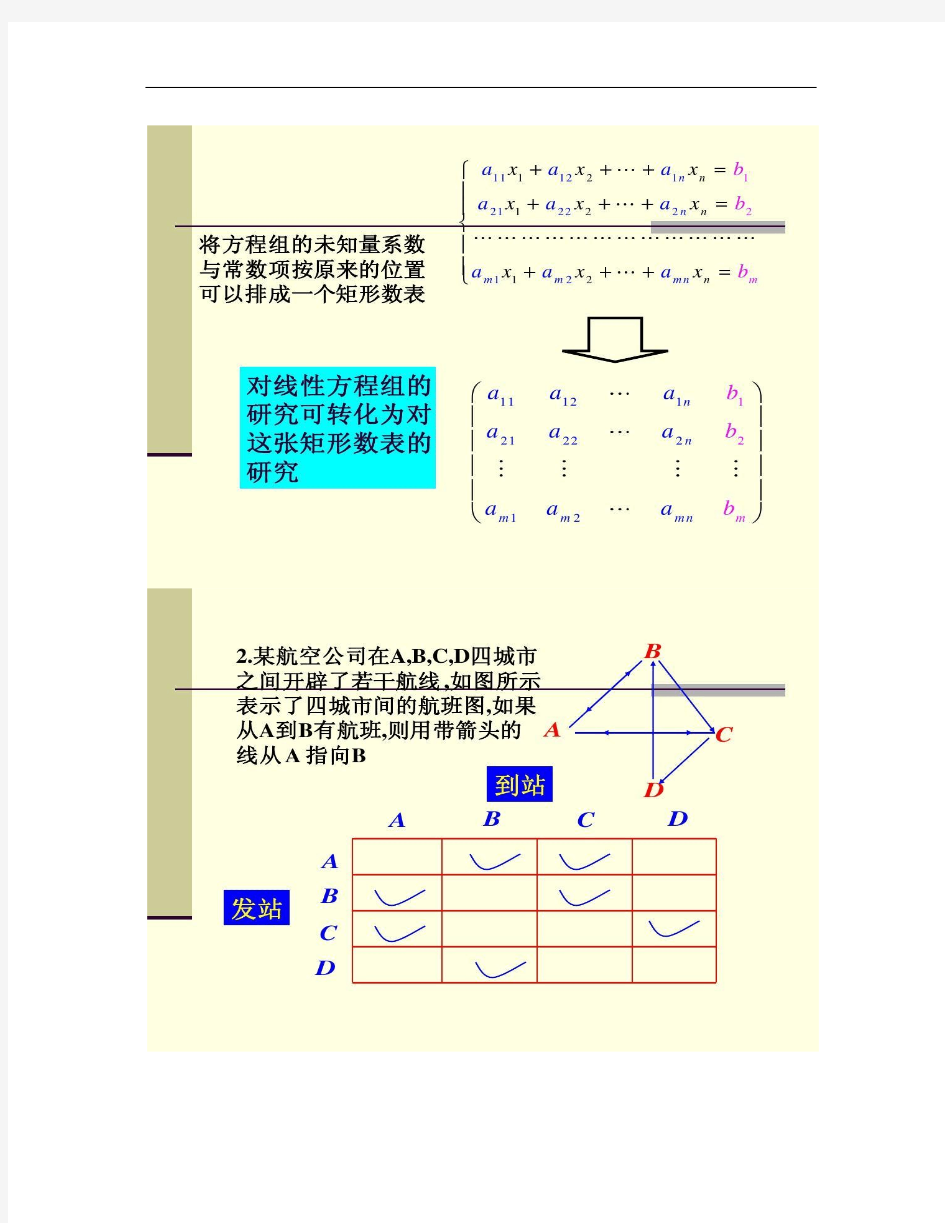
1。4 矩阵的概念和运算 教学要求 : (1) 掌握矩阵的加减、数与矩阵相乘的运算。 (2) 会矩阵相乘运算掌握其算法规则 ( 以便演示算法规则及行列间的对应关系〉 教学内容: 前面介绍了利用行列式求解线性方程组,即Cramer 法则。但是Cramer 法则有它的局限性: 1.0 2. D ≠?? ?所解的线性方程组存在系数行列式(行数=列数) 同学们接下来要学习的还是关于解线性方程组,即Cramer 法则无法用上的-――用“矩阵”的方法解线性方程组。本节课主要学习矩阵的概念。 一.矩阵的概念 123123123 23124621x x x x x x x x x -+=?? -+-=-??+-=? 它的系数行列式 1 232 4601 1 1 D -=--=- 此时Cramer 法则失效,我们可换一种形式来表示: 123124621111A ?-? ?=--- ? ?-?? 这正是“换汤不换药”, 以上线性方程组可用这张“数表”来表示,二者之间互相翻译。 这种数表一般用圆括号或中括号括起来,排成一个长方形阵式,《孙子兵法》中说道:长方形阵为矩阵。 123246111A -?? ?=-- ? ?-?? 这也是矩阵,是由以上线性方程组的系数按照原来顺序排列而成,称为“系数矩阵” 而“A ”多了一列常数列,称为以上方程组的“增广矩阵”。 注意:虽然D 和A 很相像,但是区别很大。D 是行列式,实质上是一个数,而A 是一张表格,“数是数,表是表,数不是表,表也不是数”,这是本质意义上不同。况且,行列式行数必须与列数相同,矩阵则未必。 关于以上线性方程组我们后面将介绍。 更一般地,对于线性方程组:
矩阵行列式的概念与运算(标准答案)
矩阵、行列式的概念与运算 知识点总结: 一、矩阵的概念与运算 1、 矩阵1112 132122 23a a a a a a ?? ??? 中的行向量是()111213a a a a =r ,()2122 23b a a a =r ; 2、 如:111213111211122122 2321222122,,c c c a a b b A B C c c c a a b b ?? ???? === ? ? ? ?????? ,那么 11111212111221212222212233,333a b a b a a A B A a b a b a a ++???? +== ? ? ++????, 1111122111121222 111312232111222121122222 21132223a c a c a c a c a c a c AC a c a c a c a c a c a c +++?? = ?+++?? 矩阵加法满足交换律和结合律,即如果,,A B C 是同阶的矩阵,那么有: ,()()A B B A A B C A B C +=+++=++。 同理如果矩阵,A B 是两个同阶矩阵,那么将它们对应位置上的元素相减所得到的矩阵C 叫做矩阵A 与B 的差,记作C A B =-。 实数与矩阵的乘法满足分配律:即()a A B aA aB +=+。 矩阵对乘法满足:()A B C AB AC +=+,()B C A BA CA +=+,()()()a AB aA B A aB == ()()AB C A BC = 3、 矩阵乘法不满足交换率,如1 11 11 11 122222222.a b c d c d a b a b c d c d a b ????????≠ ??? ??????????? 矩阵乘法能进行的条件是左边的矩阵A 的列数与右边矩阵B 的行数相等,而且矩阵的乘法不满足交换率,不满足消去律。 二、行列式概念及运算 1.用记号 2 2 11b a b a 表示算式1221b a b a -,即 2 2 11b a b a =1221b a b a -,其中 2 2 11b a b a 叫做二阶行列式; 算式1221b a b a -叫做二阶行列式的展开式;其计算结果叫做行列式的值;2121,,,b b a a 都叫做行列式的元素.利用对角线 2 2 11b a b a 可把二阶行式写成它的展开式,这种方法叫做二阶行列式展开的 对角线法则;即在展开时用主对角线元素的乘积减去副对角线元素的乘积. 2.二元一次方程组的解
矩阵的概念及其线性运算
第二章 矩阵 §2.1 矩阵的概念及其线性运算 学习本节内容,特别要注意与行列式的有关概念、运算相区别。 一.矩阵的概念 矩阵是一张简化了的表格,一般地 ?????? ? ??mn m m n n a a a a a a a a a 212222111211 称为n m ?矩阵,它有m 行、n 列,共n m ?个元素,其中第i 行、第j 列的元素 用j i a 表示。通常我们用大写黑体字母A 、B 、C ……表示矩阵。为了标明矩阵的行数m 和列数n ,可用n m ?A 或() i j m n a ?表示。矩阵既然是一张表,就不能象行 列式那样算出一个数来。 所有元素均为0的矩阵,称为零矩阵,记作O 。 两个矩阵A 、B 相等,意味着不仅它们的行、列数相同,而且所有对应元素都相同。记作B A =。 如果矩阵A 的行、列数都是n ,则称A 为n 阶矩阵,或称为n 阶方阵。n 阶矩阵有一条从左上角到右下角的主对角线。n 阶矩阵A 的元素按原次序构成的n 阶行列式,称为矩阵A 的行列式,记作A 。 在n 阶矩阵中,若主对角线左下侧的元素全为零,则称之为上三角矩阵;若主对角线右上侧的元素全为零,则称之为下三角矩阵;若主对角线两侧的元素全为零,则称之为对角矩阵。主对角线上元素全为1的对角矩阵,叫做单位矩阵,记为E ,即 ???? ?? ? ??=100010001 E n ?1矩阵(只有一行)又称为n 维行向量;1?n 矩阵(只有一列)又称为n 维列向量。行向量、列向量统称为向量。向量通常用小写黑体字母a ,b ,x ,y …… 表示。向量中的元素又称为向量的分量。11?矩阵因只有一个元素,故视之为数量,即()a a =。 二.矩阵的加、减运算 如果矩阵A 、B 的行数和列数都相同,那么它们可以相加、相减,记为B A +、B A -。分别称为矩阵A 、B 的和与差。B A ±表示将A 、B 中所有对应位置的元素相加、减得到的矩阵。例如
矩阵的基本概念
§1 矩阵及其运算 教学要求:理解矩阵的定义、掌握矩阵的基本律、掌握几类特殊矩阵(比如零矩阵,单位矩阵,对称矩阵和反对称矩阵 ) 的定义与性质、注意矩阵运算与通常数的运算异同。能熟练正确地进行矩阵的计算。 知识要点: 一、矩阵的基本概念 矩阵,是由个数组成的一个行列的矩形表格,通常用大写字母表示,组成矩阵的每一个数,均称为矩阵的元素,通常用小写字母其元素表示,其中下标都是正整 数,他们表示该元素在矩阵中的位置。比如, 或表示一个矩阵,下标表示元素位于该矩阵的第行、第列。元素全为零的矩阵称为零矩阵。 特别地,一个矩阵,也称为一个维列向量;而一个矩阵,也称为一个维行向量。
当一个矩阵的行数与烈数相等时,该矩阵称为一个阶方阵。对于方阵,从左上角到右下角的连线,称为主对角线;而从左下角到右上角的连线称为付对角线。若一个阶方阵的主对角线上的元素都是,而其余元素都是零,则称为单位矩阵,记为,即: 。如一个阶方阵的主对角线上(下)方的元素都是零,则称为下(上)三角矩阵,例如,是 一个阶下三角矩阵,而则是一个阶上三角矩阵。今后我们用表示数域上的矩阵构成的集合,而用或者表示数域上的阶方阵构成的集合。 二、矩阵的运算 1、矩阵的加法:如果是两个同型矩阵(即它们具有相同的行数和列数,比如说),则定义它们的和 仍为与它们同型的矩阵(即),的元素为和对应元素的和,即:。 给定矩阵,我们定义其负矩阵为:。这样我们可以定义同型矩阵的减法为:。由于矩阵的加
法运算归结为其元素的加法运算,容易验证,矩阵的加法满足下列运算律: ( 1)交换律:; ( 2)结合律:; ( 3)存在零元:; ( 4)存在负元:。 2 、数与矩阵的乘法: 设为一个数,,则定义与的乘积仍为中的一个矩阵,中的元素就是用数乘中对应的元素的道德,即。由定义可知:。容易验证数与矩阵的乘法满足下列运算律: (1 ); (2 ); (3 ); (4 )。 3 、矩阵的乘法:
矩阵的定义及其运算规则
矩阵的定义及其运算规则
矩阵的定义及其运算规则 1、矩阵的定义 一般而言,所谓矩阵就是由一组数的全体,在括号()内排列成m行n 列(横的称行,纵的称列)的一个数表,并称它为m×n阵。 矩阵通常是用大写字母A 、B …来表示。例如一个m 行n 列的矩阵可以简记为:,或 。即: (2-3)我们称(2-3)式中的为矩阵A的元素,a 的第一个注脚字母,表示矩阵的行数,第二个注脚字母j(j=1,2,…,n)表示矩阵的列数。 当m=n时,则称为n阶方阵,并用 表示。当矩阵(a ij)的元素仅有一行或一列时,则称它为行矩阵或列矩阵。设两个矩阵,有相同的行数和相同的列数,而且它们的对应元素一一相等,即,则称该两矩阵相等,记为A=
B。 2、三角形矩阵 由i=j的元素组成的对角线为主对角线,构成这个主对角线的元素称为主对角线元素。 如果在方阵中主对角线一侧的元素全为零,而另外一侧的元素不为零或不全为零,则该矩阵叫做三角形矩阵。例如,以下矩阵都是三角形矩阵: ,,,。 3、单位矩阵与零矩阵 在方阵中,如果只有的元素不等于零,而其他元素全为零,如: 则称为对角矩阵,可记为。如果在对角矩阵中所有的彼此都相等且均为1,
如:,则称为单位矩阵。单位矩阵常用E来表示,即: 当矩阵中所有的元素都等于零时,叫做零矩 阵,并用符号“0”来表示。 4、矩阵的加法 矩阵A=(a ij)m×n和B=(b ij)m×n相加时,必须要有相同的行数和列数。如以C=(c ij)m ×n 表示矩阵A及B的和,则有: 式中:。即矩阵C的元素等于矩阵A和B 的对应元素之和。 由上述定义可知,矩阵的加法具有下列性质(设A、B、C都是m×n矩阵): (1)交换律:A+B=B+A
矩阵的概念及其线性运算
.. 第二章 矩阵 §2.1 矩阵的概念及其线性运算 学习本节内容,特别要注意与行列式的有关概念、运算相区别。 一.矩阵的概念 矩阵是一张简化了的表格,一般地 ?????? ? ??mn m m n n a a a a a a a a a ΛΛΛΛΛΛΛ212222111211 称为n m ?矩阵,它有m 行、n 列,共n m ?个元素,其中第i 行、第j 列的元素 用j i a 表示。通常我们用大写黑体字母A 、B 、C ……表示矩阵。为了标明矩阵的行数m 和列数n ,可用n m ?A 或() i j m n a ?表示。矩阵既然是一张表,就不能象行 列式那样算出一个数来。 所有元素均为0的矩阵,称为零矩阵,记作O 。 两个矩阵A 、B 相等,意味着不仅它们的行、列数相同,而且所有对应元素都相同。记作B A =。 如果矩阵A 的行、列数都是n ,则称A 为n 阶矩阵,或称为n 阶方阵。n 阶矩阵有一条从左上角到右下角的主对角线。n 阶矩阵A 的元素按原次序构成的n 阶行列式,称为矩阵A 的行列式,记作A 。 在n 阶矩阵中,若主对角线左下侧的元素全为零,则称之为上三角矩阵;若主对角线右上侧的元素全为零,则称之为下三角矩阵;若主对角线两侧的元素全为零,则称之为对角矩阵。主对角线上元素全为1的对角矩阵,叫做单位矩阵,记为E ,即 ?????? ? ? ?=10 0010001Λ ΛΛΛΛΛΛE n ?1矩阵(只有一行)又称为n 维行向量;1?n 矩阵(只有一列)又称为n 维列 向量。行向量、列向量统称为向量。向量通常用小写黑体字母a ,b ,x ,y ……表示。向量中的元素又称为向量的分量。11?矩阵因只有一个元素,故视之为数量,即()a a =。 二.矩阵的加、减运算 如果矩阵A 、B 的行数和列数都相同,那么它们可以相加、相减,记为B A +、B A -。分别称为矩阵A 、B 的和与差。B A ±表示将A 、B 中所有对应位置的元素相加、减得到的矩阵。例如
矩阵的定义及其运算规则
矩阵的定义及其运算规则 This model paper was revised by the Standardization Office on December 10, 2020
矩阵的定义及其运算规则 1、矩阵的定义 一般而言,所谓矩阵就是由一组数的全体,在括号()内排列成m行n 列(横的称行,纵的称列)的一个数表,并称它为m×n阵。 矩阵通常是用大写字母A 、B …来表示。例如一个m 行n 列的矩阵可以简记为:,或 。即: (2-3) 我们称(2-3)式中的为矩阵A的元素,a的第一个注脚字母,表示矩阵的行数,第二个注脚字母j(j=1,2,…,n)表示矩阵的列数。 当m=n时,则称为n阶方阵,并用表示。当矩阵(a )的元素仅有一 ij 行或一列时,则称它为行矩阵或列矩阵。设两个矩阵,有相同的行数和相同的列数,而且它们的对应元素一一相等,即,则称该两矩阵相等,记为A=B。 2、三角形矩阵 由i=j的元素组成的对角线为主对角线,构成这个主对角线的元素称为主对角线元素。 如果在方阵中主对角线一侧的元素全为零,而另外一侧的元素不为零或不全为零,则该矩阵叫做三角形矩阵。例如,以下矩阵都是三角形矩阵:
,,,。 3、单位矩阵与零矩阵 在方阵中,如果只有的元素不等于零,而其他元素全为零,如: 则称为对角矩阵,可记为。如果在对角矩阵中所有的彼此都相等且均为1,如:,则称为单位矩阵。单位矩阵常用E来表示,即: 当矩阵中所有的元素都等于零时,叫做零矩阵,并用符号“0”来表示。 4、矩阵的加法 矩阵A=(a ij ) m×n 和B=(b ij ) m×n 相加时,必须要有相同的行数和列数。如以C= (c ij ) m ×n 表示矩阵A及B的和,则有: 式中:。即矩阵C的元素等于矩阵A和B的对应元素之和。
矩阵行列式的概念与运算标准答案
矩阵、行列式的概念与运算 知识点总结: 一、矩阵的概念与运算 1、 矩阵111213212223a a a a a a ?? ??? 中的行向量是()111213a a a a =,()212223b a a a =; 2、 如:111213111211122122 2321222122,,c c c a a b b A B C c c c a a b b ?? ???? === ? ? ??????? ,那么 11111212111221212222212233,333a b a b a a A B A a b a b a a ++???? +== ? ? ++????, 11111221 11121222111312232111222121122222 21132223a c a c a c a c a c a c AC a c a c a c a c a c a c +++?? = ?+++?? 矩阵加法满足交换律和结合律,即如果,,A B C 是同阶的矩阵,那么有: ,()()A B B A A B C A B C +=+++=++。 同理如果矩阵,A B 是两个同阶矩阵,那么将它们对应位置上的元素相减所得到的矩阵C 叫做矩阵A 与B 的差,记作C A B =-。 实数与矩阵的乘法满足分配律:即()a A B aA aB +=+。 矩阵对乘法满足:()A B C AB AC +=+,()B C A BA CA +=+,()()()a AB aA B A aB == ()()AB C A BC = 3、 矩阵乘法不满足交换率,如1 11 11 11 122222222.a b c d c d a b a b c d c d a b ????????≠ ??? ??????????? 矩阵乘法能进行的条件是左边的矩阵A 的列数与右边矩阵B 的行数相等,而且矩阵的乘法不满足交换率,不满足消去律。 二、行列式概念及运算 1.用记号 2 2 11b a b a 表示算式1221b a b a -,即2 2 11b a b a =1221b a b a -,其中 2 2 11b a b a 叫做 二阶行列式;算式1221b a b a -叫做二阶行列式的展开式;其计算结果叫做行列式的值;2121,,,b b a a 都叫做行列式的元素.利用对角线 2 2 11b a b a 可把二阶行式写成
矩阵概念及运算
第一讲 矩阵概念及运算 一、矩阵概念 矩阵是本课程的一个重要概念,在生产活动和日常生活中,我们常常用数表表示一些量或关系,如工厂中的产量统计表,市场上的价目表等等. 例1 某户居民第二季度每个月水(单位:吨)、电(单位:千瓦时)、天然气(单位:立方米)的使用情况,可以用一个三行三列的数表表示为 水 电 气 ?? ?? ??????16210101519010141659 由例1以及教材中的例子可以看到,对于不同的问题可以用不同的数表来表 示,我们将这些数表统称为矩阵. 定义2.1 有m ?n 个数排列成一个m 行n 列,并括以方括弧(或圆括弧)的数表 ????? ???????mn m m n n a a a a a a a a a 212222111211 称为m 行n 列矩阵,简称m ?n 矩阵.矩阵通常用大写字母A , B , C …表示. 记作 [] n m ij a A ?= 其中a ij (i = 1, 2, …, m ;j = 1, 2, …, n )称为矩阵A 的第i 行第j 列元素. 注:矩阵的行数m 与列数n 可能相等,也可能不等. 特别地,当m = 1时,即 A = []n a a a 11211 称为行矩阵.当n = 1时,即 A = ????? ???????121 11m a a a 称为列矩阵.当m = n 时,即 A = ????? ???????nn n n n n a a a a a a a a a 212222111211 称为n 阶矩阵,或n 阶方阵. (再介绍几个特殊矩阵) 所有元素全为零的m ?n 矩阵,称为零矩阵,记作O m n ?或O .例如 4月 5月 6月
矩阵的定义及其运算规则
矩阵得定义及其运算规则 1、矩阵得定义 一般而言,所谓矩阵就就是由一组数得全体,在括号内排列成m行n 列(横得称行,纵得称列)得一个数表,并称它为m×n阵。 矩阵通常就是用大写字母A 、B …来表示。例如一个m 行n 列得矩阵可以简记为:,或 。即: (23) 我们称(23)式中得为矩阵A得元素,a得第一个注脚字母,表示矩阵得行数,第二个注脚字母j(j=1,2,…,n)表示矩阵得列数。 当m=n时,则称为n阶方阵,并用表示。当矩阵(a ij)得元素仅有一行或一列时,则称它为行矩阵或列矩阵。设两个矩阵,有相同得行数与相同得列数,而且它们得对应元素一一相等,即,则称该两矩阵相等,记为A=B。 2、三角形矩阵 由i=j得元素组成得对角线为主对角线,构成这个主对角线得元素称为主对角线元素。 如果在方阵中主对角线一侧得元素全为零,而另外一侧得元素不为零或不全为零,则该矩阵叫做三角形矩阵。例如,以下矩阵都就是三角形矩阵: , ,, 。 3、单位矩阵与零矩阵 在方阵中,如果只有得元素不等于零,而其她元素全为零,如: 则称为对角矩阵,可记为。如果在对角矩阵中所有得彼此都相等且均为1,如: ,则称为单位矩阵。单位矩阵常用E来表示,即: 当矩阵中所有得元素都等于零时,叫做零矩阵,并用符号“0”来表示。 4、矩阵得加法 矩阵A=(a ij)m×n与B=(b ij)m×n相加时,必须要有相同得行数与列数。如以C=(c ij)m ×n表示矩阵A及B得与,则有: 式中:。即矩阵C得元素等于矩阵A与B得对应元素之与。 由上述定义可知,矩阵得加法具有下列性质(设A、B、C都就是m×n矩阵): (1)交换律:A+B=B+A (2)结合律:(A+B)+C=A+(B+C) 5、数与矩阵得乘法 我们定义用k右乘矩阵A或左乘矩阵A,其积均等于矩阵中得所有元素都乘上k之后所得得矩阵。如: 由上述定义可知,数与矩阵相乘具有下列性质:设A、B都就是m×n矩阵,k、h为任意常数,则: (1) k(A+B)=kA+kB (2)(k+h)A=kA+hA
矩阵的运算及其运算规则
矩阵基本运算及应用 牛晨晖 在数学中,矩阵是一个按照长方阵列排列的复数或实数集合。矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中。在物理学中,矩阵于电路学、力学、光学和量子物理中都有应用;计算机科学中,三维动画制作也需要用到矩阵。矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。在电力系统方面,矩阵知识已有广泛深入的应用,本文将在介绍矩阵基本运算和运算规则的基础上,简要介绍其在电力系统新能源领域建模方面的应用情况,并展望随机矩阵理论等相关知识与人工智能电力系统的紧密结合。 1矩阵的运算及其运算规则 1.1矩阵的加法与减法 1.1.1运算规则 设矩阵,, 则 简言之,两个矩阵相加减,即它们相同位置的元素相加减! 注意:只有对于两个行数、列数分别相等的矩阵(即同型矩阵),加减
法运算才有意义,即加减运算是可行的. 1.1.2运算性质 满足交换律和结合律 交换律; 结合律. 1.2矩阵与数的乘法 1.2.1运算规则 数乘矩阵A,就是将数乘矩阵A中的每一个元素,记为或.特别地,称称为的负矩阵. 1.2.2运算性质 满足结合律和分配律 结合律:(λμ)A=λ(μA);(λ+μ)A =λA+μA. 分配律:λ(A+B)=λA+λB. 1.2.3典型举例 已知两个矩阵 满足矩阵方程,求未知矩阵.
解由已知条件知 ? 1.3矩阵与矩阵的乘法 1.3.1运算规则 设,,则A与B的乘积是这样一个矩阵: (1) 行数与(左矩阵)A相同,列数与(右矩阵)B相同,即. (2) C的第行第列的元素由A的第行元素与B的第列元素对应相乘,再取乘积之和. 1.3.2典型例题 设矩阵 计算 解是的矩阵.设它为
矩阵的概念、运算(一)
第五章矩阵 辞海:将mn个元素排成m行n列的矩形称为m行n列矩阵。当m=n时称为n 阶方阵。矩阵可按某些规则进行加法、乘法以及数与矩阵相乘等运算。矩阵的概念最初是由解线性方程组产生。我国古代用筹算法解线性方程组时就是用筹码排成矩阵来进行的。 矩阵是数学中的一个重要的基本概念,是代数学的一个主要研究对象,也是数学研究和应用的一个重要工具。 百度“矩阵”,找到约约60,100,000条结果; Google“matrix”,找到约467,000,000 条结果. 背景知识:矩阵的历史 ?矩阵的概念是在解线性方程组中产生的。如我国《九章算术》(公元前1 世纪)用筹算解线性方程组时,就是把算筹排列成矩阵形式来进行的。 ?1850年由西尔维斯特(Sylvester)(英)首先提出矩阵的概念。 ?1857年卡莱(A.Cayley)(英)建立了矩阵运算规则。 ?矩阵由最初作为一种工具经过近两个世纪的发展,现在已成为独立的一 门数学分支——矩阵论。而矩阵论又可分为矩阵方程论、矩阵分解论和广义逆矩阵论等矩阵的现代理论。 ?矩阵及其理论现已广泛地应用于自然科学、工程技术、社会科学等许多领 域。如在观测、导航、机器人的位移、化学分子结构的稳定性分析、密码通讯、模糊识别、图像处理等方面都有广泛应用。 5.0矩阵的概念 一、教学内容 1、矩阵的概念 2、矩阵相等 3、几种特殊矩阵 二、教学目的 了解矩阵的产生背景,掌握矩阵的概念,理解矩阵相等的涵义,认识几种特殊矩阵 三、重点难点 矩阵相等 一、引例
我们先看几个例子 例1:设有线性方程组:???????=++-=+-+=++--=--+7 73918333215432143214 3214321x x x x x x x x x x x x x x x x 这个方程组未知量系数及常数项按方程组中的顺序组成一个4行5列的数表如下: ?????? ? ??------71317391118331211151 这个数表决定了给定方程组是否有解?以及如果有解,解是什么等问题,因此对这个数表的研究就很有必要。 例2:在解析几何中考虑坐标变换时,如果只考虑坐标的旋转(逆时针方向旋转 θ角),那么平面直角坐标变换公式为: ?? ?'+'='-'=θ θθ θcos sin sin cos y x y y x x 显然,新旧坐标之间的关系,完全可以通过公式中系数所排成的2×2数表 ??? ? ??-θθθθcos sin sin cos 表示出来。空间线性变换也有类似的情形。 例3:生产m 种产品需用n 种材料,如果以ij a 表示生产第i 种产品(i=1,2,…,m)耗用第j 种材料(j=1,2,…,n )的定额,则消耗定额可以用一个矩形表来表示。 这个表也可以简单地表示为m 行n 列的数表:
矩阵的定义及其运算规则(2)
矩阵的定义及其运算规则 1矩阵的定义 一般而言,所谓矩阵就是由一组数的全体,在括号()内排列成 m 行n 列(横的称行, 纵的称列)的一个数表,并称它为 mxn 阵。 矩阵通常是用大写字母 A 、 B …来表示。例如一个 m 行n 列的矩阵可以简记为: 示矩阵的行数,第二个注脚字母 j (j = 1, 2,…,n )表示矩阵的列数。 当m = n 时,则称’ 「为n 阶方阵,并用 *表示。当矩阵(丙)的元素仅有 行或一列时,则称它为行矩阵或列矩阵 。设两个矩阵,有相同的行数和相同的列数,而且 它们的对应元素一一相等,即 :,则称该两矩阵相等,记为 A = B 。 2、三角形矩阵 由i = j 的元素组成的对角线为主对角线,构成这个主对角线的元素称为主对角线元素。 如果在方阵中主对角线一侧的元素全为零, 而另外一侧的元素不为零或不全为零, 则该 矩阵叫做三角形矩阵。例如,以下矩阵都是三角形矩阵: 盘 12 叽 7 +1 十》 °门创说 23 屍1爲2 0 +1 +3 广 +2 (P < 0 0知丿 务 対 (0 0+6 L +呂 +1」 3、单位矩阵与零矩阵 在方阵-中,如果只有'的元素不等于零,而其他元素全为零,如: 则称为对角矩阵,可记为亠"1「一。如果在对角矩阵中所有的’ ' 彼此 。即: (2-3) 我们称(2-3)式中的,为矩阵 的元素,a 的第一个注脚字母=….,表
式中:1 '「’。即矩阵C 的元素等于矩阵 A 和B 的对应元素之和。 由上述定义可知,矩阵的加法具有下列性质 ( 设 A 、 B 、 C 都是mxn 矩阵) (1)交换律: A + B = B + A (2)结合律: (A + B ) + C = A +( B + C ) 5、数与矩阵的乘法 我们定义用k 右乘矩阵A 或左乘矩阵A ,其积均等于矩阵- - 中的所有元素都 乘上k 之后所得的矩阵。如: 由上述定义可知,数与矩阵相乘具有下列性质:设 常数,则: (1) k (A + B )= kA + kB (2) ( k + h ) A = kA + hA (3) k (hA )= khA n 0 -2 0 1 9- …0 都相等且均为1,如: 2 0 …1丿 ,则称为单位矩阵。单位矩阵常 用 E 来表示,即: 1 0 0 1 E = 9- ■ I 2 0 0 1 当矩阵中所有的元素都等于零时,叫做零矩阵,并用符号 “ 0来表示。 4、矩阵的加法 矩阵A = ( a ij ) mxn 和B = (b ij ) rnxn 相加时,必须要有相同的行数和列数。 m 勺表示矩阵 A 及 B 的和,则有: 如以 C = ( c ij ) A 、 B 都是mXn 矩阵,k 、h 为任意
