椭圆,双曲线,抛物线,导数知识点
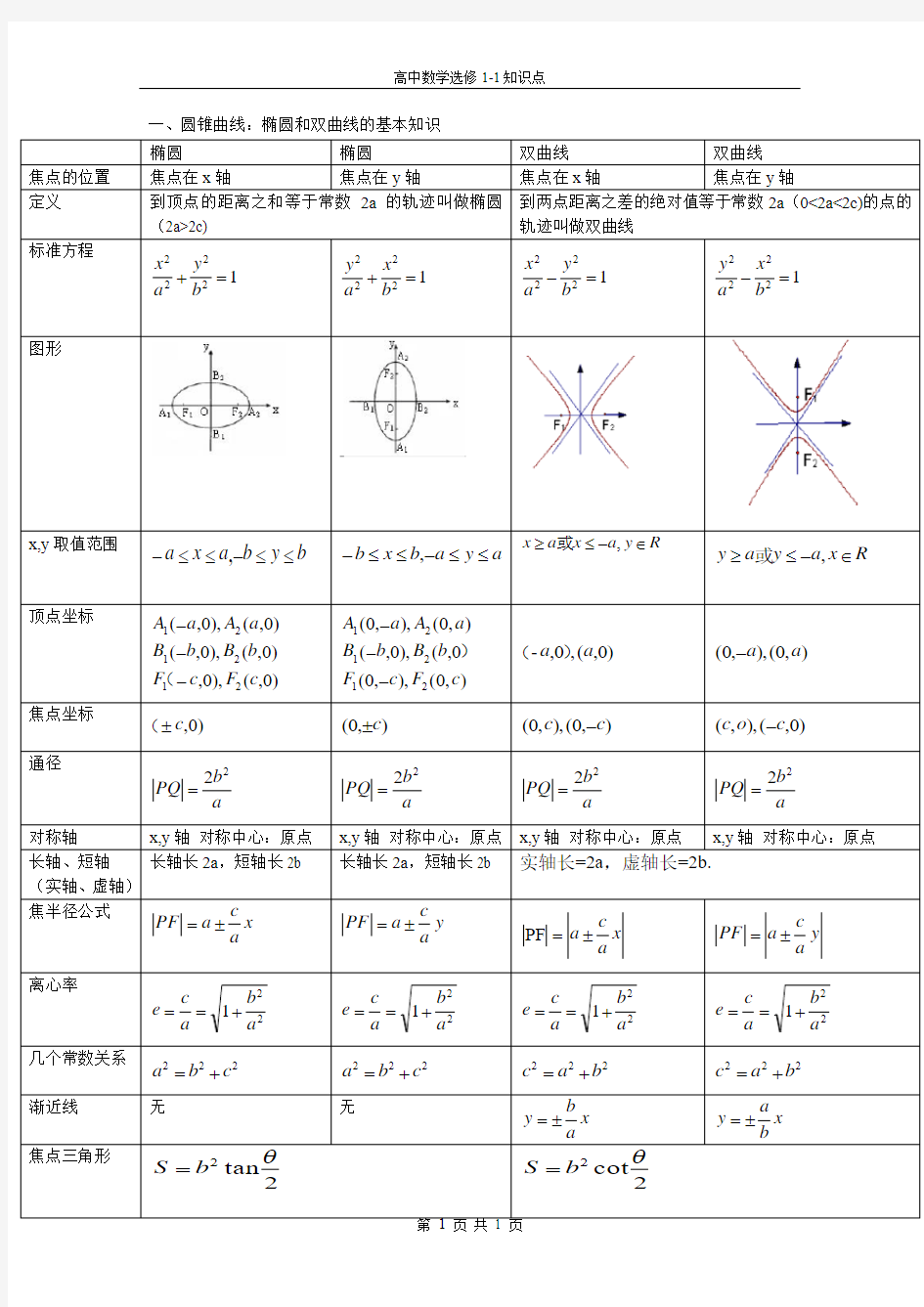

一、圆锥曲线:椭圆和双曲线的基本知识
椭圆 椭圆 双曲线 双曲线 焦点的位置 焦点在x 轴
焦点在y 轴
焦点在x 轴
焦点在y 轴
定义 到顶点的距离之和等于常数2a 的轨迹叫做椭圆(2a>2c) 到两点距离之差的绝对值等于常数2a (0<2a<2c)的点的轨迹叫做双曲线
标准方程
122
22=+b y a x 12
2
22=+b x a y 122
22=-b y a x
12
2
22=-b x a y 图形
x,y 取值范围
b y b a x a ≤≤-≤≤-,
a
y a b x b ≤≤-≤≤-,
R y a x a x ∈-≤≥,或
R x a y a y ∈-≤≥,或
顶点坐标
)
0,(),0,)0,(),0,()0,(),0,(212121c F c F b B b B a A a A ---( )
,0(),,0(0,(),0,(),0(),,0(212121c F c F b B b B a A a A ---)
)0,(,0,-a a )(
),0(),,0(a a -
焦点坐标 )0,c ±( ),0(c ± ),0(),,0(c c - )0,(),,(c o c - 通径
a
b PQ 22=
a
b PQ 2
2=
a
b PQ 2
2=
a
b PQ 2
2=
对称轴 x,y 轴 对称中心:原点
x,y 轴 对称中心:原点 x,y 轴 对称中心:原点
x,y 轴 对称中心:原点
长轴、短轴 (实轴、虚轴) 长轴长2a ,短轴长2b 长轴长2a ,短轴长2b
实轴长=2a ,虚轴长=2b.
焦半径公式
x a
c a PF ±
= y a
c a PF ±
= x a
c
a ±=PF y a
c a PF ±
= 离心率
221a b a c e +==
22
1a b a c e +==
22
1a b a c e +==
22
1a
b a
c e +==
几个常数关系 222c b a +=
222c b a +=
222b a c += 222b a c +=
渐近线 无
无
x a
b y ±
= x b
a y ±
= 焦点三角形
2
tan
2θ
b S =
2
cot
2θ
b S =
二、椭圆与直线的位置关系
判断直线l 椭圆C 的位置关系时,可将直线l 的方程代入椭圆C 的方程消去y 得到一个关于变量x 的方程02
=++c bx ax
(1)0>?,l 与C 相交,0=?,l 与C 相切,0
k x x x x k x x k AB ?+=-++=-+=2
212212
212
14)(11 三、双曲线与直线的位置关系
判断直线l 双曲线C 的位置关系时,可将直线l 的方程代入椭圆C 的方程消去y 得到一个关于变量x 的方程02
=++c bx ax
(1)0≠a 时,则有0>?,l 与C 相交;0=?,l 与C 相切;0
(2)0=a 时,即得到一个方程则l 与C 相交,并且只有一个焦点l 平行于双曲线的渐近线 四、抛物线的基础知识 定义 平面内到顶点F 和定直线l 的距离相等的点的轨迹叫做抛物线(点F 不在直线l 上)定点F 叫做抛物线的焦点,定直线叫做抛物线的准线
标准方程
)0(22>=p px y
)
0(22>-=p px y
)
0(22>=p py x
)0(22>-=p py x
图形
对称轴 x 轴
x 轴
y 轴
y 轴
焦点 )0,2p F (
)0,2p F -
( )2
,0p F (
)2,0p
F -(
顶点 顶点(0,0)
准线 2
p x -
= 2
p x =
2
p y -
= 2
p y =
离心率 1=e
通径 2p ,这是抛物线的过焦点的所有弦中最短的弦
焦半径公式
20p x +
02
x p
- 20p y +
02
y p
-
五、导数的定义: 1.函数的平均变化率
已知函数)(x f y =在0x 及其附近有定义,则比值)0()()(00≠??-?+=??x x
x f x x f x y 叫做函数的平均变化率
2.平均速度与瞬时速度
设物体运动路程与时间的关系是)(t s s =,从0t 到t t ?+0这段时间内,物体的平均速度
t
t s t t s t s ?-?+=
??)
()(00当0→?t 时,比值常数→?-?+=??t t s t t s t s )()(00,那么把这个常数称为)(t s s =在0t 处的瞬时速度 3.导数x
x f x x f x y
x f o x x ?-?+=??=→?→?)()(lim
lim
)('0000 4.求函数)(x f y =在0x 处的导数的步骤 ①求函数值的变化量)()(0x f x x f y o -?+=?
②求平均变化率x
x f x x f x y ?-?+=
??)
()(00 ③求导数:x
y
x f x ??=→?00lim )('
六、导数的运算 1.基本函数的导数
x x x x nx x C C n n sin )'(cos ,cos )'(sin ,)'(,(0'1-====-为常数)
a
x x x a a a e e x
a x x x x ln 1)'(log ,1)'(ln ,ln )'(,)'(=
=
== 2.运算法则:①[])(')('')()(x v x u x v x u ±=± ②[])(')()()(')()(x v x u x v x u x v x u += ③2
)()
(')()()('' )()(x v x v x u x v x u x v x u -=??
??
?? 3.复合函数的求导数步骤:分解—求导—回代。法则:
dx
du
du dy dx dy ?= 4.导数的几何意义;曲线)(x f y =在点))(,(00x f x P 处的切线的斜率 七、函数的应用 1.单调性
一般地,设函数)(x f y =在某个区间内可导
如果在这个区间内0)('>x f ,则)(x f y =在这个区间上是增函数 如果在这个区间内0)(' 函数)(x f y =在(a,b)有0)('>x f ?)(x f 在(a,b)上单调递增?0)('≥x f 在(a,b)上恒成立
