截长补短与倍长中线法证明三角形全等

1.截长补短法证明三角形全等
例1已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:
AE=AD+BE
练习1如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。求证:BC=AB+DC。
AC-AB=2BE
2.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证:
3如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求
证:AD+BC=AB.
P
C
E
D
B
A
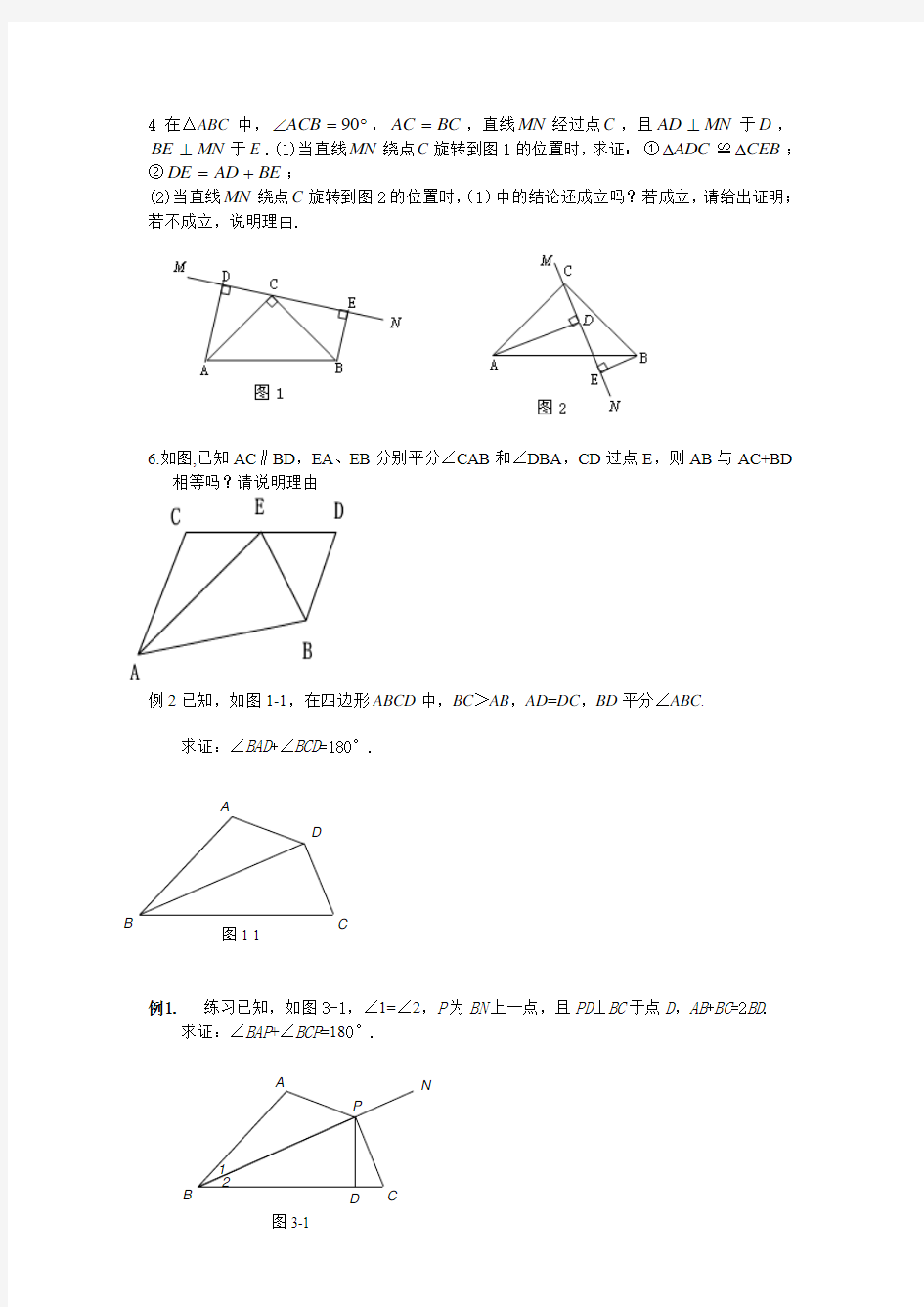
4在△ABC 中,?=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ?≌CEB ?;②BE AD DE +=;
(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.
6.如图,已知AC ∥BD ,EA 、EB 分别平分∠CAB 和∠DBA ,CD 过点E ,则AB 与AC+BD 相等吗?请说明理由
例2已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC .
求证:∠BAD +∠BCD =180°.
例1. 练习已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD .
求证:∠BAP +∠BCP =180°.
A B C D 图1-1 A P 12N
2、倍长中线法证三角形全等
例1 、求证:三角形一边上的中线小于其他两边和的一半。
练习 1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围
例2.已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE
练习2已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF
例3已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交
F
E C A B D
F E D
A B C
AE于点F,DF=AC.
求证:AE平分BAC
练习3已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE
作业
1、已知:如图,ABCD是正方形,∠FAD=∠FAE. 求证:BE+DF=AE.
2、五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:AD平分∠CDE
C
E D
B A
E D
A
B C
第 1 题图A
B
F
D E C
F
E
D
C
B
A
相交于点F 。试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论
4、已知:如图,?ABC 中,∠C=90?,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.
5:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC
于F ,求证:AF=EF
6:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE
F E A B C D D A B C M T E F E D
A B C E D A
B C
相交于点F 。试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论
F E A B C D
全等三角形之倍长中线法资料讲解
课题:《全等三角形之巧添辅助线——倍长中线法》 【方法精讲】常用辅助线添加方法一一倍长中线 △ ABC中,AD是BC边中线方式1 :直接倍长延长AD至U E, 例2: ABC中,AD是BAC的平分线,且BD=CD,求证AB=AC 方法1:作DE丄AB于E,作DF 丄AC于F,证明二次全等 方法2 :辅助线同上,利用面积 方法3 :倍长中线AD E 方式2 :间接倍长 作CF丄AD于F,作BE丄AD的延长线于E延长MD到 C 【经典例题】 例1 :△ ABC中,AB=5, AC=3求中线AD的取值范围. 提示:画出图形,倍长中线AD,利用三角形两边之和大于第三边 N,使DN=MD连接CN C 例3:已知在△ ABC中,AB=AC , D在AB 上, E在AC的延长线上,DE交BC于F,且DF=EF ,求证:BD=CE 方法1 :过D作DG // AE交BC于G,证明△ DGF^A CEF 使DE=AD,连接BE
方法2:过E 作EG // AB 交BC 的延长线于 G ,证明△ EFG^A DFB 方法3:过D 作DG 丄BC 于G,过E 作EHL BC 的延长线于 H,证明A BDG^A ECH 例4:已知在△ ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF 例5:已知:如图,在 ABC 中,AB 求证:AE 平分 BAC 方法1倍长AE 至G ,连结DG 方法2:倍长FE 至H ,连结CH 例 6:已知 CD=AB ,/ BDA= / BAD , AE 是厶 ABD 的中线,求证:/ C=Z BAE 提示:倍长 AE 至F ,连结DF,证明A ABE^A FDE ( SAS ,进而证明A ADF ^A ADC( SAS A 提示:倍长 AD 至G ,连接BG ,证明A BDG^A CDA 三角形BEG 是等腰三角形 AC , D E 在 BC 上,且 DE=EC 过 D 作 DF // BA 交 AE 于点 F , DF=AC. 第1题图
初中数学全等三角形截长补短
全等三角形——截长补短法 一、知识梳理: 截长补短法 截长补短法是几何证明题中十分重要的方法。通常来证明几条线段的数量关系。 截长法: (1)过某一点作长边的垂线 (2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等. 补短法 (1)延长短边。 (2)通过旋转等方式使两短边拼合到一起。…… 二、典型例题: 例1、如图,在ABC ?中,60BAC ∠=?,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数. 及时练习: 如图所示,在Rt △ABC 中,∠C=90°,BC=AC ,AD 平分∠BAC 交BC 于D ,求证:AB=AC+CD . 例2、已知ABC ?中,60A ∠ =,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明. D O E C B A
M D C B A P C B A 及时练习: 如图,已知在ABC 内,0 60BAC ∠=,0 40C ∠=,P ,Q 分别在BC ,CA 上,并且AP , BQ 分别是BAC ∠,ABC ∠的角平分线。求证:BQ+AQ=AB+BP 例3、如图.已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点,且∠BAE =2∠DAM . 求证:AE =BC +CE . 及时练习: 如图,AD ⊥AB ,CB ⊥AB ,DM =CM =a ,AD =h ,CB =k , ∠AMD =75°,∠BMC =45°,则AB 的长为 ( ) A . a B . k C . 2 k h + D . h 例4、以ABC ?的AB 、AC 为边向三角形外作等边ABD ?、ACE ?,连结CD 、BE 相交于点O . 求证:OA 平分DOE ∠.
a全等三角形之手拉手模型倍长中线截长补短法
手拉手模型 要点一:手拉手模型 特点:由两个等顶角的等腰三角形所组成,并且顶角的 顶点为公共顶点 结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180° (3)OA平分∠BOC 变形: 例1.如图在直线ABC的同一侧作两个等边三角形ABD ?,连结AE与CD,?与BCE 证明 (1)DBC ? ? ABE? (2)AE与DC之间的夹角为? 60 (3)BH平分AHC ∠ 变式精练1:如图两个等边三角形ABD ?,连结 ?与BCE AE与CD, 证明(1)DBC ? ABE? ? (2)AE与DC之间的夹角为? 60
(3)AE 与DC 的交点设为H ,BH 平分AHC ∠ 变式精练2:如图两个等边三角形ABD ?与BCE ?,连结AE 与CD , 证明(1)DBC ABE ??? (2)AE 与DC 之间的夹角为?60 (3)AE 与DC 的交点设为H ,BH 平分AHC ∠ 例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ???是否成立 (2)AG 是否与CE 相等 (3)AG 与CE 之间的夹角为多少度 (4)HD 是否平分AHE ∠ 例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ???是否成立 (2)AG 是否与CE 相等 (3)AG 与CE 之间的夹角为多少度 (4)HD 是否平分AHE ∠ 例4:两个等腰三角形ABD ?与BCE ?,其中 BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,
三角形全等之倍长中线(类倍长一)(人教版)(含答案)
学生做题前请先回答以下问题 问题1:“三角形全等”的辅助线: 见中线,要________,________之后___________,全等之后_________,_________. 问题2:倍长中线的作法,图中的虚线为辅助线,请叙述图1、图2的辅助线. 三角形全等之倍长中线(类倍长一)(人教版) 一、单选题(共4道,每道25分) 1.已知:如图,点E是BC的中点,∠BAE=∠D. 求证:AB=CD. 如图,先在图上走通思路后再填写空格内容: ①因为点E是BC的中点,考虑延长AE到点F,使EF=AE,连接CF; ②进而利用全等三角形的判定_________,证明_______≌_______; ③由全等可得________________;
④结合已知条件∠BAE=∠D,得∠F=∠D,在△DCF中,利用________________,可得CF=CD,等量代换得AB=CD. 以上空缺处依次所填最恰当的是( ) A.②SAS,△ABE,△ECF; ③AB=CF; ④等角对等边 B.②SAS,△ABE,△DEC; ③AB=CF,∠BAE=∠F; ④等边对等角 C.②SA S,△ABE,△FCE; ③∠ABE=∠FCE,∠BAE=∠F; ④等边对等角 D.②SAS,△ABE,△FCE; ③AB=FC,∠BAE=∠F; ④等角对等边 答案:D 解题思路:
试题难度:三颗星知识点:三角形全等之倍长中线 2.已知:如图,点E是BC的中点,∠BAE=∠D. 求证:AB=CD. 证明:如图,延长DE到点F,使EF=DE,连接BF.
∵E是BC的中点 ∴BE=CE 在△BEF和△CED中 ∴△BEF≌△CED(SAS) ∴____________________________ ∵∠BAE=∠D ____________________________ ∴AB=CD 请你仔细观察下列序号所代表的内容: ①BF=CD,∠EBF=∠C; ②BF=CD,∠F=∠D; ③; ④. 以上空缺处依次所填最恰当的是( ) A.①③ B.②③ C.①④ D.②④ 答案:B 解题思路:
全等三角形作辅助线专题一重点截长补短法可
D C B A E D F C B A 全等三角形作辅助线经典例题 常见辅助线的作法有以下几种: 1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”. 2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全 等变换中的“旋转”. 3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中 的“对折”,所考知识点常常是角平分线的性质定理或逆定理. 4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻 转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形) 5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是 之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目. 特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答. 一、倍长中线(线段)造全等 1:已知,如图△ABC中,AB=5,AC=3,则中线AD的取值范围是_________. 2:如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小. 3:如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE. E D C B A 中考应用: 以ABC ?的两边AB、AC为腰分别向外作等腰Rt ABD ?和等腰Rt ACE ?,90, BAD CAE ∠=∠=? 连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.(1)如图①当ABC ?为直角三角形时,AM与DE的位置关系是,线段AM与DE的数量关系是; (2)将图①中的等腰Rt ABD ?绕点A沿逆时针方向旋转?θ(0<θ<90)后,如图②所示,(1)
人教版初中数学全等三角形倍长中线法和截长补短法
专题2:倍长中线法和截长补短法 例1:如图,AD 为△ABC 中BC 边上的中线(AB >AC ) (1)求证:AB ﹣AC <2AD <AB +AC ; (2)若AB=8cm ,AC=5cm ,求AD 的取值范围. 针对训练:1、在△ABC 中,AC=5,中线AD=7,则BC 边的取值范围是________________. 2、如图,AD 为△ABC 的中线,∠ADB 和∠ADC 的平分线分别交AB 、AC 于点E 、F . 求证:BE +CF >EF . 3.如图,点D 、E 三等分△ABC 的BC 边,求怔:AB +AC >AD +AE . 例2:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF 针对训练:1.已知:如图,?ABC 中,∠C=90?,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作 DE//AB B
交BC 于E ,求证:CT=BE. 2、如图,已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:(1)AC=2AE (2)∠C=∠BAE 3、已知△ABC 中,AD 是BC 边上的中线,分别以AB 边、AC 边为直角边各向外作等腰直角三角形,求证:EF=2AD 例3、在△ABC 中,∠B=2∠C ,AD 是∠BAC 的平分线.求证:AC=AB +BD . 针对训练: 1、如图,在△ABC 中,∠B=2∠C ,且AC=AB +BD .求证:AD 是∠BAC 的平分线. D A B C M T E
八年级数学 全等三角形截长补短法专题
A D B C E 图2-1 截长补短法 人教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法,在无法进行直接证明的情形下,利用此种方法常可使思路豁然开朗.请看几例. 例1. 已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC . 求证:∠BAD +∠BCD =180°. 分析:因为平角等于180°,因而应考虑把两个不在一起的通过全等转化成为平角,图中缺少全等的三角形,因而解题的关键在于构造直角三角形,可通过“截长补短法”来实现. 证明:过点D 作DE 垂直BA 的延长线于点E ,作DF ⊥BC 于点F ,如图1-2 ∵BD 平分∠ABC ,∴DE =DF , 在Rt △ADE 与Rt △CDF 中, ?? ?==CD AD DF DE ∴Rt △ADE ≌Rt △CDF (HL ),∴∠DAE =∠DCF . 又∠BAD +∠DAE =180°,∴∠BAD +∠DCF =180°, 即∠BAD +∠BCD =180° 例2. 如图2-1,AD ∥BC ,点E 在线段AB 上,∠ADE =∠CDE ,∠DCE =∠ECB . 求证:CD =AD +BC . 分析:结论是CD =AD +BC ,可考虑用“截长补短法”中的“截长”,即在CD 上截取CF =CB ,只要再证DF =DA 即可,这就转化为证明两线段相等的问题,从而达到简化问题的目的. 证明:在CD 上截取CF =BC ,如图2-2 在△FCE 与△BCE 中, ?? ? ??=∠=∠=CE CE BCE FCE CB CF ∴△FCE ≌△BCE (SAS ),∴∠2=∠1. A B C D 图1-1 F E D C B A 图1-2 A D B C E F 1 234 图2-2
最新倍长中线法(经典例题)
倍长中线法 知识网络详解: 中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线. 所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法. 倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角) 倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。 【方法精讲】常用辅助线添加方法——倍长中线 △ABC中 方式1:延长AD到 E,AD是BC边中线 使DE=AD, 连接BE 方式2:间接倍长 作CF⊥AD于F,延长MD到N, 作BE⊥AD的延长线于使DN=MD, 连接BE 连接CN 经典例题讲解: 例1:△ABC中,AB=5,AC=3,求中线AD的取值范围
例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE 过D 作DG//AC 例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF 例4:已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠ B A B F D E C
例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE 自检自测: 1、如图,△ABC中,BD=DC=AC,E是DC的中点,求证,AD平分∠BAE. 2、在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。试探究线段AB与AF、CF之间的数量关系,并证明你的结论. A B F E A B C
最新全等三角形截长补短拔高练习(含答案)
八年级数学全等三角形辅助线添加之截长补短 (全等三角形)拔高练习 试卷简介:本讲测试题共两个大题,第一题是证明题,共7个小题,每小题10分;第二题解答题,2个小题,每小题15分。 学习建议:本讲内容是三角形全等的判定——辅助线添加之截长补短,其中通过截长补短来添加辅助线是重点,也是难点。希望同学们能学会熟练通过截长补短来做辅助线,进而构造出全等的三角形。 一、解答题(共1道,每道20分) 1.如图,已知点C是∠MAN的平分线上一点,CE⊥AB于E,B、D分别在AM、AN上,且AE=(AD+AB).问:∠1和∠2有何关系? 答案: 解:∠1+∠2=180° 证明:过点C作CF⊥AN于点F,由于AC平分∠NAM,所以CF=CE,则在Rt△ACF和Rt△ACE 中 ∴△ACF≌△ACE(HL),∴AF=AE,由于2AE=AD+AB,所以AB-AE=AF-AD ∴DF=BE,在△CFD和△CEB中所以△CFD≌△CEB(SAS),∴∠2=∠FDC,又∠1+∠FDC=180°,∴∠1+∠2=180°。 解题思路:见到角平分线就要想到作垂直,找到全等关系是解决此类问题的关键
易错点:找到三角形全等的所有条件 试题难度:四颗星知识点:三角形 二、证明题(共8道,每道10分) 1.如图,已知△ABC中,∠A=90°,AB=AC,BE平分∠ABC,CE⊥BD于E,求证:CE=BD. 答案: 延长CE交BA的延长线于点H,由BE平分ABC,BE CE,得CE=EH=CH。 又1+H=90°,,2+H=90° 1= 2 在△ACH和△ABD中 HAC=DAB=90° AC=AB 1= 2 △ACH≌△ABD(ASA) CH=BD CE=CH=BD 解题思路: 根据题意,要证明CE=BD,延长CE与BA,由题意的垂直平分线可得CE的两倍长CH,只需证明CH=BD即可,很显然有全等可以证明出结论 易错点:不能正确利用题中已知条件BF平分∠ABC,CE⊥BD于E,做出辅助线,进而解答。试题难度:三颗星知识点:全等三角形的判定与性质 2. 如图,已知正方形ABCD中,E为BC边上任意一点,AF平分∠DAE.求证:AE-BE=DF.
截长补短与倍长中线法证明三角形全等
1.截长补短法证明三角形全等 例1已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证: AE=AD+BE 练习1如图,四边形ABCD中,AB∥DC,BE、CE分别平分∠ABC、∠BCD,且点E在AD上。求证:BC=AB+DC。 AC-AB=2BE 2.已知∠ABC=3∠C,∠1=∠2,BE⊥AE,求证: 3如图,已知AD∥BC,∠P AB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求 证:AD+BC=AB. P C E D B A
4在△ABC 中,?=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D , MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时, 求证: ①ADC ?≌CEB ?;②BE AD DE +=; (2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由. 6.如图,已知AC ∥BD ,EA 、EB 分别平分∠CAB 和∠DBA ,CD 过点E ,则AB 与AC+BD 相等吗?请说明理由 例2已知,如图1-1,在四边形ABCD 中,BC >AB ,AD =DC ,BD 平分∠ABC . 求证:∠BAD +∠BCD =180°. 例1. 练习已知,如图3-1,∠1=∠2,P 为BN 上一点,且PD ⊥BC 于点D ,AB +BC =2BD . 求证:∠BAP +∠BCP =180°. A B C D 图1-1 A P 1 2 N
2、倍长中线法证三角形全等 例1 、求证:三角形一边上的中线小于其他两边和的一半。 练习 1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围 例2.已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE 练习2已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF 例3已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交 F E C A B D F E D A B C
三角形全等之倍长中线
三角形全等之倍长中线 课前预习 1. 填空 (1)三角形全等的判定有: 三边分别___________的两个三角形全等,即(____); 两边和它们的_____分别相等的两个三角形全等,即(____); 两角和它们的_____分别相等的两个三角形全等,即(____); 两角和其中一个角的______分别相等的两个三角形全等,即(____); 斜边和_______边分别相等的两个直角三角形全等,即(____). (2)要证明两条边相等或者两个角相等,可以考虑放在两个三角形中证________;要证明两个三角形全等需要准备______组条件,这三组条件里面必须有______;然后依据判定进行证明,其中AAA ,SSA 不能证明两个三角形全. 2. 想一想,证一证 已知:如图,AB 与CD 相交于点O ,且O 是AB 的中点. (1)当OC =OD 时,求证:△AOC ≌△BOD ; (2)当AC ∥BD 时,求证:△AOC ≌△BOD . O B C D A ? 知识点睛 1. “三角形全等”辅助线: 见中线,要__________,构造______________. 2. 中点的思考方向: ① (类)倍长中线 延长AD 到E ,使DE =AD , 延长MD 到E ,使DE =MD , 连接BE 连接CE D C B A M A B C D
②平行夹中点 F E D C B A 延长FE 交BC 的延长线于点G ? 精讲精练 1. 如图,在△ABC 中,AD 为BC 边上的中线. (1)按要求作图:延长AD 到点E ,使DE =AD ;连接BE . (2)求证:△ACD ≌△EBD . (3)求证:AB +AC >2AD . (4)若AB =5,AC =3,求AD 的取值范围. 2. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD . 求证:AB =AC . 3. 如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AB =AC . 求证:①CE =2CD ;②CB 平分∠DCE . D C B A D B A D C B A
全等三角形之截长补短法
例题1 如图所示,在Rt△ABC中,∠C=90°,BC=AC,AD平分∠BAC交BC于D,求证:AB=AC+CD. 考点:全等三角形的判定与性质. 专题:证明题. 分析:利用已知条件,求得∠B=∠E,∠2=∠1,AD=AD,得出△ABD≌△AED(AAS),∴AE=AB.∵AE=AC+CE=AC+CD,∴AB=AC+CD. 解答:证法一:如答图所示,延长AC,到E使CE=CD,连接DE. ∵∠ACB=90°,AC=BC,CE=CD, ∴∠B=∠CAB=45°,∠E=∠CDE=45°, ∴∠B=∠E. ∵AD平分∠BAC, ∴∠1=∠2 在△ABD和△AED中, ∠B=∠E,∠2=∠1,AD=AD, ∴△ABD≌△AED(AAS). ∴AE=AB. ∵AE=AC+CE=AC+CD, ∴AB=AC+CD. 证法二:如答图所示,在AB上 截取AE=AC,连接DE, ∵AD平分∠BAC, ∴∠1=∠2. 在△ACD和△AED中, AC=AE,∠1=∠2,AD=AD, ∴△ACD≌△AED(SAS). ∴∠AED=∠C=90,CD=ED, 又∵AC=BC,
∴∠B=45°. ∴∠EDB=∠B=45°. ∴DE=BE, ∴CD=BE. ∵AB=AE+BE, ∴AB=AC+CD. 点评:本题考查了全等三角形的判定和性质;通过SAS的条件证明三角形全等,利用三角形全等得出的结论来求得三角形各边之间的关系. 例题2 图,AD是△ABC中BC边上的中线,求证:AD<(AB+AC). 考点:全等三角形的判定与性质;三角形三边关系. 专题:计算题. 分析:可延长AD到E,使AD=DE,连BE,则△ACD≌△EBD得BE=AC,进而在△ABE中利用三角形三边关系,证之. 解答:证明:如图延长AD至E,使AD=DE,连接BE. ∵BD=DC,AD=DE,∠ADC=∠EDB ∴△ACD≌△EBD∴AC=BE 在△ABE中,AE<AB+BE,即2AD<AB+AC∴AD<(AB+AC) 点评:本题主要考查全等三角形的判定及性质以及三角形的三边关系问题,能够熟练掌握.
倍长中线法
全等三角形的类型题 常见辅助线的作法有以下几种: 1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”. 2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的 “旋转”. 3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”, 所考知识点常常是角平分线的性质定理或逆定理. 4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠” 5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线 段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答. 倍长中线法 1.已知:AB=4,AC=2,D是BC中点,AD是整数,求AD 2、已知:D是AB中点,∠ACB=90°,求证: 1 2 CD AB 3、已知:∠1=∠2,CD=DE,EF//AB,求证:EF=AC 4、已知,E是AB中点,AF=BD,BD=5,AC=7,求DC A D B C D A B C B A C D F 2 1 E
截长补短法 1、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C 2、如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。求证:BC=AB+DC 。 3、如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB . 4、已知∠ABC=3∠C ,∠1=∠2,BE ⊥AE ,求证:AC-AB=2BE 边加减的问题 1、已知:点A 、F 、E 、C 在同一条直线上, AF =CE ,BE ∥DF ,BE =DF .求证:△ABE ≌△CDF . 2、如图:DF=CE ,AD=BC ,∠D=∠C 。求证:△AED ≌△BFC 。 C D B F A E D C B A F E D C P E D C B A
全等三角形之中线倍长法讲课讲稿
授课教案 教学标题 教学目标 教学重难点 上次作业检查 授课内容:— 一.热身训练 1. 如图,已知:AD 是BC 上的中线,且DF=DE 求证:BE // CF. 2. 如图,AE BC 交于点 M, F 点在AM 上,BE / CF, BE=CF 求证:人“是厶ABC 的中线. 3. AB=AC , DB=DC F 是AD 的延长线上的一点。求证: BF=CF 4. 如图:AB=CD AE=DF CE=FB 求证:AF=DE 5. 已知:如图所示, AB = AD BC = DC E 、F 分别是 DC BC 的中点,求证: AE = AF. 二.知识梳理 1?中点的定义 2?中点的表示方法:等量关系、倍的关系、分的关系 3?三角形中线的作用:等分面积 全等) 三?典型例题 例1.(“希望杯”试题)已知,如图△ ABC 中, AB=5 AC=3则中线AD 的取值范围是 _____________ . 分析:①将AD 边放在某个三角形中,利用三边关系求出取值范围; A ② 中线倍长法的具体应用:延长 AD 至M,使DM=AD 连接BM 利用SAS 证明三、 角形全等; ③ 将线段AC 转换成BM 在厶ABM 中利用三边关系求出 2AD 取值范 ——L \ 中线倍长法证明全等 熟练掌握有中点为背景的全等三角形证明的方法 重点掌握中线倍长法模型的建立,能利用中线倍长法解决问题 4?全等三角形中中线的作用:倍长中线(延长中线至 *,连接**,利用SAS 证明三角形
例2.如图:在厶ABC中,BA=BC D是AC的中点。求证:BDL AC. 分析:中线倍长法,延长BD至M,使DM=BD连接AM,两次全 等,再证明角相等. 1 例3.已知:D是AB中点,/ ACB=90,求证:CD AB 2 分析:中线倍长法,延长CD至M,使DM=CD连接AM, 两次全等,解决线段分的证明 例4.已知,E 是AB 中点,AF=BD, BD=5, AC=7,求DC 分析:中线倍长法,E为中点,可倍长DE FE、CE至M (具体是哪条线段尝试之后再引导学生下结论),连接AM,利用SAS证明三角形全等,有部分等腰三角形的知识参与解题,可引导学生回忆三角形按边分类时所传授的等腰三角形的知识 D 四?课堂练习 1. 已知:AB=4, AC=2 D是BC中点,AD是整数, 2. 已知:/ 仁/2, CD=DE EF//AB,求证:EF: 五?课后反思: 1. 三角形全等证明的方法,注意两次全等的问题; 2. 有中点为背景参与的问题,常见思路是“中线倍长法”
倍长中线构造全等三角形
巧添辅助线——倍长中线 【夯实基础】 例:ABC ?中,AD 就是BAC ∠的平分线,且BD=CD,求证AB=AC 方法1:作D E ⊥AB 于E,作D F ⊥AC 于F,证明二次全等 方法2:辅助线同上,利用面积 方法3:倍长中线AD 【方法精讲】常用辅助线添加方法——倍长中线 △ABC 中 方式1: 延长AD 到E, AD 就是BC 边中线 使DE=AD, 连接BE 方式2:间接倍长 作CF ⊥AD 于延长MD 到N, 作BE ⊥AD 的延长线于使DN=MD, 连接BE 连接CD 【经典例题】 例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围 提示:画出图形,倍长中线AD,利用三角形两边之与大于第三边 例2:已知在△ABC 中,AB=AC,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F,且DF=EF,求证:BD=CE 方法1:过D 作DG ∥AE 交BC 于G,证明ΔDGF ≌ΔCEF 方法2:过E 作EG ∥AB 交BC 的延长线于G,证明ΔEFG ≌ΔDFB 方法3:过D 作DG ⊥BC 于G,过E 作EH ⊥BC 的延长线于H 证明ΔBDG ≌ΔECH
例3:已知在△ABC 中,AD 就是BC 边上的中线,E 就是AD 上一点,且BE=AC,延长BE 交AC 于F,求 证:AF=EF 提示:倍长AD 至G ,连接BG,证明ΔBDG ≌ΔCDA 三角形BEG 就是等腰三角形 例4:已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC,过D 作BA DF //交AE 于点F,DF=AC 、 求证:AE 平分BAC ∠ 提示: 方法1:倍长AE 至G,连结DG 方法2:倍长FE 至H,连结CH 例5:已知CD=AB,∠BDA=∠BAD,AE 就是△ABD 的中线,求证:∠C=∠BAE 提示:倍长AE 至F,连结DF 证明ΔABE ≌ΔFDE(SAS) 进而证明ΔADF ≌ΔADC(SAS) 【融会贯通】 1、在四边形ABCD 中,AB ∥DC,E 为BC 边的中点,∠BAE=∠EAF,AF 与DC 的延长线相交于点F 。试探究线段AB 与AF 、CF 之间的数量关系,并证明您的结论 提示:延长AE 、DF 交于G 证明AB=GC 、AF=GF 所以AB=AF+FC B 第 1 题图 A B F D E C
(精品)全等三角形——截长补短法
D C B A 全等三角形——截长补短法 一、知识梳理: 截长补短法 截长补短法是几何证明题中十分重要的方法。通常来证明几条线段的数量关系。 截长法: (1)过某一点作长边的垂线 (2)在长边上截取一条与某一短边相同的线段,再证剩下的线段与另一短边相等. 补短法 (1)延长短边。 (2)通过旋转等方式使两短边拼合到一起。…… 二、典型例题: 例1、如图,在ABC ?中,60BAC ∠=?,AD 是BAC ∠的平分线,且AC AB BD =+,求ABC ∠的度数. 及时练习: 如图所示,在Rt △ABC 中,∠C=90°,BC=AC ,AD 平分∠BAC 交BC 于D ,求证:AB=AC+CD . 例2、已知ABC ?中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.
N E B M A D M D C B A D O E C B A 及时练习: 如图,点M 为正三角形ABD 的边AB 所在直线上的任意一点(点B 除外),作60DMN ∠=?,射线MN 与DBA ∠外角的平分线交于点N ,DM 与MN 有怎样的数量关系? 例3、如图.已知正方形ABCD 中,M 为CD 的中点,E 为MC 上一点,且∠BAE =2∠DAM . 求证:AE =BC +CE . 及时练习: 如图,AD ⊥AB ,CB ⊥AB ,DM =CM =a ,AD =h ,CB =k , ∠AMD =75°,∠BMC =45°,则AB 的长为 ( ) A . a B . k C . 2 k h + D . h 例4、以ABC ?的AB 、AC 为边向三角形外作等边ABD ?、ACE ?,连结CD 、BE 相交于点O . 求证:OA 平分DOE ∠.
珍藏二——_全等三角形证明辅助线作法之倍长中线问题
几何综合部分倍长中线问题 巧添辅助线——倍长中线 【夯实基础】 例:ABC ?中,AD是BAC ∠的平分线,且BD=CD,求证AB=AC 方法1:作D E⊥AB于E,作D F⊥AC于F,证明二次全等 方法2:辅助线同上,利用面积 方法3:倍长中线AD 【方法精讲】常用辅助线添加方法——倍长中线 △ABC中方式1:延长AD到E, AD是BC边中线使DE=AD, 连接BE 方式2:间接倍长
几何综合部分倍长中线问题 2 作CF⊥AD于F,延长MD到N, 作BE⊥AD的延长线于E 使DN=MD, 连接BE 连接CD 【经典例题】 例1:△ABC中,AB=5,AC=3,求中线AD的取值范围 例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且 BD=CE 例3:已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF B
几何综合部分 倍长中线问题 3 提示:倍长AD 至G ,连接BG ,证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形 例4:已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠ 提示: 方法1:倍长AE 至G ,连结DG 方法2:倍长FE 至H ,连结CH 例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE 提示:倍长AE 至F ,连结DF 证明ΔABE ≌ΔFDE (SAS ) 进而证明ΔADF ≌ΔADC (SAS ) 第 1 题图 A B F D E C
全等三角形问题中常见的辅助线倍长中线法
D C B A 全等三角形问题中常见的辅助线——倍长中线法 △ABC 中,AD 是BC 边中线 方式1:直接倍长,(图1): 延长AD 到E ,使DE=AD ,连接BE 方式2:间接倍长 1) (图2)作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E, 连接BE 2) (图3)延长MD 到N ,使DN=MD ,连接CD 【经典例题】 例1已知,如图△ABC 中,AB=5,AC=3, 则中线AD 的取值范围是_________. (提示:画出图形,倍长中线AD ,利用三角形两边之和大于第三边) 例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上, DE 交BC 于F ,且DF=EF. 求证:BD=CE.(提示:方法1:过D 作DG ∥AE 交BC 于G ,证明ΔDGF ≌ΔCEF E D A B C F D C B A N D C B A M
E D F C B A 方法2:过E 作EG ∥AB 交BC 的延长线于G ,证明ΔEFG ≌ΔDFB 方法3:过D 作DG ⊥BC 于G ,过E 作EH ⊥BC 的延长线于H ,证明ΔBDG ≌ΔECH ) 例3、如图,△ABC 中,E 、F 分别在AB 、AC 上,DE ⊥DF ,D 是中点,试比较BE+CF 与EF 的大小.
变式:如图,AD 为ABC ?的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+ (提示:方法1:在DA 上截取DG=BD ,连结EG 、FG , 证明ΔBDE ≌ΔGDE ΔDCF ≌ΔDGF 所以BE=EG 、CF=FG 利用三角形两边之和大于第三边 方法2: 倍长ED 至H ,连结CH 、FH ,证明FH=EF 、CH=BE ,利用三角形两边之和大于第三边) 例4:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF (提示:方法1:倍长AD 至G ,连接BG ,证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形。 _ D _ F _ C _ B _ E _ A _ D _ F _ C _ B _ E _ A
全等三角形作辅助线专题一(重点_截长补短法)可打印版
全等三角形作辅助线经典例题 常见辅助线的作法有以下几种: 1) 遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折” ? 2) 遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全 等变换中的“旋转” ? 3) 遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中 的“对折”,所考知识点常常是角平分线的性质定理或逆定理. 4) 过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻 转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形) 5) 截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是 之与特定线段相等,再利用三角形全等的有关性质加以说明?这种作法,适合于证明线段的和、差、倍、分等类的题目. 特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答. 一、倍长中线(线段)造全等 1:已知,如图△ ABC中,AB=5,AC=3,则中线AD的取值范围是 _______________ . 2 :如图,△ ABC中,E、F分别在AB、AC 上, DE丄DF,D是中点,试比较BE+CF 与EF的大小. 3 :如图,△ ABC中,BD=DC=AC ,E是DC的中点,求证:AD平分/ BAE. 中考应用: ABC的两边AB、AC为腰分别向外作等腰Rt ABD和等腰Rt ACE BAD CAE 90,连接DE,M、N分别是BC、DE的中点?探究:AM与DE的位 置关系及数量关系. (1 )如图① 当ABC为直角三角形时,AM与DE的位置关系 是________________ ,线段AM与DE的数量关系是________________ ; (2 )将图①中的等腰Rt ABD绕点A沿逆时针方向旋转(0< <90)后,如图②所示,(1 )
全等三角形之倍长中线法
全等三角形之倍长中线 1. 如图,AD 为△ABC 的中线. (1)求证:AB +AC >2AD . (2)若AB =5,AC =3,求AD 的取值范围. 2. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD . 求证:AB =AC . 3. 如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AB =AC . 求证:①CE =2CD ;②CB 平分∠DCE . D C B A C A D B A
4. 如图,在△ABC 中,D 是BC 边的中点,E 是AD 上一点,BE =AC , BE 的延长线交AC 于点F . 求证:∠AEF =∠EAF . 5. 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 的中点,EF ∥AD 交CA 的延长线于点F ,交 AB 于点G ,BG =CF . 求证:AD 为△ABC 的角平分线. 6. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中 点,且AF ⊥AB ,已知AD =2.7,AE =BE =5,求CE 的长. 7. 如图,在正方形ABCD 的边CB 的延长线上取一点E ,△FEB 为等腰直角三角形,∠FEB =90°, 连接FD ,取FD 的中点G ,连接EG ,CG . 求证:EG =CG 且EG ⊥CG . 1. 已知:如图,在梯形ABCD 中,AD ∥BC ,AB =AD +BC ,E 是CD 的中点. 求证:AE ⊥BE . F E D C A G F E D A F E D C B A G F E D C B A E D C B A
倍长中线构造全等三角形
倍长中线构造全等三角 形 -CAL-FENGHAI.-(YICAI)-Company One1
巧添辅助线——倍长中线 【夯实基础】 例:ABC ?中,AD是BAC ∠的平分线,且BD=CD,求证AB=AC 方法1:作DE⊥AB于E,作DF⊥AC于F,证明二次全等方法2:辅助线同上,利用面积 方法3:倍长中线AD 【方法精讲】常用辅助线添加方法——倍长中线 △ABC中 AD到E, AD是BC边中线, 连接BE 方式2 ⊥AD于F, AD的延长线于 连接 【经典例题】 例1:△ABC中,AB=5,AC=3,求中线AD的取值范围 提示:画出图形,倍长中线AD,利用三角形两边之和大于第三边 例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE 方法1:过D作DG∥AE交BC于G,证明ΔDGF≌ΔCEF 方法2:过E作EG∥AB交BC的延长线于G,证明ΔEFG 方法3:过D作DG⊥BC于G,过E作EH⊥BC 证明ΔBDG≌ΔECH 2
3 例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交 AC 于F ,求证:AF=EF 提示:倍长AD 至G ,连接BG ,证明ΔBDG ≌ΔCDA 三角形BEG 是等腰三角形 例4:已知:如图,在ABC ?中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠ 提示: 方法1:倍长AE 至G ,连结DG 方法2:倍长FE 至H ,连结CH 例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE 提示:倍长AE 至F ,连结DF 证明ΔABE ≌ΔFDE (SAS ) 进而证明ΔADF ≌ΔADC (SAS ) 【融会贯通】 1、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论 提示:延长AE 、DF 交于G 证明AB=GC 、AF=GF 所以AB=AF+FC B 第 1 题图 A B F D E C
