第2章 力矩和力偶理论
合集下载
力系的简化和平衡-2.2力矩和力偶
定理叙述：平面汇交力系的合力对平面内任一点的矩等
于各分力对同一点力矩的代数和
n
M o FR
M o Fi
i 1
定理证明：
FR
F1
r
A
O
Fn
F2 Fi
若 n 个力汇交于A点，则其合力为：
n
FR F1 F2 Fn Fi
i 1
r 用 同时矢积上式两端
r FR
r F1
zFx
xFz
j
xFy yFx k
由此可得：
M x
F
yFz zFy
M y
F
zFx xFz
M z F xFy yFx
Fz Fx Fy
18
力矩的单位： N m 或 kN m
B
Mo(F)
r
O
h
F
A
③力对点之矩矢的性质： a) 当力沿其作用线移动时，
M O F 保持不变。
12
①力对点之矩矢的概念 力对刚体产生的绕点转动效应取决于三要素： a.强度：力与力偶臂乘积 b.方位：转动轴的方位 c.方向：转动方向
13
力矩矢量的方向
MO
r
F
按右手定则
MO r F
14
②力对点之矩矢的矢量积和解析表达式
B
Mo(F)
r
O
h
F
A
力矢： F Fx , Fy , Fz
求： 光滑螺柱AB所受水平力。
解：由力偶只能由力偶平衡的 性质，其受力图为：
M 0
FAl M1 M 2 M 3 0
解得
FA
FB
M1
M2 l
M3
200N
人教版高中物理选修(2-2)《力矩和力偶》ppt课件1
看图 §2-2
力矩、力偶
§2-2 力矩、力偶
第二节 念、力偶矩计算公式
(力 §2-21、力对点之矩 力矩、力偶
扳手拧螺母，使得扳手与螺母绕定点O转动，称为
矩)
力F对O点之矩，简称力矩。
矩心 ：O
力臂：d
2、力矩计算公式（重点）
§2-2 力矩、力偶
O
§2-2 力矩、力偶
3、力矩的性质 （1）当力的大小等于零或力的作用线通过矩心时，力 矩为零 （2）当力沿其作用线移动时，力矩不变。 （3）力矩的大小不仅与力的大小有关，同时与矩心的 位置有关。
§2-2 力矩、力偶
4、讨论：如图所示，怎样利用力矩的原理来 提高转动效应？
1、增加力的大小
O
2、增加力臂的长度
M。（F）=±Fd
M。（F）—力矩，力F对点0之矩。
符号：“＋ ”—— 使物体逆时针转动时为正； “－” —— 使物体顺时针转动时为负。
F—力
d—力臂，力F作用线与矩心的垂直距离。
单位：N.m(牛顿.米)
§2-2 力矩、力偶
例：如图，已知F＝100N，d=10cm,求力F对O 点之矩。
M O ( F ) Fd 100 0.1 10 N .m
§2-2 力矩、力偶
第二节 力矩、力偶
力矩概念、计算公式、性质 力偶概念、力偶矩计算公式
§2-2 力矩、力偶
二、力偶
力偶实例
§2-2 力矩、力偶
1、力偶
力偶作用面——力偶所在平面。
A
F
d
B
F
力偶——两个大小相等、方 向相反、作用线平行的一对 平行力。(Fˊ、F) 力偶臂——力偶中两力作用线 之间的垂直距离。(d)
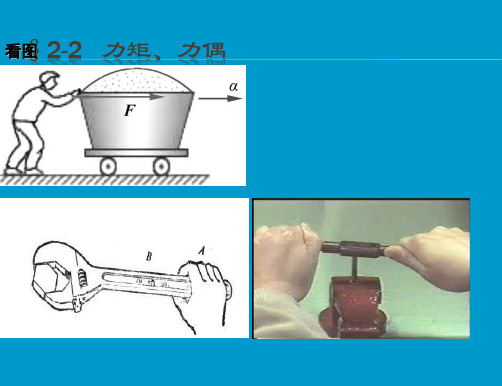
力矩、力偶
§2-2 力矩、力偶
第二节 念、力偶矩计算公式
(力 §2-21、力对点之矩 力矩、力偶
扳手拧螺母，使得扳手与螺母绕定点O转动，称为
矩)
力F对O点之矩，简称力矩。
矩心 ：O
力臂：d
2、力矩计算公式（重点）
§2-2 力矩、力偶
O
§2-2 力矩、力偶
3、力矩的性质 （1）当力的大小等于零或力的作用线通过矩心时，力 矩为零 （2）当力沿其作用线移动时，力矩不变。 （3）力矩的大小不仅与力的大小有关，同时与矩心的 位置有关。
§2-2 力矩、力偶
4、讨论：如图所示，怎样利用力矩的原理来 提高转动效应？
1、增加力的大小
O
2、增加力臂的长度
M。（F）=±Fd
M。（F）—力矩，力F对点0之矩。
符号：“＋ ”—— 使物体逆时针转动时为正； “－” —— 使物体顺时针转动时为负。
F—力
d—力臂，力F作用线与矩心的垂直距离。
单位：N.m(牛顿.米)
§2-2 力矩、力偶
例：如图，已知F＝100N，d=10cm,求力F对O 点之矩。
M O ( F ) Fd 100 0.1 10 N .m
§2-2 力矩、力偶
第二节 力矩、力偶
力矩概念、计算公式、性质 力偶概念、力偶矩计算公式
§2-2 力矩、力偶
二、力偶
力偶实例
§2-2 力矩、力偶
1、力偶
力偶作用面——力偶所在平面。
A
F
d
B
F
力偶——两个大小相等、方 向相反、作用线平行的一对 平行力。(Fˊ、F) 力偶臂——力偶中两力作用线 之间的垂直距离。(d)
第二章 力 力矩 力偶
G
1.画出AC、CG、CD、DE、结点D、C的受力图
本章重点：
熟练画受力图
C A
1.画出AC、BC的受力图 2.BC为二力体，AC不是二力体
B
本章重点：
熟练画受力图
小结
熟记4类支座 熟记3类结点 作用力与反作用力 二力体与二力杆 绳索、皮带 光滑接触面 已知荷载不能漏
本章重点：
本章重点：
熟练画受力图
第二章 力 力矩 力偶
§2.1 力的性质
1、力的三要素：大小、方向、作用点 力为矢量，其表示方法：书上用 黑体 字表示， 手写可用
F
本章重点：
熟练画受力图
§2.1 力的性质
对于刚体力的三要素：大小、方向、作用线
刚体：力具有可传性 （沿力的作用线） 变形体：力不具有可传性 同一物体在不同的场合有时看做刚体，有时为变形体
2）所谓代数和是指带正负号的。
3）该定理重在会应用。
2.2力矩
4.力矩的平衡 所有力对同一点矩的代数和等于0
M
A
0
已知宽度为4m，混凝土密度为2600kg/m3,砖密度为1900kg/m3,在雨 篷边缘有一施工荷载1kN
3000
350 70
A
240
1000
2.3力偶
1.力偶的定义：
大小相等、方向相反、作用线不同、 作用在同一的物体上 一对平行力
D A E
4.当DE为一绳索和为一杆时有啥区别
B
本章重点：
熟练画受力图
理想光滑接触面约束
本章重点：
熟练画受力图
C
B
D
1.画出AB、BC、BD、DE的受力图
G
第2章力、力矩、力偶
同样，在图 中线段aˊbˊ加上正号或负号是力F在y 轴上的 投影，用Fy 表示。 通常采用力F与坐标轴x所夹的锐角来计算投影，其正号或 负号可根据上述规定直观判断得出。由图可见，投影 Fy 和 可用下列式子计算 F
x
Fx F cos a Fy F sin a
•式中α 为力F与x轴所夹的锐角。
2. 加减平衡公理
在作用于某物体的力系中，加入或减去一个平衡力系， 并不改变原力系对物体的作用效果。这是因为一个平衡力系 作用在物体上，对物体的运动状态是没有影响的，所以在原 来作用于物体的力系中加入或减去一个平衡力系，物体的运 动状态是不会改变的，即新力系与原力系对物体的作用效果 相同。
推论(力的可传性原理)：作用在物体上的力可沿其作用 线移到物体的任一点，而不改变该力对物体的运动效 果。
对一个物体的运动趋势起制约作用的装置，我们称之为该物 体的约束。例如上面所提到的柱子是大梁的约束，基础是柱子 的约束，桥墩是桥梁的约束。约束给被约束物体的力，称为约 束力。 如上例中绳给球的作用力，柱子给梁的力。约束力作用点， 在约束与被约束物体的接触点上。
约束力方向：与约束所阻碍的物体运动方向相反。如上 图中约束力T 的方向与球向下运动的方向相反。 约束力大小：可由平衡条件求得。 物体受到的力一般可以分为两类。一类是使物体运动或使物 体有运动趋势的力，称为主动力，例如重力、水压力、土压力 等。主动力在工程上称为荷载。主动力往往是给定的或可测定 的。另一类则是约束力。约束力是阻止物体脱离约束的力，是 因其阻碍物体的运动而产生对物体的作用力，这种作用力因主 动力的存在而被动产生，并随着主动力的变化而改变，又称为 被动力或约束反力，简称反力。一般情况下，约束力都是未知 的。
图1-7
2力、力矩、力偶-2
力臂
顺时针转向为负。
矩心 h
力矩的单位 N.m, kN.m
O
F
注意：同一个力对不同点之矩是不同的， 计算力矩时一定要指明矩心。
力F 对A点之矩 ,为 力F 对B点之矩 ,为 力F 对C点之矩 ,为
MA(F )=FhA MB(F )= –FhB MC(F )=0
A hA C
F
hB B
力的作用线通过 矩心时，力对该点 之矩等于零。
W3 2gV3 19009.8 (240103 3 4) 53625 N
例2-7 带雨篷的门顶过梁长4m，横向尺寸如图。试验算 雨篷会不会绕A点倾覆
3000 350
ρ1=2600kg/m3
W3
F=1kN
W2
70
A
W1
ρ2=1900kg/m3
240 1000
计算倾覆力矩
W3
2.力矩的矢量表示 用右手螺旋法则将力矩表示为矢量 拇指表示力矩矢量的方向
MO (F)
n MO(F )
O
平面内，力对O点之矩实际上是力使物体绕着 过O点垂直于该平面的轴转动的物理量。
力对轴的矩
n F
Oh
n MO(F )
O
O
F
例2-7 带雨篷的门顶过梁长4m，横向尺寸如图。试验算 雨篷会不会绕A点倾覆
平衡？分别是多少？
1.1m
M A(W1) W1 1.1 82.5kN.m M A(W2) W2 2 240kN.m M A(F) F 1.6 144kN.m
F
W1
W2
1.6m
A
1m
3m
作业
P.27: 2-9
= –4 kN.m
第2章 平面力系-平面力对点之矩及平面力偶
即
MO(F) F d
O点为力矩的中心，称为矩心； d 为O点到力F 作用线的垂直
距离，称为力臂。 力矩的正负号：力使物体绕逆时针方向转动时为正，反
之为负。
应注意： 在平面问题中，力对点之矩只取决于力矩的大小及其旋 转方向（力矩的正负），因此它是一个代数量。
力矩的单位： 国际制 N·m，kN·m 工程制 公斤力米（kgf·m）
偶矩的代数和等于零，即 ∑Mi=0
利用这个平衡条件，可以求解一个未知量。
例题
两力偶作用在板上，尺寸如图，已知 F1 = F2=1.5 kN , F3
=F4 = 1 kN, 求作用在板上的合力偶矩。
F 1 180mm
解：由式
F2
M = M1 + M2
F4
则
M =-F1 ·0.18 –F3 ·0.08
FBA
B
A
FAB
M1
FO
O
M2 D
FD
M1 - FABrcosq 0 - M 2 2FBArcosq 0
因为 FAB FBA
所以求得 M 2 2M1
思考题1 一力偶(F1,F1′)作用在Oxy平面内,另一力偶(F2 ，F2′)作用在
Oyz平面内,它们的力偶矩大小相等(如图)。试问此两力偶是否 等效，为什么？
F1
d1
F2 d2
F1′
=
F2′
M1 F1 d1 , M 2 -F2 d2
F22 d F11
F11′
=
F22′
d
FR
FR′
M1 F11 d , M 2 -F22 d
FR F11 - F22 , FR F11 - F22
力偶
第2章 力矩与力偶2.1力对点的矩 从实践中知道，力对物体的作用效果除了能使物体移动外，还能使物体转动，力矩就是度量力使物体转动效果的物理量。
力使物体产生转动效应与哪些因素有关呢?现以扳手拧螺帽为例，如图2.1所示。
手加在扳手上的力F ，使扳手带动螺帽绕中心O 转动。
力F越大，转动越快；力的作用线离转动中心越远，转动也越快；如果力的作用线与力的作用点到转动中心O 点的连线不垂直，则转动的效果就差；当力的作用线通过转动中心O 时，无论力F 多大也不能扳动螺帽，只有当力的作用线垂直于转动中心与力的作用点的连线时，转动效果最好。
另外，当力的大小和作用线不变而指向相反时，将使物体向相反的方向转动。
在建筑工地上使用撬杠抬起重物，使用滑轮组起吊重物等等也是实际的例子。
通过大量的实践总结出以下的规律：力使物体绕某点转动的效果，与力的大小成正比，与转动中心到力的作用线的垂直距离d 也成正比。
这个垂直距离称为力臂，转动中心称为力矩中心(简称矩心)。
力的大小与力臂的乘积称为力F 对点O 之矩(简称力矩)，记作()o m F 。
计算公式可写为()o m F F d =±⋅ (2.1)式中的正负号表示力矩的转向。
在平面内规定：力使物体绕矩心作逆时针方向转动时，力矩为正；力使物体作顺时针方向转动时，力矩为负。
因此，力矩是个代数量。
力矩的单位是N m ⋅或kN m ⋅。
由力矩的定义可以得到如下力矩的性质：(1)力F 对点O 的矩，不仅决定于力的大小，同时与矩心的位置有关。
矩心的位置不同，力矩随之不同；(2)当力的大小为零或力臂为零时，则力矩为零；(3)力沿其作用线移动时，因为力的大小、方向和力臂均没有改变，所以，力矩不变。
(4)相互平衡的两个力对同一点的矩的代数和等于零。
例2.1 分别计算图2.2中1F 、2F 对O 点的力矩。
解 从图2–2中可知力1F 和2F 对O 点的力臂是h 和2l 。
故m o(F)=±F 11l = F 11l sin30=49×0.1×0.5=2.45N.mm o(F)=±F 22l =－F 22l =－16.3×0.15=2.45N.m必须注意：一般情况下力臂并不等于矩心与力的作用点的距离，如1F 的力臂是h ,不是1l 。
第2章 力 力矩 力偶
分析：
(1) 受力状态 雨篷板自重：G1 雨篷梁自重：G2 梁上墙自重：G3 雨篷板上的检修荷载： P=1kN / m
例2：已知钢筋混凝土雨蓬，梁上的墙高3m，雨篷板
宽4m，判断结构的安全性。
G3 350 G2 A 240 P 70 G1 1000 解： G1=25〓0.07〓1〓4=7kN L1=0.5m G2=25〓0.24〓0.35〓4=8.4kN L2=0.12m G3=19〓0.24〓3〓4=54.7kN L3=0.12m P=1〓4=4kN LP=1m
公理 人类经过长期实践和经验而得到的结论，它
被反复的实践所验证，是无须证明而为人们 所公认的结论。 公理1 作用力和反作用力定律 公理2 力的平行四边形法则 公理3 二力平衡公理 公理4 加减平衡力系原理
• 公理1 作用力与反作用力公理
作用力和反作用力总是同时存在，两力的大小 相等，方向相反，沿着同一直线，分别作用在两个相 互作用的物体上。
m O（F）=r 〓 F
m O（F）=〒2⊿OAB面积
• 2.2.2 合力矩定律
平面汇交力系的合力对平面内任一点的矩，等 于所有各分力对同一点的矩的代数和。
M O ( R ) M O ( Fi )
i 1
n
FR F1 F2 ...... Fn
r FR r F1 r F2 ...... r Fn
• 例题 1：已知P1=P2=P3=2kN，a=4m,求∑mA(Pi)。
P3
300
A a/2 C a/2 B
P2 P1
P1y
P3 300 P1x
解： M A ( P 1 ) 0kN m
M A ( P2 ) P2 a 2 4 8kN m
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B A A O
α
m1 m2
FAB
m1
FBA
B
NO D
O
m2
D ND
浙江水利水电专科学校 15
解： 杆AB为二力杆。
§2-7
力偶系的合成与平衡
A O
α FAB M1
分别写出杆AO 和BD 的平衡方程：
m 0
l1 S ABr cos 0 l2 2S BAr cos 0
S AB S BA l2 2l1
P d m1 1 P2 d m2
R A P1 P2' RB P1' P2
M RAd ( P P2 )d P d P2d m1 m2 1 1
浙江水利水电专科学校 13
平面力偶系合成的结果为作用于同一平面内 的合力偶，合力偶矩等于诸力偶矩的代数和。
量纲单位：
•
牛顿.米[N.m]或千牛.米[kN.m]
M o (F ) F d
浙江水利水电专科学校 3
力矩的性质： 1、力沿作用线移动时，对某点的矩不变 2、力作用过矩心时，此力对矩心之矩等于零 3、互成平衡的力对同一点的矩之和等于零
浙江水利水电专科学校 4
合力矩定理
力系中合力对一点的矩，等于力系中各分力 对同一点之矩的代数和。
试计算力对A点之矩 试计算力对A点之矩
试计算力对A点之矩
方法一：按力矩的定义计算
方法二：利用合力矩定理计算
浙江水利水电专科学校 6
力偶
定义： – 两个大小相等，方向相反，且不共线的平 行力组成的力系称为力偶。
力偶的表示法 – – 书面表示（F，F’） 图示
力偶的三要素 力偶矩的大小、力偶的转向、力偶的作用面
浙江水利水电专科学校 7
力偶
力偶 ⑴、作用效果：引起物体的转动。
⑵、力和力偶是静力学的二基本要素。
» 力偶特性一： 力偶中的二个力，既不平衡，也不可能合成为 一个力。 » 力偶特性二： 力偶只能用力偶来代替（即只能和另一力偶 等效），因而也只能与力偶平衡。
浙江水利水电专科学校 8
工程实例
浙江水利水电专科学校 9
NO
FBA
B
m2 α
D
ND
浙江水利水电专科学校 16
师生交流
浙江水利水电专科学校 17
M mi
二、平面力偶系的平衡条件 ——合力偶矩等于零 平面力偶系平衡的必要和充分条件：力偶 系中诸力偶矩的代数和等于零。
浙江水利水电专科学校 14
图示的铰接四连杆机构OABD，在杆OA 和BD 上分 别作用着矩为 m1 和 m2 的力偶，而使机构在图示位 置处于平衡。已知OA = r，DB = 2r，α= 30°，不 计杆重，试求 m1 和 m2 间的关系。
第2 章 力矩和力偶理论
力矩
力偶系
浙江水利水电专科学校 1
力矩
力对物体的运动效应，包括力对物体的移动 和转动效应，其中力对物体的转动效应用力 矩来度量。
– 力矩是力对物体的转动效应的度量
浙江水利水电专科学校 2
力矩
力矩的表示
– – 力矩的矩心、力臂 大小、转向、作用面
–
–
正负号规定
•
右手螺旋法则
– 设某力系为Fi（i=1,2,…n），其合力为FR，根据 以上理论，则有表达式：
其中：FR F1 F2 ... Fn Fi
M o ( FR ) M o ( F1 ) M o ( F2 ) ... M o ( Fn ) M o ( Fi )
浙江水利水电专科学校 5
F
d d
F
=
浙江水利水电专科学校 11
力对点的矩与力偶矩的区别： 相同处：力矩的量纲与力偶矩的相同。 不同处：力对点的矩可随矩心的位置改变而改 变，但一个力偶的矩是常量。 联 系：力偶中的两个力对任一点的之和是常 量，等于力偶矩。来自浙江水利水电专科学校 12
平面力偶系的合成
d
d
m1 F1d1 m2 F2 d 2
力偶矩
力偶臂——力偶中两个力的作用线之间的距离
力偶矩——力偶对刚体的转动效应，力偶中任何 一个力的大小与力偶臂d 的乘积，加上适当的正 负号。
M Fd
力偶矩正负号规定： 若力偶有使物体逆时针旋转的趋势 ，力偶矩取正号；反之，取负号
浙江水利水电专科学校 10
力偶的等效条件
作用在刚体内同一平面上的两个力偶相互等 效的充要条件是二者的力偶矩代数值相等。 因此，以后可用力偶的转向箭头来代替力偶。
α
m1 m2
FAB
m1
FBA
B
NO D
O
m2
D ND
浙江水利水电专科学校 15
解： 杆AB为二力杆。
§2-7
力偶系的合成与平衡
A O
α FAB M1
分别写出杆AO 和BD 的平衡方程：
m 0
l1 S ABr cos 0 l2 2S BAr cos 0
S AB S BA l2 2l1
P d m1 1 P2 d m2
R A P1 P2' RB P1' P2
M RAd ( P P2 )d P d P2d m1 m2 1 1
浙江水利水电专科学校 13
平面力偶系合成的结果为作用于同一平面内 的合力偶，合力偶矩等于诸力偶矩的代数和。
量纲单位：
•
牛顿.米[N.m]或千牛.米[kN.m]
M o (F ) F d
浙江水利水电专科学校 3
力矩的性质： 1、力沿作用线移动时，对某点的矩不变 2、力作用过矩心时，此力对矩心之矩等于零 3、互成平衡的力对同一点的矩之和等于零
浙江水利水电专科学校 4
合力矩定理
力系中合力对一点的矩，等于力系中各分力 对同一点之矩的代数和。
试计算力对A点之矩 试计算力对A点之矩
试计算力对A点之矩
方法一：按力矩的定义计算
方法二：利用合力矩定理计算
浙江水利水电专科学校 6
力偶
定义： – 两个大小相等，方向相反，且不共线的平 行力组成的力系称为力偶。
力偶的表示法 – – 书面表示（F，F’） 图示
力偶的三要素 力偶矩的大小、力偶的转向、力偶的作用面
浙江水利水电专科学校 7
力偶
力偶 ⑴、作用效果：引起物体的转动。
⑵、力和力偶是静力学的二基本要素。
» 力偶特性一： 力偶中的二个力，既不平衡，也不可能合成为 一个力。 » 力偶特性二： 力偶只能用力偶来代替（即只能和另一力偶 等效），因而也只能与力偶平衡。
浙江水利水电专科学校 8
工程实例
浙江水利水电专科学校 9
NO
FBA
B
m2 α
D
ND
浙江水利水电专科学校 16
师生交流
浙江水利水电专科学校 17
M mi
二、平面力偶系的平衡条件 ——合力偶矩等于零 平面力偶系平衡的必要和充分条件：力偶 系中诸力偶矩的代数和等于零。
浙江水利水电专科学校 14
图示的铰接四连杆机构OABD，在杆OA 和BD 上分 别作用着矩为 m1 和 m2 的力偶，而使机构在图示位 置处于平衡。已知OA = r，DB = 2r，α= 30°，不 计杆重，试求 m1 和 m2 间的关系。
第2 章 力矩和力偶理论
力矩
力偶系
浙江水利水电专科学校 1
力矩
力对物体的运动效应，包括力对物体的移动 和转动效应，其中力对物体的转动效应用力 矩来度量。
– 力矩是力对物体的转动效应的度量
浙江水利水电专科学校 2
力矩
力矩的表示
– – 力矩的矩心、力臂 大小、转向、作用面
–
–
正负号规定
•
右手螺旋法则
– 设某力系为Fi（i=1,2,…n），其合力为FR，根据 以上理论，则有表达式：
其中：FR F1 F2 ... Fn Fi
M o ( FR ) M o ( F1 ) M o ( F2 ) ... M o ( Fn ) M o ( Fi )
浙江水利水电专科学校 5
F
d d
F
=
浙江水利水电专科学校 11
力对点的矩与力偶矩的区别： 相同处：力矩的量纲与力偶矩的相同。 不同处：力对点的矩可随矩心的位置改变而改 变，但一个力偶的矩是常量。 联 系：力偶中的两个力对任一点的之和是常 量，等于力偶矩。来自浙江水利水电专科学校 12
平面力偶系的合成
d
d
m1 F1d1 m2 F2 d 2
力偶矩
力偶臂——力偶中两个力的作用线之间的距离
力偶矩——力偶对刚体的转动效应，力偶中任何 一个力的大小与力偶臂d 的乘积，加上适当的正 负号。
M Fd
力偶矩正负号规定： 若力偶有使物体逆时针旋转的趋势 ，力偶矩取正号；反之，取负号
浙江水利水电专科学校 10
力偶的等效条件
作用在刚体内同一平面上的两个力偶相互等 效的充要条件是二者的力偶矩代数值相等。 因此，以后可用力偶的转向箭头来代替力偶。