高考数学临场解题策略之线性规划
高考数学一轮复习 简单的线性规划

2008高考数学一轮复习 简单的线性规划【知识概要】1、二元一次不等式表示平面区域: (1)二元一次不等式0>++C By Ax 在平面直角坐标系中表示直线0=++C By Ax 一侧所有点组成的平面区域,直线应画成 虚线 ;0<++C By Ax 表示直线0=++C By Ax 另一侧 所有点组成的 平面区域 。
画不等式0≥++C By Ax ()0≤所表示的平面区域时,应把边界直线画成 实线 。
(2)画二元一次不等式表示的平面区域常用直线定界,特殊点定域(原点不在边界上时,用原点定域;原点在边界上时,用)0,1(或)1,0(定域)。
(3)二元一次不等式组所表示的平面区域是各个不等式所表示的平面点集的 交集 ,因而是各个不等式所表示的平面区域的 公共部分 。
2、线性规划:(1)对于变量y x ,的约束条件,都是关于y x ,的一次不等式,称为 线性约束条件 ,),(y x f z =是欲达到最值所涉及的变量y x ,的解析式,叫做 目标函数 ,当),(y x f 是关于y x ,的一次解析式时,叫做 线性目标函数 。
(2)求线性目标函数在约束条件下的最值问题称为 线性规划 问题,满足线性约束条件的解),(y x 称为 可行解 ,由所有解组成的集合叫 可行域 ,使目标函数取得最大值或最小值的可行解叫 最优解 。
【基础训练】1、不等式094≥-+y x 表示直线094=-+y x ( )A 右上方的平面区域B 左下方的平面区域C 右上方的平面区域及直线本身D 左下方的平面区域及直线本身 解:选C 。
注意指导学生从不等式直接看出,如094≥-+y x 可转化为x y -≥94,表示在y 的上方,即直线的上方;还要注意观察有无等号。
2、设变量x 、y 满足约束条件⎪⎩⎪⎨⎧-≥≥+≤632x y y x xy ,则目标函数y x z +=2的最小值为 。
解:设变量x 、y 满足约束条件2,36y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩在坐标系中画出可行域△ABC ,A(2,0),B(1,1),C(3,3),则目标函数2z x y =+的最小值为3。
高考数学丨线性规划知识点汇总

高考数学丨线性规划知识点汇总一、知识梳理1 目标函数:P=2x+y是一个含有两个变量x和y的函数,称为目标函数。
2 可行域:约束条件表示的平面区域称为可行域。
3 整点:坐标为整数的点叫做整点。
4 线性规划问题:求线性目标函数在线性约束条件下的最大值或最小值的问题,通常称为线性规划问题。
只含有两个变量的简单线性规划问题可用图解法来解决。
5 整数线性规划:要求量整数的线性规划称为整数线性规划。
线性规划是一门研究如何使用最少的人力、物力和财力去最优地完成科学研究、工业设计、经济管理中实际问题的专门学科,主要在以下两类问题中得到应用:一是在人力、物力、财务等资源一定和条件下,如何使用它们来完成最多的任务;二是给一项任务,如何合理安排和规划,能以最少的人力、物力、资金等资源来完成该项任务。
1 对于不含边界的区域,要将边界画成虚线。
2 确定二元一次不等式所表示的平面区域有种方法,常用的一种方法是“选点法”:任选一个不在直线上的点,检验它的坐标是否满足所给的不等式,若适合,则该点所在的一侧即为不等式所表示的平面区域;否则,直线的另一端为所求的平面区域。
若直线不过原点,通常选择原点代入检验。
3 平移直线y=-kx+P时,直线必须经过可行域。
4 对于有实际背景的线性规划问题,可行域通常是位于第一象限内的一个凸多边形区域,此时变动直线的最佳位置一般通过这个凸多边形的顶点。
5 简单线性规划问题就是求线性目标函数在线性约束条件下的最优解,无论此类题目是以什么实际问题提出,其求解的格式与步骤是不变的:(1)寻找线性约束条件,线性目标函数;(2)由二元一次不等于表示的平面区域做出可行域;(3)在可行域内求目标函数的最优解。
基础知识:一、1.占P(x0,y0)在直线Ax+By+C=0上,则点P坐标适合方程,即Ax0+ y0+C=02.点P(x0,y0)在直线Ax+By+C=0上方(左上或右下),则当B>0时,Ax0+ y0+C >0;当B<0时,Ax0+ y0+C<03.点P(x0+,y0)D在直线Ax0+ y0+C=0下方(左下或右下),当B>0时,Ax0+ y0+C<0;当B>0时,Ax0+ y0+C>0注意:(1)在直线Ax+ By+C=0同一侧的所有点,把它的坐标(x,y)代入Ax+ By+C=0,所得实数的符号都相同。
高考理科数学一轮复习 简单的线性规划

(第2题)
第6页
栏目导航
高考总复习 一轮复习导学案 ·数学理科
第八章
不等式
3.
y≤x, (必修 5P95 习题 7 改编)若变量 x,y 满足约束条件x+y≤4, y≥k,
且 z=2x+y
2 的最小值为-6,则 k=________.
【解析】作出不等式组表示的平面区域,如图中阴影 部分所示,z=2x+y,则 y=-2x+z.易知当直线 y=-2x +z 过点 A(k,k)时,z=2x+y 取得最小值,即 3k=-6, 所以 k=-2.
第13页
栏目导航
高考总复习 一轮复习导学案 ·数学理科
第八章
不等式
【精要点评】(1) 二元一次不等式组所确定的平面区域是不等式组中各个不等式 所表示的半平面区域的公共部分,画出平面区域的关键是把各个半平面区域确定准 确,其基本方法是“直线定界、特殊点定域”; (2) 在不等式中,无等号时直线画成虚线,有等号时直线画成实线.测试点可以 选一个,也可以选多个.直线不过原点,测试点常选取原点.
(4)可行域: 所有可行解组成的集合 称为可行域.
第9页
栏目导航
高考总复习 一轮复习导学案 ·数学理科
第八章
不等式
(5)最优解:使目标函数取得最大值或最小值的可行解称为 最优解 . (6)求线性目标函数在线性约束条件下的最大值或最小值问题称为 线性规划
问题 .
2.解线性规划问题的步骤 (1)画,即 画出线性约束条件所表示的可行域 ;
第八章
不等式
课堂导学 目标 1 确定二元一次不等式(组)所表示的平面区域 x+y≥0, 在平面直角坐标系中, 已知不等式组x-y+4≥0, x≤a 域的面积是 9,则实数 a 的值为________ 1 .
高中数学高考总复习------简单的线性规划知识讲解及考点梳理

高中数学高考总复习------简单的线性规划知识讲解及考点梳理【考纲要求】1.了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景。
2.会从实际情境中抽象出一元二次不等式模型。
3.会从实际情境中抽象出二元一次不等式组;了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组;4.会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决。
5.熟练应用不等式性质解决目标函数的最优解问题。
【知识网络】【考点梳理】【高清课堂:不等式与不等关系394841知识要点】考点一:用二元一次不等式(组)表示平面区域二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域.(虚线表示区域不包括边界直线)要点诠释:画二元一次不等式或表示的平面区域的基本步骤:①画出直线(有等号画实线,无等号画虚线);②当时,取原点作为特殊点,判断原点所在的平面区域;当时,另取一特殊点判断;③确定要画不等式所表示的平面区域。
简称:“直线定界,特殊点定域”方法。
考点二:二元一次不等式表示哪个平面区域的判断方法因为对在直线Ax+By+c=0同一侧的所有点(x ,y),实数Ax+By+c 的符号相同,所以只需在此直线的某一侧任取一点(x 0,y 0)(若原点不在直线上,则取原点(0,0)最简便).把它的坐标代入Ax+By+c,由其值的符号即可判断二元一次不等式Ax+By+c>0(或<0)表示直线的哪一侧.要点诠释:判断二元一次不等式Ax+By+c>0(或<0)表示直线的哪一侧的方法:因为对在直线Ax+By+C =0同一侧的所有点(x ,y),数Ax+By+C 的符号相同,所以只需在此直线的某一简单的线性规划二元一次不等式(组)表示的区域简单应用不等式(组)的应用背景侧任取一点(x0,y0)(若原点不在直线上,则取原点(0,0)最简便),它的坐标代入Ax+By+c,由其值的符号即可判断二元一次不等式Ax+By+c>0(或<0)表示直线的哪一侧.考点三:线性规划的有关概念:①线性约束条件:在一个问题中,不等式组是一组变量x、y的约束条件,这组约束条件都是关于x、y的一次不等式,故又称线性约束条件.②线性目标函数:关于x、y的一次式z=ax+by(a,b∈R)是欲达到最大值或最小值所涉及的变量x、y的解析式,叫线性目标函数.③线性规划问题:一般地,求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.④可行解、可行域和最优解:满足线性约束条件的解(x,y)叫可行解.由所有可行解组成的集合叫做可行域.使目标函数取得最大或最小值的可行解叫线性规划问题的最优解.要点诠释:在应用线性规划的方法时,一般具备下列条件:①一定要能够将目标表述为最大化(极大)或最小化(极小)的要求。
线性规划高考题型及解题策略

线性规划高考题型及解题策略
刘允忠
【期刊名称】《高中数理化》
【年(卷),期】2015(000)007
【摘要】从近几年全国各地高考试题来看,高考对线性规划问题的考查主要题型是在不等式约束条件下,求线性或非线性目标函数的最值,或以最值为载体求含参数值、范围问题,或探求区域面积问题、解决实际问题及隐性线性规划问题等.本文就此类
常见题型与解题策略总结如下.1约束条件下的线性目标函数的最值问题线性约束
条件下的线性目标函数的最值问题是近几年高考中的重点题型,当然解决这类问题
也相对简单,解题策略主要是借助直线的截距的几何意义以及平面区域图形求解。
【总页数】4页(P11-14)
【作者】刘允忠
【作者单位】浙江宁波北仑明港中学
【正文语种】中文
【相关文献】
1.含参数的线性规划问题解题策略
2.高考数学临场解题策略之线性规划
3.线性规划问题的题型及解题策略分析——由2017年上海市一道春考题谈起
4.高考数学临
场解题策略之线性规划5.高中数学数列问题高考题型及解题策略研究
因版权原因,仅展示原文概要,查看原文内容请购买。
高考数学 线性规划——作图与求解

线性规划——作图与求解一、基础知识1、相关术语:(1)线性约束条件:关于变量,x y 的一次不等式(或方程)组(2)可行解:满足线性约束条件的解(),x y(3)可行域:所有可行解组成的集合(4)目标函数:关于,x y 的函数解析式(5)最优解:是目标函数取得最大值或最小值的可行解2、如何在直角坐标系中作出可行域:(1)先作出围成可行域的直线,利用“两点唯一确定一条直线”可选取直线上的两个特殊点(比如坐标轴上的点),以便快速做出直线(2)如何判断满足不等式的区域位于直线的哪一侧:一条曲线(或直线)将平面分成若干区域,则在同一区域的点,所满足不等式的不等号方向相同,所以可用特殊值法,利用特殊点判断其是否符合不等式,如果符合,则该特殊点所在区域均符合该不等式,具体来说有以下三种情况:① 竖直线x a =或水平线y b =:可通过点的横(纵)坐标直接进行判断② 一般直线()0y kx b kb =+≠:可代入()0,0点进行判断,若符合不等式,则原点所在区域即为不等式表示区域,否则则为另一半区域。
例如:不等式230x y -+≤,代入()0,0符合不等式,则230x y -+≤所表示区域为直线230x y -+=的右下方③ 过原点的直线()0y kx k =≠:无法代入()0,0,可代入坐标轴上的特殊点予以解决,或者利用象限进行判断。
例如:y x ≤:直线y x =穿过一、三象限,二、四象限分居直线两侧。
考虑第四象限的点0,0x y ><,所以必有y x ≤,所以第四象限所在区域含在y x ≤表示的区域之中。
(3)在作可行域时要注意边界是否能够取到:对于约束条件(),0F x y >(或(),0F x y <)边界不能取值时,在图像中边界用虚线表示;对于约束条件(),0F x y ≥(或(),0F x y ≤)边界能取值时,在图像中边界用实线表示3、利用数形结合寻求最优解的一般步骤(1)根据约束条件,在平面直角坐标系中作出可行域所代表的区域(2)确定目标函数z 在式子中的几何意义,常见的几何意义有:(设,a b 为常数)① 线性表达式——与纵截距相关:例如z ax by =+,则有a z y x b b=-+,从而z 的取值与动直线的纵截距相关,要注意b 的符号,若0b >,则z 的最大值与纵截距最大值相关;若0b <,则z 的最大值与纵截距最小值相关。
高考数学线性规划知识点梳理

高考数学丨线性规划知识点梳理1 目标函数:P=2x+y是一个含有两个变量x和y的函数,称为目标函数。
2 可行域:约束条件表示的平面区域称为可行域。
3 整点:坐标为整数的点叫做整点。
4 线性规划问题:求线性目标函数在线性约束条件下的最大值或最小值的问题,通常称为线性规划问题。
只含有两个变量的简单线性规划问题可用图解法来解决。
5 整数线性规划:要求量整数的线性规划称为整数线性规划。
线性规划是一门研究如何使用最少的人力、物力和财力去最优地完成科学研究、工业设计、经济管理中实际问题的专门学科,主要在以下两类问题中得到应用:一是在人力、物力、财务等资源一定和条件下,如何使用它们来完成最多的任务;二是给一项任务,如何合理安排和规划,能以最少的人力、物力、资金等资源来完成该项任务。
1 对于不含边界的区域,要将边界画成虚线。
2 确定二元一次不等式所表示的平面区域有种方法,常用的一种方法是“选点法”:任选一个不在直线上的点,检验它的坐标是否满足所给的不等式,若适合,则该点所在的一侧即为不等式所表示的平面区域;否则,直线的另一端为所求的平面区域。
若直线不过原点,通常选择原点代入检验。
3 平移直线y=-kx+P时,直线必须经过可行域。
4 对于有实际背景的线性规划问题,可行域通常是位于第一象限内的一个凸多边形区域,此时变动直线的最佳位置一般通过这个凸多边形的顶点。
5 简单线性规划问题就是求线性目标函数在线性约束条件下的最优解,无论此类题目是以什么实际问题提出,其求解的格式与步骤是不变的:(1)寻找线性约束条件,线性目标函数;(2)由二元一次不等于表示的平面区域做出可行域;(3)在可行域内求目标函数的最优解。
一、1.占P(x0,y0)在直线Ax+By+C=0上,则点P坐标适合方程,即Ax0+ y0+C=02.点P(x0,y0)在直线Ax+By+C=0上方(左上或右下),则当B>0时,Ax0+ y0+C >0;当B<0时,Ax0+ y0+C<03.点P(x0+,y0)D在直线Ax0+ y0+C=0下方(左下或右下),当B>0时,Ax0+ y0+C<0;当B>0时,Ax0+ y0+C>0注意:(1)在直线Ax+ By+C=0同一侧的所有点,把它的坐标(x,y)代入Ax+ By+C=0,所得实数的符号都相同。
高考数学线性规划题型总结计划
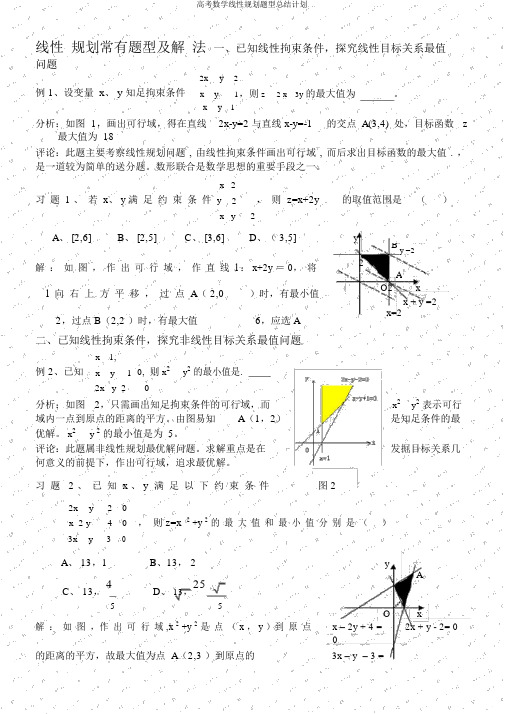
线性 规划常有题型及解 法 一、已知线性拘束条件,探究线性目标关系最值问题2x y 2例 1、设变量 x 、 y 知足拘束条件x y 1,则 z 2 x 3y 的最大值为。
x y 1分析:如图 1,画出可行域,得在直线 2x-y=2 与直线 x-y=-1 的交点 A(3,4) 处,目标函数 z最大值为 18评论:此题主要考察线性规划问题 , 由线性拘束条件画出可行域 , 而后求出目标函数的最大值 . ,是一道较为简单的送分题。
数形联合是数学思想的重要手段之一。
x 2习 题 1 、 若 x 、 y 满 足 约 束 条 件 y 2, 则 z=x+2y的取值范围是()x y2A 、 [2,6]B 、 [2,5]C 、 [3,6]D 、( 3,5]yBy =2解 : 如 图 , 作 出 可 行 域 , 作 直 线 l : x+2y = 0, 将2Axl 向 右 上 方 平 移 , 过 点 A ( 2,0)时,有最小值 O2x + y =2x=22,过点 B (2,2 )时,有最大值6,应选 A二、已知线性拘束条件,探究非线性目标关系最值问题x 1, 例 2、已知xy 1 0, 则 x 2y 2 的最小值是.2x y 2分析:如图 2,只需画出知足拘束条件的可行域,而x 2 y 2 表示可行域内一点到原点的距离的平方。
由图易知A (1,2) 是知足条件的最优解。
x 2 y 2 的最小值是为 5。
评论:此题属非线性规划最优解问题。
求解重点是在 发掘目标关系几何意义的前提下,作出可行域,追求最优解。
习 题 2 、 已 知 x 、 y 满 足 以 下 约 束 条 件图 22x y 2 0x 2 y4 0 , 则 z=x 2 +y 2 的 最 大 值 和 最 小 值 分 别 是 ()3xy3A 、 13,1B 、13, 2yAC 、 13,4D 、 13,255 5Ox解 : 如 图 ,作 出 可 行 域 ,x 2 +y 2 是 点 ( x , y )到 原 点x – 2y + 4 = 2x + y - 2= 00 的距离的平方,故最大值为点 A (2,3 )到原点的3x – y – 3 =距离的平方,即 |AO| 2 =13 ,最小值为原点到直线 2x + y - 2=0 的距离的平方,即为4,选 C 5练习 2、已知x,y 知足x 2 y50 ,则yx 1, y 0xx 2 y30的最大值为 ___________,最小值为 ____________.2,0三、设计线性规划,探究平面地区的面积问题例 3、在平面直角坐标系中,不等式组x y20x y20表示的平面地区的y0面积是() (A) 4 2 (B)4 (C) 2 2 (D)2x y 2 0分析:如图6,作出可行域,易知不等式组x y 2 0表示y 0的平面地区是一个三角形。
