北方工业大学研究生考试随机过程05年答案
北京工业大学2005年硕士研究生入学考试试题__数分_解答

北京工业大学2005年硕士研究生入学考试数学分析试题一、(15分)设0n a > ,1c <且 1limn n na c a +→∞=,试证明 0lim =∞→n n a 。
证明:取实数r 使得 1lim 1n n na c r a +→∞=<<,所以存在0>N ,当N n >时,有1n na r a +<,即有1n n a ra +<,递推得 21110n N n n N a r a r a -+-+<<<< ,令n →∞得0lim =∞→n n a 。
二、(15分)用εδ-语言证明若0lim ()x x f x A →=,0lim ()0x x g x B →=≠,则0()lim()x x f x Ag x B→=。
证明:因为 ()()()()(())()()()()f x A A g x B f x A f x B AB g x A AB g x B g x B g x g x B------=≤+由0lim ()0x x g x B →=≠,得0l i m ()0x x g x B →=>,存在10N >,当1n N >时有()2Bg x ≤, 又0lim ()x x f x A →=,0lim ()x x g x B →=,所以对任意的0ε>,存在20N >,当2n N >时有()f x A ε-<,()g x B ε-<,故当12max{,}n N N >时有2()()2()2()()()()f x A A g x B A f x A g x B g x g x B B Bε---≤+<+, 即有 0()lim()x x f x Ag x B→=。
三、(15分)设f x (),)(x g 为连续函数,试证明)}(),(max{)(x g x f x F =也为连续函数。
随机过程试题及答案

随机过程试题及答案随机过程是概率论与数理统计的重要理论基础之一。
通过研究随机过程,可以揭示随机现象的规律性,并应用于实际问题的建模与分析。
以下是一些关于随机过程的试题及答案,帮助读者更好地理解与掌握这一概念。
1. 试题:设随机过程X(t)是一个马尔可夫过程,其状态空间为S={1,2,3},转移概率矩阵为:P =| 0.5 0.2 0.3 || 0.1 0.6 0.3 || 0.1 0.3 0.6 |(1) 计算X(t)在t=2时的转移概率矩阵。
(2) 求X(t)的平稳分布。
2. 答案:(1) 根据马尔可夫过程的性质,X(t)在t=2时的转移概率矩阵可以通过原始的转移概率矩阵P的2次幂来计算。
令Q = P^2,则X(t=2)的转移概率矩阵为:Q =| 0.37 0.26 0.37 || 0.22 0.42 0.36 || 0.19 0.36 0.45 |(2) 平稳分布是指随机过程的状态概率分布在长时间内保持不变的分布。
设平稳分布为π = (π1,π2, π3),满足πP = π(即π为右特征向量),且所有状态的概率之和为1。
根据πP = π,可以得到如下方程组:π1 = 0.5π1 + 0.1π2 + 0.1π3π2 = 0.2π1 + 0.6π2 + 0.3π3π3 = 0.3π1 + 0.3π2 + 0.6π3解以上方程组可得到平稳分布:π = (0.25, 0.3125, 0.4375)3. 试题:设随机过程X(t)是一个泊松过程,其到达率为λ=1,即单位时间内到达的事件平均次数为1。
(1) 请计算X(t)在t=2时的累计到达次数的概率P{N(2)≤3}。
(2) 计算X(t)的平均到达速率。
4. 答案:(1) 泊松过程具有独立增量和平稳增量的性质,且在单位时间内到达次数服从参数为λ的泊松分布。
所以,P{N(2)≤3} = P{N(2)=0} + P{N(2)=1} + P{N(2)=2} +P{N(2)=3},其中P{N(2)=k}表示在时间间隔[0,2]内到达的次数为k的概率。
研究生《随机过程》教材课后作业答案

1.1 证明:∵1111,,,,,A F F F F ∈ΩΦ∈ΩΩ∈Φ∈Ω-Φ∈ΩΦ∈ 且∴1F 是事件域。
∵222,,,,cA A F F A F A A ∈Ω∈Ω∈-Φ∈=Ω-∴22222,,,,c c A F A F A F A F A F ∈-Φ∈-Φ∈Ω-∈Ω-∈ 且2,ccA A A A F ΦΩ=ΩΦΩ∈ ∴2F 是事件域。
且12F F ∈。
∵2ΩΩ∈∴3F Ω∈∴3F 是事件域。
且23F F ∈∴123,,F F F 皆为事件域且123F F F ∈∈。
1.2一次投掷三颗均匀骰子可能出现的点数ω为(),,,,,,16,16,16i j k i R j R k R i j k ∈∈∈≤≤≤≤≤≤∴样本空间()61,,6=,,n i j k i j k =≤≤Ω事件(){},,|,,i j k A i j k ωω==,,,,1,,6i R j R k R i j k ∈∈∈≤≤ 事件域2F Ω= 概率测度(),,1P 216i j k A =,,,,1,,6i R j R k R i j k ∈∈∈≤≤ 则(),,F P Ω为所求的概率空间。
1.3 证明:(1)由公理可知()0P Φ=(2)有概率测度的可列可加性将第n+1个集合往后都取为空集,即可得结论()11n nk k k k P A P A ==⎛⎫= ⎪⎝⎭∑∑ (3)∵,,A B F A B ∈⊂ ∴B A F -∈,()A B A -=Φ由概率测度的可列可加性可得:()()()()P B P A B A P A P B A =+-=+-即()()()P B A P B P A -=-有概率测度的非负性可得()()()0P B P A P B A -=-≥,即()()P B P A ≥ (4)若B =Ω,由(3)则有()()1P A P A =- (5)∵()()()()121212P A A P A P A P A A +=+- 假设()()()()()11211111m m m k k i j i j k m k i j m i j k m k P A P A P A A P A A A P A A A +=≤<≤≤<<≤=⎛⎫=-+-+- ⎪⎝⎭∑∑∑ 成立,则()()()()()()()()()11111111111111211111+1m m m m k k m m k m k k k k k mm k iji j k k i j mi j k mm m m m k k m k i j i k i j mP A P A A P A P A P A A P A P A P A A P A A A P A A A P A A P A P A A P A A ++++====+=≤<≤≤<<≤++=+=≤<≤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫==+-= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭+-+-⎛⎫⎛⎫+-- ⎪⎪⎝⎭⎝⎭=-+∑∑∑∑∑()()()()()()()()()()()()1121111121111212111111111n j k m i j k mm i j m i j k m m m i j m i j k m m m k i j i j k m k i j m i j k m A P A A A P A A A P A A A A P A A A A P A P A A P A A A P A A A +≤<<≤++++≤<≤≤<<≤+++=≤<≤+≤<<≤+-+-⎛⎫--+-+- ⎪⎝⎭=-+-+-∑∑∑∑∑∑也成立由数学归纳法可知()()()()()11211111n n n k k i j i j k n k i j n i j k n k P A P A P A A P A A A P A A A +=≤<≤≤<<≤=⎛⎫=-+-+- ⎪⎝⎭∑∑∑()()()()()()111122212123231231n nn n k k k k k k k k n n n k k k k k k nk k nk k P A P A A P A P A P A A P A P A P A P A A P A A P A P A P A P A =========⎛⎫⎛⎫⎛⎫⎛⎫=+=+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫=++-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫≤++ ⎪⎝⎭≤≤∑1.4 (1)()()()()()()()()()()()()()()()()()()()()()21040114P AB P A P B P AB P AB P A P B P AB P A P B P A P AB P A P B P AB P A P A B P A P A P A ≤-≤-≤≤-≤-=-=+-⎡⎤⎡⎤⎣⎦⎣⎦≤-≤(2)()()()()()()()()()()()()()()()()()()()()()()()if =1else if =P AB P BC P AB P BC P AB P AC P A B C P ABC P AB P BC P AC P A B C P ABC P BC P A B C P AB P BC P AB P BC --+=++-+=++-≤+≤--- 可由这个式子的轮换对称性证明这种情况(3)()()()()()()()()()()11111111111n nk k k k n nn nk k k k k k k k nk k nk k A A A AP A P A P A P A n P A P A n P A P A P A n ========⊂∴⊃⎛⎫≤≤=-=- ⎪⎝⎭-≤-∴≥--∑∑∑∑∑1.5()1(1)k nkk A P X k n--== 1.6由全概率公式()()()()()()()()()()()()100112211110101=1424P Y X P Y P X P Y P X P Y P X P Y P Y P Y e -≥=≥=+≥=+≥==+-=+-=-=-1.7 证明: 显然()()()()111111122,,,,,,0n n n n n F x x F x x F y x P x X y x X x X ∆=-=≤≤≤≤≥假设()()121111222,,,,,,,0i n i i i i i n n F x x P x X y x X y x X y x X x X ∆∆∆=≤≤≤≤≤≤≤≤≥ 成立 从而()()()()12+11111222111112221111122211122,,,,,,,,,,,,,,,,,,,0i i n i i i i i n n i i i i i n n i i i i i n n F x x P x X y x X y x X y x X x X P x X y x X y x X y y X x X P x X y x X y x X y x X x X +++++++++∆∆∆∆=≤≤≤≤≤≤≤≤-≤≤≤≤≤≤≤≤=≤≤≤≤≤≤≤≤≥ (分布函数对于每一变元单调不减)也成立有数学归纳法可知()()121111222,,,,0n n n n n F x x P x X y x X y x X y ∆∆∆=≤≤≤≤≤≤≥1.8()()()()()()()()()()()''''''',,0','x y x y x x y x y x y x y x y x x y y h x y eeh x y eeeee e e e x x y y -+-+-+-+-+-+----∆=-∆∆=---=--≥≤≤所以h 是二元单调不减函数。
2005年硕士研究生入学考试及答案

目录1.05年北师大物理类各方向2.05年长光所3.05年东南大学4.05年中科大5.05年南京大学6.05年华中科大7.05年吉林大学(原子所)8.05年四川大学(原子与分子)9.05年北京理工10.05年河北理工11.05年长春理工北京师范大学2005年招收硕士研究生入学考试试题专业:物理类各专业科目代号:459研究方向:各方向考试科目:量子力学[注意]答案写在答题纸上,写在试题上无效。
1.(20分)一个电子被限制在一维谐振子势场中,活动范围求激发电子到第一激发态所需要的能量(用ev表示)(,,)提示:谐振子能量本征函数可以写成2.(30分)一个电子被限制在二维各向同性谐振子势场中(特征频率为)。
(1)写出其哈密顿量,利用一维谐振子能级公式找到此电子的能级公式和简并度。
(2)请推导电子的径向运动方程。
并讨论其在时的渐近解。
提示:极坐标下3.(50分)两个质量为的粒子,被禁闭在特征频率为的一维谐振子势场中,彼此无相互作用(此题中波函数无须写出具体形式):(1)如果两个粒子无自旋可分辨,写出系统的基态(两个都在自己的基态)和第一激发能级(即一个在基态,另一个在第一激发态)的波函数和能量(注意简并情形)。
(10分)(2)如果两个粒子是不可分辨的无自旋波色子,写出系统的基态和第一激发态的能量和波函数。
如果粒子间互作用势为,计算基态能级到一级微扰项。
(15分)(3分)如果两个粒子是不可分辨的自旋1/2粒子,写出基态能级和波函数(考虑自旋)。
如果粒子间互作用能为,计算基态能量。
(15分)(4)同(3),解除势阱,两个粒子以左一右飞出。
有两个探测器分别(同时)测量它们的y方向自旋角动量。
请问测量结果为两电子自旋反向的几率是多少?(10分)4.(30分)中心力场中电子自旋与轨道角动量存在耦合能。
总角动量,是的共同本征态。
现有一电子处于态,且。
(1)在一基近似下,可用代替,请问电子的能量与态差多少?(2)请计算该电子产生的平均磁矩,并由此计算在z方向均匀磁场B中电子的能量改变多少?(),当,,当,5.(20分)一个定域(空间位置不动)的电子(自旋1/2)处于z方向强磁场中。
北京工业大学2002-2005年硕士研究生入学考试试题与答案解析

北京工业大学2002年硕士研究生入学考试试题科目代码:551 科目名称:工程热力学适用专业:热能工程一、名词解释(每题3分,共30分)1 开口系统:热力系与外界之间有物质交换2 热力循环:封闭的热力过程3 可逆过程:当系统完成某一过程后,如能使过程逆行而使系统及外界回复到原始状态不遗留下任何变化,则称此过程为可逆过程。
4 孤立系统的熵增原理:在孤立系内,一切实际过程都朝着使系统熵增加的方向进行,或在极限情况下维持系统的熵不变,而任何使系统熵减少的过程是不可能发生的。
5 临界流速:在缩放喷管的喉部,流速恰好达到当地声速6 压气机的容积效率:气缸吸气的有效进气容量与活塞的排量容积之比。
7 水的三相点:水呈现气、液、固三相平衡共存状态8 水的气化潜热:在一定压力下,1kg饱和水转变为饱和蒸气吸收的热量9 制冷系数:制冷机循环中从冷源移出的热量与所耗功量之比。
10 含湿量:湿空气中包含的水蒸气质量与干空气质量之比值。
二、填空题(每题2分,共20分)1 工程热力学是热力学的一个分支,它着重研究与热能工程有关的热能和机械能相互转换的规律。
2 闭口系统中包含的物质是固定的,故也称闭口系统为控制质量系统。
3 系统吸热时它的熵增大;系统放热时它的熵增大、减少或不变;系统与外界不发生热的交换时它的熵增大或不变。
4 理想气体的热力学能的性质是1845年焦耳通过著名的焦耳实验确定的。
5 在任何过程中,单位质量的理想气体的温度升高1K时比热力学能增加的数值即等于其比定容热容的值;而比焓增加的数值即等于其比定压热容的值。
6 指出提高燃气轮机装置热效率的两条措施:将汽轮机出口的低压湿蒸汽完全凝结为水;采用过热蒸汽作为汽轮机的进口蒸汽。
7 固体和液体的比定压热容和比定容热容的数值近似相等。
8 完全不含水蒸气的空气称为干空气。
9 卡诺定理一的内容为:在两个给定的热源间工作的所有热机,不可能具有比可逆热机更高的热效率。
10通常把湿饱和蒸汽中 饱和蒸气 的质量分数称为干度,并用x 表示。
北京工业大学2010-2013学年数理统计与随机过程(研)试卷
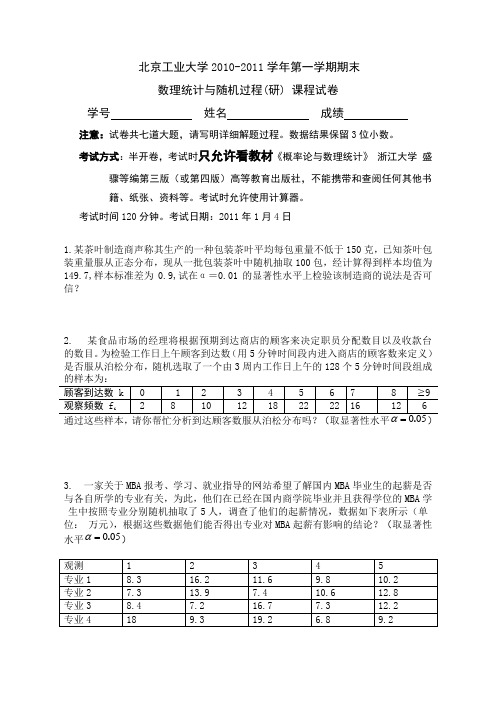
北京工业大学2010-2011学年第一学期期末数理统计与随机过程(研) 课程试卷学号 姓名 成绩 注意:试卷共七道大题,请写明详细解题过程。
数据结果保留3位小数。
考试方式:半开卷,考试时只允许看教材《概率论与数理统计》 浙江大学 盛骤等编第三版(或第四版)高等教育出版社,不能携带和查阅任何其他书籍、纸张、资料等。
考试时允许使用计算器。
考试时间120分钟。
考试日期:2011年1月4日1.某茶叶制造商声称其生产的一种包装茶叶平均每包重量不低于150克,已知茶叶包装重量服从正态分布,现从一批包装茶叶中随机抽取100包,经计算得到样本均值为149.7,样本标准差为0.9,试在α=0.01的显著性水平上检验该制造商的说法是否可信?2. 某食品市场的经理将根据预期到达商店的顾客来决定职员分配数目以及收款台的数目。
为检验工作日上午顾客到达数(用5分钟时间段内进入商店的顾客数来定义)是否服从泊松分布,随机选取了一个由3周内工作日上午的128个5分钟时间段组成通过这些样本,请你帮忙分析到达顾客数服从泊松分布吗?(取显著性水平)3.一家关于MBA 报考、学习、就业指导的网站希望了解国内MBA 毕业生的起薪是否与各自所学的专业有关,为此,他们在已经在国内商学院毕业并且获得学位的MBA 学生中按照专业分别随机抽取了5人,调查了他们的起薪情况,数据如下表所示(单 位: 万元),根据这些数据他们能否得出专业对MBA 起薪有影响的结论?(取显著性水平050.=α)4.为定义一种变量,用来描述某种商品的供给量与价格之间的相关关系.首先要收集(1) 试确定(2) 对回归方程进行显著性检验(α=0.05);(3) 当x=20时,求y 的95%的预测区间。
5.6.设{,}n X n T ∈是一个齐次马尔可夫链,其状态空间{0,1,2}I =,其一步转移概率矩阵为 3104411142431044P ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭其初始状态的概率分布为01(0)(),0,1,2,3i i p P X i i ====求: (1)求2{1}P X =;(2)求2{2|1}n n P X X +==;(3)求012{1,2,1}P X X X ===;(4)讨论此链是否具有遍历性,若是遍历的求其极限分布。
随机过程试题及答案说课材料

随机过程试题及答案收集于网络,如有侵权请联系管理员删除1.设随机变量X 服从参数为λ的泊松分布,则X 的特征函数为 。
2.设随机过程X(t)=Acos( t+),-<t<ωΦ∞∞ 其中ω为正常数,A 和Φ是相互独立的随机变量,且A 和Φ服从在区间[]0,1上的均匀分布,则X(t)的数学期望为 。
3.强度为λ的泊松过程的点间间距是相互独立的随机变量,且服从均值为 的同一指数分布。
4.设{}n W ,n 1≥是与泊松过程{}X(t),t 0≥对应的一个等待时间序列,则n W 服从 分布。
5.袋中放有一个白球,两个红球,每隔单位时间从袋中任取一球,取后放回,对每一个确定的t 对应随机变量⎪⎩⎪⎨⎧=时取得白球如果时取得红球如果t t t e t t X ,,3)(,则 这个随机过程的状态空间 。
6.设马氏链的一步转移概率矩阵ij P=(p ),n 步转移矩阵(n)(n)ij P (p )=,二者之间的关系为 。
7.设{}n X ,n 0≥为马氏链,状态空间I ,初始概率i 0p P(X =i)=,绝对概率{}j n p (n)P X j ==,n 步转移概率(n)ijp ,三者之间的关系为 。
8.设}),({0≥t t X 是泊松过程,且对于任意012≥>t t 则{(5)6|(3)4}______P X X ===9.更新方程()()()()0tK t H t K t s dF s =+-⎰解的一般形式为 。
10.记()(),0n EX a t M M t μ=≥→∞-→对一切,当时,t +a 。
二、证明题(本大题共4道小题,每题8分,共32分)1.设A,B,C 为三个随机事件,证明条件概率的乘法公式:P(BC A)=P(B A)P(C AB)。
2.设{X (t ),t ≥0}是独立增量过程, 且X (0)=0, 证明{X (t ),t ≥0}是一个马尔科夫过程。
3.设{}n X ,n 0≥为马尔科夫链,状态空间为I ,则对任意整数n 0,1<n l ≥≤和i,j I ∈,n 步转移概率(n)()(n-)ij ik kjk Ip p p l l ∈=∑ ,称此式为切普曼—科尔莫哥洛夫方程,证明并说明其意义。
随机过程课后习题答案

标准教材:随机过程基础及其应用/赵希人,彭秀艳编著索书号:O211.6/Z35-2备用教材:(这个非常多,内容一样一样的)工程随机过程/彭秀艳编著索书号:TB114/P50历年试题(页码对应备用教材)2007一、习题0.7(1)二、习题1.4三、例2.5.1—P80四、例2.1.2—P47五、习题2.2六、例3.2.2—P992008一、习题0.5二、习题1.4三、定理2.5.1—P76四、定理2.5.6—P80五、1、例2.5.1—P802、例2.2.2—P53六、例3.2.3—P992009(回忆版)一、习题1.12二、例2.2.3—P53三、例1.4.2与例1.5.5的融合四、定理2.5.3—P76五、习题0.8六、例3.2.22010一、习题0.4(附加条件给出两个新随机变量表达二、例1.2.1三、例2.1.4四、例2.2.2五、习题2.6六、习题3.3引理1.3.1 解法纠正 许瓦兹不等式()222E XY E X E Y ⎡⎤⎡⎤≤⎡⎤⎣⎦⎣⎦⎣⎦证明:()()()()222222222220440E X Y E X E XY E Y E XY E X E Y E XY E X E Y λλλ +⎡⎤⎡⎤=++≥⎣⎦⎣⎦∴∆≤⎡⎤⎡⎤∴-≤⎡⎤⎣⎦⎣⎦⎣⎦⎡⎤⎡⎤∴≤⎡⎤⎣⎦⎣⎦⎣⎦例1.4.2 解法详解已知随机过程(){},X t t T ∈的均值为零,相关函数为()121212,,,,0a t t t t et t T a --Γ=∈>为常数。
求其积分过程()(){},t Y t X d t T ττ=∈⎰的均值函数()Y m t 和相关函数()12,Y t t Γ。
解:()0Y m t =不妨设12t t >()()()()()()1212222112121122122100,,Y t t t t t t t t t EY t Y t E X d X d d d τττττττττΓ===Γ⎰⎰⎰⎰()()()()()222121122221222112222212221212121212000220022002200222211||111111||211ττττττττττττττττττττττττ--------------=+-=+=---=+-+⎡=++--⎣⎰⎰⎰⎰⎰⎰⎰⎰t t t a a t t a a a a t t t a a at a t a at t a t t at at ed d ed de d e d a ae d e d a a t t e e a a a a t e e e a a⎤⎦同理当21t t >时()()2112112221,1a t t at at Y t t t e e e a a----⎡⎤Γ=++--⎣⎦ (此处书上印刷有误)例1.5.5解法同上例1.5.6 解法详解 普松过程公式推导:(){}()()()()()()()()()()()1lim !lim 1!!!1lim 1!!lim 1lim !lim lim !第一项可看做幂级数展开:第二项将分子的阶乘进行变换:→∞-→∞-→∞---∆-→∞→∞-→∞→∞===-∆∆-⎡⎤⎡⎤⎡⎤=-∆∆⎢⎥⎢⎥⎣⎦-⎣⎦⎣⎦⎡⎤⎡⎤-∆==⎢⎥⎣⎦⎣⎦⎡⎤⋅∆=∆⎢⎥--⎣⎦N k N N kkN N k kN N kN kq t qtN N k N kk k N N P X t k C P N q t q t k N k N q t q t N k k q t e e N N N q t q t N k N ()()()()()!lim 1!-→∞⎡⎤⎢⎥⎣⎦⎡⎤⎡⎤=∆⋅=⋅=⎢⎥⎣⎦-⎣⎦N k k k k kN k N q t N qt qt N k (){}()()()()!1lim 1!!!N kkN kqt P X t k N q t q t N k k qt ek -→∞-∴=⎡⎤⎡⎤⎡⎤=-∆∆⎢⎥⎢⎥⎣⎦-⎣⎦⎣⎦=例2.1.2 解法详解设(){},X t t -∞<<+∞为零均值正交增量过程且()()2212121,E X t X t t t t t -=->⎡⎤⎣⎦,令()()()1Y t X t X t =--,试证明(){},Y t t -∞<<+∞为平稳过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2005-2006年第一学期研究生随机过程
试题答案及评分标准
一、(10分)
设随机变量X 服从参数为λ的泊松分布,求
(1)X 的特征函数)(t ϕ;
(2)利用特征函数计算X 的数学期望及方差。
解:(1) ∑∞
====0}{)()(k itk itX k X P e e
E t ϕ…………………………..3分 ∑∑∞
=-∞=-==00!)(!k k
it k k itk k e e k e e
λλλλ……………………..5分 )1(it e e
-=λ ……………………………………………….6分 (2) 由)()0()(k k k X E i =ϕ得
λλϕλ=-='-==-0)1(|)0()(t it e e ie
i i X E it …………………….8分 22)0()(λλϕ+=''-=X E
所以 λ=-=22)]([)()(X E X E X D ……………………………10分
二、(15分)
设随机过程∑=+-=101)()(k V t i k k e U
t X ,其中k U 服从参数为2的指数分布,k V 服从(0,2)上
的均匀分布,且k U ,k V (k=1,2,……10)以及它们之间都是相互独立的。
求)(t X 的均值函数和协方差函数。
解:)(t X 的均值函数为
][
)()(101)(∑=+-==k V t i k X k e U E t EX t m ……………………….4分
∑=+-=101
)(][)(k V t i k
k e E U E ……………………………..6分 )2cos 2(sin 2
52121020)(i i e dx e it x t i -+==-+-⎰ …….8分
)(t X 的协方差函数为
)()(])()([),(t m s m t X s X E t s B X X X -= …………………..11分
而 ∑∑≤≠≤---=--+=10101))(101)(2
)()()(j k iV iV t s i j k k t s i k j k e e e U U e U t X s X
4sin 2
455)]12(cos 2[sin 161905)()()()(210])()([2)()(22)()(1010
1))()(t s i t s i t s i t s i j k iV iV j k t s i t s i e e e e e E e E U E U E e e t X s X E j k --------≤≠≤-----+=-+⨯
+=+=∑..14分⎪⎭
⎫ ⎝⎛-=-+=--------4sin 21154sin 254sin 2455),(2)(2)(2)()(t s i t s i t s i t s i X e e e e t s B ……15分 三、(15分)
设某服务台在],0(t 内接待的顾客数)(t X 是具有强度(每分钟)为1=λ的泊松过程,求
(1) 三分钟内接待3个顾客的概率;
(2) 第三分钟内接待第三个顾客的概率。
解:(1)333
2
9!33}3)()3({--===-+e e t X t X P ……………………………5分 (2)所求概率为
∑=-≥-=-=2
}3)2()3(,)0()2({k k X X k X X P p ……………….9分
∑=-≥-=-=20
}3)2()3({})0()2({k k X X P k X X P ……………...11分
)1(2
4)21(2)2121(1212112--------+-+--=e e e e e e e ……………14分 322
175---=e e
………………………………………15分 四、(15分) 某电话总机在],0(t 内被呼叫的次数)(t X 是具有参数为λ的泊松过程,每次呼叫被接线员接听的概率为p ,且每次呼叫是否被接听是相互独立的,设}0,{≥t Y t 是呼叫被接听数,问
}0,{≥t Y t 是否为泊松过程?说明理由。
解:令 ⎩⎨⎧=.i 0i ,1次呼叫未被接听第,次呼叫被接听;
第i ξ ……………………………………3分…
由题意可知 ),2,1( =i i ξ独立同分布,且),1(~p B i ξ ………………….8分
则 ∑==)
(1)(t X i i t Y ξ
是复合泊松过程 …………………………………11分
pt t EY λ=)( …………………………………………13分
所以 )(t Y 是参数为p λ的泊松过程。
…………………………………..15分
五、(25分)
设马氏链的转移矩阵为
⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛=00010001000054512121
P (1) 求两步转移矩阵;
(2) 按定理4.10分解状态空间为不相交集合的并;
(3) 求出各类的周期,并讨论其常返性。
解:(1)两步转移矩阵为
⎪⎪⎪⎪⎪⎪⎭
⎫ ⎝⎛=021*********
0001521010212P …………………….7分 (2)马氏链的状态转移图如下:略
可看出4个状态是互通的 ………………………………….. 12分
状态集I 是不可约的,按定理10.4的分解为一个集合I. …………..15分
(3) 计算得
211542115121,2
1)3(11)2(11=⨯⨯+⨯⨯==f f ……….18分 其他 )3,2(0)(11≠=k f k
所以 1)(1111==
∑k k f f ……………………………21分
即状态1是常返的
因而四个状态均是常返的 ……………………………….23分
又 ∞<==∑∞=2
51)(11
1k k kf μ,且状态1是非周期的 每一个状态是遍历状态。
…………………………………..25分
六、(20分)
考虑一个具有随机相位的余弦波,它由如下的随机过程描述,))(cos()(R t t t X ∈+=θλ,其中λ是常数,θ为一个具有有限二阶矩的随机变量。
(1) )}({t X 是否为宽平稳过程?
(2) 若θ服从),(ππ-上的均匀分布,)}({t X 是否为宽平稳过程?
解:(1)相关函数
)]cos()[cos(),(θλθλτλτ+++=+t t E t t R ……………………..4分
)2(sin )2(sin )2(cos )2([cos 2
1cos 21θτλθτλλτE t E t +-++= …………………………………8分
它与t 有关,)}({t X 不是为宽平稳过程 ……………………………...10分
(2)θθλπ
ππd t t X E ⎰-+=)(cos 21)]([22 存在 )}({t X 是一二阶矩过程 ………………………………………14分
0)cos(21)]([=+=⎰-θθλπ
ππd t t X E 为常数 …………….16分 而 0)2(s i n )2(c o s ==θθE E
),(τ+t t R λτcos 2
1= 与t 无关 ………………………..18分 若θ服从),(ππ-上的均匀分布,)}({t X 是宽平稳过程 ………20分。
