几何证明角平分线模型(高级)

几何证明——角平分线模型(高级)

【经典例题】

例1、已知如图，ABC ?中，BC AC =，AD 平分CAB ∠，若ο

100=∠C ，求证：CD AD AB +=。

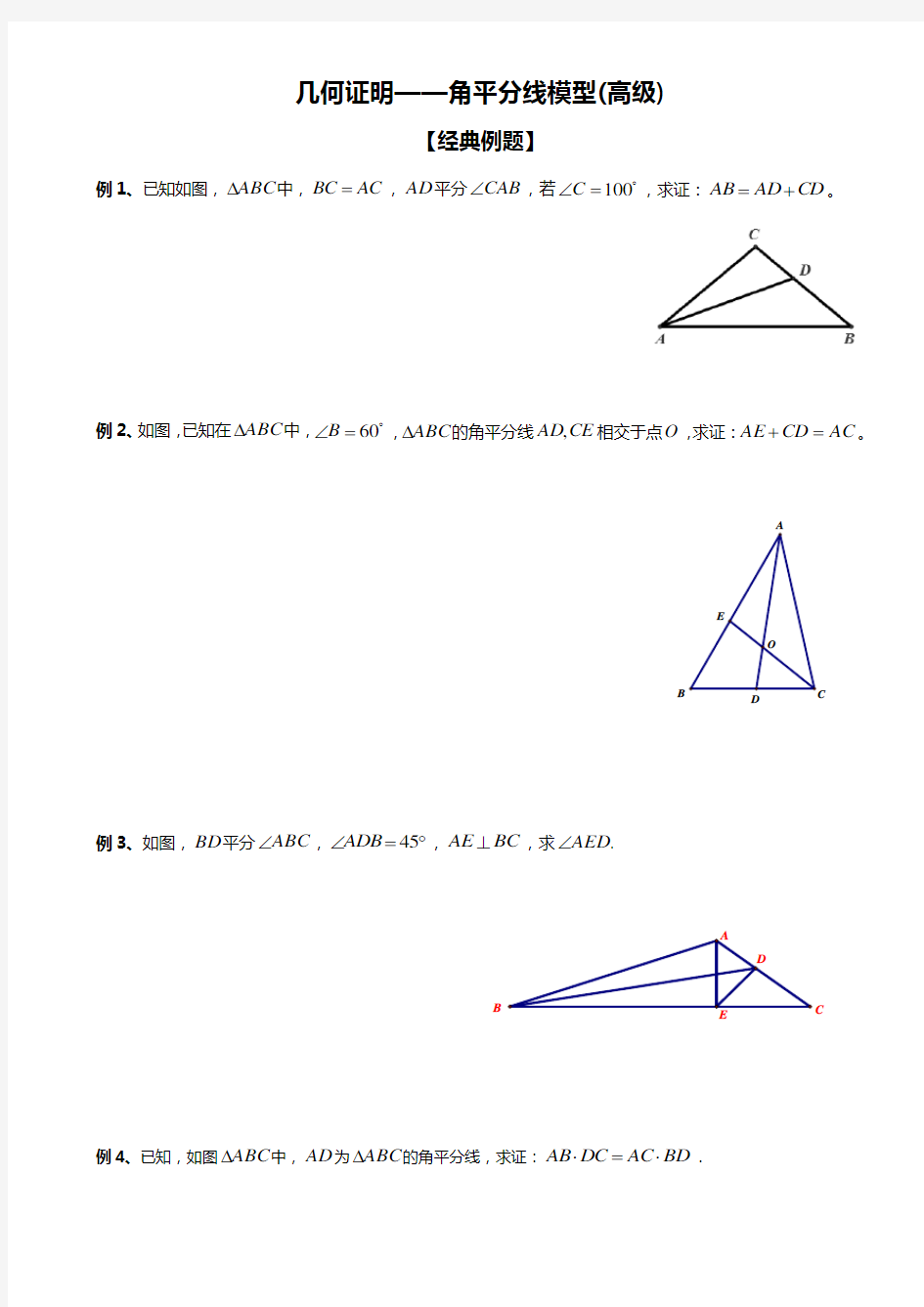
例2、如图，已知在ABC ?中，ο

60=∠B ，ABC ?的角平分线CE AD ,相交于点O ，求证：AC CD AE =+。

E

O

B

例3、如图，BD 平分ABC ∠，?=∠45ADB ，BC AE ⊥，求AED ∠.

A

B

C

D

例4、已知，如图ABC ?中，AD 为ABC ?的角平分线，求证：BD AC DC AB ?=?．

例5、如图，已知P 为锐角△ABC 内一点，过P 分别作AB AC BC ，，的垂线，垂足分别为F E D ，，，BM 为ABC ∠的平分线，MP 的延长线交AB 于点N ；如果PF PE PD +=，求证：CN 是ACB ∠的平分线。

A

B

C

N

M

P

D

E

F

例6、如图，在梯形ABCD 中，BC AD //，DC AB =，?=∠80ABC ，E 是腰CD 上一点，连接BE 、AC 、

AE ，若?=∠60ACB ，?=∠50EBC ，求EAC ∠的度数．

B

C

E

例7、已知：ABC ?中，BC AB <，AC 的中点为M ，AC MN ⊥交ABC ∠的角平分线于N ．

（1）如图1，若?=∠60ABC ，求证：BN BC BA 3=

+；

（2）如图2，若?=∠120ABC ，则BA 、BC 、BN 之间满足什么关系式，并对你得出的结论给予证明．

A

C

【提升训练】

1、在ABC ?中，AB AC >，AD 是BAC ∠的平分线．P 是AD 上任意一点．求证：AB AC PB

PC ->-．

B

2、如图，在ABC ?中，A ∠等于ο

60，BE 平分CD ABC ,∠平分ACB ∠，求证：EH DH

=。

3、如图所示，在ABC ?中，AD 平分BAC ∠，AD AB =，CM AD ⊥于M ，求证：2AB AC AM +=。

4、已知I 是ABC ?内角平分线的交点，AI 交对应边于D 。求证：

BC

AC

AB ID AI +=

。

B

5、（1）如图，BD 、CE 分别是ABC ?的外角平分线，过点A 作BD AF ⊥，CE AG ⊥，垂足分别为F 、

G ，连接FG ，延长AF 、AG ，与直线BC 相交，求证：()AC BC AB FG ++=

2

1

。 （2）若BD 、CE 分别是ABC ?的内角平分线（如图（2）），过点A 作BD AF ⊥，CE AG ⊥，垂足分别为F 、G ，连接FG ，线段FG 与ABC ?三边有怎样的数量关系？；

（3）若BD 为ABC ∠的内角平分线，CE 为ABC ?的外角平分线（如图（3）），过点A 作BD AF ⊥，

CE AG ⊥，垂足分别为F 、G ，连接FG ，则线段FG 与ABC ?三边又有怎样的数量关系？

（3）

(2)

(1)

6、如图，已知BD ，CE 为ABC ?的角平分钱，F 为DE 的中点，点F 到AC ，AB ，BC 的距离分别为

a FG =，

b FH =，

c FM =，若025

221222=+-+--m m ab c c 。

（1）求a ，b ，c ，m 的值；（2）求证：)(4

1

CD BC DG -=。

A B

C

E

D

F

M

H G

7．已知如图，CD 是ABC Rt ?斜边上的高，A ∠的平分线交CD 于H ，交BCD ∠的平分线于G ， 求证：BC HF //．

8．如图，BD 、CE 为△ABC 的两条内角平分线，K 为ED 的中点，KF ⊥AB 于F ，KG ⊥AC 于G ，KH ⊥BC 于H ，求证：KF+KG=KH ．

9．已知BC AC =，?=∠90ACB ，?=∠15DCB ，CD BD =，AD CE ⊥

于点E ，求证：CE BC 2=．

10．（1）如图1，BP 为△ABC 的角平分线，PM ⊥AB 于M ，PN ⊥BC 于N ，AB=30，BC=23，请补全图形，并求△ABP 与△BPC 的面积的比值；

（2）如图2，分别以△ABC 的边AB 、AC 为边向外作等边三角形ABD 和等边三角形ACE ，CD 与BE 相交于点O ，判断∠AOD 与∠AOE 的数量关系，并证明；

（3）在四边形ABCD 中，已知BC=DC ，且AB ≠AD ，对角线AC 平分∠BAD ，请直接写出∠B 和∠D 的数量关系．

11．（1）已知：如图1，Rt△ABC中，∠ACB=90°，∠BAC=60°，CD平分∠ACB，点E为AB中点，PE⊥AB 交CD的延长线于P，猜想：∠PAC+∠PBC= °（直接写出结论，不需证明）．

（2）已知：如图2，Rt△ABC中，∠ACB=90°，∠BAC≠45°，CD平分∠ACB，点E为AB中点，PE⊥AB交CD 的延长线于P，（1）中结论是否成立，若成立，请证明；若不成立请说明理由．

12．如图1，分别过线段AB的端点A、B作直线AM、BN，且AM∥BN，∠MAB、∠NBA的角平分线交于点C，过点C的直线l分别交AM、BN于点D、E．

（1）求证：△ABC是直角三角形；

（2）在图1中，当直线l⊥AM时，线段AD、BE、AB之间有怎样的数量关系？证明你的猜想；

（3）当直线l绕点C旋转到与AM不垂直时，在如图2、3两种情况下，（2）中的三条线段之间又有怎样的数量关系？请写出你的猜想，并选择一种情况给予证明．

13．如图，在Rt △ABC 中，∠ACB=90°，CD ⊥AB 于D ，AE 平分∠BAC ，交CD 于K ，交BC 于E ，F 是BE 上一点，且BF=CE ，求证：FK ∥AB ．

14．在ABC ?中，AD 是∠BAC 的平分线． （1）如图①，求证：

AC

AB

S S ACD ABD =??； （2）如图②，若BD=CD ，求证：AB=AC ；

（3）如图③，若AB=5，AC=4，BC=6．求BD 的长．

中，∠ABC=90°，D为BC上一点，在△ADE中，∠E=∠C，∠1=90°﹣∠EDC．求证：15．如图，在ABC

（1）∠1=∠2；

（2）ED=BC+BD．

16．如图，一个直角三角形纸片的顶点A在∠MON的边OM上移动，移动过程中始终保持AB⊥ON于点B，AC⊥OM于点A．∠MON的角平分线OP分别交AB、AC于D、E两点．

（1）点A在移动的过程中，线段AD和AE有怎样的数量关系，并说明理由．

（2）点A在移动的过程中，若射线ON上始终存在一点F与点A关于OP所在的直线对称，判断并说明以A、D、F、E为顶点的四边形是怎样特殊的四边形？

（3）若∠MON=45°，猜想线段AC、AD、OC之间有怎样的数量关系，只写出结果即可．不用证明．

17．定义：到凸四边形一组对边距离相等，到另一组对边距离也相等的点叫凸四边形的准内点．如图1，PH=PJ，PI=PG，则点P就是四边形ABCD的准内点．

（1）如图2，∠AFD与∠DEC的角平分线FP，EP相交于点P．求证：点P是四边形ABCD的准内点．

（2）分别画出图3平行四边形和图4梯形的准内点．（作图工具不限，不写作法，但要有必要的说明）

（3）判断下列命题的真假，在括号内填“真”或“假”．

①任意凸四边形一定存在准内点．（）

②任意凸四边形一定只有一个准内点．（）

③若P是任意凸四边形ABCD的准内点，则PA+PB=PC+PD或PA+PC=PB+PD．（）

18．如图，已知平行四边形ABCD中，AE平分∠BAD交DC于E，DF⊥BC于F，交AE于G，且AD=DF．过点D作DC的垂线，分别交AE、AB于点M、N．

（1）若M为AG中点，且DM=2，求DE的长；

（2）求证：AB=CF+DM．

19．如图，在平行四边形ABCD 中，∠BAD 、∠ABC 的平分线AF 、BG 分别与线段CD 交于点F 、G ， AF 与BG 交于点E ．

（1）求证：AF ⊥BG ，DF=CG ；

（2）若AB=10，AD=6，AF=8，求FG 和BG 的长度．

20、平行四边形ABCD 中，

4

3

=BC AB ，ABC ∠的平分线交AD 于点E ，BCD ∠ 的平分线交AD 于点F ，BE 、CF 交于点G ，若BC FG 4

1

=。求证：223CF BE =。

G

B

21、如图，在ABC ?中，D 是BAC ∠外角平分线上一点，求证：DC DB AC AB +<+。

D

A

B C

22．在?ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．

（1）在图1中证明CE=CF；

（2）若∠ABC=90°，G是EF的中点（如图2），直接写出∠BDG的度数；

（3）若∠ABC=120°，FG∥CE，FG=CE，分别连接DB、DG（如图3），求∠BDG的度数．