5.6同底数幂的除法2
5.6同底数幂的除法(2)

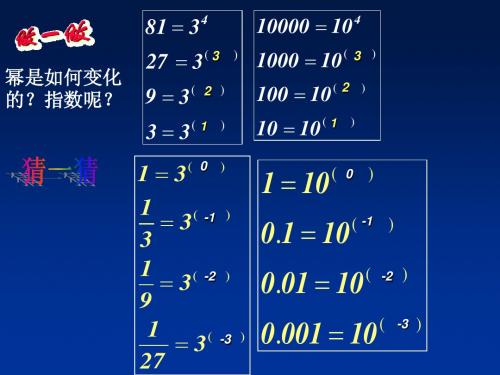
复习回顾:
同底数幂的除法的法则: 同底数幂相除,底数不变 指数相减 ;
即:am÷an=am—n
(a≠0,m,n都是正整数,且m>n)
抢答1:
10÷x8 2 (2) x =x (1) 5÷(ab) 4b4 11 2 (4)(ab) =a 9 (3) (-t) ÷(-t) =-t 100÷a100 6 2 (6)a =1 (5) (-3) ÷(-3) =81
(n为正整数)
10 1 0.1 10 10
2
0.01 0.0001
10 0.0001 n 个0
n
10 3 0.001
4
例5 把下列各数表示成a×10n (1≤a<10, n为整 数)的形式:
①12000
② 0.0021
③ 0.0000501
注意:我们可以用科学记数法表示绝对值较小的数。
s7÷s3
=s4
抢答2:
5 ).a3=a8 8 . (2) ( a (1) ( x )=x (3) b4.b3.( b14 )=b21
x7
(4) c8÷( c3 )=c5
抢答3:
1、x8÷(-x2) =-x6 2、a3n÷an =a2n 3、(y2)3÷y3 =y3 4、27÷(-2)3 =27÷(-23)=-24=-16
(1)10-3
(3)(-3)-4 (5) 950
(2)
(-0.5)-3
(4) ( 2 )
3
2
×(-5)-1
(6) a3 ÷(-10)0 (8) 3-3×37
(7)
(-3)5
÷3 6
练一练:
1、下列计算对吗?为什么?错的请改正。
①(—3)0=—1
幂的运算法则公式

幂的运算法则公式
幂运算法则公式:同底数幂相乘,底数不变,指数相加,即a m×a n=a(m+n);同底数幂相除,底数不变,指数相减,即a m÷a n=a(m-n)。
(1)同底数幂的乘法:同底数幂相乘,底数不变,指数相加。
a m×a n=a(m+n)(a≠0,m,n均为正整数,并且m>n)
(2)同底数幂的除法:同底数幂相除,底数不变,指数相减。
a m÷a n=a(m-n)(a≠0,m,n均为正整数,并且m>n)
(3)幂的乘方:幂的乘方,底数不变,指数相乘。
(a m)n=a(mn),(m,n都为正整数)
(4)积的乘方:等于将积的每个因式分别乘方,再把所得的幂相乘。
(ab)n=a n b n,(n为正整数)
(5)分式的乘方:把分式的分子、分母分别乘方即为乘方结果
(a/b)n=(a n)/(b n),(n为正整数)
(6)零指数:
a0=1 (a≠0)
(7)负整数指数幂
a-p=1/a p(a≠0, p是正整数)
(8)负实数指数幂
a(-p)=1/(a)p或(1/a)p(a≠0,p为正实数)(9)正整数指数幂
①a m a n=a m+n
②(a m)n=a mn
③a m/a n=a m-n(m大于n,a≠0)
④(ab)n=a n b n。
同底数幂的除法二

将幂的运算和同底数幂的除法应用于实际问题中,如金融、物理等 领域,提高数学应用能力。
THANKS FOR WATCHING
感谢您的观看
也可以使用等式性质进行推导
设a^m = b,a^n = c,则b ÷ c = a^m ÷ a^n = a^(m-n)。
性质应用举例
计算表达式
2^5 ÷ 2^3 = 2^(5-3) = 2^2 = 4。
化简复杂表达式
(x^5 ÷ x^2) ÷ x^3 = x^(5-2) ÷ x^3 = x^3 ÷ x^3 = x^(3-3) = x^0 = 1(x≠0)。
由于底数相同,我们可以将分子和分 母中的相同因子约去,得到a^(m-n)。
法则应用举例
计算2^5 ÷ 2^3
根据同底数幂的除法法则,2^5 ÷ 2^3 = 2^(5-3) = 2^2 = 4。
计算x^10 ÷ x^7
同样应用同底数幂的除法法则,x^10 ÷ x^7 = x^(10-7) = x^3。
运算技巧应用举例
例1
计算2^5÷2^3。
解
根据同底数幂的除法法则,2^5÷2^3=2^(53)=2^2=4。
例2
计算(3^2)^3。
解
根据幂的乘方法则,(3^2)^3=3^(2*3)=3^6=729 。
计算(2x)^3。
例3
解
根据积的乘方法则,(2x)^3=2^3×x^3=8x^3。
注意事项
在进行同底数幂的除法运算时,需要注意以下几点 1. 底数必须相同;
具体来说,如果a是一个非零实数,m和n是整数,那么a^m ÷ a^n = a^(m-n)。
法则证明
可以通过指数的定义和性质来证明同 底数幂的除法法则。
同底数幂的除法(2)
• [6-2
1997 0 × ] 1988
-2
说说零指数和负整数幂的意义
P61
练一练1,2,3
P63 3、4 本 子 上 百分百:P78 2
代数作业格式 P79 3
评价手册:P28 第2课时
0
用文字概括为: 任何一个非零数的0次幂等于1.
你2 222 1 4 2 2222 2
2 2 2
3 4
2 5
34
2
3
1
1 2 2
1
请计算 10 10 , 3 3
1 规定:a -n= a n
为正整数)
( a≠0, n
即: 任何非零数的- n ( n 为正整数)次幂等于这个数n次幂 的倒数
1 -3 ;(π-3.14) 0 2
(-0.1)0×10-2;
3、把下列各数写成负整数指数幂的形式:
1 1 ;0.0001; 64 8
(5 5 5 ) 5
2 0
2
3
2 (2)
0
3
1 -5 1 3 1 2 • × × 2 2 2
1 10
(
0
)
0.1 10
( -1 ) (
-2
0.01 10
)
)
-3
0.001 10
(
)
8.3 同底数幂的除法(2)
零指数幂与负指数幂
2 2
3 3
10 10
2 2
3 3
5 5
1 1 1
2 3
33
2 3
0
10
2 2
10 0
0
同底数幂的除法(二)

反馈拓展
(2)拓展延伸: 如果一滴水的质量约为 0.05g,请根据(1) 中提供的数据回答: ①一滴水中大约有多少个水分子? 用科学记数法表示 . ②如果把一滴水中的水分子依次排成一列 (中间没有空隙),能排多少米? 用科学记数法表示 .
小结
• • 这节课你学到了哪些知识? 用科学记数法表示小于1的正数与表示 大于10的数有什么相同之处?有什么 不同之处?
用科学记数法表示容易出现哪些错误? 你有哪些经验?与同伴交流. 在估测微小事物时你用到了哪些方法 和策略?
• •
作业
• 完成课本习题1.5 • 拓展作业: 阅读课本“读一读”,你想了解更多的 有关纳米技术或微小世界中的有趣问题吗? 请你查阅资料,制作成手抄报,一周后带来 与同学分享.
能用科学记数 法表示这些数吗? 请你与同伴交流
交流引入
一般地,一个小于1的正数可以用 科学记数法表示为: a× 10 (其中1≤a<10,n是负整数)
怎样确 定a和n?
n
巩固落实
1.用科学记数法表示下列各数: 0.000 000 000 1= 0.000 000 000 002 9= 0.000 000 001 295=
巩固落实
2.下面的数据都是用科学记数法表示的, 请你用小数把它们表示出来: 7×10-5= 1.35×10-10= 7×10-5与7-5 有什么区别? 2.657×10-16=
感受数据
1. PM2.5是指大气中直径小于或等于 2.5μm的颗粒物,也称为可入肺颗粒物. 虽然他们的直径还不到人的头发丝粗细 的二十分之一,但它们含有大量的有毒、 有害物质,并且在大气中停留的时间长、 输送距离远,因而对人体健康和大气环 境质量有很大的危害.
1纳米= 1× 10 米? 这个结果还能用科学记数法表示吗?
同底数幂的除法讲解

同底数幂的除法讲解
嘿,朋友们!今天咱来聊聊同底数幂的除法呀!这玩意儿就好像是一场奇妙的数字游戏。
你看啊,同底数幂就像是一群有着相同“姓氏”的小伙伴。
比如说 2 的几次方,那这些幂都是“2 家族”的。
那同底数幂的除法呢,就像是在这个家族里分东西。
比如说 2 的 5 次方除以 2 的 3 次方,这就好比是“2 家族”里有一堆东西,5 个 2 相乘那么多,然后要分成 3 个 2 相乘那么多份,那最后剩下多少呢?嘿嘿,不就是 2 个 2 相乘嘛,也就是 2 的 2 次方呀!这是不是挺有意思的?
咱再打个比方,就好像你有一堆苹果,都是同一个品种的,然后你要把它们分成几堆。
同底数幂的除法就是在计算这样的分法之后,还剩下多少个苹果。
而且啊,同底数幂的除法还有个特别重要的规则,那就是底数不变,指数相减。
这就像是分苹果的时候,苹果的品种不变,只是数量在变化。
你想想,要是没有这个规则,那咱得多混乱呀!就好像分苹果的时候没个准儿,那可不行。
同底数幂的除法在我们生活中其实也有不少应用呢!虽然可能不是那么直接明显,但你仔细想想,很多地方都有它的影子。
比如说计算一些比例关系的时候,或者在科学研究中分析数据的时候,都可能会用到同底数幂的除法。
这就像是一把神奇的钥匙,可以帮我们打开很多知识的大门。
哎呀呀,说了这么多,同底数幂的除法真的很重要啊!它就像是数字世界里的一个小魔法,能让我们更清楚地了解数字之间的关系。
所以啊,大家可一定要好好掌握这个知识呀,别把它当成一个难事儿,就当成是和数字小伙伴们玩游戏,多有趣呀!只要用心去理解,去感受,你肯定能把同底数幂的除法搞得明明白白的。
相信我,没错的!。
不同底数同幂的运算法则

不同底数同幂的运算法则
摘要:
一、引言
二、同底数幂的乘法法则
三、同底数幂的除法法则
四、幂的乘方与积的乘方
五、同幂的加法与减法法则
六、结论
正文:
一、引言
在代数学中,幂运算是一种基本的运算方式,它表示将一个数不断乘以自身,可以用来表示一个数的多次方。
本文将详细介绍不同底数同幂的运算法则。
二、同底数幂的乘法法则
当两个幂的底数相同时,它们的乘积等于底数不变,指数相加。
例如,同底数幂2^3 与2^4 的乘积为2^(3+4)=2^7。
三、同底数幂的除法法则
当两个幂的底数相同时,它们的商等于底数不变,指数相减。
例如,同底数幂2^4 除以2^3 等于2^(4-3)=2^1=2。
四、幂的乘方与积的乘方
当一个幂与一个数相乘时,等于将这个数的每个因数分别乘以幂的指数次
方。
例如,2^3 × 3^2 等于(2×3)^3=6^3。
当一个幂与一个数相除时,等于将这个数的每个因数分别除以幂的指数次方。
例如,2^4 ÷ 3^2 等于
(2÷3)^4=8^4/9^2。
五、同幂的加法与减法法则
当两个幂的底数相同时,它们的和等于底数不变,指数相加。
例如,同底数幂2^3 与2^4 的和为2^(3+4)=2^7。
当两个幂的底数相同时,它们的差等于底数不变,指数相减。
例如,同底数幂2^4 与2^3 的差为2^(4-
3)=2^1=2。
六、结论
总的来说,不同底数同幂的运算法则主要涉及到同底数幂的乘法、除法,幂的乘方与积的乘方,以及同幂的加法和减法。
第五讲 同底数幂的除法

一、基础知识:1、 同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加。
公式:为正整数)n m a a a n m n m ,(+=⋅ 2、幂的乘方法则:幂的乘方,底数不变,指数相乘。
公式:mn n m a a =)((为正整数n m ,)3、积的乘方法则:积的乘方等于积中各因式的乘方的积。
公式:)()(为正整数n b a ab n n n =4、同底数幂的除法法则:同底数幂相除,底数不变,指数相减。
公式:是正整数),(n m a a a n m n m -=÷5、零指数幂的意义:.100)0(10次幂都等于的数的即任何不等于≠=a a6、负整数指数幂的意义:等于是正整数),即任何不p a aa p p ,0(1≠=-零的数的次幂的倒数。
次幂都等于这个数的p p - 二、典型例题:同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加。
公式:为正整数)n m a a a n m n m ,(+=⋅例题1:计算:(1)103×102= (2) 23×22=(3)32x x ⋅ = (4)3)()x x -⋅-(=(5)42)m m ⋅-( = (6))()32a a a -⋅⋅-(=例题2:计算:(1)=÷2522___________; (2)=371010÷___________;(3)=÷37a a ___________(a ≠0)第五讲 同底数幂的除法同底数幂的除法法则:同底数幂相除,底数不变,指数相减。
公式:是正整数),(n m a a a n m n m -=÷变式2—1:计算:(1) a 8÷a 3; (2)(-a )10÷(-a ) 3;(3)(2a )7÷(2a )4; (4)x 6÷x(5) (6)(-x)6 ÷x 2(7)(a +b )4÷(a +b )2 (8) (-a 2)4÷(a 3)2×a 4变式2—2:(1)下面运算正确的是( )A .6332x x x =+B .6212x x x =÷C .x x x n n =÷++12D .2045)(x x -=-(2)在下列计算中,①422523a a a =+ ②632632a a a =⋅ ③a a a -=-÷-23)()( ④632336)2(2a a a a -=-⋅正确的有( )个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10 1000
n
(n为正整数)
10 0.0001 n 个0
n
例2 把下列各数表示成a×10n(1≤a<10,n为整 数)的形式(科学记数法):
(1)12000
(2)19600000
(2)0.0021
(3)0.0000501
理一理
畅所欲言
通过这堂课的学习,你觉得 有什么收获!
祝同学们学习进步!
同底数幂的除法的法则:
同底数幂相除,底数 不变 指数 相减
m n m — n 即:a ÷a =a
(a≠0,m,n都是正整数,且m>n)
小组比一比!
1、x8÷(-x2) 2、a3n÷an
=-x6 =a2n =y3 =27÷(-23)=-24=-16
3、(y2)3÷y3
4、27÷(-2)3
5、38÷(34.34) =38÷38 =1
想一想
38÷38=
m n m — n 公式:a ÷a =a
1
又38÷38= 38-8=30
∴ 30=1
所以我们规定:
a 1(a 0)
0
任何一个非零数的0次幂等于1.
你会计算
3 4 2 ÷2 =?
1 规定:a-p = p (a≠0,p是正整数) a
即: 任何非零数的- p ( n为正整数)次幂 等于这个数p次幂的倒数
(6) a3 ÷(-10)0
(8) 3-3×37
一起去探险吧
第一关 第二关
第三关
第四关
第一关:法官审判
(1)下列计算对吗?为什么? 错的请改正。
①(—3)0=—1
错
1
1 2
② ③
(—2)—1
错
=1
2—2=
错
—4
1 4
④ a3÷a3=0
错
1
对
⑤ ap· a-p =1 (a≠0)
第二关:牛刀小试
1、用分数或整数表示下列各值
(1) 100-2
(2) (-1)-3
(3) 0.1-3 (5) (-3)0
(4) (-71)-1 (6)-30
第三关:激流勇进
计算 1、76÷78 3、25×2-7 5、(-4)8÷410
3 2 7、 4 3 0
2、30×3-2
4、a4÷(a3.a2)
m n m — n 理一理:a ÷a =a
(a≠0,m,n都是正整数)
(1)、m>n(已学过) (2)、 m=n
a ห้องสมุดไป่ตู้ 1(a 0)
0
1 -p = a p (3)、 m<n a
学以致用
求下列各式的值
(1)10-3 (3) (-3)-4
(2) (-0.5)-3 (4)
2 2 ( ) 3
(5) 950 ×(-5)-1 (7) (-3)5 ÷36
6、(-5)-2×(-5)2
1 8、 5
100
1 5
100
归 纳 拓 展
104 10000 103 1000 10 100
2
n 个0 找规律
10 10
1
100 1 101 0.1 10 0.01 10 3 0.001 10 4 0.0001
例2 计算 7 4 2 (1)a ÷(a · a)
(2)
7 2 (-x) ÷x
(3) (ab)5÷ (ab)2 (4)a6÷a2·a4
(5)(a+b)6÷ (a+b)4
让我们一起给它拓展一下!
m n m — n 公式:a ÷a =a
(a≠0,m,n都是正整数,且m>n) (1)、m>n(已学过) (2)、 m=n (3)、 m<n
