关于罗尔(Rolle)中值定理条件的研究
同济版高等数学 在利用罗尔定理证明拉格朗日中值定理问题

同济版高等数学在利用罗尔定理证明拉格朗日中值定理问题拉格朗日中值定理(LagrangeMeanValueTheorem)是一个重要的数学定理,它可以有效地帮助我们解决微分方程和积分方程等问题,并且在多个领域有广泛的应用,尤其是在计算机科学领域。
在拉格朗日中值定理的证明中,利用罗尔定理(Rolle Theorem)是一种有效的方法。
因此,利用同济版高等数学证明拉格朗日中值定理成为一个重要的研究课题。
首先,我们介绍一下拉格朗日中值定理。
拉格朗日中值定理定义了一个函数在某段区间上的行为,它认为:如果一个函数$f(x)$在区间$[a,b]$上连续,并且在$a,b$点上可导,那么在$(a,b)$内一定存在一个点$c$,使得$frac{f(b)-f(a)}{b-a}=f^{}(c)$,即拉格朗日中值定理成立。
然后,我们介绍一下罗尔定理。
罗尔定理的定义为:如果一个函数$f(x)$在区间$[a,b]$上连续,并且在$a,b$点上可导,那么在区间$(a,b)$内一定存在一个点$c$,使得$f^{}(c)=0$。
罗尔定理可以用来证明拉格朗日中值定理。
将罗尔定理和拉格朗日中值定理联系起来,可以得到证明拉格朗日中值定理的结论:设函数$f(x)$在区间$[a,b]$上连续,并且在$a,b$处可导,那么一定存在一个点$c$,使得$f^{}(c) =frac{f(b)-f(a)}{b-a}$,即拉格朗日中值定理成立。
接下来,我们来看看如何利用同济版高等数学进行拉格朗日中值定理的证明。
首先,我们需要用罗尔定理证明函数$f(x)$在$[a,b]$上连续、可导,存在一个点$c$使得$f^{}(c)=0$,即:函数$f(x)$在$[a,c]$上单调递增,在$[c,b]$上单调递减。
在此基础上,我们继续做出下列的假设:设$f^{}(x)$在$[a,b]$上连续可积,当$f^{}(x)$在$[a,c]$上单调递增时,$f(x)$的积分是一单调递增函数,当$f^{}(x)$在$[c,b]$上单调递减时,$f(x)$的积分是一单调递减函数。
罗尔中值定理的内容及证明方法

罗尔中值定理的内容及证明方法罗尔中值定理(Rolle’s theorem)是微积分中的一个基本定理,它是拉格朗日中值定理(Lagrange mean value theorem)的特殊情况之一、罗尔中值定理描述了在一些条件下,函数在区间两个端点对应的函数值相等时,在这个区间内必然存在至少一点使函数的导数为零。
定义:假设函数$$f(x)$$满足以下条件:1.在区间$$[a,b]$$内连续2.在开区间$$(a,b)$$内可导3.在区间端点点$$x=a$$和$$x=b$$处的函数值相等,即$$f(a)=f(b)$$。
则在区间$$(a,b)$$内至少存在一个点$$c$$,使得$$f'(c)=0$$。
下面我们来证明罗尔中值定理:首先,根据条件,函数$$f(x)$$在区间$$[a,b]$$上连续,且在开区间内可导。
根据罗尔中值定理的定义,我们需要找到一个点$$c$$,使得函数$$f'(c)=0$$,也就是找到这个点的横坐标。
我们可以进行以下思路:由于函数$$f(x)$$在开区间内可导,根据导数的定义,$$f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$。
由于函数在区间端点处的函数值相等,即$$f(a)=f(b)$$,我们可以将$$x=a$$代入上式,得到$$f'(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}$$。
由于函数是在开区间可导的,所以$$f'(a)$$存在。
同样的,我们可以将$$x=b$$代入$$f'(x)$$的定义式,得到$$f'(b)=\lim_{h \to 0}\frac{f(b+h)-f(b)}{h}$$。
同样地,由于函数是在开区间可导的,所以$$f'(b)$$存在。
根据函数连续的性质,我们可以知道函数在区间$$[a,b]$$上连续,那么函数在开区间$$(a,b)$$内也连续。
罗尔定理内容及证明

罗尔定理内容及证明罗尔定理(RolleTheorem)是求解单变量函数微分方程的一个基本定理,它最初是由法国数学家特朗罗尔在1691年提出来的。
罗尔定理它说明了在满足某些特定条件的情况下,某一个函数的一阶导数存在且满足某一条件,它是实变函数微分方程的理论和应用的一个基础性定理。
一、罗尔定理的内容罗尔定理是指,设在[a,b]上已知f(a) = f(b),且f(x)在区间[a,b]上连续可导,则存在某个c∈(a,b),使得f(c)= 0。
它概括地说明了,在函数f(x)在区间[a,b]上有f(a)=f(b),并且f(x)在区间[a,b]上连续可导的情况下,那么函数f一定存在极值点,也就是一阶导数f(x)在某一点存在且为零,也就是f(c)=0。
二、罗尔定理的证明设f(x)在区间[a,b]上连续可导,f(a)=f(b)(设f(a)≠f(b),不妨设f(a)>f(b)),证明f(c)=0。
我们假定c∈(a,b),如果f(a)>f(b),那么说明f在[a,b]上是连续的凸函数,其一阶导数f(x)也是连续的,存在一点c∈(a,b),使得f(c)=0。
由此,根据函数微分的定义,可知$$f(c)=lim_{xrightarrowc}frac{f(x)-f(c)}{x-c}=frac{f(b)-f(c)}{b-c}+frac{f(c)-f(a)}{c-a}=frac{f(b)-f(a)}{b-c} +frac{f(a)-f(a)}{c-a}=frac{f(b)-f(a)}{b-a}$$由于f(a)=f(b),以f(c)=0,即c为f(x)的极值点。
综上所述,罗尔定理说明了在满足某些特定条件的情况下,一个函数f一定存在一个极值点,其一阶导数f(x)在某一点存在且为零,由此可以应用在解决实变函数微分方程的应用中,成为实变函数微分方程的理论和应用的一个基础性定理。
详细的推导过程在本文中已经完全说明,罗尔定理在实际中不断发挥着重要作用。
罗尔Rolle中值定理

[ f ( x) sin x ] x 0 解题关键
证明至少存在一点 ( 0 ,
2
), 使
f ( ) cos 0.
容易验证: g( x ) 在 [ 0, ] 上满足罗尔定理条件. 2 由罗尔定理得: 至少存在一点 ( 0, ), 使得 2 g( ) 0
即
f ( ) cos 0.
证明: 设 g( x ) f ( x ) sin x
0
1
x
例2 f ( x ) x , x [1,1];
y
(1) f ( x ) C[1,1]; ( 2) f ( x ) D( 1,1); ( 3) f ( 1) f (1).
1
0
1 x
不存在 ( 1,1), 使 f ( ) 0.
例3 f ( x ) x , x [0,1];
罗尔(Rolle)中值定理
主讲:潘 洁
安徽理工大学
微分中值定理
罗尔中值定理
泰勒中值定理
拉格朗日中值定理
柯西中值定理
问题的引出:
y
C
T 与x轴
这样的 可能有多个
a
1
2
b
x
一、罗尔(Rolle)中值定理
y
D
若函数 f ( x ) 满足:
(1) 在 [a , b] 上连续;
f ( x )在 [a , b] 上 连续, f ( x)在 [a, b] 上必有最大值 M 和最小值 m.
(1)若 M m.则 f ( x) M . 由此得 f ( x ) 0, x (a, b). (a, b),都有 f ( ) 0.
f (a ) f (b), (2)若 M m. 最值不可能同时在端点处取得. 不妨设 M f (a ),
拉格朗日中值定理
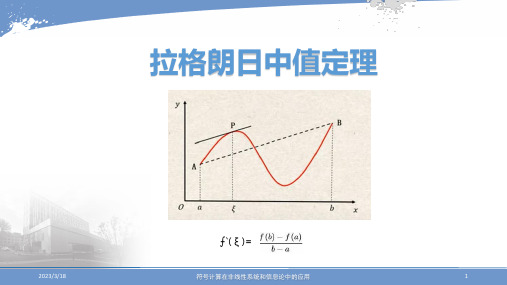
⨍`(ξ) ⨍ −⨍()
则 存在ξ ∈(a,b),使得
=
g`(ξ) −()
取g(x)=x,即为拉格朗日中值定理
2023/3/18
符号计算在非线性系统和信息论中的应用
8
x
证明:当x>0时,1+ <ln(1+x)<x,
证 设f(x)=ln(1+x),
f(x)在[0,x]上满足拉氏定理的条件,
4
二、拉格朗日(Lagrange)中值定理
若函数⨍满足如下条件:
(1) ⨍在闭区间[a,b]上连续
(2) ⨍在开区间(a,b)内可导
则在(a,b)内至少存在一点ξ,使得⨍`(ξ)=
等价形式: ⨍(a)- ⨍(b)= ⨍`(ξ )(b-a),a<ξ<b
几何意义:在满足定理条件的曲线y= ⨍(x)上至少存在一点P(ξ , ⨍(ξ )),
=
−
−
F(b)= ⨍(b)b=
F(a)=F(b),且F在[a,b]上满足罗尔定理的另外两个条件,故存在ξ ∈(a,b),使得
F`(ξ)=⨍`(ξ)=0,即⨍`(ξ)=
2023/3/18
符号计算在非线性系统和信息论中的应用
6
证明2:作辅助函数F(x)= ⨍ (x)-⨍(a)-
(x-a)
F(a)=F(b)=0
则在曲线弧内,曲线至少有一条切线平行于曲线两端点的连线。
证明:做辅助函数(不唯一),运用罗尔定理
2023/3/18
符号计算在非线性系统和信息论中的应用
11
小结:罗尔定理、拉格朗日中值定理之间的关系
2023/3/18
符号计算在非线性系统和信息论中的应用
12
试讲罗尔中值定理

注意:
1) 定理条件不全具备, 结论不一定成立. 例如:
缺条件(1)闭区间上连续.
y
缺条件(2)开区间内可导.
o 1x
y
缺条件(3) 端点处函数值相等.
1 o 1 x
y
o
2) 罗尔定理的三个条件是充分非必要的.
1x
机动 目录 上页 下页 返回 结束
例1:设 f 为 上可导函数,证明:若方程
使 f ( ) 0.
几何解பைடு நூலகம்:
y
在每一点都可导的连续 曲线上,如果曲线的两 端点高度相等,则至少 存在一条水平切线。
yf(x)
A
B
Oa 1
2 bx
机动 目录 上页 下页 返回 结束
证明: f(x)在区间 [a , b] 上连续,必有最大值M和最小值m
(1) 若 m=M , 因m f (x) M. 即, M f (x) M, 所以f (x)=M.
机动 目录 上页 下页 返回 结束
谢谢!
数学分析
罗尔中值定理
一.预备定理——费马(Fermat)定理
(或 )
y
o x0 x
机动 目录 上页 下页 返回 结束
二.罗尔(Rolle)定理
满足:
(1) 在区间 [a , b] 上连续 (2) 在区间 (a , b) 内可导 (3) f ( a ) = f ( b )
在( a , b ) 内至少存在一点
没有实根,则方程
至多只有一个实根。
证明:这可反证如下,倘若
有两个实根
和 (设 ),则函数 f 在闭区间
上满足罗尔定理三个条件,从而存在
使得
,这与
什么是“罗尔定理”?他有什么用?

什么是“罗尔定理”?他有什么⽤?1.罗尔定理的定义以法国数学家⽶歇尔·罗尔命名的罗尔中值定理(英语:Rolle's theorem)是微分学中⼀条重要的定理,是三⼤微分中值定理之⼀,叙述如下:如果函数 f(x)满⾜(1)在闭区间 [a,b]上连续;(2)在开区间 (a,b)内可导;(3)在区间端点处的函数值相等,即 f(a)=f(b),那么在 (a,b)内⾄少有⼀点ε(a<ε<b)使得2.⼏何理解下⾯是⼏何图解罗尔定理。
函数y=f(x)在 [a,b]上连续,(a,b)内可导,并且f(a)=f(b),那么f(x)曲线⾄少存在⼀点,其斜率为0.(下图显⽰有2个点斜率为0)3.通俗解释你站在地上,垂直向天空抛出⼀⼩球,⼩球⼜落在地上,那么在⼩球运动过程中,⼀定有⼀个时刻t,在t时刻速度是0.(在这个t时刻之前,速度是向上的,过了这个时刻t,速度向下,⽽在这个t,就是物体运动的最⾼点,速度是0)4.注意罗尔定理要求的条件如果函数在区间内的某个点不可导,则罗尔定理的结论不⼀定成⽴。
对于某个a > 0,考虑绝对值函数:f(x)=|x| x取值在[-a,a],其图形如下:虽然f(−a) = f(a),但−a和a之间不存在导数为零的点。
这是因为,函数虽然是连续的,但它在点x = 0不可导。
因此就不存在 f'(ε)=04.罗尔定理有什么⽤呢?罗尔定理最常⽤的是来判断⽅程有没有解。
求下列⽅程,在(0,1)内⾄少有⼀个根。
解:原⽅程相当于求解f'(x)=ax^2 +2bx-(a+b) 在(0,1)内⾄少有⼀个根,所以,我们要先构造f('x)的原型。
根据微分公式,很容易构造f'(x)的原型为:⼜, F(x) 在 [0,1] 上连续,在 (0,1) 内可导,F(0)=F(1),所以⾄少存在⼀个点F'(ε)=0,既ax^2 +2bx-(a+b) =0 ⾄少有⼀个根。
5.中值定理

f ( x)在[0, x]上满足拉氏定理的条件 ,
f ( x) f (0) f ()(x 0), (0 x)
f (0) 0, f ( x) 1 , 由上式得 1 x
ln(1 x) x , 1
又0 x 1 1 1 x
1 1 1,
f()
lim
x 0
f
(
x) x
f
()
0;
f ()存在,
f() f(). 只有 f () 0.
注意:若罗尔定理的三个条件中有一个不满足,其 结论可能不成立.
例如, y x , x [2,2]; 在[2,2]上除f (0)不存在外,满足罗尔定理的 一切条件, 但在内找不到一点能使f ( x) 0.
水平的.
o a 1
物理解释:
y f (x)
2 b x
变速直线运动在 折返点处,瞬时速 度等于零.
点击图片任意处播放\暂停
证 f ( x) 在 [a,b] 连续, 必有最大值 M 和最小值 m.
(1) 若 M m. 则 f ( x) M . 由此得 f ( x) 0. (a, b), 都有 f () 0. (2) 若 M m. f (a) f (b), 最值不可能同时在端点取得. 设 M f (a),
二、拉格朗日(Lagrange)中值定理
拉格朗日(Lagrange)中值定理 (1)如果函数 f(x)在 闭区间[a, b]上连续(,2在) 开区间(a, b) 内可导,那末在 (a, b)内至少有一点(a b),使等式
f (b) f (a) f ' ()(b a) 成立.
注意 : 与罗尔定理相比条件中去掉了 f (a) f (b). 结论亦可写成 f (b) f (a) f (). ba
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第2 8卷 第 5期
20 0 7年 1 O月
河 南 科 技 大 学 学 报 :自 然 科 学 版
J u n l fHe a i est fS in e a d T c n lg Nau a c e c o r a n n Un v r i o ce c n e h oo y: tr lS in e o y
中图 分 类 号 : 1 2 1 07. 文 献 标 识 码 : A
U
刖 舌
罗尔 中值定 理是 微分 学 的重 要 基 本定 理 之一 , 内容 为 若 函数 厂 ) 足 如 下 条 件 : i 在 闭 区 间 其 ( 满 ()
[ ,] 口 b 上连 续 ; i 在 开 区间 ( , ) (i ) 口 b 内可导 ; i) ( )= ( ) (i 厂 口 厂 b 。 i 则在 ( , ) 口 b 内至少 存在 一点 , 得 厂 ( 使 )=0 3。 ¨-]
(。 : , )内某 点 达 到 , 时 点必为 极 小值 点 , 此 故有 厂 ( =0 因此 在 ( , )内 至少存 在 一点 , 得 ) 。 口b 使
如 函数 厂 ) = 丁 (
l 一 J
,在 区 间 ( , ) 内 可 导 ,且 l f ) = l f ) =+ o 01 i ( m i ( m 。,而 厂( = )
() i在开 区间 ( , ) 口 b 内可 导 ;
(i i ( i m厂 )=l ( )l i )=+o ( 一o ) 则在 ( , ) 至少 存在 一点 , 得 厂 ( m厂 。或 。 , 口b 内 使 )= 。 0
证明 下面仅 证 “+o ” 的情形 , 对 “一o ” 的情 形 , 。 时 而 。 时 同样 可 证 。
Vo . No. 128 5
2 0 ) 5—0 9 0 1 7 6 7 (0 7 0 0 6— 2
关 于 罗 尔 ( ol) R l 中值 定 理 条 件 的研 究 e
齐 春 玲 李 晓 培 ,
( . 门 峡 职 业 技 术 学 院 , 南 三 门 峡 4 2 0 ;. 国 一 拖 集 团公 司 拖 拉 机 学 院 , 南 洛 阳 4 10 ) 1三 河 7002 中 河 7 0 3
罗尔 中值定理 要 求 函数在 闭 区间上 连续 、 区 间 内可导 , 且文 献 [ ] 出 , 罗尔 中值定 理 中 , 开 而 1指 在 若 三个 条件 中有一个 不 成立 , 则定 理 的结论 就 可能 不成 立 。但 是 , 我们 知道 这 三个条 件仅是 结 论成 立 的充 分条件, 而非 必要 条件 。本 文将 对罗 尔 中值定 理 的条 件做 进 一 步探讨 , 究在 区 间的端点 处 不连 续 的 函 研 数 以及 无穷 区间上 的 可导 函数 的相关 问题 。下面 是本 文 的一 些重 要 结论 , 以定 理 的形 式 给 出 。
t( f )
∈ ( ,) 口 b
显然 函数 F )在 区间 [ , ]上 满 足 罗 尔 中值 定 理 的 条 件 , 在 ( ,)内至 少 存 在 一 点 , 得 ( 口b 则 口b 使 F ( =0 而 当 ∈ ( ,)时 , ) =厂( , 有 厂( =0 ) , 口b F( ) 故 ) 。 定理 2 设 函数 厂 ) 足 : ( 满
摘 要 : 尔 中 值 定 理 指 出 , 函数 ) 足 三 个 特 定 条 件 时 , 区 间 内部 至 少 存 在 一 点 , 得厂 ( 罗 当 满 在 使 )=0 本 文 , 针 对 在 区 间 [ ,]端 点 处 不 连 续 的 函数 以 及无 穷 区 间 上 的可 导 函 数 的 相 关 问 题 作 了进 一 步 研 究 , 得 结 论 推 ob 所 广 和 完 善 了文 献 中 相 应 的定 理 。 关 键 词 : 尔 中值 定 理 ; 连 续 ; 穷 区 间 罗 不 无
证 明 设 l ( i )=l 厂 )=A, m厂 i ( m 由函数 厂 )在 开 区间 ( , )内可 导知 ,( ( 口b 厂 )在开 区 间 ( ,)内连 口b
续 , 对 函数 厂 )在 区间 [ , ]上作 连续 开 拓 , 再 ( 口b 令
F( ) : A 口或 6
・9 ・ 7
令 厂 )=o, 得 解
,
1
。
上 述两个 定 理告诉 我们 , 函数 , ) 闭 区 间[ , ] 两端 点 。与 b 既使 不连 续 , ( 在 ob 的 处 只要 在两 端点 处
取 ∈( ,) 因 l ( 口 b , i )=l ( m厂 i )=+o 则 由极 限定义 知 , m厂 。, 存在 。∈ ( , ) 口 ‰ ,:∈ ( , ) 使 得 b, 厂 。 ( )>厂 ) (
厂( )=0 。
1
: )>
) 而 函数 厂 ) [ 。 : , ( 在 , ]上连 续 , 而存 在最 小值 , 从 显然 最 小值 只能 在 区间
0 , l 一
作 者 简 介 : 春玲 ( 93一), , 南 陕 县 人 , 齐 16 女 河 副教 授
收 稿 日期 :0 6—1 20 2一l O
维普资讯
第 5期
齐 春 玲 : 于 罗 尔 ( o e 中 值 定 理 条 件 的研 究 关 Rl ) l
1 区 间端 点处 不 连续 的 情 形
定 理 1 若 函数 厂 ) ( 满足 : i在开 区间 ( , ) () 口 b 内可 导 ; i l 厂 )=l ( 。 (i i ( )r a i 厂 ) a r
… , + — 6一
则在 ( , )内至少存 在一 点 , 得 厂 ( =0 口b 使 ) 。
