第9章2 振动学基础2
振动基础必学知识点

振动基础必学知识点
以下是振动基础必学的知识点:
1. 振动的定义:振动是物体围绕某个平衡位置来回周期性地运动。
2. 振动的周期和频率:振动的周期是振动一个完整循环所需要的时间,单位是秒;频率是单位时间内振动的次数,单位是赫兹。
它们之间有
以下关系:频率 = 1/周期。
3. 振动的幅度:振动的幅度是指物体离开平衡位置的最大距离。
4. 简谐振动:简谐振动是指物体在没有阻力的情况下,围绕平衡位置
做匀速往复运动的振动。
简谐振动的特点是周期恒定、频率固定且幅
度不断变化。
5. 谐振:谐振是指当外力作用频率与物体固有频率相同时,物体容易
发生共振现象,振幅会明显增大的现象。
6. 弹簧振子:弹簧振子是指一个质点通过与弹簧连接,形成一个可以
进行振动的系统。
弹簧振子的运动方程可以用简谐振动的方程表示。
7. 摆钟:摆钟是指一个由质点与一个固定的绳或杆连接,形成可以进
行振动的系统。
摆钟的运动方程可以用简谐振动的方程表示。
8. 声音的传播和振动:声音是由物体的振动引起的机械波。
声音的传
播需要介质的存在,并且介质中的分子通过相互振动来传递能量。
9. 波动的特征:波动的特征包括传播速度、波长、频率和振幅。
10. 波的类型:根据波动传播介质的性质,波可以分为机械波和电磁波两种类型。
以上是振动基础必学的知识点,掌握这些知识可以帮助理解振动和波动以及它们在不同物理现象中的应用。
第9章振动学基础习题

第9章振动学基础习题9.1 质量为10×10-3kg的小球与轻弹簧组成的系统,按x=0.1cos(8πt+2π/3)(SI)的规律振动,求:(1)振动的圆频率、周期、振幅、初相以及速度与加速度的最大值;(2)最大回复力、振动能量、平均动能和平均势能;(3)t=1、2、5、10s等各时刻的相位;(4)分别画出振动的x-t图线,v-t图线和a-t图线;(5)画出这些振动的转动矢量图示,并在图中指明t=1、2、5、10s时矢量的位置。
9.2 一个弹簧振子m=0.5kg,k=50N/m,振幅A=0.04m,求:(1)振动的圆频率,最大速度和最大加速度;(2)当振子对平衡位置的位移为x=0.02m时的瞬时速度、加速度和回复力;(3)以速度具有正的最大值时为计时起点,写出振动的表达式。
9.3 一质点在x=0附近沿x轴作简谐振动。
在t=0时位置为x=0.37cm,速度为零,振动频率为0.25Hz。
试求:(1)周期、圆频率、振幅;(2)在时刻t的位置和速度;(3)最大速度和最大加速度的值;(4)在t=3.0s时的位置和速率。
9.4 作简谐振动的小球,速度最大值为v m=3cm/s,振幅A=2cm,若从速度为正的最大值时开始计算时间,求:(1)振动的周期;(2)加速度的最大值;(3)振动表达式。
9.5 如图,两轻弹簧与小球串联在一直线上,将两弹簧拉长后系在固定点A、B之间,整个系统放在水平面上。
设弹簧的原长为l1、l2,倔强系数为k1、k1,A、B间距离为L,小球的质量为m。
(1)试确定小球的平衡位置。
(2)使小球沿弹簧长度的方向作一微小位移后放手,小球将作振动,这一振动是否是简谐振动?振动的周期为多少?9.6 一轻弹簧的倔强系数为k,其下悬有一质量为m的盘子。
现有一质量为M的物体从离盘h高度处自由下落到盘中并和盘子粘在一起,盘子开始振动起来。
(1)此时振动周期与空盘振动的周期各为多少?(2)此时振动的振幅。
大学物理振动学基础2汇总

3
v 0.12 sin( 0.5 )m s1 0.18m s1
3
a dv 0.12 2 cos( 0.5 )m s2
dt
3
6 3 2m s2 1.03m s2
例4 一物体作简谐振动,其振幅为0.08m,周期为4s , 起始时刻物体在x=0.04m 处,向Ox轴负方向运动,如 图所示,试求:
由起始位置运动到-0.04m处所需的最短时间
2
3
/3 /3
0.08 0.04
O
x/m
0.04 0.08
0.08 0.04
O 0.04 0.08 x/m
解:
而状态对应的旋转矢量如图
2 s1
T
2
t
2 3
3
s
2
s
0.667 s
3
2
例5.一物体沿X轴作简谐振动,振幅为0.24m,周期为
2s,当t=0时,X0=0.12m 且向X轴正方向运动,试求: (1)振动方程;
求: (1) 振动方程 (2) 从初始位置到平衡 位置所需最 短时间
解: (1) x Acos(t )
x0 A cos
v0 A sin
k 15.8 12.57(rad / s) 4s1
m 0.1
A
x02
v02
2
0.052
(0.628)2 (12.57)2
7.07102 m
tg v0 0.628 1 x0 12.57 0.05
2)从x=-0.12m且向X轴正方向运动这一状态,回到平衡
位置所需的最短时间.
解:1
2
T
3
当t=0, X0=0.12m, V0>0;
《振动力学基础》课件

各自由度之间相互独立,可分别进行分析。
固有频率和主振型
多自由度系统具有多个固有频率和相应的主振型 。
连续系统的振动
分布参数系统
描述长弦、长杆等连续介质的振动,需要考虑空间位 置的变化。
集中参数系统
将连续介质离散化,用弹簧、质量等元件模拟,适用 于简单模型。
波的传播
连续系统中振动能量的传播形式,如声波、地震波等 。
线性振动和非线性振动
线性振动
满足叠加原理,各激励之间互不影响,系统响应与激励成正比。
非线性振动
不满足叠加原理,激励之间存在相互作用,系统响应与激励不成正 比。
周期性振动和非周期性振动
根据振动是否具有周期性进行分类。
CHAPTER 03
振动分析方法
频域分析法
01
频域分析法是一种通过将时间域的振动问题转换为频率域的振动问题 ,从而利用频率特性来分析振动的方法。
CHAPTER 02
振动的基本原理
单自由度系统的振动
自由振动
无外力作用下的振动,系统具有固有频率和固有振型。
强迫振动
在外力作用下产生的振动,其频率与外力频率相同或相近。
阻尼振动
由于系统内部摩擦或外部阻尼作用导致的振动,能量逐渐耗散。
多自由度系统的振动
耦合振动
多个自由度之间相互影响,振动频率和振型较为 复杂。
汽车悬挂系统和路面激励会导致车内振动,影响乘客舒适性。
船舶与海洋工程
船舶和海洋结构的振动会影响其性能和安全性,需要进行有效的振 动控制。
建筑领域
结构健康监测
对建筑物和桥梁等大型结构进行振动监测,可以评估其健康状况和 安全性。
地震工程
地震引起的振动对建筑结构的影响非常大,需要进行抗震设计和分 析。
第九章振动学基础

9-1 简谐振动的规律
学习要点
1. 注意简谐振动的规律和特点. 知道如何判断一个振 动是否为简谐振动?
2. 简谐振动的能量有什么特点?
3. 简谐振动的周期由什么因素决定?如何计算一简谐 振动的周期?
4. 了解研究谐振子模型的意义何在?
一 简谐振动的定义
1m2A2si2n(t)
2
1kA2sin2(t)
2
弹簧振子的总的机械能
EEk
Ep
1kA2 2
弹簧振子在振动过程中,系统的动能和势能都随时
间发生周期性变化,但动能和势能的总合保持为一个常
量,即作简谐运动的系统机械能守恒.
简谐运动能量图
E
1 kA 2 2
o T T 3T 42 4
x1
xx
A A 1 2 A 2 2 2 A 1 A 2 co 2 s1 )(
tanA A 1 1c sio n 1 1s A A 2 2s cio n2 2s
两个同方向同频率简谐运动合成后仍为简谐运动, 角速度不变.
1.当 21 2 k时, (k0 , 1 , 2 , )
解 A' x02v022 0.070m7
tan'v0 1 x0
o π 4 x
'π 或3π
A'
44
因为 v0 0,由旋转矢量图可知 ' π4
xA co ts ()0.070c7o6s.0(tπ)
4
9-3 简谐振动的合成
学习要点 1. 了解两个同方向同频率简谐振动的合振动规律. 2. 知道同方向同频率简谐振动合成后,合振动的振幅、
tanA A 1 1c sio n 1 1s A A 2 2s cio n2 2s
9-振动学基础

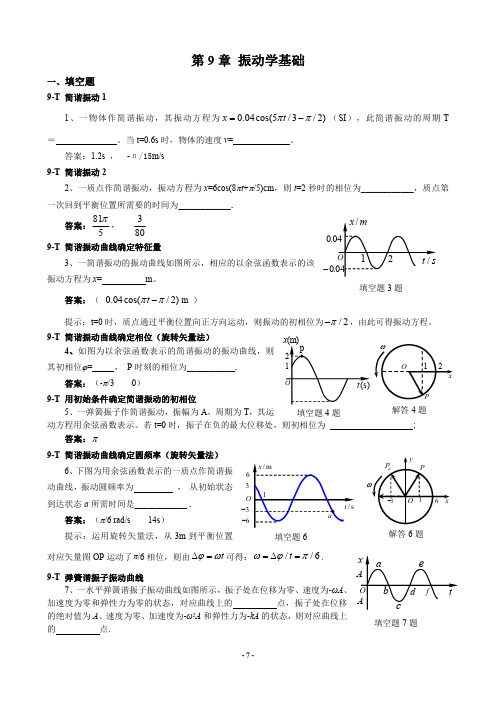
,初位相2=___________.
答案:4cm 2π/3 提示:运用旋转矢量法,如图。
y
A
A2
A1
O
x
解答 12 题
-7-
二、选择题
1、下列说法正确的是: (A) 简谐振动的运动周期与初始条件无关;(B) 一个质点在返回平衡位置的力作用下,一定做简谐振 动;(C) 已知一个谐振子在 t =0 时刻处在平衡位置,则其振动初相为π/2;(D) 因为简谐振动机械能守恒, 所以机械能守恒的运动一定是简谐振动。
周期 T;2)当速度是 12cm/s 时的位移。
9-S 简谐振动的运动规律
4、如图,一质点在一直线上作简谐振动,选取该质点向右运动通过 A 点时作为计时起点(t=0),经
2 秒后质点第一次经过 B 点,再经过 2 秒后第 2 次经过 B 点,若己知该质点在 A,B 两点具有相同的速率,
AB=10cm,求:1)质点的振动方程;2)质点在 A 点(或 B 点)处的速率。
计算 5 题
mF
7、有两个振动方向相同的简谐振动,其振动方程分别为
x1
10 cos(2t
)
cm,
x2
10 cos(2t
)
2
cm,
O
计算 6 题
1) 求它们的合振动方程;
2) 另有一同方向的简谐振动 x3 2 cos(2t 3 ) cm,问当3 为何值时, x1 x3 的振幅为最大值?
8、一个沿 x 轴作简谐振动的弹簧振子,振幅为 A,周期为 T,其振动方程用余弦
(A) Asin ;
(B) Asin ; (C) A cos ; (D) A cos
y
Hale Waihona Puke 4、如图所示质点的简谐振动曲线所对应的振动方程是:
振动的基本知识课件

振动的基本知识
9
多频率成分的产生
• 每个振源都要产生自己独特的振动频率成分 或振动形态。
• 对已知的设备,找到了它所产生的各振动频 率成分,也就知道了振源所在。
• 对一台机器所进行的振动分析1/3 是由其振 动频率成分查找振源。
• 其余2/3 的振动分析是从已知机器的历史中 找到问题所在。
• 参考脉冲也用于测量转子的转速。
振动的基本知识
43
振动相位
• The relationship of the movement of part of a machine to a reference – for example the position of the shaft as it rotates
• 传感器质量小, 可测很高振级。
• 现场测量要注意 电磁场、声场和 接地回路的干扰。
振动的基本知识
50
非接触式位移传感器
振动的基本知识
51
加速度传感器的频响特性
振动的基本知识
52
波德图和极坐标图
波德图(Bode Plot)和极坐标图(Polar Plot)两者所含信息相同,都表示基频振动 的幅值和相位随机器转速的变化规律。
风机转速 = 5 Hz or 300 RPM
振动的基本知识
17
一个简单振动试验--提高频率
➢风机转速提高一倍 ➢波形图中的波形靠得很近 ➢风机转速 = 10 Hz or 600 RPM
振动的基本知识
18
一个简单振动试验--提高幅值
➢由于加在风机叶片上的不平衡重量,当 风机转速提高后,其振动幅值增加 ➢波形的高度是幅值.
• Phase indicates how a machine is moving
文档震动学
位差为:
A
A2
(A) 0
(B)π/2
(C)π/3
(D)π/4
A1
答案: B 提示:其矢量图如图所示, A1 10 , A 20 ,根据矢量的叠加, O
1
x
- 10 -
可知 A2 为第二振动的振幅。矢量 A 在 A1 的投影大小为 A cos / 3 20 1/ 2 10 A1 ,所以 A1 与 A2 垂直
(A) Asin ;
(B) Asin ; (C) A cos ; (D) A cos
答案:B
x/m
9-X 简谐振动曲线
2
4、如图所示质点的简谐振动曲线所对应的振动方程是:( D )
2
(A) x=2cos(3t/4+π/4)(m) (B) x=2cos( t/4+5 /4)(m) (C) x=2cos( t O
2
22
2
9-X 简谐振动的动能变换频率
9、当质点以频率 v 作简谐振动时,它的动能的变化频率为
(A) v 答案:B
(B) 2v
(C) 4v
(D) v / 2
提示:利用 sin2 x 1 cos 2x 半角公式即可求频率。 2
9-X 简谐振动的能量
10、一弹簧振子作简谐振动,当位移为振幅的一半时,其动能为总能量的
速度最大值和加速度最大值。
解:将该简谐振动的表达式与简谐运动方程的一般形式 x A cos(t 0 ) 作比较后可得:
- 11 -
8 rad/s,振幅 A=0.1m,初相位0 2 / 3 ,于是周期 T 2 / 0.25 s
速度最大值 vmax A 8 0.1 m/s 0.8 m/s
1
t/s
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
17
旋转矢量图示法
A A1 A2
A2
2
O
A1 sin 1 A2 sin 2 tan A1 cos 1 A2 cos 2x1 Nhomakorabea1
A1
x2
X
x
A矢量沿X 轴之投影表征了合运动的规律。
2 A A12 A2 2 A1 A2 cos 2 1
2014年6月28日星期六 18
2014年6月28日星期六
1
9.2.4 简谐振动的旋转矢量表示
除了用运动学方程(振动 方程)和位移时间曲线 (振动曲线)来表示以外, 还可以用旋转矢量表示.
旋转矢量法: 简洁、直观、方便 常用的方法
2014年6月28日星期六
2
旋转矢量
用旋转矢量图画简谐运动的
x t
* * * T
图
x
A
x
A *
2014年6月28日星期六
16
9.3.1 同方向同频率的简谐振动的合成
设一个质点同时参与在同一直线上进行的两个独立 的同频率的简谐振动. 这一直线为x 轴, 设两个简谐振动 的运动方程分别为
x1 A1 cos t 1 x2 A2 cos t 2
解:(1)根据题意,画出旋转矢量图
A tg
2 A12 A2 0.052 0.062 0.078(m )
v A
A1 5 39.8 3948 A2 6 0 20 8448
(2)……….
v A1
v A2
4
x
o
2014年6月28日星期六
1. 解析法即运动方程法
x(t)=Acos( t+)
A x
2 0
2
2 v0
v0 arctg ( ) x0
x
v0>0
2. 曲线法(振动曲线)
A 由图一般可知振幅A,周期T , o 初始位置x0 和初始速度 v0的正负。 -A
A B
T
V0<0
t
3. 旋转矢量法
x
x
A1
o A2
2014年6月28日星期六 10
A cos(t )
π π x (0.08m)cos t 3 2
t 1.0s 代入上式得
x 0.069 m
F kx m 2 x
π 1 2 (0.01kg )( s ) (0.069 m) 1.70 103 N 2
2014年6月28日星期六 31
所以
0.4
作
业
9-18,9-19
2014年6月28日星期六
32
(3分)已知一质点沿y轴作简谐运动,其振动方程为
y = Acos(ωt + 3π/4)。与之对应的振动曲线是:
[B]
2014年6月28日星期六
33
(3分)一个质点作简谐振动,振幅为A,在起始时刻质点
6
2)对于两个同频率的简谐运动,旋转矢量图可明显的 表示出相位差,显示它们间步调上的差异.
x1 = A1 cos( t + 1) x2 = A2 cos( t + 2) 相位差:
=( t+ 2)-( t+ 1) = 2 - 1
2014年6月28日星期六
7
简谐振动的描述方法
2π π (s 1) T 2
0.08 0.04
A
o
π3
0.04
x/m
0.08
t 0, x 0.04m
代入 x
v
0.04m (0.08m) cos π π v0 0 3 3 π π x (0.08m)cos t 3 2
x
多个同方向同频率简谐运动合成仍为简谐运动
2014年6月28日星期六 24
两个同方向不同频率简谐运动的合成
2014年6月28日星期六
25
9.3.2 相互垂直的两个简谐振动的合成
两 相 互 垂 直 同 频 率 不 同 相 位 差
简 谐 运 动 的 合 成 图
2014年6月28日星期六
26
2014年6月28日星期六
x2 A2 cos(t π )
x ( A2 A1 ) cos(t π)
A A1 A2
x
x
o 2
A 2
A1
2
o
T
t
21
A
2014年6月28日星期六
1)相位差
2 1 2k π
A A1 A2
(k 0 , 1, )
相互加强
2)相位差 2
x1=A1cos( t+ 1) , x2=A2cos( t+ 2)
x =A cos( t+ )
2014年6月28日星期六
19
讨论
1)相位差
A
2 A12 A2 2 A1 A2 cos( 2 1 )
2 1 2k π (k 0 , 1, 2,)
(负号表示速度沿x 轴负方向)
(3)如果物体在 x 0.05 m 处时速度不等于零,而是具有向 右的初速度 v0 0.30m s1 ,求其运动方程.
解
A' x
2 0
2 v0 2
0.0707m
v0 tan' 1 x0
π 3π ' 或 4 4
2014年6月28日星期六 14
2014年6月28日星期六
30
解 根据振动方程画出它们的旋转矢量图如下 图所示. A1 A2 y
A
2 A12 A2 0.10m A1 0.06 而 tan 0.75 o 0.08 0.6 A2
x
3 因此合振动方程为 x 0.10cos 2t 0.4m
旋转矢量在x 轴上的投影坐标作简谐振动。
2014年6月28日星期六 4
• 矢量端点在半径为A的圆周上以圆频率ω做匀速圆周 运动 • 以旋转矢量在x轴上投影 x=Acos( t+ )代表谐振动
圆周运动速率 vm= A 投影v = - vm sin( t+ ) 圆运动向心加速度an= 2 A 投影a=- ancos( t+ ) = - 2 A cos( t+ ) y M
23
多个同方向同频率简谐运动的合成
x1 A1 cos(t 1 ) x2 A2 cos(t 2 ) xn An cos(t n )
v v A A 3
x x1 x2 xn
x A cos(t )
o
v 1 A1
2
3 v A2
1 (2k 1)π (k 0 , 1, )
A A1 A2
3)一般情况
相互削弱
A1 A2 A A1 A2
2014年6月28日星期六 22
例:有两个同方向、同频率的简谐振动,它们的振动表 式为:(SI制) 3 1 x1 0.05 cos10t x 2 0.06 cos10t 4 4 (1)求它们合成振动的振幅和初相位。 10t 0 ) ,问 0 为何值 (2)若另有一振动 x3 0.07 cos( x1 x3 的振幅为最大;为何值时,的振幅为最小。 时,
an= 2 A
vm
v
x O
t+
v A
x
2014年6月28日星期六
5
简谐振动旋转矢量表示法的应用
应用: 1)可以方便地确定初相位φ和任意时刻的相位
x0 0 v0 0 x0 0
x0 0 v0 0
φ1
x0 0 v0 0
x P
v0 0
φ2
x
2014年6月28日星期六
x A cos(t )
π 4
O
O * T
4
*
T * 3T 2 4
-A
-A
*
*
5T 4
t
T 2π (旋转矢量旋转一周所需的时间)
2014年6月28日星期六 3
振幅 : 旋转矢量的模A 圆频率 : 旋转矢量的角速度 位相 : 旋转矢量与OX 轴的夹角 t
在任意时刻该质点的位移为
x x1 x2 Acos t
合振动是简谐振动, 其频率仍为
2 A A12 A2 2 A1 A2 cos(2 1 )
A1 sin 1 A2 sin 2 tan A1 cos 1 A2 cos 2
2014年6月28日星期六
m 0.02kg
2 v0 v 2 0 0 A x0 2 x0 0.05m tan x0 由旋转矢量图可知 0
x/m
o
0.05
0 或 π
o
A
x A cos(t ) (0.05m) cos[(6.0s )t ]
1
x
13
2014年6月28日星期六
由图一般可知振幅 A ,初始 位置 x0 和初始速度 v0 的正负。
2014年6月28日星期六 8
例9-3. 一个作简谐振动的弹簧振子历时四分之一 周期,先后通过相对于平衡位置为对称的B,C 两点, 设简谐振动的振幅为A,试确定B,C 两点的位置.
解:
T T 2 , 4 2
t2
2
t1
(2)求物体从初位置运动到第一次经过A/2处时的速度;
解
x A cos(t ) A cos( t )
