工程力学:第16章 压杆稳定
压杆稳定(工程力学课件)

桁架结构
在轴向压力作用下,
短粗压杆 只要满足杆受压时的强度
条件,就能正常工作
细长压杆
破坏形式呈现出与强度问题 截然不同的现象
FN [ ]
A
压杆失稳
细长压杆:
临界压力或临界力ห้องสมุดไป่ตู้Fcr
F Fcr F Fcr
稳定的平衡 不稳定的平衡
压杆失稳
在轴向压力 F 由小逐渐增大 的过程中,压杆由稳定的平衡 转变为不稳定平衡,这种现象 称为压杆失稳。
首先判断压杆的失稳方向
(1)两端约束 1
(2)截面形状
Fcr (2 El)I2
Iz
hb3 12
140 803 12
597.3104
mm4
Iy
bh3 12
80 1403 12
1829.3104
mm4
Fcr1
2 EImin
(l)2
2 10 103 MPa 597.3104 (1 3103 mm)2
mm4
65 435 N 65.44 kN
(N、mm、MPa)
【例 1】 细长压杆,两端为球形铰支,
矩形横截面, E 10 GPa ,求其临界力。
Fcr (2 El)I2
长度影响
【例 2】细长压杆,上端约束为球形铰支,
下端约束在 xOz平面内可视为两端铰支,
Fcr (2 El)I2
在 xOy 平面内可视为一端铰支、一端固定
M
Wz
[ ]
81.67
πD4 i I 64 D 40mm
A πD2 4 4
l 1 3103 75
i
40
查表: 0.54
81.67
工程力学——压杆稳定

欧拉公 式
其中:i
I — 截面的惯性半径;为截 面的几何性质; A
=
l
i
称为压杆的柔度(长细 比);反映压杆的柔软 程度。
15N
32 mm
1mm
第一节
压杆稳定的概念
FP<FPcr :直线平衡形式(稳定平衡)
在扰动作用下,直线平衡形式转为弯曲平衡形式,扰动除 去后,能够恢复到直线平衡形式,则称原来的直线平衡构形是 稳定的。 FP>FPcr :弯曲平衡形式(不稳定平衡) 在扰动作用下,直线平衡形式转为弯曲平衡形式,扰动除去 后,不能恢复到直线平衡形式,则称原来的直线平衡形式是不稳 定的。
F
F
1.
计算柔度判断两杆的临界荷载
5m
d
9m
d
d 4 64 d I i 4 d 2 4 A 1 5 L a 125 d i 0 .5 9 4 112.5 b d 4
(a)
(b )
a b
1
0.5
2. 计算各杆的临界荷载
b a P 101
(n ) EI Fcr 2 L Fcr
n 1
kL sin 2
A
适用条件: •理想压杆(轴线为直线,压力 与轴线重合,材料均匀) •线弹性,小变形 •两端为铰支座
y sin
x 挠曲线中点的挠度 l
挠曲线为半波正弦曲线
由此得到两个重要结果:
临界载荷
(a)
z
b
h
正视图:
工程力学第16章(压杆稳定问题)

解:⑴ 计算压杆柔度
i d 11.25mm 4
两端为铰链约束
1
il11.1 2 5 0.1 70362.2
P
2E P
2200109
200106 100
62.2
压杆平衡稳定
压力小于一定的数值
时,压杆的直线平衡是 稳定的。
压杆平衡非稳定
当压力达到一定数值,压 杆仍具有直线平衡方式;在 外界扰动下,压杆偏离直线 平衡位置,但当扰动除去后, 在某一弯曲状态下达到新的 平衡
压力达到一定的数值时, 压杆存在直线和弯曲两种平 衡形式,压杆的直线平衡是 不稳定的。
压杆失稳
解: ⑴ 梁的强度校核(拉伸与弯曲的组合) 经过分析,AB 的危险截面为C 截面
F N F c o s 3 0 o 2 5 0 .8 6 6 2 1 .6 5 k N
M y F s i n 3 0 o l 1 2 5 0 .5 1 .2 5 1 5 .6 3 k N m 查型钢表
1 0 5 .5 2
4 7 3 k N
钢柱的许可载荷
F2 F nsctr
473157.7kN 3
例:图所示结构中,梁AB 为No.14 普通热轧工字钢,支承的杆 直径d = 20mm ,二者的材料均为Q235钢。结构受力如图所示,A 、B 、C 三处均为球铰约束。已知F = 25kN ,l1 = 1.25m ,l2 = 0.55m ,E = 206GPa 。规定稳定安全因数nst = 2.0 ,梁的许用应力 [σ] = 170MPa 。试校核此结构是否安全。
解:⑴ 压杆稳定校核(折减因素法)
工程力学:第16章 压杆稳定

IminI z 3.8910 8 m4
(4545 6)
等边角钢
图(b)
FPcr
2 Imin E (2l)2
20.389200 (20.5)2
76
.8kN
12.2.3 超过比例极限时压杆临界应力
一、 基本概念
1.临界应力:压杆处于临界状态时横截面上的平均应力。
cr
FPcr A
2.细长压杆的临界应力: cr
P
一、稳定平衡与不稳定平衡 : 1. 不稳定平衡:在平衡状态受扰动后无法回复到原状态
2. 稳定平衡:在平衡状态受扰动后物体将回复到原状态
3. 稳定性:构件在何在作用下保持其原有平衡状态(构形)的能力
4. 稳定性判据:构件丧失稳定性的条件 5. 失稳或屈曲:构件丧失稳定能力的现象 5. 临界荷载(屈曲荷载):构件由稳定平衡状态转化为不稳 定平衡状态时荷载
cr 235 0.006682 MPa <c 123
对于16Mn钢(E=206MPa, s=343MPa ),有
cr 343 0.014472 MPa <c 109
例4 一压杆长L=1.5m,由两根 56568 等边角钢组成,两端铰
支,压力F=150kN,角钢为A3钢,试用欧拉公式或抛物线公式
A 3.35103m2, imin 21.2mm
所以,若选用No.20a工字钢作立柱,其柔度及横截面的工作应力 分别为
l
imin
0.6 3 21.2 103
84.9
F A
250 103 3.55 103
70.4 106 Pa
查表12-3查得,对应于=84.9 的折减系数为
1
0.731
0.731 0.669 10
材料力学之压杆稳定课件

分析实验数据,得出压 杆的临界压力和失稳形式。
实验结果分析
分析压杆在不同压力 下的变形情况,判断 压杆的稳定性。
总结临界压力与失稳 形式的规律,为实际 工程应用提供依据。
对比不同长度、直径、 材料等因素对压杆稳 定性的影响。
总结词
机械装置中的压杆在承受载荷时,其稳 定性对于机械的正常运转和安全性至关 重要。
VS
详细描述
在机械装置中,如压力机、压缩机等,压 杆是重要的承载元件。通过材料力学的方 法,可以分析压杆的稳定性,确定其临界 载荷和失稳模式,从而优化机械装置的设 计,提高其稳定性和安全性。
05
压杆稳定的应用与发展
工程实例二:建筑压杆
总结词
建筑压杆在高层建筑、大跨度结构等建筑中广泛应用,其稳定性是保证建筑安全的重要 因素。
详细描述
高层建筑和大跨度结构的稳定性分析中,建筑压杆的稳定性分析占据重要地位。通过材 料力学的方法,可以对建筑压杆的承载能力和稳定性进行精确计算,从而为建筑设计提
供可靠的支持。
工程实例三:机械装置压杆
数值模拟
随着计算机技术的发展,数值模 拟方法在压杆稳定性分析中得到 广泛应用,能够更精确地预测结
构的稳定性。
材料性能研究
新型材料的不断涌现,对压杆稳定 性的影响也日益受到关注,相关研 究正在不断深入。
多因素耦合分析
在实际工程中,多种因素如载荷、 温度、腐蚀等会对压杆稳定性产生 影响,因此需要开展多因素耦合分析。
欧拉公式是由瑞士科学家欧拉提出的一个公式,用于计算等截面直杆的临界应力。 根据欧拉公式,临界应力只与压杆的材料性质和截面形状有关,而与压杆的长度 和外载大小无关。
稳定性校核
《工程力学》第十六章 压杆稳定
• 式中:I和A都是与截面有关的几何量,如果将 惯性矩写成横截面面积与某一距离平方的乘积, 即I=Ai2。i称为此横截面面积对于某一轴的惯性 半径。如果截面对y轴或z轴的惯性半径分别为
• 其量纲为长度一次方。常见图形的惯性半径 可从有关手册中查到。将I=Ai2代入(a)式得
•或
• 式中 P——工作压力; • Plj——压杆临界压力; • nw——压杆工作时实际具有的稳定安全
系数; • [nw]——规定的稳定安全系数。 • 也可采用应力形式表示压杆稳定性条件,
将式(16-10)及式(16-11),同除以压杆 的横截面面积A得
•或
• 式中[σw]——稳定许用应力。
• 二、折减系数法 • 由式(16-12)可知,压杆的稳定条件为
• 一、减小压杆的支承长度
• 由大柔度杆的临界应力公式
可
知在压杆材料一定的条件下,临界应力与
柔度的平方成反比,压杆的柔度愈小,相
应的临界应力愈高。而柔度
与压
杆长
• 度l成正比,减小压杆支承长度是降低柔度的方 法之一,在条件允许的情况下,应尽可能地减 小压杆的长度。例如,钢铁厂无缝钢管车间的 穿孔机的顶杆(图16-14),为了提高其稳定性, 在顶杆中段增加一个抱辊装置,这就达到了提 高顶杆稳定性的目的。
于是,压杆稳定性条件可以写成
• 对于已有压杆,其λ已知,可直接查表163得φ,代入式(16-14)进行稳定性校核。至
于设计截面尺寸,可采用逐次逼近法,即先
设定一个φ值,由式(16-14)计算出A值,然
后进行验算、调整,使杆件的工作应力逐渐 靠近许用应力。
表16-3.tif
《工程力学》压杆稳定

塑性材料的低碳钢短圆柱 被压扁; 铸铁短圆柱 脆断;
2、工程中的某些细长杆在轴向压力的作用下
表现出与强度完全不同的失效形式;
细长竹片受压时
开始轴线为直线,接着必被压弯,发生较大的弯曲变形; 最后被折断;
两端承受压力的细长杆:
当压力超过一定的数值时,压杆会由原来的直线平衡形式, 突然变弯,致使结构丧失承载力;
实际使用的压杆
轴线的初曲率、压力的偏心、材料的缺陷和不均匀 等因素总是存在的,为非理想受压直杆。
4、Euler解、精确解、实验结果的比较:
F
B
C 精确解
D
E
A F
Fcr
G
A’ Euler解 H 实验结果
δ
O
截面惯性矩 临界力
269103 N 269kN
§9-3其他支座条件下细长压杆的临界压力
.
§9-1 压杆稳定的概念 §9-2 两端铰支细长压杆的临界压力 §9-3 其他支座条件下压杆的临界压力 §9-4 压杆的临界应力 §9-5 压杆的稳定校核 §9-6 提高压杆稳定性的措施
§9-1 压杆稳定的概念 1、杆件在轴向拉力的作用下:
塑性材料:工作应力达到屈服极限时出现屈服失效; 脆性材料: 工作应力达到强度极限时断裂;
2.0 l )2
2 EI
Fcr ( 1.0 l )2
Fcr
(
2 EI
0.7 l )2
两端固定
Fcr
2 EI ( l )2
Fcr
2 EI
( 0.5 l )2
欧拉公式普遍形式
长度系数
l 相当长度
2
1
建筑力学压杆稳定课件

由此可以计算压杆在保证稳定的前提下,能承受的最大轴压力,又称为压杆的临界荷载 或容许荷载。当施加的压力小于容许荷载时,构件不会发生失稳破坏,反之,构件将发生失
稳破坏。对于此类问题,一般也要首先计算出压杆的长细比 ,根据 查出相应的折减系 数 ,再按照上式进行计算。
建筑力学压杆稳定
3. 对压杆进行截面设计
建筑力学压杆稳定
• 应用压杆的稳定条件,可以进行三个方面的问题计 算:
• 1. 稳定校核 • 已知压杆的截面形状和尺寸,杆件长度及支承条件
,杆件的轴心压力,根据公式(9-16)即可以验证 压杆是否会发生失稳破坏,即验证其稳定性。
建筑力学压杆稳定
例 9-4 如图 所示,构架由两根直径相同的圆杆构成,杆的材料为 Q235 钢,直径
立,由此可得的适用条件为:
cr
2E 2
p
令
p
2E p
则
p
(9-7) (9-8)
式(9-8)是欧拉公式适用范围的柔度表达形式,表明只有当压杆的实际柔度 p 时,才能
用欧拉公式来计算其临界应力和临界力。显然, p 是应用欧拉公式的最小柔度。压杆的实
际柔度 λ 随压杆的几何形状尺寸和杆端约束条件变化,但 p 是仅由材料性质确定的值。
d=20mm,材料的许用应力 =170MPa,已知 h=0.4m,作用力 F=15kN。试在计算平面内校核
二杆的稳定。
图 9-3
建筑力学压杆稳定
解:(1)计算各杆承受的压力 取结点 A 为研究对象,根据平衡条件列方程
x 0 FAB cos 450 FAC cos 300 0 Y 0 FAB sin 450 FAC sin 300 F 0
建筑力学压杆稳定
第二节 临界力和临界应力 1、影响临界力的因素 实践表明,影响细长压杆临界力的主要因素是材料的特性、截面几何形状和杆件的长度, 以及压杆两端的约束条件。 (1)材料的特性 对于两个截面几何形状及杆件长度相同的木杆和钢杆,受轴向压力 作用,木杆会先失稳,即木杆的临界力比钢杆的小,说明弹性模量 E 小的材料,其临界力也 小。 (2)截面几何形状 当截面尺寸相同,而截面形状不同时,其临界力也会不相同。影 响临界力的截面参数是截面惯性矩,惯性矩越大,杆件就越不容易失稳,说明截面的惯性矩 大,临界力也大。 (3)杆件的长度 其他条件相同时,长杆比短杆更易失去稳定,故临界力要小些。 (4)压杆两端的约束条件 对同一根细长压杆,两端的约束越强,压杆的轴心受压承 载力越大,因而,压杆两端的约束条件对压杆的稳定临界力也有很大的影响。当其他条件相 同时,一端固定、而一端铰支的压杆比两端铰支的更不容易失稳,说明两端支承越牢固,压 杆的临界力就越大。
工程力学:压杆稳定 习题与答案

一、单选题1、压杆一般分为三种类型,它们是按压杆的()。
A.惯性半径分B.杆长分C.柔度分D.杆端约束情况分正确答案:C2、细长压杆,若其长度系数增加一倍,则()。
A.Pcr增加一倍B.Pcr增加到原来的4倍C.Pcr为原来的二分之一倍D.Pcr为原来的四分之一倍正确答案:D3、下列结论中正确的是()。
①若压杆中的实际应力不大于该压杆的临界应力,则杆件不会失稳;②受压杆件的破坏均由失稳引起;③压杆临界应力的大小可以反映压杆稳定性的好坏;④若压杆中的实际应力大于scr=πE2/λ2,则压杆必定破坏。
A.①+②B.②+④C.①+③D.②+③正确答案:C4、压杆临界力的大小()。
A.与压杆所承受的轴向压力大小有关B.与压杆的柔度大小有关C.与压杆材料无关D.与压杆的柔度大小无关正确答案:B5、两端铰支的圆截面压杆,若λp=100,则压杆的长度与横截面直径之比l/d在时,才能应用欧拉公式()。
A.25B.50C.400D.200正确答案:A6、若两根细长压杆的惯性半径i相等,当()相同时,它们的柔度相等。
①杆长;②约束类型;③弹性模量;④外部载荷A.①+②B.①+②+③C.①+②+④D.①+②+③+④正确答案:A7、a、b两根都是大柔度杆,材料、杆长和横截面形状大小都相同,杆端约束不同。
其中a为两端铰支,b为一端固定,一端自由。
那么两杆临界力之比应为()。
A.4B.1/4C.2D.1/2正确答案:A8、提高水稻抗倒伏性能的可能措施包括()。
A.选用茎秆强壮品种B.选用节间较短的矮秆品种C.使用植物生长调节剂,以调控节间长度与株高等D.以上都是正确答案:D9、圆形压杆和矩形压杆在稳定性校核时有何区别()。
A.圆形压杆不需要考虑失稳方向性,而矩形压杆需要考虑B.圆形压杆需要考虑失稳方向性,而矩形压杆不需要考虑C.两者都不需要考虑D.两者都需要考虑正确答案:A10、压杆合理设计措施包括:①合理选用材料;②合理选择截面;③合理安排压杆约束与杆长()。
工程力学精品课程压杆稳定.ppt

F
b y
解:(a) 判断发生弯曲的方向。由于杆截面是矩形, 杆在不同方向弯曲的难易程度不同,如图:
l
h
z
y
因为
h z
b
Iy Iz
所以在各个方向上发生弯曲时约束条件相同的情况下,压杆最易在xz平面内发生弯曲
(b) 判断欧拉公式的适用范围。因为是细长杆
1
(c) 计算临界压力。由欧拉公式
所以可用欧拉公式
d
A
1 d 2
4
4
l 4l 120
i
d
(b) 判别压杆的性质。
1
2 E 102 p
1
压杆是大柔度杆,用欧拉公式计算临界力。
(c) 计算临界应力。
Pcr
cr
A
2E 2
A
269 kN
(d) 当l1=0.75l时,计算压杆的柔度,判别压杆的性质。
0.75120 90
2
a s
解决压杆稳定问题的关键是确定其临界压力。
二。临界压力的欧拉公式
1 两端铰支压杆的临界压力
y
P
xv
l
v xP
P
M x
P
压杆距支座x处截面上的弯矩是
M Pv
代入挠曲线的近似微分方程
d 2v dx2
M EI
Pv EI
令: k 2 P
则有:
EI
d 2v k2v 0 dx 2
以上微分方程的通解是
z b
y
y
x z
h
解:(a) 求在xz平面内弯曲时的柔度。
iy
Iy A
1 hb3
12
hb
b 12
y
1l
压杆的稳定ppt

定义
01
边界条件是指压杆在支撑条件下的限制条件,如固定、自由、
简支等。
描述
02
不同的边界条件对压杆的稳定性产生不同的影响。例如,固定
边界条件下的压杆比自由边界条件下的压杆更稳定。
影响因素
03
边界条件对压杆稳定性的影响主要表现在支撑反力的分布和大
小上,从而影响压杆的临界载荷和屈曲载荷。
03
压杆稳定性问题的解决策略
合理选择材料和截面形状
选择高强度材料
如合金钢、不锈钢等,能够提高压杆的屈服强度和抗拉强度 ,增加压杆的稳定性。
选择合适的截面形状
如圆形、方形、工字形等,能够改变压杆的截面面积和惯性 矩,进而改变压杆的稳定性。
对压杆进行合理支撑和固定
增加支撑点
通过在压杆的适当位置增加支撑点,能够提高压杆的稳定性,防止其发生屈 曲变形。
船舶设计
在船舶设计中,压杆被用于船体结构的支撑和固定。特 别是在海洋环境中,压杆的稳定性对于抵御海浪冲击和 保证船舶的安全至关重要。
地下工程
在隧道、地铁等地下工程中,压杆被用于支撑和固定土 石方及结构物。其稳定性对于保障地下工程的稳定性和 安全性至关重要。
06
总结与展望
总结
压杆稳定的定义
压杆稳定的重要性
05
压杆稳定性问Leabharlann 的工程应用建筑结构中的压杆稳定性问题
建筑物的支撑结构
在建筑设计中,压杆常被用于支撑和固定建筑结构,如桥梁、高层建筑等。其稳定性直接 影响到建筑物的安全性和使用寿命。
抗风和抗震设计
在地震或强风天气中,建筑物的压杆稳定性显得尤为重要。压杆能够提供必要的支撑力, 帮助建筑物抵御自然灾害。
定义
16压杆稳定

EIzw M (x) Fcr ( w)
x
w F cr w F cr
EI z EI z
令
Fcr k2 EI z
w
y z
y
w F cr w F cr
EI z EI zFcr 源自2 EI zw k2 w k2
方程的解为
w Asin kx Bcoskx
A,B,k 均为待定的量
取 n=1
x
F cr
m
m
w
x
o
w
F cr
x
F
Cr
2 EI l2
F cr
上式为两端铰支细长压杆的
l
m
m
y
x
临界力计算公式(欧拉公式)
o
y
F cr
三、其它支承情况下细长压杆的临界力
(1)两端绞支
F
cr
2 EI l2
(2)一端固定另绞支端
C 为拐点
F
cr
2 EI
(0.7l )2
F cr
B
l
0.7l
c
的临界荷载的计算公式。 l x
式中,Iz 是杆在 Fcr 作用下微弯时
横截面对于形心主惯性轴 z 的惯性矩。
x
Fcr
w
y z
y
x
Fcr
l
x
w
y z
y
F
cr
2 EI z
(2l)2
x
l y
z y
x
F
cr
2 EI y
(2l)2
l
y z
y
在 “偶然” 因素下,杆将在 xz 平面内弯曲,Fcr 计算公式中的 惯性矩应为Iy。
《工程力学压杆稳定》课件

压杆的应用案例
建筑
机械
压杆广泛应用于建筑领域,提供 结构稳定和支撑。
在机械工程中,压杆用于连接零 部件和传递力量。
通过案例演示,加深对压杆稳定的理解和应用。
桥梁
桥梁结构中的压杆可以增加桥梁 的稳定性和承重能力。
压杆稳定的条件
压杆稳定是杆件不发生屈曲的状态,包括杆件的截面形状、材料性质、长度等因素。
压杆的计算方法
1
确定杆件的受力状态
根据杆件受力情况进行分析。
2
计算杆件的临界压力
使用适当的公式计算杆件的临界压力。
3
判断是否稳定
根据计算结果判断杆件是否稳定。
压杆稳定的公式有等弯曲时压杆稳定公式和弯矩影响时压杆稳定公式。
《工程力学压杆稳定》 PPT课件
以图文并茂的方式介绍《工程力学压杆稳定》,让你轻松学习压杆的定义、 分类、稳定条件、计算方法和应用案例。
目录
1. 压杆的定义和分类 3. 压杆的计算方法
2. 压杆稳定的条件 4. 压杆的应用案例
压杆的定义和分类
压杆是指受到力作用的细长构件,可分为圆杆、方杆、角杆等多个分类。
(整理)压杆稳定计算

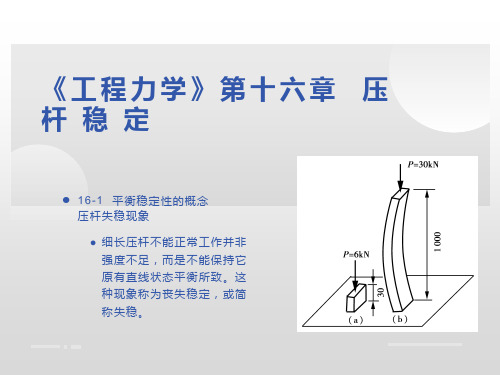
第16章压杆稳定16.1 压杆稳定性的概念在第二章中,曾讨论过受压杆件的强度问题,并且认为只要压杆满足了强度条件,就能保证其正常工作。
但是,实践与理论证明,这个结论仅对短粗的压杆才是正确的,对细长压杆不能应用上述结论,因为细长压杆丧失工作能力的原因,不是因为强度不够,而是由于出现了与强度问题截然不同的另一种破坏形式,这就是本章将要讨论的压杆稳定性问题。
当短粗杆受压时(图16-1a),在压力F由小逐渐增大的过程中,杆件始终保持原有的直线平衡形式,直到压力F达到屈服强度载荷F s(或抗压强度载荷F b),杆件发生强度破坏时为止。
但是,如果用相同的材料,做一根与图16-1a所示的同样粗细而比较长的杆件(图16-1b),当压力F比较小时,这一较长的杆件尚能保持直线的平衡形式,而当压力F逐渐增大至某—数值F1时,杆件将突然变弯,不再保持原有的直线平衡形式,因而丧失了承载能力。
我们把受压直杆突然变弯的现象,称为丧失稳定或失稳。
此时,F1可能远小于F s(或F b)。
可见,细长杆在尚未产生强度破坏时,就因失稳而破坏。
图16-1失稳现象并不限于压杆,例如狭长的矩形截面梁,在横向载荷作用下,会出现侧向弯曲和绕轴线的扭转(图16-2);受外压作用的圆柱形薄壳,当外压过大时,其形状可能突然变成椭圆(图16-3);圆环形拱受径向均布压力时,也可能产生失稳(图16-4)。
本章中,我们只研究受压杆件的稳定性。
图16-3所谓的稳定性是指杆件保持原有直线平衡形式的能力。
实际上它是指平衡状态的稳定性。
我们借助于刚性小球处于三种平衡状态的情况来形象地加以说明。
第一种状态,小球在凹面的O点处于平衡状态,如图16-5a所示。
先用外加干扰力使其偏离原有的平衡位置,然后再把干扰力去掉,小球能回到原来的平衡位置。
因此,小球原有的平衡状态是稳定平衡。
第二种状态,小球在凸面上的O点处于平衡状态,如图16-5c所示。
当用外加干扰力使其偏离原有的平衡位置后,小球将继续下滚,不再回到原来的平衡位置。
《压杆稳定教学》课件

增加约束
总结词
通过增加支撑、固定或增加附加约束,可以 提高压杆的稳定性。
详细描述
约束是影响压杆稳定性的重要因素。通过增 加支撑、固定或附加约束,可以限制压杆的 自由度,从而增强其稳定性。例如,在压杆 的适当位置增加支撑或固定点,可以减小压 杆的弯曲变形,提高其稳定性。此外,通过 增加附加约束,如套箍或加强筋等,也可以 提高压杆的稳定性。
实验结果与分析
实验结果
通过实验观察和数据记录,得到不同条件下 压杆的稳定性表现。
结果分析
根据实验数据,分析影响压杆稳定性的因素 ,如压杆的材料、截面形状、长度、直径等 。通过对比不同条件下的实验结果,总结出
压杆稳定性的一般规律和特点。
THANKS
感谢观看
REPORTING
稳定性安全系数
通过比较临界载荷与实际载荷的大小,来判断压杆的 稳定性。
稳定性试验
通过试验的方法,对压杆进行稳定性测试,以验证其 在实际使用中的稳定性。
PART 02
压杆的分类与计算
REPORTING
长细比较小的压杆
弹性失稳
当受到垂直于杆轴的压力时,杆件会 弯曲并丧失承载能力。
临界压力
当压杆达到临界压力时,杆件将发生 屈曲。
PART 05
压杆稳定性的实验研究
REPORTING
实验目的与原理
实验目的
通过实验研究,掌握压杆稳定性的基本概念和原理,了解影响压杆稳定性的因 素。
实验原理
压杆稳定性是指细长杆在受到轴向压力时,抵抗弯曲变形的能力。当轴向压力 超过某一临界值时,压杆会发生弯曲变形,丧失稳定性。本实验通过观察不同 条件下压杆的变形情况,分析影响压杆稳定性的因素。
根据欧拉公式计算临界应力:$sigma_{cr} = frac{EI}{A}$
压杆稳定教学课件PPT1

=69 kN
FNBC 4.5q ≤Fcr =69
得:q=15.3 kN/m
例 图示矩形截面压杆,h=60mm,b=40mm,杆长l=2m, 材料为Q235钢,E=206GPa 。两端用柱形铰与其它构件 相连接,在正视图的平面(xy平面)内两端视为铰支; 在俯视图的平面(xz平面)内两端为弹性固定,长度因
当x=0时,w=0。
0 A0 Bcoskx
得:B=0,
w Asin kx
w Asin kx
又当x=l时, w=0。
得 Asin kl = 0
要使上式成立,
x
1)A=0
w=0;
Fcr
代表了压杆的直线平衡状态。
A
2) sin kl = 0
w
Fcr
此时A可以不为零。
w
M (x)= Fcrw
l x x
sin
30 20Fra bibliotekFNBC 4.5q
2)求BC杆的临界力
I (D4 d 4 ) (50 4 40 4 ) =181132mm4。
64
64
2m
1m
q
Fcr
2EI ( l ) 2
A
30°
B
Ⅰ Ⅰ C
2 206103×181132
(1.0×2/cos30°×103 )2
[FNBC ] 120kN
例:托架的撑杆为钢管,外径D=50mm,内径d=40mm,
2m
A 30°
Ⅰ Ⅰ C
1m q
B
两端球形铰支,材料为Q235钢, E=206GPa。试根据该杆的稳定性 要求,确定横梁上均布载荷集度 q之许可值。
Ⅰ-Ⅰ截面
解:1)求BC杆的轴力
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
IminI z 3.8910 8 m4
(4545 6)
等边角钢
图(b)
FPcr
2 Imin E (2l)2
20.389200 (20.5)2
76
.8kN
12.2.3 超过比例极限时压杆临界应力
一、 基本概念
1.临界应力:压杆处于临界状态时横截面上的平均应力。
cr
FPcr A
2.细长压杆的临界应力: cr
第12章 压杆稳定
§12–1 压杆稳定性的概念 §12–2 细长压杆临界力的欧拉公式 §12–3 超过比例极限时压杆临界应力 §12-4 压杆的稳定校核及其合理截面
12.1 压杆稳定性的概念 构件的承载能力: ①强度
②刚度 ③稳定性
工程中有些构 件具有足够的强度、 刚度,却不一定能 安全可靠地工作。
②挠曲线近似微分方程:
y M FP y EI EI
y FP y y k 2 y 0 EI
其中:k 2
FP EI
③微分方程的解: ④确定积分常数:
yAsinxBcosx y(0)y(L)0
即:
A0B0 As ink LBc osk
L0
0
1
0
sinkL coskL
sinkL0
k
n
L
AD
F
Pcr
2EI
(0.5l)
2
l
C
B
4 一端固定另端自由
F Pcr
F
Pcr
2EI
(2l)2
FP
FPcr
2 EI min ( L)2
压杆临界力欧拉公式的一般形式
—长度系数(或约束系数)。
讨论:
(1)相当长度 l 的物理意义
1 压杆失稳时,挠曲线上两拐点间的长度就是压杆的相当
长度 l 。
FPb 18.45 kN FPcr 1 kN
工程实例
拱合梁的失稳
压杆的稳定性试验
工程实例
工程实例
12.2 细长压杆临界力的欧拉公式 12.2.1 两端铰支压杆的临界力:
假定压力已达到临界值,杆已经处于微弯状态,如图, 从挠曲线入手,求临界力。
FP FP
y
x M
FP x
FP ①弯矩:M ( x, y) FP y
线拐点 曲线拐点
C— 挠曲线拐点
临界力FPce 欧拉公式
FPcr
2EI l2
FPcr
2EI (0.7l)2
FPcr
2EI (0.5l )2
FPcr
2EI (2l )2
长度系数μ =1 0.7 =0.5 =2
FPcr
2EI l2
=1
约束在不同方向对失稳的影响
例1 试由挠曲线近似微分方程,导出下述细长压杆的临界力
(0.7 L1 )2
y
③压杆的临界力 FPcr min(FPcry , FPcrz )
例3 求下列细长压杆的临界力。
解:图(a)
P
P
I
m
in
5010 12
3
10
12
4.1710
9
m
4
10 30
z
y
FPcr
(2I1mli)n2E
24.17200 (0.70.5)2
67
.14
kN
图(b)
L L
图(a)
FPcr A
2EI (L)2 A
2E (L /i)2
2E 2
即: cr
2E 2
i I ——惯性半径。 A
3.柔度: L ——杆的柔度(或长细比)
i
12.3 压杆的临界应力总图
12.3.1大柔度杆的分界:
cr
2E 2
P
2E P
P
满足 P 的杆称为大柔度杆(或 长细杆),其临界力用 欧拉公式求。
图12–1 各种支承约束条件下等截面细长压杆临界力的欧拉公式
支承情况
两端铰支
一端固定 另端铰支
两端固定
一端固定 另端自由
两端固定但可沿 横向相对移动
FPce
FPce
FPceFPceFra bibliotekFPce
失
l l 0.7l l 0.5l
l 2l l 0.5l
稳 时
B
B
B
挠
D
曲
线 形
C
C
状
A
A
A
C— 挠曲 C、D— 挠
12.2 压杆的失稳或屈曲 1.理想压杆:材料绝对理想;轴线绝对直;压力绝对沿轴线作用。
2.压杆的稳定平衡与不稳定平衡:
FP FPcr
FP FPcr
FP FPcr
稳
不
定
稳
平
定
衡
平
衡
3.压杆失稳:
4.压杆的临界压力
临界状态
稳
定 平
过
衡
对应的 压力
临界压力:
不 稳 度定 平 衡 Pcr
失稳与强度破坏的区别
P
一、稳定平衡与不稳定平衡 : 1. 不稳定平衡:在平衡状态受扰动后无法回复到原状态
2. 稳定平衡:在平衡状态受扰动后物体将回复到原状态
3. 稳定性:构件在何在作用下保持其原有平衡状态(构形)的能力
4. 稳定性判据:构件丧失稳定性的条件 5. 失稳或屈曲:构件丧失稳定能力的现象 5. 临界荷载(屈曲荷载):构件由稳定平衡状态转化为不稳 定平衡状态时荷载
2 l 是各种支承条件下,细长压杆失稳时,挠曲线中相当于
半波正弦曲线的一段长度
(2)横截面对某一形心主惯性轴的惯性矩 I
1 若杆端在各个方向的约束情况相同(球形绞等),则 I 应取最小的形心主惯性矩。
2 若杆端在各个方向的约束情况不同(柱形绞),应分别 计算杆在不同方向失稳时的临界力。I 为其相应的对 中性轴的惯性矩。
FP EI
临界力 FPcr 是微弯下的最小压力,故,只能取n=1 ;且
杆将绕惯性矩最小的轴弯曲。
FPcr
2 EI min
L2
FPcr
2 EI min
L2
二、此公式的应用条件:
两端铰支压杆临界力的欧拉公式
1.理想压杆; 2.线弹性范围内; 3.两端为球铰支座。
12.2.2 其它支承情况下,压杆临界力的欧拉公式
公式。
解:变形如图,其挠曲线近似微分方程为:
F
F
EIy M (x) Fy M0
M0
令:k 2 F
EI
x
Fx
y k 2 y k 2 M 0
M0
F
yccoskxdsinkx
L
M0 F
M0 F
边界条件为:
x0,yy0;xL,yy0
c
M F
,d
0 , kL 2n
并 kL n
kL2n
为求最小临界力,“k”应取除零以外的最小值,即取:
FPcr
2 EI min ( L)2
压杆临界力欧拉公式的一般形式
—长度系数(或约束系数)。
12.2.2 其它支承情况下,压杆临界力的欧拉公式
1 两端绞支
2EI
F l Pcr
2
2 一端固定另端铰支
C为拐点
F Pcr
F
Pcr
2EI
(0.7l)
2
A
FP
l
C
B
3 两端固定
F Pcr
FP
C,D为拐点
所以,临界力为:
kL2
FPcr
4 2EI
L2
2EI
(L / 2)2
= 0.5
例2 求下列细长压杆的临界力。
y y
x
z
z
h
L1
解:①绕 ②绕
y z
L2
轴,两端铰支: =1.0, I y
轴,左端固定,右端铰支:
=0.7,
I
z
bh3 12
,
b3h , 12
b 2EI
FPcry L22
FPcry
2EI z
