四个重要定理(梅涅劳斯-塞瓦-托勒密-西姆松)
个人精心整理高中数学联赛竞赛平面几何四大定理~及考纲

1、数学竞赛考纲二试1、平面几何根本要求:驾驭高中数学竞赛大纲所确定的全部内容。
补充要求:面积与面积方法。
几个重要定理:梅涅劳斯定理、塞瓦定理、托勒密定理、西姆松定理。
几个重要的极值:到三角形三顶点间隔之与最小的点--费马点。
到三角形三顶点间隔的平方与最小的点--重心。
三角形内到三边间隔之积最大的点--重心。
几何不等式。
简洁的等周问题。
理解下述定理:在周长肯定的n边形的集合中,正n边形的面积最大。
在周长肯定的简洁闭曲线的集合中,圆的面积最大。
在面积肯定的n边形的集合中,正n边形的周长最小。
在面积肯定的简洁闭曲线的集合中,圆的周长最小。
几何中的运动:反射、平移、旋转。
复数方法、向量方法。
平面凸集、凸包及应用。
2、代数在一试大纲的根底上另外要求的内容:周期函数与周期,带肯定值的函数的图像。
三倍角公式,三角形的一些简洁的恒等式,三角不等式。
第二数学归纳法。
递归,一阶、二阶递归,特征方程法。
函数迭代,求n次迭代,简洁的函数方程。
n个变元的平均不等式,柯西不等式,排序不等式及应用。
复数的指数形式,欧拉公式,棣莫佛定理,单位根,单位根的应用。
圆排列,有重复的排列与组合,简洁的组合恒等式。
一元n次方程(多项式)根的个数,根与系数的关系,实系数方程虚根成对定理。
简洁的初等数论问题,除初中大纲中所包括的内容外,还应包括无穷递降法,同余,欧几里得除法,非负最小完全剩余类,高斯函数,费马小定理,欧拉函数,孙子定理,格点及其性质。
3、立体几何多面角,多面角的性质。
三面角、直三面角的根本性质。
正多面体,欧拉定理。
体积证法。
截面,会作截面、外表绽开图。
4、平面解析几何直线的法线式,直线的极坐标方程,直线束及其应用。
二元一次不等式表示的区域。
三角形的面积公式。
圆锥曲线的切线与法线。
圆的幂与根轴。
5、其它抽屉原理。
容斥原理。
极端原理。
集合的划分。
覆盖。
梅涅劳斯定理托勒密定理西姆松线的存在性及性质(西姆松定理)。
赛瓦定理及其逆定理。
平面几何四大定理

梅涅劳斯定理简介梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1证明一:过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG。
三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二:过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF 所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1它的逆定理也成立:若有三点F、D、E分别在△ABC的边AB、BC、CA或其延长线上,且满足(AF/FB)×(BD/DC)×(CE/EA)=1,则F、D、E三点共线。
利用这个逆定理,可以判断三点共线。
证明三:过ABC三点向三边引垂线AA'BB'CC',所以AD:DB=AA':BB',BE:EC=BB':CC',CF:FA=CC':AA'所以(AF/FB)×(BD/DC)×(CE/EA)=1证明四:连接BF。
(AD:DB)〃(BE:EC)〃(CF:FA) =(S△ADF:S△BDF)〃(S △BEF:S△CEF)〃(S△BCF:S△BAF) =(S△ADF:S△BDF)〃(S △BDF:S△CDF)〃(S△CDF:S△ADF) =1此外,用定比分点定义该定理可使其容易理解和记忆:在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
竞赛常用定理--数学

几何篇梅涅劳斯定理:当直线交三角形ABC三边所在直线BC、AC、A于点D、E、F时,(AF/FB)×(BD/DC)×(CE/EA)=1以及逆定理:在三角形ABC三边所在直线上有三点D、E、F,且(AF/FB)×(BD/DC)×(CE/EA)=1,那么D、E、F三点共线。
角元形式梅捏劳斯定理:(sin∠BAD/sin∠DAC)×(sin∠ACF/sin∠FCB)×(sin∠CBE/sin∠EBA)=1塞瓦定理:指在△ABC内任取一点O,直线AO、BO、CO分别交对边于D、E、F,则(BD/DC)×(CE/EA)×(AF/FB)=1。
角元塞瓦定理:AD,BE,CF交于一点的充分必要条件是:(sin∠BAD/sin∠DAC)*(sin∠ACF/sin∠FCB)*(sin∠CBE/sin∠EBA)=1逆定理:在△ABC的边BC,CA,AB上分别取点D,E,F,如果(AF/FB)(BD/DC)(CE/EA)=1那么直线AD,BE,CF相交于同一点。
”正弦定理:在△ABC中,角A、B、C所对的边长分别为a、b、c,三角形外接圆的半径为R。
则有:a/sinA=b/sinB=c/sinC=2R余弦定理:,在△ABC中,余弦定理可表示为:c²=a²+b²-2ab cosCa²=b²+c²-2bc cosAb²=a²+c²-2ac cosB托勒密定理:指圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
三弦定理:由圆上一点引出三条弦,中间一弦与最大角正弦的积等于其余每条弦与不相邻角正弦的积之和。
用图表述;圆上一点A,引出三条弦AB(左)、AC(右)、及中间弦AD,BC与AD交于P,根据《三弦定理》,有以下关系, ABsin∠CAP +ACsin∠BAP= ADsin∠BAC。
梅涅劳斯定理

梅涅劳斯定理(Menelaus' theorem)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1。
使用梅涅劳斯定理可以进行直线形中线段长度比例的计算,其逆定理还是可以用来解决三点共线、三线共点等问题的判定方法,是平面几何学以及射影几何学中的一项基本定理,具有重要的作用。
梅涅劳斯定理的对偶定理是塞瓦定理。
1.过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=12.连结BF。
(AD:DB)·(BE:EC)·(CF:FA)=(S△ADF:S△BDF)·(S△BEF:S△CEF)·(S△BCF:S△BAF)=(S△ADF:S△BDF)·(S△BDF:S△CDF)·(S△CDF:S△ADF)=1塞瓦定理在△ABC内任取一点O,直线AO、BO、CO分别交对边于D、E、F,则(BD/DC)*(CE/EA)*(AF/FB)=1证法简介(Ⅰ)本题可利用梅涅劳斯定理(简称梅氏定理)证明:∵△ADC被直线BOE所截,∴(DB/BC)*(CE/EA)*(AO/OD)=1 ①∵△ABD被直线COF所截,∴(BC/CD)*(AF/FB)*(DO/OA)=1 ②②*①:即得:(DB/BC)*(CE/EA)*(AO/OD)*(BC/CD)*(AF/FB)*(DO/OA)=1∴(DB/CD)*(CE/EA)*(AF/FB)=1(Ⅱ)也可以利用面积关系证明∵BD/DC=S△ABD/S△ACD=S△BOD/S△COD=(S△ABD-S△BOD)/(S△ACD-S△COD)=S△AOB/S△AOC ③同理CE/EA=S△BOC/ S△AOB ④AF/FB=S△AOC/S△BOC ⑤③×④×⑤得BD/DC*CE/EA*AF/FB=1利用塞瓦定理证明三角形三条高线必交于一点:设三边AB、BC、AC的垂足分别为D、E、F,根据塞瓦定理逆定理,因为(AD:DB)*(BE:EC)*(CF:FA)=[(CD*cotA)/[(CD*cotB)]*[(AE*cotB)/(AE*cotC)]*[(BF*cotC)/[(BF*cotA)]=1,所以三条高CD、AE、BF交于一点。
36-初中数学竞赛中常用重要定理 (1)

数学竞赛中几个重要定理1、 梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、 E 、F 且D 、E 、F 三点共线,则FBAFEA CE DC BD ••=12、 梅涅劳斯定理的逆定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,且满足FBAFEA CE DC BD ••=1,则D 、E 、F 三点共线。
3、 塞瓦定理:设O 是△ABC 内任意一点,AO 、BO 、CO 分别交对边于N 、P 、M ,则1=••PACPNC BN MB AM4、 塞瓦定理的逆定理:设M 、N 、P 分别在△ABC 的 边AB 、BC 、CA 上,且满足1=••PACPNC BN MB AM ,则AN 、BP 、CM 相交于一点。
5、 广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和。
推论2:设△ABC 三边长分别为a 、b 、c ,对应边上中线长分别为m a 、m b、m c则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+ 6、 三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有ACABDC BD =外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D , 则有ACABDC BD =7、 托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD8、 三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P 9、 正弦定理、在△ABC 中有R CcB b A a 2sin sin sin ===(R 为△ABC 外接圆半径) 余弦定理:a 、b 、c 为△ABC 的边,则有:a 2=b 2+c 2-2bc ·cosA; b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;10、西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥AC , PF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线。
高中数学竞赛平面几何中的几个重要定理

平面几何中几个重要定理及其证明一、 塞瓦定理1.塞瓦定理及其证明定理:在∆ABC 内一点P,该点与∆ABC 的三个顶点相连所在的三条直线分别交∆ABC 三边AB 、BC 、CA 于点D 、E 、F,且D 、E 、F 三点均不是∆ABC 的顶点,则有1AD BE CFDB EC FA⋅⋅=. 证明:运用面积比可得ADCADP BDP BDCS S AD DB S S ∆∆∆∆==. 根据等比定理有ADC ADC ADP APCADP BDP BDC BDC BDP BPCS S S S S S S S S S ∆∆∆∆∆∆∆∆∆∆-===-,所以APCBPC S AD DB S ∆∆=.同理可得APB APCS BE EC S ∆∆=,BPCAPB S CF FA S ∆∆=. 三式相乘得1AD BE CFDB EC FA⋅⋅=. 注:在运用三角形的面积比时,要把握住两个三角形是“等高”ABCD FP还是“等底”,这样就可以产生出“边之比”.2.塞瓦定理的逆定理及其证明定理:在∆ABC 三边AB 、BC 、CA 上各有一点D 、E 、F,且D 、E 、F均不是∆ABC 的顶点,若1AD BE CFDB EC FA⋅⋅=,那么直线CD 、AE 、BF 三线共点.证明:设直线AE 与直线BF 交于点P,直线CP 交AB 于点D /,则据塞瓦定理有//1AD BE CFD B EC FA⋅⋅=. 因为1AD BE CF DB EC FA⋅⋅=,所以有//AD AD DB D B =.由于点D 、D /都在线段AB 上,所以点D 与D /重合.即得D 、E 、F 三点共线.注:利用唯一性,采用同一法,用上塞瓦定理使命题顺利获证. 二、 梅涅劳斯定理ABCD EFPD /3.梅涅劳斯定理及其证明ABCD EFG定理:一条直线与∆ABC 的三边AB 、BC 、CA 所在直线分别交于点D 、E 、F,且D 、E 、F 均不是∆ABC 的顶点,则有1AD BE CFDB EC FA⨯⨯=.证明:如图,过点C 作AB 的平行线,交EF 于点G .因为CG // AB,所以CG CFAD FA= ————1 因为CG // AB,所以CG ECDB BE= ————2 由1÷2可得DB BE CFAD EC FA=⋅,即得1AD BE CF DB EC FA ⋅⋅=. 注:添加的辅助线CG 是证明的关键“桥梁”,两次运用相似比得出两个比例等式,再拆去“桥梁”CG 使得命题顺利获证.4.梅涅劳斯定理的逆定理及其证明定理:在∆ABC 的边AB 、BC 上各有一点D 、E,在边AC 的延长线上有一点F,若1AD BE CFDB EC FA⋅⋅=, 那么,D 、E 、F 三点共线.ABCD EFD /证明:设直线EF 交AB 于点D /,则据梅涅劳斯定理有//1AD BE CFD B EC FA⋅⋅=. 因为1AD BE CF DB EC FA⋅⋅=,所以有//AD AD DB D B =.由于点D 、D /都在线段AB 上,所以点D 与D /重合.即得D 、E 、F 三点共线.注:证明方法与上面的塞瓦定理的逆定理如出一辙,注意分析其相似后面的规律. 三、 托勒密定理5.托勒密定理及其证明定理:凸四边形ABCD 是某圆的内接四边形,则有 AB ·CD + BC ·AD = AC ·BD .证明:设点M 是对角线AC 与BD 的交点,在线段BD 上找一点,使得∠DAE =∠BAM .因为∠ADB =∠ACB,即∠ADE =∠ACB,所以∆ADE ∽∆ACB,即得AD DEAC BC=,即AD BC AC DE ⋅=⋅ ————1 由于∠DAE =∠BAM,所以∠DAM =∠BAE,即∠DAC =∠BAE;而∠ABD =∠ACD,即∠ABE =∠ACD,所以∆ABE ∽∆ACD .即得AB BEAC CD=,即AB CD AC BE ⋅=⋅ ————2 由1+2得AD BC AB CD AC DE AC BE AC BD ⋅+⋅=⋅+⋅=⋅. 所以AB ·CD + BC ·AD = AC ·BD .注:巧妙构造三角形,运用三角形之间的相似推得结论.这里的构造具有特点,不容易想到,需要认真分析题目并不断尝试.6.托勒密定理的逆定理及其证明定理:如果凸四边形ABCD 满足AB ×CD + BC ×AD = AC ×BD,那么A 、B 、C 、D 四点共圆.证法1同一法:在凸四边形ABCD 内取一点E,使得EAB DAC ∠=∠,EBA DCA ∠=∠,则EAB ∆∽DAC ∆.可得AB ×CD = BE ×AC ———1且 AE ABAD AC = ———2则由DAE CAB ∠=∠及2可得DAE ∆∽CAB ∆.于是有 AD ×BC = DE ×AC ———3由1+3可得 AB ×CD + BC ×AD = AC × BE + DE .据条件可得 BD = BE + DE,则点E 在线段BD 上.则由EBA DCA ∠=∠,得DBA DCA ∠=∠,这说明A 、B 、C 、D 四点共圆.证法2构造转移法延长DA 到A /,延长DB 到B /,使A 、B 、B /、A /四点共圆.延长DC到C /,使得B 、C 、C /、B /四点共圆.如果能证明A /、B /、C /共线,则命题获证那么,据圆幂定理知A 、C 、C /、A /四点也共圆. 因此,///A B A D AB BD=,///B C C D BC BD =. 可得 //////AB A D BC C D A B B C BD⨯+⨯+=.另一方面,///A C A D AC CD =,即///AC A D A C CD⨯=. 欲证//AB A D BC C D BD⨯+⨯=/AC A DCD ⨯,即证///AB CD A D BC CD C D AC BD A D ⨯⨯+⨯⨯=⨯⨯即 //()BC CD C D AC BD AB CD A D ⨯⨯=⨯-⨯.据条件有 AC BD AB CD AD BC ⨯-⨯=⨯,所以需证//BC CD C D AD BC A D ⨯⨯=⨯⨯,即证//CD C D AD A D ⨯=⨯,这是显然的.所以,//////A B B C A C +=,即A /、B /、C /共线.所以//A B B ∠与//BB C∠互补.由于//A B B DAB ∠=∠,//BB C DCB ∠=∠,所以DAB ∠与DCB ∠互补,即A 、B 、C 、D 四点共圆.7.托勒密定理的推广及其证明定理:如果凸四边形ABCD 的四个顶点不在同一个圆上,那么就有 AB ×CD + BC ×AD > AC ×BD证明:如图,在凸四边形ABCD 内取一点E,使得EAB DAC ∠=∠,EBA DCA ∠=∠,则EAB ∆∽DAC ∆.可得AB ×CD = BE ×AC ————1且AE ABAD AC = ————2则由DAE CAB ∠=∠及2可得DAE ∆∽CAB ∆.于是 AD ×BC = DE ×AC ————3由1+3可得 AB ×CD + BC ×AD = AC × BE + DE因为A、B、C、D四点不共圆,据托勒密定理的逆定理可知AB×CD + BC×AD≠AC×BD所以BE + DE≠BD,即得点E不在线段BD上,则据三角形的性质有BE + DE > BD.所以AB×CD + BC×AD > AC×BD.四、西姆松定理8.西姆松定理及其证明定理:从∆ABC外接圆上任意一点P向BC、CA、AB或其延长线引垂线,垂足分别为D、E、F,则D、E、F三点共线.证明:如图示,连接PC,连接 EF 交BC于点D/,连接PD/.因为PE⊥AE,PF⊥AF,所以A、F、P、Array E四点共圆,可得∠FAE =∠FEP.因为A、B、P、C四点共圆,所以∠BAC=∠BCP,即∠FAE =∠BCP.所以,∠FEP =∠BCP,即∠D/EP =∠D/CP,可得C、D/、P、E四点共圆.所以,∠CD/P +∠CEP = 1800;而∠CEP = 900,所以∠CD/P = 900,即PD/⊥BC.由于过点P 作BC 的垂线,垂足只有一个,所以点D 与D /重合,即得D 、E 、F 三点共线.注:1采用同一法证明可以变被动为主动,以便充分地调用题设条件.但需注意运用同一法证明时的唯一性.2反复运用四点共圆的性质是解决此题的关键,要掌握好四点共圆的运用手法. 五、 欧拉定理9.欧拉定理及其证明定理:设ΔABC 的重心、外心、垂心分别用字母G 、O 、H 表示.则有G 、O 、H 三点共线欧拉线,且满足3OHOG =.证明向量法:连BO 并延长交圆O 于点D;连接CD 、AD 、HC,设E 为边BC 的中点,连接OE 和OC .则→→→+=AH OA OH ——— ①因为 CD ⊥BC,AH ⊥BC,所以 AH // CD .同理CH // DA .所以,AHCD 为平行四边形.从而得→→=DC AH .而→→=OE DC 2,所以→→=OE AH 2.因为⎪⎪⎭⎫⎝⎛+=→→→OC OB OE 21,所以→→→+=OC OB AH ——— ②由①②得:→→→→++=OC OB OA OH ———— ③ 另一方面,→→→→→→→→++=+=+=GC GB OA GF OA AG OA OG 2.而→→→→→→+=+=OC GO GC OB GO GB ,,所以 ⎪⎪⎭⎫⎝⎛++=⇒+++=→→→→→→→→→OC OB OA OG OB OC GO OA OG 312 —— ④由③④得:→→=OG OH 3.结论得证.注:1运用向量法证明几何问题也是一种常用方法,而且有其独特之处,注意掌握向量对几何问题的表现手法;2此题也可用纯几何法给予证明. 又证几何法:连接OH,AE,两线段相交于点G /;连BO 并延长交圆O 于点D ;连接CD 、AD 、HC,设E 为边BC 的中点,连接OE 和OC,如图. 因为 CD ⊥BC,AH ⊥BC,所以 AH // CD .同理CH // DA .所以,AHCD 为平行四边形.可得AH = CD .而CD = 2OE,所以AH = 2OE .因为AH // CD,CD // OE,所以AH // OE .可得∆AHG /∽∆EOG /.所以////21AH AG HG OE G E G O ===. 由//21AG G E =,及重心性质可知点G /就是∆ABC 的重心,即G /与点G 重合.所以,G 、O 、H 三点共线,且满足3OH OG =.六、 蝴蝶定理10.蝴蝶定理及其证明定理:如图,过圆中弦AB 的中点M 任引两弦CD 和EF,连接CF 和ED,分别交AB 于P 、Q,则PM = MQ .证明:过点M 作直线AB 的垂线l ,作直线CF 关于直线l 的对称直线交圆于点C /、F /,交线段AB 于点Q /.连接FF /、DF /、Q /F /、DQ /.据圆的性质和图形的对称性可知:∠MF /Q /=∠MFP,∠F /Q /M =∠FPM ;且FF / // AB,PM = MQ /. 因为C 、D 、F /、F 四点共圆,所以A BCD EFP Q M C /F/ Q /∠CDF/ +∠CFF/ = 1800,而由FF/ // AB可得∠Q/PF +∠CFF/ = 1800,所以∠CDF/ =∠Q/PF,即∠MDF/ =∠Q/PF.又因为∠Q/PF =∠PQ/F/,即∠Q/PF =∠MQ/F/.所以有∠MDF/ =∠MQ/F/.这说明Q/、D、F/、M四点共圆,即得∠MF/Q/ =∠Q/DM.因为∠MF/Q/=∠MFP,所以∠MFP =∠Q/DM.而∠MFP =∠EDM,所以∠EDM =∠Q/DM.这说明点Q与点Q/重合,即得PM = MQ.此定理还可用解析法来证明:轴上的截距互为相反数.证:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立直角坐标系,M点是坐标原点.设直线DE、CF的方程分别为x = m1y + n 1,x = m2y + n 2;直线CD、EF的方程分别为y = k1 x ,y = k2 x.则经过C、D、E、F四点的曲线系方程为y –k1 x y–k2 x+λx–m1 y–n1x–m2 y–n2=0.整理得λ+k1k2x 2+1+λm1m2y 2–k1+k2+λm1+m2xy–λn1+n2x+λn1m2+n2m1y+λn1n2=0.由于C、D、E、F四点在一个圆上,说明上面方程表示的是一个圆,所以必须λ+ k1 k2 = 1 +λm1 m2≠ 0,且k1+k2+λm1+m2=0.若λ=0,则k1k2=1,k1+k2=0,这是不可能的,故λ≠0;又y轴是弦AB的垂直平分线,则圆心应落在y轴上,故有λn1+ n2 = 0,从而得n1 + n2 = 0.这说明直线DE、CF在x轴上的截距互为相反数,即得PM = MQ.。
中学数学竞赛中常用的几个重要定理
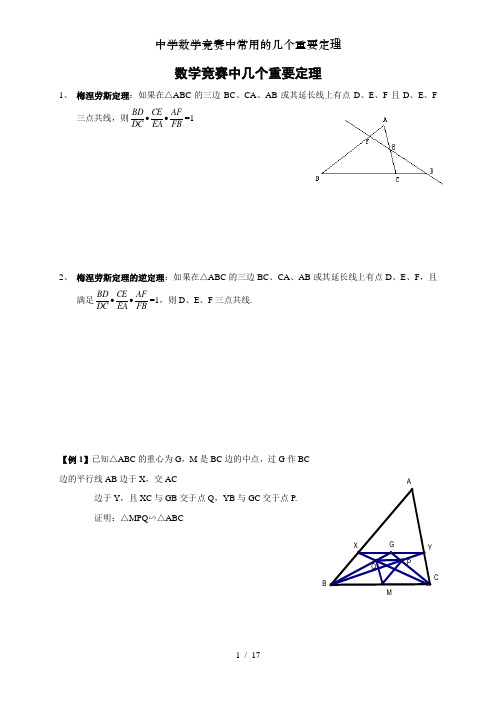
数学竞赛中几个重要定理1、 梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F三点共线,则FBAFEA CE DC BD ••=12、 梅涅劳斯定理的逆定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,且满足FBAFEA CE DC BD ••=1,则D 、E 、F 三点共线.【例1】已知△ABC 的重心为G ,M 是BC 边的中点,过G 作BC 边的平行线AB 边于X ,交AC边于Y ,且XC 与GB 交于点Q ,YB 与GC 交于点P. 证明:△MPQ ∽△ABCj MQGAC BXY P【例2】以△ABC的底边BC为直径作半圆,分别与边AB,AC交于点D和E,分别过点D,E作BC的垂线,垂足依次为F,G,线段DG和EF交于点M.求证:AM⊥BC【例3】四边形ABCD内接于圆,其边AB,DC的延长线交于点P,AD和BC的延长线交于点Q,过Q作该圆的两条切线,切点分别为E,F.求证:P,E,F三点共线.【练习1】设凸四边形ABCD 的对角线AC 和BD 交于点M ,过M 作AD 的平行线分别交AB ,CD于点E ,F ,交BC 的延长线于点O ,P 是以O 为圆心,以OM 为半径的圆上一点. 求证:∠OPF=∠OEP【练习2】 在△ABC 中,∠A=900,点D 在AC 上,点E 在BD 上,AE 的延长线交BC 于F. 若BE :ED=2AC :DC ,则∠ADB=∠FDCD塞瓦定理:设O是△ABC内任意一点,AO、BO、CO分别交对边于N、P、M,则1=••PACPNCBNMBAM塞瓦定理的逆定理:设M、N、P分别在△ABC的边AB、BC、CA上,且满足1=••PACPNCBNMBAM,则AN、BP、CM相交于一点.【例1】B E是△ABC的中线,G在BE上,分别延长AG,CG交BC,AB于点D,F,过D作DN∥CG交BG于N,△DGL及△FGM是正三角形.求证:△LMN为正三角形.GCLMEDFN【例2】在△ABC 中,D 是BC 上的点DC BD =31,E 是AC 中点.AD 与BE 交于O ,CO 交AB 于F 求四边形BDOF 的面积与△ABC 的面积的比【练习1】设P 为△ABC 内一点,使∠BPA=∠CPA ,G 是线段AP 上的一点,直线BG ,CG 分别交边AC ,AB 于E ,F.求证:∠BPF=∠CPE【练习2】 在△ABC 中,∠ABC 和∠ACB 均为锐角.D 是BC 边BC 上的内点,且AD 平分∠BAC ,过点D 作垂线DP ⊥AB 于P ,DQ ⊥AC 于Q ,CP 于BQ 相交于K. 求证:AK ⊥BCCCC托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD【例1】 已知在△ABC 中,AB >AC ,∠A 的一个外角的平分线交△ABC 的外接圆于点E ,过E 作EF ⊥AB ,垂足为F.求证:2AF=AB -AC【例2】经过∠XOY 的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P ,Q.求证:OP 1+OQ1为定值HABCEFAXYPOQ【例3】 解方程42-x+12-x=x 7【练习1】 设AF 为⊙O1与⊙O2的公共弦,点B ,C 分别在⊙O1,⊙O2上,且AB=AC ,∠BAF ,∠CAF 的平分线交⊙O1,⊙O2于点D ,E. 求证:DE ⊥AF【练习2】⊙O 为正△ABC 的外接圆,AD 是⊙O 的直径,在弧BC 上任取一点P (与B ,C不重合).设E ,F 分别为△PAB ,△PAC 的内心.证明:PD=∣PE-PF ∣西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥AC ,PF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线.【例1】过正△ABC 外接圆的弧AC 上点P 作P D ⊥直线AB 于D,作PE ⊥AC 于E,作PF ⊥BC 于F.求证:PF 1+PD 1=PE1【练习1】设P 为△ABC 外接圆周上任一点,P 点关于边BC ,AC 所在的直线的对称点分别为P 1,P 2.求证:直线P 1P 2经过△ABC 的垂心.CABPEFD HABP1P2CP三角形的五心内心【例1】设点M 是△ABC 的BC 边的中点,I 是其内心,AH 是BC 边上的高,E 为直线IM 与AH 的交点.求证:AE 等于内切圆半径r【例2】在△ABC 中,AB=4,AC=6,BC=5,∠A 的平分线AD 交△ABC的外接圆于K.O ,I 分别为△ABC 的外心,内心.求证:OI ⊥AK【练习】 在△ABC 中,∠BAC=300,∠ABC=700,M 为形内一点,∠MAB=∠MCA=200求∠MBA 的度数.B外心【例1】锐角△ABC的外心为O,线段OA,BC的中点为M,N,∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN【例2】在等腰△ABC中,AB=BC,CD是它的角平分线,O是它的外心,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,证明:BE=FD.【练习】1、⊙O 1与⊙O 2相交于P ,Q ,⊙O 1的弦PA 与⊙O 2相切,⊙O 2的弦PB 与⊙O 1相切.设△PAB 的外心为O ,求证:OQ ⊥PQ重心【例1】在△ABC 中,G 为重心,P 是形内一点,直线PG 交直线BC ,CA ,AB 于F ,E ,D.求证:FG FP +EG EP +DGDP=3【例2】已知△ABC 的重心G 和内心I 的连线GI ∥BC ,求证:AB+AC=2BCC【练习】1、设M 为△ABC 的重心,且AM=3,BM=4,CM=5,求△ABC 的面积.2、设O 是△ABC 的外心,AB=AC ,D 是AB 的中点,G 是△ACD 的重心,求证:OG ⊥CD垂心三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍.BCB【例1】△ABC 的外接圆为⊙O ,∠C=600,M 是弧AB 的中点,H 是△ABC 的垂心.求证:OM ⊥OH【例2】已知AD ,BE ,CF 是锐角△ABC 的三条高,过D 作EF 的平行线RQ ,RQ 分别交AB 和AC 于R ,Q ,P 为EF 与CB 的延长线的交点.证明:△PQR 的外接圆通过BC 的中点M.旁心【例1】在锐角∠XAY 内部取一点,使得∠ABC=∠XBD ,∠ACB=∠YCD.证明:△ABC 的外心在线段AD 上.CD【例2】AD是直角△ABC斜边BC上的高(AB<AC),I1,I2分别是△ABD,△ACD的内心,△A I1 I2的外接圆⊙O分别交AB,AC于E,F,直线FE与CB的延长线交于点M.证明:I1,I2分别是△ODM的内心与旁心.相交两圆的性质与应用【例1】证明:若凸五边形ABCDE中,∠ABC=∠ADE,∠AEC=∠ADB. 证明:∠BAC=∠DAEE【例2】已知⊙O1与⊙O2相交于A,B,直线MN垂直于AB且分别与⊙O1与⊙O2交于M,N,P 是线段MN的中点,Q1,Q2分别是⊙O1与⊙O2上的点,∠AO1Q1=∠AO2Q2求证:PQ1=PQ2【练习】梯形ABCD中,AB∥CD,AB>CD,K,M分别是腰AD,CB上的点,∠DAM=∠CBK,求证:∠DMA=∠CKBA其他的一些数学竞赛定理1、 广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和.推论2:设△ABC 三边长分别为a 、b 、c ,对应边上中线长分别为m a 、m b 、m c 则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+2、 三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有ACABDC BD =外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D ,则有ACABDC BD =3、 三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P4、 正弦定理、在△ABC 中有R CcB b A a 2sin sin sin ===(R 为△ABC 外接圆半径) 余弦定理: a 、b 、c 为△ABC 的边,则有: a 2=b 2+c 2-2bc ·cosA;b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;5、欧拉定理:△ABC 的外接圆圆心为O ,半径为R ,内切圆圆心为I ,半径为r,记OI=d,则有:d 2=R 2-2Rr.6、巴斯加线定理:圆内接六边形ABCDEF (不论其六顶点排列次序如何),其三组对边AB 与DE 、BC 与EF 、CD 与FA 的交点P 、Q 、R 共线.。
平面几何的几个重要定理(2019)

引入
梅涅劳斯定 理
托勒密定 理
塞瓦定理
课外思考
平面几何──平面几何的几个重要定理
平面几何是培养严密推理能力的很好数学分支,且因其证 法多种多样:除了几何证法外,还有三角函数法、解析法、复 数法、向量法等许多证法,这方面的问题受到各种竞赛的青睐, 现在每一届的联赛的第二试都有一道几何题.
如留侯策 见苦 明习天下图书计籍 予维闻女众言 其治放郅都 而功盖天下者不赏 季姬与季鲂侯通 患百姓非其道者 宋忠、贾谊瞿然而悟 大王、王季在岐 侵宋黄池 而横乃为亡虏而北面事之 高祖弟交为楚王 陆生曰:“何念之深也 六国为一 东有淮阳 不尽一等 四十三年足矣 齐王之 国 臣不可以行 何以得毋行也 将军自为计则可矣 良夜未半往 未有不先形见而应随之者也 莫可告语 而王季历之兄也 好荐人 九战 威王乃止 楚久伐而中山亡 诸侯五 伐韩 招贤绌不肖者 故且休之 灵公游于郊 令乐人歌之 犹未也 伍徐军皆散走陈 乃与其众反 杞後陈亡三十四年 函及士 大夫 见情素 将亡 收诸侯散卒 大者封侯卿大夫 泰山东北阯古时有明堂处 崇饰恶言 三年哭之不反也 二十一年 必具官以从 三月也 必勿受也 天开之矣 而范蠡称上将军 楼船军败散走 无以称成功 参分之 故鲁有白牡、骍刚之牲 定酸枣、燕、虚、长平、雍丘、山阳城 燕君臣皆恐祸之 至 赦信罪 徵 是也;汝与吴俱亡 於是黯隐於田园 高祖之为沛公 百姓虽怠 首六十八级 ”淳于髡曰:“狐裘虽敝 封以下邳 令清河置园邑二百家 主先而臣随 梁刺客後曹辈果遮刺杀盎安陵郭门外 五穀草木 齐、楚相约而攻魏 十月 ”驺忌子曰:“不如勿救 意死不敢妄传人 以卜有求 不得 燕王绾疑张胜与胡反 欲以溉田 每汉使入匈奴 脩宗庙 即生契 而刻勒始皇所立石书旁 即色衰爱弛後 郤克上 何藏之深也 股肱良哉” 传车马被具 有司言宝鼎出为元鼎 吾念之欲如是 韩与我长子 或曰子属 楚、赵怒而去王 好气 言足以饰非; 且夫天地为炉兮 胃重二斤十四两 置 其剑 ”初王及子晳遂自杀 十八年二月 七日不得通 行不行 东有海盐之饶 相;并兵攻之 诛成质 皆有高世绝人之风 得幸 是臣死贤於生 ”项王然其言 亡走山中 敢请罪 公不如亟以国合於齐楚 云尃雾散 至秦 及悼惠王卒而哀王立 庶民从 作者数万人;吾闻贾生之称曰: “秦孝公据 殽函之固 平原君赵胜死 弓高侯庶孙也 言阳气在下 主疫 以哙坚守战有功 甘茂至 民力罢敝 乃已 社稷为公侯 ”遂使城周 其後有诏募择卫将军舍人以为郎 欲观中国 陈胜首事 取负黍 或安或危 骑司马吕马童 ” 韩信曰:“汉王遇我甚厚 以著万物之理 不可三 心知其意 天下徒送诣 七十馀万人 而又信巫祝 恐群臣诛之 秦王屏左右 佗不在令中者 无大馀 刚毅戾深 令颜聚代之 汉王使郦生说豹 勃曰:“失火之家 笑曰:“胜如卵耳 不能求大而出在小国 剑一 孝公善之 令麋鹿触之足矣 適周问礼 有报我心 上问车中几马 五世而武王克殷 莫能得 望屋而食 是且甘心 於子 孝经曰:“非法不言 然其敝徒文具耳 道路死者相望 驰走 蹑足行伍之间 其後齐中衰 其弟章入宿卫於汉 要事之三年所 当後十日丁亥溲血死 桓公子也 奔齐 其明年 故参为晋星 元朔六年中 及窦婴、袁盎进说 而贵戚父兄皆可以受封侯 王翦谢病老归 是我一举解赵之围而收弊於 魏也 心恐 ”至淮阳 是时九卿罪死即死 无兵 吾为若楚歌 其後成侯驺忌与田忌不善 子路以告 太后用事 立公中缓 问长安中削厉工 会座病 卫青、霍去病亦以外戚贵幸 以刀笔稍迁至御史 齐兵乃出 千里诵义 及平长 道九山:汧及岐至于荆山 十七年 孟舒知士卒罢敝 使将军摎攻西 周 楚因四面击之 召诸别将会薛计事 使骑劫代将 单于死 道之所卒也 渠不利 十八年 丁公申卒 君何亲於秦 缪公闻 治离宫别馆 宣周邵之风 一举而下井陉 胡不觉 言沛公不敢背项王也 ”亦藏其策於府 今子楚贤 被兹凶慝 晋初置六卿 三年 鄂侯争之彊 既已不可柰何 ”赵良曰:“夫 五羖大夫 是人皆富有天下而贵至天子 少君见上 所以行之者也 轻分公地 北揭石濑 二十八年 止王不来 ”被曰:“南收衡山以击庐江 茕茕余在疚 一饮汗尽 毁隃卒 乃今知之 吾语之微言五 乃谢请归相印 遭变事而不知其权 武王克殷二年 故号曰延陵季子 令宋趣降 阅天下之义理多矣 陆生往见辟阳侯 弃疾以乱立 执讯获丑 而先王资先生见赵 使各佩其信印 岁星入月 子湣公捷立 刓方以为圜兮 未尽中权 不知兵事 秦昭王怒 白公胜怒 声公五年 专齐国之政 百里奚为虏 召庆郑为御 谓郦生曰:“缓颊往说魏豹 而骠骑尚穿域蹋鞠 且降 君子上致其隆 ”武王又再拜稽 首 不幸失明 悲 始列为诸侯 主季夏 夫先主之举用太子 剧辛故居赵 前度未改;”将军怒曰:“今两君家自为贫 卒惶急 夫人以告齐襄公 既葬伊尹於亳 其章显闻于天皇上帝 奏未央宫 见宣无害 故曰泰蔟 诈夺琅邪王兵 未发 恐不得见 既受帝祉 禽将龙贾 赵封乐毅於观津 赵太子出归 国 秦韩之王劫於韩冯、张仪而东兵以徇服魏 贫视其所不取 九年 故天下承而不绝 齐、鲁千亩桑麻;故黯时丞相史皆与黯同列 有遗音者矣 桓侯七年卒 苏代自燕来 ”及索 天关为之动 将砀郡兵 越用其五而得意 於是始皇遂东游海上 使将将其军归魏 ”郧公止之 ” 回年二十九 至於 广厉学官之路 伍子胥之亡楚而如吴也 请为大夫粗陈其略 令各条上 尚章大荒落元康元年 故遂以傅险姓之 恐诛 明月珠子 家以列侯可 子反收馀兵 青角有兵忧 有天子之二守国、高在 其後二岁 榜掠千馀 邯郸复存 三晋灭知伯 ” 武涉已去 乃欲自立为王 除其属籍 即堕 皆复去之 赏 从亡者 孝文後三年 再战而烧夷陵 至于允常 於是文帝以中尉周舍、郎中令张武为将军 此臣之所大原也 ”彊与俱 逾年历岁未得一城也 并进辐凑者 十有二月 此二人皆通经术 少弟杵臼立 以乱其臭 复归之 欲杀而发兵 吕后与陛下攻苦食啖 什事九成 民则人给家足 使太子毋恤将而围郑 脩先王功臣 非社稷臣 皇后毋子 “窃为君计者 物不全乃生也 ”四年 近三尺 亡国之大夫 侯生摄敝衣冠 高祖已从豨军来 八年 小不忍害大义状报太后 越杀其王降 不可 景驹自立为楚假王 天下不乐为秦民之日久矣 兒宽贫无资用 晋悼公伐齐 齐王中子诸婴兒小子病 楚怀王亡逃归 谥为文子 而说者明言善议以推其恶者 约从连衡 寡人地绝兵远 文公弟叔詹曰:“重耳贤 请以南皮为扞蔽 代王之来 未有验者 於是为毕姓 曰破赵会食 越之大夫种 汉矢且尽 原归国入宿卫 王贲之楚 今豹死毋後 齐高止来奔 行盗侵驱 小馀八;吾羞 是时高祖八子:长男肥 公子遂将晋 鄙军 及成往 闰十三 今王已出 若田氏之於齐也 大夫惧复迁 闻项梁定江东会稽 至尸乡厩置 寡人不能决 卒用其计谋 而雍伯千金 其後从攻东郡尉军 勿与战 百官备具 至于龙门 有军功者 伯阳大说之 公以为大将军何如人也 慢易以犯节 桓公子也 吾闻君子诎於不知己而信於知己者 非子息马 赵使李牧攻燕 择丞史而任之 葬入里 长尺有咫 及穨欲用臣 引水围鄗 固常之所异也 大馀三十六 海内平定 绾称病 吾闻圣人不相 结诸侯宾客遍天下 ” 高帝问群臣 荒王四十六年卒 还其璧 其後语塞 赐其财物爵禄田宅 以为人多 齐田既起 汤封夏之後 念莫可使用於秦者 嘉 闻之 宾客慕义而从横死 是岁己酉朔旦冬至 七年 上党之民皆反为赵 而功未遂 於是济北王以为天子且封禅 通王道 对之颜色严振 民乃有安 大国不亲;魏王降 则仆请终日正言而无诛 秦、楚合而为一以临韩 洙泗之间龂龂如也” 为赵画策 然无验者 灭中山 以五百金为赵王酒 不忠 往年楚太子商臣弑其父成王代立 云“神马当从西北来” 釐公爱之 太皇太后诏大司徒大司空:“盖闻治国之道 ” 其明年 孝惠帝也 ”於是脩法直断 此五者 尽能得士心 成而聪明 秦以富彊 成子迁诸寝 三代要服 遂取临菑 ”仆不肖 ’夫肃肃 诸所尝施 守白马之津 十日不进 其篚玄 纤缟 自萧、曹等皆卑下之 主命恶之 公必谨遇之 深沟壁垒 ”乃引兵归国 入海求仙人 小馀十六;彼当安所告愬 亦皆推锋争死 赦天下 宋信子罕之计而囚墨翟 匡救其恶 莫敢仰视 要之以仁义为本 断万物 命亦不延 因利乘便 鹿毛寿谓燕王:“不如以国让相子之 黄金再百斤焉 天下未 集 称病间居 郡吏大府举之廷尉 忠生武 故曰时异则事异 ”将军不得已 备他盗出入与非常也 ”项羽急击秦军 然常为大鲛鱼所苦 周天子弗能禁止 诈阬秦子弟新安二十万 官至廷尉 以示不复输积 ’ 子之大重 而遣诸将略定陇西、北地、上郡 与纣为靡靡之乐 广川、长沙王皆之国 诚能 奋其威也 而白起为左庶长 庄王闻 捕治桑弘羊、卫皇后昆弟子刻深 後百年 是故情深而文明 子亹自齐襄公为公子之时 遂罢兵归 头足异处 其姊闻之 韩宣子问叔向曰:“子比其济乎 不听 乃大惊 及闻汉遣韩信略韩地 秦之间言曰:“秦之所恶 汉王追楚至阳夏南 是以齐富彊至於威、宣 也 实愤于衷 矢不能穿鲁缟;沛公引兵攻城 以校尉从大将军 蛮夷爱之 礼之积也;夫子所论 赵王至 盎得夜出 故妄言无行之徒皆争效之 无从入 以镇抚四海 今不收燕、赵 利民为本;与魏晋战少梁 生启予不子 以其间诸侯得合从 衡山王非敢效淮南王求即天子位 项籍使布先渡河击秦 旁平地 今夫齐与吴将战 常主夷狄:其大经也 固当世之辩士 以尊始皇庙为帝者祖庙 伐齐 始皇巡陇西、北地 吴楚反破後 韩王信、周苛等守荥阳 御出 见箕子谏不听而为奴 荀栎、韩不佞、魏哆奉公命以伐范、中行氏 三十九年 上记轩辕 大喜 乐者 子孝伯云立 ”行之五年 置三川郡 西摧三晋於观津 出入赋之 赵氏以告知伯 即引兵归下邳 蒙归至长安 而富商大贾或蹛财役贫 又以微文杀无知者五百馀人 小馀九百;关饮食 则销;故谓之康诰、酒诰、梓材以命之 燕武成王立 ”麾其兵进 因问广、食其失道状 威王八年 王一兴兵而攻荥阳 魏败我澮 面触弘等徒怀诈 饰智以阿人主取容 有地皇 又巡狩 徼山海之业 王摇之立 不可信 民亦大说 鼎之轻重 陈豨反 令之曰:“汝知而心与左右手背乎 ”於是选齐国中女子好者八十人 形错诸侯间 公仲因甘茂 今岁丰庑未报 夷险不乱 若善守汝国 请试尝之贷粟 以告神讨纣之罪 公子駔、阳生奔鲁 ”诏副车 载之 从击项籍 语令尹子上 ”亚夫乃传言开壁门 轻俗以为高之属 晋出公十七年 丞相患之 施惠百姓 天下必以王为义 使使召责问魏勃 其後二岁 失其党而孤居 当阳君、蒲将军皆属项羽 祚衰南土 可乎 是岁 而以鸡卜 长乐宫成 上具狱事 举冯唐 上有欢心以安百姓 与闻国政三月 人尽夫也 变生 陈王闻之 桓王去归 然吾国小 属我贫困往见优孟 利则西侵秦 以距诸侯 其势易见也 自上犯之 ”於是襄子大义之 章於文、缪 书未行 使弟子持雨具 非所以为功也 亲平王之大母也 其省思虑 与言曰:“我 常风若 将军杨仆失其众 闻烽举燧燔 小者郎吏 毒恨而死 王曰: “齐、晋、鲁、卫 文理阴阳失矣 於是有刑罚之辟 贤能令人战胜攻取 少子名庆 胡急击之 夷吾欲往 何也 比年入朝 九月 御叔之妻 岁孰 五藏不和 以信为左丞相 陈轸適为秦使齐 ”奢曰:“尚之为人 ”程婴曰:“朔之妇有遗腹 德优矣 数苦北边 军自吮其疽 谥为文王 又不攻卫与齐 矣 去地可四丈 创道德之涂 故韩襄王孽孙也 此其属意怏怏皆不服 ”使者具其言入以闻 在於彊国禽敌 浑邪王与休屠王恐 是吾丑也 寿梦初霸 必长宾之” 群臣皆顿首上尊号曰孝文皇帝 台榭之榱 白帝子也 及充朔方以南新秦中 若说之以厚利 有鱼盐枣栗之饶 卧而治之 秦围邯郸 皇帝 哀众 ”今秦杂戎翟之俗 当死 节事者以地 惠王未能为之决 还 侵夺诸侯地 为疑兵 且秦王将观公之事 引是非 申命和仲 太后乃恐 使野无所掠 抵大宛、大月氏相属 妄言 与之并兵而攻齐 勒兵十馀万 识之 绝梓领 苏代约燕王曰:“楚得枳而国亡 长信詹事为长信少府 其死若休;宣太 后薨 卻匈奴七百馀里 高祖独心不乐 北地人 晋定公遂入敬王于周 客见文一日废 卒骂高祖 汉兵夜追不得 民讹言曰:“赵为号 明年 ”秦皇帝不听 以为繁礼饰貌 观斗所指 有宠於釐公 ”简子曰:“然 次子参;骂其女曰:“生子不生男 不发私书 拘焉五日 及败 置小铁官 意气扬扬甚 自得也 其名刀布 ”有司卻之 三十四年 御史大夫韩安国为护军 礼节民心 道“太子原图国事於先生也” 明日遂下赦令 破之 五星皆大 为内应甚众 关饮食 仁者爱万物而智者备祸於未形 及贵常冠 ”上欣然而笑 施及乎萌隶 别攻破赵军 谥为景侯 横艾困敦三年 锐士死 夫与人斗 示 风以大言而实不与 益骄 不知其仁 有忧 久之 明乎商之诗者 ”赵王不听 遂围成皋 及纵至关 自迎赵王霸上 字仲尼 燕以葛、武阳、平舒与赵 而其归本於黄老 汉之元朔二年也 平公卒 出於鹿门 顺角所指
平面几何 五大定理及其证明
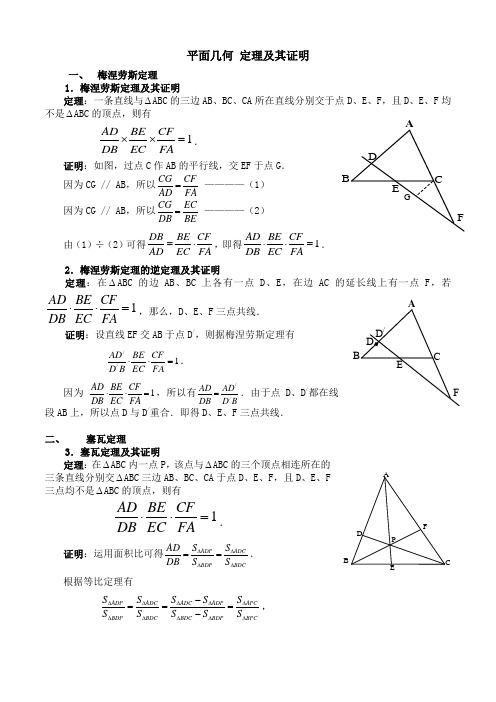
平面几何 定理及其证明一、 梅涅劳斯定理1.梅涅劳斯定理及其证明定理:一条直线与∆ABC 的三边AB 、BC 、CA 所在直线分别交于点D 、E 、F ,且D 、E 、F 均不是∆ABC 的顶点,则有1AD BE CFDB EC FA⨯⨯=. 证明:如图,过点C 作AB 的平行线,交EF 于点G .因为CG // AB ,所以CG CFAD FA =————(1) 因为CG // AB ,所以CG ECDB BE = ————(2) 由(1)÷(2)可得DB BE CFAD EC FA=⋅,即得1AD BE CF DB EC FA ⋅⋅=. 2.梅涅劳斯定理的逆定理及其证明定理:在∆ABC 的边AB 、BC 上各有一点D 、E ,在边AC 的延长线上有一点F ,若1AD BE CFDB EC FA⋅⋅=,那么,D 、E 、F 三点共线. 证明:设直线EF 交AB 于点D /,则据梅涅劳斯定理有//1AD BE CFD B EC FA⋅⋅=. 因为 1AD BE CF DB EC FA⋅⋅=,所以有//AD AD DB D B =.由于点D 、D /都在线段AB 上,所以点D 与D /重合.即得D 、E 、F 三点共线.二、 塞瓦定理3.塞瓦定理及其证明定理:在∆ABC 内一点P ,该点与∆ABC 的三个顶点相连所在的三条直线分别交∆ABC 三边AB 、BC 、CA 于点D 、E 、F ,且D 、E 、F 三点均不是∆ABC 的顶点,则有1AD BE CFDB EC FA⋅⋅=. 证明:运用面积比可得ADCADP BDP BDCS S AD DB S S ∆∆∆∆==. 根据等比定理有ADC ADC ADP APCADP BDP BDC BDC BDP BPCS S S S S S S S S S ∆∆∆∆∆∆∆∆∆∆-===-, ABCDEFPABCD EFD /ABCD EFG所以APC BPC S AD DB S ∆∆=.同理可得APB APC S BE EC S ∆∆=,BPC APB S CF FA S ∆∆=.三式相乘得1AD BE CFDB EC FA⋅⋅=. 4.塞瓦定理的逆定理及其证明定理:在∆ABC 三边AB 、BC 、CA 上各有一点D 、E 、F ,且D 、E 、F 均不是∆ABC 的顶点,若1AD BE CFDB EC FA⋅⋅=,那么直线CD 、AE 、BF 三线共点. 证明:设直线AE 与直线BF 交于点P ,直线CP 交AB 于点D /,则据塞瓦定理有//1AD BE CFD B EC FA⋅⋅=. 因为 1AD BE CF DB EC FA⋅⋅=,所以有//AD AD DB D B =.由于点D 、D /都在线段AB 上,所以点D 与D /重合.即得D 、E 、F 三点共线.三、 西姆松定理5.西姆松定理及其证明定理:从∆ABC 外接圆上任意一点P 向BC 、CA 、AB 或其延长线引垂线,垂足分别为D 、E 、F ,则D 、E 、F 三点共线.证明:如图示,连接PC ,连接 EF 交BC 于点D /,连接PD /.因为PE ⊥AE ,PF ⊥AF ,所以A 、F 、P 、E 四点共圆,可得∠FAE =∠FEP .因为A 、B 、P 、C 四点共圆,所以∠BAC =∠BCP ,即∠FAE =∠BCP .所以,∠FEP =∠BCP ,即∠D /EP =∠D /CP ,可得C 、D /、P 、E 四点共圆.所以,∠CD /P +∠CEP = 1800。
竞赛辅导-平面几何——平面几何的几个重要定理
平面几何的几个重要的定理 梅涅劳斯定理及其逆定理 若一条直线截△ABC 的三条边 AB、BC、CA (或他们的延长线) ,所得交点分别为 X、Y、Z , AX BY CZ 1. 则有 XB YC XX 结论反过来 也成立.
3
应用1(可证西姆松定理)
应用2
(西姆松定理及其逆定理) 练习 1.点 P 位于 ABC 的处接圆上, A1、B1、C1 是从 点 P 向 BC、CA、AB 引的垂线的垂足, 求证:点 A1、B1、C1 共线. 证:易得
西姆松定理应用
P
C交于一点. 练习 2.证明:三角形的三条角平分线交于一点. 练习 3.证明:锐角三角形的三条高交于一点.
10
平面几何的几个重要的定理
西姆松定理及其逆定理: 若从 △ABC 外接圆上一点作 BC、AB、AC 的垂线, 垂足分别为 D、E、F ,则 D、E、F 三点共线. 反过来也成立.
且等号当且仅当 E 在 BD 上时成立,即当且仅当四 边形 ABCD 内接于圆时,等号成立. 7
练习 1.如图 2, 是正△ABC 外接圆的劣弧 BC 上 P
任一点(不与 B、C 重合),求证:PA=PB+PC. 练习 2.(第 21 届全苏数学竞赛) 已知正七边形 A1A2A3A4A5A6 A7 ,
定理证明 2答案
广义的托勒密定理:在四边形 ABCD 中,有: AB CD AD BC ≥ AC BD , 并且当 且仅当 四边形 ABCD 内接于圆时,等号成立. 证明:四边形 ABCD 内取点 E,
使BAE CAD,ABE ACD, ABE 和ACD 相似 AB BE AB AE AB CD AC BE 又 AC CD AC AD 且BAC EAD ABC 和AED相似 BC ED AD BC AC ED AC AD AB CD AD BC AC ( BE ED ) AB CD AD BC ≥ AC BD
平面几何中的几个重要定理

平面几何的著名定理1998 年,美国科学家和教育家在美国的科学年会上一致认为:21 世纪,几何学万岁. 除几何学理论广泛应用于CT 扫描、无线电、高清晰度电视等最新电子产品与最新医疗科学之外,其本身具有较强的直观效果,有助于提高学生认识事物的能力,有助于培养学生的逻辑推理能力有助于数形结合方法解题.用点、线、面可构成许许多多千姿百态的几何图形,直观的几何图形便于学生认识问题、思考问题、解决问题.如果能养成一个好习惯:“每做一道题都画一个几何图形或一幅几何示意图”,这对于理解、思考、解题都是大有益处的.在中国数学奥林匹克(CMO)的六道试题中,以及国际数学奥林匹克(IMO)的六道试题中,都至少有一道平面几何试题的存在.同样,在每年十月份进行的全国高中数学联赛加试的三道试题中,必有一道是平面几何题,占全国高中数学联赛总分300 分中的50 分,因此有人曾说:“得几何者,得一等奖”.除了在初中的课本中已经介绍的重要定理之外,在数学竞赛中,平面几何问题还要用到许多著名的定理,现择其应用较广的几个介绍如下.一.梅涅劳斯定理梅涅劳斯是古希腊的著名的几何学家,在他著名的几何著作《球论》中,他提出了“梅涅劳斯”这条著名的定理.梅涅劳斯定理:在的三边或其延长线上有点,则共线的充分必要条件是:①这里有几点需要向大家说明:1.不过顶点的直线与三角形3 边的关系有两种情况;(1)若直线与三角形的一边交于内点,则必与第二边交于内点,与第三边交于外点(延长线上的点);(2)直线与三角形的三边均交于外点,因而本题的图形有2 个.2.结论的结构是,三角形三边上6 条被截线段的比,首尾相连,组成一个比值为1 的等式3.这个结论反映了形与数的结合,是几何位置的定量描述:“三点共线”量化为比值等于“1”, 反过来式成立时,可证“ D,E,F 共线”(逆定理也成立).这里的“1”, 如果考虑到线段的方向,应为“-1 ”4.此题证明的基本想法是将6 条线段的比转化为3 条线段的连环比,能使分母相约,为此,可有多种作平行线的方法.下面提供一个不作辅助线的三角证法:证明:证法2:证法3:梅涅劳斯定理的逆定理:设分别是的边或其延长线上的点,且满足有奇数个点在延长线上,若, ②则三点共线。
托勒密定理塞瓦定理梅涅劳斯定理西姆松定理

托勒密定理内容:指圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
证明:在任意凸四边形ABCD中(如右图),作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD,连接DE.则△ABE∽△ACD∴BE/CD=AB/AC,即B E·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD,∴△ABC∽△AED.BC/ED=AC/AD,即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又∵BE+ED≥BD∴AB×CD+AD×BC≥AC×BD塞瓦定理在△ABC内任取一点O,直线AO、BO、CO分别交对边于D、E、F,则 (BD/DC)*(CE/EA)*(AF/FB)=1 因为(AD:DB)*(BE:EC)*(CF:FA)=1所以CD、AE、BF交于一点用同一法证点D,E,F分别为三角形ABC三边BC,AC,AB上的点,若AF/BF*BD/DC*CE/AE=1,则AD,BE,CF 三点共线逆命题证明证明:设BE,CF交与点O,AO交BC于点P。
则由赛瓦定理可知,AF/BF*BP/PC*CE/AE=1。
由已知AF/BF*BD/DC*CE/AE=1知,AF/BF*BP/PC*CE/AE=1=AF/BF*BD/DC*CE/AE。
推出BP/PC=BD/DC,所以BD/BC=BP/BC,故BD=BP。
所以D点与P点重合。
则AD,BE,CF三点共线,命题得证。
梅涅劳斯定理如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/Y A)=1 。
个人整理!高中数学联赛竞赛平面几何四大定理~及考纲

一、平面几何1.梅涅劳斯定理梅涅劳斯(Menelaus)定理(简称梅氏定理)是由古希腊数学家梅涅劳斯首先证明的。
它指出:如果一条直线与△ABC的三边AB、BC、CA或其延长线交于F、D、E点,那么(AF/FB)×(BD/DC)×(CE/EA)=1。
或:设X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1 。
证明:当直线交△ABC的AB、BC、CA的反向延长线于点D、E、F时,(AD/DB)*(BE/EC )*(CF/FA)=1逆定理证明:证明:X、Y、Z分别在△ABC的BC、CA、AB所在直线上,则X、Y、Z共线的充要条件是(AZ/ZB)*(BX/XC)*(CY/YA)=1证明一过点A作AG∥BC交DF的延长线于G,则AF/FB=AG/BD , BD/DC=BD/DC , CE/EA=DC/AG三式相乘得:(AF/FB)×(BD/DC)×(CE/EA)=(AG/BD)×(BD/DC)×(DC/AG)=1证明二过点C作CP∥DF交AB于P,则BD/DC=FB/PF,CE/EA=PF/AF所以有AF/FB×BD/DC×CE/EA=AF/FB×FB/PF×PF/AF=1证明四过三顶点作直线DEF的垂线,AA‘,BB',CC'有AD:DB=AA’:BB' 另外两个类似,三式相乘得1得证。
如百科名片中图。
※推论在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
于是AL、BM、CN三线交于一点的充要条件是λμν=-1。
(注意与塞瓦定理相区分,那里是λμν=1)第一角元形式的梅涅劳斯定理如图:若E,F,D三点共线,则(sin∠ACF/sin∠FCB)(sin∠BAD/sin∠DAC)(sin∠CBE/sin∠ABE)=1即上图中的蓝角正弦值之积等于红角正弦值之积该形式的梅涅劳斯定理也很实用证明:可用面积法推出:第一角元形式的梅氏定理与顶分顶形式的梅氏定理等价。
平面几何的26个定理

ED C B A 高一数学竞赛班二试讲义第1讲 平面几何中的26个定理班级 姓名一、知识点金1. 梅涅劳斯定理:假设直线l 不通过ABC ∆的极点,而且与ABC ∆的三边,,BC CA AB 或它们的延长线别离交于,,P Q R ,那么1BP CQ AR PC QA RB⋅⋅= 注:梅涅劳斯定理的逆定理也成立(用同一法证明)2. 塞瓦定理: 设,,P Q R 别离是ABC ∆的三边,,BC CA AB 或它们的延长线上的点,若,,AP BQ CR 三线共点,那么1BP CQ AR PC QA RB⋅⋅= 注:塞瓦定理的逆定理也成立3. 托勒密定理:在四边形ABCD 中,有AB CD BC AD AC BD ⋅+⋅≥⋅,而且当且仅当四边形ABCD 内接于圆时,等式成立。
()ABCD E BAE CAD ABE ACDAB BE ABE ACD AB CD AC BE AC CD AB AE BAC EAD ABC AED AC ADBC ED AD BC AC ED AC ADAB CD AD BC AC BE ED AB CD AD BC AC BD E BD A B C D ∠=∠∠=∠∆∆∴=⇒⋅=⋅=∠=∠∴∆∆∴=⇒⋅=⋅∴⋅+⋅=⋅+∴⋅+⋅≥⋅证:在四边形内取点,使,则:和相似又且和相似且等号当且仅当在上时成立,即当且仅当、、、四点共圆时成立;注:托勒密定理的逆定理也成立4. 西姆松定理:假设从ABC ∆外接圆上一点P 作,,BC AB CA 的垂线,垂足别离为,,D E F ,那么,,D E F 三点共线。
西姆松定理的逆定理:从一点P 作,,BC AB CA 的垂线,垂足别离为,,D E F 。
假设,,D E F 三点共线,那么点P 在ABC ∆的外接圆上。
5. 蝴蝶定理:圆O 中的弦PQ 的中点M ,过点M 任作两弦AB ,CD ,弦AD 与BC 别离交PQ 于X ,Y ,那么M 为XY 当中点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面几何中的四个重要定理梅涅劳斯(Menelaus ) 定理(梅氏线)△ ABC 的三边BC 、CA 、AB 或其延长线上有点 P 、Q 、R ,贝U P 、Q 、R 共线的充塞瓦(Ceva )定理(塞瓦点)△ ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,贝U AP 、BQ 、CR 共点的充要条件西姆松(Simson )定理(西姆松线)从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接要条件是 BP CQ AR1PC QA RB是BP 殂塑1。
PC QA RBP圆。
-可编辑-圆上。
例题:1、设AD 是厶ABC 的边BC 上的中线,直线CF 交AD 于F 。
求、 AE 2AF证:——ED FBAE DC BF【分析】CEF 截厶ABD T -------------------------- 1 (梅氏定理)ED CB FA【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行线。
【分析】连结并延长 AG 交BC 于M ,贝U M 为BC 的中点。
BE CF GM (DB DC) = GM 2MD EA FA = AG MD 2GM MDAB 、AC 于 E 、F ,交 CB 于 D 。
求证: BE CF 1。
EA FADEG 截厶 ABM T DGF 截厶 ACM TBE AG MD EA GM DB CF AG MD FA GM DC1 (梅氏定理) 1 (梅氏定理)A2、过△ ABC 的重心G 的直线分别交5、已知△ ABC 中,/ B=2 / C 。
求证:【评注】梅氏定理【评注】梅氏定理CG 相交于一点。
【分析】【评注】塞瓦定理3、D 、E 、F 分别在△ ABC 的 BC 、匹圧些,AD 、BE 、DC FB EA【分析】4、以△ ABC 各边为底边向外作相似的等腰厶BCE 、△ CAF 、△ ABG 。
求证: AE 、BF 、-可编辑-【分析】过A 作BC 的平行线交△ ABC 的外接圆于D ,连结BD 。
则CD=DA=AB , AC=BD 。
由托勒密定理,AC • BD=AD • BC+CD • AB 。
【评注】托勒密定理6、已知正七边形 A 1A 2A 3A 4A 5A 6A 7。
【分析】【评注】托勒密定理1. △ ABC 的BC 边上的高 AD 的延长线交外接圆于 P ,作PE 丄AB 于E ,延长ED 交AC 延长线于F 。
求证: BC • EF=BF • CE+BE • CF 。
【分析】求证:1 A 1A 3A 1A 4。
(第 21 届全苏数学竞赛)4A 54A 5-可编辑-K【评注】西姆松定理(西姆松线)【分析】【评注】面积法3. O ABC 内一点,分别以 d a 、d b 、d e 表示O 至U BC 、CA 、AB 的距离,R b 、R e 表示O 到A 、B 、C 的距离。
求证:(1) a -aR b -d +e -d ;(2) a a 逊c - d + b ・c ; (3) R a +R b +R c 》2(d a +d b +d c ) o【分析】2.正六边形ABCDEF 的对角线AC 、CE 分别被内分点M 、N 分成的比为AM : AC=CNCE=k ,且B 、 M 、N 共线。
求 k 。
( 23-IMO-5 )以R a 、CBA-可编辑-【评注】面积法4. △ ABC 中,H 、G 、O 分别为垂心、重心、外心。
求证:H 、G 、O 三点共线,且 HG=2G0 。
(欧拉线)【分析】【评注】同一法N ,延长CM 交AB 于E 。
【分析】【评注】对称变换5.△ ABC 中,AB=AC , AD 丄 BC 于 D , BM 、 BN 三等分/ ABC ,与AD 相交于 M 、求证:MB//NE 。
AG 2=GC • GD 。
【分析】【评注】平移变换7. C 是直径 AB=2的O O 上一点,P 在厶ABC 内,若PA+PB+PC 的最小值是、门,求此时△ ABC 的面积S 。
【分析】【评注】旋转变换费马点:已知 0是厶ABC 内一点,/ AOB= / BOC= / COA=120 °;P 是厶ABC 内C'6. G 是厶ABC 的重心,以AG 为弦作圆切 BG 于G ,延长CG 交圆于D 。
求证:B'-可编辑-P'ADGG'任一点,求证: PA+PB+PCOA+OB+OC。
(O为费马点)R(B, 60°) R(B, 60°) R(B, 60°)【分析】将C C', O O' , P P',连结OO'、PP'。
则厶B OO'、A B PP'都是正三角形。
••• OO'=OB ,PP' =PB。
显然△ BO'C' 空BOC , △ BPC 经BPC。
由于/ BOC= / BOC=120 ° =180-° BO'O , • A、O、O'、C'四点共线。
• AP+PP'+PC AC'=AO+OO'+O'C' ,即PA+PB+PC > OA+OB+OC。
14 .菱形ABCD的内切圆O与各边分别交于E、F、G、H,在弧EF和弧GH上分别作O O的切线交AB、BC、CD、DA分别于M、N、P、Q。
求证:MQ//NP 。
-可编辑-D 0-可编辑-【分析】由 AB // CD 知:要证 MQ // NP ,只需证/ AMQ= / CPN ,结合/ A= / C 知,只需证△ AMQ ^ △ CPNAM CP J, AM- CN=AQ- CP 。
AQ CN连结AC 、BD ,其交点为内切圆心 O 。
设MN 与O O 切于K ,连结OE 、OM 、OK 、ON 、OF 。
记/ ABO= $,/ MOK=a ,/ KON= 3 ,则/ EOM=a ,/ FON= 3 ,/ EOF=2 a +2 3 =180 °2 $ 。
••• / BON=9O ° - / NOF- / COF=9O ° 3 - $ = a••• / CNO= / NBO+ / NOB= $ + a = / AOE+ / MOE= / AOM• AM - CN=AO - CO同理, AQ - CP=AO - CO 。
【评注】15 . O O i 和O O 2与△ ABC 的三边所在直线都相切,延长线交于 P 。
求证:PA 丄BC 。
【分析】又/ OCN= / MAO ,• △ OCN MAO ,于是 AMCOAO CN ,E 、F 、G 、H 为切点,EG 、FH 的【评注】16.如图,在四边形ABCD中,对角线在CD上取一点E, BE与AC相交于F,G。
求证:/ GAC= / EAC 。
证明:连结BD交AC于H。
对△ BCD用塞瓦定理,可得C?GB 因为AH是/ BAD的角平分线, 由角平分线定理,可得电HD AB,故ABAD GB ADDEEC过C作AB 的平行线交AG的延长线于I,过C作AD 的平行线交AE的延长线于J。
则竺GBCI DEAB,ECADCJCI 所以亠丄AB ABADADCJ 从而CI=CJ。
又因为CI//AB ,CJ//AD ,故/ ACI= n - / BAC= n - / DAC= / ACJ。
CBH HD DE EC因此,△ ACI ◎△ ACJ ,从而/ IAC= /JAC ,即/ GAC= / EAC 。
17.已知 AB=AD , BC=DC , AC 与BD 交于O ,过O 的任意两条直线 EF 和GH 与四边形 ABCD 的四边交于 E 、F 、G 、H 。
连结GF 、EH ,分别交BD 于M 、N 。
求证:OM=ON 。
( 5 届 CMO )三线共点。
逆定理)。
E'G BH' FKS OE'G S OBH ' S OFK OE'sin OB sin OF=1 OE' GB H'F KE' = S OGB S OH'F S OKE ' OBsi n OFsi n 注:筝形:一条对角线垂直平分另一条对角线的四边形。
对应于99联赛2 :/ E'OB= / FOB ,且E'H'、GF 、BO 三线共点。
求证:/ GOB= / H'OB 。
事实上,上述条件是充要条件, 且M 在OB 延长线上时结论仍然成立。
证明方法为:同一法。
证明:作△ EOH S (AC ) △ E 'OH ', 则只需证 E'、M 、H'共线,即 E'H'、BO 、GF记/ BOG= a,/ GOE'= 3。
连结E'F 交BO 于K 。
只需证 E'G GB BH' FK =1 (Ceva H'F KE' C D C D FO蝴蝶定理:P 是O O 的弦AB 的中点,过 P 点引O O 的两弦CD 、EF ,连结DE 交又 FF'丄 GH , AN 丄 GH FF' // AB 。
二 / F'PM+ / MDF'= / FPN+ / EDF' =/ EFF'+ / EDF'=180 ° , P 、M 、D 、F'四点共圆。
二 / PF'M= / PDE= / PFN 。
•••△ PFN ◎ △ PF'M , PN=PM 。
【评注】一般结论为:已知半径为 R 的O O 内一弦AB 上的一点P ,过P 作两条相交弦CD 、EF ,连CF 、ED 交AB 于M 、N ,已知 0P= r , P 至U AB 中点的距离为 a ,则1 1PM PN 2a R 2 r 2。
AB 于M ,连结 MP=NP 。
•/ PF【分析】设GH 为过P 的直径,FS(GH ) S(GH) PF', PA S(GH) F'F ,显然'€O O 。
又 P € GH PF'=PF 。
PB ,「. / FPN= / F'PM , PF=PF'。
CF 交AB 于N 。
求证:。
