第六讲 和差问题
第6讲 和差问题

第六章和差问题知识要点和差问题是已知大、小两个数的和与两个数的差,求大、小两个数各多少的问题。
大、小两个数的数量关系可表示为下面的线段图:从线段图知:(1)如果在小数中补进去一个已知的“差”,那么补后的小数与大数的和就是大数的2倍,即已知的和与已知的差之和是大数的2倍。
所以,大数=(和+差)÷2,小数=和-大数。
(2)如果在大数中去掉一个已知的差,那么去掉了“差”的大数与小数之和就是小数的2倍,即已知的和与已知的差之差是小数的2倍。
所以,小数=(和-差)÷2,大数=和-小数。
由此得到和差公式:(和+差)÷2=大数,和-大数=小数;(和-差)÷2=小数,和-小数=大数。
解决和差问题的关键,是要搞清楚两个数的“和”与“差”,而这个“和”与“差”往往又很隐蔽,需要通过条件转化而得到。
我们可以选择大数或小数作为标准数,然后进行思考。
典例巧解例1 四年一班有学生56人,其中男生比女生多6人。
你知道男、女生各多少人吗?点拨一这是一道典型的和差问题,我们先来画线段图表示题意:观察上图可知:假设女生增加6人,女生就和男生同样多。
即男、女生人数和加上差就是男生人数的2倍。
这样,我们就可以先求出男生的人数,再求女生的人数。
解法一男生:(56+6)÷2-31(人)女生:31 6=25(人)答:男生有31人,女生有25人。
点拨二观察上图可知:假设男生人数减少6人,男生就和女生同样多,即男、女生人数的和减差就是女生人数的2倍。
这样,我们就可以先求出女生的人数,再求男生的人数。
解法二女生:(56-6)÷2=25(人)男生:56-25=31(人)答:男生有31人,女生有25人。
说明像例1中的“和”与“差”直接给出的题,我们可以很容易地求出大数和小数。
如果题中没有直接给出“和”与“差”,我们可以根据题中的已知条件先求出“和”与“差”。
例2 爷爷和小明的平均年龄是39岁,如果小明的年龄再加上56岁就和爷爷的年龄一样大了。
第六讲 和倍与差

第六讲 和倍问题姓名:一、复习旧知——画线段图请帮助呆瓜兄弟用线段图闯关吧!第1关:老师买了很多巧克力分给呆瓜兄弟,阿瓜分到的是阿呆的3倍。
第2关:阿呆和阿瓜比积分,阿瓜的积分卡比阿呆的2倍多3分。
第3关:阿呆和阿瓜比赛跑步,阿瓜比阿呆的99倍多2米。
第4关:阿呆和阿瓜比赛画画,阿瓜比阿呆的3倍少2张。
二、新知引入 知识点1:和倍问题 情景引入:功夫熊猫阿宝的故事:拜师傅——吃包子——练功夫——学拳法 拜师傅:故事发生在很久以前的古代中国,而且要从一只喜欢滚来滚去、滚来滚去的大熊猫身上说起。
话说熊猫阿宝是一家面条店的学徒,虽然笨手笨脚,也勉强算是谋到了一份职业,可是阿宝天天百无禁忌地做着白日梦,梦想着自己有一天能够在功夫的世界里与明星级的大人物进行一场巅峰之战。
别看阿宝所在的“和平谷”一派欣欣向荣的安详景象,其实是一个卧虎藏龙的风水宝地,先不说五大功夫高手皆坐镇于此,更有一大师级别的宗师在这里隐居,可是在一场特殊的比武大会上胜出的人要代表“和平谷”将邪恶的大龙永久地驱除出去,啥都不会的阿宝却在经历了一系列阴差阳错之后屏雀中选,让所有人都大跌眼镜...... 吃包子:师傅买回来60个包子,阿宝和师傅抢着吃,但是师傅功夫特别好,抢到的是阿宝的5倍,阿宝吃了几个包子?练功夫:师傅让阿宝做俯卧撑,阿宝两天才做了30个。
第二天比第一天的2倍还多3个。
那么阿宝第一天和第二天分别做了几个?学拳法:师傅教阿宝拳法,两个月共学了54招。
第二个月学会的招数比第一个月的19倍少6招。
那么阿宝第一个月和第二个月分别学到了几招?和倍问题笔记:和倍问题解题顺序疯狂练习:八戒和悟空比赛吃西瓜,一共吃掉了60个。
(1)如果八戒是悟空的3倍,问两个人各吃了几个?(2)如果八戒是悟空的3倍还多4个,问两人各吃多少个?(3)如果八戒是悟空的3倍少4个,问两个各吃多少个?课本讲解:例1 纺织厂有职工480人,其中女职工人数是男职工人数的3倍,请问:男、女职工各有多少人?练1 某小学有学生1500名,其中男生人数是女生的2倍,请问男生、女生各有多少人?例2 交警一个月共开出78张罚单。
第六讲 和差问题

四年级第六讲和差问题例1:大、小两数的和是206,大数比小数多36,那么大数和小数分别是多少?例2、幼儿园分给大班3箱饮料,每箱24罐,分给小班2箱,每箱也是24罐,大班给小班多少罐饮料后,两个班的罐数就同样多了?例3:哥哥给弟弟15块糖,哥哥还比弟弟多3块糖。
原来哥哥比弟弟多几块糖?例4:甲乙两个桶里共盛水30千克,如果从甲桶里取6千克水倒入乙桶里,两个桶里的水就一样多,问甲乙两桶各有多少千克水?例5:小松期末考试时语文和数学的平均分是92分,数学比语文多得6分,问语文和数学各得了多少分?例6:今年弟弟8岁,哥哥14岁,当两人的年龄和是48岁时,两人的年龄各几岁?例7、把342分为两个数,使两个数的和是两个数的差的9倍,求这两个数各是多少?例8、师傅与徒弟二人4天共做零件264个,又知师傅每天比徒弟每天多做6个,师傅、徒弟每天各做多少个?例9、甲、乙两人同时从A、B两地相对而行,甲每小时行12千米,乙每小时行10千米,两人在相距中点5千米的地方相遇,AB两地相距多少千米?例10、某林场新运来松树、柏树和柳树三种树苗共300棵。
已知松树比柏树多50棵,柏树比柳树多20棵,林场运来松树、柏树和柳树各多少棵?例11、一个顾客买5瓶燕京啤酒,每瓶付15角,退空瓶时,售货员说:每只空瓶子的钱比酒钱少11角,顾客共退回瓶钱多少角?例12、学校买来足球、篮球、排球各一个,现知道足球和篮球共90元;排球和篮球共86元;足球和排球共80元;那么每个足球、篮球、排球各是多少元?练习题:1.填空题(1)某校科技小组共有学生51人,其中男生比女生多5人,这个科技小组有男生()人,有女生()人。
(2)买一个笔记本与一个钢笔共用10元,已知笔记本比钢笔便宜6元,那么买钢笔花了()元,买笔记本花了()元。
(3)哥哥和妹妹共存款720元,哥哥比妹妹多存80元,哥哥存款()元,妹妹存款()元。
(4)小华语文、数学两门功课的平均成绩是95分,数学比语文多8分,语文得了(),数学得了()分。
六年级上奥数第六讲和倍差倍和差问题

第六讲和倍、差倍、和差问题【知识概述】差倍问题:已知两个数的差及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类应用题叫做差倍问题。
基本公式差÷(倍数-1)=较小的数较小的数×倍数=较大的数和倍问题:已知几个数的和与这几个数之间的倍数关系求这几个数的应用题。
基本公式和÷(倍数+1)=较小数(一倍数)较小数×倍数=较大数或:和-较小数=较大数。
和差问题:已知两个数的和与差,反过来求这两个数。
基本公式(和+差)÷2 = 较大的数(和-差)÷2 = 较小的数温馨提示:为了帮助我们理解题意,弄清两种量彼此间的关系,常采用画线段图的方法来表示几种量间的这种关系,以便于找到解题的途径。
【典型例题】例1 甲班和乙班共有图书160本,甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?例2 师傅和徒弟共生产零件190个,师傅生产的个数比徒弟的3倍少10个,师、徒各生产多少个?例3妹妹有课外书20本,姐姐有课外书25本,姐姐给妹妹多少本后,妹妹课外书是姐姐的2倍?例4被除数、除数和商三个数的和是181,商是12,求被除数例5 甲乙丙三数的和是1600,乙数是甲数的2倍,丙数比乙数的2倍多60, 甲乙丙三数各是多少?【我能行】1. 小明、小红两人集邮,小明的邮票比小红多15张,小明的张数是小红的4倍,小明集邮()张,小红集邮()张。
2. 妈妈的年龄比小刚大24岁,今年妈妈的年龄正好是小刚年龄的3倍,今年妈妈()岁,小刚()岁。
3. 名士基地种的花生是白薯的16倍,现在已经知道种的花生比白薯多105棵,种花生()棵, 白薯()棵。
4. 小利的科技书比故事书少16本,故事书是科技书的3倍,小利有科技书( )本,故事书( )本。
5. 甲、乙两个数, 如果甲数加上50, 就等于乙数, 如果乙数加上350就等于甲数的3倍,问甲( ), 乙( ) 。
四年级数学奥数第6讲:和差、和倍问题-教案

星云站备课教员:***第六讲和差、和倍问题一、教学目标: 1. 会判断什么样的应用题属于和差问题.已知两个数的和以及两个数的差,要分别求这两个数就属和差问题,并掌握和差问题的特性,为以后继续学习和倍、差倍问题做准备。
2. 总结归纳出解决和差问题的方法,并解决一些实际问题。
二、教学重点:和差问题是已知大小两个数的和与这两个数的差,求大小两个数各是多少的应用题。
三、教学难点:知道两个数的和,以及它们的差,要求这两个数,解决和差问题需要我们画线段图来分析。
四、教学准备:PPT五、教学过程:第一课时(40分钟)一、外星游记(5分钟)师:同学们在上课之前我们一起来玩一个小游戏吧。
生:好的。
拍三令人数:无限制方法:多人参加,从1-99报数,有人数到“3”的倍数时,不许报数,拍一下桌子,下一个人继续报数。
如果有人报错数或拍错则出局。
奖励:最后剩下的人可以获得大拇指奖励。
师:刚才我们玩的这个游戏和我们学习的知识有一定的联系哦,今天我们要学习的是和差、和倍问题。
(板书课题:和差、和倍问题)师:我们一起去看看吧。
二、星海遨游(30分钟)(一)星海遨游1(10分钟)米德期末考试时语文和数学的平均分数是94分,数学比语文多8分,米德语文和数学各得多少分?师:米德期末考试时语文和数学平均分是94分,那么米德的语文和数学总成绩是多少分呢?生:米德语文与数学的总成绩是94×2=188分。
师:我们知道了总成绩,要想知道语文成绩应该怎么办?生:因为数学比语文多8分,从数学成绩中减去8分,此时语文与数学的成绩相等了。
师:语文成绩为多少?生:(94×2-8)÷2=90(分)。
师:知道了语文成绩,数学成绩是多少分?生:数学成绩为90+8=98(分)。
板书:语文成绩为:(94×2-8)÷2=(188-8)÷2=180÷2=90(分)则数学成绩为:90+8=98(分)答:米德的语文成绩是90分,数学成绩是98分。
和倍、差倍、和差问题解析
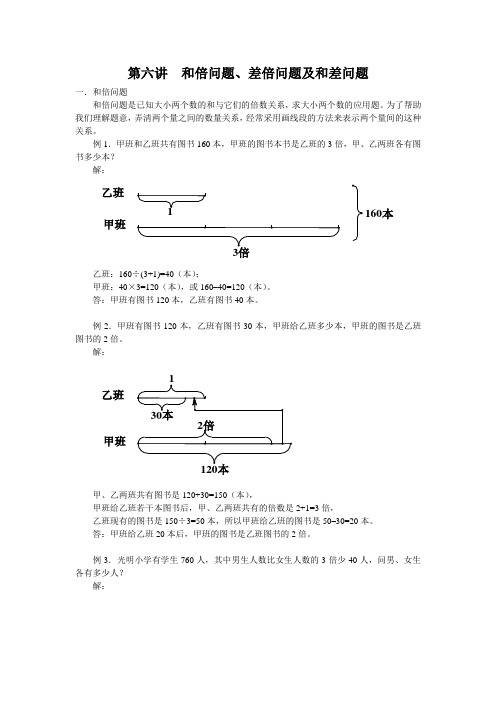
第六讲 和倍问题、差倍问题及和差问题一.和倍问题和倍问题是已知大小两个数的和与它们的倍数关系,求大小两个数的应用题。
为了帮助我们理解题意,弄清两个量之间的数量关系,经常采用画线段的方法来表示两个量间的这种关系。
例1.甲班和乙班共有图书160本,甲班的图书本书是乙班的3倍,甲、乙两班各有图书多少本?解:乙班:160÷(3+1)=40(本); 甲班:40×3=120(本),或160–40=120(本)。
答:甲班有图书120本,乙班有图书40本。
例2.甲班有图书120本,乙班有图书30本,甲班给乙班多少本,甲班的图书是乙班图书的2倍。
解:甲、乙两班共有图书是120+30=150(本),甲班给乙班若干本图书后,甲、乙两班共有的倍数是2+1=3倍,乙班现有的图书是150÷3=50本,所以甲班给乙班的图书是50–30=20本。
答:甲班给乙班20本后,甲班的图书是乙班图书的2倍。
例3.光明小学有学生760人,其中男生人数比女生人数的3倍少40人,问男、女生各有多少人?解:160本甲班乙班甲班乙班女生人数:(760+40)÷(3+1)=200(人),男生人数:200×3–40=560人,或者760–200=560(人)。
答:男生有560人,女生200人。
例4.果园里有桃树、梨树、苹果树共552棵,桃树比梨树的2倍多12棵,苹果树比梨树少20棵,求桃树、梨树和苹果树各有多少棵?解:梨树的棵树:(552+20–12)÷(1+2+1)=560÷4=140(棵); 桃树的棵树:140×2+12=292(棵); 苹果树的棵树:140–20=120棵。
答:桃树、梨树和苹果树分别有292、140、120棵。
例5.549是甲、乙、丙、丁四个数的和,如果甲数加上2,乙数减少2,丙数乘以2,丁数除以2以后,则四个数相等,求四个数各是多少?解:女生760人男生20棵苹果树梨树552棵桃树丙数是:(549+2–2)÷(2+2+1+4)=549÷9=61; 甲数是:61×2–2=120; 乙数是:61×2+2=124; 丁数是:61×4=244。
和差问题讲义

和差问题专题简析:已知大小两个数的和及它们的差,求这两个数各是多少,这类问题我们称为和差问题。
掌握了和差问题的特征和规律,我们解答起来就很方便了。
解答和差问题通常用假设法,同时结合线段图进行分析。
可以假设小数增加到与大数同样多,先求大数,再求小数;也可以假设大数减少到与小数同样多,先求小数,再求大数。
用数量关系表示:(和+差)÷2=大数(和-差)÷2=小数例题1 期中考试王平和李杨语文成绩的总和是188分,李杨比王平少4分。
两人各考了多少分?思路导航:根据题意画出线段图。
我们可以用假设法来分析。
假设李杨的分数和王平一样多,则总分就增加4分,变为188+4=192分,这就表示王平的2倍,所以王平考了:192÷2=96分,李杨考了96-4=92分。
练习一1,两筐水果共重124千克,第一筐比第二筐多8千克。
两筐水果各重多少千克?2,小宁与小慧的身高总和是264厘米,又已知小宁比小慧矮8厘米。
两人分别高多少厘米?3,三(1)班和三(2)班共有学生124人,如果从三(2)班调2人到三(1)班,两班学生同样多。
三(1)班、三(2)班原来各有学生多少人?例题2 某机床厂第一、二两个车间共有车床96部,如果第一车间拨给第二车间8部,那么两个车间车床数相等。
两个车间各有车床多少部?思路导航:用线段图表示题意。
已知第一、二两个车间共有车床96部,又根据“如果第一车间拨给第二车间8部,两个车间车床数相等”,从线段图上我们可以看出第一车间原来比第二车间多8×2=16部车床。
所以,第一车间原有:(96+8×2)÷2=56部,第二车间原有56-8×2=40部。
练习二1,红星小学一年级新108人,分成甲、乙两个班。
如果从甲班转3个学生到乙班去,两班学生就一样多。
甲、乙两班各有学生多少人?2,甲、乙两筐共有水果80千克,若从甲箱取出6千克放到乙箱中,这时两箱水果同样多。
【小学三年级数学】和差问题

第六讲和差问题目录:1、题型分类2、知识点总结使用说明3、本讲重要知识点一、题型分类1、什么是和差问题,以及和差问题的方法、公式;2、基本和差问题;3、和差不对应;4、暗和、暗差问题;二、使用说明“重要知识点”部分的作用:梳理、复习。
本部分用来梳理本讲的主要知识,孩子们可以通过本部分内容的查看复习本讲所学内容.三、重要知识点【一】和差问题、和差问题的方法、公式1、什么是和差问题已知两个数的和及它们的差,求这两个数分别是多少?2、和差问题的方法(1)思路:变成一样多(2)方法(工具):线段图3、和差问题的公式(1)(和+差)÷2=大数和-大数=小数(2)(和-差)÷2=小数和-小数=大数例题演示:两筐水果共重100千克,第一筐比第二筐少10千克,两筐水果各多少千克?解析:(1)线段图:(2)方法一:把第二筐多的10千克减掉,看成两个第一筐的重量来计算;列式:第一筐:(100-10)÷2=45(千克),第二筐:45+10=55(千克)。
方法二:把第一筐少的10千克补上,看成两个第二筐的重量来计算;列式:第二筐:(100+10)÷2=55(千克),第一筐:55-10=45(千克)。
例题演示:大明和小明各自保持相同的速度跑步,大明每分比小明多跑20米,他们两人用时3分一共跑了540米,大明和小明每分各跑多少米?解析:(1)3分一共跑了540米,那么两人1分一共跑了540÷3=180(米);(2)线段图:(3)方法一:小明:(180-20)÷2=80(米),大明:80+20=100(米)。
方法二:大明:(180+20)÷2=100(米),小明:100-20=80(米)。
【二】基本和差问题【三】和差不对应【四】暗和、暗差问题例题1演示(暗和:平均数):艾迪在期中考试中,数学、语文两科的平均分是90分,数学比语文多10分,那么艾迪数学和语文各得了多少分?解析:(1)数学语文成绩之和:90×2=180(分),数学语文成绩之差:10分;(2)线段图:方法二:数学:(180+10)÷2=95(分),语文:95-10=85(分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
和差问题
1、
有什么办法可以让和一样多呢?
圆形和三角形原来一共有()个,增加2个圆形后,两种图形的个数一样多,两种图形的总数变成了()个,也就是()个的2倍。
圆形和三角形原来一共有()个,去掉2个三角形后,两种图形的个数一样多,两种图形的总数变成了()个,也就是()个的2倍。
2、动手操作:
要求:请从奥数教程书上翻出两个页码,使这两个页码的和是121,请找到这两页分别是多少?
例题
1、刘晓每天早晨沿长和宽相差40米的操场跑步,每天跑6圈,共跑2400米。
这个操场的长和宽分别是多少米?
2、今年小勇和妈妈两人的年龄和是38岁,3年前,小勇比妈妈小26岁。
今年妈妈和小勇各多少岁?
3、两个连续奇数的和是36,这两个奇数分别是多少?
4、两筐梨子共有120个,如果从第一筐中拿10个放到第二筐中,那么两筐的梨子个数相等。
两筐原来各有多少个梨?
5、期末考试,小红语文和数学的平均分是93分,而数学比语文多6分,小红语文数学各考了多少分?
6、甲乙两个仓库共有大米800袋,如果从甲仓库中取出25袋放到乙仓库中,则甲仓库比乙仓库还多8袋。
两个仓库原来各有多少袋大米?
7、四年级3个班共有136人,已知一班比二班多3人,二班比三班少4人,求三个班各有多少人?
8、有甲乙丙3人称体重,如果每两人一起称,甲乙重83千克、乙丙重85千克、甲丙重86千克。
问其中最轻的人有多重?
9、在一个减法算式里,被减数、减数与差这3个数的和是388,减数比差大16,则减数等于几?
10、甲乙两校共有学生1050人,部分学生由于搬家需要转学,结果由甲校转入乙校20人后,甲校比乙校多10人,两校原来有学生多少人?。
