透视学(三)
透视学三点透视解释

透视学三点透视解释透视学三点透视解释:所谓三点透视就是物体有三个消失的地方,分别在眼睛、手和脑子里。
要注意的是,从各种透视图中找出来的消失点和实际消失点不完全相同。
要弄清楚消失点问题,还得知道点的位置。
通常我们把物体上两个面交线(即二点透视的消失线)称为“消失点”。
当消失点都画在某一边或某一角上,这个透视就叫作“平行透视”。
三点透视又分为三类: 1、消失于无限远处的透视——离开人眼无限远的距离仍然可以感觉到物体的存在。
例如地平线就是这样一条线,它虽然很长但由于离开了人的眼睛而感觉不到了,只有当把目光投向大海,才能真正看到它的存在。
在海平面以下,人眼是看不见物体的。
2、消失于无限近处的透视——离开人眼无限近的距离仍然可以感觉到物体的存在。
例如观察一枚硬币,人眼是看不见硬币的。
一般在画透视图时,都采用平行透视,但有些作品为了更好地表现形象,强调空间感,还是经常使用其他的透视形式,如成角透视,圆形透视,倾斜透视等。
画好透视图的关键是要做到以下几点:(1)首先要确定立体的主体及其基本比例。
(2)要了解画透视的目的是什么,如是表现近大远小的效果,还是表现景物纵深远近关系,还是仅供临摹参考等。
(3)其次是确定明暗交界线的位置和形状。
(4)第三步是定出中心线。
(5)最后要合理安排透视的次序。
1、用数学家欧几里得提出的假想线画一个圆,再把这个圆当作物体,然后用直尺将圆的四周封闭,形成一个圆柱体。
(2)看一个矩形放在哪里,就用数学家欧几里得提出的假想线把矩形框起来,然后再去观察这个矩形。
2、如图是一张屋内平面图,从屋顶、地面与窗户上看到的窗外景物图。
(1)先看一看:看得到屋顶吗?看得到地面吗?看得到窗户吗?(2)先在地面上选一点作为a点,看一看是否平行于地面。
(因为当墙角成为30°的锐角时,它就会变成一条直线,此时便没有可看的地面)(3)移动a点,重新确定b点,移动c点,并将透视线沿着窗台的方向延伸。
透视学三点透视解释

透视学三点透视解释一、透视学的定义透视学,又称“视学”,是绘画透视基础理论的总称。
包括三种透视,即平行透视、成角透视、倾斜透视。
1.平行透视即在同一个面上,把两个以上的物体看成一个整体的透视方法。
最常见的是一点透视。
2.成角透视是把物体向两边看成倾斜角度,所产生的透视现象。
最常见的是两点透视。
3.倾斜透视是把物体向前后左右都看成倾斜角度,所产生的透视现象。
最常见的是三点透视。
二、三点透视的特征( 1)在作画时,将三点透视或者更多点(即几何透视)依次安排在同一个面上,分别观察三点透视中各物体与其它物体的关系,将三个物体间相互关系的点之坐标及位置连线,就形成了立体感很强的画面。
( 2)在作画时,可运用其中任何一种透视来表现物体,使形象富有真实感。
( 3)不能认为几何透视一定要平行画面。
如构图上把山峰的外轮廓画得比较具体而明显,而内部的山头却虚掉,这样从远处看过去会出现一座漂亮的空中楼阁的透视效果。
( 4)几何透视不能成为不变的法则。
例如黄金分割法。
二、三点透视的特征( 1)在作画时,必须按照正确的规律进行画面结构的安排。
不然会出现偏差,造成透视失误。
( 2)只有一点透视才能准确地表现物体的透视现象,它在透视学中占据统治地位,只要将一点透视运用到极限,所获得的效果也是逼真的。
( 3)物体的透视变化有一个限度,超过这个限度,便会失去真实性。
三、三点透视的应用( 1)石膏像的透视法: a。
先画出石膏像的大致形状,再根据石膏像的尺寸设计好衣纹; b。
沿着衣服纹路勾勒出人物身躯的骨骼; c。
继续刻画细节,并加深暗部色调,注意眼睛、嘴巴等重点部位的塑造; d。
完善石膏像的动态姿势,增添神情气韵。
( 2)建筑模型的制作:首先选择合适的材料,做好模型的底板,利用纸壳的厚度调整好模型的体积感。
为了塑造好石膏像的体积感,可在底板上贴双面胶,这样既保证了足够的厚度,又便于拆卸模型。
为了防止石膏像的水口不好,破坏模型,还可利用彩色笔在背面涂抹,使水口附近的肌肉看起来更自然。
透视学

透视学基本原理一、基本术语:、1视平线:就是与画者眼睛平行的水平线。
2、心点:就是画者眼睛正对著视平线上的一点。
3、视点:就是画者眼睛的位置。
4、视中线:就是视点与心点相连,与视平线成直角的线。
5、消失点:就是与画面不平行的成角物体,在透视中伸远到视平线心点两旁的消失点。
6、天点:就是近低远高的倾斜物体(房子房盖的前面),消失在视平线以上的点。
7、地点:就是近高远低的倾斜物休(房子房盖的后面),消失在视平线以下的点。
8、平行透视:就是有一面与画面成平行的正方形或长方形物体的透视。
这种透视有整齐、平展、稳定、庄严的感觉。
9、成角透视:就是任何一面都不与平行的正方形成长方形的物体透视。
这种透视能使构图较有变化。
二、透视类型:1、单点透视又称为平行透视,由於在透视的结构中,只有一个透视消失点,因而得名。
平行透视是一种表达三维空间的方法。
当观者直接面对景物,可将眼前所见的景物,表达在画面之上。
通过画面上线条的特别安排,来组成人与物,或物与物的空间关系,令其具有视觉上立体及距离的表象。
2、两点透视又称为成角透视,由於在透视的结构中,有两个透视消失点,因而得名。
成角透视是指观者从一个斜摆的角度,而不是从正面的角度来观察目标物。
因此观者看到各景物不同空间上的面块,亦看到各面块消失在两个不同的消失点上。
这两个消失点皆在水平线上。
成角透视在画面上的构成,先从各景物最接近观者视线的边界开始。
景物会从这条边界往两侧消失,直到水平线处的两个消失点。
3、三点透视又称为斜角透视,是在画面中有三个消失点的透视。
此种透视的形成,是因为景物没有任何一条边缘或面块与画面平行,相对於画面,景物是倾斜的。
当物体与视线形成角度时,因立体的特性,会呈现往长、阔、高,三重空间延伸的块面,并消失於三个不同空间的消失点上。
三点透视的构成,是在两点透视的基础上多加一个消失点。
此第三个消失点可作的为高度空间的透视表达,而消失点正在水平线之上或下。
如第三消失点在水平线之上,正好象徵物体往高空伸展,观者仰头看著物体。
第三章 透视的基本原理和规律

二、 透视的基本规律
1. 近大远小 相同大小、长短、高低的物体,距离观察者近的大、长、高;距离观察者远的 小、短、低。确定物体近大远小是以物体离开画面的距离为标准的。
2. 近者清晰远者模糊 我们在写生中经常发现距离我们近的物体比较清晰,离我们远的物体就要模糊 一些,这种现象的产生主要就是近距离的物体进入视网膜的图像大,受刺激 的细胞多,所以眼睛看到的物体就会清晰,反之,远处的则会模糊。同时近 者清晰远者模糊受到大气,风、雪、雾等自然条件的影响,这些因素结合起 来,就会产生近者清晰远者模糊的现象。
图3-5 透视常用术语
图3-6 原线变线
二、 透视的种类
(一) 平行透视
在一个立方体的六面当中,只要有一个面与画面平行,那么它的变线 (共四条)在画面中消失于灭点(心点)的作图方法叫做平行透视,又称一 点透视。如图3-6所示,平行透视的立方体,无论位置高低、远近,在正常的 视圈以内,正面都是正方形,只有大小上的变化,没有透视变化。
1485年意大利画家弗朗西斯卡 写的《绘画透视学》,系统地阐明
图3-2 逃亡埃及 [意] 乔托
了空间表达的规律,即 用平面来做透视图的方 法。16世纪达芬奇《画 论》一书,把解剖、透 视、明暗和构图等零碎 的知识归纳成系统的理 论。并将透视分为三种: 线透视(形体)、空气 透视( 色彩)、隐没 透视(阴影)。,如图 3-3 所 示 , 达 芬 奇 1495 年开始绘制的壁画《最
图3-4 画家画曼陀林 [德] 丢勒
小,迫目以寸,则其形莫睹,回以数里,则可围于寸眸。诚去之稍阔,则其 见弥小。今张绡素以远映,则昆阆之形,可围于方寸之内。竖画三寸,当千 仞之高;横墨数尺,体百里之遥。”概括论述了近大远小透视规律和在绘画 中的运用半透明的薄绸做透视画面的方法。
简单易懂的透视知识图片解读美术绘画中的透视原理
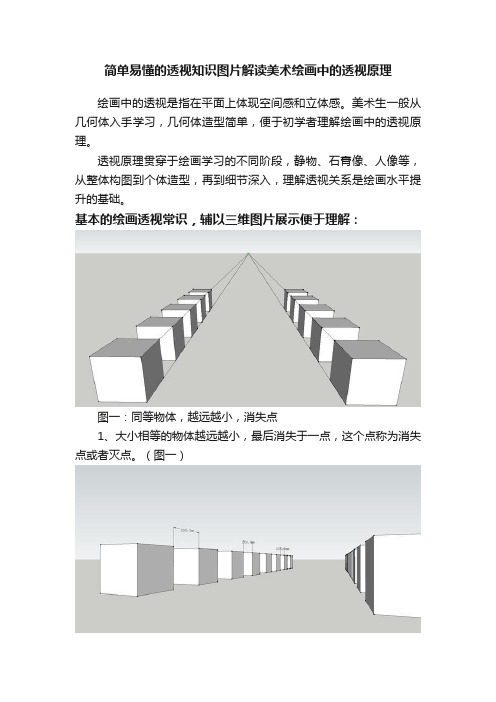
简单易懂的透视知识图片解读美术绘画中的透视原理
绘画中的透视是指在平面上体现空间感和立体感。
美术生一般从几何体入手学习,几何体造型简单,便于初学者理解绘画中的透视原理。
透视原理贯穿于绘画学习的不同阶段,静物、石膏像、人像等,从整体构图到个体造型,再到细节深入,理解透视关系是绘画水平提升的基础。
基本的绘画透视常识,辅以三维图片展示便于理解:
图一:同等物体,越远越小,消失点
1、大小相等的物体越远越小,最后消失于一点,这个点称为消失点或者灭点。
(图一)
图二:距离相等,越远越短
2、距离相等的景物越远,它们之间的距离越短。
(图二)
图三:视平线
3、观察者眼睛同高而平行的线叫视平线。
(图三)
图四:视平线以上和视平线以下对比
4、比观察者眼睛低的物体,在视平线以下,看到它的上面。
(图四)
5、比观察者眼睛高的物体,在视平线以上,看到它的下面。
(图四)
图五
6、位置在观察者右方的物体,看见它的左侧。
(图五)
7、位置在观察者左方的物体,看见它的右侧。
(图五)。
透视学

1平行透视(二)
物体 (侧面) 画面 眼睛—视点
地面
侧视图
2成角透视(一)
物体 画面 眼睛—视点
俯视图
2成角透视(二)
物体 (侧面) 画面 眼睛—视点
地面
侧视图
成角透视图例
3 倾斜透视 — 平 行 转 为 倾 斜 ( 前 倾 )
物体 (侧面) 画面 眼睛—视点
地面
侧视图
3倾斜透视—平行转为倾斜(后倾)
物体 (侧面) 画面 眼睛—视点
地面
侧视图
3倾斜透视—成角转为倾斜(前倾)
物体 (侧面) 画面 眼睛—视点
地面
侧视图
3倾斜透视—成角转为倾斜(后倾)
物体 (侧面) 画面 眼睛—视点
地面
侧视图
四、眼睛的三种位置
1高低
2左右
3前后
1高低 —— 视平线的变化
画面 物体 (侧面)
眼睛—视点
地面
侧视图
至天点
至地点
1倾斜透视的规律和画法
至天点
1倾斜透视的规律和画法
至地点
4圆形的透视画法
5物体高度的空间定位
七、作
1平行透视作业 2成角透视作业 3圆形透视作业
业
1张 1张 1张
4人在不同的空间位置上
的高度定位作业
1张
透
视
一、透视的概念
•透视是一种视觉现象
•透视是关于透视现象变化规律的科学
•透视是一种按照透视变化规律来表现
物象空间感觉的绘画技法
二、透视基本原理
透视原理示意图
画面 物体 眼睛—视点
三、物体的三种角度
1平行
2成角
3倾斜
立 方 体
达芬奇论绘画之透视篇

达芬奇论绘画之透视篇第三篇——透视学达芬奇把透视分为三个分⽀;线透视、空⽓透视与隐没透视。
线透视(即利⽤光线沿直线进⾏这⼀基本原理,阐明物体为什么愈远显得愈⼩的透视学),在希腊数学家欧⼏⾥得、⼗三世纪波兰学者维帖罗的著作中,已有论及。
在⽂艺复兴初期的建筑家布鲁涅尼斯奇和画家佛兰切斯卡等⼈的研究下,则发展得相当完备。
芬奇以前的学者主要从天⽂观测和地⽂观测的⾓度研究空⽓透视,他们认为介于眼睛和物体之间的媒介影响了⼈们对物体形状、⼤⼩、颜⾊等属性的认识,是—种消极因素,研究空⽓透视的闩的就在于寻求消除“视觉欺骗”的⽅法。
芬奇却是从画家的⾓度研究这⼀个题⽬,研究怎杆利⽤空⽓透视以补充线透视的不⾜,他认为绘画拥有空⽓透视是画胜于雕塑的⼀个⽅⾯。
空⽓透视名⾊彩透视。
眼睛接受物象是⼀个物理过程,同时也是⼀个⽣理过程。
线透视只是⼏何光学,不能说明物体在远处变得模糊不清(即我国王维所指的远⼈⽆⽬、远树⽆枝、远⼭⽆⽯、远⽔⽆波等现象)的理由,这是物理光学和⽣理光学的问题。
在这⽅⾯芬奇做了许多观察,研究了⼈对物体的视觉印象如何随距离变化,总结出⼀些经验规律,要求画家们在作画时遵守隐没透视。
从理论上阐明隐没透视的学理,则是晚到⼗九世纪的事。
透视〔总论)透视学是绘画的缰辔和舵轮。
透视学就其与绘画的关系⽽⾔可分为三个主要部分。
第⼀部分是缩形透视,研究物体在不同距离处的⼤⼩。
第⼆部分研究这些物体的颜⾊的淡褪。
第三部分研究物体在不同距离处清晰度的减低。
透视有三个分⽀:第⼀个分⽀研究物体远离眼睛时看来变⼩的原因,称为缩形透视。
第⼆个分⽀研究颜⾊离眼远去时变化的⽅式。
第三,也就是最后⼀个分⽀,阐明物体何以愈远愈模糊。
名称如下:线透视、⾊透视与隐没透视。
透视有这样的性质,它使平的物体显出浮雕,⽽使浮雕物体显得平坦。
在研究⾃然过程的各种学问之中,光的研究给研究者最⼤的愉快。
在教学的主要特征之中,最有⼒的提⾼了研究者的精神的乃是数学证明的确切性。
透视图基本知识

心点,就是画者眼睛正对着视平线上的一点。 距点,距点在视平线上主点左右两边,两者离主点的距离
与画者至心点的距离相等,凡与画面成45度角的直线,一 定消失在距点。
透视学的常用术语
余点,在视平线上心点两旁与画面形成任意角度(除45 度及90度)的水平线段的消失点,它亦是成角透视的消 失点。
2.2 两点透视(成角透视)
F2 F1
S
立方体的主要表 面与画面倾斜, 但其上的铅垂线 与画面平行,所 作的透视图有两 个灭点,称为两 点透视(成角透 视)。
平行透视
2.3 三点透视(斜透视)
F F
F E
e
长、宽、高三个方向 与画面均不平行时, 所作的透视图有三个 灭点,称为三点透视 (斜透视) 。
体越远越高,心点左右的物体越远越向心点靠 拢,最后消失于心点。
二、平行透视的条件和规律
(二)平行透视的规律 4. 平视中的平行透视只有一个灭点,就是心点,
在画面中心。 5. 方形体中只有一个面距离观察者最近。
三点透视
概念: 就是立方体相对于画面,其面及棱线都不平行
时,面的边线可以延伸为三个消失点,用俯视 或仰视等去看立方体就会形成三点透视。
透视图基本知识
三点透视
透视学的基本常识
透视学的概念 透视的三要素 透视的三种类型 透视学的常用术语和基本原理 透视的正确表现
透视学
教学内容 基本概念 平行透视 成角透视 倾斜透视 曲线透视
应用透视
透视学的概念
“透视”一词原于拉丁文“perspclre”(看透)。最初研究 透视是采取通过一块透明的平面去看景物的方法,将所见景 物准确描画在这块平面上,即成该景物的透视图。后遂将在 平面画幅上根据一定原理,用线条来显示物体的空间位置、 轮廓和投影的科学称为透视学。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.不同平面与斜面的组合透视 4.不同平面与斜面的组合透视
平视时,与地面平行与画面垂直或成角方向的透视会消失主点、距点、余点, 平视时,与地面平行与画面垂直或成角方向的透视会消失主点、距点、余点, 而与地面倾斜与画面倾斜不同方向的透视倾面会消失不同天点和地点, 而与地面倾斜与画面倾斜不同方向的透视倾面会消失不同天点和地点,这个 天点和地点的方向和位置是根据倾面倾斜位置和角度而定。 天点和地点的方向和位置是根据倾面倾斜位置和角度而定。可先求底际面的 方向和消失点再求天点或地点位置。 方向和消失点再求天点或地点位置。不同透视平面的组合会产生复杂多消失 的组合性透视图。 的组合性透视图。 成角透视的平面与上斜成角透视、下斜成角透视的组合。 成角透视的平面与上斜成角透视、下斜成角透视的组合。
第四节
倾斜透视
三.倾斜透视的特征
1.在倾斜透视中,方形平面与基面和画面都不会平行,也都不 会垂直。 2.在倾斜透视中,视向是平视,方形物体的透视斜面,上斜其 消失点是天点,下斜其消失点是地点。 3.天点和地点离开斜边底际线的天点(主点或余点)的远近取 决于斜边斜度的大小,斜度大则远,斜度小则近。 4.对称的桥梁、屋顶、斜坡的斜面,无论在视平线位置高低、 左右,只要倾角相等,它的天点和地点离视平线(地平线) 距离相等。 5.同一斜面内的变线的消失 点在同一斜面天线上。
定画幅、视高、视平线、主点,视距, V1V2点,M1M2测点,V1垂线,M1测点量上、 下两个30°角的线,延长交得天点、地 点。在基线上定最近点A,房屋长7cm线 段AB,量房屋宽3cm线段AC,高4cm线段 AD,用测点法画出长方体ADEFIHJG。
3.台阶画法 3.台阶画法
用已知条件分割法作台阶斜 面 已知画幅 已知画幅 8cm,h=5cm, 7×8cm,h=5cm,主点离画 面左框朝右3cm 3cm, 面左框朝右3cm, 最近点左 台阶左成60 60° 1cm ,台阶左成60°角,右 30° 成30°角,求作台阶倾斜透 视图。 视图。
透 视 学
Pe r spi ce r e
第四节
倾斜透视
一.倾斜透视的形成
当我们以平视的视向写生观察时, 当我们以平视的视向写生观察时,方形平面倾斜 于地面并与画面也倾斜的斜面, 于地面并与画面也倾斜的斜面,它们互相平行的边线是变 会发生透视变化,集中会消失在天点或地点上。 线,会发生透视变化,集中会消失在天点或地点上。如桥 斜坡、屋顶和楼梯等。 梁、斜坡、屋顶和楼梯等。
倾斜透视
五.天点、地点与主点、距点、余点的关系 天点、地点与主点、距点、
天点和地点的位置始终跟着底际面的主点、距点、余点。 天点和地点的位置始终跟着底际面的主点、距点、余点。 当上斜平行透视时,天点、地点的主点在垂线上, 当上斜平行透视时,天点、地点的主点在垂线上,当倾面 向左上斜或下斜时,天点和地点消失在视垂线左面距点、 向左上斜或下斜时,天点和地点消失在视垂线左面距点、 余点垂线上;当倾面向右上斜或下斜时, 余点垂线上;当倾面向右上斜或下斜时,天点和地点消失 在视垂线的右面距点、余点垂线上。 在视垂线的右面距点、余点垂线上。因它们是垂直投影关 不能主观另取偏离主点、距点、 系,不能主观另取偏离主点、距点、余点垂线位置的天点 和地点。 和地点。
第四节
倾斜透视
二.倾斜透视的概念
方形物体(正方形)与地面、 方形物体(正方形)与地面、画面倾斜成一定角 存在一组斜边消失在天点或地点的透视。 度,存在一组斜边消失在天点或地点的透视。
第四节
倾斜透视
二 .倾斜透视的概念 方形平面有一对与 基面平行的边叫平边, 基面平行的边叫平边, 平边 另一对与基面倾斜的 斜边, 边叫斜边 边叫斜边,斜面的平 面投影叫底迹面 底迹面, 面投影叫底迹面,底 迹面的边线由平边和 斜边底迹线组成。 斜边底迹线组成。
定画幅、视高、视平线、主点, 最远角2倍定X距点,画视垂线。 根据斜面与地面倾斜30°角,在 六.倾斜透视图的基本画法 视平线的X处,用量角器量30°角, 2.定角度的倾斜面的画法 2.定角度的倾斜面的画法 并与视垂线相交的天点为消失点 位置。画正方形AB在基线上居中, 画斜面时先求底际面(如原来斜面是正方形, 画斜面时先求底际面(如原来斜面是正方形,底际面就是 并消失主点。量XF线上实际正方 缩短的长方形),然后画垂线(平视时垂线是原线) ),然后画垂线 缩短的长方形),然后画垂线(平视时垂线是原线)切割 形边长尺寸4cm=XF,用直角尺在 视平线画垂线,得到XF的底际面 斜边的透视深度。 斜边的透视深度。 的长度XG,取XG底际线,在AB线 上斜平行透视图 上量出AG'(底际线比斜线短), G点与X距点相连交得A'点得到底 已知画幅7 8cm,h=5cm,主点居中,正方形斜面居中, 已知画幅7×8cm,h=5cm,主点居中,正方形斜面居中,边 际面的透视深度,从A'点画水平 长为4cm 斜面与地面倾斜30 4cm, 30° 求作上斜平行透视图。 长为4cm,斜面与地面倾斜30°角,求作上斜平行透视图。 线交得B'点,底际面就求出了。 A、B两点出发与天点相连,分别 以A'B'两点画垂线与斜线相交得 CD两点斜面透视深度,将CD两点 连接,最后将斜面ABCD画重,完 成。
பைடு நூலகம்
第四节
倾斜透视
六.倾斜透视图的基本画法
1.X距点、 1.X距点、M测点在倾斜透视中的运用 距点 我们知道在平行透视中测深度用X距点, 我们知道在平行透视中测深度用X距点,在成角透视中测深 度用M测点,而在倾斜透视中, 距点和M 度用M测点,而在倾斜透视中,X距点和M测点分别具备两种 功用。一是测透视深度,二是测天点或地点的透视高度。 功用。一是测透视深度,二是测天点或地点的透视高度。
将D、H两点连接天点, 将F、G两点连接地点并延 长交得K、N两点,K、N两 点连接消失V2点。(方法 二:当有已知屋顶到地面 的高度尺寸,可用AF与ED 相交的求中法并从中点画 垂线再量A点的垂线房屋 高度,与V1点相连,可交 得K点,另外N点可通过H、 G消失地点和天点并延长, K点消失V2得到。)最后 需要的线加重。
第四节
倾斜透视
四.倾斜透视的分类
3.成角上斜。每一对边与画面都不平行, 3.成角上斜。每一对边与画面都不平行,且有一对边与画面成 成角上斜 近低远高。 近低远高。 4.成角下斜 每一对边与画面都不平行, 成角下斜。 4.成角下斜。每一对边与画面都不平行,且有一对边与画面成 近高远低。 近高远低。
第四节
将A、D两点消失 地点,E、F两点向 下画垂线与两根消失 线相交得J、K两点, 将两点相连并消失 V1点。最后将ADKJ 的斜面画重,完成。
3.房屋画法 3.房屋画法
根据示意,已知画幅7 8cm,h=5cm,主点离画面左框右3cm,最近点左1cm, 根据示意,已知画幅7×8cm,h=5cm,主点离画面左框右3cm,最近点左1cm, 3cm 1cm 房屋左成60 60° 右成30 30° 7cm, 3cm,墙高4cm 屋顶与地面左上、 4cm, 房屋左成60°角,右成30°角,长7cm,宽3cm,墙高4cm,屋顶与地面左上、 下倾斜30 30° 求作房屋倾斜透视图。 下倾斜30°角,求作房屋倾斜透视图。
第四节
倾斜透视
四.倾斜透视的分类
根据斜面与画面的关系,一般将倾斜透视分为: 根据斜面与画面的关系,一般将倾斜透视分为: 1.平行上斜 有一对边与基面和画面都平行, 平行上斜。 1.平行上斜。有一对边与基面和画面都平行,另一对边与画面 成近低远高。 成近低远高。 2.平行下斜 有一对边与基面和画面都平行, 平行下斜。 2.平行下斜。有一对边与基面和画面都平行,另一对边与画面 成近高远低。 成近高远低。
第四节
倾斜透视
已知画幅7 8cm,h=6cm,主点离画幅左边框朝右3cm 3cm, 定画幅、视高、视平线、主 下斜平行透视图 已知画幅7×8cm,h=6cm,主点离画幅左边框朝右3cm,最近 点在右2cm 基线上方3cm 贴切画幅,斜面边长4cm 斜面与画面左成40 2cm。 3cm, 4cm; 40° 点在右2cm。基线上方3cm,贴切画幅,斜面边长4cm;斜面与画面左成40° 点,视距,左右成角角度V1V2 右成50 50° 斜面与地面倾斜40 40° 求作下斜成角透视图。 点、M1M2测点,V2点画垂线。 角,右成50°角,斜面与地面倾斜40°角;求作下斜成角透视图。 定最近点A,画水平线,定 AB=AC=4cm,A点出发消失V1V2 点,在视平线M2点上用量角器 量出与地面倾斜角度40°与V2 垂线相交得地点,在M2视平线 上量边长为4cm的M2G线段并画 垂线得M2H的底际线长度,将 M2H长度移至AC线段上,得 AH’,B、H'点测深度得D、E 两点透视深度,DE两点消失 V2V2点交得F点,ADFE底际面 画成了。
图1,天点、地点 天点、 位于主点的垂直上、 位于主点的垂直上、 下方所引变线的底 际线、 际线、面与画面成 90°角的垂直关系。 90°角的垂直关系。 天点、 图2,天点、地点 位于X 位于X距点的垂直 上、下方所引变线 的底际线、 的底际线、面与画 面成45 角的关系。 45° 面成45°角的关系。 天点、 图3,天点、地点 位于V 位于V余点的垂直 上、下方所引垂线 的底际线、 的底际线、面与画 面成除45 45° 90° 面成除45°、90° 角以外的余角关系。 角以外的余角关系。
