测量平差试题

测量平差试题一
一、 正误判断。正确“T ”,错误“F ”。(20 分) 1.在测角中正倒镜观测是为了消除偶然误差( )。
2.在水准测量中估读尾数不准确产生的误差是系统误差( )。 3.观测值与最佳估值之差为真误差( )。
4.系统误差可用平差的方法进行减弱或消除( )。 5.权一定与中误差的平方成反比( )。
6.间接平差与条件平差一定可以相互转换( )。
7.在按比例画出的误差曲线上可直接量得相应边的边长中误差( )。
8.对于特定的平面控制网,如果按条件平差法解算,则条件式的个数是一定的,形式是多样的( )。 9.定权时0σ可任意给定,它仅起比例常数的作用( )。
10.设有两个水平角的测角中误差相等,则角度值大的那个水平角相对精度高( )。 二、 用“相等”或“相同”或“不等”填空(8 分)。
已知两段距离的长度及其中误差为300.158m ±3.5cm; 600.686m ±3.5cm 。则: 1.这两段距离的中误差( )。
2.这两段距离的误差的最大限差( )。 3.它们的精度( )。 4.它们的相对精度( )。
三、 选择填空。只选择一个正确答案(25 分)。 1.取一长为d 的直线之丈量结果的权为 1,则长为D 的直线之丈量结果的权D P =( )。
a) D d b) d D c) 22D d d) 22d
D
2.有一角度测 20 测回,得中误差±0.42 秒,如果要使其中误差为±0.28秒,则还需增加
的测回数N=( )。
a) 25 b) 20 c) 45 d) 5 3.某平面控制网中一点P ,其协因数阵为:?
?????=YY YX XY XX XX Q Q Q Q Q =??
????--5.025.025.05
.0 单位权方差2
0σ =±2.0。则P 点误差椭圆的方位角 T=( )。 a) 90 b) 135 c) 120 d) 45
4.设L 的权为1,则乘积4L 的权P=( )。
a) 1/4 b) 4 c) 1/16 d) 16
5.设?????
?21y y =????????????--213112x x ;??????=4113XX D ,设F = y2+ x1,则2
F m =( )。 a) 9 b) 16 c) 144 d) 36
四、某平差问题是用间接平差法进行的,共有 10 个独立观测值,两个未知数,列出 10 个误差方程后得法方程式如下(20分):
???????
?
??????--∧∧
2182210x x =??????--146 且知[pll]=66.0。求:
1. 未知数的解 2. 单位权中误差0m 3. 设F = ∧
∧
+2134x x ;求
F
p 1
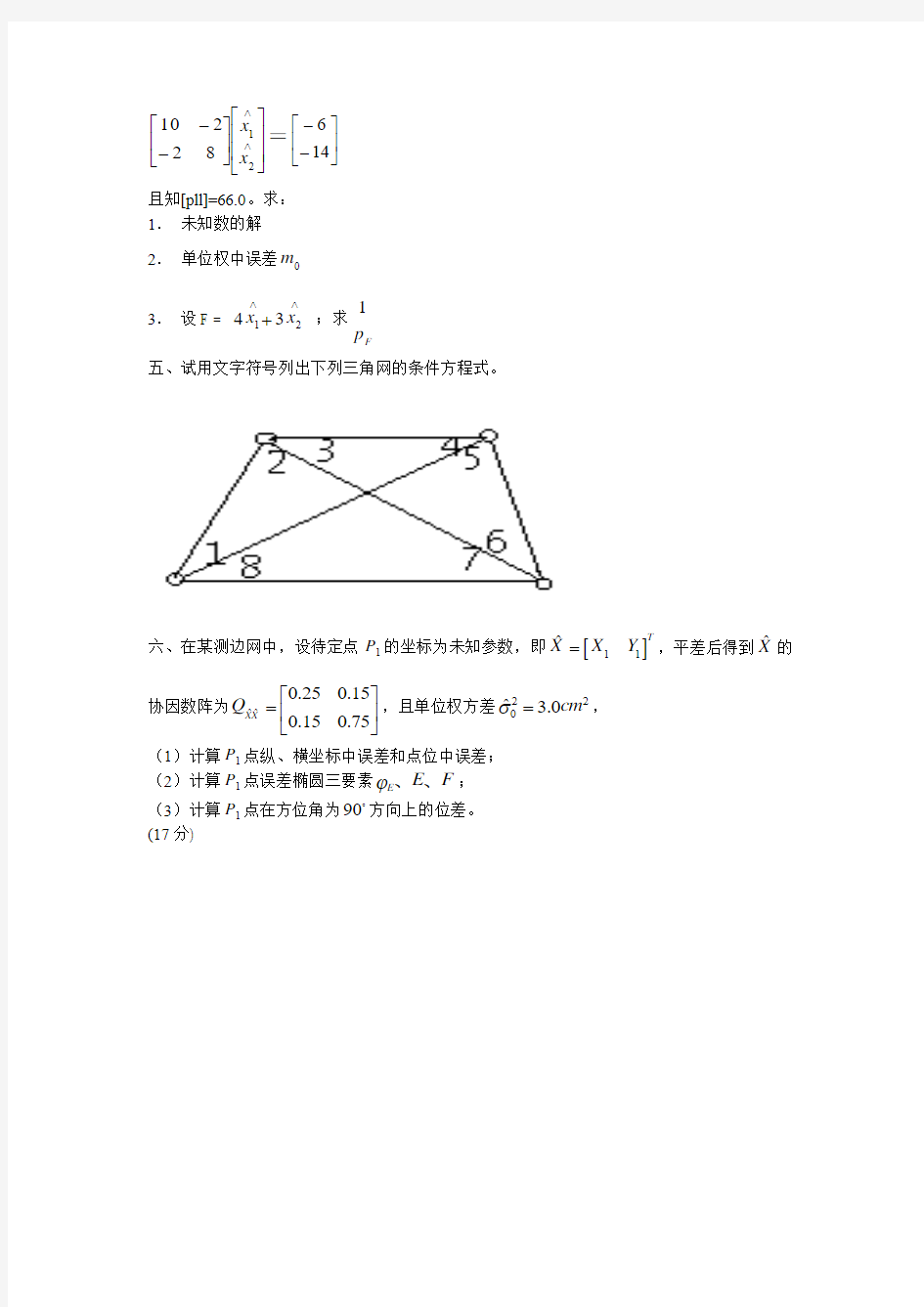
五、试用文字符号列出下列三角网的条件方程式。
六、在某测边网中,设待定点P 1的坐标为未知参数,即[]1
1?T
X X Y =,平差后得到?X
的协因数阵为??0.250.150.150.75XX Q ??=?
?
??
,且单位权方差2
20? 3.0cm σ=, (1)计算P 1点纵、横坐标中误差和点位中误差; (2)计算P 1点误差椭圆三要素E E F ?、、; (3)计算P 1点在方位角为90
方向上的位差。 (17分)
试题一答案
一、FFFFT TTTTF
二、相等 相等 相同 不等 三、aabcd
四、0=-∧
BPl x PB B T
??????
--=??????--??
????--=-∧
21146822101
x
2、t
n PV
V T -±=0σ
?????
?
--????
??---=-=∧
-2114666)(1x PB B pl l PV V T
t
T
=32 其中 n =10,t = 2
8
32
0±
=σ2±= ][??
?
???
?
=222
134σσFF
Q ?????
?34 021σσσ==
F
p 1=FF Q =25
五.
六. (1
)???1.5x y p cm σ
σ
σ===,, (2) 1.540.79E E cm F cm ?==
=74.5或254.5,,
(3)90? 1.5cm ψσ
==
014321
=++++w v v v v 028765
=++++w v v v v 048877665544332211=+-+-+-+-w v ctgL
v ctgL v ctgL v ctgL v ctgL v ctgL v ctgL v ctgL 038721
=++++w v v v v
测量平差复习题及答案
测量平差复习题及答案 一、综合题 1.已知两段距离的长度及中误差分别为cm m 5.4465.300±及cm m 5.4894.660±,试说明这两段距离的真误差是否相等?他们的精度是否相等? 答:它们的真误差不一定相等;相对精度不相等,后者高于前者。 2.已知观测值向量 ???? ??=2121 L L L 的权阵为? ??? ????=32313132 LL P ,现有函数21L L X +=, 13L Y =,求观测值的权 1 L P , 2 L P ,观测值的协因数阵XY Q 。 答:12/3L P =;22/3L P =;3XY Q = 3.在下图所示三角网中,A .B 为已知点,41~P P 为待定点,已知32P P 边的边长和方位角 分别为 S 和 0α, 今测得角度1421,,,L L L 和边长21,S S ,若按条件平差法对该网进行平差: (1)共有多少个条件方程?各类条件方程各有多少个? (2)试列出除图形条件和方位角条件外的其它条件方程(非线性条件方程不要求线性化) 答:(1)14216,6,10n t r =+=== ,所以图形条件:4个;极条件:2个;边长条件:2个;基线条件:1个;方位角条件:1个 (2)四边形14ABPP 的极条件(以1P 为极) : 34131 241314????sin()sin sin 1????sin sin sin() L L L L L L L L +??=+ 四边形1234PP P P 的极条件(以4P 为极) : 101168 91167????sin()sin sin 1????sin sin sin() L L L L L L L L +??=+
测量平差知识大全
?绪论 ?测量平差理论 ?4种基本平差方法 ?讨论点位精度 ?统计假设检验的知识 ?近代平差概论 ?绪论 §1-1观测误差 测量数据(观测数据)是指用一定的仪器、工具、传感器或其他手段获取的反映地球与其它实体的空间分布有关信息的数据,包含信息和干扰(误差)两部分。 一、误差来源 观测值中包含有观测误差,其来源主要有以下三个方面: 1. 测量仪器; 2. 观测者; 3. 外界条件。 二、观测误差分类 1. 偶然误差 定义,例如估读小数; 2. 系统误差 定义,例如用具有某一尺长误差的钢尺量距; 系统误差与偶然误差在观测过程中总是同时产生的。
3. 粗差 定义,例如观测时大数读错。 误差分布与精度指标 §2-1 正态分布 概率论中的正态分布是误差理论与测量平差基础中随机变量的基本分布。 一、一维正态分布 §2-2偶然误差的规律性
2. 直方图 由表2-1、表2-2可以得到直方图2-1和图2-2(注意纵、横坐标各表示什么?),直方图形象地表示了误差分布情况。 3. 误差分布曲线(误差的概率分布曲线) 在一定的观测条件下得到一组独立的误差,对应着一种确定的误差分布。当观测值个数的情况下,频率稳定,误差区间间隔无限缩小,图2-1和图2-2中各长方条顶边所形成的折线将分别变成如图2-3所示的两条光滑的曲线,称为误差分布曲线,随着n增大,以正态分布为其极限。因此,在以后的讨论中,都是以正态分布作为描述偶然误差分布的数学模型。
4. 偶然误差的特性 第三章协方差传播律及权 在测量实际工作中,往往会遇到某些量的大小并不是直接测定的,而是由观测值通过一定的函数关系间接计算出来的,显然,这些量是观测值的函数。例如,在一个三角形中同精度观测了3个内角L1,L2和L3,其闭合差w和各角度的平差值分别 又如图3—1中用侧方交会求交会点的坐标等。 现在提出这样一个问题:观测值函数的精度如何评定?其中误差与观测值的中误差存在怎样的关系?如何从后者得到前者?这是本章所要讨论的重要内容,阐述这种关系的公式称为协方差传播律。 § 3—1 数学期望的传播
误差理论与测量平差基础
《误差理论与测量平差基础》授课教案 2006~2007第一学期 测绘工程系 2006年9月
课程名称:误差理论与测量平差基础 英文名称: 课程编号:?? 适用专业:测绘工程 总学时数: 56学时其中理论课教学56学时,实验教学学时 总学分:4学分 ◆内容简介 《测量平差》是测绘工程等专业的技术基础课,测量平差的任务是利用含有观测误差的观测值求得观测量及其函数的平差值,并评定其精度。 本课程的主要内容包括误差理论﹑误差分布与精度指标﹑协方差传播律及权﹑平差数学模型与最小二乘原理﹑条件平差﹑附有参数的条件平差﹑间接平差﹑附有限制条件的间接平差﹑线性方程组解算方法﹑误差椭圆﹑平差系统的统计假设检验和近代平差概论等。 ◆教学目的、课程性质任务,与其他课程的关系,所需先修课程 本课程的教学目的是使学生掌握误差理论和测量平差的基本知识、基本方法和基本技能,为后续专业课程的学习和毕业后从事测绘生产打下专业基础。 课程性质为必修课、考试课。 本课程的内容将在测绘工程和地理信息系统专业的专业课程的测量数据处理内容讲授中得到应用,所需先修课程为《高等数学》、《概率与数理统计》、《线性代数》和《测量学》等。 ◆主要内容重点及深度 考虑到专业基础理论课教学应掌握“必须和够用”的原则,结合测绘专业建设的指导思想,教学内容以最小二乘理论为基础,误差理论及其应用、平差基本方法与计算方法,以及平差程序设计及其应用为主线。 测量误差理论,以分析解决工程测量中精度分析和工程设计的技术问题为着眼点,在掌握适当深度的前提下,有针对性的加强基本理论,并与实践结合,突出知识的应用。 平差方法,以条件平差和参数平差的介绍为主,以适应电算平差的参数平差为重点。 计算方法,以介绍适应电子计算机计算的理论、方法为主,建立新的手工计算与计算机求解线性方程组过程相对照的计算方法和计算格式。 平差程序设计及其应用,通过课程设计要求学生利用所学程序设计的知识和平差数学模型编制简单的平差程序,熟练掌握已有平差程序的使用方法。
测量平差练习题及参考答案
计算题 1、如图,图中已知A 、B 两点坐标,C 、D 、E 为待定点,观测了所有内角,试用条件平差的方法列出全部条件方程并线性化。 解:观测值个数 n =12,待定点个数t =3,多余观测个数r =n -2t =6 ① 图形条件4个: )180(0 )180(0 )180(0 )180(0 121110121110987987654654321321-++-==-++-++-==-++-++-==-++-++-==-++L L L w w v v v L L L w w v v v L L L w w v v v L L L w w v v v d d c c b b a a ② 圆周条件1个: )360(0963963-++-==-++L L L w w v v v e e ③ 极条件1个: ρ''--==----++)sin sin sin sin sin sin 1(0 cot cot cot cot cot cot 8 52741774411885522L L L L L L w w v L v L v L v L v L v L f f 3、如图所示水准网,A 、B 、C 三点为已知高程点, D 、E 为未知点,各观测高差及路线长度如下表所列。 用间接平差法计算未知点D 、E 的高程平差值及其中误差;
C 3、解:1)本题n=6,t=2,r=n-t=4; 选D 、E 平差值高程为未知参数2 1??X X 、 则平差值方程为: 1 615142322211?????????????X H h H X h H X h H X h H X h X X h A A B A B -=-=-=-=-=-= 则改正数方程式为: 6165154143232221211???????l x v l x v l x v l x v l x v l x x v --=-=-=-=-=--= 取参数近似值 255.24907.2220221011=+==++=h H X h h H X B B 、
测量平差题目及答案
《误差理论与测量平差基础》课程试卷A 2010-06-27 11:30:49 来源:《误差理论与测量平差基础》课程网站浏览:4次 武汉大学测绘学院 2007-2008学年度第二学期期末考试 《误差理论与测量平差基础》课程试卷A 出题者课程小组审核人 班级学号姓名成绩 一、填空题(本题共20个空格,每个空格1.5分,共30分) 1、引起观测误差的主要原因有(1)、(2)、(3)三个方面的因素,我们称这些因素为(4)。 2、根据对观测结果的影响性质,观测误差分为(5)、(6)、(7)三类,观测误差通过由于(8)引起的闭合差反映出来。 3、观测值的精度是指观测误差分布的(9)。若已知正态分布的观测误差落在区间的概率为95.5%,则误差的方差为(10),中误差为(11)。 4、观测值的权的定义式为(12)。若两条水准路线的长度为、,对应的权为2、1,则单位权观测高差为(13)。 5、某平差问题的必要观测数为,多余观测数为,独立的参数个数为。若,则平差的函数模型为(14)。若(15),则平差的函数模型为附有参数的条件平差。 6、观测值的权阵为,的方差为3,则的方差为(16)、 的权为(17)。 7、某点的方差阵为,则的点位方差为(18)、误差曲线的最大值为(19)、误差椭圆的短半轴的方位角为(20)。 二、简答题(本题共2小题,每题5分,共10分)
1、简述观测值的精度与精确度含义及指标。 在什么情况下二者相同? 2、如图1所示,A、B、C、D为已知点,由A、C分别观测位于直线AC上的点。观测边长、及角度、。问此问题的多余观测数等于几?若采用条件平差法计算,试列出条件方程式(非线性方程不必线性化)。 图1 三、(10分)其它条件如上题(简答题中第2小题)。设方位角,观测边长,中误差均为,角度、的观测中误差为 。求平差后点横坐标的方差(取)。 四、(10分)采用间接平差法对某水准网进行平差,得到误差方程及权阵(取 ) (1)试画出该水准网的图形。 (2)若已知误差方程常数项,求每公里观测
误差理论和测量平差试题+答案
误差理论与测量平差》 ( 1 ) 正误判断。正确“ T ”,错误“ F ”。(30分) 在测角中正倒镜观测是为了消除偶然误差( )。 在水准测量中估读尾数不准确产生的误差是系统误差( )。 如果随机变量 X 和 Y 服从联合正态分布,且 X 与Y 的协方差为0 ,则X 与Y 相互独立 ( )。 观测值与最佳估值之差为真误差( )。 系统误差可用平差的方法进行减弱或消除( )。 权一定与中误差的平方成反比( )。 间接平差与条件平差一定可以相互转换( )。 在按比例画出的误差曲线上可直接量得相应边的边长中误差( )。 对同一量的 N 次不等精度观测值的加权平均值与用条件平差所得的结果一定相同 ( )。 无论是用间接平差还是条件平差, 对于特定的平差问题法方程阶数一定等于必要观 测数( )。 对于特定的平面控制网,如果按条件平差法解算,则条件式的个数是一定的,形式 是多样的( )。 观测值L 的协因数阵Q LL 的主对角线元素 Q ii 不一定表示观测值 L i 的权( )。 当观测值个数大于必要观测数时,该模型可被唯一地确定( )。 定权时b 0可任意给定,它仅起比例常数的作用( )。 设有两个水平角的测角中误差相等, 则角度值大的那个水平角相对精度高( )。 用“相等”或“相同”或“不等”填空( 8 分)。 1. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10 11 12 13 14 15 16
P D = ( ) 则还需增加的 已知两段距离的长度及其中误差为 300.158m ±3.5cm; 600.686m ±3.5cm 。则: 1 .这两段距离的中误差( )。 2 .这两段距离的误差的最大限差( )。 3 .它们的精度( )。 4 .它们的相对精度( )。 17 . 选择填空。只选择一个正确答案( 25 分)。 1 .取一长为 d 的直线之丈量结果的权为 1 ,则长为 D 的直线之丈量结果的权 a ) d/D b ) D/d c ) d 2 /D 2 d ) D 2 /d 2 2. 有一角度测 20 测回,得中误差± 0.42 秒,如果要使其中误差为± 0.28 秒, 测回数 N= ( )。 a ) 25 b ) 20 c) 45 d) 5 3. 某平面控制网中一点 P , 其协因数阵为: Q Q xx Q xy 0.5 0.25 Q XX Q yx yx Q yy 0.25 0.5 2 单位权方差 0 = ±2.0 。则 P 点误差椭圆的方位角 T=( )。 a ) 90 b ) 135 c ) 120 d ) 45 4. 设L 的权为1,则乘积4L 的权P= ( )o
《误差理论与测量平差基础》试卷A(答案)
《误差理论与测量平差基础》期末考试试题A(参考答案) 一、名词解释(每题2分,共10分) 1、偶然误差 ——在相同的观测条件系作一系列的观测,如果误差在大小和符号上都表现出偶然性。即从单个误差看,该误差的大小和符号没有规律性,但就大量误差的总体而言,具有一定的统计规律。这种误差称为偶然误差。 2、函数模型线性化 ——在各种平差模型中,所列出的条件方程或观测方程,有的是线性形式,有的是非线性形式。在进行平差计算时,必须首先把非线性形式的函数方程按台劳公式展开,取至一次项,转换成线性方程。这一转换过程,称之为函数模型的线性化。 3、点位误差椭圆 ——以点位差的极大值方向为横轴X 轴方向,以位差的极值F E 、分别为椭圆的长、短半轴,这样形成的一条椭圆曲线,即为点位误差椭圆。 4、协方差传播律 ——用来阐述观测值的函数的中误差与观测值的中误差之间的运算规律的数学公式。如 0K KL Z +=,若观测向量的协方差阵为LL D ,则按协方差传播律,应有T LL ZZ K KD D =。 5、权 ——表示各观测值方差之间比例关系的数字特征,220 i i P σσ=。 二、判断正误(只判断)(每题1分,共10分) 参考答案:X √X √X X X √√X 三、选择题(每题3分,共15分) 参考答案:CCDCC 四.填空题(每空3分,共15分) 参考答案:1. 6个 2. 13个 3.1/n 4. 0.4 5. 0) () () () (432 00 2 0=''+?+?+-''+ -''- W y S X X x S Y Y C AC A C C AC A C ρρ,其中 AB A C A C X X Y Y W αββ-++--=''4300arctan 五、问答题(每题4分,共12分) 1. 几何模型的必要元素与什么有关?必要元素数就是必要观测数吗?为什么? 答:⑴几何模型的必要元素与决定该模型的内在几何规律有关;(1分) ⑵必要元素数就是必要观测数;(1分) ⑶几何模型的内在规律决定了要确定该模型,所必须具备的几何要素,称为必要元素,必要元素的个数,称为必要元素数。实际工程中为了确定该几何模型,所必须观测的要素个数,称为必要观测数,
《误差理论与测量平差基础》试卷A(答案)
《误差理论与测量平差基础》试卷A(答案)
《误差理论与测量平差基础》期末考试试题A(参考答案) 一、名词解释(每题2分,共10分) 1、偶然误差 ——在相同的观测条件系作一系列的观测,如果误差在大小和符号上都表现出偶然性。即从单个误差看,该误差的大小和符号没有规律性,但就大量误差的总体而言,具有一定的统计规律。这种误差称为偶然误差。 2、函数模型线性化 ——在各种平差模型中,所列出的条件方程或观测方程,有的是线性形式,有的是非线性形式。在进行平差计算时,必须首先把非线性形式的函数方程按台劳公式展开,取至一次项,转换成线性方程。这一转换过程,称之为函数模型的线性化。 3、点位误差椭圆 ——以点位差的极大值方向为横轴X 轴方向,以位差的极值F E 、分别为椭圆的长、短半轴,这样形成的一条椭圆曲线,即为点位误差椭圆。 4、协方差传播律 ——用来阐述观测值的函数的中误差与观测值的中误差之间的运算规律的数学公式。如0 K KL Z +=, 若观测向量的协方差阵为LL D ,则按协方差传播律, 应有T LL ZZ K KD D =。 5、权
——表示各观测值方差之间比例关系的数字特征, 2 20 i i P σσ=。 二、判断正误(只判断)(每题1分,共10分) 参考答案:X √X √X X X √√X 三、选择题(每题3分,共15分) 参考答案:CCDCC 四.填空题(每空3分,共15分) 参考答案:1. 6个 2. 13个 3.1/n 4. 0.4 5. ) () () () (432 2 0=''+?+?+-''+ -''- W y S X X x S Y Y C AC A C C AC A C ρρ,其中 AB A C A C X X Y Y W αββ-++--=''4300arctan 五、问答题(每题4分,共12分) 1. 几何模型的必要元素与什么有关?必要元素数就是必要观测数吗?为什么? 答:⑴几何模型的必要元素与决定该模型的内在几何规律有关;(1分) ⑵必要元素数就是必要观测数;(1分) ⑶几何模型的内在规律决定了要确定该模型,所必须具备的几何要素,称为必要元素,必要元素的个数,称为必要元素数。实际工程中为了确定该几何模型,所必须观测的要素个数,称为必要观测数,其类型是由必要元素所决定的,其数量,必须等于必要元素的个数。(2分) 2. 简述偶然误差的特性 答:⑴在一定条件下,误差绝对值有一定限值。或者说,
测量平差试卷E及答案200951
CXXXCCZ 中国矿业大学2008~2009学年第 二 学期 《 误差理论与测量平差 》试卷(B )卷DDDDDEF2WT AW34CQ2 考试时间:100 分钟 考试方式:闭 卷 一、填空题 (共20分,每空 2 分) 1、如下图,其中A 、B 、C 为已知点,观测了5个角,若设L 1、L 5观测值的平 差值为未知参数2 1??X X 、,按附有限制条件的条件平差法进行平差时,必要观测个数为 ,多余观测个数为 ,一般条件方程个数为 ,限制条件方程个数为 A B C D E L 1L 2L 3 L 4 L 5 2、测量是所称的观测条件包括 、观测者、 3、已知某段距离进行了同精度的往返测量(L 1、L 2),其中误差cm 221==σσ,往返测的平均值的中误差为 ,若单位权中误差cm 40=σ,往返测的平均值的权为 4、已知某观测值X 、Y 的协因数阵如下,其极大值方向为 ,若单位权中误差为±2mm ,极小值F 为 mm 。
??? ? ??--=0.15.05.00.2XX Q 二、已知某观测值X 、Y 的协因数阵如下,求X 、Y 的相关系数ρ。(10分) ??? ? ??--=25.015.015.036.0XX Q 三、设有一函数2535+=x T ,6712+=y F 其中: ? ? ?+++=+++=n n n n L L L y L L L x βββααα 22112211 αi =A 、βi =B (i =1,2,…,n )是无误差的常数,L i 的权为p i =1,p ij =0(i ≠ j )。(15分) 1)求函数T 、F 的权; 2)求协因数阵TF Ty Q Q 、。 四、如图所示水准网,A 、B 、C 三点为已知高程点, D 、E 为未知点,各观测高差及路线长度如下表所列。(20分) 用间接平差法计算未知点D 、E 的高程平差值及其中误差; C
误差理论与测量平差基础期末考试试卷样题
误差理论与测量平差基础期末考试试卷样题 一、填空题(15分) 1、误差的来源主要分为、、。 2、中误差是衡量精度的主要指标之一,中误差越,精度越。极限误差是指。 3、在平坦地区相同观测条件下测得两段观测高差及水准路线的长分别为: h 1=10.125米,s 1 =3.8公里,h 2 =-8.375米,s 2 =4.5公里,那么h 1 的精度比h 2 的精 度______,h 2的权比h 1 的权______。 4、间接平差中误差方程的个数等于________________,所选参数的个数等于 _______________。 5、在条件平差中,条件方程的个数等于。 6、平面控制网按间接平差法平差时通常选择________________为未知参数,高程控制网按间接平差法平差时通常选择________________为未知参数。 7、点位方差与坐标系,总是等于。
二、 水准测量中若要求每公里观测高差中误差不超过10mm ,水准路线全长高差 中误差不超过20mm,则该水准路线长度不应超过多少公里?(5分) 三、已知观测向量()L L L T =1 2的协方差阵为D L =--?? ?? ?3112,若有观测值函数 Y 1=2L 1,Y 2=L 1+L 2,则σy y 12等于?(5分)
四、观测向量L L L T =()1 2的权阵为P L =--()31 14 ,若有函数X L L =+12, 则函数X 与观测向量L 的互协因数阵Q XL 等于什么? (5分) 五、对某长度进行同精度独立观测,已知一次观测中误差为2mm ,设4次观测值平均值的权为2。试求:(1)单位权中误差0σ;(2)一次观测值的权;(3)若使平均值的权等于8,应观测多少次? (9分)
《测量平差》试卷D及答案(-5-1)
《 误差理论与测量平差 》试卷(D )卷 考试时间:100 分钟 考试方式:闭 卷 一、填空题 (共20分,每空 2 分) 1、观测误差产生的原因为:仪器、 、 2、已知一水准网如下图,其中A 、B 为已知点,观测了8段高差,若设E 点高程 的平差值与B 、E 之间高差的平差值为未知参数2 1??X X 、,按附有限制条件的条件平差法(概括平差法)进行平差时,必要观测个数为 ,多余观测个数为 ,一般条件方程个数为 ,限制条件方程个数为 C B 3、取一长度为d 的直线之丈量结果的权为1,则长度为D 的直线之丈量结果的权为 ,若长度为D 的直线丈量了n 次,则其算术平均值的权为 。 4、已知某点(X 、Y)的协方差阵如下,其相关系数ρXY = ,其点位方差为2 σ= mm 2 ??? ? ??=00.130.030.025.0XX D
二、设对某量分别进行等精度了n 、m 次独立观测,分别得到观测值 ),2,1(,n i L i =,),2,1(,m i L i =,权为p p i =,试求: 1)n 次观测的加权平均值] [] [p pL x n = 的权n p 2)m 次观测的加权平均值] [] [p pL x m = 的权m p 3)加权平均值m n m m n n p p x p x p x ++=的权x p (15分) 三、 已知某平面控制网中待定点坐标平差参数y x ??、的协因数为 ??? ? ??=2115.1??X X Q 其单位为()2 s dm ,并求得2?0''±=σ ,试用两种方法求E 、F 。(15分) 四、得到如下图所示,已知A 、B 点,等精度观测8个角值为:
误差理论与测量平差基础试卷
长沙理工大学考试试卷 …………………………………………………………………………………………………………………………… 试卷编号 1 拟题教研室(或教师)签名 范志勇 系主任签名 …………………………………………………………………………………………………………………………… 课程名称(含档次) 误差理论与测量平差基础 课程代号 0809021 专 业 测绘工程 层次(本、专) 本 考试方式(开、闭卷) 闭 一、 正误判断(正确“T ”,错误“F ”每题1分,共10 分)。 1.已知两段距离的长度及中误差分别为128.286m ±4.5cm 与218.268m ±4.5cm ,则其真误差与精度均相同( )。 2.如果X 与Y 的协方差0xy σ=,则其不相关( )。 3.水准测量中,按公式i i c p s = (i s 为水准路线长)来定权,要求每公里高差精度相同( )。 4.可用误差椭圆来确定待定点与待定点之间的某些精度指标( )。 5.在某一平差问题中,观测数为n ,必要观测数为t ,参数个数u <t 且不独立,则该平差问题可采用附有参数的条件平差的函数模型。( )。 6.由于同一平差问题采用不同的平差方法得到的结果不同,因此为了得到最佳平差结果,必须谨慎选择平差方法( )。 7.根据公式() 222220 cos sin 0360E F θσθθθ=+≤≤得到的曲线就是误差椭圆( )。 8.对于特定的平面控制网,如果按间接平差法解算,则误差方程的个数是一定的( )。 9.对于同一个观测值来说,若选定一定权常数0σ,则权愈小,其方差愈小,其精度愈高( )。 10.设观测值向量,1 n L 彼此不独立,其权为() 1,2 ,,i P i n = ,12(,,,)n Z f L L L = ,则有 2 221122111 1Z n n f f f P L P L P L P ?????????=+++ ? ? ?????????? ( )。 二、填空题(每空2分,共24分)。 1、设对某三角网进行同精度观测,得三角形角度闭合差分别为:3秒,-3秒,2秒,4秒,-2秒,-1秒,0秒,-4秒,3秒,-2秒,则测角中误差为 秒。 2、某平差问题函数模型)(I Q =为?? ?????=-=--=+-+=--0?0306051 54431 2 1x v v v v v v v v ,则该函数模型为 平差方法的模型;=n ,=t ,=r ,=c ,=u 。
误差理论和测量平差试卷及答案6套试题+答案
《误差理论与测量平差》课程自测题(1) 一、正误判断。正确“T”,错误“F”。(30分) 1.在测角中正倒镜观测是为了消除偶然误差()。 2.在水准测量中估读尾数不准确产生的误差是系统误差()。 3.如果随机变量X和Y服从联合正态分布,且X与Y的协方差为0,则X与Y相互独立()。4.观测值与最佳估值之差为真误差()。 5.系统误差可用平差的方法进行减弱或消除()。 6.权一定与中误差的平方成反比()。 7.间接平差与条件平差一定可以相互转换()。 8.在按比例画出的误差曲线上可直接量得相应边的边长中误差()。 9.对同一量的N次不等精度观测值的加权平均值与用条件平差所得的结果一定相同()。 10.无论是用间接平差还是条件平差,对于特定的平差问题法方程阶数一定等于必要观测数()。 11.对于特定的平面控制网,如果按条件平差法解算,则条件式的个数是一定的,形式是多样的()。 12.观测值L的协因数阵Q LL的主对角线元素Q ii不一定表示观测值L i的权()。13.当观测值个数大于必要观测数时,该模型可被唯一地确定()。 14.定权时σ0可任意给定,它仅起比例常数的作用()。 15.设有两个水平角的测角中误差相等,则角度值大的那个水平角相对精度高()。 二、用“相等”或“相同”或“不等”填空(8分)。 已知两段距离的长度及其中误差为300.158m±3.5cm; 600.686m±3.5cm。则: 1.这两段距离的中误差()。 2.这两段距离的误差的最大限差()。 3.它们的精度()。 4.它们的相对精度()。 三、选择填空。只选择一个正确答案(25分)。 1.取一长为d的直线之丈量结果的权为1,则长为D的直线之丈量结果的权P D=()。
测量平差复习题及答案
测量平差复习题及答案 一、综合题 1.已知两段距离的长度及中误差分别为cm m5.4 465 . 300±及cm m5.4 894 . 660±,试说明这两段距离的真误差是否相等他们的精度是否相等 答:它们的真误差不一定相等;相对精度不相等,后者高于前者。 ` 2.已知观测值向量 ?? ? ? ? ? = 2 1 21L L L 的权阵为 ? ? ? ? ? ? ? ? = 3 2 3 1 3 1 3 2 LL P ,现有函数2 1 L L X+ =, 1 3L Y=,求观测值的权1L P ,2L P ,观测值的协因数阵XY Q。 答: 1 2/3 L P=; 2 2/3 L P=;3 XY Q= 3.在下图所示三角网中,A.B为已知点,4 1 ~P P为待定点,已知3 2 P P 边的边长和方位角分别为0 S 和0 α ,今测得角度14 2 1 , , ,L L L 和边长 2 1 ,S S,若按条件平差法对该网进行平差: 、 (1)共有多少个条件方程各类条件方程各有多少个 (2)试列出除图形条件和方位角条件外的其它条件方程(非线性条件方程不要求线性化)答:(1)14216,6,10 n t r =+===,所以图形条件:4个;极条件:2个;边长条件:2个;基线条件:1个;方位角条件:1个 (2)四边形 14 ABPP的极条件(以 1 P为极): ~ 34131 241314 ???? sin()sin sin 1 ???? sin sin sin() L L L L L L L L + ??= + 四边形 1234 PP P P的极条件(以 4 P为极):
101168 911 67????sin()sin sin 1????sin sin sin() L L L L L L L L +??=+ 边长条件(1?AB S S - ):1 23434??????sin()sin() AB S S L L L L L = +++ 边长条件(12 ??S S - ):112 1314867 ???sin ?????sin()sin sin()S L S L L L L L ?= ++ ] 基线条件(0AB S S - ): 02 101191011?????sin()sin() S S L L L L L =+++ 4.A .B .C 三点在同一直线上,测出了AB .BC 及AC 的距离,得到4个独立观测值, m L 010.2001=,m L 050.3002=,m L 070.3003=,m L 090.5004=,若令100米量距的权为单位权,试按条件平差法确定A .C 之间各段距离的平差值L ?。 答:?[200.0147,300.0635,300.0635,500.0782]T L = ( 5.在某航测像片上,有一块矩形稻田。为了确定该稻田的面积,现用卡规量测了该矩形的 长为cm L 501=,方差为22136.0cm =σ,宽为cm L 302=,方差为2 2236.0cm =σ,又用求积 仪量测了该矩形的面积 2 31535cm L =,方差为 4 2336cm =σ,若设该矩形的长为参数1? X , 宽为参数2? X ,按间接平差法平差: (1)试求出该长方形的面积平差值;(2)面积平差值的中误差。 答:(1)令0111?X X x =+,0222 ?X X x =+,011X L =,022X L =,误差方程式为: 1122312??305035 v x v x v v v ===+- >
测量平差 第三章习题与答案
测量平差第三章思考题 3.1 下列各式中的()1,2,3i L i =均为等精度独立观测值,其中误差为σ,试求X 的中误差: (1)()12312 X L L L =++; (2)12 3 L L X L = 3.2 已知观测值1L ,2L 的中误差12σσσ==,120σ=,设11225,2X L Y L L =+=-, 12Z L L =,t X Y =+,试求X ,Y ,Z 和t 的中误差。 3.3 设有观测向量[]1 2 331 T L L L L =,其协方差阵为 4 000300 2LL D ?? ??=?????? 分别求下列函数的的方差: (1)1133F L L =-; (2)2233F L L = 3.4 设有同精度独立观测值向量[]1 2 3 31 T L L L L =的函数为113 s i n s i n AB L Y S L =, 22AB Y L α=-,式中A B α和AB S 为无误差的已知值,测角误差1"σ=,试求函数的方差1 2 y σ、 2 2 y σ 及其协方差12 y y σ 3.5 在图中△ABC 中测得A A σ∠±,边长b b σ±,c c σ±,试求三角形面积的中误差s σ 。 3.6 在水准测量中,设每站观测高差的中误差均为1mm ,今要求从已知点推算待定点的高程中误差不大于5cm ,问可以设多少站? 3.7 有一角度测4个测回,得中误差为0.42〃,问再增加多少个测回其中误差为0.28〃? 3.8 在相同观测条件下,应用水准测量测定了三角点A ,B ,C 之间的高差,设三角形的边
长分别为S 1=10km ,S 2=8km ,S 3=4km ,令40km 的高差观测值权威单位权观测,试求各段观测高差之权及单位权中误差。 3.9 以相同观测精度A ∠和B ∠,其权分别为14 A P =,12 B P =,已知8"B σ=,试求单位 权中误差0A σ∠和的中误差A σ。 3.10 已知观测值向量21L 的权阵为522 4LL P -?? =? ?-?? ,试求观测值的权1L P 和2L P 答案: 3.1 (1)x σ= , (2)3 x L σ= 3.2 2x σσ=,y σ=,z σ= ,t σ= 3.3 1 22F D =,22 2 231827F D L L =+ 3.4 ()1 222 2 2 113"2 2 3 cos sin cot sin AB y S L L L L σ ρ = +? ()222 1y σ=秒 12 0y y σ = 3.5 s σ= 3.6 最多可设25站 3.7 再增加5个测回 3.8 1 4.0P =,2 5.0P =,310.0P =,0()km σ= 3.9 "0 5.66σ=," 11.31A σ= 3.10 1 4L P =,2 165 L P =
误差理论与测量平差基础习题集
第五章条件平差 §5-1条件平差原理 条件平差中求解的未知量是什么?能否由条件方程直接求得 5. 1. 02 设某一平差问题的观测个数为n.必要观测数为t,若按条件平差法进行平差,其条件方程、法方程及改正数方程的个数各为多少? 5. 1.03 试用符号写出按条件平差法平差时,单一附合水准路线中(如图5-1所示)各观测值平差值的表达式。 图5-1 5. 1. 04 在图5-2中,已知A ,B的高程为H a= 12.123 m , H b=11. 123m,观测高差和线路长度为: 图5-2 S1=2km,S2=Ikm,S3=0.5krn,h1 =-2.003m,h2=-1.005 m,h3=-0.501 m,求改正 数条件方程和各段离差的平差值。 在图5-3的水准网中,A为已知点B、C、D为待定点,已知点高程H A=10.000m,观测了5条路线的高差: h1=1.628m, h2=0. 821 m, h3=0.715m, h4=1.502m, h5=-2.331 m。 各观测路线长度相等,试求:(1)改正数条件方程;(2)各段高差改正数及平差 值。 有水准网如图5-4所示,其中A、B、C三点高程未知,现在其间进行了水准测 量,测得高差及水准路线长度为 h1 =1 .335 m,S1=2 km; h2=1.055 m,S2=2 km; h3=-2.396 m,S3=3km。试按条件平差法求各高差的平差值。 如图5-5 所示,L1=63°19′40″,=30″;L2=58°25′20″,=20″; L3=301°45′42″,=10″. (1)列出改正数条件方程; (2)试用条件平差法求∠C的平差值(注:∠C是指内角)。 5-2条件方程 5. 2.08 对某一平差问题,其条件方程的个数和形式是否惟一? 列立条件方程时要注意哪些问题?如何使得一组条件方程彼此线性无关? 5.2. 10 指出图5-6中各水准网条件方程的个数(水准网中P i表示待定高程点,h i表 示观测高差)。 (a) (b) 图5-6
第1章习题(测量平差基础)
第一章思考题 1.1 观测条件是由那些因素构成的?它与观测结果的质量有什么联系? 1.2 观测误差分为哪几类?它们各自是怎样定义的?对观测结果有什么影响?试举例说明。 1.3 用钢尺丈量距离,有下列几种情况使得结果产生误差,试分别判定误差的性质及符号: (1) 尺长不准确; (2) 尺不水平; (3) 估读小数不准确; (4) 尺垂曲; (5) 尺端偏离直线方向。 1.4 在水准了中,有下列几种情况使水准尺读书有误差,试判断误差的性质及符号: (1) 视准轴与水准轴不平行; (2) 仪器下沉; (3) 读数不准确; (4) 水准尺下沉。 1.5 何谓多余观测?测量中为什么要进行多余观测? 1.6 为了鉴定经纬仪的精度,对已知精确测定的水平角'"450000α= 作12次同精度观测,结果为: ' " 450006 '" 455955 '" 455958 '" 450004 ' " 450003 ' " 450004 ' " 450000 ' " 455958 ' " 455959 ' " 455959 ' " 450006 ' " 450003 设a 没有误差,试求观测值的中误差。 1.7 已知两段距离的长度及中误差分别为300.465m ±4.5cm 及660.894m ±4.5cm ,试说明这两段距离的真误差是否相等?他们的精度是否相等? 1.8 设对某量进行了两组观测,他们的真误差分别为: 第一组:3,-3,2,4,-2,-1,0,-4,3,-2 第二组:0,-1,-7,2,1,-1,8,0,-3,1 试求两组观测值的平均误差1?θ、2?θ和中误差1?σ、2?σ ,并比较两组观测值的精度。 1.9 设有观测向量1 221 []T X L L =,已知1?L σ=2秒,2?L σ=3秒,12 2 ?2L L σ=-秒,试写出其协方差阵22XX D 。
测量平差基础名词解释
第一章 1、观测误差产生的原因很多,概括起有以下三种:测量仪器(感觉器官的局限、技术水平、 工作态度)、观测者(具有一定限度的准确度)、外界条件(温度、湿度、风力、大气折光等)。 2、偶然误差:在相同的观测条件下作一系列的观测,如果误差在大小和符号上都表现出偶然性,即从单个误差看,该列误差的大小和符号没有规律性,但就大量误差的总体而言,具有一定的统计规律,这种误差称为偶然误差,也叫随机误差。 采取措施:处理带有偶然误差的观测值,就是本课程的内容,也叫做测量平差。 3、系统误差:在相同的观测条件下作一系列的观测,如果误差在大小、符号上表现出一致性,或者在观测过程中按一定的规律变化,或者为一常数,这种误差就称为系统误差。 消除或削弱的方法:采取合理的操作程序(正、倒镜,中间法,对向观测等);用公式改正,即加改正数。 4、粗差:粗差即粗大误差,或者说是一种大量级的观测误差,是由于测量过程中的差错造成的。 发现、剔除粗差的方法:进行必要的重复测量或多余观测,采用必要而又严格的检核、验算等,发现后舍弃或重测。 5、测量平差两大任务:(1)、求平差值(求未知量的最佳估值);(2)、精度评定(评定测量成果精度)。 6、测量平差 7 8 9、真值:任一观测量,客观上总是存在一个能代表其真正大小的数值,这一数值就称为该观测值真值 10、真误差:真值与观测值之差 11、残差(改正数):改正数(V)= 平差值()- 观测值() 12、偶然误差的四个统计特性: (1)一定观测条件下,误差绝对值有一定限值(有限性); (2)绝对值较小的误差比绝对值较大的误差出现概率大(渐降性); (3)绝对值相等的正负误差出现概率相同(对称性); (4)偶然误差的数学期望为零(抵偿性) 13、平均误差:在一定的观测条件下,一组独立的偶然误差绝对值的数学期望,称为平均误差 14、或然误差:误差出现在(- ρ,+ ρ)之间的概率等于1/2,即 15、极限误差:通常将三倍(或两倍)的中误差作为极限误差,即 16、相对中误差的定义是:中误差与观测值之比,即 17、精度:是指误差分布的密集或离散程度,即:L与E(L)接近程度。 18、准确度:又名“准度”,是指随机变量X的真值与其数学期望之差,(是衡量系统误差大小程度的指标)
测量平差超级经典试卷含答案
一、填空题(每空 1 分,共 20 分) 1、测量平差就是在多余观测基础上,依据一定的原则,对观测值进行合理的调整,即分别给以适当的改正数,使矛盾消除,从而得到一组最 可靠的结果,并进行精度评估。 2、条件平差中,条件方程式的选取要求满足、。 3已知条件平差的法方程为{ EMBED Equation.3| 42k 140 ,则=, 23k22 =, =,=。 4、已知某平差问题,观测值个数为79,必要观测量个数为35,则按条件平差进行求解时,条件方程式个数为,法方程式个数为。 5、已知某平差问题观测值个数为50,必要观测量个数为22,若选 6 个独立参数按具有参数的条件平差进行求解,则函数模型 个数为,联系数法方程式的个数为;若在 22 个独立参数的基础上,又选了 4 个非独立参数按具有条件的参数 平差进行求解,则函数模型个数 为,联系数法方程式的个数 为。 6、间接平差中误差方程的个数等于 ________________, 所选参数的个数等于
_______________。 7、已知真误差向量及其权阵,则单位权中 误差公式为,当权阵为 此公式变为中误差公式。 二、选择题(每题2分,共20分) 1、观测条件是指: A)产生观测误差的几个主要因素: 仪 器, 观测者 , 外界条件等的综合 B)测量时的几个基本操作 : 仪器的对中 , 整平 , 照准 , 度盘配置 , 读数等要素的综 合 C)测量时的外界环境 : 温度 , 湿度 , 气压 , 大气折光??等因素的综合 . D)观测时的天气状况与观测点地理状 况诸因素的综合 答:_____ 2、已知观测向量的协方差阵为, 若有观测值函数Y1=2L1, Y2=L1+L2,则等于? (A)1/4(B)2 《测量平差基础》期末试卷本卷共 4页第2页
误差理论与测量平差基础期末考试
2009-2010学年度第二学期期末考试 误差理论与测量平差基础 课程试卷(A 卷) 出题者: 审核人: 班级: 学号: 姓名: 分数: 一. 已知观测值向量21 L 的协方差阵为?? ????--=3112LL D ,又知协因数51 12-=Q ,试求观测值的权阵LL P 及观测值的权1L P 和2L P 。(10分) 二. 在相同观测条件下观测A 、B 两个角度,设对A ∠观测4测回的权为1, 则对B ∠观测9个测回的权为多少?(10分) 三. 在图一所示测角网中,A 、B 为已知点,BC α为已知方位角,C 、D 为待 定点,721,,,L L L 为同精度独立观测值。 若按条件平差法对该网进行平差: 共有多少个条件方程?各类条件方程各有多 少个? 试列出全部条件方程(非线性条件方程要求 线性化)。(15分) 图一 四. 某平差问题有以下函数模型)(I Q = ???????=-=--=+-+=--0 ?0 30 6051 5 4 4 3 12 1x v v v v v v v v 试问: (1). 以上函数模型为何种平差方法的模型? (2). 本题中,=n ,=t , =r ,=c ,=u ,=s 。(10分) 五. 在图二所示测角网中,已知A 、B 两点的坐标和P 1、P 2两待定点的近似坐 标值(见图二,以“km ”为单位),以及0000330001'''=BP α,00003000 2'''=BP α, km BP 0.201=,km S BP 0.20 2=,721,,,L L L 65955906'''=L 。 试列出 6L 的误差方程(设5102?=ρ,x ?、 图二 y ?以dm 为单位)。(10分) 六. 有水准网如图三所示,网中A 、B 为已知点,C 、D 为待定点,51~h h 为高差观测值,设各线路等长。已知平差后算得)(482mm V V T =,试求平差后C 、 D 两点间高差5?h 的权及中误差。(10分)
