二阶对称张量的示性面
张量基础知识

张量基础知识
一、坐标变换 如图所示,设有直角坐标
系OX1X2X3,其三个方向的单
张量基础知识
此处σ不再是一个数,而是9个数构成一个方阵,称为电导率
张量,这是一个二阶张量。于是,各向异性晶体中的欧姆定
律可表示为
JE
11 12 13
21
22
23
31 32 33
张量的定义:一般来说,在物理学中,有一些量需要用9个分 量来描述,这种物理量就是二阶张量。
张量基础知识
2.2 张量的数学定义
张量基础知识
2.3 张量的运算
一、张量的加法
若 Ai,jBi(ji,j1,2,3)皆为二阶张量,则
C i j A i jB ij(i,j 1 ,2 ,3 )也为二阶张量,于是我们定义 Cij
为 Aij, Bij 之和。这就是二阶张量的加法,并表为C=A+B。
以此类推,若A,B为两个同阶张量,则A,B相应分量之和构成 新的同阶张量C,记作C=A+B。
同 样 x x1 2 : 1 2''1 1 1 2''2 2 x x1 2'' i'jT x x1 2''
由( )式得
xx12i'
j1xx12''
比较 : i'jTi'j1
[ i ' j ] 为张量正基础交知识矩阵
引用指标符号:
晶体光学 lesson5张量

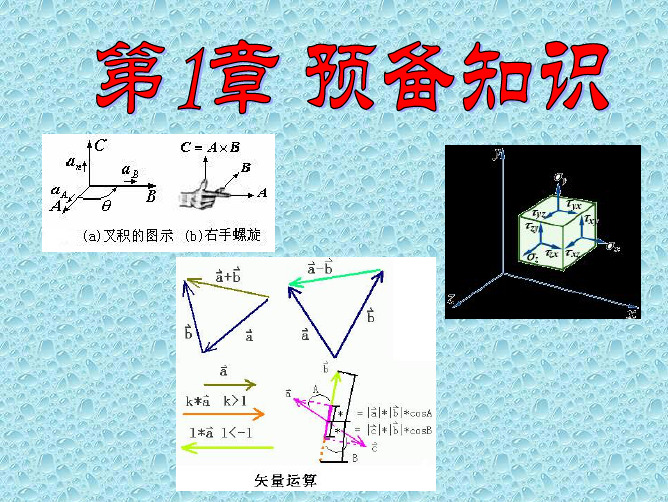
第二章晶体性质的数学描述研究内容张量的概念二阶张量-重点介绍-推导变换关系 二阶张量示性曲面及主轴化高阶张量及其变换三阶张量四阶张量晶体宏观对称性与晶体张量的关系张量的概念标量物理中常见的一些量,如密度、温度等等很多。
特点:无方向可用一个数值完全表示矢量区别于标量的另一类物理量,既有数值又有方向,如机械力就是矢量。
矢量用黑体字母表示,如F 。
在直角坐标系中用矢量在该坐标系上的分量表示矢量。
例如电场强度矢量E 记为:123[,,]T E E E =E 123E E E ++E=i j k二阶张量张量的概念以电场强度和极化强度矢量为例:123P P P =++P i j k 123E E E ++E=i j k对于各向同性晶体中,同方向则,P E0εχ=P E123[,,]T E E E =E 123[,,]T P P P =P¾如果在各向异性晶体中情况就复杂了,电场强度和它引起的极化强度的方向一般不相同¾这时电场强度的每个分量对极化强度每个方向的分量均有影响,且影响的程度不同,这时我们就不能简单的利用前面的公式()11112130111122133()()()P P E P E P E E E E εχχχ=++=++()22122230211222233()()()P P E P E P E E E E εχχχ=++=++()33132330311322333()()()P P E P E P E E E E εχχχ=++=++张量的概念我们把上述公式表示为矩阵的形式1112131120212223233313233P E P E P E χχχεχχχχχχ⎛⎞⎛⎞⎛⎞⎜⎟⎜⎟⎜⎟=⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠ 1、P 的每一个分量与电场强度的三个分量存在线性关系2、坐标系确定后为常数3、各向异性介质的电极化特性需用9各数值才能完整描述----我们接下来会详细介绍ij χ张量的概念-二阶张量111213212223313233χχχχχχχχχ⎛⎞⎜⎟⎜⎟⎜⎟⎝⎠我们称这个3×3的矩阵为二阶张量张量的概念-二阶张量推广-如果某个物理性质T ,可以表征另外两个物理量p,q 之间的关联,并具有如下关系111213112212223233313233T T T P q P T T T q P q T T T ⎛⎞⎛⎞⎛⎞⎜⎟⎜⎟⎜⎟=⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎝⎠ 我们称构成二阶张量ij T 张量的概念-二阶张量张量的习惯写法:引入爱因斯坦求和法则-略去求和符号31(1,2,3)i ij j j p T q i ===∑i ij j p T q =i 为自由下标,j 为求和下标,注意顺序1、下标符号任意选定,但要有区别2、自由下标前后呼应,求和下标成对出现张量的概念-二阶张量张量的概念-二阶张量或者表示为矩阵的形式:P Tq=对于我们晶体光学范畴研究的二阶张量均有:ij ji T T =对称张量T T ′=张量的概念-二阶张量我们可以将二阶张量的下标作如下简化:11-1 22-2 33-323 32-4 13 31-5 12 21-6121112131653212223624431323354356T T T T T T T T T T T T T T T T T T T T T T T T ⎛⎞⎜⎟⎜⎟⎛⎞⎛⎞⎜⎟⎜⎟⎜⎟⇒⇒⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠⎜⎟⎜⎟⎜⎟⎝⎠张量的概念9标量(零阶张量)9矢量(一阶张量)9二阶张量9三阶张量9四阶张量。
张量分析基础

张量的性质
张量的定义
— 张量是与坐标系有联系的一组量,并满足一定的坐标变换规律。
张量的性质
— 任何两个张量相乘所得到的新张量的阶数等于原张量阶数之和; — 两个张量间的比例系数一般是一个张量,其阶数等于原张量阶 数之和; — 张量的变换规律与坐标乘积的变换规律相同; — 变换矩阵与二阶张量的区别
二阶对称张量
δ ij =
1 i = j 0 i ≠ j
[ ]
1 0 0 δ ij = 0 1 0 0 0 1
δ ij Pj = Pi δ ij Pi = Pj
δ ijT jl = Til δ ilT jl = T ji
i, j , k顺序轮换 i, j , k反序轮换 两个以上角标同
反对称三重积
ei × e j = ε ijk e j
傀标
Pi = Tij Q j
自由 下标
[A] + [B][C][D] = [E][F]
Aij + BikCkl Dlj = Eik Fkj
坐标变换
坐标轴变换
e1* a11 * e 2 = a 21 * e3 a 31 a12 a 22 a 32
*∧
X3’
X3
θ23
a13 e1 a 23 e 2 a 33 e3
x1* a11 * x 2 = a 21 * x 3 a 31
a12 a 22 a 32
a13 x1 a 23 x 2 a 33 x 3
Neuman原理
物质张量、场张量
— 物质张量是建立晶体在外场作用下的响应与外场之间关系的物理性 能,物质张量受到晶体对称性的制约,如弹性系数 — 场张量:外场张量及晶体对外场响应后所产生的新的物理量,不受 晶体对称性的制约,如应力、电场 — 晶体响应,受外场、物理性能和晶体对称性的共同影响,如应变
张量第三章——精选推荐

张量第三章第三章⼏个基本的张量§3.1 度量张量⼀、度量张量j j i i g g δ= ji j i g g δ=协变基⽮量的逆变分量和逆变基⽮量的协变分量是单位张量。
若把每个基⽮量看成是异名基⽮量所构成的参照标架的⼀个特殊⽮量,则可以表⽰为:jij i g g g = j ijig g g =ij g 是i g 的协变分量,ij g 是i g 的逆变分量。
ij g 和ij g 称为度量张量。
ij g ——度量张量的协变分量或协变度量张量。
ij g ——度量张量的逆变分量或逆变度量张量。
证明:ijg ,ij g 是⼆阶张量:''''i j i i g g g =⼜ijj j i i j i ijj j i i j i j ij j j i i j j j ij i i jij i i i i i i g g g g g g g g g g g g '''''''''''''''''ββββββββββ==∴====同理,度量张量的混变分量是单位张量,即i ji j g δ=j i j i g δ=⼆、度量张量的性质和作⽤1、度量张量各分量等于同名基⽮量的点积。
ij k j ik j k ik j i g g g g g g g ==?=?δij j k ik j k ik j i g g g g g g g ==?=?δ2、度量张量是⼆阶对称张量。
ij j i g g g g ?=? jiij g g =i j j i g g g g ?=?ji ij g g =3、度量张量的协变分量和逆变分量相乘并按⼀对指标求和等于单位张量。
ji jk ik g g δ=jk ik hl jl ih l jl k ik j i j i g g g g g g g g g g ==?=?=δδ由上式,可由度量张量的协变分量求逆变分量或者反过来求。
2.5几种特殊的二阶张量

Ai j
j
A:A
tr A A
T
满足范数公理的三个条件:非负性、对称性与三角不等式, 可作为二阶张量空间的一种范数。
2.5.6
2.5.6.1
反对称二阶张量
定义
满足 T 的张量称为反对称张量。在任一笛卡儿 坐标系中
i j
0 1 2 1 3
T
n
T
-1
T
-1
T
-1
n 个T -1
2.5.4
正张量、非负张量及其方根、对数
正张量、非负张量都是对称二阶张量。 定义 正张量N >O满足u· u=N:uu>0 对于任意u≠0 N· 非负张量N ≥O满足u· u=N:uu≥0 对于任意u≠0 N· 对称二阶张量必定可在一组正交标准化基中化为对角标准形
u u
易证:
e3
( 包含了 的全部信息)
1
:
J2
2.5.6.5
反对称二阶张量所对应的线性变换
e1 e 2
e 2 e1
e3 0
e3 u
×u
u+ · u e2
· e u 1
对于空间任一矢量 u u1e1+u2e2+u3e3,
可证:利用任意一个非对称二阶张量T 可构造两个非负张量
X T T
T
O
Y T
T
T O
如果T 是正则的,则X,Y 是正张量:
X T T
T
>O >O
Y T
T
T
一般来说,X,Y 是两个不同的张量。可证:它们具有相同 的主分量,只是主轴方向不同而已。
二阶对称张量场可视化的一种新模式

二阶对称张量场可视化的一种新模式宋伟杰;崔俊芝;叶正麟;周敏【摘要】目前二阶对称张量场的可视化均是基于最大(次大)和最小特征向量场的,但这样定义的特征向量场存在着方向不连续的问题,而应力场的特征向量的方向却是永远连续的,鉴于此,提出了基于特征向量方向连续的一种可视化的新模式.从原理上阐述了问题产生的机理,提出了特征向量场的新定义-根据特征向量方向的连续性将特征向量场定义为第一和第二(第三)特征向量场,并对新定义的特征向量场在每一点包括退化点处的取值问题进行了研究.新定义克服了传统定义方向不连续的缺点,保持了特征向量场在每一点包括退化点处的方向上的连续性,同时,基于新定义的可视化从本质上体现了应力场及其他对称张量场本身具有的属性.【期刊名称】《计算机工程与应用》【年(卷),期】2011(047)006【总页数】4页(P1-4)【关键词】对称张量场;可视化;特征向量场【作者】宋伟杰;崔俊芝;叶正麟;周敏【作者单位】西北工业大学理学院应用数学系,西安,710072;中国科学院,数学与系统科学研究院,北京,100080;西北工业大学理学院应用数学系,西安,710072;西北工业大学理学院应用数学系,西安,710072【正文语种】中文【中图分类】TP391.4二阶对称张量场在物理、力学及生物医学等诸多领域有着非常广泛的应用。
例如,固体力学中的应力和应变,流体力学中的应力、粘性应力、雷诺应力和应变率都被描述为二阶对称张量。
另外,二阶对称张量场在核磁共振成像中也扮演着重要角色。
因此,研究二阶对称张量场的可视化技术具有非常重要的科学意义和跨学科的应用价值。
二阶对称张量场的可视化方法可以划分为两类。
起初,研究人员采用标量场的可视化方法来实现张量场的可视化。
这类方法除了不能从整体上展现张量场的结构之外,存在一个致命的缺点:可视化的结果严重依赖于坐标系的选择,这显然不是我们所希望的。
第二类方法是通过对与之等价的特征向量场进行可视化来实现张量场的可视化。
第六讲:二阶对称张量及其主轴化

1. 6. 2 二阶对称张量的主轴化
什么样的二阶张量可以主轴化(对角化)
数学要求:所有实对称矩阵都可以被对角化
张量主轴化方法
• 线性代数方法 • 求解张量矩阵特征值、特征向量
6
1. 6. 2 二阶对称张量的主轴化
例子 1 :对如下介电常数矩阵进行对角化
3 1 0 1 3 0 0 0 4
2 0 0 0 4 0 0 0 4
为了得到矩阵的上述变换,坐标轴发生了什么变化?
1/ 2 1/ 2 坐标变换矩阵: 1 / 2 1 / 2 0 0
0 0 1
7
1. 6. 2 二阶对称张量的主轴化
例子 2 :对如下介电常数矩阵进行对角化
2F ji E j Ei
ij ji
二阶偏微分结果与微分次序无关
4
1. 6. 1 二阶对称张量
对称张量的判断Байду номын сангаас
• 电导率张量
A J E J i Ei
单位时间电阻消耗的能量
A J i Ei ij Ei E j
ij ji
从能量的角度可以证明,介电张量、电导率张量为二阶对称张量! 应力张量、应变张量如何呢?
2
1. 6. 1 二阶对称张量
二阶对称张量举例 介电张量 电导率张量
应力张量
应变张量
3
1. 6. 1 二阶对称张量
对称张量的判断
• 介电张量
广义力 广义位移 电能表达式
dF E d D Ei dDi
Ei dDi Ei ijdE j
2F ij Ei E j
二阶张量的定义

二阶张量的定义二阶张量是线性代数中的一个重要概念。
在数学和物理学领域中,二阶张量被广泛应用于描述物质的性质、力学系统的行为以及电磁场的传播等问题。
本文将介绍二阶张量的定义和一些基本性质,以及其在实际应用中的意义。
我们来定义二阶张量。
在线性代数中,一个二阶张量可以被视为一个二维矩阵,它具有两个索引,通常用小写字母的下标表示。
一个二阶张量可以用以下形式表示:T_ij其中,i和j是张量的两个索引,可以取1、2、3等整数值。
这个二阶张量有四个分量,分别是T_11、T_12、T_21、T_22。
这些分量可以对应于矩阵的四个元素。
二阶张量的分量具有特定的变换规律。
当坐标系发生变换时,二阶张量的分量也会相应地发生变化。
具体而言,对于一个二阶张量T_ij,在坐标系变换下,其分量会按照以下规则进行变换:T_ij' = R_i^k * R_j^l * T_kl其中,T_ij'是变换后的二阶张量的分量,R_i^k和R_j^l是坐标系变换矩阵。
这个变换规律保证了二阶张量在不同坐标系下的表示是相容的。
二阶张量具有一些重要的性质。
首先,二阶张量可以进行加法和数乘运算,即两个二阶张量可以相加,一个二阶张量可以与一个标量相乘。
其次,二阶张量还可以进行张量积运算,即两个二阶张量可以进行分量乘积并相加的运算。
这些运算使得二阶张量具有了更强大的描述能力。
在实际应用中,二阶张量有着广泛的应用。
在物质力学中,二阶张量可以描述物质的应力和应变。
通过应力张量和应变张量的组合,可以得到物质的弹性模量和刚度矩阵等重要性质。
此外,在电磁学中,电磁场的张量表示也是一个二阶张量,可以用来描述电磁场的分布和传播。
二阶张量还在图像处理、机器学习等领域中有着重要的应用,例如图像的卷积运算和神经网络的权重矩阵等。
总结起来,二阶张量是线性代数中的一个重要概念,用于描述具有两个索引的二维矩阵。
二阶张量具有特定的变换规律和运算性质,可以用于描述物质的性质、力学系统的行为以及电磁场的传播等问题。
弹性力学第二章

强调指出:张量必须满足坐标变换,否则不能视为张量。也就是 说,从一个坐标系旋转到另一个新的坐标系,张量的表达形式不变。 即应有:T
= Ti1i2 ⋅⋅⋅in ei1 ⊗ ei2 ⊗ ⋅⋅⋅ ⊗ ein = Ti1i2 ⋅⋅⋅in βi1′i1 ei1′ ⊗ β i2′ i2 ei2′ ⊗ = βi1′i1 β i2′ i2
n n 12 n 1
⊗ β in′ in ein′
2
βi′ i Ti i ⋅⋅⋅i ei′ ⊗ ei′ ⊗
⊗ ein′
⊗ ein′
= Ti1′i2′ ⋅⋅⋅in′ ei1′ ⊗ ei2′ ⊗
注:1.对于一个给定的张量,其各分量必须满足式(2.19)的转换 关系;否则,不能视为一个张量。 2.虽然张量的分量是随坐标系的变化而变化的,但张量的本身 则不随坐标系的变化而变化。 3.在一个给定的坐标系,若某一张量的所有分量都为零,则由 式(2.19)可知,在任意的坐标系中这一张量的所有分量也 必为零。这种张量称为零张量,用O表示。
a1 a2 = b1 c1 b2 c2 a3 b3 c3
(2.9)
设: a = ai ei
eijk和δij之间的关系及其证明 :
若i、j、k三个指标中有两个取相同的值,则显然 (2.10) 式(2.10)两边都为零值;或l、m、n中有两个 取相同的值,上式两边也同样为零。下面证明: 当指标i、j、k取三个不同的值,且同时l、m、n 由式(2.10)等号右端行列式的 也取三个不同的值时,式(2.10)是否成立。 分析可知,任意两行或两列较 如: 换一次,行列式的绝对值不 变,仅改变符号,且其符号改 变规则与置换符号的定义是相 (b) 符合的。
12 n
12 n
(2.19)
第2章 二阶张量

4. 二阶张量的幂:
1)正整数次幂:T n = T ⋅T ⋅ ⋅T 2)零次幂:T 0 = G 3)负整数次幂:T ⋅ T −1 = T −1 ⋅ T = G,T −n = T −1 ⋅ T −1 T −1
◊ det(T )−1 = 1 det(T ) ◊ (T T )−1 = (T −1 )T ◊ ( A ⋅ B)−1 = B−1 ⋅ A−1
Q
=
Qi •
j
g i
g
j
= Q• j gi g
i
j
Q
=
Qi •k
g i
g
k
=
g gk,Q k
=
gk g k
若变化前是标准正交化基(指标无需分上、下),
正交变换后仍为标准正交化基
(5)正规正交张量与非正规正交张量
正常正交张量:det Q = +1;反常正交张量 det Q = −1 (6)正交张量的标准型和线性变换
Ni ij
=
N
ii j
,
Nij i
=
Nj ii
(而一般:N
i •
j
≠
Nj •i
N • j ≠ N •i
i
j
混变分量的转置 ≠ 系数矩阵的转置)
N ⋅u = u⋅N
(4) 反对称张量::Ω = −ΩT
Ωij
= −Ωji、Ω ij
= −Ω
、Ω ji
i
•j
= −Ωj•i、Ωi • j
= −Ω•ij
(而一般:Ω i •j
定理:[T ⋅ u, T ⋅ v, T ⋅ w] = det T [u, v, w]
光学材料复习概要

光学玻璃的色散
n2 ()
1
B1 2 2 C1
B2 2 2 C2
B3 2 2 C3
对于大多数无色光学玻璃而 言,色散来源于紫外与红外 波段的两个吸收带
Sellmeier 模型
n2 () A0 A1 2 A2 2 A3 4 A4 6 A5 8
Cauthy模型
光学玻璃的折射率与成分之间的关系
密度:对原子价相同的的氧 化物来说,其阳离子半径越 大,玻璃分子体积就越大, 密度越小。
分子折射度:原子价相同的 阳离子其半径越大(原子核 对外层电子吸引力越弱)则 离子极化率越高。
离子极化率还受其周围离子 极化的影响,当阳离子半径 增加时不仅其本身极化率上 升也提高了氧离子的极化率, 因而促使玻璃分子折射度迅 速上升。
激光玻璃:稀土离子
激活离子一般是发光谱带窄,色纯度高,转换效率高,荧光寿命跨度大, 具有四能级(或三能级系统)的稀土元素或离子。
基质玻璃是具有优良光学性能、机械性能以及热性能的硅酸盐玻璃,硼酸 盐及硼硅酸盐玻璃,磷酸盐玻璃和氟磷酸盐玻璃。
Nd 3+离子的4F3/2→4I11/2的跃迁 :1.064μm,室温
哑下标尽可能地靠近
T' ij
aik a Tjl kl
奇数阶的张量在具有反演中心i的晶体中是不存在的
晶体中具有物理意义的二阶张量都是对称张量:如应变张量不是 位移对位置的偏导eij,而是其中的对称部分。
张量的定义
张量的示性面:二阶张量的示性面是椭球或双曲面,其中椭球上 任意一点的径矢与法矢分别表示该二阶张量所跨居的作用矢量及 感生矢量。
在硅酸盐玻璃中逐渐增加氧化硼的含量,其性质变化曲线往往会出现极大 或极小值,称为“硼反常”,合理地应用这一反常现象可以改善玻璃的某 些物理化学性质,制得化学稳定性好,热膨胀系数小,折射率高而色散小 的玻璃。
二阶对称张量的示性面

⼆阶对称张量的⽰性⾯
⼆阶对称张量的⽰性曲⾯
⼆阶对称张量与⼆次曲⾯
1(,1,2,3)
ij i j S x x i j ==⼆阶曲⾯
i ki k
j lj l x a x x a x ′=′
=1ij ki lj k
l S a a x x ′′=kl
ij ki lj S S a a ′=kl
ki lj ij S a a S ′=
光率体
称⼆次曲⾯包围的椭球为光率体?椭球⾯上⽮径的长度即为折射率?沿晶体不同⽅向传输具有不同的折射率我们可以获得相互垂直两个偏振态在晶体某个波⽮⽅向的折射率。
K D E S
⊥⊥
折射率曲⾯
为什么研究折射率曲⾯
研究⽅便
形象直观
如何获得折射率曲⾯
取任意过晶体中⼼的直线⽅向为光线传输⽅向
利⽤该⽅向⽮量定义该⽅向过晶体中⼼的垂直截⾯,求出它与光率体外表⾯的交线(椭圆)
求该椭圆的长轴和短轴
由于取得⽅向任意获得的即为椭圆长短轴曲⾯-即两互相垂直偏振态的折射率曲⾯。
第五讲 二阶对称张量的性质

H ijkl ij kl ik
jl
il
jk
1.13 应力张量和变形速度张量---本构方程
1 定义
H 'i i
1
2 ... i n
Hii
1 2
... i n
2 置换定理
x3
x '1
x '2
H '12 H 12 H 23 H 31
jikl
jl
il
jk
ik
jl
il
jk
ji kl jk il jl ik jk il jl ik
H ijkl
1 2
H
jikl H ijkl1 ij kl ik jl il jk ik jl il jk ji kl jk il jl ik jk il jl ik 2
0 1 0
0 0 1
1 0 0 0 0 1
H ijkl H ' ijkl im
下标3出现单数次:
jn
kp lp H mnpq
jn
ij
0 1 0
H ijkl H ' ijkl im
x '3 x 3
kp lp H mnpq H ijkl
1 0 0 0 1 0 0 0 1
x '3 x 3
x2 x1 x '2 x 2
x '1 x 1
01 张量基础

第一章 张量基础晶体的物理性质一般是各向异性的,这 些性质常常需要用与方向有关的两个可测量 的量之间的关系来定义,而用张量来描述, 张量是晶体物理的数学基础。
第一章 张量基础张量的基本知识 张量的变换定律 张量的几何表示法 晶体对称性对晶体性质的影响 晶体物理性质的相互关系1.1 张量的基本知识(1)一、标量与矢量1、标量在物理学中,常遇到这样一些量,如物体的温 度、密度等等,它们都与方向无关。
这些无方向的 物理量,称为标量(也称零阶张量)。
它们完全由 给定的某一数值来确定。
1.1 张量的基本知识(2)2、矢量与方向有关的物理量,称为矢量(也称一阶张 量)。
它们不仅有大小,而且有一定的方向。
如电 场强度、电位移、温度梯度等都是矢量。
矢量用上 方带箭头的字母表示,如电场强度可表示为 E 。
矢量还可以用直角坐标系(x1,x2,x3 )中三个坐 标轴上的分量来决定它的大小和方向,于是 就可以 E 写成: E = [E , E , E ]1 2 3——字母的下标1、2、3分别代表x1, x2, x3轴。
这 样,当坐标轴选定后,矢量就完全由其在这些轴 上的分量来确定。
1.1 张量的基本知识(3)二、二阶张量在各向同性介质中,电场强度矢量 E 和电位移矢量 D 的 方向永远保持一致,在电场强度不高的情况下,两者成线形 关系,因此,它们间的关系可以直接表示为:D =εEε——介电常数在各向异性介质中,电场强度矢量 E 和电位移矢量 D 的 E 方向经常不一致,因此, D 在三个坐标轴上的分量都与 的三 个分量相关,此时,它们间的关系可表示为: D1 = ε 11 E1 + ε 12 E 2 + ε 13 E3 D2 = ε 21 E1 + ε 22 E 2 + ε 23 E3 D3 = ε 31 E1 + ε 32 E 2 + ε 33 E31.1 张量的基本知识(4)即⎛ D1 ⎞ ⎛ ε 11 ε 12 ⎜ ⎟ ⎜ ⎜ D2 ⎟ = ⎜ ε 21 ε 22 ⎜ D ⎟ ⎜ε ⎝ 3 ⎠ ⎝ 31 ε 32ε 13 ⎞⎛ E1 ⎞ ⎟⎜ ⎟ ε 23 ⎟⎜ E 2 ⎟ ⎜E ⎟ ε 33 ⎟ ⎠⎝ 3 ⎠ε 11 ε 12 ε 13 方形表 ε 21 ε 22 ε 23 就是一个二阶张量。
第二章 二阶张量

第二章:二阶张量1. ij T ij ji i j j i i j T T T ;=⊗=⊗=⊗T g g T g g g g ij i j ij i j T ; T =⋅⋅=⋅⋅g T g g T g2. T =T.u u.TT ij ij ij ij j i j i i j j i ( = T T u ;T T u )⋅⊗==⊗⋅=u.T u g g g T.u g g u g 3.i .j det()T =T行列式不等于零的二阶张量定义为正则二阶张量 正则二阶张量存在逆张量:1-⋅T T =G 4.主不变量①1)()()ζ⋅⋅⨯⋅⋅⨯⋅⨯⋅=⋅⨯T u (v w)+u (T v w)+u (v T w )u (v w)(1.()::i i Tr T ζ====T T G G T)()()i j k ijk S u v w ⋅⋅⨯⋅⋅⨯⋅⨯⋅=T u (v w)+u (T v w)+u (v T w )(m m mijk .i mjk .j imk .k ijm S T T T εεε=++由于mik imkmmmiik .i mik.i imk.k iimS T T T εεεεε=-⇓=++=当i,j,k 当中有两个相等时,0iik S = 当i j k ≠≠时i j k m ijk .i .j .k ijk not sum ijk .m ijk S (T T T )T εε=++=②2)[)][()(]()[()]()ξ⋅⋅⋅⨯⋅⋅⨯⋅⋅⋅⨯⋅=⋅⨯T u (T v w +u T v T w)+T u (v T w u v w (2......122123323113.1.2.1.2.2..3.2..3.3.1.3.1112233.1.2.2..3.3.1223311.1.2.2..3.3.111()22ij l mi j i l lm i j i j l j T T T T T T T T T T T T T T T T T T T T T T T T TTTTT T ζδ==-=-+-+-=++注意:ij ijklm lmkδδ=是张量的分量张量T 行列式中各阶主子式之和)[)][()(]()[()]i j k ijk S u v w ⋅⋅⋅⨯⋅⋅⨯⋅⋅⋅⨯⋅=T u (T v w +u T v T w)+T u (v T w ( 其中......()m n m n n mijk i j mnk j k imn k i mjn S T T T T T T εεε=++..........()0m n m n n m iik i i mnk i k imn k i min m n i i mnk m n i i nmk iik S T T T T T T T T T T S εεεεε=++===-=当i,j,k 当中有两个相等时,0iik S = 当i j k ≠≠时 (122123323113).1.2.1.2.2..3.2..3.3.1.3.12()()i j j i j k k j k i i k ijk i j i j j k j k k i k i ijk not sumijkijkijkS T T T T T T T T T T T T T T T T T T T T T T T T εεζε=-+-+-=-+-+-=③()[()()]det()()⋅⋅⋅⨯⋅=⋅⨯T u T v T w T u v w...()[()()]()()()i j k l m nl m n ijkl m n lmn T T T u v w det u v w det εε⋅⋅⋅⨯⋅===⋅⨯T u T v T w T T u v w ④()()det()()T T -⋅⨯⋅=⨯T v T w T v w()[()()]det()()[()()]det()()T⋅⋅⋅⨯⋅=⋅⨯⋅⋅⋅⨯⋅=⋅⨯T u T v T w T u v w u T T v T w T u v w由于上式对任意矢量u 都成立[()()]det()()()()det()()T T-⋅⋅⨯⋅=⨯⋅⨯⋅=⨯T T v T w T v w T v T w T T v w⑤主不变量与矩之间的关系*1*2..*3...()()()ii i kk i i j kj k i Tr T Tr T T Tr T T T ζζζ===⋅==⋅⋅=T T T T T T2212112212ij k li j j i kl .i .j .i .j .i .j *T T (T T T T )[()]ζδζζ==-=-3.....................*3***13121611()()661(()23)6ijk l m nlmn i j ki j k j k i k i j j i k i k j k j i i j k i j k i j k i j k i j k i j k e e T T T T T T T T T T T T T T T T T T T T T ζζζζζ==++-++=+- 二阶张量标准形 1. 特征值、特征向量 λ⋅=T v v ()λ-⋅=T G v 01111232221233331230.........T T T T T T T T T λλλ--=-特征方程 321230λζλζλζ-+-= 特征根是不变量2. 实对称二阶张量标准形 1. 特征根是实根*************; ; ()0 () λλλλλλλλ⋅=⋅=⋅⋅=⋅⋅⋅=⋅-⋅=⇒=⋅-=⇒=N v N v v v N v v v v N v v v v v N v v 0v v2. 特征向量互相正交1112222112112212121212 ; ; ()00λλλλλλ⋅=⋅=⋅⋅=⋅⋅⋅=⋅-⋅=⇒⋅=N v v N v v v N v v v v N v v v v v v v 3. 不存在约当链如果λ是n 重根,但不存在相应的特征向量12,v v ,使1122 ; λλ⋅=⋅=T v v T v v则一定存在约当链11221λλ⋅=⋅=+T v v T v v v然而对对称张量112212112121211110λλλλ⋅=⋅=+⇓⋅⋅=⋅⋅⋅=⋅+⋅⇓⋅=N v v N v v v v N v v v v N v v v v v v v这是不可能的。
高等流体力学-第4讲
·二次曲面 F ( r ) = ± 1 可看作二阶对称张量的几何表示,是有心二次曲面; ·在主轴坐标系下:如果主值 λ1 λ 2 λ 3 同号,表示的半径分别为:
G
1
1
1
λ1
λ2
λ3
的椭球面;
·在主轴坐标系下: 如果主值异号,则表示的双曲椭圆面。
G 1 (5) 对称张量 S 与矢径的内积为 : S ⋅ r = gradF 2
∇P= ∂ pi i "i ∂xk
1 2
n
其梯度运算的结果是一个 (n+1) 阶张量 。
( )
JGJG ∂aij JGJGJG ∂ JG ek aij ei e j = ek ei e j ∇A = ∂xk ∂xk
(
)
1.5 张量初步
1.5.6 张量的微分运算
¾ 张量的散度运算 n 阶张量P 的散度 — 定义为哈密顿算子与张量P 的左向内积:
ei′ = α ij ei′
α isα js = α siα sj = δ ij
ai′ = αij a j a j = α ji ai′
′ = αisα jt pst pij ′ pij = αsiαtj pst
1.5 张量初步
1.5.5 二阶张量
⎛ p11 ⎜ {pij } ↔ ⎜ p21 ⎜p ⎝ 31 p12 p 22 p32 p13 ⎞ ⎟ p 23 ⎟ p33 ⎟ ⎠
+
p11 p31
p11 p12 ⎞ ⎟− p =0 + p33 p21 P22 ⎟ ⎠ p13
由根与系数的关系得知: —— 二阶张量的三个不变量 ——
I1 = p11 + p22 + p33 =λ1 +λ2 +λ3
【南航研究生课程】[张量分析]第 2 章 二阶张量
![【南航研究生课程】[张量分析]第 2 章 二阶张量](https://img.taocdn.com/s3/m/d4503a0aa216147917112883.png)
第2章 二阶张量研究定义在空间一个固定点(张量的元素是实常数,i g 也是常数)上的二阶张量随坐标系转动的不同形式,不涉及与另一个张量的关系,也不涉及张量运动。
2.1 二阶张量与矩阵的对应分量同一坐标系:j i ijj i i ij ij i j i ij T T T T g g g g g g g g T ====∙∙ 另一坐标系:j i j i j i i i j i j i j i j i T T T T ''''''''∙'''∙'''''====g g g g g g g g● 对应不同坐标的分量不同:,,,jj i i iji j iji j i i jj T T T T T T T T ''''∙∙''''∙∙≠≠≠≠● 对应不同并矢的分也不同:iji i j i ij T T T T ≠≠≠∙∙● 指标满足升降:mm mniji mj im iim nj T T g g T g T g ∙∙===转置()()()()jiijTTijTiTjTj i i j ijijTT TT ∙∙====T g g g g g g g gi jj ii j jiji ij ji i j T T T T ∙∙====g g g g g g g g 分量指标互换 jijii jijij i j ii j i T T T T ∙∙====g g g g g g g g 并矢指标交换一般情况混变分量的转置≠系数矩阵的转置对称 T=N Nji ij N N =、ji ij N N =、i j i j N N ∙∙=、j i j i N N ∙∙=N u u N ⋅=⋅反对称 T=-ΩΩij ji ΩΩ=-、ijjiΩΩ=-、i i jjΩΩ∙∙=-、jj i iΩΩ∙∙=-,Ωu u Ω⋅-=⋅行列式的值 定义:i jT∙=T det , iji jjiij T g g T T g T 2===∙∙, ij g G =ji ij T T =、jiijTT =、jj iiT T ∙∙=、i iT tr ∙=T ,()i iiiS T tr ∙∙+=+S T ,()S T S T ⋅⋅=⋅tr ,():Ttr ⋅=T ST S二阶张量与矢量的点积—矢量线性变换=⋅w T u , ii jjw T u ∙=⋅,⋅≠⋅T u u T2.2 正则与退化的二阶张量定理:任意二阶张量将一个线性相关的矢量集映射为线性相关的矢量集 【设矢量集()i u 线性相关,则存在不全为零的实数()i α使:1()()I i i i α==∑u 0,()11()()()()I Ii i i i i i αα===⋅=⋅∑∑0T u T u , 所以()i ⋅T u 也线性相关】定理:[][],,det ,,⋅⋅⋅=T u T v T w T u v w[det T 为两个平行六面体的体积比,三维空间中3个矢量是否线性相关取决与它们的混合积是否为零] 正则与退化det 0≠T 正则二阶张量;否则为退化的二阶张量(1) T 为正则⇔()i u (i =1,2,3) 性无关,则()i ⋅T u 也线性无关。
二阶反对称张量

二阶反对称张量一、引言在数学和物理中,张量是一个多维数组,它可以描述不同类型的数据和满足各种数学运算的规则。
反对称张量是一种特殊的张量,其特点是任意两个不同的指标互换后,张量值会变号。
二阶反对称张量是所有反对称的二阶张量,它们形成一个线性空间。
本文将详细介绍二阶反对称张量的定义、性质和在物理中的应用。
二、二阶反对称张量的定义二阶张量是一个二维数组,而二阶反对称张量则是满足特定对称性质的二阶张量。
具体来说,对于一个二阶张量T,如果任意两个不同的指标i和j互换后,T[i][j]=-T[j][i],则称T为二阶反对称张量。
三、二阶反对称张量的性质1. 对称性:如上所述,二阶反对称张量具有反对称性,即对于任意两个不同的指标i和j,T[i][j]=-T[j][i]。
2. 零元:在所有二阶反对称张量中,零张量是最小的元素,即对于任意指标i和j,T[i][j]=0。
3. 线性空间:所有二阶反对称张量构成一个线性空间。
在这个空间中,零元是唯一的零元素,任意一个元素T可以表示为零元素的线性组合。
四、二阶反对称张量的物理应用1. 电磁学:在电磁学中,电磁场是一个典型的二阶反对称张量。
磁场B的分量满足B[i][j]=-B[j][i],电场E的分量也满足同样的性质。
因此,电磁场可以看作是二阶反对称张量的实例。
2. 晶体学:在晶体学中,晶体结构的对称性可以通过对称元素(如反射面、旋转轴等)来描述。
这些对称元素可以用二阶反对称张量来表示。
通过计算这些对称元素的组合和变换,可以得出晶体的完整对称性。
3. 弹性力学:在弹性力学中,应力张量和应变张量都是二阶张量。
当物体受到外力作用时,会产生应力和应变,这些应力和应变可以通过二阶张量来表示。
特别地,当物体具有对称性时(如球形或立方体),其应力张量和应变张量可能成为二阶反对称张量。
4. 量子力学:在量子力学中,角动量算符是一个典型的二阶反对称张量。
角动量算符由三个分量组成,满足L[i][j]=-L[j][i],其中i和j是空间方向的指标。
曲面的度量张量与积分表示问题

曲面的度量张量与积分表示问题曲面的度量张量是几何学中的重要概念之一,它描述了曲面上每一点处的曲率性质。
在本文中,我们将探讨曲面的度量张量以及利用度量张量进行积分表示的相关问题。
一、曲面的度量张量曲面的度量张量是一个对称的二阶张量,用来测量曲面上的长度、角度以及曲率等几何性质。
设曲面为Σ,参数化表示方式为u,v,则度量张量的分量可以表示为:g_ij = r_u • r_v其中,r_u和r_v分别为曲面上两个参数u和v方向的切向量。
二、度量张量的性质1. 正定性:度量张量是正定的,即对于任意曲面上的切向量v,有v • g • v ≥ 0,其中v • g • v表示内积。
2. 对称性:度量张量是对称的,即g_ij = g_ji,其中i和j为张量的指标。
三、度量张量的计算方法通过给定曲面的参数化表示,我们可以计算出度量张量的分量。
具体而言,可以分别计算出r_u和r_v的分量,然后代入度量张量的表达式即可得到结果。
例如,对于球面的参数化表示x(u,v) = (sinu*cosv, sinu*sinv, cosu),可以计算出度量张量的分量。
四、度量张量与曲面积分利用度量张量,我们可以定义曲面上的面积元素dA。
对于参数化表示的曲面Σ,面积元素可以表示为:dA = √(g)·dudv其中√(g)表示度量张量的行列式的平方根,dudv为参数域上的面积元素。
基于曲面上的度量张量,我们可以进一步定义曲面上的曲线积分和曲面积分。
曲线积分可以用来计算曲面上的向量场沿某条曲线的积分值,而曲面积分用于计算曲面上的标量场或者向量场的积分。
这些积分的具体计算方法需要借助度量张量的分量来实现。
五、应用与拓展曲面的度量张量在几何学中应用广泛,不仅用于描述曲面的几何性质,还可以用于求解曲面上的最短路径、计算曲面的曲率等。
在物理学中,度量张量也被应用于描述时空的几何结构。
此外,度量张量的概念可以拓展到更高维的流形,如三维空间中的曲面、四维时空中的曲面等。
柯西格林应变张量

柯西格林应变张量1. 引言柯西格林应变张量(Cauchy’s strain tensor)是描述物体变形程度和方向的重要工具。
它在固体力学、材料科学和工程领域中被广泛应用。
本文将介绍柯西格林应变张量的定义、性质和应用,并探讨其在实际问题中的意义。
2. 定义柯西格林应变张量是一个二阶对称张量,用于描述物体在受力作用下发生的形变情况。
它可以表示为一个3×3的矩阵,其中每个元素代表了物体在各个方向上的拉伸或压缩程度。
具体而言,对于一个三维空间中的物体,其柯西格林应变张量可以表示为:其中εij表示物体在i方向上相对于j方向的形变程度。
由于柯西格林应变张量是对称的,因此εij=εji。
3. 性质柯西格林应变张量具有以下几个重要性质:3.1 对称性柯西格林应变张量是一个对称矩阵,即εij=εji。
这意味着物体在不同方向上的形变是相互关联的,不存在剪切形变。
3.2 形变测量柯西格林应变张量可以用来测量物体在受力作用下的形变程度。
通过计算张量的各个分量,可以了解物体在各个方向上的拉伸或压缩情况。
3.3 形变率柯西格林应变张量还可以用来计算物体的形变率。
通过对时间求导,可以得到形变率张量,进一步分析物体形变的快慢和方向。
4. 应用柯西格林应变张量在材料科学和工程领域中有广泛的应用。
以下是一些典型的应用场景:4.1 结构力学在结构力学中,柯西格林应变张量被用来分析建筑、桥梁、航天器等结构物在受力作用下的形变情况。
通过计算应变张量,可以评估结构物是否存在过大的形变,从而设计出更加安全可靠的结构。
4.2 材料工程柯西格林应变张量对于材料工程的研究也非常重要。
通过分析材料在受力作用下的形变情况,可以评估材料的强度、刚度和韧性等力学性能。
这对于材料的选择、设计和加工具有指导意义。
4.3 地质学在地质学中,柯西格林应变张量被用来研究地壳运动和地震活动。
通过分析地壳中的形变情况,可以预测地震的发生概率和地质灾害的风险。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二阶对称张量的示性曲面
二阶对称张量与二次曲面
1(,1,2,3)
ij i j S x x i j ==二阶曲面
i ki k
j lj l x a x x a x ′=′
=1ij ki lj k
l S a a x x ′′=kl
ij ki lj S S a a ′=kl
ki lj ij S a a S ′=
光率体
•称二次曲面包围的椭球为光率体•椭球面上矢径的长度即为折射率•沿晶体不同方向传输具有不同的折射率
•我们可以获得相互垂直两个偏振态在晶体某个波矢方向的折射率。
K D E S
⊥⊥
折射率曲面
为什么研究折射率曲面
研究方便
形象直观
如何获得折射率曲面
取任意过晶体中心的直线方向为光线传输方向
利用该方向矢量定义该方向过晶体中心的垂直截面,求出它与光率体外表面的交线(椭圆)
求该椭圆的长轴和短轴
由于取得方向任意获得的即为椭圆长短轴曲面-即
两互相垂直偏振态的折射率曲面。
