浅谈矩阵在信息学竞赛中的应用

浅谈矩阵在信息学竞赛中的应用

天津南开中学 肖天

矩阵，是线性代数中的基本概念之一。一个m ×n 的矩阵就是m ×n 个数排成m 行n 列的一个数阵。由于它把许多数据紧凑的集中到了一起，所以有时候可以简便地表示一些复杂的模型。矩阵乘法看起来很奇怪，但实际上非常有用。它是这样定义的，只有当矩阵A 的列数与矩阵B 的行数相等时A ×B 才有意义。一个m ×n 的矩阵(a i ,j )左乘一个n ×p 的矩阵(b i ,j )，会得到一个m ×p 的矩阵(c i ,j )，满足

p j m i b a c n k j

k k i j i ≤≤≤≤?=∑=1,11,,,

矩阵乘法满足结合率，但不满足交换率。

还有一个与矩阵紧密相关的概念——向量。（行）向量可以看成是一个行数为1的矩阵，因此它可以左乘一个矩阵得到一个新的（行）向量。

本文讨论的是矩阵一方面的作用：它能表示一组事物变化的过程。而矩阵乘法就是把事物变化过程连接起来的工具。具体地说，就是用向量表示一个对象的一组属性，用矩阵表示这些属性变化的过程，用表示初始属性的向量与若干个矩阵连乘，所得向量表示的就是一系列变化后的属性。

上面说得有些抽象，让我们来看两个实际应用中的例子。

几何变换

图形的几何变换有着广泛的应用，矩阵在其中起到了重要作用。图形变换是以点变换为基础的，把一个图形看作若干顶点和连结它们的边，对顶点进行变换后重新把边连起来，就得到了变换后的图形。下面我们介绍如何进行点的变换。

在介绍之间先要明确一下点的表示法。通常应用的是齐次坐标表示法——用(n +1)维向量表示一个n 维坐标（我也不理解为什么叫“齐次”）。例如一个二维空间内的点P (x ,y )可以表示为(kx ,ky ,k )。也就是说，一个点的表示并不唯一。这样表示有诸多好处，这里不再赘述。

下面我们以二维图形的几何变换为例进行说明。

对点的变换是通过矩阵完成的。用表示点P 的向量(kx ,ky ,k )左乘一个3阶矩

设

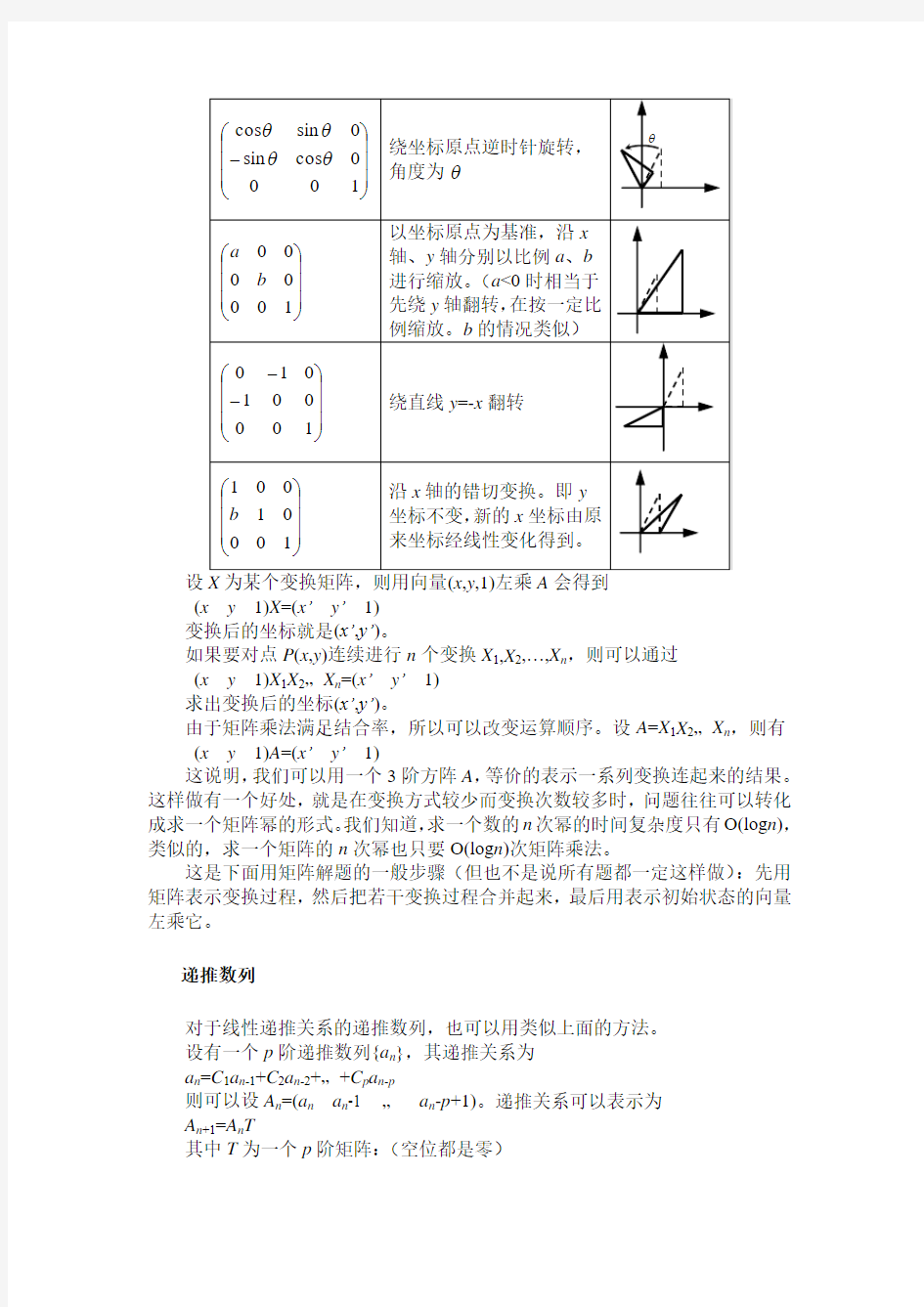
(x y1)X=(x’y’1)

变换后的坐标就是(x’,y’)。

如果要对点P(x,y)连续进行n个变换X1,X2,…,X n，则可以通过

(x y1)X1X2…X n=(x’y’1)

求出变换后的坐标(x’,y’)。

由于矩阵乘法满足结合率，所以可以改变运算顺序。设A=X1X2…X n，则有(x y1)A=(x’y’1)

这说明，我们可以用一个3阶方阵A，等价的表示一系列变换连起来的结果。这样做有一个好处，就是在变换方式较少而变换次数较多时，问题往往可以转化成求一个矩阵幂的形式。我们知道，求一个数的n次幂的时间复杂度只有O(log n)，类似的，求一个矩阵的n次幂也只要O(log n)次矩阵乘法。

这是下面用矩阵解题的一般步骤（但也不是说所有题都一定这样做）：先用矩阵表示变换过程，然后把若干变换过程合并起来，最后用表示初始状态的向量左乘它。

递推数列

对于线性递推关系的递推数列，也可以用类似上面的方法。

设有一个p阶递推数列{a n}，其递推关系为

a n=C1a n-1+C2a n-2+…+C p a n-p

则可以设A n=(a n a n-1 …a n-p+1)。递推关系可以表示为

A n+1=A n T

其中T为一个p阶矩阵：（空位都是零）

?????

??

? ??=-p p C C C C T 111121 这样，求数列中第n 项时（n 远大于p ），我们可以根据S n =S p T n -p 通过矩阵求幂得到一个时间复杂度O(p 3log n )的算法。

到这里，你已经可以基本看到矩阵在解题中起到什么作用了。下面让我们看一道具体的题目。

例1：细菌（IPSC2003）

题目大意：（这里略去了题目背景）

有N （

这些数重复执行着M （M ≤20）条指令（编号从0开始），即第S 时刻执行第((S -1) mod M )条指令。求在第T （T ≤109）时刻执行指令后，所有b i 的值。

分析：

由数据规模就可以看出，时间复杂度O(NT )的模拟是不可行的。观察到M 的值比较小，所以我们应该找出这一组指令的特点，然后用高效的算法重复这一过程。

每一时刻的状态显然可以用一个向量(b 0

,b 1,…,b N -1)来表示，因此我们来看看能不能把每条指令都用一个N 阶方阵来表示。实际上，在找到这些矩阵之前，就可以断定这是一定可行的。因为，每条指令执行后，每个新的b i 的值都与原来的(b 0,b 1

这样，问题转化为给定一个向量B =(b 0,b 1,…,b N -1)，以及M 个N 阶矩阵C i (0≤i

B ’=B

C 0C 1…C M -1C 0C 1…C M -1……

这个可以转化为

B ’=B (

C 0C 1…C M -1)T div M C 0…C (T mod M )-1

求幂的部分只需要对数次矩阵乘法。因此这个算法的时间复杂度只有O(N 3(log(T div M )+M ))。

（div 表示做除法并去商的整数部分，mod 表示取余数）

可以看出，矩阵可以简洁地表示出一个线性转化关系的全部信息。在重复这种转化过程时，对数时间的求幂算法就会发挥重要的作用。

类似的题目还有下面这一道。

例2：硬币（Sgu173）

题目大意：

有N 枚硬币，开始时正面或反面朝上。还有一个(K -1)维二进制向量A 。接下来，我们要对这N 枚硬币进行M 次操作。第i 次操作是：选定K 个连续的硬币，然后对这K 个硬币进行D i 次转换。

对于给定的K 个硬币一排C ，转换过程是这样的：

? 把C 中的硬币向左循环一个位置；

? 从左起第一个到第(K -1)个依次检查每一个硬币，如果C i 是反面朝上且A i =1，则翻转最右面一枚硬币。

显然，对确定的K 枚硬币进行转换，结果由向量A 完全确定。但向量A 并不是已知的，你只知道L 次转换的情况（转换前及转换后硬币的状态）。保证只有一个满足条件的向量A 。

给定每次操作选了哪些硬币以及重复了多少次，你的任务是通过这N 枚硬币所有操作完成后的最终状态求出初始状态。

数据规模：2≤N ≤50，1≤M ≤10，1≤L ≤200，2≤K ≤N ，D i ≤106

分析：

解这题显然要分两步。先要求出向量A ，这一步就是解一个线性方程组，不再赘述。第二步就是通过向量A 对转换进行倒推。由于D i 很大，显然不能一步一步地倒推。

可以发现，每一次转换后，前(K -1)枚硬币的状态很容易确定，而最后一枚的状态也不过是它原先的状态加上前(K -1)枚硬币的状态与向量A 对应元素乘积之和模2的余数，都是线性关系（用1表示反面，0表示正面）（你可以把它看成一个K 阶递推数列）。因此，一个K 阶矩阵就可以表示一次转换过程。设A =(a 1,a 2,…,a K -1)，则这个矩阵为（空位都是零）

?????

??? ?

?=-1211111K a a a T 接下来的工作就简单了。对第i 次操作，求出T 的D i 次幂。设转换前的硬

币状态为X =(X 1,X 2,…,X K )，转换后为C =(C 1,C 2,…,C K )，则可列方程XT =C 。这是一个线性方程组。从后向前对每次操作解一次方程就可以求出初始状态了。算法复杂度为))log (O(3

2N D M K LK M

i i +++∑。 我在最初做这道题的时候，找到的算法时间复杂度比上面这个稍高一点，为))log (O(3

2∑++M

i i D M N LN 。当时，我没有注意到每次转换只与K 枚硬币有关，而是用一个N 阶矩阵表示。（上面那个矩阵是这个N 阶矩阵的一个子矩阵，而其它位置中只有主对角线上是1，其余的是0。）忽略了每次转换只与K 枚硬币有关这一点造成了时间上的浪费，不过解题的过程稍微简化了一点：表示M 次操作的矩阵都是面向所有硬币的，所以可以把这些操作的矩阵乘起来，得到一个表示所有操作的矩阵，这样只需要解一个方程组就可以了。

比较一下上面两种方法。一个是以每一次操作的矩阵为系数矩阵解方程（系数矩阵通常写成上面给出的操作矩阵转置的形式），前一次方程组的解是后一个方程组的常数项；另一个是以所有操作矩阵的乘积为系数矩阵解方程，只解一次方程。这是不是说可以把线性方程组的系数矩阵相乘呢？让我们来看下面这道题。

例3：开关灯（笔者原创）

题目描述：（呵呵，这是我自己出的第一道题，也许有些罗嗦。如果您嫌长，可以跳过前四段）

天天在小时候玩过一个开关灯的小游戏。游戏是这样的，有5×5的方格，每个格子里有一盏灯和一个按钮。按下一个按钮会改变其所在格以及与之相邻的格子内灯的状态（由开到关，或由关到开）。一开始，有一些灯是开的，另一些是关的。通过按动按钮使所有灯都关上是游戏的目标。

玩了一段时间后，天天就觉得没意思了。因为每次只要尽量把亮的灯都集中到一条边上或一个角落里，之后往往出现相同的局面。时间长了，他记住了很多局面的定式，经常轻而易举地就过关了。于是天天给游戏增加了难度。游戏中每个按钮所支配的灯仍是确定的，但没有规律，可以在游戏开始前由游戏者规定或由计算机随机产生。游戏的目的不变。

这样，天天创造出了自己数不清的游戏，于是又产生了浓厚的兴趣，一直持续到他接触了信息学竞赛。

天天学会编程实现高斯消元法之后，发现改造后的游戏不过等价于一个线性方程组，他只要编个程序就可以解决了，甚至连N ×N （N ≤10）的问题程序都可以在瞬间出解。游戏又变得没有意思了。

玩了这么长时间，天天对这个游戏颇有感情，特别想恢复它的挑战性，于是苦思冥想之后将游戏扩展到了三维。一个M ×N ×N （M ≤100000，N ≤10）的方块，划分为M 层，每层N 行N 列个单元。每个单元内有一盏灯和一个按钮。每个按钮控制着与它同一层的某些灯（由游戏者规定或计算机随机产生），若它不是在最底层，它还控制与它所在单元相邻（有公共面）的下面一个单元里的灯。另外，层间的控制关系在所有层中都是一样的。也就是说，如果某一层中第X 行Y 列

的按钮控制着该层第X’行Y’列的灯，那么每一层第X行Y列的按钮都控制着同层第X’行Y’列的灯。按下一个按钮，就会改变所有它控制的灯的状态。一开始，只有最上面一层的某些灯是开的，其余都是关着的。游戏的目的还是通过按动按钮使所有灯都关上。显然，每个按钮至多被按一次。（游戏开始前，天天已经确认了在第一层中存在唯一的方案使该层所有灯都关上。）

这么大的规模，当然要用程序解决了。即使这样，由于按钮太多，找到一个完整的方案也不太现实。不过，天天还是关心给定所有按钮的支配关系，问题是否有解，如果有解最下面一层哪些按钮要被按下——这就是你的任务。

分析：

显然，下面的决策不会影响到上面，所以我们可以从上到下一层一层的解决。

与扩展前的问题一样，每一层都可以列一个线性方程组。层与层之间的关系只有每个按钮能控制它下面一盏灯，这相当于每一个方程组的解就是下一个方程的常数项。所以，我们的任务就是连续解这(M-1)个方程组，最后一个方程组的解就是答案。简单的解这些方程，时间复杂度会达到O(N6M)。由于所有方程组的系数矩阵都相同，所以消元的过程只需要做一次。所以对每个方程我们只要做一次时间复杂度O(N4)的回代。不过，总的时间复杂度为O(N4M)，还是不理想。

因此，我们应该用数学语言分析一下这样一些方程组有什么性质。虽然每一层是一个二维的事物，但它并没有体现出比一维事物更多的性质。所以，我们可以用一个N2维的向量表示一层中所有灯的状态，或一层中对所有按钮的决策（按或不按）。其中，灯是开着的或按钮要被按下用1表示，否则用0表示。并用一个N2×N2的矩阵A表示一层中按钮与灯的控制关系，其中一个元素等于1表示它所在行对应的按钮控制着它所在列对应的灯，等于0则表示相反意义。设X0表示第一层所有灯的初始状态，X i表示对第i层所有按钮的决策，则可以列方程组X1A=X0

（注：例2中提到过，人们通常用列向量表示未知数和常数项，写作A T X1T=X0T的样子。这里是为了与上下文一致才这样写的。）

根据不同层之间按钮与灯的控制关系，X1又可以表示第一层决策进行完而其他决策尚未进行时第二层所有灯的状态。所以

X2A=X1

将A分别右乘上式左右两边，得到

X2A2=X1A，所以X2A2=X0

类似的，我们可以推出

X M A M=X0

这样，我们只要解一次方程组即可，而其系数矩阵是一个矩阵的幂，用上文提到的方法即可。

容易证明，如果一个线性方程组有唯一解，那么无论如何改变其常数项，它总有唯一解。所以问题的答案一定是存在的。

这个算法时间复杂度为O(N6log M)。

另外还有一个类似的复杂度相同的办法，即先求出A的“逆矩阵”A-1（实际就相当于消元的过程），然后可以得到X M=X0(A-1)M，进行计算。这里有个问题，如果A-1不存在，这个办法就不可行了。但我尚未确定此时问题是否一定有解，所以题目中只好作了有唯一解的规定。

注意，解方程过程中讨论的所有运算像例2中一样都要对2取模，或者说都是二进制运算。即加法相当于二进制异或，乘法相当于二进制与。在这种情况下，

很多问题的性质会有一定改变（所以上面的“逆矩阵”加了引号），需要引起重视。

提到线性方程组，我们就会想起系数矩阵，而且刚才惊奇地发现他们居然能够相乘。想一想还有没有其他的模型与矩阵关系密切呢？也许我们还会有同样惊人的发现。图！说到图，邻接矩阵是一种很常用的表示方法。难道它也可以做乘法？没错。不信就接着往下看。

例4：好看的图案（Sgu197）

题目大意：

有一个N ×M 的方格，将每个格子染成黑色或白色，使得不存在一个2×2的方格其中4个格子同色。求有多少种满足条件的染色方案。输出结果模P 的余数。

数据规模：1≤N ≤10100，1≤M ≤5，1≤P ≤10000。

分析：

非常奇怪的数据规模应该很容易引起我们的注意。逐行递推可以得到一个O(22M N )动态规划算法，但它在庞大的N 面前显得毫无用处。而每行不超过5个格子暗示我们应该认真研究一下行的性质。

其实，在动态规划中我们已经用到了一点，那就是题目中任意2×2的方格不

同色的要求只对相邻的两行起作用。又因为每行可能的状态只有2M 种，所以可

以知道哪两个状态可以相邻。由此我们就可以建一个图G =(V ,E )。一行中每一个状态对应一个点，如果两个状态可以相邻，就从每一个点向另一个点各引一条有向边。

这样，问题转化为了在一个有向图中求长度为(N -1)的路径有多少条。这里的路径可以经过重复的点和重复的边。上面的动态规划实际就是沿着图中的边进行状态转移的。设f (i ,u )表示以点u 结尾的长度为i 的路径有多少条，则状态转移方程为

∑∈-=

)(),1(),(u N v v i f u i f

其中N (u )表示从点u 出发的边指向点的集合。

可以发现，每一阶段的状态转移都要从每个点出发从每条边经过一次。这说明，状态转移实际被重复了(N -1)次，这里有没有可改进的余地呢？

我们将图中的点从0到(2M -1)编号，则一个阶段中所有状态可以表示为一个向量

()),(),(),(1210-=M v i f v i f v i f S i

由于状态转移方程是线性的，所以我们一定能找到一个2M 阶矩阵A ，使得S i A =S i +1。通过状态转移方程可以知道，矩阵A =(a i ,j )应该是

??

???∈?=E v v E v v a j i j i j i 10, 这不就是图的邻接矩阵么！

接下来的事情就好办了。S 0=(1 1 … 1)，我们求的是S N -1=S 0A N -1种所有

元素的和。这个算法的复杂度只有O(23M log N )。

类似的题目Sgu201，那个题虽然要用动态规划解，但如果改动一下数据规模，把状态数k 改小，把串长度N 和字符集改大，就也要用这种方法做了。

上面的方法不仅能找出一个图中所有一定长度路径的个数，还可以限制路径的起点和终点。限制起点时，将S 0中不能作为起点的对应元素置为0。限制终点时，结果为S L 中能作为终点对应元素之和。

Strassen 矩阵乘法

从上面几个例子中，我们已经可以感受到用矩阵解题的缺点，那就是矩阵乘法的代价太大。O(n 3)的矩阵乘法对稍微大一点儿的矩阵就无能为力了。因此，最后我们以一种稍好一点的矩阵乘法的算法作为本文的结束。

这个算法的时间复杂度约为O(n 2.81)，虽然并没有小多少，但好一点是一点吧。（还有更好的算法，不过那个比较复杂，我也不会了。）

1969年，V ．Strassen 提出一个方法，对于两个2阶矩阵相乘只要7次乘法就够了。设

???? ??=22211211a a a a A ，???? ??=22211211b b b b B ，???

? ??==22211211c c c c AB C 先计算下面7个量，每个量用1次乘法

???????????+-=+-=+=-=-=+=++=)

)(())(()()

()()())((2221221271211112162212115

112122422121131122212

221122111b b a a x b b a a x b a a x b b a x b b a x b a a x b b a a x 根据矩阵乘法的规则，可以发现

???????+-+=+=+=+-+=6

231224221

5312754111x x x x c x x c x x c x x x x c 根据上面这个方法，我们可以进一步处理n =2k 阶的两个矩阵相乘的问题。 设有两个n =2k 阶的矩阵A 和B ，我们要求C =A ×B 。

首先，把矩阵A 和B 都划分为四块2k -1阶矩阵，然后应用类似上面2阶矩阵乘法的办法，转化为7次2k -1阶矩阵乘法和若干次加减法，然后递归运行。

易证，总共需要的乘法次数和加法次数都为)()(81.27log 2n O n O ≈。

如果矩阵A 或B 的行数或列数不是2的整数次幂也不要紧，只要在矩阵的下侧或右侧补零，使其成为阶数为2的整数次幂的方阵。实际结果就是这样计算出的结果左上角的子矩阵。