电路分析简明教程(第二版)习题详解
电路分析基础(第二版) 曾令琴 人民邮电出版社 课后答案 指导与解答9 课后答案【khdaw_lxywyl】

aw
后
答
案
.c o
网
m
指波形的后半周重复波形前半周的变化, 因此必定包含直流成分。 波形的平滑性好坏取决于其 含有的高次谐波是否严重,正弦波不含有高次谐波,因此正弦波的平滑性非常好,三角波和方 波相比,方波一个周期内出现两次波形的跳变,而三角波没有上、下跳变点,因此三角波的平 滑性较方波好,其高次谐波成分也没有方波显著。 (4) .脉冲技术中常说: “方波的前沿和后沿代表高频成分” ,你如何理解这句话? 解析:一个非正弦周期函数的波形如果不平滑且存在跳变点时,它必定包含高次谐波。 波形中跳变点越陡峭, 波形所包含的高效谐波成分越显著, 方波的前沿和后沿都是最陡峭的跳 变点,也是产生显著高次谐波的直接原因,因此可以说“方波的前沿和后沿代表高频成分” 。
9. 3
1、学习指导
非正弦周期信号的有效值、平均值和平均功率
的数值表示表述的。 但非正弦周期量的有效值与正弦量有效值的计算方法不同, 非正弦量的有 有效值平方和的开方。
正弦周期信号在一个周期内的平均值就等于它的恒定分量。 (2)非正弦周期信号的平均功率 讨论非正弦量平均功率问题时应注意:只有同频率的电压和电流才能构成该次谐波的平
什么典型的对称性,因此利用谐波分析法进行讨论时,其分析过程就会显得繁琐且不够直观。 为了简化这类周期信号电流电路的分析,本章引入了比较直观而且较为方便的频谱图表示法。 所谓的频谱图表示法有两种, 一种是把各谐波分量的相位用一个个线段表示, 并按频率的高低 图称为相位频谱图; 另一种就是教材中介绍的振幅频率图。 图中的每一条谱线代表一个相应频 这一谐波分量的频率,各条谱线的顶点连接起来构成了非正弦周期函数振幅的包络线。显然, 量所占的“比重” ,从而给工程实际问题的分析带来很大的方便。要求学习者能够理解和掌握 排成谱状, 显然这些高低不同的线段就是非正弦周期信号的相位频谱, 由相位频谱构成的谱状 率的谐波分量, 谱线的高度代表这一谐波分量的振幅频谱, 振幅频谱的谱线所在的横坐标代表 振幅频谱图能够非常直观地表示出一个非正弦周期信号包含的各次谐波分量以及每个谐波分 这种周期信号频谱图的表示方法。 2、学习检验结果解析
电工学简明教程第二版答案(第一章)

第一章习题问案之阳早格格创做A 采用题1.4.1(A) 1.4.2(C)1.4.3(C)1.4.4(B)1.5.1(B)1.5.2(B) 1.6.1(B)1.6.2(B) 1.8.1(B)1.9.1(B)1.9.2(B)1.9.3 (B)1.11.1(A) 1.12.1(B)1.12.3 (B) 1.12.4 (B) 1.12.5 (B)B 基原题1.4.5 (1)略(2)元件1战2为电源,元件3,4战5为背载(3)(-560-540+600+320+180)*w=0 仄稳1.4.6 380/(,W=(8/110)×3.7K≈20W1.4.7 电阻R=U/I=6/50*=120,应选者(a)图.1.4.8 解:220/(R1+315)=0.35A,得R1≈314.220/(R2+315)=0.7A,得R2≈0.1.4.9(1)并联R2前,I1=E/( +2R+)=220/(0.2+0.2+10)≈21.2A.并联R2后,I2=E/( +2R+∥??≈?? A??并联R 前,U ??R ??I ??VU ??R????I ????V并联R 后,U ??∥????I ??VU ??R∥??V????并联R 前,P??????????KW并联R 后,P????????KW??????I????I I ?? ??uA,I????I??I???????? ????????uA,I????I I????????uA??????果为电桥仄稳,所以没有管S断启仍旧关合=∥(+)∥(+)=200.??1.6.4 解:==16V,=<[(45+5) ≈5.5]+45>×16/<[(45+5) ∥5.5] ∥5.5+45>≈1.6. =(45+5)∥5.5×/≈/10=0.16V,共理≈/10=0.016V.1.6.5 解:当滑动端位于上端时,=(R1+RP)/(R1+RP+R2)≈8.41V.当滑动端位于下端时,=R2*/(R1+RP+R2)≈5.64V.所以输出范畴为5.64-8.14.1.7.1 解:等效电路支路电流圆程:IL=I1+I2E2-RO2*I2+RO1*I1-E1=0RL*IL+RO2*I2-E2=0戴进数据得I1=I2=20A,IL=40A1.8.2解:先利用叠加定理估计R1上的电流分成二个分电路①U1单独效率:解②IS单独效率:分流所以,1.9.4解:根据KCL得则1A电流源吸支的功率:2A电流源吸支的功率:R1电阻吸支功率:R2电阻吸支功率:1.9.5解:将电流源变更成电压源,如下图则 ,A1.9.6解:将二个电压源变更成电流源再合并为一个1.9.7解:设E单独效率uab’ = E/4 = 1/4 ×12 = 3V则二个电流源效率时uab’’ = u ab- uab’=10-3=7V1.10.1解:设1Ω电阻中的电流为I(从上到下)Uoc=4×10-10 = 30VReq=4ΩI=30/(4+1)= 6A解:先利用电源等效变更得下图:解:先利用网孔电流法解出解:先用网孔法供出1.10.41.10.5 解:设有二个二端心搜集等效为则(a)图等效为有U1=E1=4V(b)图等效为有I1=2E1/2R1=4/R1=1A =>R1=4ΩI=4/4+1=4/5A1.11.4 解:V AVBV A V AVCVBuc(0+)=uc(0-)=10v从1-72后, uc(--)=0, t搁=RC=10ms Uc(t)=10exp(-100t)V(0<=t<= )Uc(--)=10, t充=10/3msUc(t)=10-6.32exp(-300(t-0.01))vuc(--)=0 t=10msuc(t)=9.68exp(-100(t-0.02))1.12.10 解: i(0+)=i(0-)=-6/5AI(--)=6/5AT=i/R=9/5sI(t)=6/5-12/5exp(-5/9t)A利用叠加法得: i(t)=9/5-8/5exp(-5/9t)A1.11.2 解:1.11.3 解:利用叠加定理估计1.12.6解:(a)i(0+)=i(0-)=0,i()=3A(b)i(0+)= i(0-)=0,i((c)i(0+)= i(0-)=6A,i()=0(d)i(0+)= i(0-)=1.5A,i()=1A1.12.7 解: uc(0+)=uc(0-)=R3I=60VUc()=0=RC=[(R2//R3)+R1]C=10mSUc(t)=60e-100ti1(t)=Uc(t)/(R1+(R2//R3))=12e-100t mA 1.12.8 解: uc(0+)=uc(0-)=54VUc()=18v=RC=4mSUc(t)=36e-250t+181.9.9 解: (1) 利用叠加定理供IU1单独效率:I’=U1/(R1+R)=5AIS单独效率:I’’=R1/(R1+R) IS=1AI=6A(2) KCL: IR1=IS-I=-4AIR3=U1/R3=2AIU1=IR3-IR1=6AUIS=RI+R2IS=10V(3) PU1=60WPIS=20WPR3=20W PR1=16W PR2=8W PR=36 PU1+PIS=PR1+PR2+PR3+PR=80W 功率。
电工学简明教程第二版标准答案

电工学简明教程第二版标准答案(B)1、11、1(A)1、12、1(B)1、12、3 (B)1、12、4 (B)1、12、5 (B)B 基本题1、4、5 (1)略(2)元件1和2为电源,元件3,4和5为负载(3)(-560-540+600+320+180)*w=0 平衡1、4、6380/(/8+R)=8/110,所以R≈3、7K,W=(8/110)3、7K≈20W1、4、7 电阻R=U/I=6/50*=120,应选者(a)图、1、4、8 解:220/(R1+315)=0、35A,得R1≈314、220/(R2+315)=0、7A,得R2≈0、1、4、9(1)并联R2前,I1=E/( +2R+)=220/(0、2+0、2+10)≈21、2A、并联R2后,I2=E/( +2R+∥)≈50A、(2)并联R2前,U2=R1*I1=212V,U1=(2R+)*I1=216V、并联R2后,U2=(∥)*I1=200V,U1=2R+∥=210V、(3)并联R2前,P=212*21、2=4、5KW、并联R2后,P=200*50=10KW、1、5、3I3=I1+I2=0、31uA,I4=I5-I3=9、61-0、31=9、3uA,I6=I2+I4=9、6uA、1、6、3 因为电桥平衡,所以不管S断开还是闭合=∥(+)∥(+)=200、1、6、4 解:==16V,=<[(45+5)≈5、5]+45>16/<[(45+5)∥5、5] ∥5、5+45>≈1、6、 =(45+5)∥5、5/≈/10=0、16V,同理≈/10=0、016V、1、6、5 解:当滑动端位于上端时,=(R1+RP)/(R1+RP+R2)≈8、41V、当滑动端位于下端时,=R2*/(R1+RP+R2)≈5、64V、所以输出范围为5、64-8、14、1、6、61、7、1 解:等效电路支路电流方程:IL=I1+I2 E2-RO2*I2+RO1*I1-E1=0 RL*IL+RO2*I2-E2=0带入数据得I1=I2=20A,IL=40A1、8、2解:先利用叠加定理计算R1上的电流分成两个分电路① U1单独作用:解② IS单独作用:分流所以,1、9、4解:根据KCL得则1A电流源吸收的功率:2A电流源吸收的功率:R1电阻吸收功率:R2电阻吸收功率:1、9、5解:将电流源转换成电压源,如下图则 ,A1、9、6解:将两个电压源转换成电流源再合并为一个1、9、7解:设E单独作用uab’ = E/4=1/412 =3V则两个电流源作用时uab’’ = uab3=7V1、10、1解:设1Ω电阻中的电流为I(从上到下)Uoc=410-10 =30V Req=4ΩI=30/(4+1)=6A1、10、2解:先利用电源等效变换得下图:1、10、3解:先利用网孔电流法解出1、10、4 解:先用网孔法求出1、10、5 解:设有两个二端口网络等效为则(a)图等效为有U1=E1=4V(b)图等效为有I1=2E1/2R1=4/R1=1A=>R1=4ΩI=4/4+1=4/5A1、11、4 解:VA VBVAVA VCVB1、12、9 解:1、开关第一次动作uc(0+)=uc(0-)=10v从1-72后, uc(--)=0, t放=RC=10ms Uc(t)=10exp(-100t)V(0<=t<= ) Uc(t)=10exp(-1)v=3、68v2、开关第二次动作 Uc(t+)=uc(t-)=3、68v Uc(--)=10, t充=10/3ms Uc(t)=10-6、32exp(-300(t-0、01))v Uc(2*10E-2s)=10-6、32exp(-3)v=9、68v3、开关第三次动作 Uc(0、02+)=uc(0、02-)=9、68v uc(--)=0 t=10msuc(t)=9、68exp(-100(t-0、02))1、12、10 解:i(0+)=i(0-)=-6/5A I(--)=6/5A T=i/R=9/5s I(t)=6/5-12/5exp(-5/9t)A 利用叠加法得:i(t)=9/5-8/5exp(-5/9t)A1、11、2 解:1、11、3 解:利用叠加定理计算1、12、6 解:(a)i(0+)=i(0-)=0,i()=3A(b)i(0+)= i(0-)=0,i()=1、5A(c)i(0+)= i(0-)=6A,i()=0(d)i(0+)= i(0-)=1、5A,i()=1A1、12、7 解: uc(0+)=uc(0-)=R3I=60V Uc()=0=RC=[(R2//R3)+R1]C=10mS Uc(t)=60e-100ti1(t)=Uc(t)/(R1+(R2//R3))=12e-100t mA1、12、8 解: uc(0+)=uc(0-)=54V Uc()=18v =RC=4mSUc(t)=36e-250t+181、9、9 解: (1)利用叠加定理求I U1单独作用:I’=U1/(R1+R)=5A IS单独作用:I’’=R1/(R1+R)IS=1A I=6A (2)KCL: IR1=IS-I=-4A IR3=U1/R3=2A IU1=IR3-IR1=6AUIS=RI+R2IS=10V(3)PU1=60W PIS=20W PR3=20W PR1=16W PR2=8WPR=36PU1+PIS=PR1+PR2+PR3+PR=80W 功率第二章2-1 图2-1所示的电路中,US=1V,R1=1Ω,IS=2A、,电阻R消耗的功率为2W。
电工学简明教程(第二版)第九章课后答案(完整资料).doc

【最新整理,下载后即可编辑】9.2.4 如图所示各电路图中,V E 5=,tV u i ωsin 10=,二极管的正向压降可忽略不计,试分别画出输出电压0u 的波形解:首先分析二极管的两个状态:正向导通,反向截止;根据状态,正向导通时二极管两端电压为其正向压降,反向截止时相当于开路;最后分析输出电压a ) 二极管正极接正弦电压,负极接直流5V ,当正弦电压瞬时值大于5V 时,二极管导通,V u 50=;当正弦电压瞬时值小于5V 时,二极管截止,i u u =0b ) 二极管正极接5V 直流电压,负极接正弦电压,当正弦电压瞬时值小于5V 时,二极管导通,i u u =0,当正弦电压瞬时值大于5V 时,二极管截止,V E u 50==c ) 二极管正极接5V 直流电压,负极接正弦电压,当正弦电压瞬时值小于5V 时,二极管导通,V u 50=,当正弦电压瞬时值大于5V 时,二极管截止,i u u =0d ) 二极管正极接正弦电压,负极接直流5V ,当正弦电压瞬时值大于5V 时,二极管导通,i u u =0;当正弦电压瞬时值小于5V 时,二极管截止, V u 50=9.3.4 有两个稳压管其稳压电压分别为5.5V和8.5V,正向压降都是0.5V,如果要得到0.5V,3V,6V,9V和14V几种稳定电压,这两个稳压管(还有限流电阻)应该如何连接?画出各个电路解:理解稳压二极管的三个状态,正向导通时两端电压为正向压降;若反向电压小于稳压电压,则处于反向截止状态,相当于开路;反向电压大于稳压电压,则处于稳压状态,两端电压为稳压电压。
设DZ1稳压电压为5.5V,DZ2稳压电压为8.5V。
9.4.10 如图所示各个电路,试问晶体管处于何种工作状态解:首先看清楚晶体管类型,NPN 还是PNP ,CBE 极各在哪一端,电阻分别是什么电阻方法一:定性判断,a 中B C E E >,0>B E ,放大状态;b 中B C E E =,0>B E ,非放大非截止,可能是饱和;c 中0<BE U ,截止但是定性判断并不能百分百确定,有不确定性,因此最好采用定量判断a )mA R U I O CC C 12=≈,饱和时基极电流mA I I C B 24.0=='β,此时基极电流'<=-=B BBE B B I mA R U U I 11.0,放大状态 b )mA R U I O CC C 8=≈,饱和时基极电流mA I I C B 2.0=='β,此时基极电流'>=-=B BBE B B I mA R U U I 24.0,饱和状态 c )mA R U I O CC C 12=≈,饱和时基极电流mA I I C B 3.0=='β,此时基极电流mA R U U I B BE B B 33.0-=-=,为负数,截止状态。
电工学简明教程第二版习题答案(第十一章)
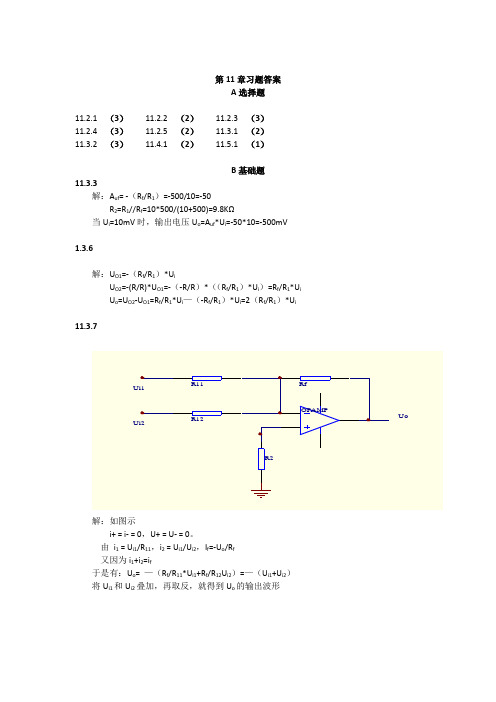
I1=5mA I2=0.5mA I3=0.1mA I4=50A I5=10A
于是Rf1=U0/-Ix
故RF1=5V/5mA=1k
RF2=5V/0.5mA-KF1=9k
RF4=5V/0.1mA-RF1-RF2=50k
RF3=5V/50*10-6mA-RF1-RF2-RF3=40k
RF5=5V/10*10-6mA-RF1-RF2-RF3-RF4=400K
Uox=-Rf/RixU; (x=1.2.3.4.5)
即:R1x=-Ui/UoxRf
每个量程上输入最大时,输出均为5V。
故R11=50/5*1M=10M
R12=10/5*1M=2M
R13=5/5*1M=1M
R14=1/5*1M=200K
R15=0.5/5*1M=100K
11.3.18
解:输出电压U=-i*RF
即有
R1=100k,Cf=1uF或者R1=10k,Cf=10uF
11.3.13
解:由“虚断”可知
U-=U+=R3/(R2+R3)Ui2
由“虚短”可知
(Ui1—U-)/R1=(U—Uo1)/Rf
所以Байду номын сангаас
Uo1=-Rf/R1*Ui1+R3/(R2+R3)*(1+Rf/R1)Ui2
=-20/10x1.1+20/(10+20)x(1+20/10)x1
R2=R1//Rf=10*500/(10+500)=9.8KΩ
当Ui=10mV时,输出电压Uo=Auf*Ui=-50*10=-500mV
1.3.6
解:UO1=-(Rf/R1)*Ui
UO2=-(R/R)*UO1=-(-R/R)*((Rf/R1)*Ui)=Rf/R1*Ui
电路分析简明教程(第二版)习题详解

A2d d 32s 32 ==-=<<tqi t q t ,则时,《电路分析简明教程》(第二版)习题解答 第一章1-1 解:当A 21d d 21s 20===<<t q i t q t 则,时, 0 s 3 =>i t 时,0s 5.3A ;2s 5.2;A 5.0s 5.1======i t i t i t 时,时,时,∴方向均为A 流向B 。
1-2 解:,产生功率参考方向相反同。
向均与图示参考方向相:电流、电压的实际方图习题W 1A 1V 1 )a ( 21-=⨯-=-=∴-UI P UI,吸收功率)(参考方向相反向相反。
实际方向与图示参考方参考方向相同;电压的电流的实际方向与图示图W 4A 22V - : b)(=⨯-=-=∴UI P UI ,吸收功率)(参考方向相同与图示参考方向相反。
电流、电压的实际方向图W 12A 3-V 4 : )(=⨯-==∴UI P UI C1-3 解:V 20A1W20 W 201=====I P U UI P ,则)( A 2V 10W20 W 202=--=-=-=-=U P I UI P ,则)(A 1V10W10 W 103=---==-==U P I UI P ,则)(1-4 解:的函数式为得出图由习题u a)( 41-t u t 10s 10=<<时, t u t 1020s 20-=<<时, 的函数式为得出由图 b)(iA 1s 10=<<i t 时,A20A 266-==+I I A 1s 20-=<<i t 时,∴t t ui P t 10110s 10=⨯==<<时,2010)1()1020(s 20-=-⨯-==<<t t ui P t 时,则P 的波形为习题1-4解图所示。
习题1-4解图时s 30 在<<t⎰⎰⎰⎰=-+=⨯+-+==tt t t t t t P W 0121320J )5(J 5d 0d )2010(d 10d1-5 解: 得:由KCL A 10A 2A 8A 2A8A )2(A )15(121-=--=--==--+=i i i1-6 解:解图示虚线)得:应用于习题由6-1KCL(据KVL ,列回路电压方程(取顺时针绕向),得V1V )10615(0V 10V 6)V 15(55=++-==----U U1-7 解:W 250W )8012050( W 250W )100150( W 80)A 4(V 20 5V 20V 50V 30 5KVL W 120)A 4(V 30 4 W 100A 2V 50 3A 2A )]4(13[ 3KCL W 50A 150V 的功率 2元件 150W 3A 50V 的功率 1元件 5423154321=++=++==+=+=-=-⨯===+-=-=-⨯===⨯===--+-=-=⨯-=-==⨯==P P P P P P P UI P U UI P UI P I UI P UI P UI 产生功率吸收功率的功率则元件的电压得元件由的功率元件的功率则元件的电流得元件由参考方向是否一致,得根据1-8 解:V23 V 24 V 59 V 23V )]16(7[ V 24V ]168[ V59V )]16()8(530[ KVL gd g fd f ad a gd fd ad -==-==-==-=-+-=-=--=-=-+-+--=U V U V U V U U U 故得由A 6.1A )28.14.1(0A ](-2)8.14.1[ 8-1KCL(cd cd -=-+-==+--I I 则)得解图示虚线假想闭合面应用于习题由1-9 解:V 10V 110 :a)( 9-1 -=⨯-=-=RI U 图习题 A 1V 55 : b)( -=-===I I RI U ,则图V 10V )1(10 : c)( -=-⨯==RI U 图1-10 解:mA 8.15mA 10401032=⨯===RPI RI P 故V 632V 104010 32=⨯⨯===PR U RU P 故1-11 解V 5sin 100 : a)( 11-1 t Ri u ==图习题 Ω===--4A 2V 8 : b)( 66t t e e i u R 图W 5sin 182)V 5sin 6( : c)( 222)2(t t R u p =Ω==Ω图W 5sin 123)V 5sin 6( 22)3(t t p =Ω=Ω1-12 解:V 5-V 5-V 10-V 10ab: a)( 12-1 ==U图习题A2 0A 2 KCL( : b)( -==+I I 则应用于闭合面)得由图U =-2×3V=-6V1-13 解: 如习题1-13解图所示1AA 10550.5A A 1050.5A A 105321=+=====I I I据KCL 可得:-1.5A1)A -(-0.5--00.5)A (-0.5- 1.5AA 1(0.532c 21b 31a ====+=+==+=+=I I I I I I )I I I1-14 解:A 22V4V 8 V 5V 3V 8 )1(ab =Ω-==-=I U 点阻上电压未变。
电工学简明教程第二版秦曾煌主编第二章答案

,J.J)有一正炫电嫌•其初相位分_的'初鰌值“獬镢电戴•^黴O^loAA (2) ^ A (3> 10i m i⑶J.2J—“了#,in(w—30.〉示式为(^(1) £/ 10 2^-—V C2yt>*io /—30* V ⑶ lj眶 10«^_>r)"f J⑵----2.2.2*~l1~l~*2'f'^=*4V2s i n c t A4-8V2»i n C o»t4-90*>A-V-4V2*m C«t90°) A,则总电流i的相貴表示式为()•(1> ^ = 4 V^"Z45_A (2) J=4 V2/—45° V C3> 1=4 /45° Aimi⑴.么3. 1在电感兀件的交流电路中,已知M= V^Jsinoit,興K >•⑴/=在(2"=j S (3) i='}coLU imi⑴2.3-2在电容元件的交流电路中,已知u=V^U s i n o i t,则C)。
⑴/=S(2) /=j£ (3)i=io>a> i m(3)2.4.1在及L C串联电路中,阻抗模()。
(1)\Z\=^~(2)l Z I=^f(3)|Z|=^1 1If解 J (2)___________________________(3)V图2. 4.1习题2. 5.1的图 '9^ (3) Z\ =Z2=Zzfi:2. 4.2在zee 串联电路中•( ⑴卜為⑵卜為【解J (3)2.4.3在/?IX •串联电路中,已知及= 则电辂的■ 率因数cos 炉等于( )• (1) 0. 8 (2) 0. 6 (3X J £解】(2)2.4.4在/?1^串联电路中,已知及=<^==叉£:==5 0』=1/2!八,则电路 端电压&等于( )。
电工学简明教程大二 第二版答案
图 1
)。
.
图 1
.
图 2
.
7 理 想 电 压 源 和 理 想 电 流 源 间( )。 (a) 有 等 效 变 换 关 系 (b) 没 有 等 效 变 换 关 系 (c) 有 条 件 下 的 等 效 变 换 关 系 8 图 示 电 路 中,用 一 个 等 效 电 源 代 替,应 该 是 一 个( (a) 2 A 的 理 想 电 流 源 (b) 2 V 的 理 想 电 压 源 (c) 不 能 代 替,仍 为 原 电 路
(a) u = 380sin(100 t+180°) V (b) u =-311sin200πt V (c) u = 220sin(628 t+180°) V 2.某 正 弦 电 流 的 有 效 值 为 7.07 A,频 率 f =100 Hz,初 相 角ϕ = -60°, 则 该 电 流 的 瞬 时 表 达 式 为 ( )。 (a) i = 5sin( 100 πt-60° ) A (b) i = 7.07sin( 100 πt+30° ) A (c) i = 10sin( 200 πt-60° ) A &= 4 + j3 对 应 的 正 弦 电 流 可 写 作 i = ( 3.与 电 流 相 量 I )。 (a) 5 sin(ωt+53.1°) A (b) 5 2 sin(ωt+36.9°)A (c) 5 2 sin(ωt+53.1°)A 4. 用 幅 值 ( 最 大 值 ) 相 量 表 示 正 弦 电 压 u = 537sin(ωt-90° ) V ( )。
i + u
R + u - R + uL
L
-
uC + C
-
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(b)
习题3-2解图
3-3解:
根据曲线相加法,得串联电路的VAR曲线3。取坐标纵轴的36V与曲线3相交,将相交点与坐标横轴相交,得串联电路的电流I=21.7mA,同时与两个非线电阻VAR曲线相交,分别得出这两个电阻的电压为12V、24V。以上见习题3-3解图
习题3-3解图
3-4解:
与上题解法类似,略。
解得
2-12解:
标出各支路电流参考方向如习题2-12解图所示。
习题2-12解图
由习题2-12解图,利用KCL列出独立节点电流方程3个(选取1、2、3为独立节点),即
由习题2-12解图,利用KVL列出独立回路L1、L2、L3电压方程(选回路绕行方向为顺时针方向),即
2-13解:
习题2-13解图
各支流电流参考方向如习题2-13解图所示。
2-6解:
应用Y-△等效变换,将习题2-6图中的三个2Ω电阻的Y形联结变换为三个6Ω电阻的△形联结,如习题2-6解图所示。
习题2-6解图
2-7解:
习题2-7解图
2-8解:
将习题2-8图等效为习题2-8解图,变换步骤如图(a)―(e)所示,由图(e)得
(e)
习题2-8解图
2-9解:
习题2-9解图
将习题2-9图等效为习题2-9解图,得
而P=UI=5.7×4.3W=24.5W
3-6解:
(a)
(b) (c)
习题3-6解图
(1)用曲线相交法
首先作出习题3-6解图(a)电路虚线框内的戴维宁电路如习题3-6解图(b),其中
9V=6V
由习题3-6解图(b),得出线性有源支路的外特性方程为:
u=6-2i
令i=0得u=6V
令u=0得i=3A
故作出线性有源支路的外特性,如习题3-6解图(c)中的红线。该红线与非线性电阻VAR曲线交于一点,得
3-5解:
习题3-5解图
根据曲线相交法解此题。首先据上表作出非线性电阻VAR曲线,如习题3-5解图曲线1所示。
据题,得出电源的外特性方程为
U=10-I
令I=0得U=10V,U=0得I=10A
作出外特性如习题3-5解图所示直线2。
直线2与曲线1的交点所对应的U、I即为本题的解。
即U=5.7VI=4.3A
u2=r21i1+r22i2
将习题2-40解图(a)所示电路等效为习题2-40解图(b)。
将习题2-40解图(b)输出端口开路,即i2=0,得
则
将习题2-40解图(b)输入端口开路,即i1=0,得
则
2-41解:
习题2-41图
将习题2-41解图输出端口短路,即u2=0,得
则
将习题2-41解图输入端口短路,即u1=0,得
2-10解:
将习题2-10图等效为习题2-10解图,变换步骤如图(a)(b)所示,(习题2-10图中与50V电压源并联的10A电流源和30Ω电阻及与5A电流源串联的10V电压源,对外电路而言均为多余元件),由图(b)得
习题2-10解图
2-11解:
习题2-11解图
由习题2-11解图,利用KCL列出节点1的电流方程和利用KVL列出回路L的电压方程各一个,即
得诺顿等效电路如习题2-33解图(e),故
2-34解:
习题2-34解图
由习题2-34解图(a)、图(b)求得
由习题2-34解图(c)得
2-35解:
习题2-35解图
移去习题2-35图示电路中的电阻R5,应用叠加定理求该电路的Uoc,其求解电路如习题2-35解图(a)、(b)所示,得
将图(b)电路中的并联电阻(3Ω、6Ω)等效合并如图(b')电路,则
1-9解:
习题1-9图
1-10解:
1-11解:
习题1-11图
1-12解:
习题1-12图
U=-2×3V=-6V
1-13解:
习题1-13解图
如习题1-13解图所示
据KCL可得
1-14解:
习题1-14图
1-15解:
习题1-15解图
1-16解:
习题1-16解图
=12× =(12×2) =24 吸收功率
1-17解:
习题2-15解图
设i4支路的2A无伴电流源的端电压为u。列出两个网孔的电压方程为:
即
对i4支路的2A无伴电流源列辅助方程为
联立求解上述三个方程得
则
2-16解:
习题2-16解图
由习题2-16解图列出网孔电压方程为
联立上述方程解得
( )
2-17解:
习题2-17解图
由习题2-17解图列出网孔电压方程为
联立上述方程解得
工作点超出OA段工作范围,故解答无效。
AB段:工作范围为1.5V≤u≤4.5V,i=1.5A,其VAR方程为
i=1.5A
将其等效电路与电压为6V、内阻为2Ω的电源电源相联,如习题3-6解图(e)所示,得
设二端网络的戴维宁等效电路由Uoc和Req串联而成,由习题2-32图得出习题2-32解图所示电路。
当开关打开时,有
当开关闭合时,有
联立上述两方程解得
2-33解:
(d) (e)
习题2-33解图
由习题2-33解图(a)及(b)得
得戴维宁等效电路如习题2-33解图(c),故
由习题2-33解图(d)所示,得
习题2-20解图
联立上述方程解得
2-21解:
习题2-21解图
设2V无伴电压源支路电流为I,由习题2-21解图列出节点方程为
联立上述方程解得
2-22解:
由习题2-22解图列出节点方程为
联立上述方程解得
习题2-22解图
2-23解:
习题2-23解图
由习题2-23解图列出节点方程为
2-24解:
习题2-24解图
故
则
将习题2-43解图的输入端口开路,即I1=0,得
即
则
习题2-43解图
2-44解:
(1)作出T形等效电路如图习题2-44解图(a)所示。
其中
(2)作出π形等效电路如图习题2-44解图(b)所示。
其中
(3)作出混合参数等效电路如习题2-44解图(c)所示。
习题2-44解图
第三章
3-1解:
u=us-Rsi=50-400i
则
习题2-41解图
2-42解:
习题2-42图
将习题2-42解图输出端口开路,即I2=0,得
则
将习题2-42解图输入端口开路,即I1=0,得
则
习题2-42解图
2-43解:
习题2-43图
由习题2-43解图,得h参数方程为
U1=h11I1+h12U2
I2=h2 1I1+h2 2U2
将习题2-43解图的输出端口短路,即U2=0,利用分流公式得
令i=0u=50V
令u=0 =125mA
作出外特性曲线AB如习题3-1解图所示,与非线性电阻VAR曲线交得Q点,可见
IQ=45mAUQ=34V
静态电阻
过Q点作VAR曲线的切线与横轴相交,构成一个直角三角形如习题3-1解图所示,则动态电阻
习题3-1解图
3-2解:
对于两个非线性电阻串联电路,有
u=u1+u2=f1(i1) +f2(i2)
利用KCL和KVL列出独立节点电流方程和列出独立回路电压方程如下:
2-14解:
在习题2-14解图所示电路中,选取如图所示参考方向的三个网孔电流,设定网孔绕行方向与网孔电流相同,利用KVL列出三个网孔电压方程为
习题2-14解图
解得
2-15解:
各支流电流和各网孔电流如习题2-15解图所示。
由于 ,故只需列两个网孔电压方程求解网孔电流im1、im2。
联立上述方程解得
由习题2-31解图(b2)得
习题2-31图(b)所示电路的戴维宁等效电路如习题2-31解图(b3)所示。
习题2-31解图
习题2-31图(c):
由该图所示电路求得
利用开路-短路法求Req,将该图所示电路a、b端短路,得习题2-31解图(c1)所示电路,由于 ,故受控电流源电流( )为零,做开路处理。由习题2-31解图(c1)电路得
2-37解:
习题2-37解图
由习题2-37图示电路得
则
利用外加电压法求Req,其电路如习题2-37解图(a)所示,得
∴
该题的戴维宁等效电路如习题2-37解图(b)所示。
2-38解:
习题2-38解图
用节点电压法就求解uoc,设无伴受控电流源(2i)支路的电流为i',其电路如习题2-38解图(a)所示,节点方程为
u=3Vi=1.5A
(2)用分段线性法
习题3-6解图
将图3-6解图(c)VAR曲线分为三段:OA、AB、BC。
OA段:工作范围为0≤u≤1.5V,0≤i≤1.5A,其VAR方程为
u=uOA+ROAi
由图(c)得
uOA=0V
它是AO直线与电压轴交点的电压值。
而
故u=i
将其等效电路与电压为6V、内阻为2Ω的电源相联,如习题3-6解图(d)所示,得
习题2-29解图
2-30解:
习题 2-30 图
由习题2-30图(a)得
则
2-31解:
习题2-31解图
习题2-31图(a):
由该图所示电路求得
由习题2-31解图(a1)得
习题2-31图(a)所示电路的戴维宁等效电路如习题2-31解图(a2)所示。
习题2-31解图
习题2-31图(b):
利用节点电压法求Uoc,由习题2-31解图(b1)列节点方程
习题2-27图
由齐性定理和叠加定理可知
