第五章 时间序列分析案例[24页]
时间序列分析ppt课件

目录
• 时间序列分析简介 • 时间序列的基本概念 • 时间序列分析方法 • 时间序列分析案例 • 时间序列分析的未来发展
01 时间序列分析简介
时间序列的定义与特点
定义
时间序列是指按照时间顺序排列的一 系列观测值。
特点
时间序列具有动态性、趋势性和周期 性等特点,这些特点对时间序列分析 具有重要的影响。
时间序列的季节性
总结词
时间序列的季节性是指时间序列在固定周期内重复出现的模式,这种模式可能是由于季节性因素、周 期性事件或数据采集的频率所引起的。
详细描述
季节性是时间序列中的一个重要特征,许多时间序列都表现出季节性。例如,一个表示月度销售的序 列可能会在每个月份都出现类似的销售模式。在进行时间序列分析时,需要考虑季节性对模型的影响 ,以便更准确地预测未来的趋势和模式。
时间序列分析在金融领域的应用广泛,如股票价格预测 、风险评估等。未来将进一步探索时间序列分析时间序列分析可用于医学影像分析、疾病 预测等方面。未来将进一步拓展其在健康领域的应用范 围,为医疗保健提供有力支持。
谢谢聆听
时间序列分析的意义
01
预测未来趋势
通过对时间序列进行分析,可以了解数据的变化趋势, 从而预测未来的走势,为决策提供依据。
02
揭示内在规律
时间序列分析可以帮助我们揭示数据背后的内在规律和 机制,进一步理解事物的本质。
03
优化资源配置
通过对时间序列的预测和分析,可以更好地优化资源配 置,提高资源利用效率。
03 时间序列分析方法
图表分析法
总结词
通过图表直观展示时间序列数据,便 于观察数据变化趋势和异常点。
详细描述
第五章、时间序列分析1

3、平均数时间数列 它是把一系列同类平均数指标按时间向后顺序 排列而成的数列 。
绝对数时间数列的分类
绝对数时间数列按数列反映时间状态的不同; 又可分为时期数列和时点数列。 时期数列
当数列中的指标为时期指标,反映现象在各段时期 内发展过程的总量时,即为时期数列。
—— 27.8 84.2 173.4
—— 27.8 56.4 89.2
—— 106.7 120.4 142.0
—— 106.7 112.8 118.0
四、增长速度
概念:由增长量与基期水平之比。 作用:说明报告期水平较基期水平增长的相对程度。 种类:增长速度也分为定基增长速度和环比增长速度。 定基增长速度的一般通式为;
a1-a0, a2-a1, a3-a2,……,an-1-an-2 ,an-an-1。
两种增长量之间关系: 各逐期增长量之和,等于相应时期的
累计增长量:
(a i a i 1) a n a 0
两相邻时期累计增长量之差,等于相 应时期的逐期增长量:
(a i a 0 ) (a i 1 a 0 ) a i a i 1
作用:说明现象报告期水平较基期水平的相对增 长结果。
种类:由基期水平选择的不同可把增长量分为累 计增长量和逐期增长量。
累计增长量是指报告期水平与固定基期水平之差。 一般通式为:
a1-a0, a2-a0, a3-a0,……,an-1-a0 ,an-a0。 逐期增长量是指报告期水平与前一期水平之差。
一般通式为:
(7) ——
(8)
举例
年份
发展水 增长量(万 平(万 元) 元) 累计 逐期
第五章_时间序列分析_102-122_

第二篇 预测方法与模型预测是研究客观事物未来发展方向与趋势的一门科学。
统计预测是以统计调查资料为依据,以经济、社会、科学技术理论为基础,以数学模型为主要手段,对客观事物未来发展所作的定量推断和估计。
根据社会、经济、科技的预测结论,人们可以调整发展战略,制定管理措施,平衡市场供求,进行各种各样的决策。
预测也是制定政策,编制规划、计划,具体组织生产经营活动的科学基础。
20世纪三四十年代以来,随着人类社会生产力水平的不断提高和科学技术的迅猛发展,特别是近年来以计算机为主的信息技术的飞速发展,更进一步推动了预测技术在国民经济、社会发展和科学技术各个领域的应用。
预测包含定性预测法、因果关系预测法和时间序列预测法三类。
本篇对定性预测法不加以介绍,对后两类方法选择以下几种介绍方法的原理、模型的建立和实际应用,分别为:时间序列分析、微分方程模型、灰色预测模型、人工神经网络。
第五章时间序列分析在预测实践中,预测者们发现和总结了许多行之有效的预测理论和方法,但以概率统计理论为基础的预测方法目前仍然是最基本和最常用的方法。
本章介绍其中的时间序列分析预测法。
此方法是根据预测对象过去的统计数据找到其随时间变化的规律,建立时间序列模型,以推断未来数值的预测方法。
时间序列分析在微观经济计量模型、宏观经济计量模型以及经济控制论中有广泛的应用。
第一节时间序列简介所谓时间序列是指将同一现象在不同时间的观测值,按时间先后顺序排列所形成的数列。
时间序列一般用 ,,,,21n y y y 来表示,可以简记为}{t y 。
它的时间单位可以是分钟、时、日、周、旬、月、季、年等。
一、时间序列预测法时间序列预测法就是通过编制和分析时间序列,根据时间序列所反应出来的发展过程、方向和趋势,进行类推或延伸,借以预测下一段时间或以后若干年内可能达到的水平。
其内容包括:收集与整理某种社会现象的历史资料;将这些资料进行检查鉴别,排成数列;分析时间序列,从中寻找该社会现象随时间变化而变化的规律,得出一定的模型,以此模型去预测该社会现象将来的情况。
【精品】121第四章时间序列分析

-0.36
1989
2
15.04
-0.69
1998
11
9.14
-0.92
1990
3
14.39
-0.65
1999
12
8.18
-0.96
1991
4
12.98
-1.41
2000
13
7.58
-0.6
1992
5
11.6
-1.38
2001
14
6.95
-0.63
1993
6
11.45
-0.15
2002
15
6.45
STAT
简捷计算法:
奇数项: a=17.43,b=1.72 yc=17.43+1.72t
STAT
偶数项: a=16.55,b=0.85 yc=16.55+0.85t b:半年平均增长量注:A、变量y与变量t之间并不存在因果(相关)关系; B、预测时需假定现象的变动不大,故长期预测效果不佳。
STAT
三、增长量与平均增长量(一)增长量1、定义:报告期水平—基期水平
STAT
2、数量关系(1)逐期增长量=累计增长量。
(2)相邻的两个累计增长量的差等于相应的逐期增长量。
STAT
(二)平均增长量1、定义:逐期增长量的平均水平
STAT
三、发展速度与增长速度(一)发展速度1、定义:报告期水平/基期水平
首尾折半法n指标值个数n1时间长度
STAT
(4)间隔不等的间断的时点数列
STAT
[计算公式]
STAT
(三)相对数、平均数时间数列求序时平均数[例]某厂第二季度有关资料如下。试据此求该厂第二季度平均的计划完成程度。
第五章 时间序列分析PPT

Y Y 18547.9 21617.9 89403.6 54425.(7 亿元)
n
11
5.2.2.2 根据时点数列计算序时平均数
要精确计算时点数列序时平均数就应该有每一瞬间都登记的资 料,这在实际中几乎是不可能的。在社会经济统计中一般是将一天 看作一个时点,即以“一天”作为最小时间单位。这样时点序列可 认为有连续时点和间断时点序列之分;而连续和间断时点序列又有 间隔相等与间隔不等之别。其序时平均数的计算方法略有不同。
(1)间隔相等连续时点序时平均数的计算: 在统计中,以“天”为统计间隔的时点序列,视其为间隔相等 的连续时点。其序时平均数可按式5–3计算。
n
Y
Y1 Y2 Yn
Yi
i 1
n
n
5.2.2.2 根据时点数列计算序时平均数
(2)间隔不相等连续时点序时平均数的计算: 如果数据资料登记的时间单位仍然是天,但实际上只在观察值 发生变动时才记录一次。此时需采用加权算术平均数的方法计算序 时平均数,权数是每一观察值的持续天数。计算公式如下:
2 140 2 340 2 711 3 371 4 538 5 500 6 210 6 470 7 479 8 346 9 371
103.1 103.4 106.4 114.7 124.1 117.1 108.3 102.8 99.2 98.6
100.4
5.1.1.1 绝对数时间序列
绝对数时间序列又称总量指标序列,指总量指标在不同时间上 的观察值按时间顺序排列而成的序列。总量指标序列是计算分析相 对数和平均数时间序列的基础。
42(台)
5.2.2.2 根据时点数列计算序时平均数
时间序列分析课件_理论与案例介绍
第9章时间序列分析根据社会经济现象在不同时间下的数量表现来研究它的发展变化过程,认识它的发展规律并预测其发展变化趋势,为科学的预测和决策提供依据。
本章将重点介绍编制时间数列的方法和进行时间数列的分析。
9.1 时间序列的对比分析一、时间序列的概念时间数列是将社会经济现象的某一指标在不同时期或时点上的指标数值按时间的先后顺序加以排列而形成的数列,又称为动态数列。
例如,为了说明改革开放以来中国的经济发展状况,总是把香港地区从1988年-2003年经济发展的数据按年度顺序排列起来。
象这样形成的随时间记录的数据序列称为时间序列,有时也称为动态数列。
任何一个时间序列都具有两个基本要素:一是被研究现象所属的时间范围;二是反映该现象一定时间条件下数量特征的数值,即在不同时间上的统计数据。
时间序列中每一项数据反映了现象在各个时间上达到的规模或水平,也称为相应时间上的发展水平。
【例9.1】表9.1所列出的是中国1990年至2002年国内生产总值、人口、消费等数据:表9.1 香港1988-2003年生产总值年份本地生产总值(按当年价格计算)本地生产总值与上年人均本地生产总值(按当年价格计算) (亿港元)(亿美元)比较的实际增长(%)(港元)(美元)19884572 586 8.0 81251 10409 19895271 676 2.6 92695 11884 19905876 754 3.7 103010 13225 19916772 872 5.6 117741 15151 19927913 1022 6.6 136423 17623 19939128 1180 6.3 154687 19996 199410298 1333 5.5 170622 22078 199510963 1417 3.9 178078 23019 199612109 1566 4.3 188163 24329 199713445 1737 5.1 207194 26762 199812799 1652 -5.0 195585 25253 199912461 1606 3.4 188622 24313 200012883 1654 10.2 193299 24811 200112699 1628 0.5 188835 24213 200212474 1599 1.9 183790 23566 200312198 1567 3.2 179308 23027对时间序列进行分析的目的,一是,它可以描述社会经济现象的发展变化过程和结果;二是,它可以研究社会经济现象的发展趋势和发展速度;三是,对时间数列进行长期趋势测定,对以揭示社会经济现象发展变化的规律性;四是,利用时间数列资料可预测社会经济现象。
第05章多元时间序列分析方法

第05章多元时间序列分析⽅法142第五章多元时间序列分析⽅法[学习⽬标]了解协整理论及协整检验⽅法;掌握协整的两种检验⽅法:E-G 两步法与Johansen ⽅法; ? 熟悉向量⾃回归模型VAR 的应⽤; ? 掌握误差修正模型ECM 的含义及检验⽅法; ? 掌握Granger 因果关系检验⽅法。
第⼀节协整检验前⾯介绍的ARMA 模型要求时间序列是平稳的,然⽽实际经济运⾏中的⼤多数时间序列都是⾮平稳的,通常采取差分⽅法消除时间序列中的⾮平稳趋势,使得序列平稳后建⽴模型,这就是第四章所介绍的ARIMA 模型。
但是,变换后的时间序列限制了所要讨论问题的范围,并且有时变换后的序列由于不具有直接的经济意义,从⽽使得转换为平稳后的序列所建⽴的时间序列模型的解释能⼒⼤⼤降低。
1987年,Engle 和Granger 提出的协整理论及其⽅法,为⾮平稳时间序列的建模提供了另⼀种重要途径。
①⽬前,协整问题研究已经成为20世纪80年代末到90年代以来经济计量学建模理论的⼀个重⼤突破,在分析变量之间的长期均衡关系中得到⼴泛应⽤。
⼀、协整概念与定义在经济运⾏中,虽然⼀组(两个或两个以上)时间序列变量(例如⼈民币汇率与外汇储备、货币供应量和股票指数)都是随机游⾛,但它们的某个线性组合却可能是平稳的,在这种情况下,我们称这两个变量是平稳的,既存在协整关系。
其基本思想是,如果两个(或两个以上)的时间序列变量是⾮平稳的,但它们的某种线性组合却表现出乎稳性,则这些变量之间存在长期稳定关系,即协整关系。
根据以上叙述,我们将给出协整这⼀重要概念。
⼀般⽽⾔,协整(cointegration)是指两个或两个以上同阶单整的⾮平稳时间序列的组合是平稳时间序列,则这些变量之间的关系的就是协整的。
为何会有协整问题存在呢?这是因为许多⾦融、经济时间序列数据都是不平稳的,但它们可能受到某些共同因素的影响,从⽽在时间上表现出共同趋势,即变量之间存在⼀定稳定关系,他们的变化受到这种关系的制约,因此它们的某种线性组合可能是平稳的,即存在协整关系。
时间序列分析课件.pptx
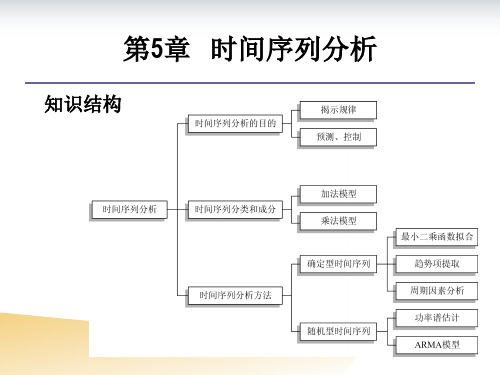
知识结构
第5章 时间序列分析
What is time series analysis?
Why to do ?
How to do?
日行迹
第5章 时间序列分析
时间序列
➢ 时间序列的概念 ➢ 时间序列的表示 ➢ 时间序列分析 ➢ 时间序列的分类 ➢ 时间序列的组合成分
时间序列分析方法
时间序列分析方法
时间序列分析的一般步骤: (1) 序列的预处理:如果原始序列为非等间隔序列,通常采用 曲线拟合及等距化重采样得到等距序列。 (2) 描述性时序分析:通过直观的数据比较或绘图观测,寻找 序列中蕴含的发展规律,往往可直观地判断序列是否具有趋势 项、周期变化等特性。 (3) 统计时序分析:计算时间序列的各种统计量,如均值,方 差,正态性检验等。利用统计特性剔除不符合统计规律的异常 样本。 (4) 判断时间序列的组合成分,对不同的成分采用不同的分析 方法。 (5) 利用不同成分的模型进行预测后叠加,得到最终的时间序 列预测值。
时间序列可能是应用最普遍的数据表现形式和数据存储格式。 在生物医学领域也存在着大量的时间序列,
人体从清晨到深夜的体温记录 人体餐后血糖浓度的变化 不同睡眠阶段的脑电波形等都是时间序列 。。。。。。
绝大多数情况下时间序列被看作为随机序列。
时间序列
时间序列的表示
X {x(T ), x(2T ),, x(kT )} {x[n]}
时间序列
时间序列分析
时间序列分析的实现是通过对观察值序列的性质进行推断,即 通过对历史观察值的分析预测而得出未来观察值的预测值。
cool! What will be next?
汽车发展的时间序列
时间序列
时间序列分析 时间序列分析的目的主要在于: (1) 描述事物在过去时间的状态。 (2) 分析事物发展变化的规律。 (3) 对事物的发展变化趋势进行预测或施加控制。
时间序列分析课件

• 某一城市从2003年到2013年中,每年参加体育锻炼的人口数,排列起来,共 有10个数据构成一个时间序列。人们希望用某个数学模型,根据这10个历史 数据,来预测2014年或以后若干年中每年的体育锻炼人数是多少,以便于该 城市制订一个有关体育健身的发展战略。
年份
参加锻炼人数(万人)
2004
1500
周
天
天数
1
星期一
1
星期二
2
星期三
3
星期四
4
星期五
5
2
星期一
6
星期二
7
星期三
8
星期四
9
星期五
10
3
星期一
11
星期二
12
星期三
13
星期四
14
星期五
15
4
星期一
16
星期二
17
星期三
18
星期四
19
星期五
20
5
星期一
21
星期二
22
星期三
23
星期四
24
星期五
25
6
星期一
26
星期二
27
星期三
28
星期四
29
星期五
0.700+2.767=3.467
2018
19×0.0389
0.739+2.767=3.506
表 7—7 年份
2014 2015 428 3.467 3.506
把Yˆ 转换为收入
预测收入
2241 2451 2681 2932 3207
表 7—8
新计数之后,得到如下数据集:
时间序列分析案例

时间序列分析案例(总17页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除《时间序列分析》案例案例名时间序列分析在经济预测中的应用称:内容要确定性与随机性时间序列之比较求:设计作者:许启发,王艳明设计时间:2003年8月案例四:时间序列分析在经济预测中的应用一、案例简介为了配合《统计学》课程时间序列分析部分的课堂教学,提高学生运用统计分析方法解决实际问题的能力,我们组织了一次案例教学,其内容是:对烟台市的未来经济发展状况作一预测分析,数据取烟台市1949—1998年国内生产总值(GDP)的年度数据,并以此为依据建立预测模型,对1999年和2000年的国内生产总值作出预测并检验其预测效果。
国内生产总值是指一个国家或地区所有常住单位在一定时期内生产活动的最终成果,是反映国民经济活动最重要的经济指标之一,科学地预测该指标,对制定经济发展目标以及与之相配套的方针政策具有重要的理论与实际意义。
在组织实施时,我们首先将数据资料印发给学生,并讲清本案例的教学目的与要求,明确案例所涉及的教学内容;然后给学生一段时间,由学生根据资料,运用不同的方法进行预测分析,并确定具体的讨论日期;在课堂讨论时让学生自由发言,阐述自己的观点;最后,由主持教师作点评发言,取得了良好的教学效果。
经济预测是研究客观经济过程未来一定时期的发展变化趋势,其目的在于通过对客观经济现象历史规律的探讨和现状的研究,求得对未来经济活动的了解,以确定社会经济活动的发展水平,为决策提供依据。
时间序列分析预测法,首先将预测目标的历史数据按照时间的先后顺序排列,然后分析它随时间的变化趋势及自身的统计规律,外推得到预测目标的未来取值。
它与回归分析预测法的最大区别在于:该方法可以根据单个变量的取值对其自身的变动进行预测,无须添加任何的辅助信息。
本案例的最大特色在于:它汇集了统计学原理中的时间序列分析这一章节的所有知识点,通过本案例的教学,可以把不同的时间序列分析方法进行综合的比较,便于学生更好地掌握本章的内容。
统计学 第五章 时间序列分析(课件)

STAT
5 41 a5
38 42 39 37 41 a a 计算公式 : a 11111 n 38台 1 42 1 39 1 37 1 41 1 日 11111 197 台日/ 5 39.4(台) 日
第七章 时间序列分析
(四)平均发展速度与平均增长速度※ 1、定义 (1)平均发展速度:环比发展速度的平均数 x (2)平均增长速度:环比增长速度的平均数 x x x 1 x x 1
[例]某厂有关产值及速度资料如下 年份 1996 1997 产值(万元) 100(a0) 120(a1) 环比发展速度 —— 120 x(%) x1=a1/a0 环比增长速度 —— 20 x1 x(%) 1998 118(a2) 98.33 x2=a2/a1 -1.67 1999 125(a3) 105.93 x3=a3/a2 5.93
第七章 时间序列分析
2、数量关系 n ai an () 1 a0 i 1 ai 1
ai ai 1 ai (2) a0 a0 ai 1
年份 产值(万元) 环比发展速度 % 定基发展速度 %
STAT
a1 a2 a2 1.20 0.9833 a0 a1 a0
1.18 a2 a1 a2 1.20 a0 a0 a1
第七章 时间序列分析
(2)间隔不等的连续的时点数列
STAT
[例]某厂成品仓库库存变动时登记如下 日期 1 6 10 25 31 库存量 a 38(a1) 42(a2) 39(a3) 37(a4) 41(a5) 试求该仓库该月的平均库存量 xf af x x a 库存量 a f f 38 38 5 42 4 39 15 37 6 41 1 a 42 5 4 15 6 1 39 1206 38 .90 (台) 37 31 41 af 计算公式: a 合计 f
统计学原理时间序列分析PPT课件
(二)增减速度
❖ 1、定义:增长量与基期水平之比 ❖ 2、反映内容:现象的增长程度 ❖ 3、公式:增长速度
vi
增长量 基期 水平 1 0% 0
发展水平1
第26页/共77页
(三)平均发展速度
❖ 1、定义 ❖ 各个时间单位的环比发展速度的序时平均数 ❖ 2、反映内容: ❖ 较长时期内逐期平均发展变化的程度 ❖ 3、平均发展速度的计算
年 份 旅游人数
季平均旅游人数
1999
1614020来自0202512001
272
68
第40页/共77页
缺点 ❖ 扩大的时距大小要符合现象的自身特点。 ❖ 扩大的时距要一致。 ❖ 信息损失过多,无法预测。
第41页/共77页
移动平均法
❖(1)原理:是时距扩大法的改良,
按照事先规定的移动时间长度K,采取逐项 向后递移,计算出序时平均数序列,主要 修匀不规则变动和季节变动的影响,使序 列呈现出比较明显的趋势。
均增长速度。
第29页/共77页
例题
某企业第四季度总产值和劳动生产率资料如下:
要求:(1)计算该企业第四季度的月平均劳动生产率。 (2)计算该企业第四季度劳动生产率。
第30页/共77页
第三节 时间序列模型分析
一、时间序列的构成及模型 二、长期趋势的测定和分析 三、季节变动的分析原理与方法 四、循环变动分析 五、不规则变动分析
第42页/共77页
移动平均法
首先,确定移动平均数的移动周期长度。
①移动周期一般以季节周期、循环变动周期长度为准; ②如若不存在明显的季节周期和循环周期,一般而言,我们在确
i1
a a 累计增长量:
i
0
4、二者关系:各逐期增长量第之12页和/共等77于页 相应的累计增长量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 2.分析品种构成,以便预测各种啤酒销量
年序 瓶装啤酒
散装啤酒
散装扎啤
合计
数量 比重% 数量 比重% 数量 比重% 数量 比重%
1 86 45.7 102 54.3 — — 188 100 2 182 52.6 164 47.4 — — 346 100 3 293 56.6 205 39.5 20 3.9 518 100 4 409 59.7 236 34.5 40 5.8 685 100 5 517 60.4 284 33.2 55 6.4 856 100
(5)曲线拟合法
• 曲线拟合法亦称趋势拟合法或时间回 归法,该方法根据时间序列随时间变 化趋势,运用最小二乘法拟合一条曲 线,而后利用该曲线随时间变化规律 对时间序列的未来取值进行预测。在 进行曲线拟合时,可以选取多项式曲 线、指数曲线、对数曲线和增长曲线 等,这里只是拟合了其中的多项式曲 线
• 2.随机性时间序列分析方法
1021
• 说明: 数学模型预测是定量分析方法,但在不同情况下应 用什么方法合适,需要从实际出发,首先进行定性 分析。本案例销售预测采用直线趋势模型是定量分 析,而对趋势类型的分析判断则使定性分析。一般 统计分析都要经过定性——定量——定性的过程。
案例2 时间序列分析在烟台市GDP预测
中的应用
本案例数据取自烟台市1949—1998年 国内生产总值的年度数据,并以此为依据 建立预测模型,对1999年和2000年的国内 生产总值作出预测并检验其预测效果。本 案例的最大特色在于:汇集了统计学原理 中的时间序列分析这一章节的所有知识点 ,通过本案例的教学,可以把不同的时间 序列分析方法进行综合的比较,便于更好 地掌握时间序列分析的内容。
从表中看出,瓶装啤酒和散装扎啤比重逐渐增大,散装啤酒比 重逐渐缩小。这与销售地区和运输条件有关。但第4、5年构成比重
趋于稳定,故可以按第5年构成比重预测第6年分 品种销量。 结合表中第5年各种啤酒构成比重,预计第6年分品种销量 为:瓶装啤酒1021吨×60.4%≈617吨,散装啤酒 1021吨×33.2%≈339吨,散装扎啤1021吨×6.4%≈65吨 3. 分析啤酒销售季节比重,以便进行季节预测
一、案例分析
1.数据的搜集
时间序列数据按照不同的分类标准可以划分 为不同的类型,最常见的有:年度数据、季 度数据、月度数据。本案例主要讨论对年度 数据如何进行预测分析。
2.确定性时间序列分析法
(1)平均增长量法
该方法是利用历史资料计算出平均 增长量,然后假定以后各期仍按这 样的平均增长量增长,从而得出在 未来一段时期内的预测值。计算平 均增长量有两种方法,即水平法与 总和法
t-N期以前的数据则完全不考虑,这往 往不符合实际。
(4)指数平滑法 指数平滑法可以看作是对移动平均法的改 进。 二阶指数平滑是在一阶指数平滑的基础上 再进行一次指数平滑,高阶的依此类推。 由于指数平滑存在滞后现象,因此,无论 一次指数平滑或二次、三次指数平滑值, 都不宜直接作为预测值。但可以利用它来 修匀时间序列,以获得时间序列的变化趋 势,从而建立预测模型。
啤酒销售存在季节变化 季节预测值=年预测值x季节比重 预测结果见下表
月份
1 2 3 4 5 6 7 8 9 10 11 12
合计
季节比重%
5.90 4.09 2.32 2.47 7.67 10.68 15.00 5.59 4.71 12.84 16.00 12.73
100.00
季节预测值
60 42 24 26 78 109 153 57 48 131 163 130
(2)平均发展速度法
• 该方法利用时间序列资料计算出平 均发展速度,然后假定以后各期仍 按这样的平均发展速度变化,从而 得出时间序列的预测值。平均发展 速度的计算方法也有两种,即几何 法和方程法
(3)移动平均法
• 移动平均法是根据时间序列资料, 采取逐项移动平均的办法,计算一 定项数的序时平均数,以反映长期 趋势的方法。移动平均法主要有简 单移动平均法,加权移动平均法, 趋势移动平均法等。这里主要介绍 简单移动平均法
一、 分析过程
1. 分析啤酒销量发展趋势并预测第6年销量 根据统计数字计算动态指标
年度
1
2
3
4
Hale Waihona Puke 5指标啤酒销量
188 346 518 685 856
逐期增长量
— 158 172 167 171
从表中看出,啤酒逐期增长量大体相同,属直线发展趋势, 故拟合直线方程。 计算表如下:
年序
X
Y
X2
XY
1
-2
188
4
-376
2
-1
346
1
-346
3
0
518
0
0
4
1
685
1
685
5
2
856
4
1712
合计
0
2593 10 1675
• 这里用中间年份为原点,使 X 0,可以使计算公式简化
。
• 设直线方程为:Y=a+bX
a Y 2593 518.6 n5
b
XY X2
1675 10
167.5
Y 518.6 167.5X • 第6年X=3,故预测值为:Y=518.6+167.5(3)=1021.1(吨)
第五章 时间序列分析案例
案例1 珍珠泉啤酒销售趋势预测和 季节预测
案例2 时间序列分析在烟台市GDP 预测中的应用
案例1 珍珠泉啤酒销售趋势预测和 季节预测
珍珠泉啤酒近5年销量直线上升。为正确制定第6年生产 经营计划,组织好原材料和包装物的采购供应,搞好生 产设备检修、产品储存设备的准备,销售网点增设等工 作,需要对第6年啤酒销售进行趋势预测。
• 移动间隔的选择
• 移动平均法对原始序列产生了一个 修匀作用,并且移动平均所使用的 间隔期越长,即N越大,修匀的程度 也越大,但对原始数据的反应越不 灵敏;反之,亦然。为此,需要依 据误差分析选择间隔时期N
• 移动平均法评价
• 简单移动平均法只适合作近期预测,若 目标的发展趋势存在较大的变化,采用 简单移动平均法会产生较大的预测偏差 和滞后;移动平均法会损失一部分数据 ,因而需要的数据量较大;移动平均法 对所平均的N个数据等权看待,而对
