多笔画问题(二)

多笔画问题（二）(★★★)下图是不凡绘制的地图，哪些地图可以一笔画。

(★★★)在下列的各个地图中，加一条线或去一条线后，一笔画出每个图形。

(★★★)下图是大房子的平面图，它由6间房间组成，每相邻两室有一门相通。

请设计一个出口，使不凡能够从入口A进去，一次不重复地经过所有的门，最后由出口走出房子。

【例3改编】(★★★)右图是某展览厅的平面图，它由五个展室组成，任两展室之间都有门相通，囫囵展览厅还有一个入口和一个出口，问游人能否一次不重复地穿过所有的门，并且第 1 页/共 4 页从入口进，从出口出？(★★★★)寻宝虫沿正方体的棱爬行，经过所有的顶点，且它没有重复走任何一条棱，最后回到出发点，它有几条棱没有经过？在线测试题温馨提醒：请在线作答，以便及时反馈孩子的薄弱环节。

1．(☆☆)下图中( )可以一笔画出，( )不能一笔画出。

（1）（2）（3）A．⑴⑵；⑶⑷B．⑴⑵⑶；⑷C．⑴；⑵⑶⑷D．⑵⑶；⑴⑷2．(☆☆☆)在下列的各图中，加一条线后使每个图都可以一笔画出。

下列做法准确的是( )。

A．B．C．D．第 3 页/共 4 页3．(☆☆☆)图中的线段代表公园的通道，小爱和小冉两人分离站在点A、B两处，他们约定以相同的速度同时从各自所在的位置出发，走遍公园中的每一条小路，最后到达C点。

下列说法准确的是( )。

C BAA．小爱先到C点B．小冉先到C点C．两人同时到达C点D．以上答案均不准确4．(☆☆☆☆)如图是一个超市的平面图，超市共有六个门，小爱想一次走遍所有通道而又不走重复路线。

倘若小爱从C进入，那么从( )出去。

A．A B．B C．D D．F5．(☆☆☆☆)有一个城市的街道图是由一些长方形所构成，如下图。

小冉要从A点出发，经过每一条路段至少一次后回到A点。

那么他至少要行走( )米。

50m60m70m400m100m300mAA．4100 B．4140 C．4200 D．4240。

二年级奥数.几何.一笔画问题(1)

如果用笔在纸上连续不断又不重复，一笔画成某种图形，这种图形就叫一笔画。

那么是不是所有的图形都能一笔画成呢？这一讲我们就一起来学习一笔画的规律。

能否一笔画成，先看是不是连通图形，不连通图形一定不能一笔画成。

连通图形，关键在于判别奇点、偶点的个数。

一、只有偶点，可以一笔画，并且可以以任意一点作为起点。

二、只有两个奇点，可以一笔画，但必须以这两个奇点分别作为起点和终点。

三、奇点超过两个，则不能一笔画。

对于一些比较复杂的路线问题，可以先转化为简单的几何图形，然后根据判定是否能一笔画的方法进行解答。

【例1】下面这些图形，哪个能一笔画？哪个不能一笔画？（1）（2）（3）（4）【例2】下面这些图形，哪个能一笔画？哪个不能一笔画？（1）（2）（3）（4）【例3】下面的各个小图形都是由点和线组成的．请你仔细观察后回答：一笔画问题发现不同知识框架例题精讲①与一条线相连的有哪些点?②与二条线相连的有哪些点?③与三条线相连的有哪些点?④与四条线或四条以上的线相连的有哪些点?【例4】下面各图能否一笔画成？（1）（2）（3）【例5】下面这几个字都能一笔写出来吗?【例6】下面这几个字母都能一笔写出来吗?【例7】下面的图形，哪些能一笔画出？哪些不能一笔画出？【例8】下图中，至少要画几笔才能画成？【随练1】德国有个城市叫哥尼斯堡．城中有条河，河中有个岛，河上架有七座桥，这些桥把陆地和小岛连接起来，这样就给人们提供了一个游玩的好去处(见下图)．俗话说，“人是万物之灵”，他们就是在游玩时候想出了这样一个问题：如果在陆地上可以随便走，而对每座桥只许通过一次，那么一个人要连续地走完这七座桥怎么个走法?好动脑筋的小朋友请先不要接着往下读，你也试一试，走一走．【随练2】在我国著名数学家陈景润写的《数学趣谈》一书中，有下面的这样一道题，大意是说：在法国的首都巴黎有一条河，河中有两个小岛，那里的人们建了15座桥把两个小岛和河岸连接起来，如下图所示，请你说一说，从任一岸出发，一次连续地通过所有的桥到达另一岸，可能吗?(每座桥只能走一次)AB CD 课堂检测【作业1】下面的图形都是由点和线组成的．请你仔细观察后回答：①与一条线相连的有哪些点?②与三条线相连的有哪些点?③与四条线或四条以上的线相连的有哪些点?【作业2】下面各图能否一笔画成？（1）（2）（3）（4）【作业3】下面这几个字母都能一笔写出来吗?【作业4】下面这几个字都能一笔写出来吗?【作业5】下图中，至少要画几笔才能画成？PONMLKJIHGFEDCBA家庭作业。

笔画问题

在行测考试中，图形推理中的一笔画问题，一直都是考生在考试中容易失分的题目。

其实主要问题存在于几个方面。

一、考生无法判断，什么样的图形考查的是一笔画;二、对一笔画图形的判断方法不了解。

接下来，中公教育专家卢志喜会从这两个方面给大家揭开一笔画的神秘面纱。

一、什么样的图形是一笔画图形定义：一笔画图形是一个图形从起点到终点可由一笔画成而中间没有间断，一笔画图形点可以重复，而线不可以重复。

一笔画图形具有两个比较明显的特点。

①图形相异;②图形简单;③图形一部分。

因此考生在复习图形推理时，除了要掌握相异图形常考的考点，点、线之外，还要掌握一笔画。

在复习备考的过程中首先要掌握一些简单的一笔画图形。

例如：长方形、正方形、三角形、五角星、圆。

当出现这些基本图形，或者在简单图形上增减了部分线条时，有一定的敏感性。

二、如何判断一个图形是否是一笔画图形方法一、奇偶点判断法奇点：从一个点引出的线条数为奇数;偶点：从一点引出的线条数为偶数。

规律：⒈凡是奇点数为2或者0的图形，一定可以一笔画成。

画时必须把一个奇点为起点，另一个奇点终点。

(利用奇点数判断，图形必须是一部分，比如“回”，奇点数为0，但是不能一笔画)2.其他情况的图都不能一笔画出。

(有偶数个奇点除以二便可算出此图需几笔画成。

)利用奇偶点法判断下列几个图形是否为一笔画图形，非一笔画图形需几笔画成分析：图形1.奇点数为2，偶点为2，可以一笔画成。

图2.奇点为0，偶点为3，可一笔画。

图3.奇点为6，偶点为0，三笔可画成。

图4.奇点为0，偶点为10，可一笔画。

图5.奇点为4，偶点为5，可2笔画。

图6.奇点为4，可2笔画。

奇偶点判断法规律适合一切一笔画图形。

方法二、区域连通法规律：1、平面内区域可以构成两两连通的区域(表示图形没有单独的出头的线条)，且区域之间属于单连通，这样的图形可以一笔画。

(单连通表示从一个区域到另一个区域只有唯一的路径，且经过的区域不能重复)利用区域连通法，判断下列几个图形是否为一笔画图形分析：首先对图形进行区域划分，如下：图1.区域1到区域2是单连通，可以一笔画。

小学奥数奇妙的一笔画精选练习例题含答案解析(附知识点拨及考点)

所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点．一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点； (3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点； (4)奇点个数超过两个的图形，一定不能一笔画．多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔画成．模块一、判断奇偶点【例 1】我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？J O I H G FED CBA【考点】一笔画问题【难度】2星【题型】解答【解析】奇点： D H J O 偶点：A B C E F G I 【答案】奇点： D H J O 偶点：A B C E F G I【例 2】同学们野营时建了9个营地，连接营地之间的道路如图所示，贝贝要给每个营地插上一面旗帜，要求相邻营地的旗帜色彩不同，则贝贝最少需要种颜色的旗子，如果贝贝从某营地出发，不走重复路线就（填“能”或“不能”）完成任务.【考点】一笔画问题【难度】2星【题型】填空例题精讲知识点拨4-1-5.奇妙的一笔画【关键词】华杯赛，六年级，初赛，第10题【解析】最少需要3种颜色的旗子。

因为中间的三点连成一个三角形，要使这三点所代表营地两粮相邻，要使相邻营地没有相同颜色的旗子，必须各插一种与其它两点不同颜色的旗子。

第八讲邮递线路问题

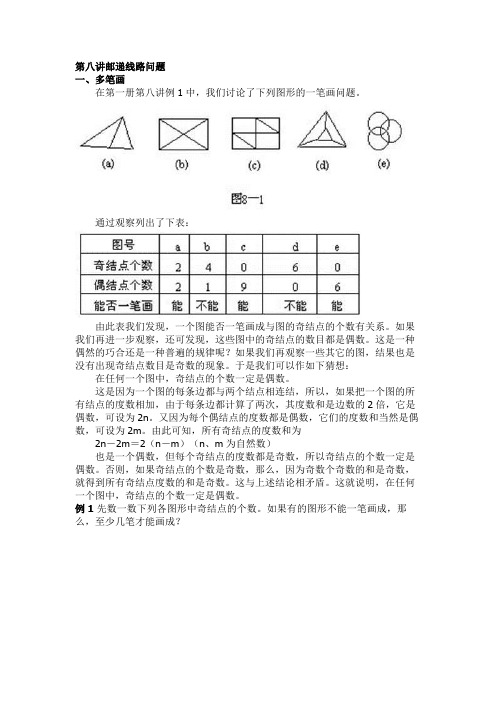
第八讲邮递线路问题一、多笔画在第一册第八讲例1中，我们讨论了下列图形的一笔画问题。

通过观察列出了下表：由此表我们发现，一个图能否一笔画成与图的奇结点的个数有关系。

如果我们再进一步观察，还可发现，这些图中的奇结点的数目都是偶数。

这是一种偶然的巧合还是一种普遍的规律呢？如果我们再观察一些其它的图，结果也是没有出现奇结点数目是奇数的现象。

于是我们可以作如下猜想：在任何一个图中，奇结点的个数一定是偶数。

这是因为一个图的每条边都与两个结点相连结，所以，如果把一个图的所有结点的度数相加，由于每条边都计算了两次，其度数和是边数的2倍，它是偶数，可设为2n。

又因为每个偶结点的度数都是偶数，它们的度数和当然是偶数，可设为2m。

由此可知，所有奇结点的度数和为2n－2m＝2（n－m）（n、m为自然数）也是一个偶数，但每个奇结点的度数都是奇数，所以奇结点的个数一定是偶数。

否则，如果奇结点的个数是奇数，那么，因为奇数个奇数的和是奇数，就得到所有奇结点度数的和是奇数。

这与上述结论相矛盾。

这就说明，在任何一个图中，奇结点的个数一定是偶数。

例1 先数一数下列各图形中奇结点的个数。

如果有的图形不能一笔画成，那么，至少几笔才能画成？分析与解：图8－2（a）中只有两个奇结点，根据欧拉定理，可从A点出发一笔画出到B点结束，图（b）中有四个奇结点，不能一笔画成。

图8－2（b）与图（a）比较，多出了折线CEFD。

如果先一笔画出图（a），再添一笔画出折线CEFD，就可得到图（b）。

因此，图（b）至少两笔才能画成。

图8－2（c）中共有六个奇结点，也不能一笔画成。

图（c）与图（b）比较又多出了一面旗子。

它也含有两个奇结点，于是在两笔画出图（b）的基础上，再添一笔画上旗子，就成了图（c）。

因此，图（c）至少三笔才能画成。

例2 图8－3（a）表示一所房子，问至少几笔才能画成？分析与解：1图8－3（a）所示的图中共有B、E、F、G、I、J六个奇结点，所以不能一笔画成。

小学奥数教程：奇妙的一笔画_全国通用(含答案)

所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点．一笔画问题：(1)能一笔画出的图形必须是连通的图形；(2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点； (3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点； (4)奇点个数超过两个的图形，一定不能一笔画．多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔画成．模块一、判断奇偶点【例 1】我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？J O I H G FED CBA【考点】一笔画问题【难度】2星【题型】解答【解析】奇点： D H J O 偶点：A B C E F G I 【答案】奇点： D H J O 偶点：A B C E F G I【例 2】同学们野营时建了9个营地，连接营地之间的道路如图所示，贝贝要给每个营地插上一面旗帜，要求相邻营地的旗帜色彩不同，则贝贝最少需要种颜色的旗子，如果贝贝从某营地出发，不走重复路线就（填“能”或“不能”）完成任务.【考点】一笔画问题【难度】2星【题型】填空【关键词】华杯赛，六年级，初赛，第10题【解析】最少需要3种颜色的旗子。

因为中间的三点连成一个三角形，要使这三点所代表营地两粮相邻，要使相邻营地没有相同颜色的旗子，必须各插一种与其它两点不同颜色的旗子。

三年级数学奥数题(有答案)

三年级数学奥数题(有答案)1) 工程问题绿化队种树任务，前四天种了200棵，还剩下400棵需要种。

根据这个工作效率，需要多少天才能完成任务？解答：先计算出一天能种多少棵树：200÷4=50棵。

然后计算总共需要的天数：(200+400)÷50=12天。

小结】归一思想，先求出一天种多少棵树，再求共需几天完成任务。

单一数：200÷4=50棵，总共的天数是：(200+400)÷50=12天。

2) 还原问题三个笼子里共养了78只鹦鹉。

如果从第1个笼子里取出8只放到第2个笼子里，再从第2个笼子里取出6只放到第3个笼子里，那么3个笼子里的鹦鹉一样多。

求3个笼子里原来各养了多少只鹦鹉？解答：三个班级每天共叠千纸鹤2400只，所以每个班级平均每天叠800只。

根据“相同时间”计算，三(一)班和三(二)班分别叠了2430只和2370只，共用了6天。

因此，三(一)班每天叠的个数是2430÷6=405只，三(二)班每天叠的个数是2370÷6=395只。

3) 楼梯问题1) 上楼梯问题某人要到一座高层楼的第8层办事，但电梯停电不能用。

如果从1层走到4层需要48秒，那么以同样的速度走到八层，需要多少秒？解答：上一层楼梯需要的时间是48÷(4-1)=16秒。

从4楼走到8楼共走4层楼梯，所以还需要的时间是16×4=64秒。

答：还需要64秒才能到达8层。

2) 楼梯问题晶晶从1楼走到3楼需要走36级台阶。

如果各层楼之间的台阶数相同，那么晶晶从第1层走到第6层需要走多少级台阶？解答：每一层楼梯有36÷(3-1)=18级台阶。

晶晶从1层走到6层需要走18×(6-1)=90级台阶。

答：晶晶从第1层走到第6层需要走90级台阶。

3) 页码问题1) 黑白棋子有黑白两种棋子共300枚，按每堆3枚分成100堆。

其中只有1枚白子的共27堆，有2枚或3枚黑子的共42堆，有3枚白子的与有3枚黑子的堆数相等。

第三讲多笔画及应用问题

第三讲多笔画及应用问题上一讲中，我们主要研究了利用奇偶点来判别一笔画，学习了利用一笔画来研究一些简单的实际问题.然而，实际生活中，许多问题的图并不能一笔画出，也就是说，一笔画理论不能直接用来解决这些问题.因此，在一笔画的基础上，我们有必要对这一类的问题作一些深入研究。

一、多笔画我们把不能一笔画成的图，归纳为多笔画.首先，我们来考虑一个不能一笔画成的图，至少用几笔才能画完呢？（为了研究的方便，我们仍然只研究连通图，非连通图可转化为连通图.）下面，我们就用简单熟悉的图来研究这个问题.通过前面的学习我们已经知道：当奇点个数不是0或2时，图不能一笔画出.因此，我们可以猜想；奇点个数是研究多笔画问题的关键。

观察下面的图形，并列出奇点的个数与笔画数（至少几笔画完此图）的关系表格。

为了表示得清楚一些，我们把图中第一笔画出的部分用实线表示，第二笔画出的部分用虚线表示，第三笔画出的部分用点线表示，其余部分请大家自己画出.奇点个数与笔画数的关系可列表如下：容易看出，笔画数恰等于奇点个数的一半.事实上，对于任意的连通图来说，如果有2n 个奇点（n为自然数），那么这个图一定可以用n笔画成.公式如下：奇点数÷2=笔画数，即2n÷2=n。

细心的同学可能会问：2n是表示一个偶数，但假若有奇数个奇点怎么办？实际上，这种情况不可能出现，连通图中，奇点的个数只能是偶数.想一想，这是为什么呢？例1 观察下面的图，看各至少用几笔画成？分析解答（1）图中有8个奇结点，因此需用4笔画成。

（2）图中有12个奇点，需6笔画成。

（3）图是无奇点的连通图，可一笔画成。

例2 判断下面的图能否一笔画成；若不能，你能用什么方法把它改成一笔画？分析解答图中共有4个奇点，因此，显然无法一笔画成.要想改为一笔画，关键在于减少奇点的数目（把奇点的个数减少到0或2），具体方法有两种：①去边.即将多余的两奇点间的边去掉.这种方法只适用于多余的两奇点间有边相连的情况，如对下图就不适用.本题中，可去掉连结奇点B、C的边BC。

一年级笔画教学存在的问题及对策

一年级笔画教学存在的问题及对策今年，我接手一四班，由于一年级年龄小，一些孩子的学习习惯仍带有幼儿班的味道。

存在的主要问题：比如上课跑位，讲话，坐姿歪歪斜斜，冷不防地来一声巨响。

说真的，一开始真有点头疼。

因为我从教三十年，教一年级小朋友还是头一回。

从幼儿班升到一年级，是一个过渡期，出现这些现象也很正常。

课上一年级任务重，那么多的识字量，如果不学扎实一点，基础打牢一点，到了高年级学习起来就很吃力。

因此，一年级拼音、识字教学就显得尤为重要。

从最初的拼音字母发音到简单的汉字书写，再到进一步的拼读，书写，这是一个渐进的过程。

基础好一点的，很快步入正轨；稍差一点的，需要反复强调，多次拼写。

拼音学完，就开始接触课文，而课文中的汉字给孩子们带来不小的困难。

如何让刚上一年级的新生喜欢汉字，就必须根据孩子的兴趣特点以及学生的认知规律进行识字教学。

一年级新书，编排很有特色，每一个字配有图画，具有形象性，而孩子的思维以形象思维为主。

因此，要对字形细心观察，比对图画，增强对汉字形体美的感知。

结合孩子特点，制定如下对策：一、练好笔画，重在得法笔画是汉字最简单的组成单位，练好基本笔画是练好字的基础。

基本笔画一般有横、竖、撇、捺、点、钩、提和折。

其他笔画都是在此基础上变化而来的。

古人发明了“永”字八法，就是专讲基本笔画的，可见基本笔画在练字中的重要性。

练好基本笔画，方法很多，但重在得法。

1.体验中悟古人对书法的用笔作了精准的论述“用笔须沉着，虽一点一画之间，皆须三过其笔”，也就是在写笔画的过程中，都要关注三个组成部分，即起笔、行笔和收笔。

学生写的是铅笔字，虽无需讲各种复杂的笔法，但从教学“横”开始，教师必须有这个意识，要告诉学生：起笔就是一个笔画的开始，行笔就好比这个笔画的行走过程和方向，收笔就是这个笔画的结束。

每一笔画都由这三部分组成。

以“横”为例，一般起笔重，行笔轻，收笔要顿笔有力，轻轻收起。

如何让学生真正体会到轻、重、有力的感觉，最常用的方法不外乎古人蒙童初学写字的“扶手润笔法”，即教师手把手地教。

多笔画

第三讲多笔画及应用问题上一讲中，我们主要研究了利用奇偶点来判别一笔画，学习了利用一笔画来研究一些简单的实际问题.然而，实际生活中，许多问题的图并不能一笔画出，也就是说，一笔画理论不能直接用来解决这些问题.因此，在一笔画的基础上，我们有必要对这一类的问题作一些深入研究。

一、多笔画我们把不能一笔画成的图，归纳为多笔画.首先，我们来考虑一个不能一笔画成的图，至少用几笔才能画完呢？（为了研究的方便，我们仍然只研究连通图，非连通图可转化为连通图.）下面，我们就用简单熟悉的图来研究这个问题.通过前面的学习我们已经知道：当奇点个数不是0或2时，图不能一笔画出.因此，我们可以猜想；奇点个数是研究多笔画问题的关键。

观察下面的图形，并列出奇点的个数与笔画数（至少几笔画完此图）的关系表格。

为了表示得清楚一些，我们把图中第一笔画出的部分用实线表示，第二笔画出的部分用虚线表示，第三笔画出的部分用点线表示，其余部分请大家自己画出.奇点个数与笔画数的关系可列表如下：容易看出，笔画数恰等于奇点个数的一半.事实上，对于任意的连通图来说，如果有2n个奇点（n为自然数），那么这个图一定可以用n笔画成.公式如下：奇点数÷2=笔画数，即2n÷2=n。

细心的同学可能会问：2n是表示一个偶数，但假若有奇数个奇点怎么办？实际上，这种情况不可能出现，连通图中，奇点的个数只能是偶数.想一想，这是为什么呢？例1观察下面的图，看各至少用几笔画成？分析解答（1）图中有8个奇结点，因此需用4笔画成。

（2）图中有12个奇点，需6笔画成。

（3）图是无奇点的连通图，可一笔画成。

例2判断下面的图能否一笔画成；若不能，你能用什么方法把它改成一笔画？分析解答图中共有4个奇点，因此，显然无法一笔画成.要想改为一笔画，关键在于减少奇点的数目（把奇点的个数减少到0或2），具体方法有两种：①去边.即将多余的两奇点间的边去掉.这种方法只适用于多余的两奇点间有边相连的情况，如对下图就不适用.本题中，可去掉连结奇点B、C的边BC。

小学数学奥数测试题笔画问题_人教版-学习文档

2019年小学奥数智巧趣题专题——一笔画问题1．判断下列图a、图b、图c能否一笔画．2．下面图形能不能一笔画成？若果能，应该怎样画？3．下图中不能一笔画成，请你在下图中添加最少的线段，将其改成一笔画的图形，并画出路线图．4．下图中的线段表示小路，请你仔细观察，认真思考，能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁？该怎样爬？5．下图是儿童乐园的道路平面图，要使游客走遍每条路并且不重复，那么出、入口应设在哪里？6．邮递员叔叔向11个地点送信一次信，不走重复路，怎样走最合适？7．观察下面的图，看各至少用几笔画成？8．判断下列图形能否一笔画．若能，请给出一种画法；若不能，请加一条线或去一条线，将其改成可一笔画的图形．9．18世纪的哥尼斯堡城是一座美丽的城市，在这座城市中有一条布勒格尔河横贯城区，这条河有两条支流在城市中心汇合，汇合处有一座小岛A和一座半岛D，人们在这里建了一座公园，公园中有七座桥把河两岸和两个小岛连接起来(如图a)．如果游人要一次走过这七座桥，而且对每座桥只许走一次，问如何走才能成功？10．右图是某展览厅的平面图，它由五个展室组成，任两展室之间都有门相通，整个展览厅还有一个进口和一个出口，问游人能否一次不重复地穿过所有的门，并且从入口进，从出口出？11．一条小虫沿长6分米，宽4分米，高5分米的长方体的棱爬行．如果它只能进不能退，并且同一条棱不能爬两次，那么它最多能爬多少分米？12．如图是某餐厅的平面图，共有五个小厅，相邻两厅之间有门相通，并且设有入口．请问你能否从入口进入一次不重复地穿过所有的门．如果可以，请指明穿行路线，如果不能，应关闭哪个门就可以办到？13．在3×3的方阵中每个小正方形的边长都是100 米．小明沿线段从A点到B 点，不许走重复路，他最多能走多少米？14．一个邮递员投递信件要走的街道如右图所示，图中的数字表示各条街道的千米数，他从邮局出发，要走遍各街道，最后回到邮局．怎样走才能使所走的行程最短？全程多少千米？第 1 页参考答案1．图a和图c能，图b不能。

奥数第九讲作业

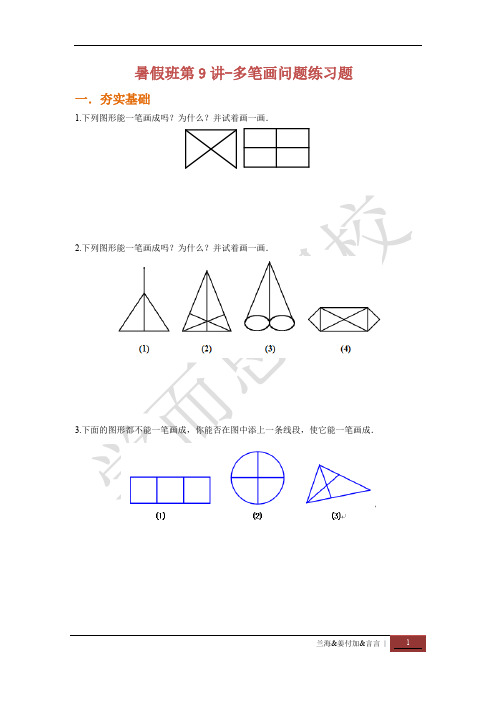
7.解析：把每个展室看作一个点，整个展厅的外部也看作一个点，两室之间有门相通，可以看作两点之间有线相连．这样，展厅的平面图就转化成 b 图，一个实际问题也就转化为这个图能否一笔画成的问题了，即能否从 A 出发，一笔画完此图，最后再回到 A ．图( b )中，所有的点都是偶点，因此，一定可以以 A 作为起点和终点而一笔画完此图．即游人可以从入口进，一次不重复地穿过所有的门，最后从出口出来．下面仅给出一种参观路线： A E B C E F C D F A ．
9.下图为某邮递员负责的邮区街道图，图中交叉点为邮户，每个小长方形的长为 180 米、宽为 150 米．如果邮递员每分钟行 200 米，在每个邮户停留半分钟，从邮局出发走遍所有邮户，再回到邮局，最少要用分钟．
150 邮局 180
兰海&姜付加&言言 |
3
四．杯赛演练：
10. “春蕾杯”小学数学邀请赛决赛下面的图形，要求画过的线段不能重复画，那么这个图形最少笔才能画出．
50m 60m 70m 300m 100m 图1 400m
A
兰海&姜付加&言言 |
6
11.(中国台湾小学数学竞赛选拔赛复赛) 有一个城市的街道图是由一些矩形所构成，如下图．一位警察要从 A 点出发巡逻，行经每一条路段至少一次后回到 A 点．请问他至少要行走多少米？50m 60m 70m 30m 100m 第12题 400m
A
兰海&姜付加&言言 |
4
答案： 1.解析：第一个图形可以一笔画，第二个图形有 4 个奇点不可以一笔画。 2.解析：⑴、⑷可以，⑵、⑶不可以；其实我们不必把所有奇点都找出来，只要发现图中的奇点多于 2 个就不能一笔画成了． 3.解析：⑴ 图中有四个点是奇点，所以不能一笔画成，要想使这个图形一笔画成，就要添加一笔，使这个图形的奇点变成两个．如下图：（答案不唯一）

笔画问题

§ 一笔画问题一、教学目标学会判断单数点和双数点，并根据单数点的个数判断一个图形能否一笔画成。

二、教学重难点如何判断一个图形能否一笔画成。

三、主要知识点1．概念：一笔画，指从图的一点出发，笔不离纸，而且每条线都只画一次不准重复而画成的图形。

2．分类：（1）双数点：从这点出发的线的数目是双数的，叫双数点。

（2）单数点：从这点出发的数目是单数的，叫单数点。

3．规律：一个图形能否一笔画成，关键在于图中单数点的多少。

（1）凡是图形中没有单数点的一定可以一笔画成。

（2）凡是图形中只有两个单数点，一定可以一笔画成，画时必须从一个单数点为起点，最后以另一单数点为终点。

（3）凡是图形中单数点的个数多于两个时，此图肯定是不能一笔画成。

四、主要方法找单数点的个数。

五、例题例1 下面的图形哪些可以一笔画成，哪些不能一笔画成？解图（1）不能一笔画出，图（2）、（3）可以一笔画出，图（4）不可以一笔画出，图（2）、（3）、（4）这样连在一起的图，叫做连通图。

而图（1）叫做不连通图，称与单数条边相连结的点为单数点，称与双数条边相连的点为双数点，（2）上的点全是双数点；图（3）是A 、B 两点是单数点，其余全是双数点；图（4）是A 、B 、C 、D4个点是单数点，其余是双数点。

评析（1）凡是由双数点组成的连通图，一定可以一笔画成，画时可以任一双点为起点，最后以这个点为终点画完全图。

（2）凡是只有两个单数点（其余均为偶点）的连通图，一定可以一笔画完，画时必须以一个单数点为起点，另一个单数点为终点。

（3）其他情况的图都不能一笔画出。

例2 右图能否一笔画成，如果能，应该怎样画？（1）（2）（3）D （4） BC分析与解此图是一个五角星，共有10个点，15条连线，10个点全是双数点，单数点为0，所以可以从任意一个双数点出发一笔画成，最后回到始点（即始点与终点重合）。

例3 下图是国际奥委会的会标，你能一笔把它画出来吗？分析与解一个连通图能否一笔画出，取决于这个图中单数点的个数。

小学奥数4-1-5 奇妙的一笔画.专项练习及答案解析

所谓图的一笔画，指的就是：从图的一点出发，笔不离纸，遍历每条边恰好一次，即每条边都只画一次，不准重复．从图中容易看出：能一笔画出的图首先必须是连通图．但是否所有的连通图都可以一笔画出呢？下面，我们就来探求解决这个问题的方法．什么样的图形能一笔画成呢？这就是一笔画问题，它是一种有名的数学游戏．我们把一个图形中与偶数条线相连接的点叫做偶点．相应的把与奇数条线相连接的点叫做奇点．一笔画问题：(1)能一笔画出的图形必须是连通的图形； (2)凡是只由偶点组成的连通图形．一定可以一笔画出．画时可以由任一偶点作为起点．最后仍回到这点；(3)凡是只有两个奇点的连通图形一定可以一笔画出．画时必须以一个奇点作为起点，以另一个奇点为终点；(4)奇点个数超过两个的图形，一定不能一笔画．多笔画问题：我们把不能一笔画成的图，归纳为多笔画．多笔画图形的笔画数恰等于奇点个数的一半．事实上，对于任意的连通图来说，如果有2n 个奇点(n 为自然数)，那么这个图一定可以用n 笔画成．模块一、判断奇偶点【例 1】我们把一个图形上与偶数条线相连的点叫做偶点，与奇数条线相连的点叫做奇点．下图中，哪些点是偶点？哪些点是奇点？J O I H G FED CBA【考点】一笔画问题【难度】2星【题型】解答【解析】奇点：D H J O 偶点：A B CEFG I【答案】奇点： D H J O 偶点：A B C E F G I【例 2】同学们野营时建了9个营地，连接营地之间的道路如图所示，贝贝要给每个营地插上一面旗帜，要求相邻营地的旗帜色彩不同，则贝贝最少需要种颜色的旗子，如果贝贝从某营地出发，不走重复路线就（填“能”或“不能”）完成任务.例题精讲知识点拨4-1-5.奇妙的一笔画【考点】一笔画问题【难度】2星【题型】填空【关键词】华杯赛，六年级，初赛，第10题【解析】最少需要3种颜色的旗子。

因为中间的三点连成一个三角形，要使这三点所代表营地两粮相邻，要使相邻营地没有相同颜色的旗子，必须各插一种与其它两点不同颜色的旗子。

多笔画问题(二)