平面单元-等效结点荷载计算PPT
结构力学Ⅱ课件:荷载及内力计算

T
0
T
1
§9.6 非结点荷载处理
q
荷载
非结点荷载
结点力、力矩
单元内分布力
集中力
温度作用
惯性力等
荷载向量
P =PD+PE
2
3
1
4
P
l
直接结点荷载PD
非结点荷载的等
效结点荷载PE
非结点荷载: 等效移置到结点上。
结构力学II
2
h/2
结点荷载
h/2
Q
q
ql
12
Q
2
2
h/2
3
2
P
q
2
ql
2
θ
1
h/2
y
4
构的结点位移向量: EI1 30.82 1.40 1.53 12.73 16.58T
30.82
E
解:因为杆件只考虑弯曲变形,包括
杆端结点的侧移和转角位移,对应的
内力为杆端剪力和弯矩,根据内力,
单元的刚度方程取四阶。
y
EI1 30.82
16.58
E
1.4
E
④ 1.53
①
ഥ ——单元坐标描述
ഥ
ത =
4. 如果梁单元内有非结点荷载,则要叠加非结点荷载引起的
固端力,得到真正的杆端内力:
F ( e ) K ( e ) ( e ) Fg ( e ) ——单元坐标描述
✓ 此时可以根据杆端内力确定单元刚度方程的阶数。
结构力学II
13
例25:计算图示结构的内力。 忽略轴向变形,已知求得结
EI
⑤
③
单
元
信
有限元分析补充内容等效节点载荷课件

有限元分析的基本步骤
01
02
03
前处理
建立模型、划分网格、定 义边界条件和载荷。
求解
对离散化的系统进行求解 ,得到各节点和单元的位 移、应力、应变等结果。
后处理
对求解结果进行可视化、 分析和评估,为设计优化 提供依据。
迭代法
对于一些复杂的有限元模型,可能需要采用迭代法来求解等效节点载荷,逐步逼近真实解。
等效节点载荷的精度与收敛性分析
精度分析
等效节点载荷的精度取决于有限元模型的离散程度、网格划分的质量以及外部载荷的施 加方式。
收敛性分析
随着有限元模型中网格的细化,等效节点载荷应逐渐收敛于真实值。收敛速度和收敛特 性可以通过收敛性分析来评估。
等效节点载荷的应用场景
01
结构静力分析
在结构静力分析中,等效节点载 荷可用于计算结构的内力和变形 。
02
结构动力分析
03
结构稳定性分析
在结构动力分析中,等效节点载 荷可用于计算结构的动态响应和 振动特性。
在结构稳定性分析中,等效节点 载荷可用于计算结构的临界载荷 和失稳模态。
03
CHAPTER
有限元分析中的等效节点载 荷
02 后处理技术:结果可视化、误差分析、优化设计 等。
03 前后处理技术的自动化和智能化:提高效率,减 少人工干预和错误。
05
CHAPTER
案例分析
等效节点载荷在结构分析中的应用案例
总结词
等效节点载荷在结构分析中应用广泛,通过 合理设置等效节点载荷,可以模拟复杂结构 的受力情况,提高分析精度。
结构力学等效结点荷载 ppt课件

q
2(1,2,3)
3(4,5,6) 2(4,5,6)
3(7,8,9)
E
F
F2 F2
结构力学等效结点荷载
内 力 相 等
结点位 移等效
4
2. 等效结点荷载的计算
2(4,5,6) FP
FPl ql 2 8 12
q
② 3(7,8,9)
①
=
ql 2
ql 2
1(1,2,3)
12
ql
2
FPl
FPl
2 FPl 2
8
+ 没有结 0
点位移
0
ql 2
0
12
ql
2
ql
ql 2
结点荷载作用下求得的即是杆端
的实际位移。
E
F
F1 F1
(C)
E
F
有非结点荷载作用的单元杆
F2 F2 端力,可以由两部分叠加而得,
一部分是单元固端力,另一部分
结构力学等效结是点杆荷载端位移产生的杆端力。 16
练习:用先处理法、后处理法分别计算结构的 综合结点荷载列阵。
M=FPl FP
FP=ql C
D
F
0
F
2
F3 F4 F5
FR1x
F
R1
y
0
FR
2
y
F1
y
F2 F2
x y
Байду номын сангаас
F3
x
F
R1
y
=
F
R
2
F2 x y F3 x
F1 y F2 y
F6
0
F3
y
F3 y
等效结点荷载 -回复

等效结点荷载-回复等效节点荷载(equivalent nodal load,ENL)是电力系统分析中的一种方法,用于简化复杂系统中节点之间的连接。
通过将一组节点的电流和电压转换为等效的荷载,可以简化系统的计算和分析过程。
本文将从基本概念、计算方法、应用和实际案例等方面逐步介绍等效节点荷载。
基本概念等效节点荷载是用来替代一组连接在节点上的元件,从而简化系统分析的方法。
它将节点上所有的电流和电压转换为等效的荷载,使得在计算过程中可以只考虑节点间的连接关系,而不用关心具体的元件参数。
常用的等效节点荷载包括恒功率荷载、恒阻抗荷载和恒导纳荷载。
计算方法等效节点荷载的计算方法通常是通过节点分析或剖分电路的方法来实现的。
首先,需要将系统中的元件连接关系转换为等效的电流和电压,然后根据转换后的电流和电压计算等效节点荷载。
具体的计算方法根据节点分析和剖分电路的不同而有所不同,但核心思想都是将节点间的连接关系转换为等效荷载。
应用等效节点荷载在电力系统分析中有广泛的应用。
它可以用于求解节点电压、电流和功率等参数,从而帮助工程师进行系统计算和分析。
等效节点荷载还可以用于评估系统的稳定性、确定潮流分布、分析故障影响等。
通过对系统中不同节点的等效节点荷载进行分析,可以更加深入地了解系统的性能和运行情况。
实际案例为了更好地理解等效节点荷载的应用,我们将通过一个实际案例来说明其在电力系统分析中的作用。
假设我们有一个复杂的电力系统,包含多个节点和元件。
我们希望计算出每个节点的电压和电流,以及各个元件的功率损耗。
如果直接对系统进行分析,将会非常繁琐和复杂。
但是,如果我们利用等效节点荷载的方法,可以将节点间的连接关系简化为等效荷载,从而简化计算过程。
通过计算等效节点荷载,我们可以更快、更准确地得到每个节点的电压和电流,以及各个元件的功率损耗。
结论等效节点荷载是一种用于简化电力系统分析的方法,通过将节点的电流和电压转换为等效荷载,可以简化系统的计算和分析过程。
第二章00 建筑结构荷载计算介绍PPT课件

1.4.4 荷载动力系数
结构受动力作用时,应将荷载增大,这个增大 系数就叫荷载动力系数
建筑结构设计的动力计算,在有充分依据时, 可将重物或设备的自重乘以动力系数后,按静力计
搬运和装卸重物以及车辆起动和刹车时的动力 系数,可采用表1.1~1.3,其动力荷载只传至楼板和
考虑一个最大荷 载
考虑两个荷 载
取大值
练习
n
S SGK SQ1K ci SQiK
i2
屋面
恒载
楼面 活载
活载
2.518 2.017 0.6 2.0 0.7
66.8kN / m2
17层
练习:位于非地震区,某工业建筑楼面梁、楼面活载标准值为
4.5 KN / m2 ,在楼面永久荷载和楼面活载作用下,该楼面梁梁 端弯矩标准值分别为240KN.m和230KN.m,楼面活荷载的组合 值系数取0.7,求该楼面梁梁端弯矩设计值。
地面粗糙度是指风在到达结构物以前吹越过 2km范围内的地面时,描述该地面上不规则障碍物 分布状况的等级。规范将地面粗糙度分为A、B、C、 D四类。
A类——指近海海面和海岛、海岸、湖岸及沙漠
B类——指田野、乡村、丛林、丘陵以及房屋比
C类—— D类——指有密集建筑群且房屋较高的城市市区。
1.6.3 风荷载体型系数
M 1.28 1.4 50 79.6KN ' m
M 1.28 0.9 (1.4 50 1.4 4) 77.64KN ' m
M 79.6KN 'm
考虑两个 荷载
例题5
某厂房排架结构,经内力计算知排架柱底截面内力 标准值为:恒载产生弯矩标准值为MGK 8KN ' m
有限元讲稿等效载荷PPT课件
October 9, 2004
第四章-2
第2页/共33页
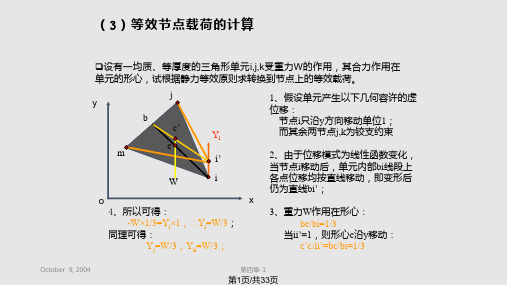
(3)等效节点载荷的计算
如果单元上有体力作用,沿x,y方向的体力分量为{P}=[X, Y]T,相当于在点 (x,y)处作用集中力为{P}tdxdy,则等效节点载荷为:
Re [N]T {P}tdxdy
V
如果单元某边界受有面力q作用,沿x,y方向的面力分量为{q}=[qx, qy]T,若将 微元体tds上的面力qtds当作集中载荷P,相当于在边界点(x,y)处作用集中力 为P={q}tds,则等效节点载荷为:
号的对应关系:
(i, j, m)=(5, 3, 2)
当许多单元共用一个节点时,作用在
该节点的合力就是每个单元刚阵中具
6
有相同下标子矩阵[kij]的迭加,也就是 总刚阵中具有相同下标的元素,即:
Kij [kij ]e
e
October 9, 2004
第四章-6
第6页/共33页
(4)结构整体刚度矩阵的集成
单元的刚性位移是指平移和转动,与单元的内部变形无关,它是由于其他 单元发生了变形后而连带发生的,因此要正确反映单元的位移形态,位移模式 中必须包含反映单元刚性位移的函数项,即常数项。 2)位移模式必须能反映单元的常应变项
当单元的尺寸越来越小时,每个单元内的应变应趋于一个确定的值。因此 对有限区域(元)讲,所选择位移模式必须包含能描述上述特性的函数项,即 包括两部分:一部分能给出常应变,另一部分给出与坐标有关的应变,即变量 应变。由于变量应变随单元尺寸减小逐渐变小,因此常应变项为应变的主要部 分。即位移模式至少需包含线性函数项。 3)位移模式应反映实际结构位移的连续性
K25
K 26 U2 =0
F2
结构力学课件等效结点荷载

F
F
(1)
ql 2 12
F F
F 5 F 6
FPl
FP 2
8
0
ql
2
ql 2
12
0
(2)
FP
2
FPl
F
F
(2)
8
0
FP
2 FPl
8
0
局部坐标系下单元等效结点荷载:
e
Fe
FE F
整体坐标系下单元等效结点荷载:
FEe
T T
1(1,2,3)
5(11,12,13)
总码
0
0
1
4
FP
FP
2
5
2 2
FE (3) T T
F
F
(3)
FPl 8
FPl 8
3
6
0 0 4 7
FP
2 FPl
8
8 9
总码
ql
2
1
4
0
2
5
FE (1)
ql 2 12
0
FP
FPl 2 8
0
FPl
FP 2
8
0
局部坐标系下单元固端力列阵
2(4,5,6) FP
② 3(7,8,9) q①
1(1,2,3)
ql 2 0
12
ql 2
ql
ql 2
2
12 0
FP
FPl 2 8
0
F
F 1 F
e
F 2
F
F
e
F
F 3 F
F 4
(1)
0
ql
2
0
平面单元等效结点荷载计算ppt课件
1 0 0 0 0 0
1 0 0 0 0
对称
*
*
*
0
* * 0
6
*
0
1
4. 边境条件的处置
3〕大数法〔适宜于计 k11
k1i
k1n a1 P1
算机处置〕 α>>1
ki1
kii
kin
ai
kiib
kn1
kni
knn an Pn
第i行展开之后:
ki1a1 kiiai kinan kiib 两边同除以:
4. 边境条件的处置
1〕直接带入法〔降阶法〕
ab为已知位移组成的列向量,Pb为对应的支座反力
KKbaaa
Kab Kbb
aaba
Pa Pb
KaaaaPaKabab
求得aa之后可按下式求得支座反力:
Pb Kba aaKbb ab
改动了原方程 的顺序,只适 用于一些简单
的问题
4. 边境条件的处置
2. N1 N 2 N 3 1
N I N 1 I N 2 I N 3
3.
N
的
i
阶
数
与
假
设
的
N
:插
i
值
函
数
(
形
状
函
数
)
位移函数阶数相同
u1
v1
0
N3
u v
2 2
N
ae
u
3
v 3
I为 二 阶 单 位 矩 阵
4. 数 值 在 0- 1之 间
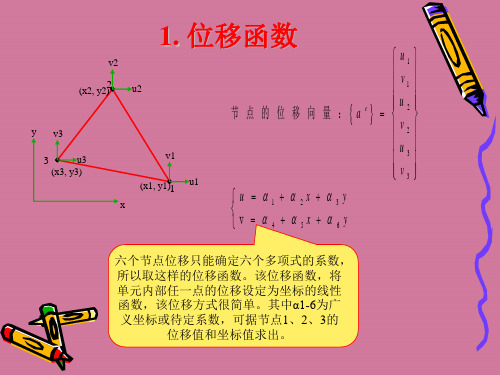
1. 位移函数-例题
1. 位移函数
v2
(x2, y2)2 u2
谭继锦有限元法课件之四 3.5 单元等效节点载荷

13
第三章 连续体问题的有限元法
P
e
1 3 1 = 3 1 = 3
I A I I
p t I I
T T
I I
A t p w
I I
T
=
1 3
1 = 3
1 0 1 0 1 0 wx w y wx wy wx wy
u 1 2 x 3 y v 4 5 x 6 y
Questions: 1. 有限元求解方法? 2. 为什么定义位移模式? 3. αi等系数如何求取?
2
第三章 连续体问题的有限元法 由节点位移表达单元内任一点位移的插值公式,即 由节点位移表达单元内任 点位移的插值公式 即 位移模式的另一种形式:
P
e
P i e P j P xi Pm
e
P
e yi
P
e xj
P
e yj
P
e xm
P
e ym
T
7
第三章 连续体问题的有限元法 设该单元发生一个任意的虚位移,n点相应的虚位移为:
f u
[k ]
e
[ B ]
T
[ D ][ B ]tdxdy
5
第三章 连续体问题的有限元法
第 节 单元等效节点载荷 第五节 单 等效节点载荷
等效节点载荷处理:将非节点载荷按一定原则移置到 节点上,也就是等效节点载荷处理。移置必须满足静 力等效原则。 力等效原则 所谓静力等效原则是指原载荷与移置后的等效节点 载荷在弹性体产生任何虚位移过程中,所做的虚功 相等。在一定的位移函数下,这种移置的结果是唯 一的。
等效结点荷载例

YP 2 12kN
8kN
2
2ห้องสมุดไป่ตู้5m
例13-3 求图示结构的等效结点荷载{P}. e ① T F 解:1)求F 0 12 10 0 12 10 P P X P2 0 单元① X P1 0
4.8kN/m
↓↓↓↓↓↓↓↓↓↓
1
x
F 0 12 10 0 12 10 F 0 4 5 0 4 5
0 +4 4
1
12 +0 2 12 10- 55 3 -10 -10 4
点击左键,一步步播放。结束播放请点“后退”。
重新播放请点
重新播放
1 0 0 0 0 0
0 0 1 0 0 0
0 0 0 0 1 0
0 0 0 1 0 0
0 0 4 0 4 0 0 5 5 0 0 4 0 4 0 5 5 1
1 2 3 {P}= 0 0 0
① P
② T P
T
2)求
P
①
①
T FP
T
T ①
①
单元①的倾角α1=0 1 2 3 0 0
①
P
T FP I FP 0
12 10
0
1 10
4
T
单元②的倾角α2=90°
0 1 ② ② T 0 P T FP 0 0 0
按单元集成法求整体结构的等效结点荷载 ⑴局部坐标系中的单元固端约束力 F e P e e ⑵整体坐标系中的单元等效结点荷载 P T T F P ⑶整体结构的等效结点荷载{P} 由各单元{P} e 中的元素按{λ}在{P}中进行定位并累加。 ⑷等效结点荷载与直接结点荷载叠加,即得结构的结点荷载。
建筑力学课件-第十二章等效载荷及地震作用

1 简化分析过程
2 提高设计效率
等效载荷将复杂的荷载情况 简化为一个或多个等效载荷, 减少了结构分析的复杂性。
通过使用等效载荷,可以快 速进行结构分析,加快设计 进程。
3 提高准确性
等效载荷的计算过程相对简单,减少了出错的可能性,提高了分析结 果的准确性。
地震反应分析法与静力分析法
地震反应分析法和静力分析法是两种常用的结构分析方法,它们在处理地震 载荷时具有一些异同。
地震响应分析是评估建筑结构地震抗震性能的重要方法之一。常用的地震响应分析方法包括:
线性弹性分析
假设结构在地震作用下保持线性弹性行为进 行分析。
非线性时程分析
考虑结构的非线性行为,在时间域内进行分 析。
频谱分析
利用结构的振动模态和地震谱,计算结构的 响应特性。
有限元分析
利用有限元法对结构进行离散化,求解结构 在地震作用下的响应。
加固柱子
对柱子进行加固,提高柱子的承载能力。
增加钢筋混凝土墙
在结构中增加钢筋混凝土墙,提供额外的刚 度和抗震能力。
建筑力学课件-第十二章 等效载荷及地震作用
本章介绍了建筑结构中的等效载荷以及地震作用。探讨了等效载荷的概念、 静力分析法和地震反应分析法的异同,以及等效载荷的计算方法和公式。
等效载荷的作用
等效载荷在建筑结构设计中起着重要的作用。通过将复杂的荷载情况转化为 等效载荷,可以简化结构分析过程,提高设计效率和准确性。
3 可靠度分析
4 灰色理论
使用可靠度理论评估结构的地震可靠度。
利用灰色理论对结构的地震安全性进行 评估和预测。
建筑结构抗震加固方法
对于现有的建筑结构,可以采取一些抗震加固措施,提高其抗震性能。常用的抗震加固方法包括:
结构力学等效结点荷载.

平面四边形4结点等参有限单元法

有限元程序设计平面四边形4结点等参有限单元法程序设计1、程序功能及特点a.该程序采用四边形4节点等参单元,能解决弹性力学的平面应力应变问题。
b.前处理采用网格自动划分技术,自动生成单元及结点信息。
b.能计算受集中力、自重体力、分布面力和静水压力的作用。
c.计算结点的位移和单元中心点的应力分量及其主应力。
d.后处理采取整体应力磨平求得各个结点的应力分量。
e.算例计算结果与ANSYS计算结果比较,并给出误差分析。
f.程序采用Visual Fortran 5.0编制而成。
2、程序流程及图框图2-1程序流程图图2-2子程序框图其中,各子程序的主要功能为:INPUT――输入原始数据HUAFEN――自动网格划分,形成COOR(2,NP),X,Y的坐标值与单元信息CBAND――形成主元素序号指示矩阵MA(*)SKO――形成整体刚度矩阵[K]CONCR――计算集中力引起的等效结点荷载{R}eBODYR――计算自重体力引起的等效结点荷载{R}eFACER――计算分布面力引起的等效结点荷载{R}eDECOP――支配方程LU三角分解FOBA――LU分解直接解法中的回代过程OUTDISP――输出结点位移分量STRESS――计算单元应力分量OUTSTRE――输出单元应力分量STIF――计算单元刚度矩阵FDNX――计算形函数对整体坐标的导数TiiyNxN⎥⎦⎤⎢⎣⎡∂∂∂∂,=i1,2,3,4。
FUN8――计算形函数及雅可比矩阵[J]SFUN ――应力磨平-单元下的‘K’=NCN‘SCN――应力磨平-单元下的右端项系数‘CN‘SUMSKN――应力磨平-单元下的右端项集成到总体的‘P‘SUMSTRS――应力磨平-单元下的集成到总体的‘K‘GAUSTRSS――高斯消元求磨平后的应力3、输入数据及变量说明当程序开始运行时,按屏幕提示,键入数据文件的名字。
在运行程序之前,根据程序中INPUT需要的数据输入建立一个存放原始数据的文件,这个文件的名字为INDAT.DAT。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
②
43
2④
13
1
5
6
3、解方程组,求节点位移; 4、根据节点位移求出应力。
a
a
14.10.2020
8
3. 总体刚度矩阵的形成与特点 —整体分析的一般步骤
1、建立整体刚度矩阵
上图中的结构有六个节点,共有12个节点位移分量(自由度) 和12个节点力分量,它们之间的关系为:
Ka P 即:
k1,1
k2,1
将载荷转移到节点上,必须遵循静力等效的原则。静力等效是指 原载荷与节点载荷在任意虚位移上做的虚功相等。前面推导时使用的 能量泛函пp对{ae}进行变分之后产生的{δae}实际上就是虚位移,以上公 式可以适用于任意复杂的荷载情况。
如果单元为线性单元(如,本章的三节点三角形单元),则可以 采用直接的静力等效法和虚功等效法。
14.10.2020
3
1. 位移函数
若令:
N1
1 2A
(a1
b1 x
c1 y )
N2
1 2A
(a2
b2 x
c2 y)
N3
1 2A
(a3
b3 x
c3 y)
插值函数 矩阵或形 函数矩阵
u
u
v
N1
0
0 N1
N2 0
0 N2
N3 0
插值函数的性质:
1 . N i ( x j , y j ) ij i , j 1 , 2 ,其3 中
最终确定6个待定系数:
12 3
1 2A
a1
b1
c1
a2 b2 c2
a3 b3 c3
uu12 u3
54 6
1 2A
a1 b1 c1
a2 b2 c2
a3 b3 c3
vv12 v3
14.10.2020
2
其中:
1. 位移函数
1 x1 y1
2 A 1 x2 y2 1 x3 y3
k11,1
k12,1
k1,2 k2,2
k11,2 k12,2
k1,11 k2,11
k11,11 k12,11
14.10.2020
k1,12 a1 P1
k2,12
a2
P2
总体刚度方程 中的自由度与 节点位移之间 的对应关系
k11,12
a11
k12,12 a12
1. 位移函数
v2
2
(x2, y2)
u2
y v3
3
u3
(x3, y3)
v1
(x1, y1) 1 u1
x
u1
v1
节 点 的 位 移 向 量 :
ae
u v
2 2
u
3
v 3
u v
1 4
2x 5x
3y 6y
六个节点位移只能确定六个多项式的系数,
所以取这样的位移函数。该位移函数,将
a1 x2 y3 x3 y2
为2A第1行各 个元素的代 数余子式
b1 y2 y3
1,2,3轮 换
c1 x3 x2
u
1 2A
[
(
a1
b1 x
c1 y )u1
(a2
b2 x
c2 y)u2
(a3
b3 x
c3 y)u3 ]
1 v 2 A [(a1 b1 x c1 y )v1 (a2 b2 x c2 y )v2 (a3 b3 x c3 y )v3 ]
P11
P12
a1 a2
u1
v1
P1 P1x
P2
P1 y
a1
1
u
6
P11
9
P6
x
a12 v6 P12 P6 y
3. 总体刚度矩阵的形成与特点 —整体分析的一般步骤
2、根据支承条件修改整体刚度矩阵。
建立整体刚度矩阵时,每个节点的位移当作未知量看待,
4
1. 位移函数-例题
例题:图示等腰三角形单元,求其插值函数矩阵[N]。
y 2 (0,a)
3 (0,0)
a1 x2 y3 x3 y2 0 b1 y2 y3 a c1 x3 x2 0
a2 x3 y1 x1 y3 0 b2 y3 y1 0 c2 x1 x3 a
x 1 (a,0)
没有考虑具体的支承情况,因此进行整体分析时还要针对 支承条件加以处理。
在上图的结构中,支承条件共有四个,即在节点1、4、6 的四个支杆处相应位移已知为零:u1=u4=v4=v6=0
建立节点平衡方程时,应根据上述边界条件进行处理。
单元内部任一点的位移设定为坐标的线性 函数,该位移模式很简单。其中α1-6为广 义坐标或待定系数,可据节点1、2、3的
位移值和坐标值求出。
14.10.2020
1
1. 位移函数
将节点位移带入:
u1 1 2x1 3 y1 v1 4 5x1 6 y1 u2 1 2x2 3 y2 v2 4 5x2 6 y2 u3 1 2x3 3 y3 v3 4 5x3 6 y3
1 2A
(a3
b3 x
c3 y)
1 a2
(a 2
ax
ay)
1
x a
y a
x
[N
]
a
0
y a
0 1 x y aa
0
0
x a
0
y a
0
1
x a
y a
14.10.2020
6
2. 关于节点等效力的一点说明
连续弹性体离散为单元组合体时,需把弹性体承受的任意分布的 载荷都向节点转移,而成为节点等效载荷(或节点等效力)。如果弹 性体承受的载荷全都是集中力,则将所有集中力的作用点取为节点, 就不存在转移的问题,集中力就是节点等效载荷。但实际问题往往受 有分布的面力和体力,都不可能只作用在节点上。因此,必须进行载 荷转移。如果集中力的作用点未被取为节点,该集中力也要向节点转 移。
a3 x1 y2 x2 y1 a 2 b3 y1 y2 a c3 x2 x1 a
14.10.2020
5
1. 位移函数-例题
三角形的面积:
a2 A
2
N1
1 2A
(a1
b1 x
c1 ya
N2
1 2A
(a2
b2 x
c2 y)
1 a2
(0
0
ay)
y a
N3
2. N1 N 2 N 3 1
N I N 1 I N 2 I N 3
3.
N
的
i
阶
数
与
假
设
的
N
:插
i
值
函
数
(
形
状
函
数
)
位 移 函 数 阶 数14.相10.同2020
4. 数 值 在 0- 1之 间
u1
v
1
0
N3
u v
2 2
N
ae
u
3
v 3
I为 二 阶 单 位 矩 阵
14.10.2020
7
3. 总体刚度矩阵的形成与特点 —整体分析的一般步骤
P1y
1
2
a
①
P3y
图示结构的网格共有四个单元 和六个节点。在节点1、4、6共 有四个支杆支承。结构的载荷 已经转换为节点载荷。
整体分析的四个步骤:
23
P2x
1 2
a
13
3
P3x
③2
1、建立整体刚度矩阵;
2、根据支承条件修改整体刚度 矩阵;
