第五版运筹学基础与应用-大题模拟试题及答案
02375《运筹学基础》复习题

《运筹学基础》模拟试题一、填空题1.决策方法可以分为定性决策、()和()。
2.判断预测法一般有下列两种:()和()。
3.网络图分为()网络图和()网络图。
4.盈亏平衡分析是以所有成本都能分为()和()两个组成部分为前提。
5.系统模拟的过程是建立模型并通过模型的运行对模型进行()和(),使模型不断趋于完善的过程6. 滑动平均预测法又分为()和()。
7.建立库存模型主要是为了探讨()与()之间的关系。
8.企业的盈亏主要取决于企业产品的()和产品的()。
二、名词解释题1.运筹学2.决策3.ABC分析法4.线性规划5.盈亏平衡分析6.预测7.经济订货量8.网络计划技术9.关键路线法10.模拟三、简答题1.简述应用运筹学进行决策过程的步骤2.简述预测的程序3.简述线性规划建模的步骤4.简述网络计划优化的内容5. 简述特尔斐法的实施程序6. 简述决策的程序7. 简述决策树方法的优点8. 简述库存管理的意义四、建模题1.某企业在计划期内要安排生产甲、乙两种产品,已知生产单位产品所需的A、B、C 三种原材料的消耗如下表所示。
该工厂每生产1吨甲种产品可获利15元,生产1吨乙种产品可获利20元。
问应如何安排生产计划使该工厂获利最多?只需建立数学模型,2.现要将三种煤混合后炼焦,每公斤混合煤产生的热量不能少于21千卡,含硫量不得超过0.00025,问应如何混合才能使每吨混合煤的成本最低?只需建立数学模型,不需要求解。
3. 某厂生产甲、乙、丙三种产品,其所需劳动力、材料等数据见下表。
问应如何安排生产计划使该工厂获利最多?只需建立数学模型,不需要求解。
五、计算题1.设有某印刷厂,下一年度需用印刷纸2000卷,经会计部门核算预测:该种纸的进厂价为200元/卷,采购该种纸的订货费用为每次500元,该种纸的年保管费用率为平均存货额的25%,试求该种纸的最佳订货量。
2. 某企业经销一种产品,产品单件可变成本为50元,售价100元,每年固定成本为90000元。
运筹学基础及应用课后习题答案(第一二章习题解答)

运筹学基础及应用课后习题答案(第一二章习题解答)第一章:线性规划一、选择题1. 线性规划问题中,目标函数可以是()A. 最大化B. 最小化C. A和B都对D. A和B都不对答案:C解析:线性规划问题中,目标函数可以是最大化也可以是最小化,关键在于问题的实际背景。
2. 在线性规划问题中,约束条件通常表示为()A. 等式B. 不等式C. A和B都对D. A和B都不对答案:C解析:线性规划问题中的约束条件通常包括等式和不等式两种形式。
二、填空题1. 线性规划问题的基本假设是______。
答案:线性性2. 线性规划问题中,若决策变量个数和约束条件个数相等,则该问题称为______。
答案:标准型线性规划问题三、计算题1. 求解以下线性规划问题:Maximize Z = 2x + 3ySubject to:x + 2y ≤ 83x + 4y ≤ 12x, y ≥ 0答案:最优解为 x = 4, y = 2,最大值为 Z = 14。
解析:画出约束条件的图形,找到可行域,再求目标函数的最大值。
具体步骤如下:1) 将约束条件化为等式,画出直线;2) 找到可行域的顶点;3) 将顶点代入目标函数,求解最大值。
第二章:非线性规划一、选择题1. 以下哪个方法适用于求解非线性规划问题()A. 单纯形法B. 拉格朗日乘数法C. 柯西-拉格朗日乘数法D. A和B都对答案:B解析:非线性规划问题通常采用拉格朗日乘数法求解,单纯形法适用于线性规划问题。
2. 非线性规划问题中,以下哪个条件不是K-T条件的必要条件()A. 梯度条件B. 正则性条件C. 互补松弛条件D. 目标函数为凸函数答案:D解析:K-T条件包括梯度条件、正则性条件和互补松弛条件,与目标函数是否为凸函数无关。
二、填空题1. 非线性规划问题中,若目标函数和约束条件都是凸函数,则该问题称为______。
答案:凸非线性规划问题2. 非线性规划问题中,K-T条件是求解______的必要条件。
运筹学基础和应用(第一二章习题解答)

运筹学基础及应用 习题解答习题一 P46 1.1 (a)该问题有无穷多最优解,即满足210664221≤≤=+x x x 且的所有()21,x x ,此时目标函数值3=z 。
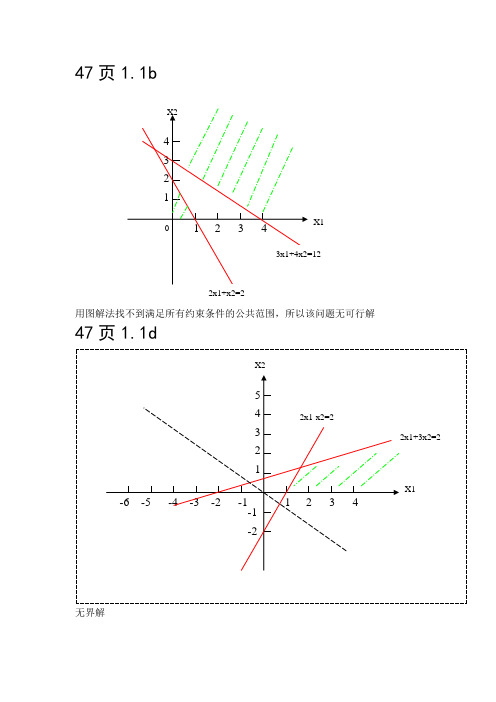
(b)用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A4最优解()T x 0,0,7,0,10,0=。
(b) 约束方程组的系数矩阵⎪⎪⎭⎫ ⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。
1.3(a)(1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ,最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式 ⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。
令021==x x得基可行解()8,9,0,0=x ,由此列出初始单纯形表 21σσ>。
5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ,2328,1421min =⎪⎭⎫ ⎝⎛=θ0,21<σσ,表明已找到问题最优解0 , 0 , 231,4321====x x x x 。
最大值 235*=z (b)(1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x ,最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩21=+x x 2621+x x则3P ,4P ,5P 组成一个基。
令021==x x得基可行解()0,0,15,24,5x =,由此列出初始单纯形表21σσ>。
《运筹学(胡运权)》第五版课后习题答案
X33.000000 0.000000
X1,X2,X3 0.000000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.200000
3) 0.000000 0.600000
4) 0.0000000.000000
6) 0.0000000.008571
7) 0.000000 0.110000
8) 0.000000 -1.500000
NO. ITERATIONS= 6
计算lindo截屏
2.1a:
对偶问题为:
maxz=2y1+3y2+5y3
s.t.
y1+2y2+y3≤2
3y3+y2+4y3≤2
4y1+3y2+3y3=4
A1 1200.000000 0.000000
A2 0.000000 9.640000
A3 285.714294 0.000000
B3 10000.0000000.000000
C1 0.000000 15.900000
B1 0.000000 0.230000
A4 342.857147 0.000000
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
第五版运筹学课后习题答案

第五版运筹学课后习题答案【篇一:运筹学课后习题答案林齐宁版本北邮出版社】>1、某织带厂生产a、b两种纱线和c、d两种纱带,纱带由专门纱线加工而工厂有供纺纱的总工时7200h,织带的总工时1200h。
(1) 列出线性规划模型,以便确定产品的数量使总利润最大;(2) 如果组织这次生产具有一次性的投入20万元,模型有什么变化?对模型的解是否有影响?解:(1)设a的产量为x1,b的产量为x2,c的产量为x3,d的产量为x4,则有线性规划模型如下:max f(x)=(168?42)x1 +(140?28)x2 +(1050?350)x3 +(406?140)x4=126 x1 +112 x2 +700 x3 +266 x4?3x1?2x2?10x3?4x4?7200?s.t. ? 2x3?0.5x4?1200?xi?0, i?1,2,3,4?(2)如果组织这次生产有一次性的投入20万元,由于与产品的生产量无关,故上述模型只需要在目标函数中减去一个常数20万,因此可知对模型的解没有影响。
2、将下列线性规划化为极大化的标准形式minf(x)?2x1?3x2?5x3解:将约束条件中的第一行的右端项变为正值,并添加松弛变量x4,在第二行添加人工变量? x1? x2? x3??5 ???6x1?7x2?9x3?16 x5,将第三行约束的绝对值号打开,变为两s.t. ?|19x1?7x2?5x3|?13个不等式,分别添加松弛变量x6, x7,并令??x,x?0, x?不限3?12x3?x3??x3??,则有max[?f(x)]= {?2 x1 ?3 x2 ?5(x3??x3??)+0 x4 ?m x5+0 x6 +0 x7} ?? x3???x4?5 ?x1 ?x2 ?x3 ???6x?7x?9x??9x?? ?x?1612335????5x3?? ?x6?13 s.t. ? 19x1?7x2?5x3??19x?7x?5x??5x?? ?x7?131233??,x3??,x4,x5,x6,x7?0?x1,x2,x3?3、用单纯形法解下面的线性规划maxf(x)?2x1?5x2?3x3?3x1?2x2?x3?610??x?6x?3x?125 ?123s. t. ???2x1?x2?0.5x3?420?x1,x2,x3?0, ?解:在约束行1,2,3分别添加x4, x5, x6松弛变量,有初始基础可行解和单纯形答:最优解为x1 =244.375, x2 =0, x3 =123.125, 剩余变量x6=847.1875;最优解的目标函数值为858.125。
第五版运筹学基础与应用大题模拟试题及答案

第五版运筹学基础与应用-大题模拟试题及答案计算题一1. 下列线性规划问题化为标准型。
(10分) 123min +5-2Z x x x =-123123121236235100,0,x x x x x x x x x x x +-≤-+≥+=≥≤符号不限2. 写出下列问题的对偶问题 (10分)123min 42+3Z x x x =+123123121234+56=78910111213140,0x x x x x x x x x x x --+≥+≤≤≥无约束,3. 用最小元素法求下列运输问题的一个初始基本可行解(10分)4.某公司有资金10万元,若投资用于项目(1,2,3)i i i x =的投资额为时,其收益分别为11122()4,()9,g x x g x x ==33()2,g x x =问应如何分配投资数额才能使总收益最大?(15分)满满5.求图中所示网络中的最短路。
(15分)计算题二1、某工厂拥有A,B,C三种类型的设备,生产甲、乙两种产品,每件产品在生产中需要使用的机时数,每件产品可以获得的利润,以及三种设备可利用的机时数见下表:求:(1)线性规划模型;(5分)(2)利用单纯形法求最优解;(15分)4.如图所示的单行线交通网,每个弧旁边的数字表示这条单行线的长度。
现在有一个人要从1v 出发,经过这个交通网到达8v,要寻求使总路程最短的线路。
(15分)5. 某项工程有三个设计方案。
据现有条件,这些方案不能按期完成的概率分别为0.5,0.7,0.9,即三个方案均完不成的概率为0.5×0.7×0.9=0.315。
为使这三个方案中至少完成一个的概率尽可能大,决定追加2万元资金。
当使用追加投资后,上述方案完不成的概率见下表,问应如何分配追加投资,才能使其中至少一个方案完成的概率为最大。
(15分)计算题三1、某工厂要制作100套专用钢架,每套钢架需要用长为2.9m , 2.1m , 1.5m的圆钢各一根。
运筹学基础模拟试卷一参考答案.doc

《运筹学基础》模拟试卷一一、单项选择题(本大题共15小题,每小题1分,共15分)1.运筹学研究和应用的模型是()A.数学模型 B.符号和图像表示的模型C.数学和符号表示的模型D.数学模型、图形表示的模型、抽象的模型2.以下不属于运用运筹学进行决策的步骤的是()A.观察待决策问题所处的环境B.分析定义待决策的问题并拟定模型C.提出解并验证其合理性D.进行灵敏度分析3.问题域的外部环境一般是指()A、问题域界面与外界的人、财、物之间的交互活动;B、问题域外界的人、财、物之间的交互活动;C、问题域界面与问题域内部的人、财、物之间的交互活动;D、问题域界外部的人、财、物之间的交互活动。
4.科技预测的短期预测时间为()A.1~3年B.3~5年C.5~10年D.3~7年5.已知一组观察值的平均值为x=15.8,y =49.5,y对x的一元线性回归方程的回归系数b=2.5,则回归方程在y轴上的截距为()A.-10B.10C.89D.107.956.在不确定的条件下进行决策,下列哪个条件是不必须具备的()A.确定各种自然状态可能出现的概率值B.具有一个明确的决策目标C.可拟订出两个以上的可行方案D.可以预测或估计出不同的可行方案在不同的自然状态下的收益值7.存货台套的运费应列入()A.订货费用B.保管费用 C.进厂价D.其它支出8.一般在应用线性规划建立模型时要经过四个步骤:(1)明确问题,确定目标,列出约束因素(2)收集资料,确定模型(3)模型求解与检验(4)优化后分析以上四步的正确顺序是()A.(1)(2)(3)(4)B.(2)(1)(3)(4)C .(1)(2)(4)(3)D .(2)(1)(4)(3)9. 在解运输问题时,若调整路线已确定,则调整运量应为( )A.负号格的最小运量B.负号格的最大运量C.正号格的最小运量D.正号格的最大运量10. 在箭线式网络图中,活动j i →的最迟完成时间ij LF 等于A.j ESB.ij LSC.j LFD.ij i T ES + 11. 箭线式网络图中,关键线路是从始结点到终结点( )A.占用时间最长的线路B.结点数目最多的线路C.作业数目最多的线路D.结点数目最少的线路12. 时间优化就是在人力、材料、设备、资金等资源基本上有保证的条件下,寻求最短的工程周期。
运筹学考试试卷及答案

运筹学考试试卷及答案一、选择题(每题2分,共20分)1. 线性规划问题的标准形式是:A. 所有变量都非负B. 目标函数是最大化C. 所有约束条件都是等式D. 所有约束条件都是不等式答案:A2. 单纯形法中,如果某个变量的检验数为负数,那么:A. 该变量可以增大B. 该变量可以减小C. 该变量保持不变D. 该变量不能进入基答案:A3. 在运输问题中,如果某种资源的供应量大于需求量,那么应该:A. 增加供应量B. 减少需求量C. 增加需求量D. 减少供应量答案:C4. 动态规划的基本原理是:A. 递归B. 迭代C. 回溯D. 分解答案:D5. 决策树中,每个节点代表:A. 一个决策B. 一个状态C. 一个结果D. 一个概率答案:A6. 排队论中,M/M/1队列的特点是:A. 到达时间服从泊松分布,服务时间服从指数分布,且只有一个服务台B. 到达时间服从指数分布,服务时间服从泊松分布,且只有一个服务台C. 到达时间服从泊松分布,服务时间服从指数分布,且有两个服务台D. 到达时间服从指数分布,服务时间服从泊松分布,且有两个服务台答案:A7. 网络流问题中,最大流最小割定理说明:A. 最大流等于最小割B. 最大流小于最小割C. 最大流大于最小割D. 最大流与最小割无关答案:A8. 整数规划问题中,分支定界法的基本思想是:A. 将问题分解为多个子问题B. 将问题转化为线性规划问题C. 将问题转化为非线性规划问题D. 将问题转化为动态规划问题答案:A9. 在多目标决策中,如果目标之间存在冲突,通常采用的方法是:A. 目标排序B. 目标加权C. 目标合并D. 目标替换答案:B10. 敏感性分析的目的是:A. 确定最优解的稳定性B. 确定最优解的唯一性C. 确定最优解的可行性D. 确定最优解的最优性答案:A二、填空题(每题2分,共20分)1. 线性规划问题的可行域是由所有_________约束条件构成的集合。
答案:可行2. 在单纯形法中,如果目标函数的系数都是正数,则该问题为_________问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算题一1. 下列线性规划问题化为标准型。
(10分)123min +5-2Z x x x =-123123121236235100,0,x x x x x x x x x x x +-≤-+≥+=≥≤符号不限2. 写出下列问题的对偶问题 (10分)123min 42+3Z x x x =+123123121234+56=78910111213140,0x x x x x x x x x x x --+≥+≤≤≥无约束,3. 用最小元素法求下列运输问题的一个初始基本可行解(10分)4.某公司有资金10万元,若投资用于项目(1,2,3)i i i x =的投资额为时,其收益分别为11122()4,()9,g x x g x x == 33()2,g x x =问应如何分配投资数额才能使总收益最大?(15分)5. 求图中所示网络中的最短路。
(15分)计算题二满足满足1、某工厂拥有A,B,C 三种类型的设备,生产甲、乙两种产品,每件产品在生产中需要使用的机时数,每件产品可以获得的利润,以及三种设备可利用的机时数见下表:求:(1)线性规划模型;(5分) (2)利用单纯形法求最优解;(15分)4. 如图所示的单行线交通网,每个弧旁边的数字表示这条单行线的长度。
现在有一个人要从1v 出发,经过这个交通网到达8v ,要寻求使总路程最短的线路。
(15分)5. 某项工程有三个设计方案。
据现有条件,这些方案不能按期完成的概率分别为0.5,0.7,0.9,即三个方案均完不成的概率为0.5×0.7×0.9=0.315。
为使这三个方案中至少完成一个的概率尽可能大,决定追加2万元资金。
当使用追加投资后,上述方案完不成的概率见下表,问应如何分配追加投资,才能使其中至少一个方案完成的概率为最大。
(15分)计算题三1、某工厂要制作100套专用钢架,每套钢架需要用长为2.9m , 2.1m , 1.5m的圆钢各一根。
已知原料每根长7.4m ,现考虑应如何下料,可使所用的材料最省?产品甲产品乙设备能力/h设备A 3 2 65设备B 2 1 40设备C 0 3 75利润/(元/件) 1500 2500求:(1(2)将上述模型化为标准型(5分)2、求解下列线性规划问题,并根据最优单纯形法表中的检验数,给出其对偶问题的最优解。
(15分)123ax437m z x x x=++12322100x x x++≤12333100x x x++≤123,,0x x x≥3.断下表中方案是否可作为运输问题的初始方案,为什么?(10分)4.用Dijkstra算法计算下列有向图的最短路。
(15分)追加投资(万元)各方案完不成的概率1 2 3120.500.300.250.700.500.300.900.700.40满足v2v6v1v4v5v7v32352173517555.某集团公司拟将6千万资金用于改造扩建所属的A、B、C三个企业。
每个企业的利润增长额与所分配到的投资额有关,各企业在获得不同的投资额时所能增加的利润如下表所示。
集团公司考虑要给各企业都投资。
问应如何分配这些资金可使公司总的利润增长额最大?(15分)计算题答案一1、max(-z)=''''123352()x x x x -+-2、写出对偶问题maxW=12371114y y y ++3、解:4.解:状态变量k s 为第k 阶段初拥有的可以分配给第k 到底3个项目的资金额;决策变量k x 为决定给第k 个项目的资金额;状态转移方程为1k k k s s x +=-;最优指标函数()k k f s表示第k 阶段初始状态为k s 时,从第k 到第3个项目所获得的最大收益,()k k f s 即为所求的总收益。
递推方程为:{}10()()()(1,2,3)max k kk k k k k k x s f s g x f s k ++≤≤=+= 44()0f s = 当k=3时有{}3323330()2max x s f s x ≤≤=当33x s =时,取得极大值223s ,即:{}332233330()22max x s f s x x ≤≤==当k=2时有:{}222222330()9()max x s f s x f s ≤≤=+{}22223092max x s xs ≤≤+={}22222092()max x s x s x ≤≤+-=令 2222222(,)92()h s x x s x =+-用经典解析方法求其极值点。
由 222292()(1)0dh s x dx =+--=解得:2294x s =-而 222240d h d x= 所以2294x s =-是极小值点。
极大值点可能在[0,2s ]端点取得:222(0)2f s =, 222()9f s s =当222(0)()f f s =时,解得 29/2s =当29/2s 时,222(0)()f f s ,此时,*20x =当29/2s 时,222(0)()f f s ,此时,*22x s =当k=1时,{}11111220()4()max x s f s x f s ≤≤=+当 222()9f s s =时,{}11111110()499max x s f s x s x ≤≤=+-{}111110959max x s s x s ≤≤=-=但此时 211100109/2s s x =-=-=,与29/2s 矛盾,所以舍去。
当2222()2f s s =时,{}121111010(10)42()max x f x s x ≤≤=+-令 2111111(,)42()h s x x s x =+-由 122144()(1)0dh s x dx =+--= 解得: 211x s =-而 222210d h d x = 所以 111x s =-是极小值点。
比较[0,10]两个端点 10x =时,1(10)200f = 110x =时,1(10)40f =*10x = 所以再由状态转移方程顺推:*21110010s s x =-=-= 因为 29/2s所以 *20x =,*32210010s s x =-=-= 因此*3310x s == 最优投资方案为全部资金用于第3个项目,可获得最大收益200万元。
5. 解:用Dijkstra 算法的步骤如下, P (1v )=0T (j v)=∞(j =2,3…7) 第一步:因为()21,v v ,()31,v v A ∈且2v ,3v 是T 标号,则修改上个点的T 标号分别为:()()()[]12122,m in w v P v T v T +==[]min ,055∞+=()()()[]13133,m in w v P v T v T +==[]min ,022∞+=所有T 标号中,T (3v )最小,令P (3v )=2 第二步:3v 是刚得到的P 标号,考察3v()34,v v ,()36,v v A ∈,且5v ,6v 是T 标号 ()()()44334min ,T v T v P v w =+⎡⎤⎣⎦=[]min ,279∞+=()[]6min ,2T v =∞+4=6所有T 标号中,T (2v )最小,令P (2v )=5 第三步:2v 是刚得到的P 标号,考察2v()()()44224min ,T v T v P v w =+⎡⎤⎣⎦=[]min 9,527+= ()()()55225min ,T v T v P v w =+⎡⎤⎣⎦=[]min ,5712∞+=所有T 标号中,T (6v )最小,令P (6v )=6 第四步:6v 是刚得到的P 标号,考察6v()()()44664min ,T v T v P v w =+⎡⎤⎣⎦=[]min 9,627+= ()()()55665min ,T v T v P v w =+⎡⎤⎣⎦=[]min 12,617+=()()()77667min ,T v T v P v w =+⎡⎤⎣⎦=[]min ,6612∞+=所有T 标号中,T (4v ),T (5v )同时标号,令P (4v )=P (5v )=7第五步:同各标号点相邻的未标号只有7v ()()()[]57577,m in w v P v T v T += =[]min 12,7310+=至此:所有的T 标号全部变为P 标号,计算结束。
故1v 至7v 的最短路为10。
计算题答案二1. 解:(1)12m ax 15002500z x x =+123265x x +≤ 满足 12240x x +≤ 2375x ≤12,0x x ≥(2)最优解 *(5,25,0,5,0)T x = 最优目标值 = 70000元2. 解:此规划存在可行解(0,1)Tx =,其对偶规划123m in 4143w y y y =++满足: 12333y y y -++≥ 123222y y y +-≥123,,0y y y ≥对偶规划也存在可行解(0,1,0)Ty =,因此原规划存在最优解。
3、解:可以作为初始方案。
理由如下: (1)满足产销平衡 (2)有m+n-1个数值格(3)不存在以数值格为顶点的避回路4.解:5.解:此题目等价于求使各方案均完不成的概率最小的策略。
把对第k 个方案追加投资看着决策过程的第k 个阶段,k =1,2,3。
k x -----------第k 个阶段,可给第k, k+1,…,3个方案追加的投资额。
k u -----------对第k 个方案的投资额{}kk k k k k k k u x x x u u u D -=≤==+12,1,0且阶段指标函数()()k k k k u x p u x C ,,=,这里的()k k u x p ,是表中已知的概率值。
过程指标函数()()()()()1,,,44113,133,min =⋅=⋅=++∈+=x f x f u x C x f V u x C V k k k k D u k k k ki k k k kk以上的k =1,2,3 用逆序算法求解 k =3时,()()3333,min 33u x C x f D u ∈= 得表:最优策略:*1u =1,*2u =1,*3u =0或*1u =0,*2u =2, *3u =0,至少有一个方案完成的最大概率为1-0.135=0.865计算题答案三1. 解 分析:利用7.4m 长的圆钢截成2.9m , 2.1 m ,1.5m 的圆钢共有如下表所示的8方案 毛胚/m 方案1 方案2 方案3 方案4 方案5 方案6 方案7 方案8 2.9 2 1 1 1 0 0 0 02.1 0 2 1 0 3 2 1 0 1.5 1 0 1 3 0 2 3 4 合计 7.3 7.1 6.5 7.4 6.3 7.2 6.6 6.0 剩余料头0.1 0.3 0.9 0 1.1 0.2 0.8 1.4 设1x ,2x ,3x ,4x ,5x ,6x ,7x ,8x 分别为上面8中方案下料的原材料根数。
