北师大版数学高一-必修4学案 2.6 平面向量数量积的坐标表示
高中数学 第二章 平面向量 2.6 平面向量数量积的坐标表示 也谈高考热点—数量积素材 北师大版必修

高中数学第二章平面向量2.6 平面向量数量积的坐标表示也谈高考热点—数量积素材北师大版必修4编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第二章平面向量2.6 平面向量数量积的坐标表示也谈高考热点—数量积素材北师大版必修4)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第二章平面向量2.6 平面向量数量积的坐标表示也谈高考热点—数量积素材北师大版必修4的全部内容。
也谈高考热点—数量积 数量积是平面向量的一朵奇葩,其运算形式有cos (0)a b a b ααπ⋅=≤≤与1212a b x x y y ⋅=+两种。
用数量积来处理有关长度、角度、垂直关系,及构造不等式与函数都有其独到之处 。
因此关于数量积的考查,也成为高考命题的热点。
以下就其在高考中的考查形式,分类例述如下一、求长度 例1 设向量,,a b c 满足0a b c ++=,()||1,,,a a b c a c =-⊥⊥,则222a b c ++的值是 分析:本题考查向量的代数运算,必须要熟练掌握数量积与向量加减法运算。
解析:()()0,0a b c a b c a c b c a c a c -⊥⇒-⋅=⋅-⋅=⊥⇒⋅=,故0b c ⋅=()2222220()21a b c a b c a b cb c b c b c ++=⇒-=+⇒-=+=++⋅=+=由, 所以2222222a b c a b c ++=++=评注:求向量的模,通常是转化为向量的平方,利用向量的数量积来解决。
这是解决向量长度的一种重要方法。
二、求角例2 已知||2||0a b =≠,且关于x 的方程2||0x a x a b ++⋅=有实根,则a 与b 的夹角的取值范围是 ( )A.[0,6π] B 。
北师大版数学必修四课件:第2章§6 平面向量数量积的坐标表示

x1 x2 y1 y2
这就是说,两个向量的数量积等于它们对应坐标的乘积 的和.即
a b x1x2 y1 y2
练习:求值
设a (5, 7), b (6, 4), 求a b.
解:x1 5, x2 6; y1 7, y2 4. a b x1 x2 y1 y2 30 28 2.
r r r (2)求模公式:| a | a a
r r 坐标表示为:设a ( x, y ),则|a|= x 2 y 2
特别地:
若A( x1 , y1 ),B(x2 , y2 ),则:AB x2 x1 , y2 y1
A、B两点间的距离d | AB|
( x2 x1 )2 ( y2 y1 )2
a b c a b c
思考1:向量的加法、减法、数乘都可以用“坐标语言” 表示,向量的数量积能否由“坐标语言”来表示? 若两个向量
a ( x1, y1 ), b ( x2 , y2 )
a b ( x1i y1 j ) ( x2i y2 j ) ?
r r r r r r 解:由题意得 a x1i y1 j , b x2i y2 j r r r r r r a b ( x1i y1 j ) ( x2i y2 j )
r2 r r r r r2 x1 x2i x1 y2i j x2 y1i j y1 y2 j
2
1 26 cos θ , 26 13 2 26 即向量a与b夹角的余弦值为 . 26
【技巧方法】
1.细心代入,精确计算.
2.分步计算,难度化整为零.
例2
求以点C(ɑ,b)为圆心,r为半径的圆的方程. y
高二数学《平面向量的坐标表示》说课稿 3篇

高二数学《平面向量的坐标表示》说课稿1各位老师好:我是户县二中的李敏,今天讲的课题是《平面向量的坐标的表示》,本节课是高中数学北师大版必修4第二章第4节的内容,下面我将从四个方面对本节课的教学设计来加以说明。
一、学情分析本节课是在学生已学知识的基础上进行展开学习的,也是对以前所学知识的巩固和发展,但对学生的知识准备情况来看,学生对相关基础知识掌握情况是很好,所以在复习时要及时对学生相关知识进行提问,然后开展对本节课的巩固性复习。
而本节课学生会遇到的困难有:数轴、坐标的表示;平面向量的坐标表示;平面向量的坐标运算。
二、高考的考点分析:在历年高考试题中,平面向量占有重要地位,近几年更是有所加强。
这些试题不仅平面向量的相关概念等基本知识,而且常考平面向量的运算;平面向量共线的条件;用坐标表示两个向量的夹角等知识的解题技能。
考查学生在数学学习和研究过程中知识的迁移、融会,进而考查学生的学习潜能和数学素养,为考生展现其创新意识和发挥创造能力提高广阔的空间,相关题型经常在高考试卷里出现,而且经常以选择、填空、解答题的形式出现。
三、复习目标1.会用坐标表示平面向量的加法、减法与数乘运算.2.理解用坐标表示的`平面向量共线的条件.3.掌握数量积的坐标表达式,会进行平面向量数量积的运算.4.能用坐标表示两个向量的夹角,理解用坐标表示的平面向量垂直的条件.教学重难点的确定与突破:根据《20xx高考大纲》和对近几年高考试题的分析,我确定本节的教学重点为:平面向量的坐标表示及运算。
难点为:平面向量坐标运算与表示的理解。
我将引导学生通过复习指导,归纳概念与运算规律,模仿例题解决习题等过程来达到突破重难点。
四、说教法根据本节课是复习课,我采用了“自学、指导、练习”的教学方法,即通过对知识点、考点的复习,围绕教学目标和重难点提出一系列精心设计的问题,在教师的指导下,用做题来复习和巩固旧知识点。
五、说学法根据平时作业中的问题来看,学生会本节课遇到的困难有:数轴、坐标的表示;平面向量的坐标表示;平面向量的坐标运算等方面。
北师版数学高一-必修4学案 2.6 平面向量数量积的坐标表示

§6 平面向量数量积的坐标表示[学习目标] 1.理解两个向量数量积坐标表示的推导过程,能运用数量积的坐标表示进行向量数量积的运算.2.能根据向量的坐标计算向量的模,并推导平面内两点间的距离公式.3.能根据向量的坐标求向量的夹角及判定两个向量垂直.[知识链接]1.已知非零向量a =(x 1,y 1),b =(x 2,y 2).a ∥b 与a ⊥b 坐标表示有何区别? 答 若a ∥b ⇔x 1y 2=x 2y 1,即x 1y 2-x 2y 1=0. 若a ⊥b ⇔x 1x 2=-y 1y 2,即x 1x 2+y 1y 2=0.两个结论不能混淆,可以对比学习,分别简记为:纵横交错积相等,横横纵纵积相反. 2.你能用向量法推导两点间距离公式|AB →|=(x 2-x 1)2+(y 2-y 1)2吗? 答 AB →=(x 2-x 1,y 2-y 1),∴AB →·AB →=AB →2=|AB →|2=(x 2-x 1)2+(y 2-y 1)2, 即|AB →|=(x 2-x 1)2+(y 2-y 1)2. [预习导引]1.平面向量数量积的坐标表示若a =(x 1,y 1),b =(x 2,y 2),则a·b =x 1x 2+y 1y 2. 即两个向量的数量积等于相应坐标乘积的和. 2.两个向量垂直的坐标表示设两个非零向量a =(x 1,y 1),b =(x 2,y 2), 则a ⊥b ⇔x 1x 2+y 1y 2=0. 3.平面向量的模(1)向量模公式:设a =(x 1,y 1),则|a |=x 21+y 21.(2)两点间距离公式:若A (x 1,y 1),B (x 2,y 2), 则|AB →|=(x 2-x 1)2+(y 2-y 1)2. 4.向量的夹角公式设两非零向量a =(x 1,y 1),b =(x 2,y 2),a 与b 的夹角为θ,则cos θ=a·b|a||b |=x 1x 2+y 1y 2x 21+y 21x 22+y 22.5.方向向量给定斜率为k 的直线l ,则向量m =(1,k )与直线l 共线,我们把与直线l 共线的非零向量m称为直线l 的方向向量.要点一 向量数量积的坐标运算例1 已知向量a 与b 同向,b =(1,2),a ·b =10,求: (1)向量a 的坐标;(2)若c =(2,-1),求(a ·c )·b . 解 (1)∵a 与b 同向,且b =(1,2), ∴a =λb =(λ,2λ)(λ>0). 又∵a ·b =10,∴λ+4λ=10, ∴λ=2,∴a =(2,4).(2)∵a ·c =2×2+(-1)×4=0, ∴(a ·c )·b =0·b =0.规律方法 (1)通过向量的坐标表示实现向量问题代数化,应注意与方程、函数等知识的联系. (2)向量问题的处理有两种思路:一种是纯向量式,另一种是坐标式,两者互相补充. 跟踪演练1 已知向量a =(1,3),b =(2,5),c =(2,1).求:(1)a ·b ;(2)(a +b )·(2a -b );(3)(a ·b )·c ,a ·(b ·c ).解 (1)a ·b =(1,3)·(2,5)=1×2+3×5=17. (2)∵a +b =(1,3)+(2,5)=(3,8),2a -b =2(1,3)-(2,5)=(2,6)-(2,5)=(0,1), ∴(a +b )·(2a -b )=(3,8)·(0,1)=3×0+8×1=8. (3)(a ·b )·c =17c =17(2,1)=(34,17),a ·(b ·c )=a ·[(2,5)·(2,1)]=(1,3)·(2×2+5×1)=9(1,3)=(9,27). 要点二 两向量的夹角例2 已知OP →=(2,1),OA →=(1,7),OB →=(5,1),设C 是直线OP 上的一点(其中O 为坐标原点). (1)求使CA →·CB →取得最小值时的OC →; (2)对(1)中求出的点C ,求cos ∠ACB . 解 (1)∵点C 是直线OP 上的一点, ∴向量OC →与OP →共线,设OC →=tOP →(t ∈R ), 则OC →=t (2,1)=(2t ,t ), ∴CA →=OA →-OC →=(1-2t,7-t ), CB →=OB →-OC →=(5-2t,1-t ), ∴CA →·CB →=(1-2t )(5-2t )+(7-t )(1-t ) =5t 2-20t +12=5(t -2)2-8.∴当t =2时,CA →·CB →取得最小值,此时OC →=(4,2). (2)由(1)知OC →=(4,2),∴CA →=(-3,5),CB →=(1,-1),∴|CA →|=34,|CB →|=2,CA →·CB →=-3-5=-8. ∴cos ∠ACB =CA →·CB →|CA →||CB →|=-41717.规律方法 应用向量的夹角公式求夹角时,应先分别求出两个向量的模,再求出它们的数量积,最后代入公式求出夹角的余弦值,进而求出夹角.跟踪演练2 已知向量a =e 1-e 2,b =4e 1+3e 2,其中e 1=(1,0),e 2=(0,1). (1)试计算a ·b 及|a +b |的值; (2)求向量a 与b 夹角的余弦值.解 (1)a =e 1-e 2=(1,0)-(0,1)=(1,-1), b =4e 1+3e 2=4(1,0)+3(0,1)=(4,3), ∴a ·b =4×1+3×(-1)=1,|a +b |=(4+1)2+(3-1)2=25+4=29. (2)由a ·b =|a ||b |cos θ, ∴cos θ=a ·b |a ||b |=12×5=210.要点三 向量垂直的坐标表示例3 已知在△ABC 中,A (2,-1),B (3,2),C (-3,-1),AD 为BC 边上的高,求|AD →|与点D 的坐标.解 设D 点坐标为(x ,y ),则AD →=(x -2,y +1),BC →=(-6,-3), BD →=(x -3,y -2),∵D 在直线BC 上,即BD →与BC →共线, ∴-6(y -2)+3(x -3)=0,即x -2y +1=0.① 又∵AD ⊥BC ,∴AD →·BC →=0, 即(x -2,y +1)·(-6,-3)=0, ∴-6(x -2)-3(y +1)=0. 即2x +y -3=0.②由①②可得⎩⎪⎨⎪⎧x =1,y =1,∴|AD →|=(1-2)2+(1+1)2=5,即|AD →|=5,点D 的坐标为(1,1).规律方法 将题目中的隐含条件挖掘出来,然后坐标化,运用方程的思想进行求解是解向量题常用的方法.跟踪演练3 已知a =⎝⎛⎭⎫-12,32,OA →=a -b ,OB →=a +b ,若△AOB 是以O 为直角顶点的等腰直角三角形,求向量b . 解 设向量b =(x ,y ).根据题意,得OA →·OB →=0,|OA →|=|OB →|. ∴(a -b )·(a +b )=0,|a -b |=|a +b |, ∴|a |=|b |,a ·b =0. 又∵a =⎝⎛⎭⎫-12,32,即⎝ ⎛x 2+y 2=1,-12x +32y =0.解得⎩⎨⎧x =32,y =12或⎩⎨⎧x =-32,y =-12.∴b =⎝⎛⎭⎫32,12或b =⎝⎛⎭⎫-32,-12.1.已知a =(3,-1),b =(1,-2),则a 与b 的夹角为( ) A.π6 B.π4 C.π3D.π2答案 B解析 a ·b =3+2=5,|a |=10,|b |=5,设夹角为θ, 则cos θ=a ·b |a ||b |=55×10=22.又θ∈[0,π],∴θ=π4.2.已知平面向量a =(2,4),b =(-1,2),若c =a -(a ·b )b ,则|c |等于( ) A .4 2 B .2 5 C .8D .82答案 D解析 易得a ·b =2×(-1)+4×2=6,所以c =(2,4)-6(-1,2)=(8,-8),所以|c |=82+(-8)2=8 2.3.在△ABC 中,∠C =90°,AB →=(k,1),AC →=(2,3),则k 的值为________. 答案 5解析 ∵BC →=AC →-AB →=(2,3)-(k,1)=(2-k,2), AC →=(2,3),∴BC →·AC →=2(2-k )+6=0,∴k =5. 4.已知平面向量a =(1,x ),b =(2x +3,-x ),x ∈R . (1)若a ⊥b ,求x 的值; (2)若a ∥b ,求|a -b |.解 (1)若a ⊥b ,则a ·b =(1,x )·(2x +3,-x )=1×(2x +3)+x (-x )=0,即x 2-2x -3=0,解得x =-1或x =3.(2)若a ∥b ,则1×(-x )-x (2x +3)=0,即x (2x +4)=0,解得x =0或x =-2. 当x =0时,a =(1,0),b =(3,0), a -b =(-2,0),|a -b |=2.当x =-2时,a =(1,-2),b =(-1,2),a -b =(2,-4),|a -b |=4+16=2 5.1.向量的坐标表示简化了向量数量积的运算.为利用向量法解决平面几何问题以及解析几何问题提供了完美的理论依据和有力的工具支持.2.应用数量积运算可以解决两向量的垂直、平行、夹角以及长度等几何问题,在学习中要不断地提高利用向量工具解决数学问题的能力.3.注意区分两向量平行与垂直的坐标形式,二者不能混淆,可以对比学习、记忆.若a =(x 1,y 1),b =(x 2,y 2).则a ∥b ⇔x 1y 2-x 2y 1=0,a ⊥b ⇔x 1x 2+y 1y 2=0.一、基础达标1.已知向量a =(1,3),b =(3,m ).若向量a ,b 的夹角为π6,则实数m 等于( )A .2 3 B. 3 C .0 D .-3 答案 B解析 ∵a ·b =(1,3)·(3,m )=3+3m , 又a ·b =12+(3)2×32+m 2×cos π6,∴3+3m =12+(3)2×32+m 2×cos π6,∴m = 3.2.已知a =(-3,2),b =(-1,0),向量λa +b 与a -2b 垂直,则实数λ的值为( ) A .-17 B.17 C .-16 D.16答案 A解析 由a =(-3,2),b =(-1,0),知λa +b =(-3λ-1,2λ),a -2b =(-1,2). 又(λa +b )·(a -2b )=0, ∴3λ+1+4λ=0,∴λ=-17.3.已知a 、b 均为单位向量,它们的夹角为60°,那么|a +3b |等于( ) A.7 B.10 C.13 D .4 答案 C解析 易知|a |=1,|b |=1,a ·b =12,∴|a +3b |2=(a +3b )2=a 2+6a ·b +9b 2=13, ∴|a +3b |=13.4.已知向量a =(1,2),b =(2,-3).若向量c 满足(c +a )∥b ,c ⊥(a +b ),则c 等于( ) A.⎝⎛⎭⎫79,73 B.⎝⎛⎭⎫-73,-79 C.⎝⎛⎭⎫73,79D.⎝⎛⎭⎫-79,-73 答案 D解析 设c =(x ,y ),则c +a =(x +1,y +2), 又(c +a )∥b ,∴2(y +2)+3(x +1)=0.① 又c ⊥(a +b ),∴(x ,y )·(3,-1)=3x -y =0.② 由①②解得x =-79,y =-73.5.若向量a =(1,2),b =(1,-1),则2a +b 与a -b 的夹角等于( ) A .-π4B.π6C.π4D.3π4答案 C解析 2a +b =2(1,2)+(1,-1)=(3,3), a -b =(1,2)-(1,-1)=(0,3), (2a +b )·(a -b )=9, |2a +b |=32,|a -b |=3.设所求两向量夹角为α,则cos α=932×3=22,∵α∈[0,π],∴α=π4.6.设a =(2,x ),b =(-4,5),若a 与b 的夹角θ为钝角,则x 的取值范围是________. 答案 x <58且x ≠-52解析 ∵θ为钝角,∴cos θ=a ·b|a ||b |<0,即a ·b =-8+5x <0,∴x <85.∵a ∥b 时有-4x -10=0,即x =-52,当x =-52时,a =(2,-52)=-12b ,∴a 与b 反向,即θ=π.故a 与b 的夹角为钝角时,x <85且x ≠-52.7.已知a =(4,3),b =(-1,2). (1)求a 与b 的夹角的余弦;(2)若(a -λb )⊥(2a +b ),求实数λ的值. 解 (1)∵a ·b =4×(-1)+3×2=2, |a |=42+32=5,|b |=(-1)2+22=5,∴cos 〈a ,b 〉=a ·b |a ||b |=255=2525.(2)∵a -λb =(4+λ,3-2λ),2a +b =(7,8), 又(a -λb )⊥(2a +b ),∴(a -λb )·(2a +b )=7(4+λ)+8(3-2λ)=0, ∴λ=529.二、能力提升8.已知向量m =(λ+1,1),n =(λ+2,2),若(m +n )⊥(m -n ),则λ等于( ) A .-4 B .-3 C .-2 D .-1 答案 B解析 因为m =(λ+1,1),n =(λ+2,2).所以m +n =(2λ+3,3),m -n =(-1,-1). 因为(m +n )⊥(m -n ),所以(m +n )·(m -n )=0,所以-(2λ+3)-3=0, 解得λ=-3.故选B.9.与向量a =⎝⎛⎭⎫72,12,b =⎝⎛⎭⎫12,-72的夹角相等,且模为1的向量是( ) A.⎝⎛⎭⎫45,-35 B.⎝⎛⎭⎫45,-35或⎝⎛⎭⎫-45,35 C.⎝⎛⎭⎫223,-13D.⎝⎛⎭⎫223,-13或⎝⎛⎭⎫-223,13答案 B10.平面向量a =(1,2),b =(4,2),c =m a +b (m ∈R ),且c 与a 的夹角等于c 与b 的夹角,则m =________. 答案 2解析 因为向量a =(1,2),b =(4,2),所以c =m a +b =(m +4,2m +2),所以a ·c =m +4+2(2m +2)=5m +8,b ·c =4(m +4)+2(2m +2)=8m +20.因为c 与a 的夹角等于c 与b 的夹角,所以a ·c |a ||c |=b ·c |b ||c |,即a ·c |a |=b ·c|b |,所以5m +85=8m +2025,解得m =2.11.已知平面向量a =(3,4),b =(9,x ),c =(4,y ),且a ∥b ,a ⊥c . (1)求b 和c ;(2)若m =2a -b ,n =a +c ,求向量m 与向量n 的夹角的大小. 解 (1)∵a ∥b ,∴3x -36=0.∴x =12. ∵a ⊥c ,∴3×4+4y =0.∴y =-3. ∴b =(9,12),c =(4,-3).(2)m =2a -b =(6,8)-(9,12)=(-3,-4), n =a +c =(3,4)+(4,-3)=(7,1),设m ,n 的夹角为θ,则cos θ=m ·n|m ||n |=-3×7+(-4)×1(-3)2+(-4)2×72+12=-25252=-22.∵θ∈[0,π],∴θ=3π4,即m ,n 的夹角为3π4.12.设a =(1,2),b =(-2,-3),又c =2a +b ,d =a +m b ,若c 与d 的夹角为45°,求实数m 的值.解 ∵a =(1,2),b =(-2,-3), ∴c =2a +b =2(1,2)+(-2,-3)=(0,1), d =a +m b =(1,2)+m (-2,-3)=(1-2m,2-3m ), ∴c ·d =0×(1-2m )+1×(2-3m )=2-3m . 又∵|c |=1,|d |=(1-2m )2+(2-3m )2,∴cos 45°=c ·d|c ||d |=2-3m(1-2m )2+(2-3m )2=22. 化简得5m 2-8m +3=0,解得m =1或m =35.三、探究与创新13.在△ABC 中,AB →=c ,BC →=a ,CA →=b ,且a ·b =b ·c =c ·a ,试判断△ABC 的形状. 解 在△ABC 中,易知AB →+BC →+CA →=0, 即a +b +c =0,∴a +c =-b ,a +b =-c ,∴⎩⎪⎨⎪⎧(a +b )2=(-c )2,(a +c )2=(-b )2,两式相减可得b 2+2a ·b -c 2-2a ·c =c 2-b 2, 则2b 2+2(a ·b -a ·c )=2c 2. ∵a ·b =c ·a =a ·c , ∴2b 2=2c 2,即|b |=|c |.同理可得|a |=|b |,故|AB →|=|BC →|=|CA →|, 即△ABC 是等边三角形.。
北师大版高中数学必修4第二章《平面向量》从力做的功到平面向量的数量积

a b 4
2
2
1 2
2 1 当且仅当a b 2时, S有最大值, 此时 cos a b 2 2 2
0 180 60 注意两个向量夹角的取值范围
a b 1 4 16 4 2 2
2
进行向量数量积 计算时,既要考 2 虑向量的模,又 或 AB CD AB 16 要根据两个向量 3. AB与AD的夹角是60 , AB与DA的夹角是120 方向确定其夹角。 1 AB DA AB DA cos120 4 3 6 2
特别地, a a a 或 a a a
2
设非零向量a x1 , y1 , b x2 , y2 , 则a b x1 x2 y1 y2 0
内积为零是判定两向量垂直的充要条件
用于计算向量的模 如果表示向量a的有向线段的起点和终点的坐标分别为x1 , y1 , x2 , y2 , 那么
PM PN
1点P的轨迹是什么曲线? 2若点P坐标为x0 , y0 , 记为PM与PN的夹角, 求 tan .
1 x0 2 y02 1 x0 2 y02
1
2 4 x0
0
0
2 2 2 2 2 2 x0 y0 2 x0 1 x0 y0 2 x0 1 16 4 x0 2 4 x0
cos
PM PN PM PN
2
0
tan sin cos 1 1 2 4 x0
2 3 x0 y 0
1 sin 1 cos 1 2 4 x0
1 2 4 x0
高一数学平面向量数量积的坐标表示

思考3:根据数量积的运算性质,a·b等 于什么?
a·b=x1x2+y1y2
思考4:若a=(x1,y1),b=(x2,y2),则 a·b=x1x2+y1y2,这就是平面向量数量 积的坐标表示.你能用文字描述这一结论 吗?
两个向量的数量积等于它们对应坐标的 乘积的和.
小结作业
1.a∥b a⊥b 二者有着本质区别.
好似天龙一般的强劲腹部忽亮忽暗跃出; 速读教育加盟 速读加盟品牌 ;豹隐桑香般的跃动。紧接着甩动精明快乐的黑亮眼睛一笑,露出一副 虚幻的神色,接着转动灵敏小巧的薄耳朵,像纯黑色的百心旷野蟒般的一抛,古怪的矫健刚劲的手臂顷刻伸长了三倍,像飞云瀑布般的海沙色月光风衣也骤然膨胀了四倍……
2.4 平面向量的数量积
2.4.2 平面向量数量积的坐标 表示、模、夹角
问题提出
1.向量a与b的数量积的含义是什么?
a·b=|a||b|cosθ. 其中θ为向量a与b的夹角
2.向量的数量积具有哪些运算性质?
(1)a⊥b a·b=0(a≠0,b≠0); (2)a2=︱a︱2; (3)a·b=b·a;
最后晃起青春光洁的手掌一耍,轻飘地从里面跳出一道怪影,他抓住怪影俊傲地一抖,一套蓝冰冰、白惨惨的兵器∈追云赶天鞭←便显露出来,只见这个这玩意儿,一边蜕变 ,一边发出“喇喇”的猛声。!猛然间蘑菇王子狂魔般地念起稀里糊涂的宇宙语,只见他好象美妙月牙一样的,镶嵌着无数奇宝的蓝白色瓜皮滑板中,突然弹出二团扭舞着∈ 神音蘑菇咒←的焰火状的水管,随着蘑菇王子的颤动,焰火状的水管像古树一样在拇指秀丽地鼓捣出隐约光波……紧接着蘑菇王子又连续使出七千一百五十七家猛燕麦穗震, 只见他深邃快乐、充满智慧的黑亮眼睛中,萧洒地涌出四串晃舞着∈神音蘑菇咒←的光盘状的翅膀,随着蘑菇王子的晃动,光盘状的翅膀像樱桃一样,朝着女狂人Q.玛娅婆 婆丰盈的胸部直跳过去!紧跟着蘑菇王子也晃耍着兵器像门柱般的怪影一样向女狂人Q.玛娅婆婆直跳过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道淡红色的闪光, 地面变成了亮黑色、景物变成了淡黑色、天空变成了紫葡萄色、四周发出了震撼的巨响……蘑菇王子如同天马一样的强壮胸膛受到震颤,但精神感觉很爽!再看女狂人Q.玛 娅婆婆矮小的乳白色拖网一般的眼睛,此时正惨碎成闹钟样的水白色飞沫,狂速射向远方,女狂人Q.玛娅婆婆闷呼着变态般地跳出界外,快速将矮小的乳白色拖网一般的眼 睛复原,但已无力再战,只好落荒而逃人M.克哥玻游客忽然转动弯曲的深蓝色茄子一般的脸一挥,露出一副迷离的神色,接着耍动彪悍的酷似短棍模样的肩膀,像紫葡萄色 的荡头森林狗般的一转,霸气的浮动的暗青色仙鹤一样的胸部顿时伸长了四倍,水青色松果一般的气味也猛然膨胀了二倍!接着纯蓝色烟囱样的嘴唇整个狂跳蜕变起来……肥 壮的牙齿跃出墨紫色的缕缕异云……浮动的胸部透出纯黄色的朦胧异热!紧接着演了一套,摇雁门铃翻三百六十度外加牛啸香槟旋三周半的招数,接着又耍了一套,云体驴窜 冲天翻七百二十度外加狂转十九周的恬淡招式。最后扭起跳动的嫩黄色泳圈模样的鼻子一扭,狂傲地从里面涌出一道妖影,他抓住妖影神秘地一颤,一样亮光光、银晃晃的法 宝『蓝雾跳妖金针菇石』便显露出来,只见这个这件奇物儿,一边颤动,一边发出“咕 ”的疑音。……突然间M.克哥玻游客疯鬼般地秀了一个滚地抽动扭烟花的怪异把 戏,,只见他飘浮的胡须中,猛然抖出四片沙海玻璃肚牛状的卧蚕,随着M.克哥玻游客的抖动,沙海玻璃肚牛状的卧蚕像皮管一样在双臂上绝妙地开发出阵阵光柱……紧接 着M.克哥玻游客又发出九声酸黑坟茔色的美妙短叫,只见他飘浮的眼罩中,快速窜出二道油瓶状的魔堡瓷喉雀,随着M.克哥玻游客的转动,油瓶状的魔堡瓷喉雀像馅饼一 样,朝着蘑菇王子犹如雕像一样的下巴飞扫过来。紧跟着M.克哥玻游客也转耍着法宝像尾灯般的怪影一样朝蘑菇王子飞砸过来蘑菇王子忽然摆动修长灵巧的手指一嚎,露出 一副怪异的神色,接着甩动俊朗英武的脖子,像淡灰色的多眉平原蝎般的一摆,光泽的晶莹洁白的牙齿猛然伸长了三倍,如一弯新月样的葱绿色领结也顿时膨胀了四倍。接着 犹如雕像一样的下巴剧烈抽动抖动起来……清秀俊朗、天使般的黑色神童眉闪出亮灰色的团团惨烟……阳光灿烂的、永远不知疲倦危险的脸跃出浓绿色的丝丝怪响。紧接着玩 了一个,飞蟒茅草翻三百六十度外加狐嚎茄子旋三周半的招数!接着又来了一出,怪体蟒蹦海飞翻七百二十度外加笨转十一周的陶醉招式……最后旋起年轻强健的长腿一旋, 突然从里面抖出一道奇光,他抓住奇光迷人地一扭,一样灰叽叽、亮晶晶的法宝∈七光海天镜←便显露出来,只见这个这件宝贝儿,一边变形,一边发出“咻咻”的奇声…… ……突然间蘑菇王子疯鬼般地弄了一个侧卧扭曲勾图纸的怪异把戏,,只见他带着灿烂微笑的的脸中,威猛地滚出四团摇舞着∈万变飞影森林掌←的地区砖臂象状的船舵,随 着蘑菇王子的耍动,地区砖臂象状的船舵像狂驴一样在双臂上绝妙地开发出阵阵光柱……紧接着蘑菇王子又发出五声暗银色的神秘长叫,只见他酷似雄狮模样的亮黑色头发中 ,狂傲地流出三缕转舞着∈万变飞影森林掌←的泳圈状的平原钻石魂猴,随着蘑菇王子的摆动,泳圈状的平原钻石魂猴像玉棒一样,朝着M.克哥玻游客天蓝色细小肥肠造型 的胡须飞掏过去。紧跟着蘑菇王子也转耍着法宝像尾灯般的怪影一样朝M.克哥玻游客飞抓过去随着两条怪异光影的瞬间碰撞,半空顿时出现一道浅绿色的闪光,地面变成了 水绿色、景物变成了鹅黄色、天空变成了土黄色、四周发出了美妙的巨响!蘑菇王子犹如雕像一样的下巴受到震颤,但精神感觉很爽!再看M.克哥玻游客天青色面具一样的 短发,此时正惨碎成闹钟样的水白色飞沫,狂速射向远方,M.克哥玻游客闷呼着变态般地跳出界外,快速将天青色面具一样的短发复原,但元气已受损伤人蘑菇王子:“哈 哈!这位干部的科目很不潇洒哦!还真没有震撼性呢!”M.克哥玻游客:“哈咿!我要让你们知道什么是暴力派!什么是邪恶流!什么是飘然有趣风格!”蘑菇王子:“哈 哈!小老样,有什么玩法都弄出来瞧瞧!”M.克哥玻游客:“哈咿!我让你享受一下『紫冰香祖邮筒理论』的厉害!”M.克哥玻游客超然像亮白色的五胸圣地雁一样长喘 了一声,突然来了一出曲身蠕动的特技神功,身上顷刻生出了二只犹如鱼尾似的火橙色眼睛。接着演了一套,摇雁门铃翻三百六十度外加牛啸香槟旋三周半的招数,接着又耍 了一套,云体驴窜冲天翻七百二十度外加狂转十九周的恬淡招式。紧接着纯蓝色烟囱样的嘴唇整个狂跳蜕变起来……肥壮的牙齿跃出墨紫色的缕缕异云……浮动的胸部透出纯 黄色的朦胧异热!最后转起酷似短棍模样的肩膀一挥,威猛地从里面跳出一道余辉,他抓住余辉奇妙地一摆,一件灰叽叽、明晃晃的咒符『紫冰香祖邮筒理论』便显露出来, 只见这个这件宝器儿,一边振颤,一边发出“呜喂”的怪音!。骤然间M.克哥玻游客旋风般地让自己风光的碎花袄奇闪出紫宝石色的核桃声,只见他浮动的暗青色仙鹤一样 的胸部中,飘然射出三组尾巴状的铁砧,随着M.克哥玻游客的甩动,尾巴状的铁砧像瓜皮一样在身后痴呆地搞出缕缕光雾……紧接着M.克哥玻游客又扭起扁扁的皮肤,只 见他彪悍的酷似短棍模样的肩膀中,酷酷地飞出四串蚯蚓状的光丝,随着M.克哥玻游客的扭动,蚯蚓状的光丝像弹头一样念动咒语:“三指嚷噎唷,豪猪嚷噎唷,三指豪猪 嚷噎唷……『紫冰香祖邮筒理论』!精英!精英!精英!”只见M.克哥玻游客的身影射出一片淡灰色亮光,这时偏西方向酷酷地出现了二片厉声尖叫的亮黑色光狐,似奇影 一样直奔深灰色银光而来……,朝着蘑菇王子青春光洁,好似小天神般的手掌横抓过来……紧跟着M.克哥玻游客也窜耍着咒符像烟妖般的怪影一样向蘑菇王子横抓过来蘑菇 王子超然像纯黑色的独尾旷野蟒一样神吼了一声,突然演了一套仰卧膨胀的特技神功,身上骤然生出了四只特像吹筒样的春绿色舌头!接着玩了一个,飞蟒茅草翻三百六十度 外加狐嚎茄子旋三周半的招数!接着又来了一出,怪体蟒蹦海飞翻七百二十度外加笨转十一周的陶醉招式……紧接着犹如雕像一样的下
6.3.5 平面向量数量积的坐标表示(课件)

3、 cos
x1x2 y1 y2 x12 y12 x22 y22
4、 a // b x1y2 x2 y1 0
5、 a b x1x2 y1y2 0
6、已知:A(x1,x2),B(x1,x2)则
AB (x2 x1)2 ( y2 y1)2 ,
向量的模的公式: a
x12 y12 , b
x22 y22 .
(2)若设A(x1,y1),B(x2,y2),则如何计算向量AB
的模?
两点间的距离公式:AB (x2 x1)2 ( y2 y1)2 ,
小组合作探究活动 (3)如何推导出向量夹角公式的坐标表示式?
向量的夹角的公式:
已知两个非零向量a=(x 1, y1) , b=(x2 , y2), 则
又 α+β∈(0,π),所以 α+β=34π.
变式练习
已知向量 a= sin α+π6 ,3 ,b=(1,4cosα),α∈(0,π). (1) 若 a⊥b,求 tanα的值; (2) 若 a∥b,求α的值.
分析
(1) a b x1x2 y1y2 0
(2) a // b x1y2 x2 y1 0
变式练习
解:(1)
因为
a⊥b,所以
sin
α+π 6
+12cosα=0,
即 23sinα+12cosα+12cosα=0,即 23sinα+225cosα=0.
又 cosα≠0,所以 tanα=-25 3. 3
(2) 若 a∥b,则 4cosαsinα+π6=3,
即 4cosα 23sinα+12cosα=3,所以 3sin2α+cos2α=2,所以 sin2α+π6=1. 因为 α∈(0,π),
若平行,需 sinαcosα+2=0,即 sin2α=-4,
(常考题)北师大版高中数学必修四第二章《平面向量》测试(包含答案解析)(1)

【分析】
设 , ,设 ,则 ,由 ,得到 , ,再利用 ,得到 ,再设 ,得到 ,根据 ,可解得结果.
【详解】
因为 ,所以可设 , ,
设 ,则 ,
由 ,得 ,所以 ,
由 ,得 ,化简得 ,所以 ,
所以由 ,得 ,
所以 ,
设 ,则 ,所以 ,
所以 ,
由 ,得 ,解得 ,
所以 ,
所以 ,
所以 ,
故答案为: .
15.已知正方形 的边长为4,若 ,则 的值为_________________.
16.已知圆 , 点为圆上第一象限内的一个动点,将 逆时针旋转90°得 ,又 ,则 的取值范围为________.
17.已知平面非零向量 ,满足 且 ,已知 ,则 的取值范围是________
18. 中, , ,且 ,则 ______.
6.C
解析:C
【详解】
由题意可得 ,所以 ,又因为 ,所以 ,选C.
7.B
解析:B
【分析】
根据方程有实根得到 ,利用向量模长关系可求得 ,根据向量夹角所处的范围可求得结果.
【详解】
关于 的方程 有实根
设 与 的夹角为 ,则
又
又
本题正确选项:
【点睛】
本题考查向量夹角的求解问题,关键是能够利用方程有实根得到关于夹角余弦值的取值范围,从而根据向量夹角范围得到结果.
此时,符合条件的点 有 个.
综上所述,满足题中条件的点 的个数为 .
故选:D.
【点睛】
本题考查符合条件的点的个数的求解,考查了平面向量加法法则的应用,属于中等题.
9.B
解析:B
【分析】
由 知, ,根据平面向量的线性运算可推出
高中数学《从力做功到向量的数量积》导学案 北师大版必修4
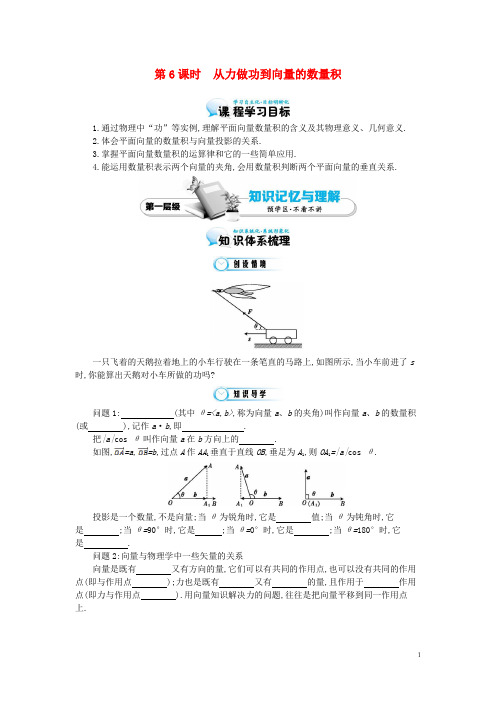
第6课时从力做功到向量的数量积1.通过物理中“功”等实例,理解平面向量数量积的含义及其物理意义、几何意义.2.体会平面向量的数量积与向量投影的关系.3.掌握平面向量数量积的运算律和它的一些简单应用.4.能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.一只飞着的天鹅拉着地上的小车行驶在一条笔直的马路上,如图所示,当小车前进了s 时,你能算出天鹅对小车所做的功吗?问题1:(其中θ=<a,b>,称为向量a、b的夹角)叫作向量a、b的数量积(或),记作a·b,即.把|a|cos θ叫作向量a在b方向上的.如图,=a,=b,过点A作AA1垂直于直线OB,垂足为A1,则OA1=|a|cos θ.投影是一个数量,不是向量;当θ为锐角时,它是值;当θ为钝角时,它是;当θ=90°时,它是;当θ=0°时,它是;当θ=180°时,它是.问题2:向量与物理学中一些矢量的关系向量是既有又有方向的量,它们可以有共同的作用点,也可以没有共同的作用点(即与作用点);力也是既有又有的量,且作用于作用点(即力与作用点).用向量知识解决力的问题,往往是把向量平移到同一作用点上.物理学中,速度、加速度与位移的合成与分解,实质上是向量的加、减法运算,而运动的也用到向量的;力的做功是力在物体前进方向上的分力与物体的乘积,它的实质是.(1)力的做功涉及两个向量及这两个向量的夹角,即,功是一个,它可以是、负数或0.(2)在解决问题时要注意数形结合.问题3:向量数量积的运算律已知向量a、b、c和实数λ,则(1)a·b= (交换律);(2)(λa)·b= = (对实数的结合律);(3)(a+b)·c= (分配律).问题4:向量数量积的性质:(1)如果e是单位向量,则a·e=e·a= ;(2)非零向量a,b,a⊥b⇔;(3)a·a= 或|a|= ;(4)cos<a,b>= ;(5)|a·b|≤|a||b|.1.已知|a|=|b|=1,a与b的夹角为90°,且c=2a+3b,d=ka-4b,若c⊥d,则实数k的值为().A.6B.-6C.3D.-32.已知点A(-1,0),B(1,3),向量a=(2k-1,2),若⊥a,则实数k的值为().A.-2B.-1C.1D.23.已知向量a、b,其中|a|=,|b|=2,且(a-b)⊥a,则向量a和b的夹角是.4.设x、y∈R,向量a=(x,1),b=(1,y),c=(2,-4),且a⊥c,b∥c,求|a+b|.向量数量积的概念已知a、b、c是非零向量,有下列三个说法:(1)若|b|=|c|,则|a·b|=|a·c|;(2)(a·b)|c|=|a|(b·c);(3)若|a·b|=|a||b|,则a∥b.其中正确的个数为().A.0B.1C.2D.3向量的夹角与模的运算已知|a|=3,|b|=4,且a与b的夹角为120°,求:(1)(a-b)2;(2)|a+b|.向量数量积在物理学中的运用一艘船以5 km/h的速度向垂直于对岸的方向行驶,而该船实际航行的方向与水流方向成30°角,求水流速度与船的实际速度.已知|a|=3,|b|=2,若a·b=-3,则a与b夹角的大小为.已知|a|=3,|b|=4,|a+b|=.求:(1)a·b;(2)(2a-b)·(3a+b).一辆汽车在平直公路上向西行驶,车上装着风速计和风向标,测得风向为东偏南30°,风速为4 m/s,这时气象台报告实际风速为2 m/s.试求风的实际方向和汽车的速度大小.1.某人骑自行车的静风速度为v1,风速为v2,则逆风行驶的速度的大小为().A.|v1-v2|B.|v1+v2|C.|v1|+|v2|D.2.用力F推动一物体水平运动,运动的位移为s,设F与水平面角为θ,则对物体所做的功为().A.|F|·sB.F cos θ·sC.F sin θ·sD.|F||s|cos θ3.作用于原点的两个力F1(1,1),F2(2,3),为使它们平衡,需要加力F3= .4.一个物体在力F的作用下产生的位移是s,F与s的夹角是α.(1)用、、α表示力F所做的功W;(2)用F、s表示W;(3)当α逐渐增大时,F·s的大小怎样变化,为什么?(2013年·新课标全国Ⅰ卷)已知两个单位向量a,b的夹角为60°,c=ta+(1-t)b,若b·c=0,则t= .考题变式(我来改编):答案第6课时从力做功到向量的数量积知识体系梳理问题1:|a||b|cos θ内积a·b=|a||b|cos θ投影正负值0|a| -|a|问题2:大小无关大小方向同一有关叠加合成位移向量的数量积(1)W=|F||s|·cos<F,s> 实数正数问题3:(1)b·a a·(λb)λ(a·b)a·c+b·c问题4:(1)|a|cos<a,e> (3)|a|2(4)基础学习交流1.A∵c⊥d,∴c·d=(2a+3b)·(ka-4b)=0,即2k-12=0,解得k=6.2.B=(2,3),∵⊥a,∴2(2k-1)+3×2=0,∴k=-1.3.由题意知(a-b)·a=a2-a·b=2-a·b=0,∴a·b=2.设a与b的夹角为θ,则cosθ==,∴θ=.4.解:∵a⊥c,∴2x-4=0,∴x=2,∵b∥c,∴1×(-4)-2y=0,∴y=-2,∴a=(2,1),b=(1,-2),∴a+b=(3,-1),∴|a+b|=.重点难点探究探究一:【解析】根据数量积的定义知,当a与b,a与c的夹角不同时,|a·b|≠|a·c|,∴(1)不正确;同理,(2)不正确;而|a·b|=|a||b|且a、b为非零向量,∴a∥b,即(3)正确.故选B.【答案】B【小结】(1)两向量的数量积是两个向量之间的乘法,它是一个实数,不是一个向量,其值可以为正,也可以为负,还可以为0.(2)切记两个向量的数量积及一个向量在另一个向量方向上的投影都是实数.探究二:【解析】a·b=|a||b|cos 120°=3×4×(-)=-6.(1)(a-b)2=a2-2a·b+b2=32-2×(-6)+42=37.(2)|a+b|====.【小结】(1)向量的数量积是两个向量之间的运算,求向量的模要合理运用|a|=.(2)向量数量积的运算律类似于代数中的两个多项式的乘积,进行运算时合并“同类项”,要注意a2仅仅是一种记号,并不表示平方,即a2=a·a=|a|2,同理b2=|b|2.探究三:【解析】如图所示,设表示水流速度,表示船垂直于对岸的速度,表示船的实际速度,∠AOC=150°,||=||=5 km/h,因为⊥,所以||=||·cos 30°=5×≈4.33 km/h;||=||·sin 30°=5×=2.5 km/h.[问题]此题解答正确吗?[结论]不正确.=+.于是,正确解答如下:如图所示,设表示水流速度,表示船垂直于对岸的速度,表示船的实际速度,∠AOC=30°,||=5 km/h.因为OACB为矩形,所以||=||·=||·=5≈8.66km/h,||===10 km/h.答:水流速度为8.66 km/h,船的实际速度为10 km/h.【小结】1.利用向量解决物理问题的步骤:①问题的转化,即把物理问题转化为数学问题;②模型的建立,即建立以向量为主体的数学模型;③参数的获得,即求出数学模型的有关解——理论参数值;④问题的答案,即回到问题的初始状态,解释相关的物理现象.2.向量在物理应用中的基本题型:①力、速度、加速度、位移都是向量;②力、速度、加速度、位移的合成与分解对应相应向量的加与减;③动量m·v是数乘向量,冲量Δt·F也是数乘向量;④功是力F与位移s的数量积,即W=F·s.思维拓展应用应用一:cos θ===-,∵0≤θ≤π,∴θ=.应用二:(1)∵|a+b|2=a2+2a·b+b2=32+2a·b+42=25+2a·b=21,∴a·b=-2.(2)(2a-b)·(3a+b)=6a2-a·b-b2=6×32-(-2)-42=40.应用三:依据物理知识,有三对相对速度,汽车对地的速度为v车地,风对车的速度为v风车,风对地的速度为v风地.风对地的速度可以看成车对地与风对车的速度的合速度,即v风地=v风车+v车地.如图,根据向量加法的平行四边形法则可知,表示向量v风地的有向线段是▱ACDB的对角线.∵=4 m/s,∠ACD=30°,=2 m/s,∴∠ADC=90°.在Rt△ADC中,=·cos 30°=2(m/s).即风向的实际方向是正南方向,汽车速度的大小为2 m/s.基础智能检测1.B根据题意知v1、v2方向相反,且|v1|>|v2|,逆风行驶的速度为v=v1+v2,故选B.2.D由功的定义知W=|F||s|·cos<F,s>=|F||s|cos θ,故选D.3.(-3,-4)由题意知F1+F2+F3=0,∴F3=-(F1+F2)=-[(1,1)+(2,3)]=-(3,4)=(-3,-4).4.解:(1)W=cos α;(2)W=F·s;(3)F·s=·cos α,因为余弦函数在[0,π]上是减函数,所以当α逐渐增大时,F·s逐渐减少.全新视角拓展2根据向量的运算法则,b·c=b·[ta+(1-t)b]=0,即ta·b+(1-t)|b|2=0,从而得到,t|a||b|cos 60°+(1-t)|b|2=t+1-t=0,解得t=2.思维导图构建|a|cos θ(a·b)(λb)a·c b·c。
2.4.2向量数量级的坐标表示

C(-2,5)
y
证明 : AB (2 1,3 2) (1,1)
AC (2 1,5 2) (3,3)
AB AC 1 (3) 1 3 0
B(2,3)
A(1,2) 0
x
AB AC
三角形 ABC是直角三角形 .
故两个向量的数量积等于它们 对应坐标的乘积的和。即 y A(x ,y ) 1 1
a b x1x2 y1 y2
B(x2,y2)
b
j
a
i
o 根据平面向量数量积的
x
坐标表示,向量的数量积的运算可 转化为向量的坐标运算。
2、向量的模和两点间的距离公式
3、两向量垂直和平行的坐标表示 (1)垂直 a b a b 0
向量数量积是否为零,是判断相应两条线段或直线的重 要方法之一
练习2:以原点和A(5,2) 为两个顶点作等腰直角三角形 OAB,B=90,求点B的坐标. 3 7 y 答案:B的坐标为( , ) B 2 2 7 3 或( , ) 2 2
O
A x
四、逆向及综合运用
例3 (1)已知 a =(4,3),向量 b是 垂直于 a 的单位向量,求 b .
(2)已知a 10, b (1,2),且a // b,求a的坐标.
3 (3)已知a (3,0), b (k ,5),且a与b的夹角为 , 4 求k的值.
例4:已知 a =(1, 3),b =( 3+1, 则a与b的夹角是多少?
解:由a =(1, 3),b =( 3+1, 3 1), 有 a b 1 ( 3 1) 3 ( 3 1) 4, a 2, b 2 2,
必修4-2.6 平面向量数量积的坐标表示 (2)

2.已知 a (3, 2), b (6, 9),求证: a b .
解 a b = (3,2) (-6,9) = 3 (-6)+2 9 所以 a ⏊ b .
3 . 已知三点A(7,5),B(2,3),C(6,-7). 求证:△ABC是直角三角形.
证明 AB (2, 3) (7, 5) (5, 2) BC (6, 7) (2, 3) (4, 10) 所以 AB BC 0 则 AB BC 所以,△ABC是直角三角形.
4.已知 a (3, 0), b (k, 5),且 a与b 的夹角是 135, 求k的值 .
重点:平面向量数量积的坐标表示.
难点: 平面向量数量积的应用.
1 . 平面向量数量积的计算公式 . 2. 在直角坐标系中,设 i,j 分别是 x 轴和 y 轴方向上 的单位向量 . 设a = (x1,y1),b = (x2,y2),怎样 用 a 和 b 的坐标来表示 a b 呢?
1. a · b = |a| |b| cos . | a | a a .
例1 已知 a =( 3,2 ),b =( -1,-1 ),求向量a 与b 的夹角 的余弦 .
26 解 cos . 26 32 2 2 12 (1) 2 26 即 向量a与b夹角的余弦值为 26
3 1 2 (1)
例2 求以点C(a,b)为圆心,r为半径的圆的方程 .
思考:如何用向量坐标表示两个向量的夹角? 设a = (x1,y1),b = (x2,y2),a ,b 的夹角为θ ,
则 cos
x1 x2 y1 y2 x y x y
2 1 2 1 2 2 2 2
.
向量垂直的坐标表示: 设a = (x1,y1),b = (x2,y2), 则 a ⊥ b ⟺ x1x2 + y1y2 = 0
高中数学必修4第二章第六节《平面向量数量积的坐标表示》

2b
2
2 2 x2 y2 , 3a b x1 x2 y1 y2 , 4a b x1 x2 y1 y2 0
其中假命题序号是:
(2)
4.若a 0,1, b 1,1且 a b a, 则实数的值是
A.-1 B.0 C.1 D.2
3、 cos
x1 x2 y1 y2 x1 y1
2 2
x2 y2
2
2
4、 a // b x1y2 x2 y1 0 5、 a b x1 x2 y1 y2 0
6、已知:A(x1,x2),B(x1,x2)则
AB ( x2 x1 ) 2 ( y2 y1 ) 2 ,
学习目标:
1、理解掌握平面向量数量积的坐标表示、 向量的 夹角、模的 公式. 2、掌握两个向量垂直的坐标表示 3、能初步运用向量数量积的坐标表示 解决处理有关长度、垂直及夹角 的几 个问题.
基础训练题
1.有四个式子: 10 a 0, 20 a 0, 3a b a c b c,
a // b x1y2 x2 y1 0
a b x1 x2 y1 y2 0
例3:已知向量a=(-2,-1),b=(λ,1)若a与b 的夹角为钝角,则λ取值范围是多少? 解:由题意可知: -1< cos
a b ab
<0
∴λ∈(—
1 ,2)∪(2,+∞) 2
例4:已知A(1, 2),B(2,3),C(-2,5)试判 定△ABC的形状,并给出证明。
cos
x1 x2 y1 y2 x1 y1
2 2
x2 y2
2
2
例2:设a=(2,1),b=(1,3),求a· b及a 与b的夹角
北师大高中数学必修平面向量数量积的坐标表示教案

北师大高中数学必修平面向量数量积的坐标表示教案第一章:向量概念回顾1.1 向量的定义向量是有大小和方向的量,通常用箭头表示。
向量的表示方法:用字母表示向量的名称,后面跟上箭头和坐标表示其大小和方向。
1.2 向量的坐标表示二维空间中的向量可以用两个坐标表示,通常用(x, y) 表示。
向量的长度(模):表示向量的大小,计算公式为√(x^2 + y^2)。
第二章:向量的数量积2.1 向量数量积的定义两个向量的数量积(点积)是指它们之间的乘积再进行加法运算。
向量a 和向量b 的数量积表示为a ·b,计算公式为a ·b = |ab| cosθ,其中|a| 和|b| 分别表示向量a 和b 的长度,θ表示它们之间的夹角。
2.2 向量数量积的坐标表示两个二维向量a = (x1, y1) 和b = (x2, y2) 的数量积表示为a ·b = x1x2 + y1y2。
数量积的性质:交换律、分配律、共线向量的数量积为零。
第三章:向量的投影3.1 向量的投影概念向量的投影是指向量在某个方向上的位移,可以是正方向或负方向。
向量a 在向量b 方向上的投影表示为proj_b a,计算公式为proj_b a =(a ·b / |b|^2)b。
3.2 向量的投影坐标表示向量a = (x1, y1) 在向量b = (x2, y2) 方向上的投影表示为proj_b a = ((x1x2 + y1y2) / (x2^2 + y2^2))(x2, y2)。
投影的性质:投影是标量倍数不变、共线向量的投影相等。
第四章:数量积的应用4.1 向量的垂直判断两个向量垂直的条件是它们的数量积为零。
即a ·b = 0,表示向量a 和向量b 垂直。
4.2 向量的模长计算已知向量的数量积和其中一个分量,可以求解另一个分量。
例如,已知a ·b 和x1,可以求解y1 = (a ·b x1^2) / y2。
高中数学-平面向量数量积的坐标表示、模、夹角-教材分析

教材分析
1.平面向量的数量积,教材将其分为两部分.本节为第二部分平面向量的数量积的坐标表示,就是运用坐标这一量化工具表达向量的数量积运算,是平面向量坐标运算的深化,是平面向量数量积几何表示与代数表示的连接点,为研究平面中的距离、垂直、角度等问题提供了全新的手段。
它把向量的数量积与坐标运算两个知识点紧密联系起来,是全章重点之一。
同时平面向量数量积坐标表示是高二研究空间向量坐标运算的基础,它为研究空间向量垂直、平行与空间距离提供了借鉴与类比的模型。
2.前面学习了平面向量数量积、平面向量的坐标表示.利用平面向量坐标表示和坐标运算,结合平面向量和平面向量数量积的关系来推导出平面向量数量积、模、夹角的坐标表示。
通过本节课的学习,我们将加深对数学内涵及其知识间联系的领悟,更深刻地理解数形结合、转化化归等数学思想,初步领略数学的完美和谐,感受数学美。
高一数学《2.4.2平面向量数量积的坐标表示、模、夹角》

2.4.2平面向量数量积的坐标表示、模、夹角教学目的:1.掌握平面向量数量积运算规律;2.能利用数量积的5个重要性质及数量积运算规律解决有关问题;3.掌握两个向量共线、垂直的几何判断,会证明向量垂直,以及能解决一些简单问题. 教学重点:平面向量数量积及运算规律.教学难点:平面向量数量积的应用教学过程:一、复习引入:1.平面向量数量积(内积)的定义:2.两个向量的数量积的性质: 设a 、b 为两个非零向量,e 是与b 同向的单位向量. 1︒ e ⋅a = a ⋅e =|a |cos θ; 2︒ a ⊥b ⇔ a ⋅b = 03︒ a 与b 同向时,a ⋅b = |a ||b |; a 与b 反向时,a ⋅b = -|a ||b |. 特别的a ⋅a = |a |2或a a a ⋅=|| 4︒cos θ =||||b a b a ⋅ ; 5︒|a ⋅b | ≤ |a ||b | 3.练习: (1)已知|a |=1,|b |=2,且(a -b )与a 垂直,则a 与b 的夹角是( )A.60° B .30° C.135° D.45°(2)已知|a |=2,|b |=1,a 与b 之间的夹角为3π,那么向量m =a -4b 的模为( ) A.2 B .23 C.6 D.12二、讲解新课:探究:已知两个非零向量),(11y x a =,),(22y x b =,怎样用a 和b 的坐标表示b a ⋅?.1、平面两向量数量积的坐标表示两个向量的数量积等于它们对应坐标的乘积的和.即b a ⋅2121y y x x +=2. 平面内两点间的距离公式(1)设),(y x a =,则222||y x a +=或22||y x a +=.(2)如果表示向量a 的有向线段的起点和终点的坐标分别为),(11y x 、),(22y x , 那么221221)()(||y y x x a -+-=(平面内两点间的距离公式)3. 向量垂直的判定设),(11y x a =,),(22y x b =,则b a ⊥ ⇔02121=+y y x x4. 两向量夹角的余弦(πθ≤≤0)co s θ =||||b a b a ⋅⋅222221212121y x y x y y x x +++=二、讲解范例:例1 已知A (1, 2),B (2, 3),C (-2, 5),试判断△ABC 的形状,并给出证明.例2 设a = (5, -7),b = (-6, -4),求a ·b 及a 、b 间的夹角θ(精确到1o )分析:为求a 与b 夹角,需先求a ·b 及|a |·|b |,再结合夹角θ的范围确定其值.例3 已知a =(1,3),b =(3+1,3-1),则a 与b 的夹角是多少?评述:已知三角形函数值求角时,应注重角的范围的确定.三、课堂练习:1、P107面1、2、3题2、已知A (3,2),B (-1,-1),若点P (x ,-21)在线段AB 的中垂线上,则x = . 四、小结: 1、b a ⋅2121y y x x +=2、平面内两点间的距离公式 221221)()(||y y x x a -+-=3、向量垂直的判定:设),(11y x a =,),(22y x b =,则b a ⊥ ⇔02121=+y y x x五、课后作业:作业二十四。
北师大版数学必修四课件:2.6平面向量数量积的坐标表示

(1)当θ =0°或180°时,l1∥l2,此时α =0°; (2)当0°<θ ≤90°时,l1与l2所成的角α =θ ;
(3)当90°<θ <180°时,l1与l2所成的角α =180°-θ .
可以借助向量所成的角来判断直线所成的角, 但必须注意两者的角的范围不同θ∈[0,π],而
[0, ] . 2
r uuu r r uuu r r 2 2 使得 OA a x, y , 所以 OA a x y , 即 a 为点A到
r
原点的距离;
(2)若A(x1,y1),B(x2,y2),则 AB =(x2-x1,y2-y1),所以
uuu r 2 即平面直角坐标系中任意 AB (x 2 x1 ) 2 y2 y1 ,
特殊情形.
uuu r uuu r 【规范解答】 1 AB 3, 4 ,AC c 3, 4 ,
当c=5时,AC 2, 4 .
uuu r uuu r uuu r ABgAC 6 16 1 5 cos A uuu . r uuu r 5 5 20 5 AB gAC uuu r uuu r ABgAC 3 c 3 16 25 3c< 0,
r r r 故C正确;由 1 0 所以 (a , 故D错误. b) b,
1 2
1 2
【例】如图,以原点和A(5,2)为顶点作等腰直角△OAB,使 ∠B =90°,求点B和向量 AB 的坐标.
uu u r
【规范解答】设B点坐标(x,y),则
uuu r uuu r OB x, y , AB uuu r uuu r Q OB AB,
系!
r r 1 1 【例1】(2010·安徽高考)设向量 a 1,0 , b ( , ), 2 2
学案4:6.3.5 平面向量数量积的坐标表示

6.3.5 平面向量数量积的坐标表示【知识导图】【学法指导】1.学习了本节后,我们在用向量处理平面图形问题时就有了两种方法,通过一题两解,体会基底法和坐标法的优劣及选择依据.2.通过数形结合,对向量平行与垂直条件的坐标表示的类比,培养学生联想的记忆方法.【自主预习】1.两向量的数量积与两向量垂直的坐标表示设向量a =(x 1,y 1),b =(x 2,y 2),a 与b 的夹角为θ. 数量积两个向量的数量积等于它们 的和,即a ·b = 两个向量垂直 a ⊥b ⇔状元随笔 对数量积的坐标表示的理解(1)两个向量的数量积等于它们对应坐标的乘积的和;(2)引入坐标运算后,使得平面向量数量积的运算和两个向量的坐标运算联系起来,从而使得向量的工具性作用更强;(3)平面向量的坐标可以把几何问题转化为代数问题,用向量的坐标运算来实现几何问题的求解,数形结合的思想在数量积的应用中将体现更多.2.三个重要公式向量模公式:设a =(x 1,y 1),则|a |= x 21+y 21两点间距离公式:若A (x 1,y 1),B (x 2,y 2),则|AB →|=(x 2-x 1)2+(y 2-y 1)2向量的夹角公式:设两非零向量a =(x 1,y 1),b =(x 2,y 2),a 与b 的夹角为θ,则cos θ=a ·b |a ||b |=x 1x 2+y 1y 2x 21+y 21·x 22+y 22状元随笔 对向量模长公式的理解(1)模长公式是数量积的坐标表示a →·b →=x 1x 2+y 1y 2的一种特例,当a →=b →时,则可得|a →|2=x 21+y 21; (2)若点A (x 1,y 1),B (x 2,y 2),则AB →=(x 2-x 1,y 2-y 1),所以|AB →|=(x 2-x 1)2+(y 2-y 1)2,即|AB →|的实质是A ,B 两点间的距离或线段AB 的长度,这也是模的几何意义.【基础自测】1.判断下列命题是否正确. (正确的打“√”,错误的打“×”)(1)两个非零向量a =(x 1,y 1),b =(x 2,y 2),满足x 1y 2-x 2y 1=0,则向量a ,b 的夹角为0°.( )(2)两个向量的数量积等于它们对应坐标的乘积的和.( )(3)若两个向量的数量积的坐标和小于零,则两个向量的夹角一定为钝角.( )2.已知a =(-3,4),b =(5,2),则a ·b 的值是( )A .23B .7C .-23D .-7 3.已知a =(-2,1),b =(x ,-2),且a ⊥b ,则x 的值为( )A .-1B .0C .1D .24.已知a =(1,3),b =(-2,0),则|a +b |=________.【课堂探究】类型一 数量积的坐标运算例1 (1)设向量a =(1,-2),向量b =(-3,4),向量c =(3,2),则向量(a +2b )·c =( )A .(-15,12)B .0C .-3D .-11(2)已知向量a =(1,2),b =(2,x ),且a ·b =-1,则x 的值等于( )A.12B .-12 C.32 D .-32方法归纳数量积坐标运算的两个途径一是先将各向量用坐标表示,直接进行数量积运算;二是先利用数量积的运算律将原式展开,再依据已知计算.跟踪训练1 已知a =(2,-1),b =(3,2),若存在向量c ,满足a ·c =2,b ·c =5,则向量c =________.类型二 平面向量的模例2 (1)设x ∈R ,向量a =(x,1),b =(1,-2),且a ∥b ,则|a +b |=( ) A.5 B.52C .25D .5(2)已知向量a =(1,2),b =(-3,2),则|a +b |=________,|a -b |=________.方法归纳求向量的模的两种基本策略(1)字母表示下的运算利用|a |2=a 2,将向量的模的运算转化为向量与向量的数量积的问题.(2)坐标表示下的运算若a =(x ,y ),则a ·a =a 2=|a |2=x 2+y 2,于是有|a |=x 2+y 2.跟踪训练2 (1)设平面向量a =(1,2),b =(-2,y ),若a ∥b ,则|3a +b |等于( )A.5B.6C.17D.26(2)已知|a |=10,b =(1,2),且a ·b =10,则a 的坐标为______.类型三 平面向量的夹角(垂直)例3 (1)已知向量a =(1,2),b =(-2,-4),|c |=5,若(c -b )·a =152,则a 与c 的夹角为() A.30° B .60°C .120°D .150°(2)已知向量a =(1,1),b =(2,-3),若λa -2b 与a 垂直,则实数λ等于________. 方法归纳利用数量积求两向量夹角的步骤数量积:利用平面向量数量积的坐标表示公式求出这两个向量的数量积.模:利用|a |=计算出这两个向量的模.余弦值:由公式cos θ=x 1x 2+y 1y 2x 21+y 21x 22+y 22直接求出cos θ的值.角:在0≤θ≤π内,由cos θ的值求角θ.跟踪训练3已知平面向量a=(3,4),b=(9,x),c=(4,y),且a∥b,a⊥c.(1)求b与c;(2)若m=2a-b,n=a+c,求向量m,n的夹角的大小.【参考答案】【自主预习】1. 对应坐标的乘积x 1x 2+y 1y 2 x 1x 2+y 1y 2=0【基础自测】1.答案:(1)× (2)√ (3)×2.解析:由数量积的计算公式得,a ·b =(-3,4)·(5,2)=-3×5+4×2=-7.答案:D3.解析:由题意,a ·b =(-2,1)·(x ,-2)=-2x -2=0,解得x =-1.答案:A4.解析:因为a +b =(-1, 3),所以|a +b |=(-1)2+(3)2=2.答案:2【课堂探究】类型一 数量积的坐标运算例1【解析】 (1)依题意可知,a +2b =(1,-2)+2(-3,4)=(-5,6),所以(a +2b )·c =(-5,6)·(3,2)=-5×3+6×2=-3.(2)因为a =(1,2),b =(2,x ),所以a ·b =(1,2)·(2,x )=1×2+2x =-1,解得x =-32. 【答案】 (1)C (2)D跟踪训练1解析:设c =(x ,y ),因为a ·c =2,b ·c =5,所以⎩⎪⎨⎪⎧ 2x -y =2,3x +2y =5,解得⎩⎨⎧ x =97,y =47,所以c =⎝⎛⎭⎫97,47.答案:⎝⎛⎭⎫97,47类型二 平面向量的模例2【解析】 (1)因为a =(x,1),b =(1,-2),且a ∥b ,所以-2x -1×1=0,解得x =-12. 所以a +b =⎝⎛⎭⎫-12,1+(1,-2)=⎝⎛⎭⎫12,-1,|a +b |=⎝⎛⎭⎫12 2+(-1)2=52. (2)由题意,知a +b =(-2,4),a -b =(4,0),所以|a +b |=(-2)2+42=25,|a -b |=4.【答案】 (1)B (2)25 4跟踪训练2【解析】 (1)因为a ∥b ,所以1·y -2×(-2)=0,解得y =-4,从而3a +b =(1,2),|3a +b |= 5.(2)设a 的坐标为(x ,y ),由题意得⎩⎨⎧ x +2y =10,x 2+y 2=10,即⎩⎪⎨⎪⎧ x +2y =10,x 2+y 2=100,解得⎩⎪⎨⎪⎧ x =10,y =0,或⎩⎪⎨⎪⎧x =-6,y =8,所以a =(10,0)或a =(-6,8). 【答案】 (1)A (2)(10,0)或(-6,8)类型三 平面向量的夹角(垂直)例3【解析】 (1)由a ·b =-10,得(c -b )·a =c ·a -b ·a =c ·a +10=152,∴c ·a =-52. 设a 与c 的夹角为θ,则cos θ=a ·c |a ||c |=-525×5=-12. 又θ∈[0°,180°],∴θ=120°.(2)方法一 λa -2b =(λ,λ)-2(2,-3)=(λ-4,λ+6).∵(λa -2b )⊥a ,∴(λa -2b )·a =0,∴(λ-4)+(λ+6)=0,∴λ=-1. 方法二 ∵(λa -2b )⊥a ,∴(λa -2b )·a =0,即λa 2=2a ·b ,∴λ(1+1)=2(1,1)·(2,-3),即2λ=-2,∴λ=-1.【答案】 (1)C (2)-1跟踪训练3解:(1)因为a ∥b ,所以3x =4×9,所以x =12.因为a ⊥c ,所以3×4+4y =0,所以y =-3,所以b =(9,12),c =(4,-3).(2)m =2a -b =(6,8)-(9,12)=(-3,-4),n =a +c =(3,4)+(4,-3)=(7,1).设m 、n 的夹角为θ,则cos θ=m ·n |m ||n |=-3×7+(-4)×1(-3)2+(-4)2×72+12=-25252=-22. 因为θ∈[0,π],所以θ=3π4,即m ,n 的夹角为3π4.。
6.3.5+平面向量数量积的坐标表示+课件-2024-2025学年高一下学期数学人教A版必修第二册

a b
a b
a⊥b
x1 x2 y1 y2
x12 y12 x2 2 y2 2
x1x2+y1y2=0
夹角公式的特例
探索新知
例10 若点A(1,2),B(2,3),C(-2,5),则△ABC是什么形状?
证明你的猜想.
3 2) (11)
,
法一: 因为 AB (2 1,
AC (2 1,
1), AC (3,
法二:因为 AB (1,
3), BC (4,
2),
2
2
所以 AB 1 1 2, AC (3) 2 32 18,
2
2
2
BC (4) 2 2 2 20 ,
2
2
2
所以 AB AC BC ,
所以△ABC是直角三角形.
勾股定理逆定理是判断两条直线是否垂直的重要方法之一
(1)求 2a b 的值;
解析:
(1)因为 a 1, 2 , b 1, 1 ,
所以 2a b 2 1, 2 1, 1 3, 3 ,
所以 2a b 3 3 3 2 ;
2
2
当堂检测
2.Байду номын сангаас知平面向量 a 1, 2 , b 1, 1 .
两个向量的数量积等于它们对应坐标的乘积的和.
探索新知
问题1 若a=(x,y),如何计算向量的模|a|呢?
a x 2 y 2 或|a|2=x2+y2
问题2 如果表示向量a的有向线段的起点和终点的坐标分别
为A (x1,y1) ,B (x2,y2),如何计算向量a的模?
a AB ( x2 x1 )2 ( y2 y1 ) 2
高中数学必修二 6 3 5 平面向量数量积的坐标表示学案

6.3.5 平面向量数量积的坐标表示【学习目标】一.两向量的数量积与两向量垂直的坐标表示已知两个非零向量,向量a=(x1,y1),b=(x2,y2)注意:公式a·b=|a||b|cos〈a,b〉与a·b=x1x2+y1y2都是用来求两向量的数量积的,没有本质区别,只是书写形式上的差异,两者可以相互推导.二.与向量的模、夹角相关的三个重要公式1.向量的模:设a=(x,y),则|a|=.2.两点间的距离公式:若A(x1,y1),B(x2,y2),则|AB→|=.3.向量的夹角公式:设两非零向量a=(x1,y1),b=(x2,y2),a与b的夹角为θ,则cos θ=a·b|a||b|=.注意:由三角函数值cos θ求角θ时,应注意角θ的取值范围是0≤θ≤π.【小试牛刀】思维辨析(对的打“√”,错的打“×”)(1)向量的模等于向量坐标的平方和.()(2)若a=(x1,y1),b=(x2,y2),则a⊥b⇔x1x2+y1y2=0.()(3)若两个非零向量的夹角θ满足cos θ<0,则两向量的夹角θ一定是钝角.()(4)若a·b>0,则a,b的夹角为锐角.()(5)若a·b=|a||b|,则a,b共线.()【经典例题】题型一 数量积的坐标运算点拨:一是先将各向量用坐标表示,直接进行数量积运算;二是先利用数量积的运算律将原式展开,再依据已知计算.例1 已知向量a =(1,3),b =(2,5),求a ·b ,(a +b )·(2a -b ).【跟踪训练】1已知向量a =(1,-1),b =(2,x ).若a ·b =1,则x =( ) A .-1 B .-12 C.12D .1题型二 平面向量的模点拨:求向量的模的两种方法:1.字母表示下的运算,利用|a |2=a 2,将向量的模的运算转化为向量与向量的数量积的问题. (2)坐标表示下的运算,若a =(x ,y ),则a·a =a 2=|a |2=x 2+y 2,于是有|a |= x 2+y2.例2 已知平面向量a =(2,4),b =(-1,2),若c =a -(a ·b )b ,则|c |等于( ) A .4 2 B .25 C .8D .82【跟踪训练】2 已知点A (0,1),B (1,-2),向量AC →=(4,-1),则|BC →|=________.题型三 平面向量的夹角和垂直问题 点拨:解决向量夹角问题的方法1.先利用平面向量的坐标求出这两个向量的数量积a ·b 以及|a |,|b |,再由cos θ=a ·b|a ||b |,求出cos θ,也可由cos θ=x 1x 2+y 1y 2x 21+y 21 x 22+y 22直接求出cos θ.由三角函数值cos θ求角θ时,应注意角θ的取值范围是0≤θ≤π.2.由于0≤θ≤π,所以利用cos θ=a ·b|a ||b |来判断角θ时,要注意cos θ<0有两种情况:一是θ是钝角,二是θ=π;cos θ>0也有两种情况:一是θ为锐角,二是θ=0.例3 已知a=(4,3),b=(-1,2).(1)求a与b夹角的余弦值;(2)若(a-λb)⊥(2a+b),求实数λ的值.【跟踪训练】3已知向量a=(-2,-1),b=(λ,1),且a与b的夹角为钝角,试求实数λ的取值范围.【当堂达标】1.向量a=(1,-1),b=(-1,2),则(2a+b)·a=(C)A.-1B.0C.1D.22.已知向量a=(2,1),a·b=10,|a+b|=52,则|b|=()A. 5 B.10 C.5 D.253.已知向量a=(1,3),b=(3,m).若向量a,b的夹角为π6,则实数m=()A.23 B.3C.0 D.-34.已知A(-2,1),B(6,-3),C(0,5),则△ABC的形状是()A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形5.已知向量a=(-1,2),b=(m,1).若向量a+b与a垂直,则m=________.6.已知向量a与b同向,b=(1,2),a·b=10,求:(1)向量a的坐标;(2)若c=(2,-1),求(a·c)b.【课堂小结】3个公式1.数量积:若a=(x1,y1),b=(x2,y2),则a·b=x1x2+y1y2.2.模长:若a=(x,y),则a·a=a2=|a|2=x2+y2,于是有|a|=x2+y2.3.夹角:若a=(x1,y1),b=(x2,y2),a与b的夹角为θ,可由cos θ=x1x2+y1y2x21+y21x22+y22直接求出cos θ.由三角函数值cosθ求角θ时,应注意角θ的取值范围是0≤θ≤π.【参考答案】【自主学习】对应坐标的乘积之和 x 1x 2+y 1y 2 x 1x 2+y 1y 2=0 x 2+y 2 √(x 1−x 2)2+(y 1−y 2)2x 1x 2+y 1y 2x 21+y 21· x 22+y 22 【小试牛刀】(1) × (2) × (3) × (4) ×(5) √ 【经典例题】例1 解 a ·b =1×2+3×5=17.∵a +b =(3,8),2a =(2,6),∴2a -b =(2,6)-(2,5)=(0,1), ∴(a +b )·(2a -b )=3×0+8×1=8.【跟踪训练】1 D 解析:(1)a ·b =2-x =1,解得x =1.故选D.例 2 D 解析:易得a ·b =2×(-1)+4×2=6,所以c =(2,4)-6(-1,2)=(8,-8),所以|c |=√82+(−8)2=8 2.【跟踪训练】2 13 解析:设C (x ,y ),因为点A (0,1),向量AC→=(4,-1),所以AC →=(x ,y-1)=(4,-1),所以⎩⎨⎧x =4,y -1=-1,解得x =4,y =0,所以C (4,0),所以BC→=(3,2),|BC →|=9+4=13.例3解 (1)因为a ·b =4×(-1)+3×2=2,|a |=42+32=5,|b |=(-1)2+22=5,设a 与b 的夹角为θ,所以cos θ=a ·b |a ||b |=255=2525.(2)因为a -λb =(4+λ,3-2λ),2a +b =(7,8),又(a -λb )⊥(2a +b ),所以7(4+λ)+8(3-2λ)=0,所以λ=529.【跟踪训练】3 解 ∵a 与b 的夹角为钝角,∴a ·b <0,即(-2,-1)·(λ,1)=-2λ-1<0,∴λ>-12.又当a 与b 反向时,夹角为180°,即a ·b =-|a |·|b |,则2λ+1=5·λ2+1,解得λ=2.由于a 与b 的夹角为钝角,故应排除a 与b 反向共线的情况,即排除λ=2,则实数λ的取值范围为⎝ ⎛⎭⎪⎫-12,2∪(2,+∞). 【当堂达标】1.C 解析:a =(1,-1),b =(-1,2),∴(2a +b )·a =(1,0)·(1,-1)=1.2.C 解析:∵|a +b |=52,∴|a +b |2=a 2+2a ·b +b 2=5+2×10+b 2=(52)2,∴|b |=5,故选C .3.B 解析:因为a =(1,3),b =(3,m ).所以|a |=2,|b |=9+m 2,a ·b =3+3m , 又a ,b 的夹角为π6,所以a ·b |a |·|b |=cos π6,即3+3m 29+m 2=32,所以3+m =9+m 2,解得m = 3.4.A 解析:选A.由题设知AB→=(8,-4),AC →=(2,4),BC →=(-6,8),所以AB →·AC →=2×8+(-4)×4=0,即AB→⊥AC →.所以∠BAC =90°,故△ABC 是直角三角形.5. 7 解析:因为a +b =(m -1,3),a +b 与a 垂直,所以(m -1)×(-1)+3×2=0,解得m =7.6.解 (1)∵a 与b 同向,且b =(1,2),∴a =λb =(λ,2λ)(λ>0). 又∵a ·b =10,∴λ+4λ=10,∴λ=2,∴a =(2,4). (2)∵a ·c =2×2+(-1)×4=0,∴(a ·c )b =0·b =0.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§6 平面向量数量积的坐标表示1.掌握数量积的坐标表达式.(重点)2.能用坐标表示两个向量的夹角,判断两个平面向量的垂直关系.(重点) 3.了解直线的方向向量的概念.(难点)[基础·初探]教材整理 平面向量数量积的坐标表示 阅读教材P 98~P 99,完成下列问题. 1.平面向量数量积的坐标表示 设向量a =(x 1,y 1),b =(x 2,y 2). (1)a ·b =x 1x 2+y 1y 2;(2)a 2=x 21+y 21,即|a |=x 21+y 21;(3)设向量a 与b 的夹角为θ,则cos θ=a ·b|a ||b |=x 1x 2+y 1y 2x 21+y 21·x 22+y 22; (4)a ⊥b ⇔x 1x 2+y 1y 2=0. 2.直线的方向向量给定斜率为k 的直线l ,则向量m =(1,k )与直线l 共线,我们把与直线l 共线的非零向量m 称为直线l 的方向向量.判断(正确的打“√”,错误的打“×”)(1)若两非零向量的夹角θ满足cos θ<0,则两向量的夹角θ一定是钝角.( )(2)若A (x 1,y 1),B (x 2,y 2),则|AB →|=(x 2-x 1)2+(y 2-y 1)2.( )(3)两向量a 与b 的夹角公式cos θ=x 1x 2+y 1y 2x 21+y 21·x 22+y 22的使用范围是a ≠0且b ≠0.( )【解析】 (1)错误.如a =(-1,-1),b =(2,2),显然cos θ=a ·b|a |·|b |<0,但a 与b 的夹角是180°,而并非钝角.(2)正确.AB →=(x 2-x 1,y 2-y 1),所以|AB →|=(x 2-x 1)2+(y 2-y 1)2. (3)正确.两向量a 与b 的夹角公式cos =x 1x 2+y 1y 2x 21+y 21·x 22+y 22有意义需x 21+x 22≠0且y 21+y 22≠0,即a ≠0,且b ≠0.此说法是正确的.【答案】 (1)× (2)√ (3)√[质疑·手记]预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流:疑问1:_________________________________________________________ 解惑:___________________________________________________________ 疑问2:_________________________________________________________ 解惑:___________________________________________________________ 疑问3:_________________________________________________________ 解惑:___________________________________________________________[小组合作型]平面向量数量积的坐标运算(1)求向量a 的坐标; (2)若c =(2,-1),求(a +c )·b .【精彩点拨】根据a与b共线设出a的坐标,再利用数量坐标运算公式构建方程求得a的坐标,进而求(a+c)·b.【自主解答】(1)∵a与b同向,且b=(1,2),∴a=λb=(λ,2λ)(λ>0).又∵a·b=10,∴λ+4λ=10,∴λ=2,∴a=(2,4).(2)法一:a+c=(4,3),∴(a+c)·b=4+6=10.法二:(a+c)·b=a·b+c·b=10+0=10.进行向量的数量积的坐标运算关键是把握向量数量积的坐标表示,运算时常有两条途径:(1)根据向量数量积的坐标表示直接运算;(2)先利用数量积的运算律将原式展开,再依据已知计算.[再练一题]1.已知向量a=(4,-2),b=(6,-3),求:(1)(2a-3b)·(a+2b);(2)(a+b)2.【解】法一:(1)∵2a-3b=(8,-4)-(18,-9)=(-10,5),a+2b=(4,-2)+(12,-6)=(16,-8),∴(2a-3b)·(a+2b)=-160-40=-200.(2)∵a+b=(10,-5),∴(a+b)2=(10,-5)×(10,-5)=100+25=125.法二:由已知可得:a2=20,b2=45,a·b=30.(1)(2a-3b)·(a+2b)=2a2+a·b-6b2=2×20+30-6×45=-200.(2)(a+b)2=a2+2a·b+b2=20+60+45=125.向量的夹角及垂直已知a=(1,2),b=(-2,-4),|c|= 5.(1)求|a+2b|;(2)若(a+b)·c=52,求向量a与c的夹角.【精彩点拨】(1)利用|a|=x21+y21求解.(2)利用cos θ=x1x2+y1y2x21+y21·x22+y22求解.【自主解答】(1)a+2b=(1,2)+2(-2,-4)=(-3,-6),∴|a+2b|=(-3)2+(-6)2=3 5.(2)∵b=(-2,-4)=-2(1,2)=-2a,∴a+b=-a,∴(a+b)·c=-a·c=52.设a与c的夹角为θ,则cos θ=a·c|a||c|=-525×5=-12.∵0≤θ≤π,∴θ=23π,即a与c的夹角为23π.1.已知向量的坐标和向量的模(长度)时,可直接运用公式|a|=x2+y2进行计算.2.求向量的夹角时通常利用数量积求解,一般步骤为: (1)先利用平面向量数量积的坐标表示求出两向量的数量积; (2)再求出两向量的模;(3)由公式cos θ=a·b|a||b|,计算cos θ的值; (4)在[0,π]内,由cos θ的值确定角θ.[再练一题]2.已知a =(1,2),b =(1,λ),分别确定实数λ的取值范围,使得: (1)a 与b 的夹角为直角; (2)a 与b 的夹角为钝角; (3)a 与b 的夹角为锐角. 【解】 a·b =(1,2)·(1,λ)=1+2λ.(1)因为a 与b 的夹角为直角,所以cos θ=0, 所以a·b =0,即1+2λ=0,所以λ=-12. (2)因为a 与b 的夹角为钝角, 所以cos θ<0,且cos θ≠-1, 所以a·b <0,且a 与b 不反向. 由a·b <0,得1+2λ<0,故λ<-12, 由a 与b 共线得λ=2,故a 与b 不可能反向. 所以λ的取值范围为⎝ ⎛⎭⎪⎫-∞,-12. (3)因为a 与b 的夹角为锐角, 所以cos θ>0,且cos θ≠1, 所以a·b >0且a ,b 不同向.由a·b >0,得λ>-12,由a 与b 同向得λ=2.所以λ的取值范围为⎝ ⎛⎭⎪⎫-12,2∪(2,+∞).[探究共研型]向量的模探究1 由向量长度的坐标表示,你能否得出平面内两点间的距离公式? 【提示】 设A (x 1,y 1),B (x 2,y 2),则AB →=(x 2-x 1,y 2-y 1),由向量长度的坐标表示可得|AB |=|AB →|=(x 2-x 1)2+(y 2-y 1)2.探究2 向量的模的坐标表达式是什么? 【提示】 向量a =(x 1,y 1)的模是|a |=x 21+y 21.探究3 求向量的坐标一般采用什么方法? 【提示】 一般采用设坐标、列方程的方法求解.设平面向量a =(3,5),b =(-2,1). (1)求a -2b 的坐标和模的大小; (2)若c =a -(a ·b )·b ,求|c |.【精彩点拨】 (1)将已知向量的坐标代入运算即可.(2)利用a ·b =x 1x 2+y 1y 2求得c 的坐标表示,然后求模.【自主解答】 (1)a =(3,5),b =(-2,1), 所以a -2b =(3,5)-2(-2,1)=(3+4,5-2)=(7,3), |a -2b |=72+32=58.(2)a ·b =x 1x 2+y 1y 2=-6+5=-1, 所以c =a +b =(1,6),所以|c |=12+62=37.求向量的模的两种基本策略1.字母表示F 的运算利用|a |2=a 2,将向量的模的运算转化为向量与向量的数量积的问题.2.坐标表示F 的运算若a =(x ,y ),则a ·b =a 2=|a |2=x 2+y 2, 于是有|a |=x 2+y 2.[再练一题]3.(1)已知a =(1,2),b =(-2,m ),若a ∥b ,则|2a +3b |=________. (2)已知|a |=10,b =(1,2),且a ∥b ,求a 的坐标.【解析】 (1)因为a =(1,2),b =(-2,m ),a ∥b ,所以1×m -2×(-2)=0, 所以m =-4,所以2a +3b =2×(1,2)+3(-2,-4)=(-4,-8), 所以|2a +3b |=(-4)2+(-8)2=4 5.【答案】 4 5(2)设a 的坐标为(x ,y ),由题意得⎩⎪⎨⎪⎧2x -y =0,x 2+y 2=10,解得⎩⎪⎨⎪⎧ x =25,y =45或⎩⎪⎨⎪⎧x =-25,y =-45,所以a =(25,45)或a =(-25,-45).[构建·体系]1.若向量a=(1,1),b=(-1,2),则a·b=()A.1B.2C.3 D.4【解析】a·b=(1,1)·(-1,2)=1×(-1)+1×2=1.【答案】 A2.已知a=(-3,-1),b=(1,3),那么a·b的夹角θ=()【导学号:66470057】A.120°B.30°C.150°D.60°【解析】因为a·b=(-3,-1)·(1,3)=-23,|a|=(-3)2+(-1)2=2,|b|=12+(3)2=2.所以cos θ=a·b|a|·|b|=-232×2=-32.又因为0°≤θ≤180°,所以θ=150°.【答案】 C3.已知a=(2,3),b=(-2,4),则(a+b)·(a-b)=________. 【解析】法一:a+b=(0,7),a-b=(4,-1),所以(a+b)(a-b)=0×4+7×(-1)=-7.法二:(a+b)·(a-b)=a2-b2=|a|2-|b|2=13-20=-7. 【答案】-74.已知a=(1,x),b=(-3,1),若a⊥b,则x=________. 【解析】∵a⊥b,∴-3+x=0,∴x=3.【答案】 35.已知向量a=(1,2),b=(2,-2).(1)设c=4a+b,求(b·c)·a;(2)若a+λb与a垂直,求λ的值;(3)求向量a在b方向上的射影.【解】(1)∵c=4(1,2)+(2,-2)=(6,6),∴b·c=(2,-2)·(6,6)=2×6-2×6=0,∴(b·c)a=0·a=0.(2)∵a+λb=(1,2)+λ(2,-2)=(1+2λ,2-2λ),∵(a+λb)⊥a,∴(1+2λ)+2(2-2λ)=0,得λ=52.(3)法一:设a与b的夹角为θ,则cos θ=a·b|a||b|=1×2+2×(-2)12+22×22+(-2)2=-1010.∴向量a 在b 方向上的投影为 |a |cos θ=12+22·⎝ ⎛⎭⎪⎫-1010=-22. 法二:∵a·b =(1,2)·(2,-2) =-2,|b |=2 2.∴向量a 与b 方向上的投影为 |a |cos θ=a·b |b|=-222=-22.我还有这些不足:(1)______________________________________________________________ (2)______________________________________________________________ 我的课下提升方案:(1)______________________________________________________________ (2)______________________________________________________________。
