工科物理大作业09-电磁感应与电磁场
《大学物理》期末复习 第八章 电磁感应与电磁场

第八章 电磁感应与电磁场§8-1电磁感应定律一、电磁感应现象电磁感应现象可通过两类实验来说明: 1.实验1)磁场不变而线圈运动 2)磁场随时变化线圈不动2.感应电动势由上两个实验可知:当通过一个闭合导体回路的磁通量变化时,不管这种变化的原因如何(如:线圈运动,变;或不变线圈运动),回路中就有电流产生,这种现象就是电磁感应现象,回路中电流称为感应电流。
3.电动势的数学定义式定义:把单位正电荷绕闭合回路一周时非静电力做的功定义为该回路的电动势,即()⎰∙=lK ld K :非静电力ε (8-1)说明:(1)由于非静电力只存在电源内部,电源电动势又可表示为⎰∙=正极负极ld Kε表明:电源电动势的大小等于把单位正电荷从负极经电源内部移到正极时,非静电力所做的功。
(2)闭合回路上处处有非静电力时,整个回路都是电源,这时电动势用普遍式表示:()⎰∙=lK ld K :非静电力ε(3)电动势是标量,和电势一样,将它规定一个方向,把从负极经电源内部到正极的方向规定为电动势的方向。
二、电磁感应定律 1、定律表述在一闭合回路上产生的感应电动势与通过回路所围面积的磁通量对时间的变化率成正比。
数学表达式:dtd ki Φ-=ε在SI 制中,1=k ,(St V Wb :;:;:εΦ),有dtd i Φ-=ε (8-2)上式中“-”号说明方向。
2、i ε方向的确定为确定i ε,首先在回路上取一个绕行方向。
规定回路绕行方向与回路所围面积的正法向满足右手旋不定关系。
在此基础上求出通过回路上所围面积的磁通量,根据dtd i Φ-=ε计算i ε。
,0>Φ00<⇒>Φi dtd ε ,0>Φ00>⇒<Φi dtd ε沿回路绕行反方向沿回路绕行方向:0:0<>iε三、楞次定律此外,感应电动势的方向也可用楞次定律来判断。
楞次定律表述:闭合回路感应电流形成的磁场关系抵抗产生电流的磁通量变化。
高考物理专题九电磁感应第2讲法拉第电磁感应定律自感和涡流课时作业

第2讲法拉第电磁感应定律自感和涡流一、单项选择题1.如图K921所示为地磁场磁感线的示意图.一架民航飞机在赤道上空匀速飞行,机翼保持水平,由于遇到强气流作用使飞机竖直下坠,在地磁场的作用下,金属机翼上有电势差.设飞行员左方机翼末端处的电势为φ1,右方机翼末端处的电势为φ2,忽略磁偏角的影响,则( )图K921A.若飞机从西往东飞,φ2比φ1高B.若飞机从东往西飞,φ2比φ1高C.若飞机从南往北飞,φ2比φ1高D.若飞机从北往南飞,φ2比φ1高2.边长为a的闭合金属正三角形框架,左边竖直且与磁场右边界平行,完全处于垂直于框架平面向里的匀强磁场中.现把框架匀速水平向右拉出磁场,如图K922所示,则下列图象与这一过程相符合的是( )图K922A B C D3.如图K923所示,a、b是用同种规格的铜丝做成的两个同心圆环,两环半径之比为2∶3,其中仅在a环所围区域内有垂直于纸面向里的匀强磁场.当该匀强磁场的磁感应强度均匀增大时,a、b两环内的感应电动势大小之比和感应电流大小之比分别为( )图K923A.1∶1,3∶2B.1∶1,2∶3C.4∶9,2∶3D.4∶9,9∶44.(2020年广东惠州一调)如图K924所示,单匝圆形金属线圈电阻恒定不变,在线圈的圆形区域内有垂直向里的匀强磁场,在时间t内要使线圈中产生大小、方向恒定不变的电流,匀强磁场的磁感应强度应按下列选项中哪种情况变化( )图K924A B C D5.如图K925所示的电路,开关原先闭合,电路处于稳定状态,在某一时刻突然断开开关S ,则通过电阻R 1中的电流I 1随时间变化的图线可能是下图中的( )图K925A B C D6.如图K926均匀磁场中有一由半圆弧及其直径构成的导线框,半圆直径与磁场边缘重合;磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B 0.使该线框从静止开始绕过圆心O 、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流.现使线框保持图中所示位置,磁感应强度大小随时间线性变化.为了产生与线框转动半周过程中同样大小的电流,磁感应强度随时间的变化率ΔB Δt 的大小应为( )图K926A .4ωB 0π B .2ωB 0πC .ωB 0πD .ωB 02π7.(2020年福建卷)如图K927,由某种粗细均匀的总电阻为3R 的金属条制成的矩形线框abcd ,固定在水平面内且处于方向竖直向下的匀强磁场B 中.一接入电路的电阻为R 的导体棒PQ ,在水平拉力作用下沿ab 、dc 以速度v 匀速滑动,滑动过程中PQ 始终与ab 垂直,且与线框接触良好,不计摩擦.在PQ 从靠近ad 处向bc 滑动的过程中( )图K927A .PQ 中电流先增大后减小B .PQ 两端电压先减小后增大C .PQ 上拉力的功率先减小后增大D .线框消耗的电功率先减小后增大二、多项选择题8.(2020年新课标全国卷Ⅰ)1824年,法国科学家阿拉果完成了著名的“圆盘实验”.实验中将一铜圆盘水平放置,在其中心正上方用柔软细线悬挂一枚可以自由旋转的磁针,如图K928所示.实验中发现,当圆盘在磁针的磁场中绕过圆盘中心的竖直轴旋转时,磁针也随着一起转动起来,但略有滞后.下列说法正确的是( )A.圆盘上产生了感应电动势B.圆盘内的涡电流产生的磁场导致磁针转动C.在圆盘转动的过程中,磁针的磁场穿过整个圆盘的磁通量发生了变化D.圆盘中的自由电子随圆盘一起运动形成电流,此电流产生的磁场导致磁针转动图K928图K9299.如图K929所示,空间存在两个磁场,磁感应强度大小均为B,方向相反且垂直纸面,MN、PQ为其边界,OO′为其对称轴.一导线折成边长为l的正方形闭合回路abcd,回路在纸面内以恒定速度v0向右运动,当运动到关于OO′对称的位置时( )A.穿过回路的磁通量为零B.回路中感应电动势大小为2Blv0C.回路中感应电流的方向为顺时针方向D.回路中ab边与cd边所受安培力方向相反10.(2020年广东珠海二模)如图K9210所示,在磁感应强度为B、方向竖直向下的匀强磁场中,有一水平放置的U形导轨,导轨左端连接一阻值为R的电阻,导轨电阻不计.导轨间距离为L,在导轨上垂直放置一根金属棒MN,与导轨接触良好,电阻为r,用外力拉着金属棒向右以速度v做匀速运动.则金属棒运动过程中( )图K9210A.金属棒中的电流方向为由N到MB.电阻R两端的电压为BLvC.金属棒受到的安培力大小为B2L2v r+RD.电阻R产生焦耳热的功率为B2L2v2 R三、非选择题11.如图K9211甲所示,光滑导轨宽0.4 m,ab为金属棒,均匀变化的磁场垂直穿过轨道平面,磁场的变化情况如图乙所示,金属棒ab的电阻为1 Ω,导轨电阻不计.t=0时刻,ab棒从导轨最左端,以v=1 m/s的速度向右匀速运动,求1 s末回路中的感应电流及金属棒ab受到的安培力.甲乙图K921112.小明同学设计了一个“电磁天平”,如图K9212甲所示,等臂天平的左臂为挂盘,右臂挂有矩形线圈,两臂平衡.线圈的水平边长L =0.1 m ,竖直边长H =0.3 m ,匝数为N 1.线圈的下边处于匀强磁场内,磁感应强度B 0=1.0 T ,方向垂直线圈平面向里.线圈中通有可在0~2.0 A 范围内调节的电流I.挂盘放上待测物体后,调节线圈中电流使天平平衡,测出电流即可测得物体的质量.(重力加速度取g =10m/s 2)甲 乙图K9212(1)为使电磁天平的量程达到0.5 kg ,线圈的匝数N 1至少为多少?(2)进一步探究电磁感应现象,另选N 2=100匝、形状相同的线圈,总电阻R =10 Ω.不接外电流,两臂平衡.如图乙所示,保持B 0不变,在线圈上部另加垂直纸面向外的匀强磁场,且磁感应强度B 随时间均匀变大,磁场区域宽度d =0.1 m .当挂盘中放质量为0.01 kg 的物体时,天平平衡,求此时磁感应强度的变化率ΔB Δt.第2讲 法拉第电磁感应定律 自感和涡流1.C 解析:由于地磁场的方向是由南到北的,若飞机从西往东飞或者从东往西飞时,机翼不切割磁感线,不产生感应电动势,所以机翼两端不存在电势差,故A 、B 错误;若飞机从南往北飞,由右手定则可判定,飞机的右机翼末端的电势比左机翼末端的电势高,即φ2比φ1高,若飞机从北往南飞,φ2比φ1低,故C 正确,D 错误.2.B 解析:该过程中,框架切割磁感线的有效长度等于框架与磁场右边界两交点的间距,根据几何关系有l 有=2 33x ,所以E 电动势=Bl 有v =2 33Bvx∝x,选项A 错误,B 正确;F 外力=B 2l 2v R =4B 2x 2v 3R∝x 2,选项C 错误;P 外力功率=F 外力v∝F 外力∝x 2,选项D 错误.3.A4.A 解析:在时间t 内要使线圈中产生大小、方向恒定不变的电流,根据法拉第电磁感应定律得ΔB Δt是个定值,即图象的斜率保持不变,故A 正确.5.D 解析:开关S 原来闭合时,电路处于稳定状态,流过R 1的电流方向向左,大小为I 1,与R 1并联的R 2和线圈L 支路中的电流I 2的方向也是向左.当某一时刻开关S 突然断开时,L 中向左的电流要减小,由于自感现象,线圈L 产生自感电动势,在回路“L→R 1→A→R 2”中形成感应电流,电流通过R 1的方向与原来相反,变为向右,并从I 2开始逐渐减小到零,故D 图正确.6.C 解析:当线框绕过圆心O 的转动轴以角速度ω匀速转动时,由于面积的变化产生感应电动势,从而产生感应电流.设半圆的半径为r ,导线框的电阻为R ,即I 1=E R =ΔΦRΔt =B 0ΔS RΔt =12πr 2B 0R πω=B 0r 2ω2R .当线框不动,磁感应强度变化时,I 2=E R =ΔΦRΔt =ΔB·S RΔt =ΔBπr 22RΔt ,因I 1=I 2,可得ΔB Δt =ωB 0π,选项C 正确. 7.C 解析:设PQ 左侧电路的电阻为R x ,则右侧电路的电阻为3R -R x ,所以外电路的总电阻R′=R x 3R -R x 3R,外电路电阻先增大后减小,所以路端电压先增大后减小,所以B 错误;电路的总电阻先增大后减小,再根据闭合电路的欧姆定律可得PQ 中的电流I =E R′+R先减小后增大,故A 错误;由于导体棒做匀速运动,拉力等于安培力,即F =BIL ,拉力的功率P =BILv ,先减小后增大,所以C 正确;外电路的总电阻R′=R x 3R -R x 3R 最大为3R 4,小于电源内阻R ,又外电阻先增大后减小,当R′=R 时,外电路消耗的功率最大,所以外电路消耗的功率先增大后减小,故D 错误.8.AB 解析:圆盘运动过程中,半径方向的金属条在切割磁感线,在圆心和边缘之间产生了感应电动势,选项A 正确;圆盘在径向的辐条切割磁感线过程中,内部距离圆心远近不同的点电势不等而形成涡流,产生的磁场又导致磁针转动,选项B 正确;圆盘转动过程中,圆盘位置、圆盘面积和磁场都没有发生变化,所以没有磁通量的变化,选项C 错误;圆盘本身呈现电中性,不会产生环形电流,选项D 错误.9.AB10.AC 解析:由右手定则可知,金属棒中的电流方向为由N 到M ,选项A 正确;因为感应电动势E=BLv ,则电阻R 两端的电压为U =ER R +r =BLvR R +r ,选项B 错误;金属棒受到的安培力大小为F =BIL =B BLv R +rL =B 2L 2v R +r ,选项C 正确;电阻R 产生焦耳热的功率为P R =I 2R =⎝ ⎛⎭⎪⎫BLv R +r 2R =B 2L 2Rv 2R +r 2,选项D 错误. 11.解:Φ的变化有两个原因,一是B 的变化,二是面积S 的变化,显然这两个因素都应当考虑在内,所以有E =ΔΦΔt =ΔB ΔtS +Blv 又ΔB Δt=2 T/s 在1 s 末,B =2 T ,S =lvt =0.4×1×1 m 2=0.4 m 2所以1 s 末,E =ΔB ΔtS +Blv =1.6 V此时回路中的电流I =E R =1.6 A根据楞次定律与右手定则可判断出电流方向为逆时针方向金属棒ab 受到的安培力为F =BIl =2×1.6×0.4 N=1.28 N ,方向向左.12.解:(1)线圈受到安培力F =N 1B 0IL ①天平平衡mg =N 1B 0IL ②代入数据得N 1=25匝. ③(2)由电磁感应定律得E =N 2ΔΦΔt ④即E =N 2ΔB Δt Ld ⑤由欧姆定律得I′=E R ⑥线圈受到安培力F′=N 2B 0I′L ⑦天平平衡m′g=N 22B 0ΔB Δt ·dL2R ⑧代入数据可得ΔB Δt =0.1 T/s.2019-2020学年高考物理模拟试卷一、单项选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的1.我国不少地方在节日期间有挂红灯笼的习俗。
大作业参考答案-电磁感应

电磁感应一、选择题⒈ D ; ⒉ B ;⒊ C ; ⒋ BD ; ⒌ C ; 6.E ; 7.B ; 8.A ; 9.A二、填空题⒈ < 。
⒉ 洛伦兹力,B x v ; 感生电场力; 变化的磁场。
⒊ S iR / 。
⒋ θω222/1B S i n L ; C A → 。
⒌ 0 ;dt dB l 4 ; dtdB l 2- 。
⒍ )ln (20d l d d l I +-πωμ; A O → 。
⒎ 1/16。
⒏ 1.6x106 J/m 3; 4.425 J/m 3; 磁场更易于存储能量。
9. ⎰⎰⎰∙∂∂=∙S S d t D l d H ;⎰⎰⎰∙∂∂-=∙SS d t B l d E ; 0=∙⎰⎰SS d B ; ∑⎰⎰=∙0q S d D S 。
三、问答题1. 答:(1) 起源不同:静止电荷激发静电场,而变化的磁场激发涡旋电场。
(2)性质不同:静电场是有源无旋、保守力场,而涡旋电场是无源有旋、非保守力场。
2. 答: (1) 传导电流源于自由电荷的定向移动,而位移电流本质上是变化的电场。
(2)传导电流通过导体时产生焦耳热,而位移电流则无热效应。
(3)传导电流只能在导体中存在,而位移电流可以在导体、电介质、真空中存在。
四、计算题1 解:(1) 因磁场分布为:r Iπμ2B 0=,则000ln 2200r lr Ix xdr r I S d B d l r r m m +==∙==⎰⎰⎰+πμπμφφ 。
(2)0m ln 2d d r lr Iv t i +-=-=πμφε00ln 2r lr R Iv R I i i +-==πμε(3)Rv r l r I dr r Ir l r R Iv Bdr I dF F l r r i 20000000)ln 2(2ln 200+=⋅⋅+===⎰⎰⎰+πμπμπμ方向垂直于导线向上。
2 解: t 时刻,磁通量为θθφc o s c o s ⋅⋅==l v t kt BS m则电动势为k l x k v t l t i -=-=-=θφεc o s 2d d m负号说明电动势方向沿顺时针3 解:(1)取顺时针方向为正绕线,则3ln 2ln 2200πμπμπμφφIac b Ia adr r I Sd B d b c m m ===∙==⎰⎰⎰则3ln 20πμφaI M m ==(2)3ln 2d d 0t m e at IM λλπμε-=-=电动势方向为顺时针。
大学物理 电磁感应与电磁场

× f× e × × × ×
× × ×
G× ○
× ×
× B v × ×
× × × ×
fm×
×
eE evB E vB
a
U El vBl
谁充当非静电力?
洛伦兹力
fm Ek (v B) e i Ek dl (v B) dl
dΦ i N dt
13
匀强磁场中,导线可在导轨上滑动, 求回路中感应电动势。
解: 在 t 时刻
Φ(t ) Bls (t )
dΦ Blds Blv dt dt
B
s (t )
l
a v
b
两个同心圆环,已知 r1<<r2,大线圈中通有电流 I ,当小
圆环绕直径以 转动时求小圆环中的感应电动势。
交变电流
交变电流
整块铁心
彼此绝缘的薄片 抽真空
高频感应加热 减小电流截面,减少涡流损耗。
2.电子感应加速器
电子感应加速器是利用感应电场来加速电子的设备
铁芯
线圈 电子束
环形真 空管道
电子感应加速器全貌
电子感应加速器的一部分
它的柱形电磁铁在两 极间产生磁场。在磁 场中安臵一个环形真 空管道作为电子运行 的轨道。当磁场发生 变化时,就会沿管道 方向产生感应电场。 射入其中的电子就受 到这感应电场的持续 作用而被不断加速。
B
a
l
dl v
b
导 线 成 为 电 源
i (v B) dl
a
b
vBdl
vBl
ch9+电磁感应和电磁场+习题及答案Word版

第9章 电稳感应和电磁场 习题及答案1. 通过某回路的磁场与线圈平面垂直指向纸面内,磁通量按以下关系变化:23(65)10t t Wb -Φ=++⨯。
求2t s =时,回路中感应电动势的大小和方向。
解:310)62(-⨯+-=Φ-=t dtd ε当s t 2=时,V 01.0-=ε由楞次定律知,感应电动势方向为逆时针方向2. 长度为l 的金属杆ab 以速率υ在导电轨道abcd 上平行移动。
已知导轨处于均匀磁场B中,B 的方向与回路的法线成60°角,如图所示,B的大小为B =kt (k 为正常数)。
设0=t 时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向。
解:任意时刻通过通过回路面积的磁通量为202160cos t kl t Bl S d B m υυ==⋅=Φ导线回路中感应电动势为 t kl tmυε-=Φ-=d d 方向沿abcda 方向。
3. 如图所示,一边长为a ,总电阻为R 的正方形导体框固定于一空间非均匀磁场中,磁场方向垂直于纸面向外,其大小沿x 方向变化,且)1(x k B +=,0>k 。
求: (1)穿过正方形线框的磁通量;(2)当k 随时间t 按t k t k 0)(=(0k 为正值常量)变化时,线框中感生电流的大小和方向。
解:(1)通过正方形线框的磁通量为⎰⎰=⋅=Φa S Badx S d B 0 ⎰+=a dx x ak 0)1()211(2a k a +=(2)当t k k 0=时,通过正方形线框的磁通量为)211(02a t k a +=Φ 正方形线框中感应电动势的大小为dt d Φ=ε)211(02a k a += 正方形线框线框中电流大小为)211(02a R k a R I +==ε,方向:顺时针方向4.如图所示,一矩形线圈与载有电流t I I ωcos 0=长直导线共面。
设线圈的长为b ,宽为a ;0=t 时,线圈的AD 边与长直导线重合;线圈以匀速度υ垂直离开导线。
大学物理电磁感应电磁场和电磁波PPT课件

③ 连接MN成一回路 常数ddt 0
NM MN NM MN2RvB
例4 已知如图 求 的大小和方向
解:
fg
① 用动生电动势公式
I
v
l2
设回路方向: e—f—g—h—e
x e l1 h
effggh he
fghe0
ef hg (v B )d l(v B )d l
作匀速转动. 求线
圈中的感应电动势.
N
enO
'
B
iR
O
已知 S, N,, 求 .
解 设 t 0 时,
en与
B同向
,
则
t
N
N NB co S ts
enO
'
B
dNBSsint
dt
ω
令 mNBS
则 msint
O
iR
msint
金属块
发接 生高 器频
抽真空 金 属 电 极
阻
尼 摆N
S
涡电流加热金属电极
*12-3 自感和互感
自感现象
L
R
通过线圈的电流变化
时,线圈自身会产生感应 现象.
一 自感电动势 自感 穿过闭合电流回路的磁通量
ΦLI
(1)自感 LΦI
若线圈有 N 匝,
IB
磁通匝数 N Φ自感 L I
一 电磁感应现象 磁铁相对线圈运动
通电线圈相对线圈 运动
磁场中运动的导体所产生的感应现象
二 电磁感应定律
电流通断时所产生的
当穿过闭合回路所围 感应现象
面积的磁通量发生变化时,
回路中会产生感应电动势,
(新课标)2020届高考物理一轮复习第九章电磁感应第二节法拉第电磁感应定律自感和涡流课时作业

2.法拉第电磁感应定律 自感和涡流时间:45分钟 一、单项选择题 1.pc X x?乞x xl如图所示,虚线区域内有一垂直纸面向里的匀强磁场,磁场宽度为 L ,磁感应强度大小为B.总电阻为R 的直角三角形导线框,两条直角边边长分别为2L 和L ,当 该线框以垂直于磁场边界的速度 v 匀速穿过磁场的过程中,下列说法正确的是( )A. 线框中的感应电流方向 始终不变B. 线框中感应电流一直在增大C. 线框所受安培力方向始终相同D. 当通过线框的磁通量最大时,线框中的感应电动势为零解析:该线框以垂直于磁场边界的速度 v 匀速穿过磁场的过程中,穿过线框的 磁通量先增大后减小,根据 楞次定律、安培定则可以判断线框中的感应电流先沿逆 时针方向后沿顺时针方向,且始终不为零,由左手定则可以判断线框在该磁场中一 直受到水平向左的安培力作用,故 A 、D 项错,C 项正确;该线框以垂直于磁场边界 的速度v 匀速穿过磁场的过程中,导线框切割磁感线的有效长度先增大、后不变、 后再增大,由E = BLv 及闭合电路欧姆定律可得线框中的感应电流先增大、后不变、 后再增大,故B 项错.答案:C如图所示,两块水平放置的金属板距离为 d ,用导线、开关K 与一个n 匝的线 圈连接,线圈置于方向竖直向上的均匀变化的磁场 B 中.两板间放一台小型压力传 感器,压力传感器上表面绝缘,在其上表面静止放置一个质量为m 电荷量为q 的带正电小球.K 没有闭合时传感器有示数,K 闭合时传感器示数变为原来的一半. 则 线圈中磁场B 的变化情况和磁通量的变化率分别为()解析:根据K 闭合时传感器示数变为原来的一半,推出带正电小球受向上的电 场力,即上极板带负电,下极板带正电,线圈感应电动势的方向从上极板经线圈流 向下极板,根据安培定则知感应磁场的方向向下,与原磁场方向相反,又由楞次定 律得线圈中磁场正在增强;对小球受力分析得 q E =罗,其中感应电动势E = n-At 代入得詈^器故B 正确.答案:B3. 如图甲所示,电路的左侧是一个电容为 C 的电容器,电路的右侧是一个环形 导体,环形导体所围的面积为 S.在环形导体中有一垂直纸面向里的匀强磁场,磁感 应强度的大小随时间变化的规律如图乙所示.则在 0〜t o 时间内,电容器()A.正在增强,△① mgd At 2qB •正在增强,△① mgd At — 2nq C.正在减弱,△① = Atmgd2qD.正在减弱,△① mgd At — 2nqA. 上极板带正电,所带电荷量为D.上极板带负电,所带电荷量为针方向,故电容器上极板带正电,E = n 字二SB ,Q= CE ^ CS :— B ,A Att 0 10正确.答案:A 4.如图所示,A 、B 、C 是三个完全相同的灯泡,L 是一个自感系数较大的线圈 (直流电阻可忽略不计).则( )C 阜 $A. S 闭合时,A 灯立即亮,然后逐渐熄灭B. S 闭合时,B 灯立即亮,然后逐渐熄灭C. 电路接通稳定后,三个灯亮度相同D. 电路接通稳定后,S 断开时,C 灯立即熄灭解析:因线圈L 的自感现象,S 闭合时,A 灯立即亮,电路中电流稳定后 A 灯逐 渐熄灭,A 正确;S 闭合时,B 灯先不太亮,然后亮,B 错误;电路接通稳定后,B 、 C 灯亮度相同,A 灯不亮,C 错误;电路接通稳定后,S 断开时,C 灯逐渐熄灭,D 错误.答案:AB.上极板带正电,所带电荷量为C B — B it 0 C.上极板带负电,所带电荷量为CS B 2— Bt 0解析: 由题图乙可知△ B B 2— B iAt 10B 增大,根据楞次定律知,感应电流沿逆时如图所示,将一根绝缘硬金属导线弯曲成一个完整的正弦曲线形状,它通过两 个小金属环a 、b 与长直金属杆导通,图中a 、b 间距离为L ,导线组成的正弦图形 顶部或底部到杆的距离都是d.右边虚线范围内存在磁感应强度大小为 B 、方向垂直以恒定的速度v 向右运动,t = 0时刻a 环刚从0点进入磁场区域,贝U 下列说法正确 的是()A •在t = 2v 时刻,回路中的感应电动势为 Bdv3LB •在t = 4V 时刻,回路中的感应电动势为 2BdvC •在t = 4v 时刻,回路中的感应电流第一次改变方向D.在t = 2v 时刻,回路中的感应电流第一次改变方向答案:D 二、多项选择题6.—环形线圈放在匀强磁场中,设第1 s 内磁感线垂直线圈平面向里,如图甲所示•若磁感应强度 B 随时间t 变化的关系如图乙所示,那么下列选项正确的是于弯曲导线所在平面的匀强磁场,磁场区域的宽度为3L~4, 现在外力作用下导线沿杆解析:c 2v 时刻,回路中切割磁感线的有效长度为0,感应电动势为0,选项A 错误;t 3L二4V 时刻,回路中切割磁感线的有效长度为d ,感应电动势为Bdv ,选项B错误;t二时刻, 回路中感应电流第一次开始改变方向,选项C 错误,D 正确.5.A. 第1 s内线圈中感应电流的大小逐渐增加B. 第2 s内线圈中感应电流的大小恒定C. 第3 s内线圈中感应电流的方向为顺时针方向D. 第4 s内线圈中感应电流的方向为逆时针方向解析:由题图分析可知,磁场在每1s内都均匀变化,B-1图象斜率恒定,线圈中产生的感应电流大小恒定,因此A错误,B正确;由楞次定律可判断出第3s、第4 s 内线圈中感应电流方向为逆时针方向,C错误,D正确.答案:BD某学习小组在探究线圈中感应电流的影响因素时,设计了如图所示的实验装置,让一个闭合圆线圈放在匀强磁场中,线圈的轴线与磁场方向的夹角为B,磁感应强度随时间均匀变化,则()A. 若把线圈的匝数增加一倍,线圈内感应电流大小不变B. 若把线圈的面积增加一倍,线圈内感应电流大小变为原来的2倍C. 改变线圈轴线与磁场方向的夹角大小,线圈内感应电流大小可能变为原来的2倍D. 把线圈的半径增加一倍,线圈内感应电流大小变为原来的2倍解析:由法拉第电磁感应定律E=门罟可知,若线圈的匝数增加一倍,感应电动势与线圈的总电阻都增加一倍,线圈内的感应电流大小不变,A正确;若线圈的面积增加一倍,感应电动势增加一倍,但线圈的电阻增大,线圈内的感应电流并不AB是原来的2倍,B错误;E= n—Scos 9,故无论怎样改变线圈轴线与磁场方向的夹At角,都不可能使线圈内的感应电流是原来的2倍,C错误;若线圈的半径增加一倍,则面积是原来的4倍,电阻是原来的2倍,线圈内感应电流变为原来的2倍,D正确.答案:AD8.如图所示,两条平行竖直虚线之间存在匀强磁场,磁场方向垂直纸面向里,虚线间的距离为I.金属圆环的直径也为I.圆环从左边界进入磁场,以垂直于磁场边界的恒定速度v穿过磁场区域.则下列说法正确的是()A. 感应电流的大小先增大后减小再增大再减小B. 感应电流的方向先逆时针后顺时针C. 金属圆环受到的安培力先向左后向右1D. 进入磁场时感应电动势平均值E =彳冗Blv解析:在圆环进入磁场的过程中,通过圆环的磁通量逐渐增大,根据楞次定律可知感应电流的方向为逆时针方向,感应电动势E= Blv,有效长度先增大后减小,所以感应电流先增大后减小,同理可以判断穿出磁场时的情况,A、B两项正确;根据左手定则可以判断,进入磁场和穿出磁场时受到的安培力都向左,C项错误;进答案:AB如图所示,固定在匀强磁场中的水平导轨 ab 、cd 的间距L i = 0.5 m 金属棒ad 与导轨左端bc 的距离为L 2= 0.8 m ,整个闭合回路的电阻为 R = 0.2 Q,磁感应强 度为B o = 1 T 的匀强磁场竖直向下穿过整个回路.ad 杆通过滑轮和轻绳连接着一个匀地增大.求:(1) 金属棒上电流的方向.⑵感应电动势的大小.(3)物体刚好离开地面的时间(g 取10 m/s 2).解析:(1)由楞次定律可以判断,金属棒上的电流由 a 到d. (2) 由法拉第电磁感应定律得△① AE == ~ = 0.08 V.At At⑶ 物体刚好离开地面时,其受到的拉力 F = mg而拉力F 又等于棒所受的安培力,即 mg= F 安=BIL 1入磁场时感应电动势平均值 E =B-〉l△①4 vAt2 1-=:n Blv , D 项错误. 4质量为m= 0.04 kg 的物体,不计一切摩擦,现使磁场以AB At °2 T/s的变化率均三、非选择题其中 B = B 0+xt解得t = 5 s.答案:⑴由 a 到 d (2)0.08 V (3)5 s10.某同学设计一个发电测速装置,工作原理如图所示.一个半径为R = 0.1 m的圆形金属导轨固定在竖直平面上, 一根长为R 的金属棒OA A 端与导轨接触良好, RO 端固定在圆心处的转轴上.转轴的左端有一个半径为r = 3的圆盘,圆盘和金属棒能随转轴一起转动.圆盘上绕有不可伸长的细线,下端挂着一个质量为详0.5 kg的铝块.在金属导轨区域内存在垂直于导轨平面向右的匀强磁场,磁感应强度 0.5 T . a 点与导轨相连,b 点通过电刷与O 端相连•测量a 、b 两点间的电势差U可算得铝块速度.铝块由静止释放,下落 h = 0.3 m 时,测得U= 0.15 V .(细线与 圆盘间没有滑动,金属棒、导轨、导线及电刷的电阻均不计,重力加速度g 取10 m/s 2)(3) 求此下落过程中铝块机械能的损失.△①解析:⑵由电磁感应定律得U = 其中△①=1BF 2A9,贝U U= *B 3R 2B=(2)求此时铝块的速度大小;“正极”还是“负所以 v = 3BR T 2 m/s.答案:⑴正极 (2)2 m/s (3)0.5 J11.如图甲所示,光滑导轨宽 0.4 m , ab 为金属棒,均匀变化的磁场垂直穿过 轨道平面,磁场的变化情况如图乙所示,金属棒ab 的电阻为1 Q,导轨电阻不计.t =0时刻,ab 棒从导轨最左端,以v = 1 m/s 的速度向右匀速运动,求1 s 末回路中的感应电流及金属棒ab 受到的安培力.解析:①的变化有两个原因,一是B 的变化,二是面积S 的变化,显然这两个 因素都应当考虑在内,所以有AB又「二 2 T/s , At在 1 s 末,B = 2 T , S = lvt = 0.4 x 1 x 1 m 2 = 0.4 m 2A B所以 1 s 末,E =A^S + Blv = 1.6 V ,此时回路中的电流EI =尸 1.6 AR根据楞次定律与右手定则可判断出电流方向为逆时针方向金属棒ab 受到的安培力为 F = BIl = 2X 1.6 x 0.4 N = 1.28 N ,方向向左.答案:1.6 A 1.28 N ,方向向左 1 2(3) A E = mgh- qmv =0.5 J.△① At AAB S + Blv At 甲。
电磁感应电磁场(一)作业答案

第九章 电磁感应 电磁场〔一〕法拉第电磁感应:t d d i Φ-=ε,假设为N 匝,那么tN d d i Φ-=ε 感应电流:t R I d d i Φ-=。
感应电量:)(1d 21i 21φφ-==⎰Rt I q t t[A ]1.〔根底训练1〕半径为a 的圆线圈置于磁感强度为B 的均匀磁场中,线圈平面与磁场方向垂直,线圈电阻为R ,当把线圈转动使其法向与B 的夹角为α=60︒时,线圈中已通过的电量与线圈面积及转动时间的关系是:(A) 与线圈面积成正比,与时间无关. (B) 与线圈面积成正比,与时间成正比. (C) 与线圈面积成反比,与时间无关. (D) 与线圈面积成反比,与时间成正比. 【分析】2.〔自测提高7〕将一个通过电流I 的闭合回路置于均匀磁场中,回路所围的面积的法线方向与磁场的夹角为α,假设均匀磁场同通过此回路的磁通大小为αtan ΦI 量为φ,那么回路所受的力矩的【分析】αcos BS S B =⋅=Φ ,αsin BIS B p M m ,大小为⨯=,因此力矩大小为αtan ΦI 。
3.〔根底训练17〕如图12-22两个半径分别为R 和r 的同轴圆形线圈相距x ,且R >>r ,x >>R .假设大线圈通有电流I 而小线圈沿x 轴方向以速率v 运动,试求x =NR 时(N 为正数)小线圈回路中产生的感应电动势的大小. 解: 在轴线上的磁场动生电动势:⎰⎰⋅⨯=⋅=B AB Al B l Ed d i )(v ε1、〔根底训练15〕如图12-20所示,一段长度为l 的直导线MN ,水平放置在载电流为I 的竖直长导线旁与竖直导线共面,并从静止由图示位置自由下落,那么t 秒末导线两端的电势差=-N M U U ala Igt +-ln 20πμ 【分析】长直导线在周围空间产生的磁场的磁感应强度为xIB πμ20=,方向与电流方向成右手螺旋关系。
在金属杆MN 处B 的方向垂直纸面向内。
电磁感应与电磁场例题

ΦD DS ΦD t
D σ
ΦD t t S qt
I (t )
S
dq dΦD I I D —位移电流(电场变化等效为一种电流) dt dt
电位移通量的变化率等于传导电流强度
dΦD d D 一般情况位移电流 I D D dS dS S S t dt dt
r
例 电荷 +q 以速度 v 向O点运动。在O点处作一半径为 a 的圆, 圆面与速度方向垂直。 求 通过该圆面的位移电流和圆周上各点处的磁感应强度? 解 在任一时刻,穿过圆面的电位移通量
D D dS DS球冠
S
q q v 2π rh r (1 cos ) 2r 4π r 2 q x dΦD qa 2 (1 ) ID 3v 2 2 2 x a dt 2r
I
NI H 2π r
B
0 r NI
2π r
R2 R1 O
1 1 0 r N 2 I 2 wm BH 2 2 4π 2 r 2
取体积元
dV 2π rhdr
R2
h
2π rhdr
Wm wmdV
V
0 r N 2 I 2
8π r
2 2
N 2 I 2 h R2
方法二(用法拉第电磁感应定律): (补逆时针回路 OCDO)
dl N
dΦ d( BLh / 2) hL dB OC CD DO CD i 2 dt dt dt
例7 设一载流回路由两根平行的长直导线组成。 求 这一对导线单位长度的自感L
解 由题意,设电流回路 I
a
Φ
大学物理作业-电磁感应二解答

电磁感应的基本原理
法拉第电磁感应定律
总结词
法拉第电磁感应定律是电磁感应的基本原理之一,它指出当磁场发生变化时,会在导体 中产生电动势。
详细描述
法拉第通过实验发现,当磁场发生变化时,会在导体中产生电动势。这个定律对于理解 电磁感应现象和发电机的运作原理非常重要。
楞次定律
总结词
楞次定律指出,当磁场发生变化时,会在导体中产生电流,且电流的方向与磁 场变化的方向相反。
详细描述
楞次定律是电磁感应中另一个重要的原理。它解释了当磁场发生变化时,导体 中电流的方向是如何决定的。这个定律对于理解电动机和变压器的运作原理非 常重要。
电磁感应的应用
总结词
电磁感应在日常生活和工业生产中有着广泛的应用,如发电机、变压器、电动机 等。
详细描述
通过利用电磁感应的原理,我们可以制造出各种设备,如发电机可以将机械能转 化为电能,变压器可以改变电压的大小,电动机可以将电能转化为机械能等。这 些设备在我们的日常生活和工业生产中发挥着重要的作用。
1. 观察到当磁铁插入和拔出线圈时,电压表有读数,说 明产生了感应电动势。
3. 根据实验数据绘制了感应电动势与磁通量变化率的曲 线,验证了法拉第电磁感应定律。
实验结论和误差分析
实验结论
通过实验验证了法拉第电磁感应定律,即感应电动势的大 小与磁通量变化率成正比。这表明当磁场变化时,会在导 体回路中产生感应电动势。
感应电动势的大小与磁通量变化率成 正比。
电磁感应的重要性
发电
利用电磁感应原理,可以将 机械能转化为电能,为现代 电力工业提供了基础。
电机控制
通过电磁感应原理,可以控 制电机的旋转方向和转速, 实现各种自动化设备。
ch9电磁感应和电磁场习题及答案.docx

第9章电稳感应和电磁场习题及答案1. 通过某冋路的磁场与线圈平而垂立指向纸面内,磁通量按以下关系变化: O = (r 2+6z + 5)xl0_3W/?o 求t = 2s 吋,冋路中感应电动势的大小和方向。
d ①o解:^ = -—= -(2r + 6)xW 3 dt 当 t = 2s 时,6: = -0.0 IV由楞次定律知,感应电动势方向为逆吋针方向2. 长度为/的金属杆必以速率u 在导电轨道abed 上平行移动。
已知导轨处于均匀磁场鸟中,B 的方向与冋路的法线成60°角,如图所示,B 的大小为B = kt(k 为正常数)。
设t = 0时杆位于cd 处,求:任一时刻f 导线回路中感应电动势的大小和方向。
解:任意时刻通过通过冋路而积的磁通量为① == B/wcos60° =丄 klut 12导线回路中感应电动势为方向沿abeda 方向。
3. 如图所示,一•边长为a,总电阻为R 的止方形导体框固定于一空间非均匀磁场中,磁场方向 垂直于纸面向外,其大小沿兀方向变化,且B = k(l + x), k>0。
求:(1)穿过止方形线框的磁通量:(2)当P 随时间/按k ⑴=如(灯为止值常量)变化时,线框中感生电流的大小和方向。
解(1)通过正方形线框的磁通量为①二 -dS - J Badx = akf (1 + x)dx(2)当k=k o t 时,通过正方形线框的磁通量为①=u~ + — 6/)正方形线框中感应电动势的大小为正方形线框线框中电流大小为a? k 1I=~ = — (1+-6Z ),方向:顺时针方向 R R 24.如图所示,一矩形线圈与载有电流/ = /()coscw 长直导线共面。
设线圈的长为b,宽为a ;(=0吋,线圈的AD 边与长直导线重合;线圈以匀速度0垂直离开导线。
求任一吋刻线圈中的感应电动势的大小。
解:建立图示坐标系,长宜导线在右边产生的磁感应强度 大小为B 卫2mt 时刻通过线圈平血的磁通量为①訂0・d4广如皿=必In 出 几 」川2加 2龙 Dt=-kl vt“Job 1 vt +a = cos cot In --------------- 2/r vt任一时刻线圈屮的感应电动势为d ① r ci cos cot • t vt + a y= ------- = 0| ------------ ^cosmcotln ---------- ]dt 17i (vt + d)t vt5. 如图所示,在两平行载流的无限长直导线的平而内有一矩形线圈。
大学物理--电磁感应与电磁场

1 BL(L
2
2r )
●
O OB
二、感生电动势 涡旋电场
1、变化的磁场产生感生电动势
1
2
当回路 1中电流发生
ε 变化时,在回路 2中
G
出现感应电动势。
电磁感应
R
动生电动势 非静电力 洛仑兹力
感生电动势 非静电力 ?
关于电荷所受的力 电荷
运动电荷
库仑力 洛仑兹力
其他电荷激发的电场 磁场
变化的磁场中的电荷受到的力--既非洛仑兹力也非库仑力
l
E
dl
l
2
1
2
k R2 dl
l 2r
kr
2r
kR
kr
2
2
由楞次定律可知,电动势的方向为逆时针方向
例题、 在半径为R 的圆柱形空间中存在着均匀磁场 ,
B
的方向与柱的轴线平行,如右图所示,
有一长为 l 的金属棒放在磁场中,
B sin dl
a
BLsin
方向a-b
B
b dl
L
B
例题、如图所示,把一半径为R 的半圆形导线OP 置于 磁感强度为B的匀强磁场中,当导线OP 以匀速率v 向 右移动时,求:导线中感应电动势大小。哪一端电势
较高?
解:作辅助线OP,形成闭合回路。P
B 0I ×
B
d
(2xB)
dl
I
x dx
ቤተ መጻሕፍቲ ባይዱ
0I sin 900 dx cos1800 20xI dx
A
0.1m
第8章电磁感应与电磁场大作业解读PPT课件

R
v
r
R 2R
2 0 IR 2R 1R r d r0 2 I R 1ln 2
电动势的方向a到b
9
D
2电. 磁方感d 法应(定1律):总的感应电动势回路A 绕向
v
dt
x
BdS BdS BS
C
B(12xtg30o x) 3 Bx2
2
3
d
dt
3B0v2t2
20Ivlna a b b
5
3.
小圆环所在处的磁场可看作匀强的:
or
B
Bo
0 I
2a
a
B SB Sco s0Ir2co st
I
2 a
id10Ir2sint
dt R 2Ra
6
4.
B
A B
v B dl
A
Io
d
A
B
vBdl
ad v 0I0 dr
A
d 2 r
R
a
v
0 I0v ln a d
S
dD dt
r20
dE dt
r20E0 et / RC
RC
方向与场强相8 反
8. (1)变化的磁场一定伴随有电场:方程(2)
(2)磁力线是无头无尾的:方程(3)
(3)电荷总伴随有电场:方程(1)
三、计算题
1.
b
ab a v B dl
2R
R
0I
dr
R
2 r
I
a dl b
b'
L
a'b' a' E kdl0E kcos dx
o
a b
a'
面向新世纪课程教材大学物理大作业答案——电磁感应与电磁场答案
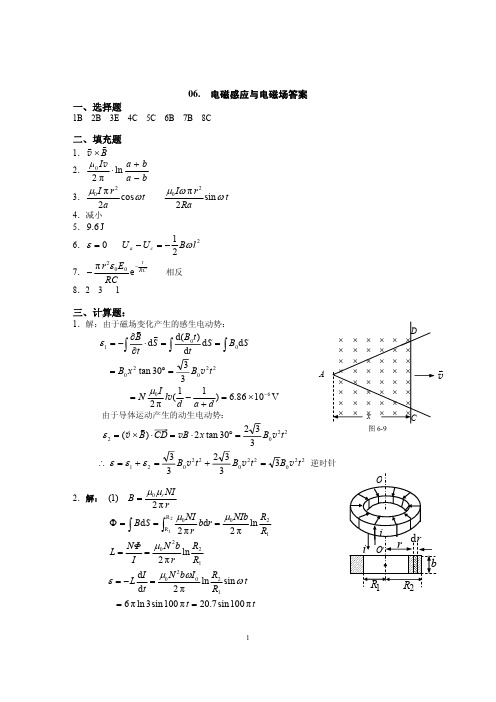
i
O′
r dr
b
R2
R1
1
3.解: (1) dΦ = B ⋅ dS = BLdx =
v
v
μ0 I
2π x b μ I IL μ b Φ = ∫ 0 Ldx = 0 ln a 2π x a 2π
Ldx
dx I L a b x
感应电动势为:
μ L b dI dΦ = − 0 ln ⋅ dt 2 π a dt dI Q I = I 0 e -4t = −4 I 0 e − 4 t dt 2 μ 0 LI 0 b −4 t ∴ εi = ln e a π ε i > 0 ,方向为顺时针 μ0 LI b ln Φ a = μ 0 L ln b (2) M = = 2π I I 2π a εi = −
2.解: (1)
图 6-9
B=
μ0 μ r NI
2πr
R2 R1
2
O
Φ = ∫ BdS = ∫
μ0 NI
2πr
bdr =
μ0 NIb
2π
ln
R2 R1
i
NΦ μ 0 N b R 2 L= = ln I 2πr R1
dI μ N 2 bωI 0 R2 ε = −L = 0 ln sin ω t R1 dt 2π = 6 π ln 3 sin 100 π t = 20.7 sin 100 π t
由于导体运动产生的动生电动势:
A
× × × × × × × ×
× × × × × × × ×
× × × × × × × × x
× × × × × × × ×
× × × × × × × ×
× × × × × × × ×
D
(完整word版)工科物理大作业09-电磁感应与电磁场

I图9-1图9-2图9-3(a)09 电磁感应与电磁场一、选择题(在下列各题中,均给出了4个~5个答案,其中有的只有1个是正确答案,有的则有几个是正确答案,请把正确答案的英文字母序号填在题后的括号内)1.如图9-1所示,在无限长载流直导线旁,放置一圆形导体线框,且线框平面与直导线共面。
则在下列情况下线框会产生感应电动势的是:A .线框与直导线相对静止;B .线框的速度v 沿纸面向上运动;C .直导线的电流t I Iωsin 0=,线框与直导线相对静止;D .线框绕过圆心O 且垂直纸面的轴以角速度ω 转动;E .线框以速度v 向右远离直导线运动。
(C 、E ) [知识点] 法拉第电磁感应定律,由磁通量m Φ变化判断。
[分析与解答] 判断线框在磁场中是否有感应电动势,只要看通过它的磁通量⎰⎰=⋅=ΦSSm S θB d cos d S B 是否发生变化即可,在A 、B 、D 所示线圈中没有感应电动势因为磁通量不变化;在C 所示线框中有感应电动势,因为直导线电流在变化,磁场B 在变化,则m Φ会发生变化;而在E 所示线框中也有感应电动势,因为离直导线越远,磁场越弱,m Φ减小;。
2.如图9-2所示,通过导体线圈的磁感线减少了,则线圈内感应电动势的方向为:A .顺时针;B .逆时针;C .0=iε; D .无法判断。
(B )[知识点] tεmi d d Φ-=的负号意义。
[分析与解答] 由楞次定理知,原来磁场方向向上并减弱,磁通量减少了,感应电流产生的磁场要阻碍向上的磁通量的减少,则会“减则同”,即其方向会与变化的磁场相同,则由右手螺旋法则知线圈内感应电动势的方向为逆时针。
3.如图9-3(a)所示,将一根导线弯折成半径为R 的3/4圆周abcde ,置于均匀磁场B 中,当导线沿aoe 的分角线方向以v 向右运动时,导线中产生的感应电动势i ε为:A .v BR 22; B .0;图9-4图9-3(b)C .v BR ;D .v BR 2。
大学物理课后习题答案 电磁感应 电磁场 (电磁场)

C
q U
q CU
dq du C 由于全电流连续得: dt dt du Id Ic C 20 10 6 1.5 10 5 3 A dt d0 dD s dDR 2 d 0 ER 2 dE 0R 2 11、 I d dt dt dt dt dt Ic
E
q 4 0 R 2
r
q 4 0 R 2
cost i sin t j
dD d q d q jd 0E cos t i sin t j sin t i cos t j 2 2 dt dt 4R dt 4R
12、充电过程中上极板带正电故 p 处电场强度 的方向向下,且电场强度增大,位移电流密度 的方向向下即位移电流向下,圆柱状向下的位移 电流在 p 处产生的 H 根据右手法则是垂直 纸 B 向里 。
i
P
H E
i d D 13、 j d 因为 E 增大 故 dD 0 , jd 的方向和 E 相同。即垂直纸面向里。 dt
n D ds q0 即q自 说明电荷总伴随有电场。
s i 1
9、当 A 板带正电, B 板带负电,当将开关 K 合上时, AB 极间的电场方向由正电荷指向负
dD 电荷即沿 x 的正方向。位移电流密度 jd 的方向即 的方向,因电容器放电, D 减少 dt
dD 0 dD 的方向和 D 的方向相反, 故沿 x 轴负方向或根据全电流连续的性质, 位移电流
第十三章 1、[D]
电磁感应 电磁场 (电磁场)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
IO图9-1BB图9-2a bcOvB e 09 电磁感应与电磁场一、选择题(在下列各题中,均给出了4个~5个答案,其中有的只有1个是正确答案,有的则有几个是正确答案,请把正确答案的英文字母序号填在题后的括号内)1.如图9-1所示,在无限长载流直导线旁,放置一圆形导体线框,且线框平面与直导线共面。
则在下列情况下线框会产生感应电动势的是:A .线框与直导线相对静止;B .线框的速度v 沿纸面向上运动;C .直导线的电流t I Iωsin 0=,线框与直导线相对静止;D .线框绕过圆心O 且垂直纸面的轴以角速度 转动;E .线框以速度v 向右远离直导线运动。
(C 、E ) [知识点] 法拉第电磁感应定律,由磁通量m Φ变化判断。
[分析与解答] 判断线框在磁场中是否有感应电动势,只要看通过它的磁通量⎰⎰=⋅=ΦSSm S θB d cos d S B 是否发生变化即可,在A 、B 、D 所示线圈中没有感应电动势因为磁通量不变化;在C 所示线框中有感应电动势,因为直导线电流在变化,磁场B 在变化,则m Φ会发生变化;而在E 所示线框中也有感应电动势,因为离直导线越远,磁场越弱,m Φ减小;。
2.如图9-2所示,通过导体线圈的磁感线减少了,则线圈内感应电动势的方向为:A .顺时针;B .逆时针;C .0=iε; D .无法判断。
(B )[知识点] tεmi d d Φ-=的负号意义。
[分析与解答] 由楞次定理知,原来磁场方向向上并减弱,磁通量减少了,感应电流产生的磁场要阻碍向上的磁通量的减少,则会“减则同”,即其方向会与变化的磁场相同,则由右手螺旋法则知线圈内感应电动势的方向为逆时针。
3.如图9-3(a)所示,将一根导线弯折成半径为R 的3/4圆周abcde ,置于均匀磁场B 中,当导线沿aoe 的分角线方向以v 向右运动时,导线中产生的感应电动势i ε为:A .v BR 22; B .0;图9-4图9-3(b)C .v BR ;D .v BR 2。
(D ) [知识点] 补偿法,动生电动势分析与计算.[分析与解答] 将圆弧导线abcde 的a 、e 端用一直导线连接,形成如图9-3(b)所示的闭合回路。
当回路整体以速度v 向右运动时,通过回路的磁通量不变,由法拉第电磁感应定律知,回路中电动势之和为零。
即 0=ε+ε=εea a bcde a bcdea 又由动生电动势公式()⎰⋅⨯=εl B v d i 分析可知直导线ea 电动势为()RvB vB ea 2ea d ae==⋅⨯=ε⎰l B v则从上分析可知,导线abcde 中的电动势与直导线ea 电动势大小必相等,即圆弧形导线abcde 上的电动势为RvB ea a bcde 2-=ε-=ε,负号表示其方向相反4. 如图9-4所示,M 、N 为水平面内的两根平行金属导轨,ab 与cd 为垂直于导轨并可在其上自由滑动的两根直导线,外磁场B 垂直于水平面且向上,当外力使ab 向右平移时,则cd 的运动情况为:A .不动;B .转动;C .向左移动;D .向右移动。
( D )[知识点] 动生电动势与安培力。
[分析与解答] 由于直导线ab 处于均匀磁场B 中,且速度、磁场与杆的方向三者垂直,有电动势ab Bv i =ε,电动势的方向就是B v ⨯的方向,则当ab 向右平移时,会在abcda 闭合回路中形成方向为b →a →d →c 顺时针的感应电流;又由安培定律B l F ⨯=d d I 知,直导线cd 会受到向右的安培力的作用,直导线将会向右移动。
5.如图9-5所示,一导体棒ab ,长为L ,处于均匀磁场B 中,绕通过c 点垂直于棒的O O '轴在水平面内转动,已知L ac 32=。
则导体棒中感应电动势和a 、b 两端点的电势大小关系为: A .261BL abωε=,b a U U >; B .261BL ab ωε=,b a U U <; C .0=abε,b a U U =;D .0=abε,有时b a U U >,有时b a U U <。
(A )图9-6(a)图9-5图9-6(b)[知识点] 动生电动势判断与计算。
[分析与解答] 以c 点为原点,建立如图所示坐标,在导体棒上任选一线元x d ,其上的动生电动势为 ()x B x d d d ω=⋅⨯=εl B v 整个导体棒上的电动势为 061d 23132<ω-=ω=ε⎰-BL x Bx L L 即感应电动势的方向为b →a ,则a 点电动势高于b 点,即b a U U >。
6.如图9-6(a)所示,在圆柱形区域内分布着均匀磁场B ,且tBd d 为正的恒量,现将ao 、ob 、ab 、b a和cd 5段导线置于图示位置,则下列说法正确的是:A .由于a 、b 两点电势确定,所以ab 和aob 上感生电动势相同,即aob ab εε=;B .cd 导线处于0=B 的空间,故cd ε=0;C .在该区域内,变化磁场激发的涡旋电场强度r E k ∝,故ab ba εε> ,0>>ao ab εε; D .oa 、ob 均垂直于E k ,故0==ob oa εε。
(D )[知识点] 感生电动势的概念、分析。
[分析与解答] 在如图9-6(b)所示的变化磁场中,在空间产生感生电场,感生电场线的分布是以o 为圆心的一系列同心圆,各点的感生电场k E 方向沿着圆周的切线方向。
由于oa 和ob 与感生电场的方向正交,由电动势定义⎰⋅=εlEd k知,00=a ε,0=ob ε,则0=aob ε;而ab 导线处在感生电场中,且感生电场沿ab 的分量不为零,则0≠εab ,且方向由a 指向b ,即0>εab 。
cd 导线虽处在磁场以外,但该空间仍有感生电场分布,且感生电场沿cd 的分量不为零,则0≠εcd 。
经计算知,圆柱形区域内涡旋电场强度为rBr E k d d 2=,即r E k ∝。
且有t B S a b d d 1=ε、tBS ba d d 2=ˆˆε,式中1S 为三角形的面积,2S 为扇形的面积,则ab b a εε>ˆˆ,但0=εao 。
7.在下列关于自感和位移电流的表述中,正确的是:A I 越大,L 越大;B .自感是对线圈而言的,对直导线回路不存在自感问题;C .位移电流的本质是变化的电场;D .位移电流只在平板电容器中存在,但它能激发磁场;E .位移电流是电荷的定向运动产生的,也能激发磁场。
(C )[知识点] 自感系数L 和位移电流的概念。
[分析与解答] 线圈的自感系数L 是反映线圈电磁惯性大小的物理量,它只和线圈本身的形状、大小、匝数、磁介质分布有关,而与线圈是否载流无关。
当然线圈中有电流时,m Φ与I 成正比,故L 与I 无关。
从自感的定义式ILmΦ=可知,m Φ是穿过一个回路的磁通量,这个“回路”即可以指线圈回路,也可以指一般的载流回路。
因而,并不是线圈才有自感,非线圈回路也有自感,只是与前者相比自感小得多。
位移电流实质上是指“变化的电场”,因而,它可存在于真空、介质、导体中。
而且变化的电场(位移电流)是能激发磁场的。
8.激发涡旋电场的场源是:A .静止电荷;B .运动电荷;C .变化的磁场;D .电流。
(C ) [知识点] 感生电场的概念。
9.已知平板电容器的电容为C ,两板间的电势差U 随时间变化,则其间的位移电流为: A .dtdD; B .0; C .CU ; D .dtdUC 。
(D ) [知识点] 位移电流d I 的计算。
[分析与解答] 设平行板电容器的极板面积为S ,其间的电位移为 Sq D =σ= 当极板间的电势差随时间变化时,极板上的带电量也同样随时间变化,则其间的位移电流为图9-7⎰⋅=Φ=S D d t t I S D d d d d d tqS t D d d d d =⋅= 由U q C =关系可知 tUC t q d d d d = 则 tUCI d d d =10.平板电容器在充电过程中,忽略边缘效应,作如图9-7所示的环路L 1和L 2,则沿两个环路的磁场强度H 的环流必有:A .⎰⎰⋅>⋅21d d L L l H l H ;B .⎰⎰⋅=⋅21d d L L l H l H ;C .⎰⎰⋅<⋅21d d L L l H l H ;D .0d 1=⋅⎰L l H ,0d 2≠⋅⎰L l H 。
(C )[知识点] 全电流安培环路定律。
[分析与解答] 根据全电流连续,平行板电容间的全部位移电流等于穿过2L 的传导电流,因此,1L 回路中的位移电流小于2L 中的传导电流,则由H 的环路定理知⎰⎰⋅<⋅21d d L L l H l H且 传I L =⋅⎰2d l H二、填空题1.法拉第电磁感应定律的表达式为 dtd mi Φ-=ε ,此式表明:感应电动势i ε的大小等于磁通量随时间的变化率 ;负号表示i ε的方向(指向)是 阻碍磁通量的变化 的方向。
已知垂直通过一平面线圈的磁通量随时间变化的规律为m Φ=1762++t t (SI ),则t 时刻线圈中的感应电动势的大小为=i ε 712+t V ,它表明i ε是随时间t 变化的。
[知识点] 法拉第电磁感应定律的意义。
[分析与解答] 1762++=Φt t m感应电动势的大小 ()V 712d d +=Φ=t tmi εN Svacb图9-8(a)ωILDab图9-9(a)N Svacb图9-8(b)ωLD I vd r Orab图9-9(b)2. 如图9-8(a)所示,一条形磁铁插入线圈,根据楞次定律可知,线圈中感应电流i 的流向是由c 点指向 a 点。
[知识点] 楞次定理的应用。
[分析与解答] 由图9-8(b)知,原来磁场方向向上并在增加,由楞次定理知,磁通量增加了,则感应电流的磁场要阻碍向上的磁通量的增加,会“增则反”,即其方向会与变化后的磁场相反,则由右手螺旋法则知,线圈内感应电流的流向为顺时针方向即(即c →a )。
3.产生动生电动势的非静电力是 洛伦兹力 ,其相应的非静电性电场强度=kE B ⨯v ;动生电动势的方向(指向)就是 B ⨯v 的方向。
产生感生电动势的非静电力是 感生电场力 。
[知识点] 动生电动势和感生电动势的概念。
4.如图9-9(a)所示,长为L 的导体杆ab 与通有电流I 的长直载流导线共面,ab 杆可绕通过a 点,垂直于纸面的轴以角速度 转动,当ab 杆转到与直导线垂直的位置时,杆中的动生电动势为=ab ε)ln (20DLD D L I +-ωπμ,a 端的电势较b 端的电势要 低 。
[知识点] 导体杆在非均匀场中转动时的动ε计算。
