二次函数与角度问题

https://www.360docs.net/doc/7014845434.html,/forum.php?mod=viewthread&tid=2737247

（2009益阳）如图11，△ABC中，已知∠BAC＝45°，AD⊥BC于D，BD＝2，DC＝3，求AD的长.

小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题.

请按照小萍的思路，探究并解答下列问题：

(1)分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，证明四边形AEGF是正方形；

(2)设AD=x，利用勾股定理，建立关于x的方程模型，求出x的值.

A

图11

(1)证明：由题意可得：△ABD≌△ABE，△ACD≌△ACF

∴∠DAB＝∠EAB，∠DAC＝∠FAC，又∠BAC＝45°，

∴∠EAF＝90°

又∵AD⊥BC

∴∠E＝∠ADB＝90°∠F＝∠ADC＝90°

又∵AE＝AD，AF＝AD

∴AE＝AF

∴四边形AEGF是正方形

(2)解：设AD＝x，则AE＝EG＝GF＝x

∵BD＝2，DC＝3

∴BE＝2 ，CF＝3

∴BG＝x－2，CG＝x－3

在Rt△BGC中，BG2＋CG2＝BC2

∴( x－2)2＋(x－3)2＝52

化简得，x2－5x－6＝0

解得x1＝6，x2＝－1（舍）

所以AD＝x＝6

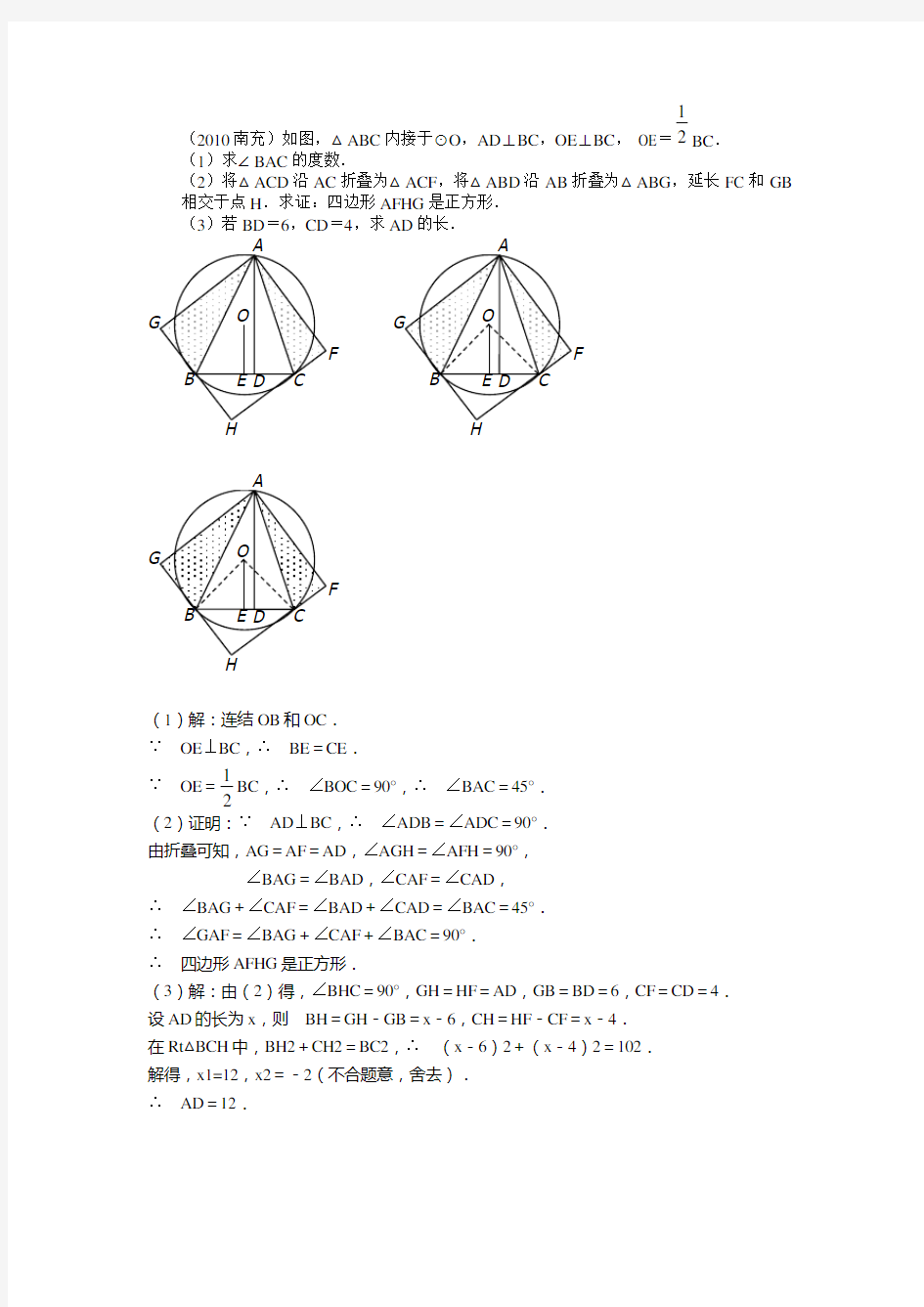
（2010南充）如图，△ABC 内接于⊙O ，AD ⊥BC ，OE ⊥BC ， OE ＝1

2BC ．

（1）求∠BAC 的度数． （2）将△ACD 沿AC 折叠为△ACF ，将△ABD 沿AB 折叠为△ABG ，延长FC 和GB 相交于点H ．求证：四边形AFHG 是正方形． （3）若BD ＝6，CD ＝4，求AD 的长．

（1）解：连结OB 和OC ． ∵ OE ⊥BC ，∴ BE ＝CE ． ∵ OE ＝

1

2

BC ，∴ ∠BOC ＝90°，∴ ∠BAC ＝45°． （2）证明：∵ AD ⊥BC ，∴ ∠ADB ＝∠ADC ＝90°． 由折叠可知，AG ＝AF ＝AD ，∠AGH ＝∠AFH ＝90°， ∠BAG ＝∠BAD ，∠CAF ＝∠CAD ， ∴ ∠BAG ＋∠CAF ＝∠BAD ＋∠CAD ＝∠BAC ＝45°． ∴ ∠GAF ＝∠BAG ＋∠CAF ＋∠BAC ＝90°． ∴ 四边形AFHG 是正方形．

（3）解：由（2）得，∠BHC ＝90°，GH ＝HF ＝AD ，GB ＝BD ＝6，CF ＝CD ＝4． 设AD 的长为x ，则 BH ＝GH －GB ＝x －6，CH ＝HF －CF ＝x －4． 在Rt △BCH 中，BH2＋CH2＝BC2，∴ （x －6）2＋（x －4）2＝102． 解得，x1=12，x2＝－2（不合题意，舍去）． ∴ AD ＝12．

（2013?呼和浩特）在平面直角坐标系中，已知点A（4，0）、B（﹣6，0），点C是y轴上的一个动点，当∠BCA=45°时，点C的坐标为（0，12）或（0，﹣12）．

注意点C有两个．

解：设线段BA的中点为E，

∵点A（4，0）、B（﹣6，0），∴AB=10，E（﹣1，0）．

（1）如答图1所示，过点E在第二象限作EP⊥BA，且EP=AB=5，则易知△PBA为

等腰直角三角形，∠BPA=90°，PA=PB=；

以点P为圆心，PA（或PB）长为半径作⊙P，与y轴的正半轴交于点C，

∵∠BCA为⊙P的圆周角，

∴∠BCA=∠BPA=45°，即则点C即为所求．

过点P作PF⊥y轴于点F，则OF=PE=5，PF=1，

在Rt△PFC中，PF=1，PC=，由勾股定理得：CF==7，

∴OC=OF+CF=5+7=12，

∴点C坐标为（0，12）；

（2）如答图2所示，在第3象限可以参照（1）作同样操作，同理求得y轴负半轴上的点C坐标为（0，﹣12）．

综上所述，点C坐标为（0，12）或（0，﹣12）．

故答案为：（0，12）或（0，﹣12）．

（2008北京）在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于

A B ，两点（点A 在点B 的左侧），与y 轴交于点C ，点B 的坐标为(30)，，将

直线y kx =沿y 轴向上平移3个单位长度后恰好经过B C ，两点． （1）求直线BC 及抛物线的解析式；

（2）设抛物线的顶点为D ，点P 在抛物线的对称轴上，且APD ACB ∠=∠，求点P 的坐标；

（3）连结CD ，求OCA ∠与OCD ∠两角和的度数． 解：（1） （2） 24．解：（1）

y kx =沿y 轴向上平移3个单位长度后经过y 轴上的点C ，

(03)C ∴，．

设直线BC 的解析式为3y kx =+．

(30)B ，在直线BC 上，

330k ∴+=．

1 O y

x

2 3 4

4

3 2 1

-1 -2 -2

-1

··

··，设抛物线对称轴与

2

AE=

··

两角和的度数为

x ∴∠+

OCA

即两角和的度数为

（2013?十堰）已知抛物线y=x2﹣2x+c与x轴交于A．B两点，与y轴交于C点，抛物线的顶点为D点，点A的坐标为（﹣1，0）．

（1）求D点的坐标；

（2）如图1，连接AC，BD并延长交于点E，求∠E的度数；

（3）如图2，已知点P（﹣4，0），点Q在x轴下方的抛物线上，直线PQ交线段AC于点M，当∠PMA=∠E时，求点Q的坐标．

考

点：

二次函数综合题．

分析：（1）将点A的坐标代入到抛物线的解析式求得c值，然后配方后即可确定顶点D的坐标；

（2）连接CD、CB，过点D作DF⊥y轴于点F，首先求得点C的坐标，然后证得△DCB∽△AOC得到∠CBD=∠OCA，根据∠ACB=∠CBD+∠E=∠OCA+∠OCB，得到∠E=∠OCB=45°；

（3）设直线PQ交y轴于N点，交BD于H点，作DG⊥x轴于G点，增大

△DGB∽△PON后利用相似三角形的性质求得ON的长，从而求得点N的坐标，进而求得直线PQ的解析式，

设Q（m，n），根据点Q在y=x2﹣2x﹣3上，得到﹣m﹣2=m2﹣2m﹣3，求得m、n的值后即可求得点Q的坐标．

解答：解：（1）把x=﹣1，y=0代入y=x2﹣2x+c得：1+2+c=0 ∴c=﹣3

∴y=x2﹣2x﹣3=y=（x﹣1）2﹣4

∴顶点坐标为（1，﹣4）；

（2）如图1，连接CD、CB，过点D作DF⊥y轴于点F，由x2﹣2x﹣3=0得x=﹣1或x=3

∴B（3，0）

当x=0时，y=x2﹣2x﹣3=﹣3

∴C（0，﹣3）

∴OB=OC=3

∵∠BOC=90°，

∴∠OCB=45°，

BC=3

又∵DF=CF=1，∠CFD=90°，

∴∠FCD=45°，CD=，

∴∠BCD=180°﹣∠OCB﹣∠FCD=90°．

∴∠BCD=∠COA

又∵

∴△DCB∽△AOC，

∴∠CBD=∠OCA

又∵∠ACB=∠CBD+∠E=∠OCA+∠OCB

∴∠E=∠OCB=45°，

（3）如图2，设直线PQ交y轴于N点，交BD于H点，作DG⊥x轴于G点∵∠PMA=45°，

∴∠EMH=45°，

∴∠MHE=90°，

∴∠PHB=90°，

∴∠DBG+∠OPN=90°

又∴∠ONP+∠OPN=90°，

∴∠DBG=∠ONP

又∵∠DGB=∠PON=90°，

∴△DGB=∠PON=90°，

∴△DGB∽△PON

∴

即：=

∴ON=2，

∴N（0，﹣2）

设直线PQ的解析式为y=kx+b

则

解得：

∴y=﹣x﹣2

设Q（m，n）且n＜0，

∴n=﹣m﹣2

又∵Q（m，n）在y=x2﹣2x﹣3上，

∴n=m2﹣2m﹣3

∴﹣m﹣2=m2﹣2m﹣3

解得：m=2或m=﹣

∴n=﹣3或n=﹣

∴点Q的坐标为（2，﹣3）或（﹣，﹣）．

（2014?威海）如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点．

（1）求这条抛物线的解析式；

（2）E为抛物线上一动点，是否存在点E使以A、B、E为顶点的三角形与△COB 相似？若存在，试求出点E的坐标；若不存在，请说明理由；

（3）若将直线BC平移，使其经过点A，且与抛物线相交于点D，连接BD，试求出∠BDA的度数．

考点：二次函数综合题

分析：（1）本题需先根据已知条件，过C点，设出该抛物线的解析式为y=ax2+bx+2，再根据过A，B两点，即可得出结果；

（2）由图象可知，以A、B为直角顶点的△ABE不存在，所以

△ABE只可能是以点E为直角顶点的三角形．由相似关系求出点E

的坐标；

（3）如图2，连结AC，作DE⊥x轴于点E，作BF⊥AD于点F，

由BC∥AD设BC的解析式为y=kx+b，设AD的解析式为

y=kx+n，由待定系数法求出一次函数的解析式，就可以求出D坐

标，由勾股定理就可以求出BD的值，由勾股定理的逆定理就可以

得出∠ACB=90°，由平行线的性质就可以得出∠CAD=90°，就可以

得出四边形ACBF是矩形，就可以得出BF的值，由勾股定理求出

DF的值，而得出DF=BF而得出结论．

解：（1）∵该抛物线过点C（0，2），

∴可设该抛物线的解析式为y=ax2+bx+2．

将A（﹣1，0），B（4，0）代入，

得，

解得，

∴抛物线的解析式为：y=﹣x2+x+2．

（2）存在．

由图象可知，以A、B为直角顶点的△ABE不存在，所以△ABE只可能是以点E为直角顶点的三角形．

[来源:学+科+网Z+X+X+K]

在Rt△BOC中，OC=2，OB=4，

∴BC==．

在Rt△BOC中，设BC边上的高为h，则×h=×2×4，

∴h=．

∵△BEA∽△COB，设E点坐标为（x，y），

∴=，∴y=±2

将y=2代入抛物线y=﹣x2+x+2，得x1=0，x2=3．

当y=﹣2时，不合题意舍去．

∴E点坐标为（0，2），（3，2）．

（3）如图2，连结AC，作DE⊥x轴于点E，作BF⊥AD于点F，

∴∠BED=∠BFD=∠AFB=90°．

设BC的解析式为y=kx+b，由图象，得

，

∴，

y BC=﹣x+2．

由BC∥AD，设AD的解析式为y=﹣x+n，由图象，得

0=﹣×（﹣1）+n

∴n=﹣，

y AD=﹣x﹣．

∴﹣x2+x+2=﹣x﹣，

解得：x1=﹣1，x2=5

∴D（﹣1，0）与A重合，舍去，D（5，﹣3）．∵DE⊥x轴，

∴DE=3，OE=5．

由勾股定理，得BD=．

∵A（﹣1，0），B（4，0），C（0，2），

∴OA=1，OB=4，OC=2．

∴AB=5

在Rt△AOC中，Rt△BOC中，由勾股定理，得AC=，BC=2，

∴AC2=5，BC2=20，AB2=25，

∴AC2+BC2=AB2

∴△ACB是直角三角形，

∴∠ACB=90°．

∵BC∥AD，

∴∠CAF+∠ACB=180°，

∴∠CAF=90°．

∴∠CAF=∠ACB=∠AFB=90°，

∴四边形ACBF是矩形，

∴AC=BF=，

在Rt△BFD中，由勾股定理，得DF=，

∴DF=BF，

∴∠ADB=45°．

（2009武汉）如图，抛物线24y ax bx a =+-经过()10A -，

、()04C ，两点，与x 轴交于另一点B ．

⑴求抛物线的解析式；

⑵已知点()1D m m +，

在第一象限的抛物线上，求点D 关于直线BC 对称的点的坐标； ⑶在⑵的条件下，连接BD ，点P 为抛物线上一点，且45DBP ∠=?，求点P 的坐标．

【答案】解：⑴∵抛物线24y ax bx a =+-经过()10A -，

，()04C ，两点， ∴40

44a b a a --=??

-=?

解得1

3

a b =-??

=? ∴抛物线的解析式为234y x x =-++．

⑵∵点

在抛物线上，∴2134m m m +=-++， 即2230m m --=，∴1m =-或3m =．

∵点D 在第一象限，∴点D 的坐标为()34，

． 由⑴知OC OB =，∴45CBA ∠=?．

设点D 关于直线BC 的对称点为点E ．

∵()04C ，

，∴CD AB ∥，且3CD =， ∴45ECB DCB ∠=∠=?，

∴E 点在y 轴上，且3CE CD ==．

∴1OE =，∴()01E ，

．

即点D 关于直线BC 对称的点的坐标为()01，

． ⑶方法一：作PF AB ⊥于F ，DE BC ⊥于E ． 由⑴有：4OB OC ==，∴45OBC ∠=?， ∵45DBP ∠=?，CBD PBA ∠=∠．

∵()04C ，

，()34D ，，∴CD OB ∥且3CD =． ∴45DCE CBO ∠=∠=?，

∴DE CE ==

∵4OB OC ==

，∴BC =

BE BC CE =-= ∴3

tan tan 5

DE PBF CBD BE ∠=∠=

=． 设3PF t =，则5BF t =，∴54OF t =-，

∴()543P t t -+，

． ∵P 点在抛物线上，

∴()()2

3543544t t t =--++-++， ∴0t =（舍去）或2225t =

，∴266525P ??- ???

，．

D BD PB 于点Q ，过点D 作DH x ⊥轴于

H ．过Q 点作

QG DH ⊥于G ． ∵45PBD ∠=?,∴QD DB =． ∴90QDG BDH ∠+∠=?，

又90DQG QDG ∠+∠=?，∴DQG BDH ∠=∠．

∴QDG DBH △≌△，∴4QG DH ==，1DG BH ==．

由⑵知()34D ，

，∴()13Q -，． ∵()40B ，

，∴直线BP 的解析式为31255

y x =-+．

解方程组23431255y x x y x ?=-++??=-+??得1140x y =??

=?，2

2

25

6625x y ?

=-????=

??

点P 的坐标为266525??

- ???

，．

（2013年河南省中考数学试卷）如图，抛物线2y x bx c =-++与直线1

22

y x =

+交于,C D 两点，其中点C 在y 轴上，点D 的坐标为732?

? ??

?，．点P 是y 轴右侧的抛物线上

一动点，过点P 作PE x ⊥轴于点E ，交CD 于点F . ⑴ 求抛物线的解析式；

⑵ 若点P 的横坐标为m ，当m 为何值时，以O ，C ，P ，F 为顶点的四边形是平行四边形？请说明理由．

⑶ 若存在点P ，使45PCF ∠=?，请直接写出相应的点P 的坐标．

【解答】⑴ ∵直线1

22y x =

+经过点C ， ∴()02C ，

． ∵抛物线2y x bx c =-++经过点(02)C ，，732D ?

? ??

?，，

∴2

27332c b c =???=-++??∴722

b c ?

=

???=?． ∴抛物线的解析式为2

722

y x x =-++

⑵ ∵点P 的横坐标为m 且在抛物线上

∴2

722P m m m ??-++ ???，，122F m m ??+ ???

，

∵PF CO ∥，

∴当PF CO =时，以O ，C ，P ，F 为顶点的四边形是平行四边形．

①当3m ＜时，22

7122322PF m m m m m ??=-++-+=-+ ???

∴232m m -+=，

解得：11m =，22m =．

即当1m =或2时，四边形OCPF 是平行四边形．

②当3m ≥时，22

1722322PF m m m m m ????=+--++=- ? ?????

232m m -=，

解得：1m =

，2m =（舍去）

即当1m =时，四边形OCFP 是平行四边形．

⑶ 如图，当点P 在CD 上方且45PCF ∠=?时， 作PM CD ⊥，CN PF ⊥，则

PMF CNF △∽△，

∴2

12

PM CN m

MF FN m === ∴2PM CM CF ==

∴5522

PF CN m ===== 又∵23PF m m =-+

∴2

532m m m -+=

解得：11

2

m =，20m =（舍去）

∴1722P ?? ???

，．

同理可以求得：另外一点为2313618P ?? ?

??，．