大学物理第三章动量与角动量教学总结
合集下载
第三章 动量与角动量

在光滑桌面上运动,速度分别为
v1
10i ,
v2
3.0i
5.0
j
(SI制)碰撞后合为一体,求碰撞后的速度?
解:方法一,根据动量守恒定律
m1v1 m2v2 (m1 m2 )v
解得:
v
7i
25
j
7
方法二,利用动量守恒分量式:
(m1 m2 )vx m1v1x m2v2x vx 7m / s
例 题 12
12、一子弹在枪筒里前进时所受的合力大小为 F 400 4105 t
3
(SI),子弹从枪口射出时的速率为300m/s。假设子弹离
开枪口时合力刚好为零,则
(1)子弹走完枪筒全长所用的时间;
(2)子弹在枪筒中所受力的冲量; (3)子弹的质量 m ;
解:(1)根据题意,子弹离开枪口时合力为零,
f mg
f t(N)
30N L L L 0 t 4 30 ft 70 10tL 4 t 7
0
Ft ft f
t(s) 47
当 t 4s 时 Ftt mv4 mv0 v4 8m / s
(2)当 t 6s 时
6
4 Ftdt mv6 mv4 v6 v4 8m / s
人造卫星的角动量守恒。
A1 : L1 mv1(R l1)
l2
l1 m
A2 : L2 mv2 (R l2 )
A2
A1
mv1(R l1) mv2 (R l2 )
v2 6.30km/s
v2
v1
R l1 R l2
o
B
第3章动量角动量

(3)动量守恒定律只适用于惯性系, 使用时所有速度必须相 对于同一惯性系。
(4)动量守恒定律是物理学中最普遍、最基本的定律之一。 在微观高速范围同样适用。
例3-3 如图,在光滑的水平面上,有一质量为M、长为l 的小车, 车上一端站有质量为m的人,起初m、M均静止,若人从车 的一端走到另一端,则人和车相对地面走过的距离为多少?
为ω,杆长均为l 。(2)如系统作加速转
动,系统的动量和角动量变化吗?
三、质点的角动量(动量矩)定理
Lrp
求
dL
导
d (r
p)
dr
p
r
dp
F
dt
dt
M
dL
dt
dt
dt
质点的角动量定理(微分形式)
质点所受合力对点O 的力矩, 等于质点对点O的角 动量的时间变化率。
M
dL
dt
改写
Mdt dL
t2 t1
F dt
p2
p1
(1)定理中的冲量指的是质点所受合力的冲量,或者质点所
受冲量的矢量和。
I
t2 t1
F合
dt
= =
t2 t1
(
F1+F2++Fn
)
d
t
t2 t1
F1dt
t2 t1
F2dt+
+
t2 t1
Fndt =
i 1
Ii
(2)冲量是过程量,动量是状态量,冲量的方向可用动量变化的
由动量定理 I p2 得 p1
(3) 2.7 m/s
(2)3s末质点的加速度
a(3) F (3) 1.5 m/s2 m
3.1.2 质点系的动量定理 动量守恒定律
(4)动量守恒定律是物理学中最普遍、最基本的定律之一。 在微观高速范围同样适用。
例3-3 如图,在光滑的水平面上,有一质量为M、长为l 的小车, 车上一端站有质量为m的人,起初m、M均静止,若人从车 的一端走到另一端,则人和车相对地面走过的距离为多少?
为ω,杆长均为l 。(2)如系统作加速转
动,系统的动量和角动量变化吗?
三、质点的角动量(动量矩)定理
Lrp
求
dL
导
d (r
p)
dr
p
r
dp
F
dt
dt
M
dL
dt
dt
dt
质点的角动量定理(微分形式)
质点所受合力对点O 的力矩, 等于质点对点O的角 动量的时间变化率。
M
dL
dt
改写
Mdt dL
t2 t1
F dt
p2
p1
(1)定理中的冲量指的是质点所受合力的冲量,或者质点所
受冲量的矢量和。
I
t2 t1
F合
dt
= =
t2 t1
(
F1+F2++Fn
)
d
t
t2 t1
F1dt
t2 t1
F2dt+
+
t2 t1
Fndt =
i 1
Ii
(2)冲量是过程量,动量是状态量,冲量的方向可用动量变化的
由动量定理 I p2 得 p1
(3) 2.7 m/s
(2)3s末质点的加速度
a(3) F (3) 1.5 m/s2 m
3.1.2 质点系的动量定理 动量守恒定律
大学物理第三章知识点

dt dt
t2 Mdt
t1
2 d(J) J
1
2 1
d
J2
J1
冲量矩
---角动量定理(积分式)
X. J. Feng
作用于刚体上冲量矩等于刚体角动量的增量
3.角动量守恒定律
t2
t1
Mdt
J2
J1
M 0时,J2 J1
若转动物体的合外力矩为零,则系统的角动量守恒
转动系统由两个或两个以上物体组成时:
X. J. Feng
M合 0时 Jii 常数
若系统的合外力矩为零,则系统的角动量守恒
讨论:1. J、ω均不变, J ω=常数 2. J、ω都改变, 但 J ω不变
注意: 1).运用角动量守恒时,系统中各物体均绕同一转轴转动
2).角动量定理、角动量守恒定律中各角速度或速度均需 相对同一惯性参照系。
花样滑冰运动员通过改变 身体姿态即改变转动惯量 来改变转速
ω
X. J. Feng
猫的下落
例: 杆( m,l ),可扰固定端O在竖直平面内自由转动, X. J. Feng
一子弹( m,v0 )射入杆的下端,求杆上摆的最大角度?
O 判断:
m,l
mv0 (m m)V
1 2
mv 0 2
刚体定轴转动定律: 功能关系:
M 合 J
刚体转动动能定理:
A
1 2
J2 2
1 2
J12
刚体重力势能: EP mghc
机械能守恒定律:
若W外+ W内非=0 则Ek +Ep =常量
X. J. Feng
t2 Mdt
t1
2 d(J) J
1
2 1
d
J2
J1
冲量矩
---角动量定理(积分式)
X. J. Feng
作用于刚体上冲量矩等于刚体角动量的增量
3.角动量守恒定律
t2
t1
Mdt
J2
J1
M 0时,J2 J1
若转动物体的合外力矩为零,则系统的角动量守恒
转动系统由两个或两个以上物体组成时:
X. J. Feng
M合 0时 Jii 常数
若系统的合外力矩为零,则系统的角动量守恒
讨论:1. J、ω均不变, J ω=常数 2. J、ω都改变, 但 J ω不变
注意: 1).运用角动量守恒时,系统中各物体均绕同一转轴转动
2).角动量定理、角动量守恒定律中各角速度或速度均需 相对同一惯性参照系。
花样滑冰运动员通过改变 身体姿态即改变转动惯量 来改变转速
ω
X. J. Feng
猫的下落
例: 杆( m,l ),可扰固定端O在竖直平面内自由转动, X. J. Feng
一子弹( m,v0 )射入杆的下端,求杆上摆的最大角度?
O 判断:
m,l
mv0 (m m)V
1 2
mv 0 2
刚体定轴转动定律: 功能关系:
M 合 J
刚体转动动能定理:
A
1 2
J2 2
1 2
J12
刚体重力势能: EP mghc
机械能守恒定律:
若W外+ W内非=0 则Ek +Ep =常量
X. J. Feng
第三章-动量-角动量

对于同一点的角动量对时间的变化率,这一结论称为质点的角
动量定理。
质点的角动量定理可以写为
Mdt dL
其中 Mdt 称为dt 时间内力矩 M对质点的冲量矩。两边
积分有:
t2 t1
Mdt
L2
L1
上式表明:作用于质点的合外力矩M 从 t1 到 t2 时间间隔 内的冲量矩,等于质点在同一时间间隔内角动量的增量。
力心
例4、一质点在x-y平面内运动,已知质点的质量为20 g,在A 、
B 两位置处的速率都是20 m/s ,vA与X轴成45 o角,vB垂 直于y轴。求质点由A点到B点这段时间内,作用在质点
上外力对O点的总冲量矩(已知OA=2m,OB=4m)。
解: 由质点的角动量定理知:
y vB B
由A到B,角动量的方向均垂 直于x-y平面向上
标量式为
(3-5)
对于冲量 I 应注意:
(1)冲量是力对时间的积累作用。
I
t2
Fdt
t1
mv1
mv
mv2
(2)冲量是矢量,其方向与动量增量方向相同。 即 I 的方向与 P 或 mv 的方向相同。
对动量原理应注意:
(1) F 是指物体所受的合外力,I 是合外力的冲量。 (2) 动量原理是矢量式,常用其分量式。 (3) 动量原理用于惯性系。
②已知炮弹对炮车的相对速度为v ,仰角
为时速θ ,度由v速’ 的度水叠平加分原量理为,炮弹对V地的瞬
v’ x = v cosθ – V
系统总动量为 m (v cosθ - V) – MV 系统总动量的水平分量守恒方程:
m (v cos θ - V) – MV = 0
代入数字 解得:
v v
大学物理第三章动量与角动量分解

mg=Mgx/L
所以
F总=F+mg=2Mgx/L+Mgx/L=3mg
19
例2:(page72)一辆装煤车以v=3m/s的速率从煤斗下通过,每
秒钟落入车厢的煤为Δ m=500kg.如果使车厢的速率保持不
变,应用多大的牵引力拉车厢?
v
dm m F
20
例3:质量为M的滑块正沿着光滑水平地面向右滑动.一质量 为m的小球水平向右飞行,以速度 v 1 (相对地面)与滑块斜 面相碰,碰后竖直向上弹起,速度为 v (相对地面).若碰撞
F 可分解为两个分量 F//
与水对船的垂直阻力相平衡 与船平行,并指向船前进的方 向 10
例4.一篮球质量m = 0.58kg,从h = 2.0m的高度下落,到达 地面后以同样速率反弹,接触地面时间 t 0.019 s 。 求:篮球对地面的平均冲力 F 球对地
解:篮球到达地面的速率为:
f f’
m1
m2
F2
碰撞后两质点的速度分别为
1和 2
相碰时的相互作用内力为 f 和f
同时受系统外其它物体的作用外力为 F1和F 2
d P1 对质点m1: F1 f dt d P2 对质点m2:F2 f dt
两式相加,得
13
f f
d P1 d P2 F1 F2 f f dt dt
p 2mv 篮球接触地面前后动量改变(大小)为:
由动量定理有: F 地对球 t p 2mv 由牛顿第三定律有: F 球对地 F 地对球
v 2 gh 2 9.80 2 6.26 m/s
2mv 2 0.58 6.26 t 0.019 3.82 10 2 N
大学物理第3章动量与角动量

力在时间上的积累效应:
平动 转动 冲量 冲量矩 动量的改变 角动量的改变
一、力的冲量
, 定义:力 f 作用时间为 t
则 f t 称为力
f
f
I
I f t
在 t 时间间隔内的冲量。 定义式:
I f t
I F t
1
量纲
pe
α
因为
pe p pN 0 2 2 1/ 2 pe 与 p 垂直: p N pe p
pN
θ
p
pe 1.2 10 23 所以: =arctg 61.9 6.4 10 23 p
= -61.9 118.1 180
A A
v
B
u
Mv mu (M m)v
Mv mu v M m m u v v M
mu v v v v M m
v dm u v 6 a lim u v t 0 t dt M M
i
常矢量 P=mv
P= mivi 常矢量
动量守恒定律:一个质点系所受的合外力为零时, 这个系统的总动量将保持不变.
在直角坐标系中的分量表示:
px miv ix C1
i
p y miv iy C2
i
pz miv iz C3
i
讨论
1.动量守恒定律是牛顿第三定律的必然推论。 2. 动量定理及动量守恒定律只适用于惯性系。质点 系内各质点的速度必须是相对同一惯性参照系而言。 3. 动量若在某一惯性系中守恒,则在其他 一切惯性系中 均守恒。 4. 若某个方向上合外力为零,则该方向上动量守恒,尽管 总动量可能并不守恒 5. 当外力<<内力且作用时间极短时(如碰撞) 可认为动量近似守恒。 6. 动量守恒定律比牛顿定律更普遍、更基本 , 在宏观和 微观领域均适用。
大学物理 动量与角动量解读

t2 t1
F外
dt
P2
P1
—质点系动量定 理(积分形式)
系统总动量由外力的冲量决定,与内力无关。
用质点系动量定理处理问题可避开内力。 8
§3.2动量守恒定律 (law of conservation of momentum)
质点系所受合外力为零时,质点系的总动量
不随时间改变。这就是质点系的动量守恒定律。
zC
mi zi m
质量为权重的平均值。 17
二.几种系统的质心
● 两质点系统
· · m1
C× m2
r1
r2
● 连续体
z
dm
r
×C
rc m
0
x
m1 r1 = m2 r2
rC
r dm
m
xC
xdm
……m
18
● 均匀杆、圆盘、圆环、球,质心为其几何中心。
● “小线度”物体的质心和重心是重合的。
[例]如图示,求挖掉小圆盘后系统的质心坐标。 解:由对称性分析,质心C应在x轴上。
2
3.1 冲量与动量定理
冲量:力和力作用时间的乘积 (单位:牛顿·秒 (N·s))
恒力 变力
在 dt 时间内的元冲量: dI Fdt
在 t1至 t2 时间段内的冲量:
(力对时间的积累效应)
动量:质点质量 m 和速度 的乘积
P mv
单位:千克·米·秒-1 (kg·m·s-1) 3
一、质点的动量定理
经整理得: Mdv = -udM
d v u d M M
f
Mf dM
d v u
i
M Mi
速度公式:
vf
vi
大学物理3_3 角动量 角动量守恒定律

将
R 、 h1 、h2 和 v1 各值代入,得
2 6.13公里/ 秒
3 – 3 角动量 角动量守恒定律 第三章 刚体的转动 例3-8 两个转动惯量分别为 J1 和 J2 的圆盘 A和 B. A 是机器上的飞轮, B 是用以改变飞轮转速的离合器 圆盘. 开始时, 他们分别以角速度ω 1 和ω 2 绕水平轴 转动. 然后,两圆盘在沿水平轴方向力的作用下.啮合 为一体, 其角速度为 ω, 求 齿轮啮合后两圆盘的角速度. 解: 系统角动量守恒
( L mR )
2
得
LdL m gR cosd
3 – 3 角动量 角动量守恒定律
第三章 刚体的转动
LdL m gR cosd
2 3
由题设条件积分上式
L
0
LdL m gR
2
32
3
0
cosd
12
L mR (2 g sin )
L mR
2
2g 12 ( sin ) R
3 – 3 角动量 角动量守恒定律
第三章 刚体的转动
力的时间累积效应 力矩的时间累积效应 角动量定理.
一
冲量、动量、动量定理. 冲量矩、角动量、
刚体定轴转动运动状态的描述 L J Ek J 2 2 0, p 0 0, p 0
质点的角动量定理和角动量守恒定律 质点运动状态的描述 p mv Ek mv 2 2
2
航天器调姿
1
3 – 3 角动量 角动量守恒定律 第三章 刚体的转动 例3-6 如图所示,有一质量为 m1 、长度为 l 的均质细 棒,原先静止地平放在水平桌面上,它可绕通过其端点O 且与桌面垂直的固定轴转动,另有一质量为 m2 的水平运动 的小滑块,从棒的侧面沿垂直于棒的方向与棒的另一端A 相碰撞,并被棒反向弹回,设碰撞时间极短。已知小滑块 碰撞前、后的速率分别为 和 u ,桌面与细棒的滑动摩 擦系数为 。求:(1)从碰撞到细棒停止运动所需的时 间;(2)从碰撞到细棒停止运动,细棒转过的圈数。
大学物理学习指导(第3章)

,'定轴转动时刚体的转动定律
^ 刚体紐定轴转动时,刚体的角加速度与它所受的合外力矩成正比,与刚体的转 动惯量成反比,这称为刚体的转动定律。 31
:
//?
叫
式 ^ 、 7、必须是对同一刚体、同一转轴而言。
8,角动量守恒定律
物体所受的合外力矩等于零,或者不受外力矩的作用,物体的角动量保持不 变。这个结论叫做角动量守恒定律。 I 二加^常矢量
一 转动惯量为/ ^ ^ ^ ^
、
12001^8 ^ 0 1 2 。 一 质 量 为 ^ : 801^8的人,开始时站在转台的中心, ^ 2111时,转台的角速度是多大?
^ 』:2
"; 2 ^ 。 第 页
山# 、理工大学备课紙
年
质量连续分布的刚体 】二 厂2(1^ ^ 厂2一3^
月
日
刚体的转动惯量是刚体作转动时惯性大小的量度。其大小决定于刚体转轴的 位置,刚体本身的形状,质量的大小及其质量分布情况。 6,刚体的角动量 刚体上各质点的角动量之和,即为刚体的角动量。一个刚体绕某一定轴转动, 其角动量为 :加
+ 爐 2 ―威2
由碎块和破盘组成的系统总角动量守恒。
】00 ―】产;十771^^^
^为破盘的角速度。
~ ^ 嫩 、 ^ (^]^!!^^
―
7 ^ ^ 十 卿 0 尺
^ = 0
^0
圆盘余下部分的角动量为
第
页
山系理工大学备课紙
年
I ^ (告魔2 一肌尺2》
月
日
一平面转台绕中心轴转动,每转一周所需时间为纟^ 108,转台对轴的
距轴为「处,取一小段^!厂,其质量01加: 9^^ ,这一小段(!"所受摩擦力矩 习题3-6图 整个杆所受摩擦力矩 1^1 ^2 「2 〃
3.2第三章-动量与角动量讲义

初 F2 + F1 + F n dt = P末 − P初
若
F i = 0 则有 P末 = P初
动量守恒
i
dL =M= rF
角动量守恒
dt
若 M = 0 则有 L = r mv =常数
例:一个力学系统由两个质点组成,他们之间只有引力 作用。若两质点所受外力的矢量和为零,则系统:
动量守恒? 机械能守恒?角动量守恒?
质点在有心力作用下运动,角动
量守恒。
L = pr = mvr = 常量
r F
五、质点系的角动量
质元 i :质量 mi
Fi mi ri • fi
外力Fi 内力 fi
o
L = Li = ri pi = ri mvi
rj
fj •
Fj
mj
i
i
i
由质点的角动量定理 r F = M = dL
dt
mv0 (l0 + ) = ml0v sin( − )
1 2
mv02
+
1 2
k2
=
1 2
mv2
则有
v=
v02
+
k m
2
= arcsin v0 (l0 + )
l0v
A外+A内 = Ek末- Ek初
A外+A非保内 = E末- E初
复习
若 A外+A非保内=0
则有 E末=E初 机械能守恒定律
( ) 末
( ) 末
初 F2 + F1 dt = P末 − P初
或 注意:
I
=
P末
−
P初
……质点系的动量定理
a、外力可改变系统的动量,也可改变某一个质点的动
若
F i = 0 则有 P末 = P初
动量守恒
i
dL =M= rF
角动量守恒
dt
若 M = 0 则有 L = r mv =常数
例:一个力学系统由两个质点组成,他们之间只有引力 作用。若两质点所受外力的矢量和为零,则系统:
动量守恒? 机械能守恒?角动量守恒?
质点在有心力作用下运动,角动
量守恒。
L = pr = mvr = 常量
r F
五、质点系的角动量
质元 i :质量 mi
Fi mi ri • fi
外力Fi 内力 fi
o
L = Li = ri pi = ri mvi
rj
fj •
Fj
mj
i
i
i
由质点的角动量定理 r F = M = dL
dt
mv0 (l0 + ) = ml0v sin( − )
1 2
mv02
+
1 2
k2
=
1 2
mv2
则有
v=
v02
+
k m
2
= arcsin v0 (l0 + )
l0v
A外+A内 = Ek末- Ek初
A外+A非保内 = E末- E初
复习
若 A外+A非保内=0
则有 E末=E初 机械能守恒定律
( ) 末
( ) 末
初 F2 + F1 dt = P末 − P初
或 注意:
I
=
P末
−
P初
……质点系的动量定理
a、外力可改变系统的动量,也可改变某一个质点的动
大学物理第3章动量与角动量

§3.2 动量守恒定律
动量守恒定律的分量形式:
若 若 若
F F F
x
0, px 0, p y 0, pz
y z
m v m v m v
i i i
i ix i iy
常量 常量 常量
i iz
动量守恒可以在单一方向上守恒。 动量守恒定律在惯性系中成立。 动量守恒定律是自然界的普遍规律,它不依赖于牛顿 定律而成立。
微观粒子的实验(如电子转化为光子)
§3.2 动量守恒定律
t2
F外dt P P0
t1
动量定理
dP 微分形式? F dt
可以写成
0 P 当F C 外
动量守恒定律
吗? F m a
注意后面 的讲解。
讨论
1.动量守恒定律是牛顿第三定律的必然推论。
m x m y m z x , y , z m m m
i i i i i i i i i C i C i C i i i i
z
C
质心的位置矢量表为
rC
m
i i
m i ri
i
x
O
r C
y
§3.4 质心
对连续质量的物体,质心位置可用积分式计算:
xdm ydm zdm x , y , z dm dm dm
C C C
rC
dm
r dm
质元dm视为质点
说明: 质心的位置由质点系各质点的相对位置决定,与 坐标原点的位置无关。 重力的着力点——重心,就在物体的质心上。
§3.4 质心
v
解:以M和dt时间里落到车厢 的煤粒dm为质点系。
动量守恒定律的分量形式:
若 若 若
F F F
x
0, px 0, p y 0, pz
y z
m v m v m v
i i i
i ix i iy
常量 常量 常量
i iz
动量守恒可以在单一方向上守恒。 动量守恒定律在惯性系中成立。 动量守恒定律是自然界的普遍规律,它不依赖于牛顿 定律而成立。
微观粒子的实验(如电子转化为光子)
§3.2 动量守恒定律
t2
F外dt P P0
t1
动量定理
dP 微分形式? F dt
可以写成
0 P 当F C 外
动量守恒定律
吗? F m a
注意后面 的讲解。
讨论
1.动量守恒定律是牛顿第三定律的必然推论。
m x m y m z x , y , z m m m
i i i i i i i i i C i C i C i i i i
z
C
质心的位置矢量表为
rC
m
i i
m i ri
i
x
O
r C
y
§3.4 质心
对连续质量的物体,质心位置可用积分式计算:
xdm ydm zdm x , y , z dm dm dm
C C C
rC
dm
r dm
质元dm视为质点
说明: 质心的位置由质点系各质点的相对位置决定,与 坐标原点的位置无关。 重力的着力点——重心,就在物体的质心上。
§3.4 质心
v
解:以M和dt时间里落到车厢 的煤粒dm为质点系。
大学物理 第三章 动量守恒和角动量守恒

mv 2 y − mv1y = ∫
t2 t1 t2
t1 t2
I mv 2
Fx dt
Fy dt
mv 2 z − mv1z = ∫
冲量的任何分量等于 在它自己方向上的动 量分量的增量
t1
Fz dt
在力的整个作用时间内, 在力的整个作用时间内 , 平均力 的冲量等于变力的冲量: 的冲量等于变力的冲量:
F F F
∑ miv i − ∑ miv i 0 = ∑ ∫ t i i i
t
Fi dt
0
注意
内力不改变质点系的动量
两人二人相推.swf相推
初始速度 推开后速度
v g 0 = v b0 = 0
m b = 2m g
p0 = 0
= 0
且方向相反, v g = 2 v b 且方向相反,也有 p
推开前后系统动量不变
•
2) 弹性碰撞 动量守恒: 动量守恒: 动能守恒: 动能守恒: v10 v20 v1 v2
3) 完全非弹性碰撞 动量守恒: 动量守恒: 机械能损失: 机械能损失: v10 v20 v
4) 非弹性碰撞: 非弹性碰撞: 动量守恒: 动量守恒: 碰撞定律: 碰撞后两球的分离速度(v 碰撞定律: 碰撞后两球的分离速度 -v )与碰撞前两球的接近速度 -v ) 与碰撞前两球的接近速度(v 2 1 与碰撞前两球的接近速度 10 20 成正比。 等大球碰撞.avi; 成正比。比值由两球的质料决定:等大球碰撞 ;大球碰小球
t
∆t
I =∫
t2 t1
Fdt = F (t2 − t1 )
O
1
t
2
t
例1:一篮球质量0.58kg,从2.0m高度下落,到达地面后,以同 样速率反弹,接触时间仅0.019s,求:对地平均冲力?
t2 t1 t2
t1 t2
I mv 2
Fx dt
Fy dt
mv 2 z − mv1z = ∫
冲量的任何分量等于 在它自己方向上的动 量分量的增量
t1
Fz dt
在力的整个作用时间内, 在力的整个作用时间内 , 平均力 的冲量等于变力的冲量: 的冲量等于变力的冲量:
F F F
∑ miv i − ∑ miv i 0 = ∑ ∫ t i i i
t
Fi dt
0
注意
内力不改变质点系的动量
两人二人相推.swf相推
初始速度 推开后速度
v g 0 = v b0 = 0
m b = 2m g
p0 = 0
= 0
且方向相反, v g = 2 v b 且方向相反,也有 p
推开前后系统动量不变
•
2) 弹性碰撞 动量守恒: 动量守恒: 动能守恒: 动能守恒: v10 v20 v1 v2
3) 完全非弹性碰撞 动量守恒: 动量守恒: 机械能损失: 机械能损失: v10 v20 v
4) 非弹性碰撞: 非弹性碰撞: 动量守恒: 动量守恒: 碰撞定律: 碰撞后两球的分离速度(v 碰撞定律: 碰撞后两球的分离速度 -v )与碰撞前两球的接近速度 -v ) 与碰撞前两球的接近速度(v 2 1 与碰撞前两球的接近速度 10 20 成正比。 等大球碰撞.avi; 成正比。比值由两球的质料决定:等大球碰撞 ;大球碰小球
t
∆t
I =∫
t2 t1
Fdt = F (t2 − t1 )
O
1
t
2
t
例1:一篮球质量0.58kg,从2.0m高度下落,到达地面后,以同 样速率反弹,接触时间仅0.019s,求:对地平均冲力?
大学物理第3章第2节-角动量定理及其守恒定律
用角动量定理和守恒定律处理问题 (i) 确定研究对象 (单一刚体、刚体系、刚 体+质点); (ii) 确定是对点还是对轴; (iii) 受力分析 (外力) 并求各力的力矩; (iv) 求初、末状态的角动量; (v) 用角动量定理和角动量守恒定律 (对 点或对轴) 列方程求解.
例3.9 一半径为 R 、质量为 m 的匀质圆 R 盘平放在粗糙的水平面 上. 设盘与桌面的摩擦因 数为 , 令圆盘最初以角 速度0 绕过其中心且垂直于盘面的轴旋转, 问它经过多少时间才停止转动? 解 圆盘与桌面间有摩擦, 在转动过程 中受到摩擦力矩的作用, 对圆盘上半径为 r 宽度为 d r 的圆环, 受到的阻力矩为
解 受力分析 N N 人: m M 重力 mg R 支持力 N1 mg 转台: 重力 Mg 支持力 N 2 Mg 合外力为零, 不产生力矩, 角动量守恒.
2 1
设转台沿逆时 M 针转动, 对地的角速 度为 , 人沿顺时针运 动, 人对转台的角速度为 , 则人对地的角速度为 . 转动惯量 2 I MR 2 转台: 2 I mR 人:
dM f rd f
f ( d m) g d r (d m) g m d S d r ( d S ) g
m
R
m r (2 rd r ) g 2 R
m R 2 , d S 2 rd r
m
R
角动量守恒
I I ( ) 0
M
R
m
MR mR2 ( ) 0 2
2
解得
2m M , M 2m M 2m
当人在转台上跑一周时
大学物理 第三章 角动量守恒定律 刚体汇总

求它由此下摆 角时的角加速度和角速度。
解:棒下摆为加速过程,外
力矩为重力对O的力矩。在 O
棒上取质元dm,当棒处在下
摆 角时,棒 的重力矩为:
M l d(mg)
l
设 m
L
L
gl sin(
)dl
1
mgL cos
0
2
2
X dm
dmg
J 1 mL2
3
M
1 mgL cos
2
3g cos
J
1 mL2
整个刚体绕轴的角动量为所有质元角动量之和:
L Li ( miri2 )
i
i
令:J miri2 称为刚体对轴的转动惯量。
i
则刚体对轴的角动量为:L J
力对转轴的力矩
f 在转动平面内 Mz r f
Mz fr sin
Z
Mz
Or
d
P
f
转动平面
方向如图
例题P40:3-3
f 不在转动平面内,有时间可以补讲。
(2)通过棒的中点并与棒垂直的转轴的转动惯量。
解:(1) m
l
dm dx
x dx
x l
J x2dm l x2dx 1l3 1 ml2
0
33
例1、求质量为m、半径为R的均匀圆环的转动 惯量。轴与圆环平面垂直并通过圆心。
解: J R2dm R2 dm mR2
OR dm
例2、求质量为m、半径为R、厚为l 的均匀圆 盘的转动惯量。轴与盘平面垂直并通过盘心。
平行轴定理
若有任一轴与过质心的轴平行,相距
为d,刚体对其转动惯量为J,则有:
l
J=JC+md2。
z
刚体的质心: xc
解:棒下摆为加速过程,外
力矩为重力对O的力矩。在 O
棒上取质元dm,当棒处在下
摆 角时,棒 的重力矩为:
M l d(mg)
l
设 m
L
L
gl sin(
)dl
1
mgL cos
0
2
2
X dm
dmg
J 1 mL2
3
M
1 mgL cos
2
3g cos
J
1 mL2
整个刚体绕轴的角动量为所有质元角动量之和:
L Li ( miri2 )
i
i
令:J miri2 称为刚体对轴的转动惯量。
i
则刚体对轴的角动量为:L J
力对转轴的力矩
f 在转动平面内 Mz r f
Mz fr sin
Z
Mz
Or
d
P
f
转动平面
方向如图
例题P40:3-3
f 不在转动平面内,有时间可以补讲。
(2)通过棒的中点并与棒垂直的转轴的转动惯量。
解:(1) m
l
dm dx
x dx
x l
J x2dm l x2dx 1l3 1 ml2
0
33
例1、求质量为m、半径为R的均匀圆环的转动 惯量。轴与圆环平面垂直并通过圆心。
解: J R2dm R2 dm mR2
OR dm
例2、求质量为m、半径为R、厚为l 的均匀圆 盘的转动惯量。轴与盘平面垂直并通过盘心。
平行轴定理
若有任一轴与过质心的轴平行,相距
为d,刚体对其转动惯量为J,则有:
l
J=JC+md2。
z
刚体的质心: xc
大学物理_角动量_转动惯量汇总

df dm g 2 gr dr
df
dM r df 2 2 gr dr
R
r O
2 3 M 2 gr dr gR 3 0
R
dr
2
问题: 若圆盘以ω0 的初角速度转动,圆盘转多少圈静止? (解答需要转动情况下的动能定理)
刚体(rigid body) :在外力作用下,形状和大小都不 发生变化的物体。(或:任意两质点间距离保持不变 的特殊质点系)。 刚体的运动形式: 平动(translation)、 转动(rotation)。 平动: 刚体内任意两点间连线 的空间方向总保持不变
特点:各点位移、速度、 加速度均相同。 刚体平动 质点运动
M ij
O
M rF sin θ Fd
Mij M ji
力矩的计算:
M ji
d
ri
F ji iF
ij
rj
j
计算变力对某一转轴的力矩则应当采取分小段的 办法,将每一小段的力视为恒力,再按照恒力矩的计 算方法进行计算,最后求和。
计算对定轴的力矩时,可用正负号来反映力矩方向。
转动:刚体中所有点同时都绕同一直线做圆周运动。 转动又分定轴转动、非定轴转动(绕定点转动或绕瞬心 转动)。
刚体的平面运动:
例:曲柄连杆机构中连杆AB的运动。
A点作圆周运动,B
点作直线运动,因此,
AB 杆的运动既不是平动
也不是定轴转动,而是
平面运动。
刚体的一般运动: 质心的平动 质心 :刚体的质量分布的中心
二、质点的角动量定理 1、质点的角动量[旧称动量矩] (Angular Momentum) 在空间运动,某时刻相对原点 O 的位矢为 r,质点相对于原 点的角动量定义为
大学物理教程-动量与角动量

N i 1
pi
大学物理教程
●
m F ● i● i
●
Fi合
fij ●
●
f ji
●
fi
●
p●i
●
mj
●
2023/2/26
12
3.1
哈尔滨工业大学(威海)
动量 Harbin Institute of Technology at Weihai
大学物理教程
N N
Fi fij
i 1
i1 i j
N
d pi
动量 Harbin Institute of Technology at Weihai
大学物理教程
例1. 如图所示,汽锤质量为m=2t,由h=1m高处自由下
落,达到工件上后经Δt=10-4s速度为零,试求:
x
(1)打击过程汽锤所受合力的冲量;
(2)工件所受锤作用的平均冲力N。
h
解 (1)汽锤刚与工件接触时 v1x 2gh
哈尔滨工业大学(威海)
动量 Harbin Institute of Technology at Weihai
大学物理教程
➢ 说明:
I
t2 t1
F
dt
p2
p1
①分量式
I
x
t2 t1
Fxdt
p2 x
p1x
I
y
t2 t1
Fydt
p2 y
p1y
I
z
t2 t1
Fz dt
p2 z
p1z
② 合外力的冲量方向和质点的
解:炸裂时爆炸力是物体内力,它远大于重力,故在爆炸
前后,可认为动量守恒。
即: 0 m1v1 m 2v2 m 3v3
第三章动量与角动量

mg Mgx / L
F总 F mg 2Mgx / L Mgx / L 3mg
例3:传送带由马达牵引以 v = 2m/s 的速率水平匀速前进。漏 斗中的沙子以 40kg/s 的速率落料。漏斗口在传送带上方 h=0.5m处。求落料过程中落沙对传送带的作用力以及马达对传 送带的牵引力。 解:设落料过程中传送带对沙的作用 力为 F y ︱F ydt︱=︱0-dmVy︱
v M t时刻
(u)
x
v+dv
dm
)
M dm t+dt时刻
由动量守恒定律,有(t 时刻总动量 = t+dt 时刻总动量) Mv ( M dm)(v dv) dm(v u )
Mv Mdv udm dmdv
Mdv udm 0
Mdv udM 0(因 dm dM) dM dv u M
•对称物体的质心就是物体的对称中心。 •重心——地球对物体各部分引力的合力作用点,
•对于不太大的实物,质心与重心重合。
例:一段均匀铁丝弯成半径为R的半圆形,求此半圆形铁丝的 质心。 解:选如图坐标系,取长为dl的铁丝, 质量为dm,以λ 表示线密度,dm=dl. 分析得质心应在y轴上。
d
yc
ydl
例 4,水平地面上一静止的炮车发射炮弹,炮车 质量为 M ,炮身仰角 ,炮弹质量 m ,炮弹刚出 口时,相对炮身的速度为u,不计地面摩擦。 1) 求炮弹刚出口时,炮车的速度。
2) 若炮筒长为l (即在发炮过程中,炮弹相对炮的行 程)求发炮过程中炮车移动的距离。
解:( A )以炮弹,炮车为一系统, 地面为参照系(水平向右为坐标正向) 此系统在水平方向 受合外力为零,动 量守恒。
大学物理——第3章-角动量定理和刚体的转动
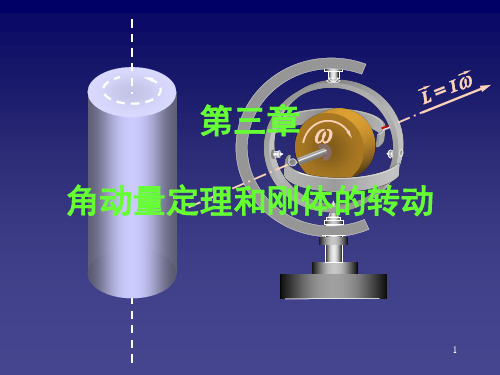
M
α
I
有何联系?
13
实验指出,定轴转动的刚体的角加速度 α与刚体所受的合外 力矩 M 成正比,与刚体的转动惯量 I 成反比.
v dω v M = Iα = I dt
v
定轴转动定理
v v F = ma
定轴转动定律在转动问题中的地 位相当于平动时的牛顿第二定律
应用转动定理解题步骤与牛顿第二定律时完全相同.
1 1 2 2 2 Eki = miυi = mi ri ω 2 2
质点质量 整个刚体的动能:
N
圆周运动的速率和半径
1 N 2 2 Ek = ∑Eki = (∑mi ri )ω 2 i=1 i=1
刚体对转轴的转动惯量:I
7
刚体定轴转动动能公式
物体的平动动能(质点动能)
1 2 Ek = Iω 2
角速度 ω 转动惯量 I 物体绕轴的转动惯性
λ :质量线密度 σ :质量面密度 ρ :质量体密度
10
I = ∫ r 2dm
单位: kg m2
转动惯量的大小取决于刚体的质量,质量分布及转轴的位置.
O
O l/2 O′
1 I= ml2 12
O
O O′
1 2 I = ml 3
r
O′
1 I = mr2 4
O′
1 I = mr2 2
11
平行轴
垂直轴
平行轴定理 质量为 m 的刚体,如果对其质心轴的转动惯量为 IC,则对任 一与该轴平行,相距为 d 的转轴的转动惯量:
2 θ 3Rω0 n= = 2π 16π g
26
讨论
用定轴转动的动能定理较之用转动定律求解, 省去了求角加速度,而直接求得,更为简捷.
动量角动量小结

四、质点系的角动量定理
• 对质点系中的任一质点应用质点的角动量定理:
dLi dL Mi M i内 + M i外 = i dt dt d M i内 + M i外=dt ( Li ) 质点系
m1 r1 r12 r2
f1
m2
f2
M i内=0 dL M 外= dt
(质点系角定理动量)
0 f1 r2 f 2 M i内 r1 f1 f 2 M i内 (r1 r2 ) f 2 r12 f 2 0
dp F合 dt
F合dt dp d (mv) 定义:冲量dI Fdt
p mv
I 合 P (质点的动量定理)
分量式
I x Fx dt px mv2 x mv 1x
t1
t2
意义:合力在某一方向上的冲量,等于该方向上动量 的增量。
平均冲力作用效果与实际冲力一样:
t2
t1
Fdt F (t2 t1 ) P
p F t
质点系动量定理
t2
t1
n n F外力i dt mi vi mi vi 0 i 1 i 1
I 外 p p0
作用于系统的外力的冲量和等于系统动量的增量.
动量守恒定律
由质点系动量定理
t I外
t0
F外i dt pi pi 0
i i i
若质点系所受的合外力为零 F外 F外i 0 i 则系统的总动量守恒,即 p pi=C 保持不变 .
分量表述 F外x 0 ,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
F风对帆 F横
F进
v1 v2 帆
风 v1
Δv v2 F帆对风 Δv
F阻
F横
龙骨
9
F帆对风
帆给风团的冲力为:
方向向斜后方
根据牛顿第三运动定律,风团对帆有一反作用力 F :
可分解为两个分量 F F//
与水对船的垂直阻力相平衡
与船平行,并指向船前进的方 向
10
例4.一篮球质量m = 0.58kg,从h = 2.0m的高度下落,到达
•动量表征了物体的运动状态.
•牛顿第二定律的另外一种表示方法
F
ma
m dv
d
(mv)
dP
dt dt
dt
4
3、质点的动量定理(theorem of momentum of
F
dP
a particle)
dt
质点动量定理的微分形式
dP Fdt
P2
dP
P1
t2 t1
Fdt
F
是否平衡.
α mg
刚好不下滑时:
mgsin f smg cos s tg
当一物体竖直坠入箱中,在冲力作用下,时的瞬间应满足:
s ( mg cos F cos ) ( mg sin F sin ) ma
代入 s tg 得 a=0
12
§3.2 质点系的动量定理
(theorem of mometum of a system of particles)
I
P2
P1
质点动量定理的积分形式
注: F为恒力时,可以得出I=F t
F作用时间很短时,可用力的平均值来代替。
物理意义:在给定的时间间隔内,外力作用在质点上
的冲量,等于该质点在此时间内动量的增量.
冲力
平均冲力
F
t2 t1
F dt
p
t2 t1 t
5
说明:
1.动量定理将始末时刻的动量与冲量联系起来,而忽略细节变化;
2.碰撞或冲击过程,牛顿第二定律无法直接使用,用动量定理解;
3.变质量物体的运动过程,用动量定理较方便;
4.动量定理说明质点动量的改变是由外力和外力作用时间两个因
素,即冲量决定的;
5.动量定理的分量式. I x Fxdt m v2x m v1x t
I y Fydt m v2 y m v1 y t
•冲量是矢量: 大小和方向;
•冲量是过程量, 改变物体机械运动状态的原因。 3
2、动量(momentum)
定义:物体的质量与速度的乘积叫做物体的动量
P
mv
•单位: kg·m·s-1
•量纲:MLT-1
说明:
•动量是矢量,大小为 mv,方向就是速度的方向;冲量的方向
不是与动量的方向相同,而是与动量增量的方向相同.
f
f
d P1 dt
d P2 dt
f f
d F1 F2 dt ( P1 P2 )
t2
( F1 F2 )dt d ( P1 P2 ) ( m11 m22 ) ( m110 m220 )
t1
t2 F1+F2 dt (m1v1 m2v2 ) (m1v10 m2v20 )
第三章 动量与角动量
(Momentum and Angular Momentum) 教学要求:
1)理解动量,冲量,角动量的概念及它们的矢量性. 2)掌握及应用动量定理,动量守恒定律以及质点的角动
量守恒定律来计算力学问题. 3)理解质心的概念,了解质心运动定理.
1
§3.1 冲量与动量定理
牛顿定律是瞬时的规律。——力在任意时刻的作用,是使 质点产生加速度,运动状态发生变化。 但在有些问题中,如:碰撞(宏观)、散射(微观)… 我们往往只关心力的作用按时间累积起来的总的效果, 即只关心始末态间的关系,对过程的细节不感兴趣。
2mv 2 0.58 6.26
t
0.019
3.82102 N
方向向上
11
例5.在斜面上放着一个盛有细沙的箱子,在摩擦力的作用 下箱子刚好不下滑.若有一物体m’从竖直方向坠入箱中,试 问在该物体的冲力作用下,箱子是否还能保持静止?
m’
已知μs
N
f
解:箱子是否下滑,决定于物体坠入
箱子时,在冲力的作用下箱子的受力
1、两个质点组成的系统
F1
已知:
f m1
f’ m2
碰撞前两质点的速度分别为 10和 20 碰撞后两质点的速度分别为 1和 2
F2
相碰时的相互作用内力为 f和f
同时受系统外其它物体的作用外力为 F1和F2
对质点m1: F1
f
d P1 dt
两式相加,得
对质点m2:F2
f
d P2 dt
13
F1
F2
地面后以同样速率反弹,接触地面时间 t 0.019s 。 求:篮球对地面的平均冲力 F 球对地
解:篮球到达地面的速率为:
v 2gh 2 9.80 2 6.26m/s
篮球接触地面前后动量改变(大小)为:p 2mv
由动量定理有: F 地对球 t p 2mv
由牛顿第三定律有:F 球对地 F 地对球
t1
意义:两个物体总动量的改变只决定于外力的冲量,
而与内力无关.
内力的冲量呢?只会使每一个物体的动量发生改变,
但对总动量没有任何影响.
14
2、多个质点组成的系统
共有N个粒子
pi
· i
······ Fi fij
fj i j
Fi
为质点
i
受的合外力,
fij为质点 i 受质点 j 的内力,
pi
为质点
i
t2
t1
F外
dt
P2
P1
的动量。
· 质点系
对质点
i
:
(Fi
fij)d ij)d t
d
pi
i
ji
i
由牛顿第三定律有: fij 0
i ji
15
所以有:
(
Fi)d
t
d
pi
令
i Fi
F外
,
i
pi
P
i
i
则有: 或
F外 d t d P
F外
dP dt
质点系动量定理 (微分形式)
力在时间上的积累效应:
平动 冲量,改变动量 转动 冲量矩,改变角动量
2
1、冲量(impulse)
定义:力对一段时间的积累
大小: I=
t2
Fdt
t1
F F
方向:速度变化的方向
单位:N·s
量纲:MLT-1
0
t
t1 dt
t2
微分形式: d I F d t d p
说明
•冲量是表征力持续作用一段时间的累积效应;
6.应用:
Iz Fzdt m v2z m v1z t
利用冲力:增大冲力,减小作用时间——冲床 避免冲力:减小冲力,增大作用时间——轮船靠岸时的缓冲6
应用举例: 例1.
例2.问题:人为什 么从高处跳到地面 时,要把腿弯一下?
7
例3. “船行八面风”---帆船靠风力推动前进,只要有风,不
管风从什么方向吹来,都可借助风力前进。
F风对帆 F横
F进
v1 v2 帆
风 v1
Δv v2 F帆对风 Δv
F阻
F横
龙骨
9
F帆对风
帆给风团的冲力为:
方向向斜后方
根据牛顿第三运动定律,风团对帆有一反作用力 F :
可分解为两个分量 F F//
与水对船的垂直阻力相平衡
与船平行,并指向船前进的方 向
10
例4.一篮球质量m = 0.58kg,从h = 2.0m的高度下落,到达
•动量表征了物体的运动状态.
•牛顿第二定律的另外一种表示方法
F
ma
m dv
d
(mv)
dP
dt dt
dt
4
3、质点的动量定理(theorem of momentum of
F
dP
a particle)
dt
质点动量定理的微分形式
dP Fdt
P2
dP
P1
t2 t1
Fdt
F
是否平衡.
α mg
刚好不下滑时:
mgsin f smg cos s tg
当一物体竖直坠入箱中,在冲力作用下,时的瞬间应满足:
s ( mg cos F cos ) ( mg sin F sin ) ma
代入 s tg 得 a=0
12
§3.2 质点系的动量定理
(theorem of mometum of a system of particles)
I
P2
P1
质点动量定理的积分形式
注: F为恒力时,可以得出I=F t
F作用时间很短时,可用力的平均值来代替。
物理意义:在给定的时间间隔内,外力作用在质点上
的冲量,等于该质点在此时间内动量的增量.
冲力
平均冲力
F
t2 t1
F dt
p
t2 t1 t
5
说明:
1.动量定理将始末时刻的动量与冲量联系起来,而忽略细节变化;
2.碰撞或冲击过程,牛顿第二定律无法直接使用,用动量定理解;
3.变质量物体的运动过程,用动量定理较方便;
4.动量定理说明质点动量的改变是由外力和外力作用时间两个因
素,即冲量决定的;
5.动量定理的分量式. I x Fxdt m v2x m v1x t
I y Fydt m v2 y m v1 y t
•冲量是矢量: 大小和方向;
•冲量是过程量, 改变物体机械运动状态的原因。 3
2、动量(momentum)
定义:物体的质量与速度的乘积叫做物体的动量
P
mv
•单位: kg·m·s-1
•量纲:MLT-1
说明:
•动量是矢量,大小为 mv,方向就是速度的方向;冲量的方向
不是与动量的方向相同,而是与动量增量的方向相同.
f
f
d P1 dt
d P2 dt
f f
d F1 F2 dt ( P1 P2 )
t2
( F1 F2 )dt d ( P1 P2 ) ( m11 m22 ) ( m110 m220 )
t1
t2 F1+F2 dt (m1v1 m2v2 ) (m1v10 m2v20 )
第三章 动量与角动量
(Momentum and Angular Momentum) 教学要求:
1)理解动量,冲量,角动量的概念及它们的矢量性. 2)掌握及应用动量定理,动量守恒定律以及质点的角动
量守恒定律来计算力学问题. 3)理解质心的概念,了解质心运动定理.
1
§3.1 冲量与动量定理
牛顿定律是瞬时的规律。——力在任意时刻的作用,是使 质点产生加速度,运动状态发生变化。 但在有些问题中,如:碰撞(宏观)、散射(微观)… 我们往往只关心力的作用按时间累积起来的总的效果, 即只关心始末态间的关系,对过程的细节不感兴趣。
2mv 2 0.58 6.26
t
0.019
3.82102 N
方向向上
11
例5.在斜面上放着一个盛有细沙的箱子,在摩擦力的作用 下箱子刚好不下滑.若有一物体m’从竖直方向坠入箱中,试 问在该物体的冲力作用下,箱子是否还能保持静止?
m’
已知μs
N
f
解:箱子是否下滑,决定于物体坠入
箱子时,在冲力的作用下箱子的受力
1、两个质点组成的系统
F1
已知:
f m1
f’ m2
碰撞前两质点的速度分别为 10和 20 碰撞后两质点的速度分别为 1和 2
F2
相碰时的相互作用内力为 f和f
同时受系统外其它物体的作用外力为 F1和F2
对质点m1: F1
f
d P1 dt
两式相加,得
对质点m2:F2
f
d P2 dt
13
F1
F2
地面后以同样速率反弹,接触地面时间 t 0.019s 。 求:篮球对地面的平均冲力 F 球对地
解:篮球到达地面的速率为:
v 2gh 2 9.80 2 6.26m/s
篮球接触地面前后动量改变(大小)为:p 2mv
由动量定理有: F 地对球 t p 2mv
由牛顿第三定律有:F 球对地 F 地对球
t1
意义:两个物体总动量的改变只决定于外力的冲量,
而与内力无关.
内力的冲量呢?只会使每一个物体的动量发生改变,
但对总动量没有任何影响.
14
2、多个质点组成的系统
共有N个粒子
pi
· i
······ Fi fij
fj i j
Fi
为质点
i
受的合外力,
fij为质点 i 受质点 j 的内力,
pi
为质点
i
t2
t1
F外
dt
P2
P1
的动量。
· 质点系
对质点
i
:
(Fi
fij)d ij)d t
d
pi
i
ji
i
由牛顿第三定律有: fij 0
i ji
15
所以有:
(
Fi)d
t
d
pi
令
i Fi
F外
,
i
pi
P
i
i
则有: 或
F外 d t d P
F外
dP dt
质点系动量定理 (微分形式)
力在时间上的积累效应:
平动 冲量,改变动量 转动 冲量矩,改变角动量
2
1、冲量(impulse)
定义:力对一段时间的积累
大小: I=
t2
Fdt
t1
F F
方向:速度变化的方向
单位:N·s
量纲:MLT-1
0
t
t1 dt
t2
微分形式: d I F d t d p
说明
•冲量是表征力持续作用一段时间的累积效应;
6.应用:
Iz Fzdt m v2z m v1z t
利用冲力:增大冲力,减小作用时间——冲床 避免冲力:减小冲力,增大作用时间——轮船靠岸时的缓冲6
应用举例: 例1.
例2.问题:人为什 么从高处跳到地面 时,要把腿弯一下?
7
例3. “船行八面风”---帆船靠风力推动前进,只要有风,不
管风从什么方向吹来,都可借助风力前进。
