专题04 椭圆知识点和常见题型(解析版)
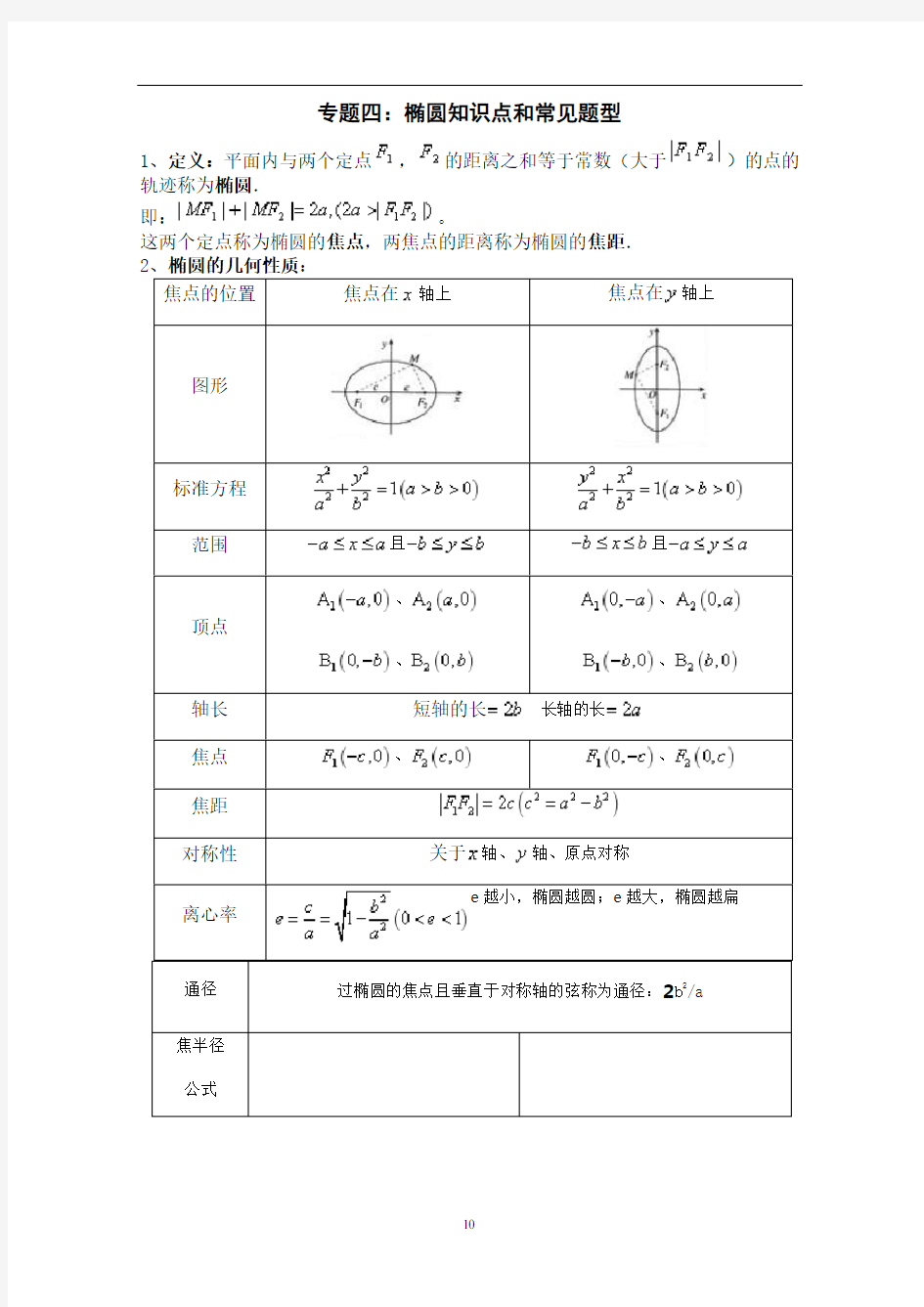

专题四:椭圆知识点和常见题型
1、定义:平面内与两个定点,的距离之和等于常数(大于)的点的轨迹称为椭圆.
即:。
这两个定点称为椭圆的焦点,两焦点的距离称为椭圆的焦距.
焦点的位置焦点在轴上焦点在轴上图形
标准方程
范围且且
顶点
、
、、、
轴长短轴的长长轴的长
焦点、、
焦距
对称性关于轴、轴、原点对称
离心率
e越小,椭圆越圆;e越大,椭圆越扁通径过椭圆的焦点且垂直于对称轴的弦称为通径:2b2/a
焦半径
公式
题型一:求椭圆的解析式
例1.求椭圆2
2
4936x y +=的长轴长、焦距、焦点坐标、顶点坐标;
【详解】椭圆2
2
4936x y +=化为标准方程22
194
x y +=,
∴3a =,2b =,
∴c ==∴椭圆的长轴长为26a =
,焦距为2c =
焦点坐标为()
1F
,)
2
F ,
顶点坐标为()13,0A -,()23,0A ,()10,2B -,()20,2B . 例2.求适合下列条件的椭圆标准方程:
(1)与椭圆2
212x y +=有相同的焦点,且经过点3(1,)2
(2
)经过(2,(2A B 两点 【详解】(1)椭圆2
212
x y +=的焦点坐标为(1,0)±,
∵椭圆过点3(1,)2
,
∴24a =,
∴2,a b ==,
∴椭圆的标准方程为22
143
x y +=.
(2)设所求的椭圆方程为22
1(0,0,)x y m n m n m n
+=>>≠.
把(2,(22
A B -两点代入, 得:1
4
213241m
n
m
n
??+=???
??+=??,解得81m n ==,, ??? ??-232
5
,
∴椭圆方程为2
218
x y +=.
题型二:求轨迹
例3.在同一平面直角坐标系xOy 中,圆22
4x y +=经过伸缩变换:12x x y y ?=???=''??
后,得到曲
线C .
求曲线C 的方程; 【详解】
设圆22
4x y +=上任意一点(),M x y 经过伸缩变换:12x x
y y ω=???=''??
得到对应点(),M x y '''.
将x x '
=,2y y '=代入224x y +=,得()
2
2
24x y ''+=,化简得2214
x y ''+=.
∴曲线C 的方程为2
214
x y +=;
例4.已知ABC 中,角、、A B C 所对的边分别为,>>、、a b c a c b ,且2,2=+=c a b c ,求点C 的轨迹方程. 【详解】
由题意,以AB 所在直线为x 轴,线段AB 的垂直平分线为y 轴建立平面直角坐标系, 如图所示,
因为2c =,则(1,0),(1,0)A B -,设(,)C x y , 因为2a b c +=,即||||2||CB CA AB +=,
4=,整理得所以22143
x y +=,
因为a b >,即||||CB CA >,所以点C 只能在y 轴的左边,即0x <. 又ABC 的三个顶点不能共线,所以点C 不能在x 轴上,即2x ≠-.
所以所求点C 的轨迹方程为22
1(20)43
x y x +=-<<.
例5在圆2
2
8x y +=上任取一点P ,过P 作x 轴的垂线PD ,D 为垂足.当点P 在圆上运动时,
求线段PD 的中点Q 的轨迹方程. 【详解】
解:已知在圆2
2
8x y +=上任取一点P ,过P 作x 轴的垂线PD ,D 为垂足,
设0(P x ,0)y ,(,)M x y ,0(D x ,0),
M 是PD 的中点,
0x x ∴=,02y y =,
又P 在圆22
8x y +=上,
22008x y ∴+=,即2248x y +=,
∴22
182
x y +=, ∴线段PD 的中点M 的轨迹方程是22
182
x y +=.
题型三:求参数的范围
例6:已知椭圆22
22:1(0)y x C a b a b
+=>>的上下两个焦点分别为12,F F ,过点1F 与y 轴垂直
的直线交椭圆C 于 ,M N 两点,2MNF ?
C
. (1)求椭圆C 的标准方程;
(2)已知O 为坐标原点,直线:l y kx m =+与y 轴交于点P ,与椭圆C 交于,A B 两个不同的点,若存在实数λ,使得4OA OB OP λ+=,求m 的取值范围.
由题意2MNF ?
的面积为21212||2b c
F F MN c MN a
===
由已知得
2
c a =
,∴21b =,∴24a =, ∴椭圆C 的标准方程为2
2
14
y x +=.
(Ⅱ)若0m =,则()0,0P ,由椭圆的对称性得AP PB =,即0OA OB +=, ∴0m =能使4OA OB OP λ+=成立. 若0m ≠,由4OA OB OP λ+=,得144
OP OA OB λ
=
+, 因为A ,B ,P 共线,所以14λ+=,解得3λ=.
设()11,A x kx m +,()22,B x kx m +,由22,{440,
y kx m x y =++-= 得(
)
2
22
4240k x mkx m +++-=,
由已知得(
)(
)
2
2
2
2
44440m k k m ?=-+->,即2240k m -+>,
且12224km x x k -+=+,21224
4
m x x k -=+,
由3AP PB =,得123x x -=,即123x x =-,∴()2
1212340x x x x ++=, ∴
()
(
)222
2
2
2
44120
4
4
m k m k k
-+
=++,即222240m k m k +--=.
当2
1m =时,2
2
2
2
40m k m k +--=不成立,∴2
2
241
m k m -=-,
∵2
2
40k m -+>,∴22
24401m m m --+>-,即()
222401
m m m ->-, ∴214m <<,解得21m -<<-或12m <<.
综上所述,m 的取值范围为{|21012}m m m m -<<-=<<或或.
直线与圆锥曲线的位置关系
2.直线与圆锥曲线的位置关系: ⑴.从几何角度看:(特别注意)要特别注意当直线与双曲线的渐进线平行时,直线与双曲线只有一个交点;当直线与抛物线的对称轴平行或重合时,直线与抛物线也只有一个交点。 ⑵.从代数角度看:设直线L 的方程与圆锥曲线的方程联立得到
。
①. 若=0,当圆锥曲线是双曲线时,直线L 与双曲线的渐进线平行或重合;
当圆锥曲线是抛物线时,直线L 与抛物线的对称轴平行或重合。 ②.若,设
。.
时,直线和圆锥曲线相交于不同两点,相交。
b.时,直线和圆锥曲线相切于一点,相切。
c.
时,直线和圆锥曲线没有公共点,
相离。
题型四:直线与椭圆的位置关系
例7已知椭圆C :22
221x y a b
+=(0a b >>)的左,右焦点分别为()12,0F -,)
2
2,0F ,
且经过点)
2,1M
.
(1)求椭圆C 的标准方程;
(2)若斜率为2的直线与椭圆C 交于A ,B 两点,且2AB =,求该直线的方程. 【详解】
(1)依题意可知2c =
根据椭圆的定义可知122MF MF a +=,
即
24a =
=,2
a =
,b ==
所以椭圆C 的标准方程为22
142
x y +=.
(2)设直线AB 的方程为2y x t =+,
由22214
2y x t
x y =+??
?+=??消去y 并化简得2298240x tx t ++-=,
由于直线AB 和椭圆相交,所以()()
2
2
849240t t ?=-??-
>
,解得t -<<设()()1122,,,A x y B x y ,则21212824
,99t t x x x x -+=-?=,
所以2AB ==,
2
=
,
29=, 两边平方并化简得2
9910t =
,所以t =所以直线AB
的方程为2y x =. 例8.已知P 是椭圆2
212
x y +=上的一动点.求P 到直线220x y ++=距离的最大值.
【详解】
P 在椭圆22
12
x y +
=上,设,sin )P θθ,
则P 到直线220x y ++=
距离为
d
=
=
=
,其中1
sin ,cos 33
??=
=,?取锐角. ∴当sin()1θ?+
=
时,max d =
=
弦长问题
直线与圆锥曲线相交时的弦长问题是一个难点,化解这个难点的方
法是:
设而不求,根据
根与系数的关系,进行整体代入。即当直线
与圆锥曲线交于点
,时,则
=
=
=
=
题型四:弦长公式
例9.已知椭圆22
22:1(0)x y C a b a b
+=>>的右焦点
(
)
3,0,且经过点31,2??
- ? ???
,点M 是x 轴上的一点,过点M 的直线l 与椭圆C 交于,A B 两点(点A 在x 轴的上方) (1)求椭圆C 的方程;
(2)若2AM MB =,且直线l 与圆22
4
:7
O x y +=
相切于点N ,求MN 的长.
试题解析:(1)由题意知()2222
2
2
3
3{114a b c b -==? -??+=,即()()24430a a --=, 又2233a b =+>,故22
4,1a b ==,
椭圆C 的方程为2
214
x y +=.
(2)设(),0M m ,直线()()1122:,,,,l x ty m A x y B x y =+, 由2AM MB =,有122y y =-,
221
ax by +=
由()
2
22221
{42404
x y t y my m x yy m
+=?+++-==+, 由韦达定理得2121222
24
,44
tm m y y y y t t -+=-=++, 由2
122122222,2y y y y y y y y =-+=-+=-,则()()2
2
1212122y y y y y y ??=--+=-+??,
2
22242,244m tm t t -??=-- ?
++??,化简得()()2222448m t t m -+=-,原点O
到直线的距离
d =
,
又直线l 与圆2
2
4:7O x y +=
=2
2714t m =-,
()()
2
222
4222
448{
2116160714
m
t t m m m t m -+=-?--==
-,即()()2234740m m -+=,
解得2
43m =,此时2
43t =,满足0?>
,此时M ?? ? ???
, 在Rt OMN ?
中,21MN =
=
,所以MN
. 例10在平面直角坐标系xOy 中,已知点()2,0B ,()2,0C -,设直线AB ,AC 的斜率分别为1k ,2k ,且121
2
k k =-,记点A 的轨迹为E . (1)求E 的方程;
(2)若直线l :1y x =+与E 相交于P ,Q 两点,求PQ . 【详解】
解:(1)设点(,)A x y ,则12y k x =
-,2+2y k x =, 因为121
2k k =-,则1212
2+2y y x k x k ?=--=
, 整理得:22
142
x y +=,斜率存在,所以2x ≠±,
所以E 的方程:22
142
x y +=,
(0y ≠) (2)设11(,)P x y ,22(,)Q x y ,
由221
14
2y x x y =+???+=??,消去y 得到23420x x +-=,则2443(2)400?=-??-=>,
所以12124323x x x x ?+=-?????=-
??
,则12PQ x =-=,
所以PQ =
题型五:中点弦问题
例11设椭圆22221(0)x y a b a b +=>>的短轴长为4
,离心率为2
.
设点(2,1)M 是直线l 被椭圆所截得的线段AB 的中点,求直线l 的方程. 【详解】
设()()1122,,,A x y B x y ,由(2,1)M 在椭圆内, 过点(2,1)M 的直线与椭圆有两个交点,
再由椭圆的对称性可确定直线AB 的斜率一定存在.
则()()()()2211121212122
2
22416
40416
x y x x x x y y y y x y ?+=?-++-?+=?+=?, 整理得:()121212121
42
y y x x x x y y -+==---+
所以斜率1
2
k =-
,所以直线l 的方程为240x y +-=. [点评] 关于中点弦问题,一般采用两种方法解决:
(1)联立方程组,消元,利用根与系数的关系进行设而不求,从而简化运算. (2)利用“点差法”求解,即若椭圆方程为x 2a 2+y 2
b 2=1,直线与椭圆交于点A (x 1,y 1)、
B (x 2,y 2),且弦AB 的中点为M (x 0,y 0),则
?
?
x 21
a 2
+y 21b 2=1, ①x 22a 2+y 22b 2=1. ②
由①-②得a 2(y 21-y 22)+b 2(x 21-x 22)=0,
∴y 1-y 2x 1-x 2
=-b 2a 2·x 1+x 2y 1+y 2=-b 2a 2·x 0y 0.
这样就建立了中点坐标与直线的斜率之间的关系,从而使问题能得以解决. 题型六:定值问题
1.与圆锥曲线有关的最值和范围的讨论常用以下方法
(1)结合圆锥曲线的定义,利用图形中几何量之间的大小关系;
(2)不等式(组)求解法,根据题意结合图形(如点在曲线内等)列出所讨论的参数适合的不等式(组),通过解不等式(组),得出参数的变化范围;
(3)函数值域求解法,把所讨论的参数作为一个函数,选一个适当的参数作为自变量来表示这个函数,通过讨论函数的值域来求参数的变化范围;
(4)构造一个二次函数,利用判别式求解;
(5)利用不等式,若能将问题转化为“和为定值”或“积为定值”,则可以用基本不等式求解;
例12.(定点问题)已知椭圆()2222:10x y C a b a b +=>>的离心率为3
,1(3,)2M -是椭
圆C 上的一点.
(1)求椭圆C 的方程;
(2)过点(4,0)P -作直线l 与椭圆C 交于不同两点A 、B ,A 点关于x 轴的对称点为D ,问直线BD 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
【详解】(1)∵3c a =222a b c =+,∴22
4a b =,∴222214x y b b +=,
将1(3,)2M -代入椭圆C ,∴2
1b =,∴22:14
x C y +=.
(2)显然AB 斜率存在,设AB 方程 为:(4)y k x =+,2
222221
(14)3264404
(4)x y k x k x k y k x ?+=??+++-=??=+?
, 2161920k ?=->,∴2
112
k <.
设11(,)A x y ,22(,)B x y ,11(,)D x y -,∴21223214k x x k +=-+,2122
644
14k x x k -=+,
∵()211121
:y y BD y y x x x x ++=
--,∴0y =时211112*********()
()8x y x y kx x k x x x x y y k x x k -++=+=+++
22
3322233
2
644322()4()1288128141413232832()814k k k k k k k k k k k k k k k
k -+---++===--++-++, ∴直线BD 过定点(1,0)-.
例13(定值问题)已知直线220x y 经过椭圆22
221(0)x y C a b a b
+=>>:的左顶
点A 和上顶点D ,设椭圆C 的右顶点为B . (1)求椭圆C 的标准方程和离心率e 的值;
(2)设点S 是椭圆上位于x 轴上方的动点,求证:直线AS 与BS 的斜率的乘积为定值.
【详解】(1)由已知得,椭圆C 的左顶点为()20A -,,上顶点为()01D ,,
2a ∴=,1b =
,c =
故椭圆C 的方程为2214x y += ,离心率e
的值为
2
; (2)设()00S x y ,,且()20B ,
, 22
0014x y ∴+=,故220014
x y =-
, 故200020001·2244
SA SB y y y k k x x x =
==-+--为定值. ∴直线AS 与BS 的斜率的乘积为定值.
例14.已知椭圆2222:1(0)x y M a b a b +=>>
的离心率为2
,且过点.
(1)求椭圆M 的方程;
(2)若A ,B 分别为椭圆M 的上,下顶点,过点B 且斜率为()0k k >的直线l 交椭圆M 于另一点N (异于椭圆的右顶点),交x 轴于点P ,直线AN 与直线x a =相交于点Q .求证:直
线PQ 的斜率为定值. 【详解】
(1)设椭圆的焦距为2c
,则
2
c a =
①, 2
242
1a b
+=②,又222a b c =+③, 由①②③解得28a =,24b =,24c =,
所以椭圆M 的标准方程为22
184
x y +=.
(2)证明:易得(0,2)A ,(0,2)B -,直线l 的方程为2y kx =-,因为直线l
不过点0),
所以k ≠
由22
228
y kx x y =-??+=?,得()222180k x kx +-=,
所以2
821N k x k =+,从而222842,2121k
k N k k ??- ?++??
,2,0P k ??
???, 直线AN 的斜率为22242
21218221k k k k k --+=-+,故直线AN 的方程为122y x k =-+. 令22x =,得2
22,2Q k ??-+ ? ???
,
直线PQ 的斜率2
2
222(21)2222222(21)22PQ k k k k k k k -
+-+-====---. 所以直线PQ 的斜率为定值22
. 题型七:求离心率
例15已知椭圆22
221(0)x y a b a b
+=>>上有一点A ,它关于原点的对称点为B ,点F 为椭圆
的右焦点,且满足AF BF ⊥,设ABF α∠=,且,126ππα??
∈????
,求该椭圆的离心率e 的取值范围.
【详解】如图所示,设椭圆的左焦点为1F ,连接11,AF BF ,则四边形1AFBF 为矩形,
1||2,||||2∴==+=AB FF c AF BF a . ||2sin ,||2ccos αα==AF c BF ,
2sin 2cos 2αα∴+=c c a ,
1
1
sin cos 24παα
α∴=
=
+?
?+ ?
?
?e . ,126ππα??
?
??∈?
,
5,4312π
ππα??∴+
∈????
, 326sin ,424πα??+?
?∴+∈?? ?????,
6132sin ,422πα??+?
?∴+∈?? ?????
,
∴椭圆的离心率631,??∈-???
e .
例16:椭圆的两个焦点的坐标分别为F 1(﹣2,0),F 2(2,0),且椭圆经过点(,﹣) (1)求椭圆标准方程.
(2)求椭圆长轴长、短轴长、离心率. 解:(1)设椭圆的标准方程为
+
=1(a >b >0),
则2a=+=2,
即a=
,
又∵c=2, ∴b 2=a 2﹣c 2=6, 故椭圆的标准方程为:+
=1,
(2)由(1)得: 椭圆的长轴长:2,
短轴长2, 离心率e=
=
. 例17:已知直线:l y kx m =+与椭圆22
221(0)x y a b a b +=>>恰有一个公共点P ,l 与圆
222x y a +=相交于,A B 两点.
(I )求k 与m 的关系式;
(II )点Q 与点P 关于坐标原点O 对称.若当1
2
k =-时,QAB ?的面积取到最大值2a ,求椭圆的离心率. 【详解】
(I )由2222,1
y kx m x y a
b =+???+=??,得()()22222222
20a k b x a kmx a m b +++-=,
则()
()()
2
2222222240a km
a k
b a m b ?=-+-=
化简整理,得2222m a k b =+;
(Ⅱ)因点Q 与点P 关于坐标原点O 对称,故QAB ?的面积是OAB ?的面积的两倍.
所以当12k =-时,OAB ?的面积取到最大值2
2
a ,此时OA OB ⊥,
从而原点O 到直线l 的距离2
d =
, 又2
1
m
d k =+22212m a
k =+. 再由(I ),得22222
12a k b a k +=+,则22
221b k a =-. 又12k =-,故22
22114b k a =-=,即2238
b a =,
从而222
22518c b e a a ==-=,即10
4
e =.
例18椭圆22
221(0)x y a b a b
+=>>的中心在原点,12,F F 分别为左?右焦点,,A B 分别是椭圆
的上顶点和右顶点,P 是椭圆上一点,且1PF x ⊥轴,2//PF AB ,求椭圆的离心率. 【详解】
如图所示:()0,A b ,(),0B a ,()2,0F c ,
因为1PF x ⊥轴,所以2,b P c a ??
- ???.
222,b PF c a ??
=- ??
?,(),AB a b =-.
因为2//PF AB ,所以2
20b bc a a
-+?=,即2b c =.
所以()
2
22225a b c c c c =+=+=,5
5
c e a =
=
.
题型八:求面积
例19.已知椭圆的焦点在x 轴上,长轴长为6,焦距为5P 为椭圆上的一点,1F ,2F 是该椭圆的两个焦点,若1260F PF ∠=?,求: (1)椭圆的标准方程; (2)12PF F △的面积. 【详解】
(1)设椭圆的标准方程为()22
2210x y a b a b
+=>>,
因为长轴长为6,焦距为53a =,5c =
2b =,
故椭圆方程为22
194
x y +=.
(2)由椭圆的定义可得126PF PF +=,
由余弦定理可得2
2
12122cos6020PF PF PF PF +
-?=,
整理得到2
2
121220PF PF PF PF +-=,2
2
1212236PF PF PF PF ++=, 所以1216
3
PF PF =,故12
1231643
sin 60413
23PF F S PF PF ??=?=
=
?.
例20.椭圆()2222:10x y C a b a b +=>>的离心率为
3
,且过其右焦点F 与长轴垂直的直线被椭圆C 截得的弦长为2.
(1)求椭圆C 的方程;
(2)设点P 是椭圆C 的一个动点,直线33
:l y x =+
C 交于,A B 两点,求PAB △面积的最大值.
试题解析:解:(1)∵椭圆()22
22:10x y C a b a b +=>>的离心率为
3
2
,3232c e c a a ∴==∴=,即2243c a =,
又
椭圆右焦点F 与长轴垂直的直线被椭圆C 截得的弦长为
2,2
2
2222
31141,1a c a b a b ∴+=∴+=,即24b =,又222a b c -=,所以222
2344
a b c a =+=+,即
2
16a =,所以椭圆C 的方程为:22
1164
x y ∴+
=. (2)联立直线直线 33:42l x +与椭圆C 的方程,得22
3342
{1164
y x x y
=
+
+=,消去y ,整理可得
2712520x x +-=,即()()72620x x +-=,解得2x =或26
7
x =-
,所以不妨设(
26,,7A B ?- ??
,则AB ==, 设过P 点且与直线l 平行的直线L
的方程为:y C =
+,L 与l 的距离就是P 点到AB 的距离,即PAB △的边AB 边上的高,只要L 与椭圆相切,就有L 与的AB 最大距离,即得最大面积,
将4y x C =+代入
221164
x y +=,消元、整理,可得:
22716640x c ++-= 令判别式
()
()
2
2471664c ?=-??-225628640c =-+?=
,解得c == L ∴与AB
19
=
,PAB ∴?
面积的最大值为:
(1102197
=.
椭圆的常见题型及解法(一).
椭圆的常见题型及其解法(一) 椭圆是圆锥曲线的内容之一,也是高考的热点和重点,椭圆学习的好坏还直接影响后面的双曲线与抛物线的学习,笔者在这里就椭圆常见题型作简要的探讨,希望对学习椭圆的同学有所帮助. 一、椭圆的焦半径 椭圆上的任意一点到焦点F的长称为此曲线上该点的焦半径,根据椭圆的定义,很容易推导出椭圆的焦半径公式。在涉及到焦半径或焦点弦的一些问题时,用焦半径公式解题可以简化运算过程。 1.公式的推导 设P (,)是椭圆上的任意一点, 分别是椭圆的左、右焦点,椭圆 ,求证,。证法1: 。 因为,所以 ∴ 又因为,所以 ∴, 证法2:设P 到左、右准线的距离分别为,由椭圆的第二定义知1 1 PF e d ,又,所 以, 而 。
∴,。 2.公式的应用 例1 椭圆上三个不同的点A ()、B ()、C ()到焦点F (4, 0)的距离成等差数列,则 12 x x + . 解:在已知椭圆中,右准线方程为 25 4x = ,设A 、B 、C 到右准线的距离为 , 则、、。 ∵ , , ,而|AF|、|BF|、|CF|成等差数列。 ∴,即,。 例2.12,F F 是椭圆22 14x y +=的两个焦点,P 是椭圆上的动点,求 的最大值和最 小值。 解:设 ,则10202,2.PF x PF x =+ =-2 12034.4 PF PF x ?=- P 在椭圆上,022x ∴-≤≤,12PF PF ?的最大值为4,最小值为1. 变式练习1:. 求过椭圆的左焦点,倾斜角为的弦AB 的长度。 解:由已知 可得 ,所以直线AB 的方程 为 ,代入椭圆方程 得 设 ,则 ,从而 变式练习2. 设Q 是椭圆22 221(0)x y a b a b +=>>上任意一点,求证:以2QF (或1QF )为
中考古诗词鉴赏题的常见题型及解析
中考古诗词鉴赏题的常见题型及解析 (一)品味炼字类[题目形式](1)“某”个字或词用得好,好在哪里?(2)诗歌中的“某”字或词有什么表达效果?(3)“某”字能否改为“某”字?(4)你最欣赏哪个字或词?请赏析。 [应对策略]这类题主要考查我们对精炼词语的感悟能力。解答时要抓住诗歌中关键词语来点评,可以从词性、色彩、修辞以及所表达的思想感情去把握它的内涵。值得提醒的是分析时要结合全诗的意境和作者的情感去回答,不能孤立地谈这个词的作用。 [题型示例](xx浙江绍兴)雨过山村[唐]王建雨里鸡鸣一两家,竹溪村路板桥斜。妇姑相唤浴蚕去,闲着中庭栀子花。问题:古典诗词讲究炼字,末句中的“闲”字用得好,请你说说好在哪里。解析:“闲”字面应为“清闲、闲适”的意思,但不能孤立的分析这个词的作用。按应对策略所述,要结合全诗的意境和作者的情感去回答,通过第三句可以看出,这首诗描绘的是妇姑浴蚕的劳动生活情景,事实上没有一个人闲着,是栀子花“闲着”,用了反衬、拟人的手法,因而答案为:妙在它不从正面着墨,而从侧面落笔,以“栀子花”的“闲”来反衬人们的“忙”,巧作对照,情趣盎然(或:运用拟人手法,形象地写出了蚕妇们去后庭中栀子花的闲适自在。)
(二)名句赏析类[题目形式](1)从某句诗中领悟到什么人生哲理?(2)请谈谈对诗歌中千古传诵的名句的理解。(3)某诗句历来受到人们的赞赏,请分析原因。 [应对策略]这类题主要考查学生对诗歌中被后人传诵的名句的理解和赏析能力。这类题多为开放题,答案不要求统一,要掌握常见的鉴赏评价的角度:能指出写景特点(如景物的色彩、近景远景的结合等)或采用的修辞手法(如拟人、比喻等)或用词的生动形象等,并且还要说出表达了诗人怎样的思想感情或给人怎样的启示和思考。 [题型示例](xx年江苏连云港市)阅读下面这首唐诗,回答后面的问题。酬乐天扬州初逢席上见赠刘禹锡巴山楚水凄凉地,二三年弃置身。怀旧空吟闻笛赋,到乡翻似烂柯人。沉舟侧畔千帆过,病树前头万木春。今日听君歌一曲,暂凭杯酒长精神。问题:“沉舟侧畔千帆过,病树前头万木春”这两句因为蕴含深刻的哲理而被后世广为传诵,请谈谈你从这两句诗中领悟到了什么?解析:这两句诗之所以被后人传诵,是因为它是通过对景物的描写向人们揭示了深刻的哲理。首先应明确景物的特点,可理解为:翻覆的船只旁仍有千千万万的帆船经过;枯萎的树木前面也有万千林木欣欣向荣。然后说出这句诗所蕴含的哲理,答案不要求统一,示例供参考,(1)人在逆境面前,要积极进取,振作精神,面向未来(要有坚定的信心和执著的信念);(2)痛苦、困难、挫折、失意都是暂时的,理想、光明、胜利就在前头;
最新椭圆基本知识点总结
椭圆知识点 知识点一:椭圆的定义 平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数)2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆.这两个定点叫椭圆的焦点,两焦点的距离叫作椭圆的焦距. 注意:若2121F F PF PF =+,则动点P 的轨迹为线段21F F ; 若2121F F PF PF <+,则动点P 的轨迹无图形. 知识点二:椭圆的简单几何性质 椭圆:12222=+b y a x )0(>>b a 与 122 22=+b x a y )0(>>b a 的简单几何性质
1.椭圆标准方程中的三个量c b a ,,的几何意义 222c b a += 2.通径:过焦点且垂直于长轴的弦,其长a b 2 2 3.最大角:p 是椭圆上一点,当p 是椭圆的短轴端点时,21PF F ∠ 为最大角。 4.焦点三角形的面积2 tan 2 21θ b S F PF =?,其中21PF F ∠=θ 5. 用待定系数法求椭圆标准方程的步骤. (1)作判断:依据条件判断椭圆的焦点在x 轴上还是在y 轴上. (2)设方程: ①依据上述判断设方程为2222b y a x +=1)0(>>b a 或22 22a y b x +=1)0(>>b a ②在不能确定焦点位置的情况下也可设mx 2+ny 2=1(m >0,n >0且m ≠n ). (3)找关系,根据已知条件,建立关于a ,b ,c 或m ,n 的方程组. (4)解方程组,代入所设方程即为所求. 6.点与椭圆的位置关系: 2222b y a x +<1,点在椭圆内,2222b y a x +=1,点在椭圆上,2 2 22b y a x +>1, 点在椭圆外。 7.直线与椭圆的位置关系 设直线方程y =kx +m ,若直线与椭圆方程联立,消去y 得关于x 的一元二次方程:ax 2+bx +c =0(a ≠0). (1)Δ>0,直线与椭圆有两个公共点;(2)Δ=0,直线与椭圆有一个公共点; (3)Δ<0,直线与椭圆无公共点. 8.弦长公式: 若直线b kx y l +=:与圆锥曲线相交与A 、B 两点,),(),,2211y x B y x A (则弦长
分数加减法常见题型解析
分数加减法常见题型解析 题型一:直接写出得数 1、同分母分数加减(考点:约分、分数互化) 例题:37 +67 = 59 -29 = 练习:45 +35 = 38 +18 = 139 -19 = 712 +1112 = 127 +57 = 76 +116 = 2、异分母分数加减(考点:通分、分数互化) 例题:67 -35 = 58 +712 = 练习:56 +35 = 25 +14 = 139 -16 = 3、整数减分数(考点:分数互化) 例题:4-35 = 5-147 = 7719 -4= 练习:3-59 = 6-256 = 9-138 = 4、杂合(考点:简算) 例题:56 +35 +16 = 23 +34 -14 = 223 -(23 +14 )= 267 -56 -16 = 116 -34 -56 = 59 -(14 -49 )= 练习:34 -16 +56 = 357 -(78 +57 )= 58 +34 +54 =
237 -16 -56 = 57 -(38 -27 )= 139 -34 -49 = 5、含小数(考点:分数与小数互化) 例题:0.5+35 = 1720 -0.55= 338 +34 -0.375= 练习: 134 +0.7= 158 -0.7= 910 +0.25= 1320 +0.35= 1.3+45 = 1.3-1725 = 题型二:计算与简算 1、简算定律 要点:只有同分母加减法才有简算。先看分数、再看符号。 例题:加法交换律、加法结合律 79 +37 +29 = 连减的性质 118 -37 -47 = 118 -37 -38 = 带符号移动 59 -14 -29 = 57 -49 +27 = 练习:157 -611 -511 = 0.85+49 +1320 +59 =
(完整版)椭圆知识点复习总结
椭圆知识点总结复习 1. 椭圆的定义: (1)椭圆:焦点在x 轴上时122 22=+b y a x (222a b c =+)?{ cos sin x a y b ??==(参 数方程,其中?为参数),焦点在y 轴上时22 22b x a y +=1(0a b >>)。方程 22Ax By C +=表示椭圆的充要条件是什么?(ABC ≠0,且A ,B ,C 同号,A ≠B )。 例一:已知线段AB 的两个端点A ,B 分别在x 轴,y 轴上,AB=5,M 是AB 上的一个点,且AM=2,点M 随AB 的运动而运动,求点M 的运动轨迹方程 2. 椭圆的几何性质: (1)椭圆(以122 22=+b y a x (0a b >>)为例):①范围:,a x a b y b -≤≤-≤≤; ②焦点:两个焦点(,0)c ±;③对称性:两条对称轴0,0x y ==,一个对称中心(0,0),四个顶点(,0),(0,)a b ±±,其中长轴长为2a ,短轴长为2b ;④准线: 两条准线2a x c =±; ⑤离心率:c e a =,椭圆?01e <<,e 越小,椭圆越圆;e 越大,椭圆越扁。⑥通径2 2b a 例二:设椭圆22 221(0)x y a b a b +=>>上一点P 作x 轴的垂线,恰好过椭圆的一个焦 点1F ,此时椭圆与x 轴交于点A ,与y 轴交于点B ,且A,B 两点所确定的直线AB 与OP 平行,求离心率e
2.点与椭圆的位置关系:(1)点00(,)P x y 在椭圆外?2200 221x y a b +>; (2)点00(,)P x y 在椭圆上?220 220b y a x +=1; (3)点00(,)P x y 在椭圆内?2200 221x y a b +< 3.直线与圆锥曲线的位置关系:(往往设而不求) (1)相交:0?>?直线与椭圆相交;(2)相切:0?=?直线与椭圆相切; (3)相离:0?>与过点(2,0),(0,1)A B 的直线有且只有一个公共 点T ,且椭圆的离心率2 e = (1)求椭圆的方程 (2)设12,F F 分别为椭圆的左,右焦点,M 为线段2AF 的中点,求证:1ATM AFT ∠=∠ (3)求证:2 121 2 AT AF F =. ?4、焦半径(圆锥曲线上的点P 到焦点F 的距离)的计算方法:利用圆锥曲线的第二定义,转化到相应准线的距离,即焦半径0r ed a ex ==±,其中d 表示P 到与F 所对应的准线的距离。 例五:已知椭圆22 221x y a b +=上一点P 到椭圆左焦点的距离为3,则点P 到右 准线的距离为____(答:10/3); 例六:椭圆1342 2=+y x 内有一点)1,1(-P ,F 为右焦点,在椭圆上有一点M , 使MF MP 2+ 之值最小,则点M 的坐标为_______(答:)1,3 6 2( -) ; 5、焦点三角形(椭圆或双曲线上的一点与两焦点所构成的三角形) 问题:0||S c y =,当0||y b =即P 为短轴端点时,m ax S 的最大值为bc ;
椭圆知识点总结附例题
圆锥曲线与方程 椭 圆 知识点 一.椭圆及其标准方程 1.椭圆的定义:平面内与两定点F 1,F 2距离的和等于常数()212F F a >的点的轨迹叫做椭圆,即点集M={P| |PF 1|+|PF 2|=2a ,2a >|F 1F 2|=2c}; 这里两个定点F 1,F 2叫椭圆的焦点,两焦点间的距离叫椭圆的焦距2c 。 (212F F a =时为线段21F F ,212F F a <无轨迹)。 2.标准方程: 222c a b =- ①焦点在x 轴上:122 22=+b y a x (a >b >0); 焦点F (±c ,0) ②焦点在y 轴上:122 22=+b x a y (a >b >0); 焦点F (0, ±c ) 注意:①在两种标准方程中,总有a >b >0,并且椭圆的焦点总在长轴上; ②两种标准方程可用一般形式表示:22 1x y m n += 或者 mx 2+ny 2=1 二.椭圆的简单几何性质: 1.范围 (1)椭圆12222=+b y a x (a >b >0) 横坐标-a ≤x ≤a ,纵坐标-b ≤x ≤b (2)椭圆12222=+b x a y (a >b >0) 横坐标-b ≤x ≤b,纵坐标-a ≤x ≤a 2.对称性 椭圆关于x 轴y 轴都是对称的,这里,坐标轴是椭圆的对称轴,原点是椭圆的对称 中心,椭圆的对称中心叫做椭圆的中心
3.顶点 (1)椭圆的顶点:A 1(-a ,0),A 2(a ,0),B 1(0,-b ),B 2(0,b ) (2)线段A 1A 2,B 1B 2 分别叫做椭圆的长轴长等于2a ,短轴长等于2b ,a 和b 分别叫做椭 圆的长半轴长和短半轴长。 4.离心率 (1)我们把椭圆的焦距与长轴长的比 22c a ,即a c 称为椭圆的离心率, 记作e (10< 椭 圆 1.椭圆的定义:把平面内与两个定点21,F F 的距离之和等于常数(大于21F F )的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点的距离叫做焦距(设为2c). 2.椭圆的标准方程: 12222=+b y a x (a >b >0) 122 22=+b x a y (a >b >0) 焦点在坐标轴上的椭圆标准方程有两种情形,为了计算简便,可设方程为mx 2 +ny 2 =1(m>0,n>0)不必考虑焦点位置,求出方程 3.求轨迹方程的方法: 定义法、待定系数法、相关点法、直接法 . ,.2,,1的轨迹中点求线段段轴作垂线向从这个圆上任意一点半径为标原点已知一个圆的圆心为坐如图例M P P P P x P ''解:(相关点法)设点M(x, y),点P(x 0 , y 0 ), 则x =x 0, y = 2 0y 得x 0=x , y 0=2y. ∵x 02 +y 02 =4, 得x 2 +(2y)2 =4, 即.14 2 =+y x 所以点M 的轨迹是一个椭圆. 4.范围. x 2≤a 2,y 2≤b 2 ,∴|x|≤a ,|y|≤b . 椭圆位于直线x =±a 和y =±b 围成的矩形里. 5.椭圆的对称性 椭圆是关于y 轴、x 轴、原点都是对称的.坐标轴是椭圆的对称轴. 原点是椭圆的对称中心.椭圆的对称中心叫做椭圆的中心. 6.顶点 只须令x =0,得y =±b ,点B 1(0,-b)、B 2(0, b)是椭圆和y 轴的两个交点;令y =0,得x =±a ,点A 1(-a,0)、A 2(a,0)是椭圆和x 轴的两个交点.椭圆有四个顶点:A 1(-a, 0)、A 2(a, 0)、B 1(0, -b)、B 2(0, b).椭圆和它的对称轴的四个交点叫椭圆的顶点. 线段A 1A 2、B 1B 2分别叫做椭圆的长轴和短轴. 长轴的长等于2a. 短轴的长等于2b.a 叫做椭圆的 长半轴长.b 叫做椭圆的短半轴长. |B 1F 1|=|B 1F 2|=|B 2F 1|=|B 2F 2|=a . 在Rt △OB 2F 2中,|OF 2|2=|B 2F 2|2-|OB 2|2, 即c 2=a 2-b 2 . a A 1y O F 1F 2 x B 2 B 1 A 2c b y O F 1F 2x M c c x F 2 F 1 O y M c c y x P O P ' M 椭圆常见题型总结 1、椭圆中的焦点三角形:通常结合定义、正弦定理、余弦定理、勾股定理来解决; 椭圆 22 2 21(0)x y a b a b +=>>上一点00(,)P x y 和焦点1(,0)c F -,2(,0)c F 为顶点的12PF F ?中,12F PF α=∠,则当P 为短轴端点时α最大,且 ① 122PF PF a +=; ②22 2 12122cos 4c PF PF PF PF α=+-; ③12 121 sin 2PF F S PF PF α?= =2tan 2 b α?(b 短轴长) 2、直线与椭圆的位置关系:直线y kx b =+与椭圆22 221(0)x y a b a b +=>>交于 1122(,),(,)A x y B x y 两点,则12AB x =-=3、椭圆的中点弦:设1122(,),(,)A x y B x y 是椭圆22 221(0)x y a b a b +=>>上不同两点, 00(,)M x y 是线段AB 的中点,可运用点差法可得直线AB 斜率,且20 20 AB b x k a y =-; 4、椭圆的离心率 范围:01e <<,e 越大,椭圆就越扁。 求椭圆离心率时注意运用:c a e = ,222c b a += 5、椭圆的焦半径 若00(,)P x y 是离心率为e 的椭圆22 221(0)x y a b a b +=>>上任一点,焦点 为1(,0)c F -,2(,0)c F ,则焦半径10PF a ex =+,10PF a ex =-; 6、椭圆标准方程的求法 ⑴定义法:根据椭圆定义,确定2 a ,2 b 值,结合焦点位置直接写出椭圆方程; ⑵待定系数法:根据焦点位置设出相应标准方程,根据题中条件解出2 a ,2 b ,从而求出标准方程; ⑶在不知道焦点的情况下可设椭圆方程为221Ax By +=; 行程问题常见题型分析 在列方程解应用题问题中,行程问题是一个必不可少的内容,也是比较难的一个内容。 一、弄清行程问题中基本的量和它们之间的关系。 行程问题中有三个基本量:速度、时间、路程。 这三个量之间的关系是:路程=时间×速度。 变形可得到:速度=路程/时间 时间=路程/速度 这三个量的作用是知道其中两个就可以表示第三个。 二、行程问题常见类型 1、普通相遇问题。 2、追及(急)问题。3顺(逆)水航行问题。4、跑道上的相遇(追急)问题 三、行程问题中的等量关系 所谓等量关系就是不同的项表示的同一个量(路程、时间或速度)应该相等,并可用等式列出。 1、若路程已知,则应找时间的等量关系和速度的等量关系。 2、若速度已知,则应找时间的等量关系和路程的等量关系。 3、若时间已知,则找路程的等量关系和速度的等量关系。 在航行问题中还有两个固定的等量关系,就是: 顺水速度=静水速度+水流速度逆水速度=静水速度-水流速度 四、分类举例 例1 :小明每天早上要在7:50之前赶到距离家1000米的学校去上学。小明以80米/分的速度出发,5分钟后小明的爸爸发现他忘了带语文书。于是,爸爸立即以180米/分的速度去追小明,并且在途中追上了他。爸爸追小明用了多长时间? 分析:此题中小明的速度,爸爸的速度均已告诉。因此速度之间不存在等量关系。我们只能在父子二人的时间和父子二人的路程上找等量关系。由于小明比爸爸早出发5分钟,且相遇时在同一个时刻,因此相遇时爸爸比小明少用5分钟,可得时间的等量关系:①爸爸的时间+5分钟=小明的时间;当爸爸追上小明时,父子二人都是从家走到相遇的地点,故爸爸行的路程与小明行的路程相等。可得路程相等关系。②爸爸路程=小明路程如果爸爸追上小明用了x分钟,则由第一个相等关系得:小明用了(x +5)分钟。 又由第二个等量关系,可得此题方程: 180x(爸爸的路程)=80(x+5)(小明的路程) 高考数学 直线和圆锥曲线常考题型 运用的知识: 1、两条直线111222:,:l y k x b l y k x b =+=+垂直:则121k k =-;两条直线垂直,则直线所在的向量120v v =r r g 2、韦达定理:若一元二次方程2 0(0)ax bx c a ++=≠有两个不同的根12,x x ,则1212,b c x x x x a a +=-=。 3、中点坐标公式:1212,y 22 x x y y x ++= =,其中,x y 是点1122(,)(,)A x y B x y ,的中点坐标。 4、弦长公式:若点1122(,)(,)A x y B x y ,在直线(0)y kx b k =+≠上, 则1122y kx b y kx b =+=+,,这是同点纵横坐标变换,是两大坐标变换技巧之一, AB = 或者AB = 例题1、已知直线:1l y kx =+与椭圆22 : 14x y C m +=始终有交点,求m 的取值范围 解: 14m m ≤≠且。 例题2、过点T(-1,0)作直线l 与曲线N :2 y x =交于A 、B 两点,在x 轴上是否存在一点E(0x ,0),使得ABE ?是等边三角形,若存在,求出0x ;若不存在,请说明理由。 解:依题意知,直线的斜率存在,且不等于0。 设直线:(1)l y k x =+,0k ≠,11(,)A x y ,22(,)B x y 。 由2 (1)y k x y x =+?? =?消y 整理,得2222 (21)0k x k x k +-+= ① 由直线和抛物线交于两点,得 2242(21)4410k k k ?=--=-+> 即2 1 04 k << ② 由韦达定理,得:212221 ,k x x k -+=-121x x =。 则线段AB 的中点为22211 (,)22k k k -- 。 线段的垂直平分线方程为:2 21112()22k y x k k k --=-- 一、政治答题公式 1.初中政治每课的结构 是什么+为什么+怎么办(这也是做每个习题的最基本思路)。 2.是什么 含义+表现+特点+形成+种类(不是每个必讲,用的不多,在做题的第一句话时需要点清是什么)。 3.为什么的思考角度 作用+意义+重要性=必要性+危害性+关系+功能+原则+理念等。 4.怎么办 国家怎么办+社会怎么办+公民怎么办+青少年怎么办+{途径+方式+方法+技能技巧}。 5.国家怎么办 政治怎么办+经济怎么办+文化怎么办+法制怎么办+其它方针政策怎么办。 6.青少年怎么办 理想+品德+心理品质+学习+方法+途径(品德一般是八荣,心理品质:情绪.意志.挫折.性格,等)。 7.怎么办: 出主意+建议+办法+启示。 8.每个题的最后答案可归纳为: 是什么,为什么,怎么办。 9.人物类分析说明题的常用语句(人物类分析说明题除了心理分析外,还有以下常用语句)公式 给人物定性+涉及的课本原理+联系材料证明+表态怎么办。 10.评价问题: 注意点;引入材料+知识评析; 答案组合:行为评价(行为定性与判断)+道德角度+;法律角度+心理品质方面。 11.材料分析题:分析思路及格式 在关键是搞清涉及到那些知识(判断出是什么)点的基础上按以下格式答题: ①用课本知识分析说明观点(原因) ②结合材料分析 ③回归提问得出结论 ④表态(青少年的做法) 12.实践题 ①班会: 主题,目的,标语,歌曲,步骤活动方式,发言提纲(看法); ②做活动:调查组(调查目的,调查内容,调查方法,调查对象,提出建议),宣传组(板报,板报拦目,漫画,解说词)策划组(征文,演讲,知识竞赛,图片展); ③形式:辩论会,主题班会,故事会,板报手抄报,调查报告,参观访问,家务劳动,公益劳动,校内各种活动等。 【椭圆】 一、椭圆的定义 1、椭圆的第一定义:平面内一个动点P 到两个定点1F 、2F 的距离之和等于常数 )2(2121F F a PF PF >=+ ,这个动点P 的轨迹叫椭圆。这两个定点叫椭圆的焦点,两焦 点的距离叫作椭圆的焦距。 注意:若)(2121F F PF PF =+,则动点P 的轨迹为线段21F F ; 若)(2121 F F PF PF <+,则动点P 的轨迹无图形。 二、椭圆的方程 1、椭圆的标准方程(端点为a 、b ,焦点为c ) (1)当焦点在x 轴上时,椭圆的标准方程:12222=+b y a x )0(>>b a ,其中2 22b a c -=; (2)当焦点在y 轴上时,椭圆的标准方程:12222=+b x a y )0(>>b a ,其中2 22b a c -=; 2、两种标准方程可用一般形式表示: 221x y m n += 或者 mx 2+ny 2=1 三、椭圆的性质(以122 22=+b y a x )0(>>b a 为例) 1、对称性: 对于椭圆标准方程122 22=+b y a x )0(>>b a :是以x 轴、y 轴为对称轴的轴对称图形;并且 是以原点为对称中心的中心对称图形,这个对称中心称为椭圆的中心。 2、范围: 椭圆上所有的点都位于直线a x ±=和b y ±=所围成的矩形内,所以椭圆上点的坐标满足 a x ≤, b y ≤。 3、顶点: ①椭圆的对称轴与椭圆的交点称为椭圆的顶点。 ②椭圆122 22=+b y a x )0(>>b a 与坐标轴的四个交点即为椭圆的四个顶点,坐标分别为 )0,(1a A -,)0,(2a A ,),0(1b B -,),0(2b B 。 ③线段21A A ,21B B 分别叫做椭圆的长轴和短轴,a A A 221=,b B B 221=。a 和b 分别叫做椭圆的长半轴长和短半轴长。 4、离心率: ① 椭圆的焦距与长轴长度的比叫做椭圆的离心率,用e 表示,记作a c a c e == 22。 ② 因为)0(>>c a ,所以e 的取值范围是)10(< 椭 圆专题总结 一、直线与椭圆问题的常规解题方法: 1.设直线与方程; (提醒:①设直线时分斜率存在与不-存在;②设为y=kx+b 与x=my+n 的区别) 2.设交点坐标;(提醒:之所以要设是因为不去求出它,即“设而不求”) 3.联立方程组; 4.消元韦达定理;(提醒:抛物线时经常是把抛物线方程代入直线方程反而简单) 5.根据条件重转化;常有以下类型: ①“以弦AB 为直径的圆过点0”(提醒:需讨论K 是否存在) ②“点在圆内、圆上、圆外问题” ?“直角、锐角、钝角问题” ?“向量的数量积大于、等于、小于0问题” ?12120x x y y +>>0; ③“等角、角平分、角互补问题” ?斜率关系(120K K +=或12K K =); ④“共线问题” (如:AQ QB λ= ?数的角度:坐标表示法;形的角度:距离转化法); (如:A 、O 、B 三点共线?直线OA 与OB 斜率相等); ⑤“点、线对称问题” ?坐标与斜率关系; ⑥“弦长、面积问题”?转化为坐标与弦长公式问题(提醒:注意两个面积公式 的 合理选择); 6.化简与计算; 7.细节问题不忽略; ①判别式是否已经考虑;②抛物线、双曲线问题中二次项系数是否会出现0. 二、基本解题思想: 1、“常规求值”问题:需要找等式,“求范围”问题需要找不等式; 2、“是否存在”问题:当作存在去求,若不存在则计算时自然会无解; 3、证明定值问题的方法:⑴常把变动的元素用参数表示出来,然后证明计算结果与参数无 关;⑵也可先在特殊条件下求出定值,再给出一般的证明。 4、处理定点问题的方法:⑴常把方程中参数的同次项集在一起,并令各项的系数为零,求 出定点;⑵也可先取参数的特殊值探求定点,然后给出证明, 5、求最值问题时:将对象表示为变量的函数,几何法、配方法(转化为二次函数的最值)、 三角代换法(转化为三角函数的最值)、利用切线的方法、利用均值不等式的方法等再解决; 6、转化思想:有些题思路易成,但难以实施。这就要优化方法,才能使计算具有可行性, 关键是积累“转化”的经验; 椭圆中的定值、定点问题 一、常见基本题型: 在几何问题中,有些几何量和参数无关,这就构成定值问题,解决这类问题常通过取参数和特殊值来确定“定值”是多少,或者将该问题涉及的几何式转化为代数式或三角式,证明该式是恒定的。 (1)直线恒过定点问题 1、已知点00(,)P x y 是椭圆2 2:12 x E y +=上任意一点,直线l 的方程为0012 x x y y +=,直线0l 过P 点与直线l 垂直,点M (-1,0)关于直线0l 的对称点为N ,直线PN 恒过一定点G ,求点G 的坐标。 有关定积分问题的常见题型解析 题型一 利用微积分基本定理求积分 例1、求下列定积分: (1) ( ) 1 3 31x x dx -+? (2) 4 1dx ? (3) ? --2 2 24x 分析:根据求导数与求原函数互为逆运算,找到被积函数得一个原函数,利用微积分基本公式代入求值。 评注:利用微积分基本定理求定积分 dx x f a b )(?的关键是找出)()(/ x f x F =的函数)(x F 。 如果原函数不好找,则可以尝试找出画出函数的图像, 图像为圆或者三角形则直接求 其面积。 题型二 利用定积分求平面图形的面积 例2 如图 ,求直线y=2x+3与抛物线y=x 2 所围成的图形面积。 分析:从图形可以看出,所求图形的面积可以转化为一个梯形与一个曲边梯形面积的差,进而可以用定积分求出面积。为了确定出被积函数和积分和上、下限,我们需要求出两条曲线的交点的横坐标。 评注:求平面图形的面积的一般步骤:⑴画图,并将图形分割成若干曲边梯形;⑵对每个曲边梯形确定其存在的范围,从而确定积分上、下限;⑶确定被积函数;⑷求出各曲边梯形的面积和,即各积分的绝对值之和。 关键环节:①认定曲边梯形,选定积分变量;②确定被积函数和积分上下限。 知识小结:几种典型的曲边梯形面积的计算方法: (1)由三条直线x=a 、x=b (a <b )、x 轴,一条曲线y=()x f (()x f ≥0)围成的曲边梯形的面积: S = ()?b a dx x f ,如图1。 (2)由三条直线x=a 、x=b (a <b )、x 轴,一条曲线y=()x f (()x f ≤0)围成的曲边梯形的面积: S = ()()??-=b a b a dx x f dx x f ,如图2。 (3)由两条直线x=a 、x=b (a <b )、两条曲线y=()x f 、y=()x g (()()x g x f ≥)围成的平面图形的面积:S = ()()?-b a dx x g x f ][,如图3。 椭圆常见题型与典型方法归 纳 -标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII 椭圆常见题型与典型方法归纳 考点一 椭圆的定义 椭圆的第一定义:我们把平面内与两个定点12,F F 的距离的和等于常数 1.22(2)a a F F >的点的轨迹叫做椭圆.这两 定点12,F F 叫做椭圆的焦点,两定点间的距离叫做椭圆的焦距. 椭圆的第二定义:我们把平面内与一个定点的距离和它到一条定直线的距离的比是常数e= a c (0 一次函数常见题型解析(一) 题型一、点的坐标 方法: x 轴上的点纵坐标为0,y 轴上的点横坐标为0; 若两个点关于x 轴对称,则他们的横坐标相同,纵坐标互为相反数; 若两个点关于y 轴对称,则它们的纵坐标相同,横坐标互为相反数; 若两个点关于原点对称,则它们的横坐标互为相反数,纵坐标也互为相反数; 1、 若点A (m,n )在第二象限,则点(|m|,-n )在第____象限; 2、 若点P (2a-1,2-3b )是第二象限的点,则a,b 的范围为______________________; 3、 已知A (4,b ),B (a,-2),若A ,B 关于x 轴对称,则a=_______,b=_________;若A,B 关于y 轴对称,则a=_______,b=__________;若若A ,B 关于原点对称,则a=_______,b=_________; 4、 若点M (1-x,1-y )在第二象限,那么点N (1-x,y-1)关于原点的对称点在第______象限。 题型二、关于点的距离的问题 方法:点到x 轴的距离用纵坐标的绝对值表示,点到y 轴的距离用横坐标的绝对值表示; 任意两点(,),(,)A A B B A x y B x y ; 若AB ∥x 轴,则(,0),(,0)A B A x B x 的距离为A B x x -; 若AB ∥y 轴,则(0,),(0,)A B A y B y 的距离为A B y y -; 点(,)A A A x y 1、 点B (2,-2)到x 轴的距离是_________;到y 轴的距离是____________; 2、 点C (0,-5)到x 轴的距离是_________;到y 轴的距离是____________;到原点的距 离是____________; 3、 点D (a,b )到x 轴的距离是_________;到y 轴的距离是____________;到原点的距离 是____________; 4、 已知点P (3,0),Q(-2,0),则PQ=__________,已知点110,,0,22M N ? ???- ? ????? ,则MQ=________; ()()2,1,2,8E F --,则EF 两点之间的距离是__________;已知点G (2,-3)、H (3,4),则G 、H 两点之间的距离是_________; 5、 两点(3,-4)、(5,a )间的距离是2,则a 的值为__________; 6、 已知点A (0,2)、B (-3,-2)、C (a,b ),若C 点在x 轴上,且∠ACB=90°,则C 点坐 标为___________. 题型三、一次函数与正比例函数的识别 方法:若y=kx+b(k,b 是常数,k ≠0),那么y 叫做x 的一次函数,特别的,当b=0时,一次 函数就成为y=kx(k 是常数,k ≠0),这时,y 叫做x 的正比例函数,当k=0时,一次函数就成为若y=b ,这时,y 叫做常函数。 ☆A 与B 成正比例 A=kB(k ≠0) 1、当k_____________时,()2 323y k x x =-++-是一次函数; 椭圆的知识点总结(一) 一、椭圆的定义 1、椭圆的第一定义:平面内与两定点F 1、F 2的距离和等于常数(2a ,且2a>|F 1F 2|)点的轨迹叫做椭圆。 说明:两个定点F 1(c ,0)、F 2(-c ,0)叫做椭圆的焦点; 两焦点间的距离叫做椭圆的焦距(2c ); 建立合适的坐标系,椭圆截与两焦点连线重合的直线所得的弦为长轴,长为2a ,椭圆截垂直平分两焦点连线的直线所得弦为短轴,长为2b 。 2、椭圆的第二定义:平面上到定点的距离与到定直线的距离之比为常数e ,当0 二、椭圆的方程 1、椭圆的标准方程 ● 焦点在x 轴,22 22x 1y a b +=(a>b>0) ● 焦点在y 轴,22 22x 1y b a +=(a>b>0) 椭圆上任意一点到F 1,F 2距离的和为2a ,F 1,F 2之间的距离为2c 。而公式中的b2=a2-c2,b 是为了书写方便设定的参数,同时在椭圆的图像中,b 代表短轴的一半。 ● 当焦点位置不明确时,方程可设为2 2 m 1x ny +=(m>0,n>0,且m≠n ),即标准方程 的统一形式。 ● 根据椭圆的第一定义推导标准方程: 考虑焦点在x 轴的情况(焦点在y 轴的情况类似),根据椭圆的第一定义,建立坐标系,以F 1,F 2的连线为x 轴,F 1,F 2的中垂线为y 轴。 1222222222222 222222242222,)F -,0F ,022()44()444()() 22p x y c c a a x c y a x c y a xc a x c y a xc a x a xc a c a y a a xc x c a ==-++=--+=-??-+=-??-++=-+设点坐标为(,坐标为(),坐标为()222224222222222222422222422224222222222222222222 22)() 1x a c a y a x c b a c a x a a b a y a x a b a x a a b a y a x a x b a b a y x b x b a y a b x y a b ++=+=-+-+=+-+-+=+--+=-+=+=令,代入,有 ( ● 根据椭圆的第二定义推导标准方程: 椭圆常考题型汇总及练习 第一部分:复习运用的知识 (一)椭圆几何性质 椭圆第一定义:平面内与两定点21F F 、距离和等于常数 ()a 2(大于21F F )的点的轨迹叫做椭圆. 两个定点叫做椭圆的焦点;两焦点间的距离叫做椭圆的焦距 ()c 2. 椭圆的几何性质:以 ()0122 22>>=+b a b y a x 为例 1. 范围: 由标准方程可知,椭圆上点的坐标()y x ,都适合不等式1,122 22≤≤b y a x ,即 b y a x ≤≤,说明椭圆位于直线a x ±=和b y ±=所围成的矩形里(封闭曲线).该性质主要用 于求最值、轨迹检验等问题. 2. 对称性:关于原点、x 轴、y 轴对称,坐标轴是椭圆的对称轴,原点是椭圆的对称中心。 3. 顶点(椭圆和它的对称轴的交点) 有四个:()()()().,0B ,0B 0,0,2121b b a A a A 、、、-- 4. 长轴、短轴: 21A A 叫椭圆的长轴,a a A A ,221=是长半轴长; 21B B 叫椭圆的短轴,b b B B ,221=是短半轴长. 5. 离心率 (1)椭圆焦距与长轴的比a c e =,()10,0<<∴>>e c a Θ (2)22F OB Rt ?, 2 22 22 22OF OB F B +=,即222c b a +=.这是椭圆的特征三角形,并且 22cos B OF ∠的值是椭圆的离心率. (3)椭圆的圆扁程度由离心率的大小确定,与焦点所在的坐标轴无关.当e 接近于1时,c 越接近于a ,从而22c a b -= 越小, 椭圆越扁;当e 接近于0时,c 越接近于0,从而2 2c a b -=越大,椭圆越接近圆。 三、判断推理 一)、图形推理 (1)数量型图形推理:数量型图形推理一般包括点(交点)、线(线条数、笔画数)、面(角、图形种类、图形的封闭区间)等数量关系。 例题: 解析:数量型图形推理,所给字母都为三条线段组成;故答案为D。 (2)对称型图形推理:对称性图形推理考查图形的对称性,一般包括翻转、平移、轴对称、中心对称等。(最常见图形:九宫格) 例题:二、 解析:对称型图形推理,此题为隐藏了九宫格的平移图形推理,其中每个小块围绕九宫格的中心顺时针进行向上、向下、向左或向右的平移,且平移一个格;故答案为A。 (3)叠加型图形推理:叠加型图形推理考查图形的叠加性,一般包括两个或几个图形相加/相减、去同存异、去异存同等。 例题: 解析:叠加型图形推理,前四个图形相加能够组成B项图形;故答案为B。 (4)空间型图形推理:空间型推行推理考查图形的空间逻辑性,一般包括图形的空间立体图形与平面展开图形。 例题: 解析:空间型图形推理,从图形平面图可以看出,两个阴影正方形的位置只能是相对的,所以A、C、D可以排除;故答案为B。 二)、类比推理 一、造句法:将所给词语按照一定的逻辑关系造句,所造词语逻辑关系最为相似的一组即为答案。 例题:例1、()对于行动相当于()对于航行 A.目标灯塔 B.信心风帆 C.激情桅杆 D.毅力水手 解析:利用造句法,目标是行动的方向,灯塔市航行的方向;故答案为A。 二、词义法:根据词语的词义关系选择最佳答案,一般包括近义词、反义词、同意异名等。 例题:例2、寡对于()相当于利对于() A.孤弊 B.少害 C.众钝 D.多益 解析:此题考查的是反义词对应;故答案为C。 三、搭配法:根据词语的搭配关系选择最佳答案,一般包括动宾搭配、成语及其出处搭配、作者及其作品搭配、历史事件及其时间/人物搭配等。 例题:例3、分配:任务 A.解决:问题 B.团结:合作 C.公共:服务 D.信息:技术 解析:分配任务为动宾搭配,选项中只有A项解决问题也为动宾搭配;故答案为A。 四、总分关系法:根据词语间的总分关系选择最佳答案。 例题:例4、阳光:紫外线 A.电脑:辐射 B.海水:氯化钠 C.混合物:单质 D.微波炉:微波 解析:阳光与紫外线,海水与氯化钠都是整体与组成部分的关系;故答案为B。 五、代入法:将选项词语代入题干中,逻辑关系最为相似的一组即为答案。 例题:例5、()对于知识相当于分析对于() A.书本理论 B.学习结论 C.学问研究 D.学生研究员 解析:将A代入题干中,得到书本里面有知识,分析理论,两组词的逻辑关系不统一;将B代入题干中,得到学习知识,分析结论逻辑关系类似;故答案为B。 三)、演绎推理 ㈠三段论:由三个简单判断组成,其中两个是前提,一个是结论。 例题:不法分子都害怕法律的制裁(大前提);杀人犯是不法分子(小前提);所以杀人犯害怕法律的制裁(结论)。 ㈡假言推理:以一个假言判断作为大前提,通过对这一判断的前件或后件的肯定或否定,从而得出结论。假言推理可分为:充分条件假言推理、必要条件假言推理和充分必要条件假言推理等三种假言推理形式。 (1)充分条件假言推理:指以充分条件假言判断的大前提的演绎推理。 例题:例一、如果两条线平行,那么它们就是直线;这两条线不平行;所以,它们就不是直线。显然,这个结论是错误的,因为所有的不弯曲的两点之间最短的线都是直线。 例二、如果饮酒过量,肝脏就会生病;他的肝脏生病;所以,他饮酒过量了。 这一结论不符合实际情况,因为有时其他诸多原因,也会引起肝脏生病。 (2)必要条件假言推理:指以必要条件假言判断作为大前提的演绎推理。这种推理可分为肯定式和否定式两种。 ①必要条件假言推理(肯定式)。 例题:只有努力学习,才能取得好成绩;晓鸣取得了好成绩;可见,他努力学习了。 这种肯定的一般规则是:肯定后件,就能肯定前件;但是否定后件,不能否定前件。例如:只有忠诚党的高中数学:椭圆知识点归纳总结及经典例题
(完整版)椭圆常见题型总结
行程问题常见题型分析
高考数学-直线和椭圆(圆锥曲线)常考题型
初中政治常见题型解析
椭圆知识点总结
椭圆综合专题整理(供参考)
有关定积分问题的常见题型解析(全题型)
椭圆常见题型与典型方法归纳
一次函数常见题型解析(一)
椭圆知识点总结
椭圆常考题型汇总及练习进步
行测判断推理常见题型分析及详解
