简支钢梁计算带公式
5.简支H型钢梁计算

简支H型钢梁计算表格使用及编制说明1.凡单元格内红色字体均为需要交互输入的数据。
当选中单元格时右侧出现向下箭头,则直接选择箭头菜单内的数字或字母。
2.适用范围:2.1力学模型:单向受弯的单跨简支梁,可用于各种钢结构平台、转运站及屋面等结构计算。
2.2计算类型:可用于不多于一组满布均布荷载和六组梁跨范围任意位置的集中荷载,每组荷载均包含一个恒载和一个活载。
3.计算内容:3.1荷载:一组满布均布荷载(应包含梁自身质量),荷载距离即为梁跨;六组集中荷载分别作用于梁跨范围的1~6点位,荷载距离按计算简图依次填入荷载表中。
3.2荷载组合:荷载按标准值和设计值分别计算,以用于正常使用极限状态下的挠度计算和承载力极限状态下的强度和稳定计算。
结构重要性系数取1;荷载效应组合的设计值则采用基本组合中由可变荷载效应控制的组合,其荷载分项系数和组合值系数取值如下:永久荷载分项系数1.2;可变荷载分项系数1.4。
3.3内力计算:分别计算出了梁端支座反力和跨中及六个集中力点位(共计七个点位)处永久荷载和可变荷载下的弯矩标准值,进而得出相应的标准值之和和设计值。
内力计算采用叠加原理进行,每一点位处的内力为七个荷载在该点位处的内力叠加得出。
3.4截面计算:3.4.1截面类型:实腹截面的热轧H型钢、双轴对称的焊接H型钢。
截面尺寸参数交互输入,其中r视情况填入实际数据或0,表格自动计算截面模量等参数。
3.4.2钢材类型:梁材质为Q235、Q345、Q390和Q420。
3.4.3抗弯强度计算:选择最大弯矩值进行截面抗弯强度计算,其截面塑性发展系数γx需要交互输入。
3.4.4抗剪强度计算:梁支座反力较大值即为截面最大剪力,用于截面抗剪强度计算。
3.4.5梁整体稳定计算:梁整体稳定计算需要交互输入梁侧向支点最大距离(即受压翼缘的自由长度)l1和梁整体稳定的等效临界弯矩系数βb。
βb按《钢结构设计规范》GB50017-2003附录B的要求取用。
单跨变截面简支钢梁计算

t 1= 8 mm t 2= 8 mm t w= 6 mm
t 1= 8 mm t 2= 8 mm t w= 6 mm
kg/m
1/7
U.S.A.
JOB No.:__________
即 : 断面
350x6x180x BH 8x180x8
BY________________ DATE______________ CHK'D_____________
W 1x = 5.88E+05 mm 3
W 2x = 5.88E+05 mm 3 I y = 7.78E+06 mm 4
iy=
46.5 mm
y=
75.3
I 1 = 6.67E+06 mm 4
I 2 = 3.89E+06 mm 4
0.63 0.21 0.18
0.71 5/7
U.S.A.
JOB No.:__________
I z = 8.01E+08 mm 4
W 1x = 1.88E+06 mm 3 W 2x = 1.88E+06 mm 3
I y = 7.79E+06 mm 4
iy=
36.6 mm
y=
95.7
I 1 = 6.67E+06 mm 4
I 2 = 3.89E+06 mm 4
A 0 = 4884 mm 2 重量 38.3 y 0 = 175 mm I z = 1.03E+08 mm 4
钢梁截 面钢:梁中和 轴的位 置:
钢梁对X 轴截面惯 性矩:
钢梁上翼 缘的弹性 抵抗矩:
钢梁下翼 缘的弹性 抵抗矩:
钢梁对Y 轴截面惯 性矩:
简支钢梁计算

简 支 钢 梁 计 算基本数据输入:梁跨度: l=9000mm梁间距a=2400mm钢材:Q 345f =315N/mm 2fv =185N/mm 2 上翼缘:b 1=400mm t 1=14mm 下翼缘:b 2=300mm t 2=12mm 腹 板:h w =574mm t w =8mm即: 断面截面特性计算:钢梁截面:A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置:y 0=342mm钢梁对X轴截面惯性矩:I z =8.94E+08mm4钢梁上翼缘的弹性抵抗矩:W 1x = 3.46E+06mm 3 钢梁下翼缘的弹性抵抗矩:W 2x = 2.61E+06mm 3 钢梁对Y轴截面惯性矩:I y = 1.02E+08mm 4i y =85.9 mm y =104.8上翼缘对Y 轴的惯性矩:I 1=7.47E+07mm 4下翼缘对Y 轴的惯性矩:I 2= 2.70E+07mm 40.73 截面不对称影响系数:0.380.53 工字形截面简支梁的系数0.76 梁的整体稳定系数:0.74 修正后:0.672.截面验算:(1)弯矩及剪力的计算:=+=211I I I b α=-=)12(8.0b b αη=bβ==hb t l 111ξ=bφ='bφλ钢梁自重: 1.30KN/m恒载: 4.00KN/m2g1k=10.90KN/m活载:q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩:M=234.49KN·m剪力:V=104.22KN(2)钢梁的强度、稳定和挠度的验算:梁的整体稳定应力:σ=101.01N/mm2钢梁上翼缘应力:σ1=67.70N/mm2钢梁下翼缘应力:σ2=89.68N/mm2钢梁剪应力:τ=22.70N/mm2挠度:w=8.4mmw/l=1/1072。
简支梁计算表
U.S.A.
钢梁上翼 缘的弹性 抵抗矩:
钢梁下翼 缘的弹性 抵抗矩:
钢梁对Y 轴截面惯 性矩:
上翼缘对 Y轴的惯性 矩:
下翼缘对 Y轴的惯性 矩:
平面外 稳定系数 计算:
截面不 对称影响 系数:
工字形截 面简支梁 的系数
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
钢梁截 面钢:梁中和 轴的位 置:
钢梁对X 轴截面惯 性矩:
钢梁上翼 缘的弹性 抵抗矩:
钢梁下翼 缘的弹性 抵抗矩:
钢梁对Y 轴截面惯 性矩:
上翼缘对 Y轴下的翼惯缘性对 Y轴的惯性
截面特 性计算:
钢梁截 面钢:梁中和 轴的位 置:
钢梁对X 轴截面惯 性矩:
A 0 = 7884 mm 2 重量 61.9 y 0 = 425 mm
t 1= 8 mm t 2= 8 mm t w= 6 mm
t 1= 8 mm t 2= 8 mm t w= 6 mm
kg/m
1/7
U.S.A.
JOB No.:__________
即 : 断面
350x6x180x BH 8x180x8
BY________________ DATE______________ CHK'D_____________
U.S.A.
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
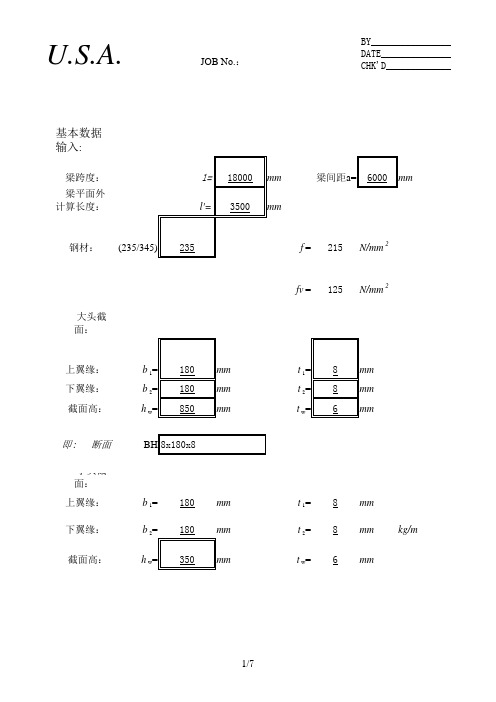
基本数据 输入:
梁跨度: 梁平面外 计算长度:
l= 18000 mm l'= 3500 mm
各种梁的弯矩计算公式

各种梁的弯矩计算公式在工程设计中,梁是一种常见的结构元素。
梁的弯曲是指当梁受到外力作用时,其截面发生弯曲变形。
为了计算梁的弯矩,设计者需要了解不同类型的梁及其特性。
1.矩形截面梁:矩形截面梁是最简单和常见的梁类型之一,其截面形状为矩形。
可以使用以下公式计算矩形截面梁的弯矩:M=(b*h^2*σ)/6其中,M是弯矩,b是梁的宽度,h是梁的高度,σ是应力。
2.T型截面梁:T型截面梁是梁的一种变体,其截面形状类似于字母“T”。
计算T 型截面梁的弯矩可以使用以下公式:M=((b1*h1^2*σ1)/6)+((b2*h2^2*σ2)/6)其中,M是弯矩,b1和b2是梁上下翼板的宽度,h1和h2是梁上下翼板的高度,σ1和σ2是应力。
3.I型截面梁:I型截面梁是一种常见且有效的梁形态,其截面形状类似于字母“I”。
计算I型截面梁的弯矩可以使用以下公式:M=(b1*h1^2*σ1/6)+(b2*h2^2*σ2/6)+(b3*h3^2*σ3/6)其中,M是弯矩,b1、b2和b3是梁的不同部分的宽度,h1、h2和h3是梁的不同部分的高度,σ1、σ2和σ3是应力。
4.简支梁:简支梁是一种在两端支承的梁结构,常见于桥梁和楼板等应用中。
计算简支梁的弯矩可以使用以下公式:M=(w*L^2)/8其中,M是弯矩,w是梁的均布载荷,L是梁的跨度。
5.连续梁:连续梁是一种具有多个支点的梁结构,常见于长跨度桥梁和大型建筑物中。
计算连续梁的弯矩可以使用以下公式:M=(w*L^2)/(8*n)其中,M是弯矩,w是梁的均布载荷,L是梁的跨度,n是支点的数量。
这里只是列举了几种常见梁的弯矩计算公式,实际上,基于梁的几何形状和加载条件,还可以有其他更复杂的公式。
因此,在实际工程设计中,如果遇到需要计算梁的弯矩的情况,应根据具体问题,选择适合的公式进行计算。
同时,为了确保计算结果的准确性,建议使用专业的结构分析软件进行梁的弯矩计算。
简支梁计算公式总汇

简支梁在各种荷载作用下跨中最大挠度计算公式:均布荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 5ql^4/384EI.式中: Ymax 为梁跨中的最大挠度mm.q 为均布线荷载标准值kn/m.E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得mm^4.跨中一个集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 8pl^3/384EI=1pl^3/48EI.式中: Ymax 为梁跨中的最大挠度mm.p 为各个集中荷载标准值之和kn.E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得mm^4.跨间等间距布置两个相等的集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = ^3/384EI.式中: Ymax 为梁跨中的最大挠度mm.p 为各个集中荷载标准值之和kn.E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得mm^4.跨间等间距布置三个相等的集中荷载下的最大挠度,其计算公式: Ymax = ^3/384EI.式中: Ymax 为梁跨中的最大挠度mm.p 为各个集中荷载标准值之和kn.E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得mm^4.悬臂梁受均布荷载或自由端受集中荷载作用时,自由端最大挠度分别为的,其计算公式:Ymax =1ql^4/8EI. ;Ymax =1pl^3/3EI.q 为均布线荷载标准值kn/m. ;p 为各个集中荷载标准值之和kn.你可以根据最大挠度控制1/400,荷载条件25kn/m以及一些其他荷载条件进行反算,看能满足的上部荷载要求。
梁钢筋长度计算公式

梁钢筋长度计算公式1.钢筋长度计算公式:在梁底面和顶面的纵向钢筋一般是按照水平面上的曲线计算,即假设梁的曲线为圆弧,常用的计算公式如下:L=2π(R-D/2)+2√(h^2+(D/2)^2)其中,L为钢筋长度,R为梁的曲率半径,D为梁的直径,h为梁高。
此公式适用于梁的跨度较大,曲率半径较小的情况。
2.梁受压钢筋长度计算公式:在梁的底部受压区域,通常会设置纵向受压钢筋(又称主筋)来承受弯矩引起的压力,其长度计算公式如下:Lc=(2h-Dc)+π(R-D/2)其中,Lc为受压钢筋长度,Dc为纵向受压钢筋的直径。
需要注意的是,梁的受压区域一般是重新计算的,通常为梁高的一半。
3.梁受弯钢筋长度计算公式:在梁的底部受拉区域,通常会设置纵向受拉钢筋(又称为弯曲钢筋),其长度计算公式如下:Ls = 2[hp - (Dc/2 + Φd)]其中,Ls为受弯钢筋长度,hp为纵向受拉钢筋到梁底面的距离,Φd为受拉钢筋的直径。
4.梁剪力钢筋长度计算公式:在梁的剪力区域,通常会设置纵向受拉钢筋(又称为剪切钢筋),其长度计算公式如下:Lv = 2d + 2hp + (D c/2 + Φd) + 2d'其中,Lv为剪力钢筋长度,d为纵向受拉钢筋到梁底面的距离,hp为纵向受拉钢筋到梁底面的距离,d'为受拉钢筋与梁边缘的最小距离。
5.其他因素的考虑:不同设计规范可能会根据特殊情况进行修正,例如温度和构造变形等因素的考虑。
此外,在实际工程中,还需要考虑钢筋的连接和延伸长度等。
因此,在具体设计时,还需要参考相关规范,并结合具体工程条件进行相关的计算和设计。
以上是常见的梁钢筋长度计算公式,需要根据具体情况和设计规范进行具体的计算。
在实际工程中,还需要注意其他因素的考虑,以确保结构的安全和合理性。
各种梁的弯矩计算公式

各种梁的弯矩计算公式在结构工程中,梁的弯矩计算是非常重要的一部分。
弯矩是描述梁在受力作用下发生弯曲变形的力学量,其计算公式可以根据梁的截面形状、材料性质和受力情况等因素来确定。
以下是一些常见梁的弯矩计算公式:1.简支梁简支梁是一种两端简支的梁,其弯矩计算公式可以根据跨度、截面形状和材料性质等因素来确定。
一般而言,简支梁的弯矩计算公式为:M = F*l/4其中,M为弯矩,F为梁所受的集中力或分布荷载,l为梁的跨度。
2.外伸梁外伸梁是一种一端固定,另一端外伸的梁。
由于其受力情况比简支梁复杂,因此需要采用更复杂的公式来计算弯矩。
一般而言,外伸梁的弯矩计算公式为:M = F a l/4 + F b l/2其中,a和b分别为梁在自由端左右两边的外伸长度。
3.固端梁固端梁是一种一端固定,另一端自由的梁。
由于其固定端受到约束,因此其弯矩计算公式与外伸梁有所不同。
一般而言,固端梁的弯矩计算公式为:M = F l l/8 + F a l/4其中,a为梁在自由端一侧的外伸长度。
4.连续梁连续梁是一种多跨相连的梁,其弯矩计算公式需要根据跨度、截面形状和材料性质等因素来确定。
一般而言,连续梁的弯矩计算公式为:M = F l/4 + F a l/2 + F b*l/4其中,a和b分别为梁在左右两边的外伸长度。
需要注意的是,以上公式仅适用于一些常见的梁类型,对于其他复杂的梁类型或特定的受力情况,可能需要采用更复杂的公式来计算弯矩。
此外,在计算过程中还需要考虑截面形状、材料性质和荷载情况等因素对弯矩的影响。
为了得到更准确的结果,可能需要借助专业的结构分析软件进行计算。
简支钢梁计算XX

简 支 钢 梁 计 算基本数据输入:梁跨度:l=6000mm 梁间距a=2000mm梁平面外计算长度:l'=6000mm钢材:Q 235f =345N/mm 2fv =185N/mm 2 上翼缘:b 1=180mm t 1=6mm 下翼缘:b 2=180mm t 2=8mm 腹 板:h w =336mmt w =6mm即: 断面BH 350x6x180x6x180x8截面特性计算:钢梁截面:A 0=4536mm 2 重量35.6kg/m钢梁中和轴的位置:y 0=162mm钢梁对X轴截面惯性矩:I z =9.23E+07mm 4 钢梁上翼缘的弹性抵抗矩:W 1x = 4.91E+05mm 3 钢梁下翼缘的弹性抵抗矩:W 2x = 5.69E+05mm 3 钢梁对Y轴截面惯性矩:I y = 6.81E+06mm 4i y =38.7 mm y =154.9上翼缘对Y 轴的惯性矩:I 1= 2.92E+06mm 4 下翼缘对Y 轴的惯性矩:I 2= 3.89E+06mm 40.43 截面不对称影响系数:-0.110.57 工字形截面简支梁的系数0.76 0.52 0.522.截面验算:(1)弯矩及剪力的验算:钢梁自重:0.43KN/m 恒 载:4.80KN/m 2=+=211I I I b a =-=)12(8.0b b a h =bb==hb t l 111x =bf='bflg=10.03KN/m1k活载:q c=10.00KN/m2p k=30.03KN/m p=38.03KN/m 弯矩:M=171.15KN·m剪力:V=114.10KN(2)钢梁的强度、稳定和挠度的验算:钢梁上翼缘应力:σ1=670.88N/mm2钢梁下翼缘应力:σ2=300.65N/mm2钢梁剪应力:τ=56.60N/mm2挠度:w=26.7mmw/l=1/225。
简支钢梁设计计算书

------------------------------- | 简支梁设计 | | | | 构件:BEAM52 | | 日期:2015/08/31 | | 时间:15:37:10 | ------------------------------------ 设计信息 -----钢梁钢材:Q235梁跨度(m): 5.200梁平面外计算长度(m): 2.600钢梁截面:焊接组合H形截面:H*B1*B2*Tw*T1*T2=300*250*250*6*12*12 容许挠度限值[υ]: l/400 = 13.000 (mm)强度计算净截面系数:1.000计算梁截面自重作用: 计算简支梁受荷方式: 竖向单向受荷荷载组合分项系数按荷载规范自动取值----- 设计依据 ----- 《建筑结构荷载规范》(GB 50009-2012)《钢结构设计规范》(GB 50017-2003)----- 简支梁作用与验算 -----1、截面特性计算A =7.6560e-003; Xc =1.2500e-001; Yc =1.5000e-001;Ix =1.3500e-004; Iy =3.1255e-005;ix =1.3279e-001; iy =6.3894e-002;W1x=9.0000e-004; W2x=9.0000e-004;W1y=2.5004e-004; W2y=2.5004e-004;2、简支梁自重作用计算梁自重荷载作用计算:简支梁自重 (KN): G =3.1252e+000;自重作用折算梁上均布线荷(KN/m) p=6.0100e-001;3、梁上活载作用荷载编号荷载类型荷载值1 荷载参数1 荷载参数2 荷载值2 1 4 8.10 2.60 0.00 0.004、单工况荷载标准值作用支座反力 (压为正,单位:KN)△恒载标准值支座反力左支座反力 Rd1=1.563, 右支座反力 Rd2=1.563△活载标准值支座反力左支座反力 Rl1=4.050, 右支座反力 Rl2=4.0505、梁上各断面内力计算结果△组合1:1.2恒+1.4活断面号: 1 2 3 4 5 6 7 弯矩(kN.m): -0.000 3.202 6.268 9.199 11.995 14.655 17.180 剪力(kN) : 7.545 7.233 6.920 6.608 6.295 5.983 -5.670断面号: 8 9 10 11 12 13弯矩(kN.m): 14.655 11.995 9.199 6.268 3.202 -0.000剪力(kN) : -5.983 -6.295 -6.608 -6.920 -7.233 -7.545△组合2:1.35恒+0.7*1.4活断面号: 1 2 3 4 5 6 7 弯矩(kN.m): -0.000 2.558 4.963 7.216 9.317 11.266 13.062 剪力(kN) : 6.078 5.727 5.375 5.024 4.672 4.321 -3.969断面号: 8 9 10 11 12 13弯矩(kN.m): 11.266 9.317 7.216 4.963 2.558 -0.000剪力(kN) : -4.321 -4.672 -5.024 -5.375 -5.727 -6.0786、局部稳定验算翼缘宽厚比 B/T=10.17 < 容许宽厚比 [B/T] =15.0腹板计算高厚比 H0/Tw=46.00 < 容许高厚比[H0/Tw]=80.07、简支梁截面强度验算简支梁最大正弯矩(kN.m):17.180 (组合:1; 控制位置:2.600m)强度计算最大应力(N/mm2):18.179 < f=215.000简支梁抗弯强度验算满足。
钢结构梁简易计算

钢结构梁简易计算在建筑和工程领域,钢结构梁的设计和计算是至关重要的环节。
它不仅关系到结构的安全性和稳定性,还直接影响着整个工程的成本和质量。
对于一些不太复杂的钢结构梁,我们可以通过一些简易的计算方法来初步评估其承载能力和性能。
接下来,就让我们一起探讨一下钢结构梁的简易计算方法。
首先,我们需要了解钢结构梁的基本组成和受力情况。
钢结构梁通常由钢材制成,其截面形状有多种,如工字梁、H 型梁、箱型梁等。
在承受荷载时,梁会产生弯曲应力、剪应力和局部承压应力等。
对于弯曲应力的计算,我们可以使用经典的弯曲公式。
假设梁受到一个均布荷载 q,跨度为 L,那么梁的最大弯矩 M 可以表示为 M =qL²/8。
然后,根据梁的截面特性,如惯性矩 I 和截面模量 W,弯曲应力σ 可以通过公式σ = M / W 计算得出。
接下来是剪应力的计算。
在均布荷载作用下,梁的最大剪力 V 为qL/2。
剪应力τ 可以通过公式τ = V S / I b 计算,其中 S 是截面的静矩,b 是截面的宽度。
除了上述的基本应力计算,还需要考虑梁的局部承压应力。
当梁上有集中荷载作用时,在荷载作用处会产生局部承压应力。
这个应力的大小与荷载大小、荷载作用面积以及钢材的强度等因素有关。
在进行钢结构梁的简易计算时,还需要注意一些实际的问题。
例如,钢材的强度取值要根据其材质和规格来确定。
同时,要考虑梁的支撑条件,是简支梁、悬臂梁还是连续梁,不同的支撑条件会影响梁的内力分布。
另外,在计算过程中,还需要考虑安全系数。
安全系数是为了保证结构在使用过程中的安全性和可靠性,通常会根据相关的规范和标准来选取。
让我们通过一个具体的例子来进一步说明钢结构梁的简易计算过程。
假设我们有一个跨度为 6 米的简支工字钢梁,承受均布荷载 5kN/m,钢材采用 Q235,我们来计算其弯曲应力和剪应力是否满足要求。
首先,计算最大弯矩 M = 5×6²/8 = 225 kN·m。
工学装配式钢筋混凝土简支形梁桥计算示例

V0 447.35KN, Vl 118.96KN m
2
假定有 232 通过支点,按《公预规》9.3.10条的构造要求,
1
a
34.5 30 2
47.3mm,
h0
h
a
1200
47.3
1252.7mm
l 2
在确定处支点处和跨中的横向分布系数以后,其他位置的荷载横向分布系 数便可以用近似处理的方法来处理,方法参见下图.
1号梁M l , M l 及Q l的计算
42
2
同理,2号梁M l , M l 及Q l的计算
42
2
3号梁M l , M l 及Q l的计算
42
2
(6)计算支点处的剪力 绘制荷载横向分布系数沿桥纵向的变化图形和支点剪力影响线,如下图所示,
0.4) 7.875 0.916
192.55KN
人群荷载下,Q0r
0.4 2.259
1 4.45 (0 0.4) 2.25 0.916 2
6.27KN
3、荷载效应组合 钢筋混凝土及预应力混凝土梁式桥,当按承载能力极限状态设计时,作用效应组合
按公式 sud 1.2s自重 1.4s汽 +0.81.4s人计算
注意:杠杆原理法适用于计算荷载位于靠近主梁支点时的荷载横向分布系数
②荷载位于跨中时,1、2、3号梁相应于公路二级和人群荷载的横向分布系数
本例采用偏心压力法计算,它适用于桥上具有可靠的横向联接,且桥的宽跨比B/L小 于或接近于0.5的情况时,跨中截面荷载横向分布系数 mc .
公式: ik
1 n
excel计算大全-钢结构计算表格-简支钢梁计算

excel计算大全-钢结构计算表格-简支钢梁计算简支钢梁计算基本数据输入:梁跨度: l=9000mm梁间距a=2400mm钢材:Q 345f =315N/mm 2fv =185N/mm 2 上翼缘:b 1=400mm t 1=14mm 下翼缘:b 2=300mm t 2=12mm 腹板:h w =574mm t w =8mm即: 断面BH 600x8x400x14x300x12截面特性计算:钢梁截面:A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置:y 0=342mm钢梁对X轴截面惯性矩:I z =8.94E+08mm 4 钢梁上翼缘的弹性抵抗矩:W 1x = 3.46E+06mm 3 钢梁下翼缘的弹性抵抗矩:W 2x = 2.61E+06mm 3钢梁对Y轴截面惯性矩:I y = 1.02E+08mm 4i y =85.9 mm y =104.8上翼缘对Y 轴的惯性矩:I 1=7.47E+07mm 4 下翼缘对Y 轴的惯性矩:I 2= 2.70E+07mm 40.73 截面不对称影响系数:0.380.53 工字形截面简支梁的系数0.76 梁的整体稳定系数:0.74 修正后:0.672.截面验算:(1)弯矩及剪力的计算:=+=211I I I b α=-=)12(8.0b b αη=bβ==hb t l 111ξ=bφ='bφλ钢梁自重: 1.30KN/m恒载: 4.00KN/m2=10.90KN/mg1k活载:q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩:M=234.49KN·m 剪力:V=104.22KN(2)钢梁的强度、稳定和挠度的验算:梁的整体稳定应力:σ=101.01N/mm2钢梁上翼缘应力:σ1=67.70N/mm2钢梁下翼缘应力:σ2=89.68N/mm2钢梁剪应力:τ=22.70N/mm2挠度:w=8.4mmw/l=1/1072。
简支H型钢梁计算

简支H型钢梁计算在工程中,H型钢梁是一种常见的结构材料,广泛应用于建筑和桥梁等领域。
H型钢梁具有高强度、高刚度和重量轻的特点,能够有效承受水平和垂直荷载,因此在结构设计中起到至关重要的作用。
H型钢梁的计算是结构设计的关键步骤,下面将详细介绍简支H型钢梁的计算方法。
1.弯矩计算:首先需要计算出简支H型钢梁受到的最大弯矩。
弯矩计算公式为:M=(qL^2)/8其中,M为弯矩,单位为N·m;q为均布荷载,单位为N/m;L为梁的长度,单位为m。
2.应力计算:H型钢梁在承受弯矩时,上翼板和下翼板呈受拉状态,而腹板则呈受压状态。
为了保证结构的安全性,需要对H型钢梁的应力进行计算。
上下翼板受拉应力的计算公式为:σ1=M/(W1*h)其中,σ1为上下翼板的受拉应力,单位为Pa;M为弯矩,单位为N·m;W1为上下翼板的截面模量,单位为m^3;h为上下翼板的高度,单位为m。
腹板受压应力的计算公式为:σ2=M/(W2*t)其中,σ2为腹板的受压应力,单位为Pa;M为弯矩,单位为N·m;W2为腹板的截面模量,单位为m^3;t为腹板的厚度,单位为m。
3.拉压强度计算:H型钢梁在受力时需要满足一定的拉压强度要求,因此需要计算H型钢梁的拉压强度。
拉压强度计算的公式为:F=σ*A其中,F为拉压强度,单位为N;σ为应力,单位为Pa;A为截面面积,单位为m^2根据弯矩计算和应力计算的结果,可以计算出H型钢梁的拉压强度,从而判断H型钢梁是否符合设计要求。
此外,在实际的H型钢梁计算中,还需要考虑梁的端部承载能力、支座的稳定性以及梁的自重等因素。
这些因素需要结合具体的工程情况进行综合考虑和计算。
综上所述,简支H型钢梁的计算是一个复杂的过程,需要综合考虑弯矩、应力和拉压强度等因素。
在实际应用中,还需要根据具体的工程情况进行细化设计和计算。
为了确保H型钢梁的结构安全和稳定性,建议由专业的结构工程师进行计算和设计。
钢结构梁简易计算

平台恒载标准值:kN/m 2活载标准值:kN/m 2恒载分项系数(r G ):活载分项系数(r Q ):截面塑性发展系数(r x ):钢材材质:计算步骤:`次梁按照简支梁设计,画计算简图,强度设计值f=f v =(1)荷载计算:次梁承担板面荷载宽度:m 次梁长度:m 荷载标准值:q k =[(+荷载设计值:q d =[(*+*(2)外荷载引起的内力:跨中最大弯矩设计值:2次梁所需截面抵抗矩:*6*(3)选择截面,进行验算:(3.1)查表选用型钢为:,质量:I x =cm 4,W x =cm 3,S x =cm 3,t w =mm,t=mm,r=mm,508.2292.78.5cm 332157115kg/m,91.875*51.4)*91.875W n =M=r x f kN/m ]kN/m=406.98kN/m kN.m()mm 3=103)kN.m=29.43.5=( 1.2418*29.4 3.541.21.41.0543.471.05Q235)*]kN/m=3.54I28a M max 215N/mm 2N/mm 23522.512513.710.5钢结构次梁计算书(3.2)验算:最大内力设计值:2==①抗弯强度验算:*6**3②抗剪强度验算:**3*4*③支座处局部受压强度验算:a =mm (取支座长度为mm)l z =+=[+(+)]mm=mm **④刚度验算:q k =(+**)kN/m=kN/m *4**4查受弯构件挠度容许值[ν]=l/>ν⑤整体稳定性验算:次梁与刚性面板连牢不验算整体稳定条件。
经验算所选截面满足要求,可作为梁的设计截面。
)kN.m *9.8*5kN.m *10* 1.2-3+18*43.47V max M max =(91.87593.473*+1*212101.05508.21093.47310)N/mm 2=N/mm 29.8*σ=M=(r x W x74.778kN *29.4*5=(τ=VS=)kN <215N/mm 2(满足要求)-374778292.7101.2*(I x t w <125N/mm 2(满足要求)108.5)N/mm 2=711536.2N/mm 2*175.17543.47a h y 10013.7100100124.2σc =10.5ψF=(l z t w 70.8N/mm 2f=215N/mm 21.074778)N/mm 2=8.5124.2(5*<9.810-322.926ν=q k l 4=EI 5384*I28a mm ≈393l1022.9265000)mm=206000250(满足要求)384711512.7(满足要求)22.543.47。
梁计算公式大全范文

梁计算公式大全范文一、受力分析公式:1.梁的受弯矩计算公式:M=W*(L-a)其中,M为弯矩,W为梁受力点的集中力,L为梁长度,a为集中力作用点到梁起点的距离。
2.梁的剪力计算公式:V=W其中,V为剪力,W为梁受力点的集中力。
3.梁的弯矩和剪力分布公式:M(x)=M1-W*(x-a)V(x)=-W其中,M(x)为距离梁起点x处的弯矩,M1为梁起点的弯矩,V(x)为距离梁起点x处的剪力。
二、截面计算公式:1.截面受弯矩计算公式:σ=M*c/I其中,σ为截面受弯应力,M为弯矩,c为截面形心到受压纤维距离,I为截面惯性矩。
2.截面抗弯承载力计算公式:Fc=σ*S其中,Fc为截面抗弯承载力,S为截面抗弯矩。
3.截面受剪力计算公式:τ=V/(b*h)其中,τ为截面受剪应力,V为剪力,b为截面宽度,h为截面高度。
4.截面抗剪承载力计算公式:Fv=τ*A其中,Fv为截面抗剪承载力,τ为截面受剪应力,A为截面面积。
三、挠度计算公式:1.简支梁挠度计算公式:δ=(5*W*L^4)/(384*E*I)其中,δ为梁的挠度,W为集中力,L为梁长度,E为弹性模量,I为惯性矩。
2.等截面梁挠度计算公式:δ=(5*q*L^4)/(384*E*I)其中,δ为梁的挠度,q为梁上的均布荷载,L为梁长度,E为弹性模量,I为惯性矩。
3.连续梁挠度计算公式:δ=(q*(L^4))/(185*E*I)其中,δ为梁的挠度,q为梁上的均布荷载,L为梁长度,E为弹性模量,I为惯性矩。
四、其他公式:1.梁的重量计算公式:G=γ*A*L其中,G为梁的重量,γ为材料的比重,A为梁的截面面积,L为梁的长度。
2.梁的弯曲刚度计算公式:EI=(E*I)其中,EI为梁的弯曲刚度,E为弹性模量,I为截面的惯性矩。
以上是梁计算中常用的公式,不同类型和形式的梁可能需要针对具体情况进行具体计算。
在进行梁的设计计算时,应根据工程实际情况选择合适的公式,并结合相关的参数进行计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I 2 = 2.70E+07 mm 4
1/3
U.S.A.
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
0.73
截面不对 称影响系 数:
工字形截 面简支梁的 系数
钢梁下翼 缘的弹性抵 抗矩:
钢梁对Y轴 截面惯性 矩:
上翼缘对Y 轴的惯性 矩:
下翼缘对Y 轴的惯性 矩:
简支
l= 9000 mm
梁间距a= 2400 mm
Q 345
b 1= 400 mm b 2= 300 mm h w= 574 mm
600x8x400x BH 14x300x12
f = 315 N/mm 2
p = 23.16
234.49 KN ·m
104.22 KN
KN/m
(2)钢梁 的强度、稳 定和挠度的 验算:
梁的
整体稳定应 力:
σ = 101.01 N/mm 2
2/3
U.S.A.
钢梁 上翼缘应 力:
钢梁 下翼缘应 力:
钢梁 剪应力:
挠 度:
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
0.38 0.53
0.76
梁பைடு நூலகம்整体 稳定系数:
0.74
修正后:
2.截面验 算:
(1)弯矩 及剪力的计 算:
钢梁自 重: 恒 载:
活 载:
0.67
1.30 KN/m 4.00 KN/m 2 g = 1k 10.90 KN/m q c = 3.0 KN/m 2
pk= 弯矩: 剪力:
18.10
KN/m M= V=
fv = 185 N/mm 2 t 1= 14 mm t 2= 12 mm t w= 8 mm
A 0 = 13792 mm 2 重量 108.3 kg/m y 0 = 342 mm
I z = 8.94E+08 mm 4
W 1x = 3.46E+06 mm 3
W 2x = 2.61E+06 mm 3
I y = 1.02E+08 mm 4 i y = 85.9 mm y = 104.8
σ 1= 67.70 N/mm 2
σ 2= 89.68 N/mm 2
τ= 22.70 N/mm 2
w= w / l=
8.4 mm 1/ 1072
3/3
U.S.A.
JOB No.:__________
BY________________ DATE______________ CHK'D_____________
基本数据 输入:
梁跨度:
钢材:
上翼缘: 下翼缘: 腹 板:
即 : 断面
截面特性
钢梁截 面:
钢梁中和 轴的位置:
钢梁对X轴 截面惯性 矩:
钢梁上翼 缘的弹性抵 抗矩:
