高中数学必修4知识点总结

必修4基础知识汇整
第一部分 三角函数与三角恒等变换
1.⑴ 角度制与弧度制的互化:π弧度180=,1180
π
=弧度,1弧度180()π='5718≈.
⑵ 弧长公式:||l R α=;扇形面积公式:211
||22
S R Rl α=
=. 2.三角函数定义:
⑴ 设α是一个任意角,终边与单位圆交于点P (x ,y ),那么y 叫作α的正弦,记作sin α;
x 叫作α的余弦,记作cos α;
y
x
叫作α的正切,记作tan α. ⑵ 角α中边上任意一点P 为(,)x y ,设||OP r =,则:
sin ,cos ,y x r r αα==tan y
x
α=.
三角函数符号规律:一全正,二正弦,三正切,四余弦. 3.三角函数线:
正弦线:MP ; 余弦线:OM ; 正切线: AT .(过定点A (1,0)) 4
六组诱导公式统一为“()2
k Z α±∈”
,记忆口诀:奇变偶不变(对k 而言),符号看象限.
5.同角三角函数基本关系:22sin cos 1αα+=(平方关系);sin tan cos
α
αα
=
(商数关系). 6.两角和与差的正弦、余弦、正切:① sin()sin cos cos sin αβαβαβ±=±;
② cos()cos cos sin sin αβαβαβ±=; ③ tan tan tan()1tan tan αβ
αβαβ
±±=.
7.二倍角公式:① sin22sin cos ααα=;
② 2222cos2cos sin 2cos 112sin α
αααα=-=-=-; ③ 22tan tan 21tan α
αα
=-.
变形:21cos2sin 2αα-=;21cos2cos 2
α
α+=. (降幂)
8.辅助角公式:sin cos )y a x b x x x =+)x ?+. 万能公式:a
a a a a cos 1sin sin cos 12tan
+=
-= 9. 物理意义:物理简谐运动sin(),[0,)y A x x ω?=+∈+∞,其中0,0A ω>>. 振幅为A ,
表示物体离开平衡位置的最大距离;周期为
2
T
π
ω
=,表示物体往返运动一次所需的时间;
频率为
1
2
f
T
ω
π
==,表示物体在单位时间内往返运动的次数;x
ω?
+为相位;?为初相.
(会根据图像求函数的解析式)
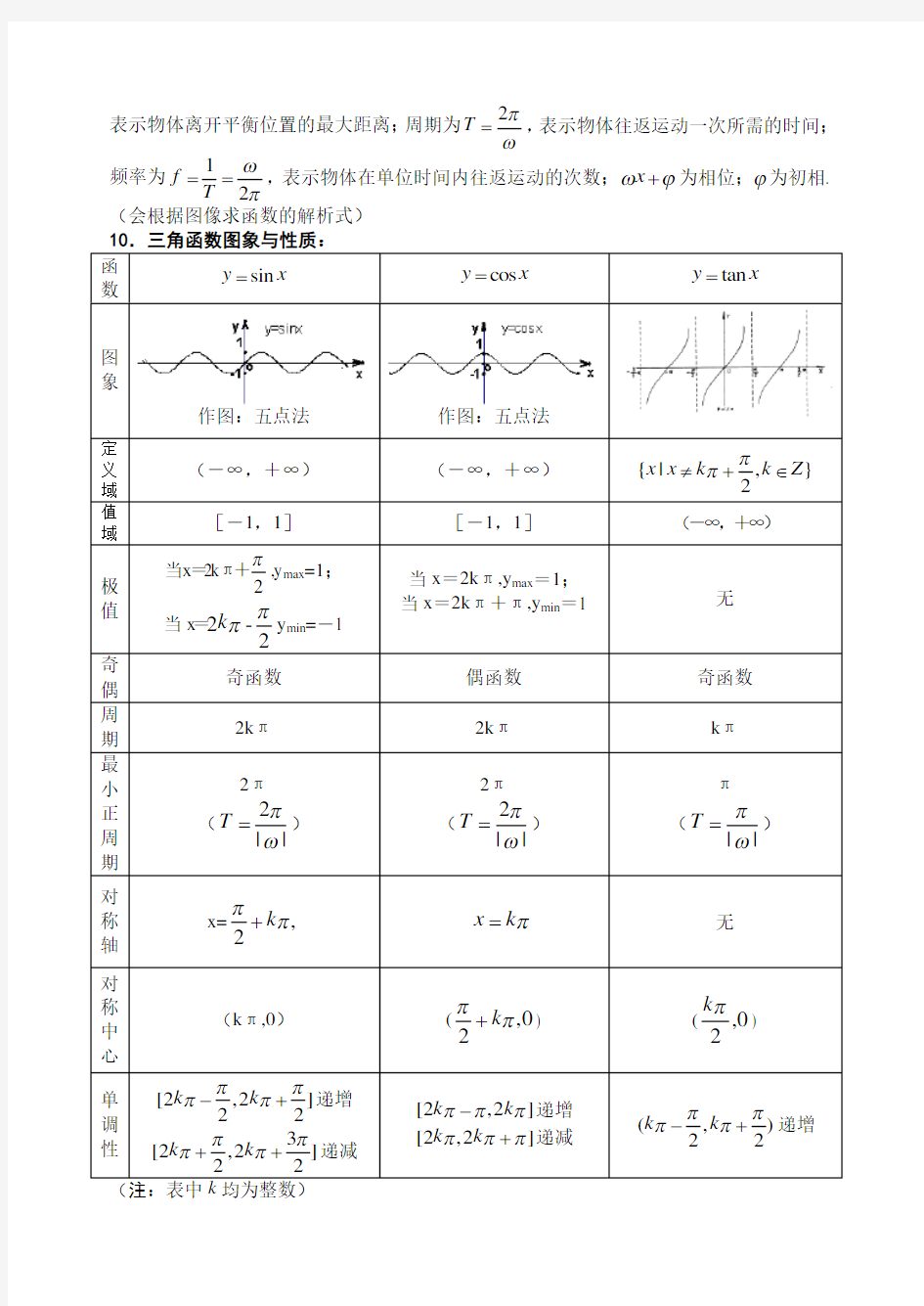
函数
sin
y x
=cos
y x
=tan
y x
=
图
象
作图:五点法作图:五点法定
义域(-∞,+∞)(-∞,+∞){|,}
2
x x k k Z
π
π
≠+∈
值
域
[-1,1][-1,1](-∞,+∞)
极值当x=2kπ+
2
π
,y max=1;
当x=
2
-
2
π
πk y min=-1
当x=2kπ,y max=1;
当x=2kπ+π,y min=1 无
奇
偶
奇函数偶函数奇函数周
期
2kπ2kπkπ最
小正周期
2π
(
|
|
2
ω
π
=
T)
2π
(
|
|
2
ω
π
=
T)
π
(
|
|ω
π
=
T)
对
称轴x=,
2
π
π
k
+πk
x=无
对
称中心(kπ,0)(,0
2
π
π
k
+) (0,
2
πk
)
单调性[2,2]
22
k k
ππ
ππ
-+递增
3
[2,2]
22
k k
ππ
ππ
++递减
[2,2]
k k
πππ
-递增
[2,2]
k k
πππ
+递减
(,)
22
k k
ππ
ππ
-+递增
11. 正弦型函数sin()(0,0)y A x A ω?ω=+>>的性质及研究思路:
先把已知函数转化为sin()(0,0)y A x A ω?ω=+>>的形式 ① 最小正周期2T π
ω
=
,值域为[,]A A -.
② 五点法图:把“x ω?+”看成一个整体,取30,
,,
,222
x π
π
ω?ππ+=时的五个自变量
值,相应的函数值为0,,0,,0A A -,描出五个关键点,得到一个周期内的图象.
③ 三角函数图象变换路线:sin y x =??????→左移个单位
sin()y x ?=+ ω
?????→1
横坐标变为倍 sin()y x ω?=+A ?????
→纵坐标变为倍
sin()y A x ω?=+. 或:sin y x = ω
?????→1
横坐标变为倍
sin y x ω=?
ω
?????
→左移个单位
sin ()y x ?ωω
=+A ?????
→纵坐标变为倍
sin()y A x ω?=+. (先伸缩后平移这种情况必须保证x 前面的系数为1)
④ 单调性:sin()(0,0)y A x A ω?ω=+>>的增区间,把“x ω?+”代入到sin y x =增
区间[2,
2]()22k k k Z π
π
ππ-
++∈,即求解22()22
k x k k Z π
π
πω?π-
+≤+≤
+∈.减区
间同理(注:求单调区间必须保证x 前面的系数为正)
⑤对称轴:sin()(0,0)y A x A ω?ω=+>>的对称轴,把“x ω?+”代入到sin y x =对
称轴x=
,2
ππ
k +(Z k ∈)
,即求解x ω?+=,2
ππ
k +(Z k ∈)
。y=Acos(x ω?+)同理 ⑥对称中心:sin()(0,0)y A x A ω?ω=+>>的对称中心,把“x ω?+”代入到sin y x =对称中心(k π,0)(Z k ∈),即求解x ω?+= k π,(Z k ∈)。y=Acos(x ω?+)同理
⑦最大,最小值(或值域):先把函数转化为sin()(0,0)y A x A ω?ω=+>>的形式 (1)当x 的范围是全体实数,那么当x ω?+=2
2π
π+
k 时,y max =A,
当x ω?+=2-
2π
πk 时,y min =-A
(2)当x 的范围是指定的,就须先根据x 的范围确定x ω?+的范围,再根据x ω?+的范围画图来确定sin(x ω?+)的取值范围,在进行计算 y=Acos(x ω?+)同理
⑧ 整体思想:把“x ω?+”看成一个整体,代入sin y x =,y=cosx 与tan y x =的性质
中进行求解. 这种整体思想的运用,主要体现在求单调区间时,对称轴,对称中心或取最大值与最小值时的自变量取值.
余弦型函数y=Acos(x ω?+),正切型函数y=Atan(x ω?+)的性质及研究思路同理(按第10点的表所列的性质)
第二部分 平面向量
平面向量
1. 向量与数量:在数学中,我们把既有大小,又有方向的量叫做向量,反之,把只有大小,没有方向的量称为数量. 向量常用有向线段来表示,记为a 或AB (起点A ,终点B ). 向量的大小叫做向量的长度(或模),记为||a 或||AB . 规定长度为0的向量叫做零向量,记为0;长度等于1个单位的向量称为单位向量.
2. 平行向量:方向相同或相反的非零向量叫做平行向量,记作//a b ,并规定零向量平行于任意一个向量. 平行向量都可以移到同一直线上,因而也叫共线向量. 方向相同且长度相等的向量称为相等向量,记作a b =. 与向量a 长度相等而方向相反的向量,称为a 的相反向量,记为a -,规定零向量的相反向量仍是零向量.
3. 向量加减法:
向量加减法运算遵循三角形法则与平行四边形法则.
如图所示,已知非零向量,a b ,在平面内任取一点O ,作,OA a AB b ==,则向量
b a AB OA OC OA OB +=+=+=.
若作,OA a OC b ==,则向量b a OC OA CA -=-=.
向量的加减法满足:交换律a b a b +=-;结合律()()a b c a b c ++=++. 向量加法:向量首尾相接,结果首尾连.
向量减法:向量起点相同,结果第二个向量终点指向第一个向量起点
4. 向量数乘运算(结果仍是一个向量):实数λ与向量a 的乘积仍然是一个向量,这种运算称为向量的数乘,记作a λ,并规定:① ||||||a a λλ=;②当0λ>时,a λ的方向与
a 的方向相同;当0λ<时,a λ的方向与a 的方向相反;当0λ=时,0a λ=. 数乘运
算满足:
分配律()u a a ua λλ+=+、()a b a b λλλ+=+;结合律()()a a λμλμ=. 对于任意向量,a b ,以及任意实数12,,u u λ,恒有1212()u a u b u a u b λλλ±=±. 向量的加、减、数乘运算统称为向量的线性运算. 5. 平面向量基本定理:如果12,e e 是同一平面内的两个不共线向量,那么对这一平面内的任意向量a ,有且只有一对实数12,λλ,使1122a e e λλ=+. 把不共线的向量12,e e 叫做表示这一平面内所有向量的一组基底.(不共线的两个向量都可以作为一组基底)
向量夹角(起点须相同):对两个非零向量,a b ,在平面内任取一点O ,作
,OA a OB b ==,则AOB θ=∠叫做向量a 与b 夹角. 当a 与b 夹角是90°时,a 与b 垂
直,记作a b ⊥.
正交分解:依据平面向量的基本定理,对平面上的任意向量a ,均可分解为不共线的两个向量11a λ与22a λ,使1122a a a λλ=+. 若把一个向量分解为两个互相垂直的向量,叫做把向量正交分解.
坐标表示:在平面直角坐标系中,分别取与x 轴、y 轴方向相同的两个单位向量,i j 作为基底,则对于平面内的一个向量a ,有且只有一对实数x 、y ,使得a xi y j =+. 即平面内的任意向量a 都可由x 、y 唯一确定,把有序数对(x ,y )叫做向量a 的坐标,记作(,)a x y =,式子(,)a x y =叫做向量的坐标表示.
6. 平面向量的数量积运算(结果是一个实数):θcos ||||b a b a =?,其中θ是a 与b 的夹角,||cos a θ叫做向量a 在b 方向上的投影.b a ?的几何意义:数量b a ?等于a 的长度
||a 与b 在a 的方向上的投影||cos b θ的乘积. 数量积运算满足:
交换律?=?;数乘结合律)()()(b a b a b a λλλ?=?=?; 分配律c a b a c b a ?+?=+?)(.
把?记作2
a ,有性质22||a a =,从而2
||a a =. 7. 平面向量的坐标运算:设11(,)a x y =,22(,)b x y =,则
加减法:1212(,)a b x x y y +=++,1212(,)a b x x y y -=--;
数乘:11(,)a x y λλλ=;向量积:2121y y x x +=?;模:21||a x =+ 距离:2||||(AB d AB b a x ==-=-(终点坐标减起点坐标) 夹角:21
1
cos ,||||
a b
a b a b x y
<>=
=+.
8. 向量共线:设11(,)a x y =,22(,)b x y =,其中0b ≠,若,a b 共线,当且仅当存在实数
λ,使a b λ=,即//a b a b λ?=12210x y x y ?-=. 由此可证明平行问题、三点共线等.
9. 向量垂直:对于平面内任意两个非零向量,a b ,0a b a b ⊥?=. 设11(,)a x y =,
22(,)b x y =,则12120a b x x y y ⊥?+=. 由此可证明一些垂直问题.
2(AB x x =-||||a b 或转化为两个非零向量,a 的数量积为b 共线,即a 11. 向量法解决平面几何问题三步曲:
(1)建立平面几何与向量的联系,用向量表示问题中涉及的几何元素,将平面几何问题转化为向量问题;
(2)通过向量运算,研究几何元素之间的关系,如距离、夹角等;
(3)把运算结果“翻译”成几何关系,得到几何问题的结论.
