运筹学动态规划

第7章 动态规划

动态规划是Bellman 在1957年提出的解多阶决策问题的方法，在那个时期，线性规划很流行，它是研究静态问题的，而Bellman 提出的解多阶决策问题的方法适用于动态问题，相对于线性规划研究静态问题，取名动态规划。动态规划方法应用范围非常广泛，方法也比较简单。动态规划是将一个多阶决策问题分解为一系列的互相嵌套的一步决策问题，序贯求解使问题得到简化。 动态规划问题按照问题的性质可以分为确定性的和随机性的，按决策变量的和状态变量的取值可以分为离散型的和连续型的。此外还有依据时间变量连续取值还是离散取值又分为连续时间动态规划问题和离散时间动态规划问题。本章重点讨论离散时间确定性动态规划问题，包括状态变量和决策变量连续取值和离散取值两种情况。

7.1解多阶决策问题的动态规划法

1.多阶决策问题的例

(1)最优路径问题—多阶决策问题的例

为了直观，先从最优路径问题谈起，它可以看作一个多阶决策过程。通过最优路径问题的解可以看到用动态规划法解多阶决策问题的基本思想。

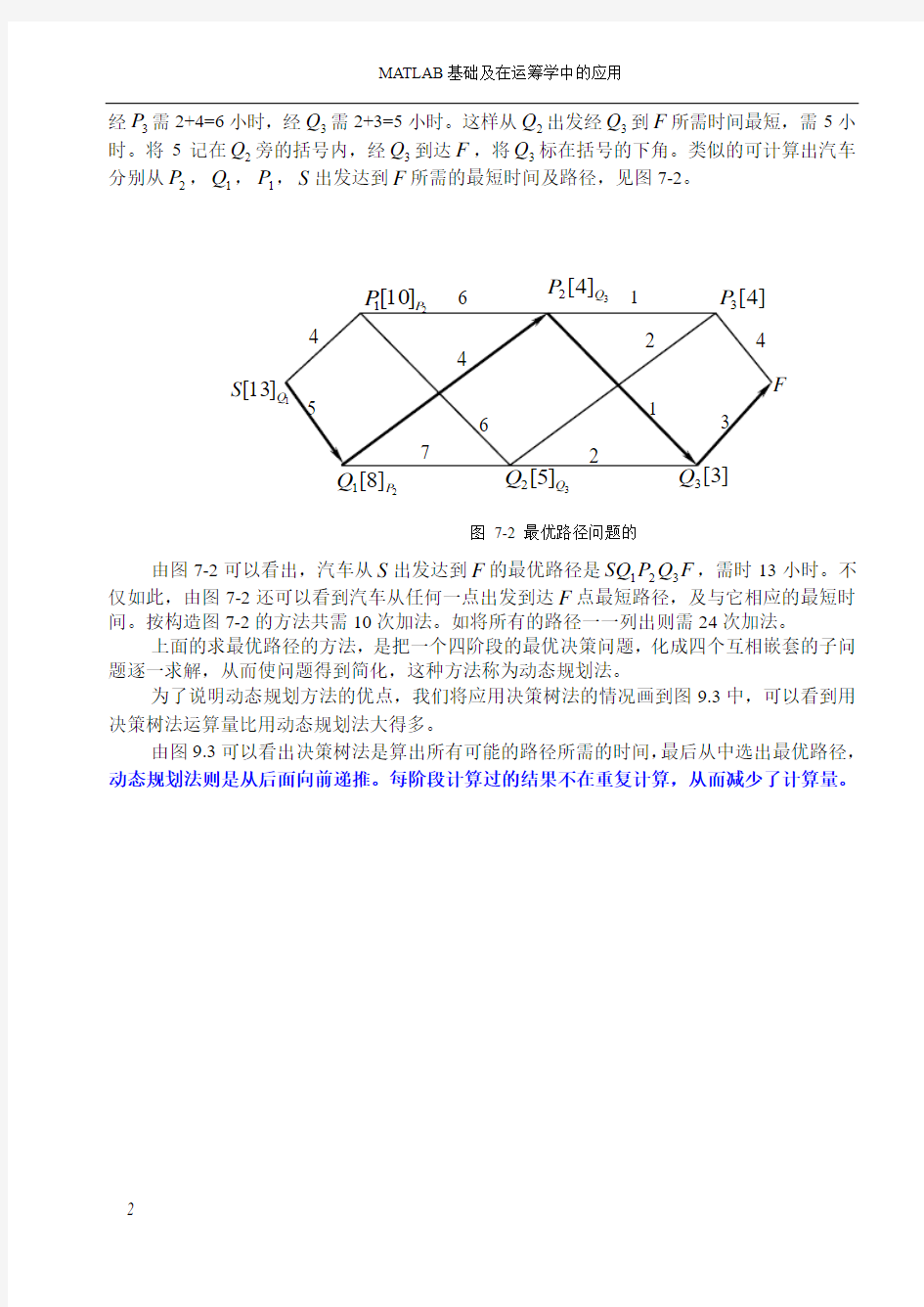
考虑图7-1所示的最优路径问题。一汽车由S 点出发到终点F ，P 和Q 是一些可以通过的点。图中两点间标出的数字是汽车走这一段路所需的时间(单位为小时)。最优路径问题是确定一个路径，使汽车沿这条路径由S 点出发达到F 点所用时间最短。最优路径问题可以看作一个多阶决策问题，由S 到城市甲是第1个阶段，第1个结点P 1或第2个结点Q 1做为第1阶段可以通过的两个站点，由城市甲到城市乙是第2阶段，这个阶段是从P 1或Q 1到P 2或

Q 2，由城市乙到城市丙是第3阶段，这个阶段是从P 2或Q 2到P 3或Q 3，由城市丙的P 3或Q 3到F 做为第四阶段。

（2）最优路径问题的解

对最优路径问题，存在一个非常明显的原理，即最优路径的一部分还是最优路径。换句话说，如果SQ P Q F 123是所求的最优路径，那么，汽车从这一路径上的任何一点，例如P 2，出发到F 的最优路径必为P Q F 23。这一原理称为最优性原理。根据这一原理可以由后向前递推求出最优路径。

如果汽车已到Q 3，由Q 3直接到F 用3小时，如果汽车已到P 3，由P 3直接到F 用4小时，这两个数字分别标在图7-2中Q 3和P 3旁的方括号内。再向前推一步，设汽车已在2Q ，

1441P 2

P 3P 1Q 2Q 3Q 42

2166753S F 图7-1最优路径问题

经P 3需2+4=6小时，经Q 3需2+3=5小时。这样从Q 2出发经Q 3到F 所需时间最短，需5小时。将5记在Q 2旁的括号内，经Q 3到达F ，将Q 3标在括号的下角。类似的可计算出汽车分别从P 2，Q 1，P 1，S 出发达到F 所需的最短时间及路径，见图7-2。

由图7-2可以看出，汽车从S 出发达到F 的最优路径是SQ P Q F 123，需时13小时。不仅如此，由图7-2还可以看到汽车从任何一点出发到达F 点最短路径，及与它相应的最短时间。按构造图7-2的方法共需10次加法。如将所有的路径一一列出则需24次加法。

上面的求最优路径的方法，是把一个四阶段的最优决策问题，化成四个互相嵌套的子问题逐一求解，从而使问题得到简化，这种方法称为动态规划法。

为了说明动态规划方法的优点，我们将应用决策树法的情况画到图9.3中，可以看到用决策树法运算量比用动态规划法大得多。

由图9.3可以看出决策树法是算出所有可能的路径所需的时间，最后从中选出最优路径，动态规划法则是从后面向前递推。每阶段计算过的结果不在重复计算，从而减少了计算量。

1442

]10[1P P 3]4[2Q P ]4[3P 2]8[1P Q 3]5[2Q Q ]3[3Q 422166

7531

]13[Q S F 图7-2最优路径问题的

2.应用动态规划解多阶决策问题的基本特征

动态规划是解多阶决策问题的一种方法。它可以求解的问题有如下特征：决策问题可以分成若干个阶段，每个阶段有若干与该阶段有关的状态和需要做的决策，系统从一个阶段的状态按一定的规律转移到下一个阶段的状态，多阶决策问题是求一个由每个阶段的决策构成的最优策略使得按决策目标最好。

应用动态规划解多阶决策问题有如下基本特征：

（1）问题可以依时间顺序或空间的自然特征划分为几个阶段，每个阶段有一个决策变量需要作出决策。用k 表示阶段数，用)(k u 表示第k 阶段的决策变量。

（2）动态规划中本阶段状态往往是上一阶段的状态和上一阶段的决策进行综合的结果．每个阶段作出决策后，使得当前的状态)(k x 转移到下一阶段的状态)1(+k x

)),(),(()1(k k u k x f k x =+ 1,,2,0-=N k

函数)),(),((k k u k x f 决定了这一转移过程，称它为转移函数。这个方程称为状态转移方程简称状态方程。

状态方程是研究对象的内在规律的数学描述，也称为研究对象的数学模型。 （3）每个阶段的决策变量的集合构成多阶决策问题的一个策略

)}1(,),1(),0({-N u u u

按照决策的目标，引进一个用于衡量所选定策略优劣的数量指标称为指标函数．一些决策过程的指标函数越大越好（例如指标函数是利润、产值等），另一些决策过程的指标函数越小越好（例如指标函数是成本、误差等）。使得指标函数最大（或最小）的策略称为最优策略。最优策略常记为)}1(*,),1(*),0(*{-N u u u

（4）以)),(),((k k u k x L 表示第k 阶段的指标函数，则N 阶决策过程的指标函数为

∑-==10

)),(),((N k N k k u k x L J

3.多阶段决策问题的一般提法

图 最短线路问题中的决策树

466

57

44315 11111

11第一第二第三第四

设多阶决策问题状态方程为

x k f x k u k k ()((),(),)+=1 （7-1）

指标函数为

∑-==1

)),(),((N k N k k u k x L J （7-2）

其中u k ()为决策变量。

多阶段决策问题是求一个策略:u ()0，u ()1，…，u N ()-1，使得指标函数J N 最大(或最小)。

使得指标函数J N 最大(或最小)的策略称为最优策略，常记为

)1(*,),1(*),0(*-N u u u

为了讨论简单，假设函数f 和L 都不依赖于时间变量，设状态方程为

x k f x k u k ()((),())+=1 （7-3）

指标函数为

J L x k u k N k N ==-∑((),())0

1

（7-4）

我们遇到的多数问题属于这种情况。

假设系统的初始状态给定为x x ()00=，在指标函数中逐次应用状态方程，可得到N 步决策的指标函数的值为

J L x u L x u L x N u N L x u L f x u u N =+++--=++((),())((),())((),())

((),())(((),()),())00111100001

经逐次代入可得到

J J x u u u N N N =-((),(),(),())0011

如果已经求出了使N J 最大（或最小）的最优策略u *

(),0u *

(),1 ,u N *

-()1，那么，将它们代入上式，就得到控制N 步的指标函数的最大值(或最小值)。由于

)1(*,),1(*),0(*-N u u u 已确定，N J 只依赖于x ()0，记为J x N *

(())0，即

))1(*,),1(*),0(*),0(())0((-=*

N u u u x J x J N N

一般地，初始条件为)(i x 时，i N -步决策的指标函数为

∑-=-=1

))(),((N i

k i N k u k x L J

如果已经求出了使i N J -最大（或最小）的最优策略)1(*,),1(*),(*-+N u i u i u ，那么，将它们代入上式，就得到控制i N -步的指标函数的最大值(或最小值)。由于

)1(*,),1(*),(*-+N u i u i u 已确定，N J 只依赖于)(i x ，记为))((i x J i N *

-，即

))1(*,),1

(*),(*),(())((-+=*

-N u i u i u i x J i x J N i N 简记为

))((i x J i N *

-

))((i x J i N *

-是第i 阶段状态为)(i x 指标函数的最优值，称为最优值函数。

4.动态规划的基本方程—Bellman 方程

(1)最优性原理

在最短路径问题中讲的最优性原理，对于一般多阶段决策问题也成立。多阶段决策问题的最优性原理，可用一句话概括：最优策略序列的一部分也构成一个最优策略序列。更具体的可叙述为如下的定理。

最优性原理：如果),0(*u ),1(*u ,)1(*-N u 是最优策略序列，那么它的一部分

),1(*u ,)1(*-N u 也是一个最优策略序列，其初始状态为))0(*),0(()1(u x f x =。

(2)动态规划的基本方程

下面导出动态规划的基本方程，它给出N 阶决策问题的指标函数最优值与它的子问题(一个N -1阶决策问题)的指标函数最优值之间的递推关系式。这个基本方程是用动态规划解一切多阶段决策问题的基础。

假设)0(*u 已求出，那么)1(*,),1(*),0(*-N u u u 的问题构成一个初始条件为

x f x u ()((),())100=*的N -1阶决策问题。这一问题的指标函数最小值记作J x N -*

11(())，

则有

???

???=∑-=-*10)

1(),1(),0())(),((min ))0((N k N u u u N

k u k x L x J ?

??

???+=∑-=-1

1)

1(),1(),0())(),(())0()0((min N k N u u u k u k x L u x L ???

?

????????+=∑-=-11)

1(),1(,)0())(),((min ))0(),0((min N k N u u u k u k x L u x L

{}))1(())0(),0((min 1)

0(x J u x L N u *

-+=

方程 {

}

J x L x u J x N u N *

-*

=+(())min ((),())(())()

000101

称为动态规划的基本方程，它给出了J x N *(())0与J x N -*

11(())之间的递推关系。 类似于上面的推导，可以得到动态规划基本方程的如下一般形式：

{}

))1(())(),((min ))((1)

(++=*--*-i x J i u i x L i x J i N i u i N （7-5）

动态规划的基本方程，也称递推方程或Bellman 方程，它给出了J x i N *

(())与

J x i N i --*

+11(())之间的递推关系。通过它可以把一个多阶决策问题化为若干个子问题，而在

决策的每一阶段，只需对一个变量进行最优化。 5.动态规划的逆向递归求解法

应用Bellman 方程（7-5），可以对以上多阶决策问题从最后一步开始递推求解。这一方法称为逆向递归求解法。该方法首先考虑一步最优化问题：

))1(),1((min ))1(()

1(1--=--*N u N x L N x J N u

))1(),1((--N u N x L 对变量u N ()-1求最小，这是一个静态最优化问题，解这个问题

得到)1(*-N u ，代入上式可以求出J x N 11*-(())。J x N 11*

-(())求出后，由Bellman 方程

{}

J x N L x N u N J x N u N 2212221*-*-=--+-(())min ((),())(())()

(7-6）

式中))2(),2(()1(--=-N u N x f N x 。在此约束条件下对花括号中的函数关于u N ()-2求最小，由于J x N 11*

-(())已经求出，这又是一个静态最优化问题，解这个问题得到

)2(*-N u 。这是通过解一阶必要条件

=-?-?--+-??)

2()

1()1())1(()2(*1N u N x N dx N x dJ N u L

0)

2())2(),2(()1())1(()2(*1=-?--?--+-??N u N u N x f N dx N x dJ N u L （7-7）

求出的。由这个一阶条件求出)2(*-N u 后，将它代回式（7-6）得到))2((2-*

N x J 。然后

就可以进行下一次递推。

一阶必要条件（7-7）的一般形式是

0)

())(),(()1(d ))1((d )(*

1=??+++??--i u i u i x f i x i x J i u L i N （7-8） 这样逐次应用基本方程，就可以由后向前逐次求出所有的决策变量。这一求解过程是把

原来的N 阶决策问题化成了一系列对单变量求最小的问题，从而使问题的求解得到了简化。最优性原理保证这种分步最优化的过程得到的结果与同时确定所有决策变量的结果相同。

以上是终端状态为自由的情况，如果终端状态是给定的，即已给N x N x =)(，则由状态方程有

))1(),1(()(--=N u N x f N x

于是由方程

))1(),1((--=N u N x f x N

可以直接解出唯一的)1(-N

u ，它就是)1(*-N u (因为没有其他选择)。

进而可以计算J x N 11*

-(())，由Bellman 方程

{}

J x N L x N u N J x N u N 2212221*-*-=--+-(())min ((),())(())()

再求)2(*-N u ，然后再继续递归。只到求出最优策略)1(*,),1(*),0(*-N u u u 。

以上推导假设了x 和u 都是标量，当x 和u 都是向量时以上结果仍然成立。

【例7-1】将前面讨论的最优途径问题看作一个四阶段决策问题，可以看出前面的解法实质上是在逐次利用动态规划基本方程求解。

从最后一个阶段开始，如果汽车已经在城市丙的站点P 3，则到达终点F 的最短时间为4)(*31=P J ，如果汽车已经在城市丙的站点3Q ，则到达终点F 的最短时间为3)(*31=Q J 。 向前递推一步，考虑3，4两个阶段，即城市乙和丙联合考虑，利用动态规划基本方程，如

果汽车已经在城市乙的站点2P ，则到达终点F 的最短时间

4}31,41min{)}(*),(*min{)(*3132313222=++=++=Q J Q P P J P P P J （选3Q ） 如果汽车已经在城市乙的站点2Q ，则到达终点F 的最短时间 5}32,42min{)}(*),(*min{)(*3132313222=++=++=Q J Q Q P J P Q Q J （选3Q ） 再递推一步，将城市甲、乙和丙联合考虑，如果汽车已经在城市甲的站点1P ，则到达终点F

的最短时间

10}56,46min{)}(*),(*min{)(*2221222113=++=++=Q J Q P P J P P P J （选2P ） 如果汽车已经在城市甲的站点1Q ，则到达终点F 的最短时间 8}57,44min{)}(*),(*min{)(*2221222113=++=++=Q J Q Q P J P Q Q J （选2P ） 最后，始点S 到达终点F 的最短时间

13}85,104min{)}(*),(*min{)(*1311314=++=++=Q J SQ P J SP S J （选1Q ） 于是得到最优途径是F Q P SQ 321。

【例7-2】资源分配问题

设某公司为了扩大生产能力拟购设备4-6套分配给3个分厂，各分厂得到设备后预期的利润见下表：

预期利润表 分厂 0套 1套 2套 3套 4套 5套 6套 1 0 3 5 6 7 6 5 2 0 4 6 7 8 9 10 3 0 2 5 9 8 8 7

按1、2、3的顺序进行分配，以)(k x 表示给k 厂分配时可分配的套数，)(k u 分配给k 厂的套数))(),((k u k x L 是由上表给出的k 厂得到)(k u 套设备所创的利润，状态转移方程为

)()()1(k u k x k x -=+

指标函数为

∑==3

1

3))(),((k k u k x L J

问题是选取策略)3(),2(),1(j u u 使满足)()(0k x k u ≤≤并使3J 最大。 记 ∑=≤≤=

3

1

)

()(01*3

))(),((max

)(k k x k u k u k x L x J

由后向前递推：

第1步：3=k ，由利润表的最后一行得到下表

)3(x )3(u ))3((*1x J

1 2 3 4 5 6

1 2 3 3 3 3

2 5 9 9 9 9

第2步：2=k ，由利润表的第2行及递推公式得到下表

)2(x 0 1 2 3 4 5 6

))

2((*2x J

)

2(*u

1 2 3 4 5 6

0 0+2 0+5 0+9=9 0+9=9 0+9=9 0+9=9 4+0=4 4+2=6 4+5=9 4+9=13 4+9=13 4+9=13 6+0=6 6+2=8 6+5=11 6+9=15 6+9=15 7+0=7 7+2=9 7+5=12 7+9=16 8+0=8 8+2=10 8+5=13 9+0=9 9+2=11 10+0=10 0 4 6 9 13 15 16

0 1 1,2 0,1 1 2 3

第2步：2=k ，由利润表的第1行及递推公式得到下表，由于公司仅购买4-6套设备，所以

6,5,4)1(=x

)

1(x 0 1 2 3 4 5 6

))1((*3x J )1(*u

4 5 6

0+13 0+15 0+16

3+9=12 3+13=16 3+15=18 5+6=11 5+9=14 5+13=18 6+4=10 6+6=12 6+9=15 7+0=7 7+4=11 7+6=13 6+0=11 6+4=10

5 12 1

6 18 1 1 1,2

最后顺序递推得到最优策略：

由上表，当6)1(=x 时，3步决策的指标函数值最大为18，这时)1(*u =1或2，于是

?

?

?===2)1(*41

)1(*5)2(u u x 对于对于 这时对于5)2(=x ，2)2(*=u ，因此=)3(x 3；对于4)2(=x ，1)2(*=u ，因此=)3(x 3 于是=)3(x 3，由第1步的表，3)1(*=u 。

最优策略的两种可能：

3)3(*,3)3(*,2)2(*,5)2(*,1)1(*,6)1(*======u x u x u x ，最大利润18。 3)3(*,3)3(*,1)2(*,4)2(*,2)2(*,6)1(*======u x u x u x ，最大利润18。

最优策略为{1,2,3}或{2,1,3}，两种策略均可获最大利润18。

【例7-3】吃糕问题 吃糕问题是资源管理中很多问题的的基础，经济管理的教材都以它为例。吃糕只是形象的说法。

已知有一块蛋糕其大小为0W （代表某种资源的初始存量），计划分N 天吃完（开采完），以)(k W 记第k 天开始时剩余的蛋糕的大小（资源的存量），以)(k C 记第k 天吃的蛋糕的量（开采量），则吃糕问题（资源开采问题）的状态方程为

∑-==1

)(ln N k k k C J Max β

0)()0()

()()1(..0

==-=+N W W W k C k W k W t s

为了具体我们设3=N ，考虑问题

∑==20

)(ln k k k C J Max β

0)3()0()

()()1(..0

==-=+W W W k C k W k W t s

解 由0)3(=W 得到0)2()2(=-C W ，即)2()2(*W C =， 于是 )2(ln )2(*ln ))2((2

2*1W C W J ββ== 应用Bellman 方程，有

))}2(()1(ln {))1((*1)

1(*2W J C Max W J C +=β)}2(ln )1(ln {2)

1(W C Max C ββ+=

)]}1()1(ln[)1(ln {2)

1(C W C Max C -+=ββ

下面需要对花括号内的函数关于)1(C 求导数，并令它等于零，解出)1(C ，这一工作可

以由MATLAB 的符号微分运算和解方程来完成，程序如下：

>> syms beta c1 w1

eq=diff('beta*log(c1)+(beta)^2*log(w1-c1)',c1) eq =

beta/c1-beta^2/(w1-c1) >> c1=solve(eq,c1) c1 =

w1/(1+beta)

得到 β

+=1)

1()1(*W C 于是 )]1()1(ln[)1(ln ))1((2*

2C W C W J -+=ββ

]1)1()1(ln[1)1(ln 2β

βββ+-++=W W W

应用bellman 方程再递推一步

))}1(()0({ln ))0((*

2)

0(*3W J C Max W J C +=

+=)0({ln )0(C Max C ]}1)

1()1(ln[1)1(ln

2β

βββ+-++W W W

+=)0({ln )0(C Max C ]}1)

1(ln[1)1(ln 2β

ββββ+++W W 其中)0()0()1(C W W -=，以上式代入花括号内，再对花括号内的函数关于)0(C 求导数，并令它等于零，解出)0(C ，这一工作仍然由MATLAB 的符号微分运算和解方程来完成：

>> syms beta c0 w0 b

b=1+beta;eq=diff('log(c0)+beta*log((w0-c0)/b)+(beta)^2*log(beta*(w0-c0)/b)',c0) eq =

1/c0-beta/(w0-c0)-beta^2/(w0-c0) >> c0=solve(eq,c0) c0 =

w0/(1+beta+beta^2)

得到 2

1)

0()0(*ββ++=

W C

在解离散的多阶决策问题时，要考虑今天采取的行动会对未来产生影响。用动态规划的Bellman 方程求解跨期最优化问题时，例如在决定当前的收入水平下今天的消费时，不仅要考虑今天的消费，还要考虑未来的消费。当决定今天消费多少时，必须考虑这一决策将影响明天的消费。在应用动态规划的Bellman 方程多阶决策问题时，总是将决策分为两个时期，当前和未来。假设未来的行为已经最优化了，当前应该如何决策。

本例中第一个必要条件

0)1()1()

1()

1(2=--+

C W C ββ

可改写为

)

1()1()

1(2

C W C -=

ββ

左边是消费的边际效用的贴现值，即在1=k 这个周期每增加1个单位蛋糕的消费增加的效用的贴现值。右边是在未来增加1个单位蛋糕的消费增加的边际效用的贴现值，即在2=k 这个周期增加1个单位蛋糕的消费增加的效用的贴现值。这恰是1=k 这个周期每增加1个单位蛋糕的消费的机会成本。因此上面的必要条件的经济意义是：在1=k 这个周期每增加1个单位蛋糕的消费增加的效用的贴现值等于1=k 这个周期每增加1个单位蛋糕的消费的机会成本。

通过例7-1，演示了如何借助于MATLAB 的符号运算，通过Bellman 方程解动态规划问题。但是多数动态规划问题不能像例12-1那样可以求出解析解。

通过例7-1的求解过程我们再概括一下动态规划解多阶决策问题的思路：

（1）将多阶段决策过程划分阶段，恰当地选择状态变量、决策变量以定义最优指标函数，从而把问题化成一族同类型的子问题，然后逐个求解。

（2）求解时从边界条件开始，逆序过程行进，逐段递推寻优．在每一个子问题求解时，都要使用它前面已求出的子问题的最优结果．最后一个子问题的最优解，就是整个问题的最优解。

（3)动态规划方法不是将每个阶段孤立地分开，而是既将当前一段与未来各段分开，又把当前效益和未来效益结合起来考虑的一种最优化方法，因此每段的最优决策选取是从全局考虑的，与仅考虑该阶段的最优选择一般是不同的。

【例7-4】生产-库存-销售系统控制问题 设某厂计划全部生产某种产品，四个季度的定货量分别为600件，700件，500件和1200件。已知该产品的生产费用与生产数量的平方成正比，比例系数为0.005。厂内有仓库可存放未销售掉的产品，其存储费用为每件每季度1元。

设第k 季度该产品的生产数量为u k ()，第k 季度初的库存量为x k ()，第k 季度的销售量(这里假设完全按定货量销售)为s k ()。那么这三个变量之间的关系为：下季度初的库存量等于本季度的库存量加本季度的生产量减去本季度的销售量。因此该系统的状态方程为

x k x k u k s k ()()()()+=+-1

如果年初没有存货，则x ()10=，如果要求年底将货销完，则有x ()50=。该控制问题的目标是使总费用(包括生产费用和存储费用)最小。指标函数为

J u k x k k 421

4

0005=+=∑[.()()]

生产库存系统的最优管理问题是求u u u u (),(),(),()1234，使J 4最小。

下面用动态规划的基本方程求这一管理问题的最优策略。 先由最后一个季度考虑起：

J u x 12000544=+.()()

由状态方程和条件x ()50=得到

x x u s x u ()()()()()()54444412000

=+-=+-= 由此得到

u x *=-()()412004

代入J 1得到

J x x x x 122

0005120044720011400054*=-+=-+.(())()

().()

第二步考虑第三、四两个季度。由动态规划的基本方程：

))}4(()3()3(005.0{min ))3((122)

3(x J x u x J u **

++=

)}4(005.0)4(117200)3()3(005.0{min

2

2)

3(x x x u u +-++= 其中x x u s x u ()()()()()()433333500=+-=+-，代入上式得到

J x u x x u x u u 222

3000533720011335000005335003*

=++-+-++-(())min{.()()(()())

.(()())}

()

对{}?中的函数关于u ()3求最小，有

??{}

()

.().()?=-+=u u x 300231600130 解得

u x 33800053*=-().()

为了保证u 330*

≥()，x ()3必须小于1600。 将u 33*()代入J x 23*

(())得到

J x x x x x x x x x 2222300058000533720011380005350000053800053500755073000753*

=-++-+--++--=-+(()).(.())()(().())

.(().())().()

第三步考虑2－4三个季度，由基本方程

J x u x J x u x x x u u 32222

2000522300052275507300025322**=++=++-+(())min{.()()(())}

min{.()()().()}

()

()

其中x x u s x u ()()()()()()322222700=+-=+-，代入上式得到

J x u x x u x u u 322

2000522755072270000025227002*

=++-+-++-(())min{.()()(()())

.(()())}

()

由

??{}

()

.().(()())?=-++-=u u x u 20015270005227000

解得

u x 227001

3

2*

=-

()() 代入J x 32*

(())得到

J x x x 32

2100006200053

2*

=-+

(())().() 最后对四个季度一起考虑，由基本方程有

J x u x J x u 422100051121**=++(())min{.()()(())}()

以x x u s x u ()()()()()()211111600=+-=+-代入上式得

J x u x x u x u u 42210005111000061160000053

116001*

=++-+-++-(())min{.()()(()())

.(()())}

()

令

??{}

()

?=u 10 得到

00116001

3

116000.().(()())u x u -+

+-= 即

u x 116001

4

1*=-

()() 代入J x 41*

(())得到

J x x x 42

1118005100054

1*=-+

(())().() 由于已设x ()10=，得u *=()1600，x ()20=，u *=()2700，x ()30=，u *=()3800，

x ()4300=，u *=()4900。

采用上策略时，总费用为

J 4011800()=元

如果采用销多少生产多少的策略，u ()1600=，u ()2700=，u ()3500=，u ()41200=，则总费用为

J 4222200005600700500120012700().[]=+++=元

最优策略节省费用900元，约合71%.。

5.指标函数有贴现因子时的Bellman 方程

设系统的状态方程为

x k f x k u k ()((),())+=1

指标函数为

∑-==1

))(),((N k k N k u k x L J β

β是贴现因子。Bellman 方程为

{}))1(())(),((min ))((1)

(++=*--*-i x J i u i x L i x J i N i i u i N β

式中

))(),((min

))1((1

1

)

1(,),1(*

1

k u k x L i x J

N i k k

N u i u i N ∑-+=-+--=

+β

因此*i N J -和*

1--i N J 都是贴现到0=k 时的值。上方程的两边同乘以i -β得到

{}))1(()())(),((min ))((11)

(++=*

----*--i x J i u i x L i x J i N i i u i N i βββ

式中记

))(())((*

*i x J i x J i N i i N ---=β

))1

(())1((*

11*1+=+------i x J i x J i N i i N β 得到

{}

))1(())(),((min ))((1)

(++=*

--*-i x J i u i x L i x J i N i u i N β

它是指标函数有贴现因子时的Bellman 方程，*

J 为当期的指标函数的最优值，没有贴

现到初始时刻。为了简化，以后仍把*

J

记为*J 。将指标函数有贴现因子时的Bellman 方程

仍记为

{}

))1(())(),((min ))((1)

(++=*--*-i x J i u i x L i x J i N i u i N β （7-9）

【例7-5】设某大学生的家长计划在四年内给该生M 元，作为大学四年的花费。设效用函数为c c U =

)(，贴现因子为β，则效用最大化问题的状态方程是

)()()1(k c k s k s -=+

)(k s 是该生第k 年开始时剩的钱，)(k c 是该生第k 年的消费，指标函数是

∑==3

04)(k k k c J β

效用最大化问题是求消费策略)3(),2(),1(),0(c c c c 使4J 最大。 这个问题可简记为

∑=3

)(k k c

k c Max β

)()()1(..k c k s k s t s -=+

由于效用函数c 是增函数，最后一年的最优消费策略必是

)3()3(*s c = 于是初始条件为)3(s 时指标函数的最大值为

)3())3((*1s s J =

由指标函数有贴现因子时的Bellman 方程，递推一步有

))}3(()2({))2((*1)

2(*2s J c Max s J c β+=})3()2({)

2(s c Max c β+=

其中)2()2()3(c s s -=,以)3(s 代入上式得到

})2()2()2({))2(()

2(*

2c s c Max s J c -+=β

下面需要对花括号内的函数关于)2(c 求导数，并令它等于零，解出)2(c ，这一工作可

以由MATLAB 的符号微分运算和解方程完成：(文件Li12_2_1)

syms beta s2 c2

eq=diff('sqrt(c2)-beta*sqrt(s2-c2)',c2) c2=solve(eq,c2)

运行这个文件得到：

>> Li12_2_1 eq =

1/2/c2^(1/2)+1/2*beta/(s2-c2)^(1/2) c2 =

s2/(1+beta^2) 即得到

2

1)

2()2(*β

+=

s c 将)2(*c 代回))2((*

2s J 得到

)2()1(1)

2()2(1)2())2((22

2*2s s s s s J ββ

ββ+=+-++=

应用指标函数有贴现因子时的Bellman 方程再递推一步

))}2(()1({))1((*

2)

1(*3s J c Max s J c β+=})2()1()1({2)

1(s c Max c ββ++=

]})1()1()[1()1({2)

1(c s c Max c -++=ββ

下面需要对花括号内的函数关于)1(c 求导数，并令它等于零，解出)1(c ，这一工作可以由MATLAB 的符号微分运算和解方程完成：(文件Li12_2_2)

syms beta s1 c1

eq=diff('sqrt(c1)+beta*sqrt((1+beta^2)*(s1-c1))',c1) c1=solve(eq,c1)

运行这个文件得到：

>> Li12_2_2 eq =

1/2/c1^(1/2)+1/2*beta/((1+beta^2)*(s1-c1))^(1/2)*(-1-beta^2) c1 =

s1/(beta^4+beta^2+1) 即得到 )

1()

1()1(*42ββ++=

s c

将)1(*c 代回))1((*

3s J 得到 ]1)1()1()[1(1)1())1((4

22

42*3β

βββββ++-++++=

s s s s J )1()1(42s ββ++= 再递推一步有

))}1(()0({))0((*

3)

0(*4s J c Max s J c β+=})1()1()0({42)

0(s c Max c βββ+++=

]})0()0()[1()0({42)

0(c s c Max c -+++=βββ

下面需要对花括号内的函数关于)0(c 求导数，并令它等于零，解出)0(c ，这一工作可以

由MATLAB 的符号微分运算和解方程完成：(文件Li12_2_3)

syms beta s0 c0

eq=diff('sqrt(c0)+beta*sqrt((1+beta^2+beta^4)*(s0-c0))',c0) c0=solve(eq,c0)

运行这个文件得到：

>> Li12_2_3 eq =

1/2/c0^(1/2)+1/2*beta/((beta^4+beta^2+1)*(s0-c0))^(1/2)*(-beta^4-beta^2-1) c0 =

s0/(beta^6+beta^4+beta^2+1)

即得到 )

1()1()0()0(*6

42642ββββββ+++=+++=

M

s c 贴现因子β取值于0，1之间，当9.0=β时，

M M c 3

1

997541.2)0(*≈=

4661

.2)

1()1(*s c =

81

.1)

2()2(*s c =

)3()3(*s c =

7.2随机动态规划

1.随机动态规划的提法

以上给出的动态规划算法都是确定型的，没有考虑有随机干扰的情况，本节给出有随机干扰的动态系统的跨期最优化问题的动态规划算法。设动态系统的状态方程为

))1(),(),(()1(+=+k k u k x f k x ε （7-12）

式中)1(+k ε对动态系统的随机干扰这里用1+k 是因为在k 时刻它是未知的，假设它的概率分布不依赖于)(,),1(k εε 。指标函数为

}))(),(({10

∑-==N k k k u k x L E J β （7-13）

由于花括号中的函数是一个随机变量，因此指标函数表示为花括号中函数的期望值，E 是期望算子。

2. 随机动态规划的Bellman 方程

对于这个随机跨期最优化问题，动态规划的Bellman 方程应改为

{}

))1(())(),((min ))((1)

(++=*--*-i x EJ i u i x L i x J i N i u i N β （7-14）

象前面一样，引进值函数

))(())((i x J i x V i N *

-=

Bellman 方程又可以改写为

{}))]1(([))(),((min ))(()(++=i x V E i u i x L i x V i u β

或者简记为 {})))](),(),((([),(min )(k k u k x f V E u x L x V u

εβ+= 问题的一阶条件是

0]),,()),,(([),(=??'+??u

u x f u x f V E u u x L εεβ 对于随机动态规划问题，方程（7-10）和（7-11）化为

0))(),(()1())(),((=++i u i x f i E i u i x L u u λβ （7-15） )())(),(()1())(),((i i u i x f i E i u i x L x x λλβ=++ （7-16）

这两个条件常称为Euler 均衡条件。

最常见的一类随机跨期最优化问题是线性二次型高斯问题，这类问题的状态方程是线性差分方程组，指标函数是状态变量和决策变量的二次型，随机干扰是高斯白噪声。

[ss,pi,xx]=dpstst(model,h,nbin,s,x);

这里用到的程序：qnwlogn ，fundefn ，funnode ，lqapprox ，dpsolve ，dpsimul 和dpsts 都可以在参考文献[18]的作者网站的CompEcon Toolbox 中找到。

7.3 MATLAB 在动态规划中的应用

动态规划问题形式多种多样，MATLAB 没有统一的解动态规划问题的函数，但对于自由始端和终端的动态规划,求指标函数最小值的逆序算法递归，有人写了函数dynprog,可以应用dyprog 求解。（参见：宋来忠，王志明：数学建模与实验 科学出版社2005 p.182或周品、赵新芬：MATLAB 数学建模与仿真 国防工业出版社 2009 p.340）

函数dynprog 的调用形式是：

[p_opt,fval]=dynprog(x,DecisFun,ObjFun,TransFun)

输入 x 是状态变量的矩阵，它的第k 列是k 阶段状态变量)(k x 的可能取值，其他输入由3个函数给出：

DecisFun(k,x)是由阶段k 的状态变量)(k x ，求出相应的允许决策变量的函数。

函数ObjFun(k,x,u)用于由阶段k 的状态变量x 和阶段k 的决策变量u 计算阶段k 指标函数。

函数TransFun(k,x,u) 是状态转移函数,其中x 是阶段k 的状态变量，u 是相应的决策变量。

应用函数dyprog 之前，需要写3个函数: DecisFun,ObjFun,TransFun 分别给出状态变量x 求出相应的允许决策变量、阶段指标函数和转移函数。

输出p_opt 由4列构成，第1列是序号组，第2列是最优轨线)(*k x ，第3列是最优策略)(k u ，第4列是阶段指标函数值；输出fval 是一个列向量，它给出p_opt 各最优策略组对

应的最优值。

下面通过实例说明如何应用函数dynpro 求解动态规划问题。

1.生产计划问题1 （参看宋来忠，王志明：数学建模与实验 科学出版社2005 p.179或周品、赵新芬：mATLAB 数学建模与仿真 国防工业出版社 2009 p.343）

设某工厂与用户订立合同，在4个月内出售一定数量的某产品，产量限制为10的倍数，工厂每月至多生产100件，产品可以存储，存储费用每件2元，最多可以存储130件，每个月的需求量及每件产品的 生产成本如表7-1 月份 每件生产成本（元） 需要量（件） 月份 每件生产成本（元） 需要量（件） 1 70 60

2 72 70

3 80 120

4 76 60

在一月初的存储量未知的情况下，确定每月的产量，要求既能满足每月的合同需求量，第4个月不剩产品，又使生产成本和存储费用的和最小。

设)(k x 是第k 月初的库存量，)(k u 是第k 月的生产量，)(k q 是第k 月的合同需求量， 指标函数：总费用最小，即

∑=+=4

1

)(200)()(min k k x k u k c z

)()()()1(..k q k u k x k x t s -+=+

100)(≤k u

为使用函数dynprog 需要定义3个函数：

eg13f1_2.m

function u=DecisF_1(k,x)

%在阶段k 由状态变量x 的值求出其相应的决策变量所有的取值 c=[70,72,80,76];q=10*[6,7,12,6];

if q(k)-x<0,u=0:100; %决策变量不能取为负值 else,u=q(k)-x:100;end; %产量满足需求且不超过100 u=u(:); eg13f2_2.m

function v=ObjF_1(k,x,u) 阶段k 的指标函数

c=[70,72,80,76];v=c(k)*u+2*x; eg13f3_2.m

function y=TransF_1(k,x,u) 状态转移方程

q=10*[6,7,12,6];y=x+u-q(k);

有了这3个函数就可以应用函数dynprog 求解这个例： 首先分析)4(),3(),2(),1(x x x X 的各种可能：

先分析)(k x 可能取值的情况，然后建立)(k x 可能取值的阵列：

由于第1个月的需求量是60，第1个月的存储量考虑0、10、20、30、40、50、60几种情况，当60)1(=x 时，第1个月最多生产100件，第1个月需求是60，因此100)2(0≤≤x ， 第2个月存储量最大100，生产最大100，第2个月需求量是70，因此130)3(0≤≤x ，第4个月不剩产品，第4个月的需求量是60，因此60)4(0≤≤x 。

建立)(k x 可能取值的阵列：

>> x=nan*ones(14,4) x =

NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN

由于第1个月的需求量是60，第1个月的存储量考虑0、10、20、30、40、50、60几种

情况：

>> x(1:7,1)=10*(0:6)' x =

0 NaN NaN NaN 10 NaN NaN NaN 20 NaN NaN NaN 30 NaN NaN NaN 40 NaN NaN NaN 50 NaN NaN NaN 60 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN

当60)1(=x 时，第1个月最多生产100件，第1个月需求是60，因此100)2(0≤≤x ： >> x(1:11,2)=10*(0:10)' x =

0 0 NaN NaN 10 10 NaN NaN 20 20 NaN NaN 30 30 NaN NaN 40 40 NaN NaN 50 50 NaN NaN 60 60 NaN NaN NaN 70 NaN NaN NaN 80 NaN NaN NaN 90 NaN NaN NaN 100 NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN

第2个月存储量最大100，生产最大100，第2个月需求量是70，因此130)3(0≤≤x ，但是由于第4个月需求是120，而第4个月的产量最大100因此130)3(20≤≤x ：

>> x(1:12,3)=10*(2:13)' x =

0 0 20 NaN 10 10 30 NaN 20 20 40 NaN 30 30 50 NaN 40 40 60 NaN

50 50 70 NaN 60 60 80 NaN NaN 70 90 NaN NaN 80 100 NaN NaN 90 110 NaN NaN 100 120 NaN NaN NaN 130 NaN NaN NaN NaN NaN NaN NaN NaN NaN

第4个月不剩产品，第4个月的需求量是60，因此60)4(0≤≤x ： >> x(1:7,4)=10*(0:6)' x =

0 0 20 0 10 10 30 10 20 20 40 20 30 30 50 30 40 40 60 40 50 50 70 50 60 60 80 60 NaN 70 90 NaN NaN 80 100 NaN NaN 90 110 NaN NaN 100 120 NaN NaN NaN 130 NaN NaN NaN NaN NaN NaN NaN NaN NaN

有了以上准备，就可以调用函数dynprog,解这个问题了，程序及运行结果如下： >> clear;x=nan*ones(14,4);% x 是10的倍数，最大范围0≤x ≤130, %因此x=0,1,...13，所以x 初始化取14行，nan 表示无意义元素 x(1:7,1)=10*(0:6)'; % 按月定义x 的可能取值 x(1:11,2)=10*(0:10)';x(1:12,3)=10*(2:13)'; x(1:7,4)=10*(0:6)';

[p,f]=dynprog(x,'eg13f1_2','eg13f2_2','eg13f3_2')

p =

1 0 100 7000

2 40 100 7280

3 70 50 4140

4 0 60 4560 1 10 100 7020 2 50 100 7300 3 80 40 3360 4 0 60 4560 1 20 100 7040 2 60 100 7320 3 90 30 2580 4 0 60 4560 1 30 100 7060