第八章第五节
同济版高等数学第六版课件第八章第五节曲面及其方程

定义
三、柱面
观察柱面的形成过程:
平行于定直线并沿定曲线 移动的直线所形成的曲面称为柱面.
这条定曲线 叫柱面的准线动直线 L 叫柱面的母线.
定义
三、柱面
观察柱面的形成过程:
平行于定直线并沿定曲线 移动的直线所形成的曲面称为柱面.
这条定曲线 叫柱面的准线动直线 L 叫柱面的母线.
这条定直线叫旋转 曲面的轴.
二、旋转曲面
定义
以一条平面曲线绕其平面上的一条直线旋转一周所成的曲面称为旋转曲面.
这条定直线叫旋转 曲面的轴.
二、旋转曲面
定义
以一条平面曲线绕其平面上的一条直线旋转一周所成的曲面称为旋转曲面.
这条定直线叫旋转 曲面的轴.
二、旋转曲面
定义
以一条平面曲线绕其平面上的一条直线旋转一周所成的曲面称为旋转曲面.
定义
三、柱面
观察柱面的形成过程:
平行于定直线并沿定曲线 移动的直线所形成的曲面称为柱面.
这条定曲线 叫柱面的准线动直线 L 叫柱面的母线.
定义
三、柱面
观察柱面的形成过程:
平行于定直线并沿定曲线 移动的直线所形成的曲面称为柱面.
这条定曲线 叫柱面的准线动直线 L 叫柱面的母线.
水桶的表面、台灯的罩子面等.
曲面在空间解析几何中被看成是点的几何轨迹.
曲面的实例:
一、曲面方程的概念
曲面方程的定义:
以下给出几例常见的曲面.
解
根据题意有
所求方程为
特殊地:球心在原点时方程为
解
根据题意有
所求方程为
根据题意有
解
化简得所求方程
例4 方程 的图形是怎的?
这条定直线叫旋转 曲面的轴.
七年级地理下册第八章第五节巴西

图32
巴西
巴西
南美热带巴西木,葡萄牙人拓疆土; 踢足球,桑巴舞, 民族混合大熔炉; 迁移农业因贫苦,热带雨林要保护; 咖啡甘蔗甜橘子,巴西高原种作物; 铁矿石,做基础,钢铁之上空海陆; 亚马孙,水量大,巴拉那河伊泰普; 人口集中东南部,圣保罗里热内卢; 噪音大,交通堵,巴西利亚做首都。
地形 支流、流域面积
气候 降水
尼罗河是世界第一长河,但其水 从地形和气候两方面分析亚马 量为什么远远不及亚马孙河? 孙河水量大的原因。
地形:北、西、南三面地
势高,便于水流汇集,支 流多,流域面积广。
气候:主要流经全年多雨
的热带雨林气候区。
返回
亚
马
孙
河
安第斯 山脉,向东注入 大西 洋。 亚马孙河发源于 全长6400公里,在世界河流中位居第二。水量充沛,占全 球入海河水总流量的五分之一。有 15000条支流 ,流域面积几 是世界上水量 最大 、流域面积 最广 的大河。 乎大如澳洲。通航河道河面宽广,不能同时看到两岸。 长度6400 多千米,仅次于尼罗 河,居世界第 二 。
耕地面积广大,约有可耕 地3.7亿公顷;丰富的水资 源、水能资源;良好的气 候条件。
巴西的农产品中,产量占世界首位的 有:
咖啡、甘蔗、柑橘
巴西的 。 、 、 等粮食的产量居世
界前列,其中
的产量仅次于美国。
2. 巴西工业 铁矿储量650亿吨,产量和
①自然资源 出口量均居世界第一。铝矾 丰富
土、铀、锰、锡、铬、石油、 天然气、煤的储量都居世界 前列。水力资源仅次于中国, 森林覆盖率达60%)
人口、城市多在东南部沿海地区原因: 1、海上交通便利 2、殖民者首先到达这里,开发较早 3、气候较温和湿润 4、工商业发达 稀少区原因 1、过度湿热 2、交通不便 3、开发不便,经济落后
(重庆大学高等数学课件)第八章第5节隐函数的微分法

解法2 微分法. 解法2 微分法. 对方程 的两边求微分: 的两边求微分:
F′⋅ d( ) +F2′ ⋅d( ) = 0 1
zdx −xdz zdy − ydz F′⋅ +F2′ ⋅ =0 1 2 2 z z F′⋅ zdx−F′⋅ xdz +F2′⋅ zdy−F2′⋅ ydz = 0 1 1 − xF′dz − yF2′dz = −zF′dx −zF2′dy 1 1
∂z ∂z 其中 F 有连续的 一阶偏导数, 求证 x 有连续的一阶偏导数 一阶偏导数, +y = z − xy ∂y z z ∂x 证明 设 G( x, y, z) = F( x + , y + )
z z 是由方程 F( x + , y + ) y x
所确定
例3. 设F( x , y)具有连续偏导数,已知方程 连续偏导数 偏导数, 解法1 解法1 设G( x, y, z) =
1 +y′+z′ +2z ⋅ z′ −1 + 1 + 2y ⋅ y′ z′+3z2 ⋅ z′ −1
13
求导, 解: 方程组两边对 x 求导, 并移项得
∂u ∂u ∂v ∂v 例4. 设 xu − yv = 0, yu + xv = 1, 求 , , . , ∂x ∂ y ∂x ∂ y
∂u ∂v u+ x + −y = −u 0 ∂x ∂x ∂u ∂v − v y + v+ x = 0 ∂x ∂x −u − y ∂u −v x −xu − yv = = x −y ∂x x2 + y2 y x
x x
在点
则方程 F( x, y) = 0
第八章 第五节 建设社会主义生态文明
◆
用生态文明的力量托起“美丽中国”
/pinglun/n/2012/1112/c78779-19549520.html
“把生态文明建设放在突出地位”,“努 力建设美丽中国,实现中华民族永续发展”, 胡锦涛同志在十八大报告中铿锵有力地进行庄 严宣示。 十八大报告将生态文明建设,与经济建设、 政治建设、文化建设、社会建设一起,列入 “五位一体”总体布局,并用专章论述。 十八大报告中提出“从源头上扭转生态环 境恶化趋势”的目标,提出“给自然留下更多 修复空间,给农业留下更多良田,给子孙后代 留下天蓝、地绿、水净的美好家园”的愿景。
文化建设,就是发展社会主义先进文化,建设社会主义精神 文明,实行依法治国和以德治国相结合,提高全民族思想道德 素质和科学文化素质,为改革开放和社会主义现代化建设提供 强大 的思想保证,精神动力和智力支持; 社会建设,就是构建社会主义和谐社会,按照民主政治、 公平正义、诚信友爱、充满活力、安定有序、人与自然和谐相 处的总要求和共同建设、共同享有的原则,以改善民生为重点, 解决好人民最关心、最直接、最现实的利益问题,努力形成全 体人民各尽其能、各得其所而又和谐相处的局面; 生态文明建设,就是树立尊重自然、顺应自然、保护自然的 生态文明理念,把生态文明建设放在突出地位,融入经济建设、 政治建设、文化建设、社会建设各方面和全过程,努力建设美 丽中国,实现中华民族永续发展。 同时,为了实现“五位一体”的总体布局,党章还从促进 人的全面发展的角度,增加了“尊重劳动、尊重知识、尊重人 才、尊重创造,做到发展为了人民,发展依靠人民,发展成果 由人民共享”的内容,充分体现了执政党“五位一体”总体布 局中以人为本的全新观念。 “五位一体”,是中国特色社会主 义事业的总体布局;“五位一体”,是党领导人民建成小康社 会伟大构想。
第八章 第五节 理学的集大成者——朱熹

就显示世界而言,理与气不能分离,天下任何事 物都是由理气两个方面结合而成,但就本源上说, 理先于气存在.这里涉及一般与个别的关系.一 类事物的理作为这一类事物的共同本质,规律, 体现在此类一切事物之中,不为此类事物中某个 个别事物所私有,因而不以个别事物产生,消灭 为转移..朱熹有见于一类事物的理对此类中个 别事物的先在性,但据此认为一类事物的理可以 先于此类事物而存在,是把理的绝对化.这是客 观的观念论.朱熹晚年强调理气的无所谓先后, 但实际上仍认为理是本,是体,是第一性的,气 则是第二性的.
《答林择之》:"未发只是思虑事物之未接时,于 此便可见物已交之际,皆得其理,故可谓之和,而 不可谓之心.心则通观乎已发未发之间,乃大易生 生流行,一动一静之全体也."(《朱文公文集》 卷43) 《已发未发说》:"思虑未萌,事物未至之时为喜 怒哀乐之未发,当此之时即是心体流行寂然不动之 处,而天明命之性体段具焉.以其无过不及,不偏 不倚,故谓之中.然已是就心体流行处见,故直谓 之性则不可."(《朱文公文集》卷67) 《胡子知言疑义》:"'圣人指明其体曰性,指明 其用曰心,新不能不动,动则心矣.'熹按:心性 体用之云,恐自上蔡谢子失之.此云性不能不动, 动则心矣.语尤未安,凡此心字皆欲作情字,如 何?"(《朱文公文集》卷73) 《朱子语类》卷98:"'心统 情,统如何?'曰: '统是主宰,如统百万军.'"
性:是人的本质属性和道德理性,认为 源于天赋予人的自然本性,性具有儒家 仁义礼智,纲常伦理的内涵.二程朱熹 还认性为宇宙本体.二成提出"性即 理",把以性为代表的儒家伦理等同于 天理,提升为宇宙本体.朱熹基本上也 是依此思路,把道德理性本体化.他们 还认为性无意识.与以后的王阳明所说 的不同.
同济版高等数学第六版课件第八章第五节曲面及其方程

直纹曲面在建筑设计中的应用
总结词
设计曲面建筑外观
VS
详细描述
直纹曲面方程在建筑设计中用于描述复杂 的曲面结构。通过直纹曲面,建筑师可以 创造出独特且富有艺术感的建筑外观。直 纹曲面在建筑设计中的广泛应用,不仅提 高了建筑的审美价值,也为建筑师提供了 更多的创作空间。
方程
锥面的方程通常表示为 x^2 + y^2 = r^2(z),其中 (x, y) 是平面上的点,r 是锥顶到平面的距离,z 是锥面的参数。
性质
锥面是一个非对称的曲面,在锥顶处曲率为无穷大。
旋转曲面
定义
旋转曲面是由一条平面曲线绕 一条直线旋转一周所形成的曲
面。
方程
旋转曲面的方程通常表示为 x = x(t), y = y(t), z = z(t),其 中 t 是参数,x(t), y(t), z(t) 是
非标准曲面
定义
01
非标准曲面是指不符合常规形式的曲面,如参数曲面、隐式曲
面等。
性质
02
非标准曲面具有一些特殊的几何性质,如曲率、法向量等,这
些性质有助于理解曲面的几何结构。
应用
03
非标准曲面在计算机图形学、计算几何等领域有广泛的应用,
如动画设计、虚拟现实、游戏开发等。
曲面的微分性质
定义
曲面的微分性质是指曲面在局部的几何性质,如切线、法线、曲率 等。
给定的平面曲线。
性质
旋转曲面是一个具有旋转对称 性的曲面,其曲率随旋转角度
而变化。
直纹曲面
定义
直纹曲面是由一条直线按一定方式移动所形成的曲面 。
方程
直纹曲面的方程通常表示为 z = f(x, y),其中 f(x, y) 是给定的函数,(x, y) 是平面上的点。
高等数学 第八章 第五节 曲面及其方程

(2) 用坐标面 xoz ( y = 0) 与曲面相截
截得中心在原点的双曲线。
x2 a2
−
z2 c2
=1
y = 0
实轴与 x 轴相合, 虚轴与 y 轴相合。
第八章 第五节
33
与平面 y = y1 ( y1 b) 的交线为双曲线。
x2
a
2
−
z2 c2
= 1−
y12 b2
双曲线的中心都在 y 轴上。
第八章 第五节
26
与平面 z = z1 (z1 0) 的交线为椭圆。
x2
2
pz1
+
y2 2qz1
=
1
z = z1
当 z1变动时,这种椭
圆的中心都在 z 轴上。
与平面 z = z1 (z1 0) 不相交。
② 用坐标面 xoz ( y = 0) 与曲面相截
截得抛物线
x2 = 2 pz
y = 0
f ( x2 + y2 , z) = 0
同理:绕 y 轴旋转的旋转曲面方程
f (y , x2 + z2 ) = 0
问:曲线 C: f ( x , y) = 0 xoy 绕 x 轴旋转生成 的旋转曲面为?绕 y 轴旋转生成的旋转曲面为一条与 L 相交的直线旋转所得旋转
x
H(z , x) = 0 表示母线平行于 y 轴;
z
准线为 xoz 面上的曲线 l3的柱面。 l3
x
y
第八章 第五节
18
例
y2 b2
+
z2 c2
=
1
椭圆柱面 // 轴
x
x2 a2
−
y2 b2
=
高中数学知识点总结(第八章 立体几何 第五节 直线、平面垂直的判定与性质)

第五节 直线、平面垂直的判定与性质一、基础知识1.直线与平面垂直 (1)直线和平面垂直的定义:直线l 与平面α内的任意一条直线都垂直, 就说直线l 与平面α互相垂直.(2)直线与平面垂直的判定定理及性质定理:文字语言 图形语言符号语言判定定理一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直⎭⎪⎬⎪⎫a ,b ⊂αa ∩b =Ol ⊥a l ⊥b⇒l ⊥α 性质定理 垂直于同一个平面的两条直线平行⎭⎪⎬⎪⎫a ⊥αb ⊥α⇒a ∥b⎣⎢⎡⎦⎥⎤❶如果一条直线与平面内再多(即无数条)的直线垂直,但这些直线不相交就不能说明这条直线与此平面垂直. 2.平面与平面垂直的判定定理与性质定理文字语言 图形语言符号语言判定定理一个平面过另一个平面的垂线❷,则这两个平面垂直⎭⎪⎬⎪⎫l ⊂βl ⊥α⇒α⊥β 性质定理两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直⎭⎪⎬⎪⎫α⊥βl ⊂βα∩β=a l ⊥a ⇒l ⊥α[❷要求一平面只需过另一平面的垂线.]二、常用结论直线与平面垂直的五个结论(1)若一条直线垂直于一个平面,则这条直线垂直于这个平面内的任意直线.(2)若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面.(3)垂直于同一条直线的两个平面平行.(4)一条直线垂直于两平行平面中的一个,则这一条直线与另一个平面也垂直.(5)两个相交平面同时垂直于第三个平面,它们的交线也垂直于第三个平面.考点一直线与平面垂直的判定与性质[典例]如图,在四棱锥PABCD中,P A⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,P A=AB=BC,E是PC的中点.求证:(1)CD⊥AE;(2)PD⊥平面ABE.[证明](1)在四棱锥PABCD中,∵P A⊥底面ABCD,CD⊂底面ABCD,∴P A⊥CD,又∵AC⊥CD,且P A∩AC=A,∴CD⊥平面P AC.∵AE⊂平面P AC,∴CD⊥AE.(2)由P A=AB=BC,∠ABC=60°,可得AC=P A.∵E是PC的中点,∴AE⊥PC.由(1)知AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD.∵PD⊂平面PCD,∴AE⊥PD.∵P A⊥底面ABCD,AB⊂底面ABCD,∴P A⊥AB.又∵AB⊥AD,且P A∩AD=A,∴AB⊥平面P AD,∵PD⊂平面P AD,∴AB⊥PD.又∵AB∩AE=A,∴PD⊥平面ABE.[解题技法]证明线面垂直的4种方法(1)线面垂直的判定定理:l ⊥a ,l ⊥b ,a ⊂α,b ⊂α,a ∩b =P ⇒l ⊥α. (2)面面垂直的性质定理:α⊥β,α∩β=l ,a ⊂α,a ⊥l ⇒a ⊥β. (3)性质:①a ∥b ,b ⊥α⇒a ⊥α,②α∥β,a ⊥β⇒a ⊥α. (4)α⊥γ,β⊥γ,α∩β=l ⇒l ⊥γ.(客观题可用) [口诀归纳]线面垂直的关键,定义来证最常见, 判定定理也常用,它的意义要记清. 平面之内两直线,两线相交于一点, 面外还有一直线,垂直两线是条件. [题组训练]1.(2019·安徽知名示范高中联考)如图,在直三棱柱ABC A 1B 1C 1中,AB =BC =BB 1,AB 1∩A 1B =E ,D 为AC 上的点,B 1C ∥平面A 1BD .(1)求证:BD ⊥平面A 1ACC 1;(2)若AB =1,且AC ·AD =1,求三棱锥A BCB 1的体积. 解: (1)证明:如图,连接ED ,∵平面AB 1C ∩平面A 1BD =ED ,B 1C ∥平面A 1BD , ∴B 1C ∥ED , ∵E 为AB 1的中点, ∴D 为AC 的中点, ∵AB =BC ,∴BD ⊥AC .∵A 1A ⊥平面ABC ,BD ⊂平面ABC ,∴A 1A ⊥BD . 又∵A 1A ,AC 是平面A 1ACC 1内的两条相交直线, ∴BD ⊥平面A 1ACC 1.(2)由AB =1,得BC =BB 1=1,由(1)知AD =12AC ,又AC ·AD =1,∴AC 2=2,∴AC 2=2=AB 2+BC 2,∴AB ⊥BC , ∴S △ABC =12AB ·BC =12,∴V A BCB 1=V B 1ABC =13S △ABC ·BB 1=13×12×1=16.2.如图,S是Rt△ABC所在平面外一点,且SA=SB=SC,D为斜边AC的中点.(1)求证:SD⊥平面ABC;(2)若AB=BC,求证:BD⊥平面SAC.证明:(1)如图所示,取AB的中点E,连接SE,DE,在Rt△ABC中,D,E分别为AC,AB的中点.∴DE∥BC,∴DE⊥AB,∵SA=SB,∴SE⊥AB.又SE∩DE=E,∴AB⊥平面SDE.又SD⊂平面SDE,∴AB⊥SD.在△SAC中,∵SA=SC,D为AC的中点,∴SD⊥AC.又AC∩AB=A,∴SD⊥平面ABC.(2)∵AB=BC,∴BD⊥AC,由(1)可知,SD⊥平面ABC,又BD⊂平面ABC,∴SD⊥BD,又SD∩AC=D,∴BD⊥平面SAC.考点二面面垂直的判定与性质[典例](2018·江苏高考)在平行六面体ABCDA1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.[证明](1)在平行六面体ABCDA1B1C1D1中,AB∥A1B1.因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,所以AB∥平面A1B1C.(2)在平行六面体ABCDA1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1=AB,所以四边形ABB1A1为菱形,因此AB1⊥A1B.因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC.因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,所以AB1⊥平面A1BC.因为AB1⊂平面ABB1A1,所以平面ABB1A1⊥平面A1BC.[解题技法] 证明面面垂直的2种方法 定义法利用面面垂直的定义,即判定两平面所成的二面角为直二面角,将证明面面垂直问题转化为证明平面角为直角的问题定理法 利用面面垂直的判定定理,即证明其中一个平面经过另一个平面的一条垂线,把问题转化成证明线线垂直加以解决[题组训练]1.(2019·武汉调研)如图,三棱锥P ABC 中,底面ABC 是边长为2的正三角形,P A ⊥PC ,PB =2.求证:平面P AC ⊥平面ABC .证明:取AC 的中点O ,连接BO ,PO . 因为△ABC 是边长为2的正三角形, 所以BO ⊥AC ,BO = 3.因为P A ⊥PC ,所以PO =12AC =1.因为PB =2,所以OP 2+OB 2=PB 2,所以PO ⊥OB . 因为AC ∩OP =O , 所以BO ⊥平面P AC . 又OB ⊂平面ABC , 所以平面P AC ⊥平面ABC .2.(2018·安徽淮北一中模拟)如图,四棱锥P ABCD 的底面是矩形,P A ⊥平面ABCD ,E ,F 分别是AB ,PD 的中点,且P A =AD .求证:(1)AF ∥平面PEC ; (2)平面PEC ⊥平面PCD .证明:(1)取PC 的中点G ,连接FG ,EG , ∵F 为PD 的中点,G 为PC 的中点, ∴FG 为△CDP 的中位线, ∴FG ∥CD ,FG =12CD .∵四边形ABCD 为矩形,E 为AB 的中点, ∴AE ∥CD ,AE =12CD .∴FG =AE ,FG ∥AE , ∴四边形AEGF 是平行四边形,∴AF ∥EG ,又EG ⊂平面PEC ,AF ⊄平面PEC ,∴AF∥平面PEC.(2)∵P A=AD,F为PD中点,∴AF⊥PD,∵P A⊥平面ABCD,CD⊂平面ABCD,∴P A⊥CD,又∵CD⊥AD,AD∩P A=A,∴CD⊥平面P AD,∵AF⊂平面P AD,∴CD⊥AF.又PD∩CD=D,∴AF⊥平面PCD.由(1)知EG∥AF,∴EG⊥平面PCD,又EG⊂平面PEC,∴平面PEC⊥平面PCD.[课时跟踪检测]A级1.设a,b是两条不同的直线,α,β是两个不同的平面,则能得出a⊥b的是() A.a⊥α,b∥β,α⊥βB.a⊥α,b⊥β,α∥βC.a⊂α,b⊥β,α∥βD.a⊂α,b∥β,α⊥β解析:选C对于C项,由α∥β,a⊂α可得a∥β,又b⊥β,得a⊥b,故选C.2.(2019·湘东五校联考)已知直线m,l,平面α,β,且m⊥α,l⊂β,给出下列命题:①若α∥β,则m⊥l;②若α⊥β,则m∥l;③若m⊥l,则α⊥β;④若m∥l,则α⊥β.其中正确的命题是()A.①④B.③④C.①②D.①③解析:选A对于①,若α∥β,m⊥α,l⊂β,则m⊥l,故①正确,排除B.对于④,若m∥l,m⊥α,则l⊥α,又l⊂β,所以α⊥β.故④正确.故选A.3.已知P A垂直于以AB为直径的圆所在的平面,C为圆上异于A,B两点的任一点,则下列关系不正确的是()A.P A⊥BC B.BC⊥平面P ACC.AC⊥PB D.PC⊥BC解析:选C由P A⊥平面ACB⇒P A⊥BC,故A不符合题意;由BC⊥P A,BC⊥AC,P A∩AC=A,可得BC⊥平面P AC,所以BC⊥PC,故B、D不符合题意;AC⊥PB显然不成立,故C符合题意.4.如图,在四面体ABCD中,已知AB⊥AC,BD⊥AC,那么点D在平面ABC内的射影H必在()A.直线AB上B.直线BC上C.直线AC上D.△ABC内部解析:选A因为AB⊥AC,BD⊥AC,AB∩BD=B,所以AC⊥平央ABD,又AC⊂平面ABC,所以平面ABC⊥平面ABD,所以点D在平面ABC内的射影H必在直线AB上.5.如图,在正四面体PABC中,D,E,F分别是AB,BC,CA的中点,则下面四个结论不成立的是()A.BC∥平面PDFB.DF⊥平面P AEC.平面PDF⊥平面P AED.平面PDE⊥平面ABC解析:选D因为BC∥DF,DF⊂平面PDF,BC⊄平面PDF,所以BC∥平面PDF,故选项A正确.在正四面体中,AE⊥BC,PE⊥BC,AE∩PE=E,所以BC⊥平面P AE,又DF∥BC,则DF⊥平面P AE,从而平面PDF⊥平面P AE.因此选项B、C均正确.6.如图,已知∠BAC=90°,PC⊥平面ABC,则在△ABC,△P AC的边所在的直线中,与PC垂直的直线有________个;与AP垂直的直线有________个.解析:∵PC⊥平面ABC,∴PC垂直于直线AB,BC,AC.∵AB⊥AC,AB⊥PC,AC∩PC=C,∴AB⊥平面P AC,又∵AP⊂平面P AC,∴AB⊥AP,与AP垂直的直线是AB.答案:317.设α和β为不重合的两个平面,给出下列命题:①若α内的两条相交直线分别平行于β内的两条直线,则α∥β;②若α外的一条直线l与α内的一条直线平行,则l∥α;③设α∩β=l,若α内有一条直线垂直于l,则α⊥β;④直线l⊥α的充要条件是l与α内的两条直线垂直.其中所有的真命题的序号是________.解析:①正确;②正确;满足③的α与β不一定垂直,所以③错误;直线l⊥α的充要条件是l与α内的两条相交直线垂直,所以④错误.故所有的真命题的序号是①②.答案:①②8.在直三棱柱ABCA1B1C1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确命题的序号是________.解析:如图所示,因为AA1∥平面α,平面α∩平面AA1B1B=EH,所以AA1∥EH.同理AA1∥GF,所以EH∥GF,又ABCA1B1C1是直三棱柱,易知EH=GF=AA1,所以四边形EFGH是平行四边形,故①正确;若平面α∥平面BB1C1C,由平面α∩平面A1B1C1=GH,平面BCC1B1∩平面A1B1C1=B1C1,知GH∥B1C1,而GH∥B1C1不一定成立,故②错误;由AA1⊥平面BCFE,结合AA1∥EH知EH⊥平面BCFE,又EH⊂平面α,所以平面α⊥平面BCFE,故③正确.答案:①③9.(2019·太原模拟)如图,在四棱锥PABCD中,底面ABCD是菱形,∠BAD=60°,P A=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.(1)求证:AD⊥平面PNB;(2)若平面P AD⊥平面ABCD,求三棱锥PNBM的体积.解:(1)证明:连接BD.∵P A=PD,N为AD的中点,∴PN⊥AD.又底面ABCD是菱形,∠BAD=60°,∴△ABD为等边三角形,∴BN⊥AD,又PN∩BN=N,∴AD⊥平面PNB.(2)∵P A=PD=AD=2,∴PN=NB= 3.又平面P AD⊥平面ABCD,平面P AD∩平面ABCD=AD,PN⊥AD,∴PN⊥平面ABCD,∴PN⊥NB,∴S△PNB=12×3×3=32.∵AD⊥平面PNB,AD∥BC,∴BC ⊥平面PNB .又PM =2MC , ∴V P NBM =V M PNB =23V C PNB =23×13×32×2=23.10.如图,在直三棱柱ABC A 1B 1C 1中,D ,E 分别为AB ,BC 的中点,点F 在侧棱B 1B 上,且B 1D ⊥A 1F ,A 1C 1⊥A 1B 1.求证:(1)直线DE ∥平面A 1C 1F ; (2)平面B 1DE ⊥平面A 1C 1F .证明:(1)在直三棱柱ABC A 1B 1C 1中,AC ∥A 1C 1, 在△ABC 中,因为D ,E 分别为AB ,BC 的中点. 所以DE ∥AC ,于是DE ∥A 1C 1,又因为DE ⊄平面A 1C 1F ,A 1C 1⊂平面A 1C 1F , 所以直线DE ∥平面A 1C 1F .(2)在直三棱柱ABC A 1B 1C 1中,AA 1⊥平面A 1B 1C 1, 因为A 1C 1⊂平面A 1B 1C 1,所以AA 1⊥A 1C 1,又因为A 1C 1⊥A 1B 1,A 1B 1∩AA 1=A 1,AA 1⊂平面ABB 1A 1,A 1B 1⊂平面ABB 1A 1, 所以A 1C 1⊥平面ABB 1A 1, 因为B 1D ⊂平面ABB 1A 1, 所以A 1C 1⊥B 1D ,又因为B 1D ⊥A 1F ,A 1C 1∩A 1F =A 1,A 1C 1⊂平面A 1C 1F ,A 1F ⊂平面A 1C 1F , 所以B 1D ⊥平面A 1C 1F , 因为直线B 1D ⊂平面B 1DE , 所以平面B 1DE ⊥平面A 1C 1F .B 级1.(2018·全国卷Ⅱ)如图,在三棱锥P ABC 中,AB =BC =22,P A =PB =PC =AC =4,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC =2MB ,求点C 到平面POM 的距离. 解:(1)证明:因为P A =PC =AC =4,O 为AC 的中点, 所以PO ⊥AC ,且PO =2 3. 连接OB , 因为AB =BC =22AC , 所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB =12AC =2.所以PO 2+OB 2=PB 2,所以PO ⊥OB . 又因为AC ∩OB =O ,所以PO ⊥平面ABC . (2)作CH ⊥OM ,垂足为H , 又由(1)可得OP ⊥CH , 所以CH ⊥平面POM .故CH 的长为点C 到平面POM 的距离.由题设可知OC =12AC =2,CM =23BC =423,∠ACB =45°,所以OM =253,CH =OC ·MC ·sin ∠ACB OM =455.所以点C 到平面POM 的距离为455.2.(2019·河南中原名校质量考评)如图,在四棱锥P ABCD 中,AB ∥CD ,AB ⊥AD ,CD =2AB ,平面P AD ⊥底面ABCD ,P A ⊥AD ,E ,F 分别是CD ,PC 的中点.求证:(1)BE ∥平面P AD ; (2)平面BEF ⊥平面PCD .证明:(1)∵AB ∥CD ,CD =2AB ,E 是CD 的中点, ∴AB ∥DE 且AB =DE , ∴四边形ABED 为平行四边形,∴AD ∥BE ,又BE ⊄平面P AD ,AD ⊂平面P AD , ∴BE ∥平面P AD .(2)∵AB ⊥AD ,∴四边形ABED 为矩形, ∴BE ⊥CD ,AD ⊥CD ,∵平面P AD ⊥底面ABCD ,平面P AD ∩底面ABCD =AD ,P A ⊥AD , ∴P A ⊥底面ABCD , ∴P A ⊥CD ,又P A ∩AD =A , ∴CD ⊥平面P AD ,∴CD ⊥PD , ∵E ,F 分别是CD ,PC 的中点, ∴PD ∥EF ,∴CD ⊥EF ,又EF ∩BE =E , ∴CD ⊥平面BEF ,∵CD ⊂平面PCD ,∴平面BEF ⊥平面PCD .。
实验心理学下第八章第五节前瞻记忆

成功的前瞻记忆有两点要求:记住发生了什么 事情(包括过去的行为和特定的目标事件);记
住必须要在将来特定的时间执行某个行为或是对
特定的目标事件作出反应。前者包含了回溯成分,
而后者不是,也就是说,成功的前瞻记忆需要回
溯记忆。
Peter Graf(2001)将前瞻记忆类比为采矿,前瞻 成分如同勘探专家,其作用是在环境中根据矿物 储存的迹象,确定是否有矿可以开采;当确定有 矿后,具体的开采任务则留待矿工去进是被动地 反映其是否能成功地完成一件任务,而且可以对 完成任务产生主动的影响。其中一种影响是通过 采用记忆策略。麦克丹尼尔-米兹扎克(1999)认 为,在个体的自我效能感形成过程中,前瞻记忆
比回溯记忆起更大的作用。
麦克丹尼尔-米兹扎克在实验中设计了两种前瞻 记忆任务和回溯记忆任务。基于时间的前瞻记忆 任务是,提醒主试20分钟后打一个重要的电话向 导师询问是否获得了奖学金,并在桌子上放有时 钟作为提示。被试的记忆成绩用4点记分,0为完 全忘记,1为准确度超过10分钟,2为准确度在210分钟之间,3为2分钟之内。
分类依据 记忆类型 特点
提取的意 外显记忆 有意识的 识性 提取 内隐记忆 无意识的 自动提取 对记忆的 客体记忆 对信息的 控制 编码、储 存和提取 元记忆 对客体记 忆的认识 评价和监 控
典型实验方法
直接测量 间接测量 加工分离程序
FOK研究中的 RJR、gameshow范式等
分类依 据 是否真 实反映 事实
记忆类型 特点 真实记忆 准确真实 反映事实
典型实验方法
错误记忆 错误虚假 联想研究范式误 反映事实 导信息干扰范式
信息指 向
是否涉 及情绪 事件
回溯记忆 记忆过去 的行为或 事件 前瞻记忆 记忆某个 意向 情绪记忆
高等代数第八章 5第五节 初等因子

事实上, 证明 事实上,令 (f1(λ)g1(λ), f2(λ)g2(λ))=d(λ), , (f1(λ), f2(λ))=d1(λ), (g1(λ), g2(λ))=d2(λ) . , 显然, 显然, d1(λ)|d(λ), d2(λ)|d(λ) . , 由于 (f1(λ), g1(λ))=1,故 (d1(λ), d2(λ))=1, , , 因而, 因而, d1(λ)d2(λ)|d(λ). 另一方面,由于 d(λ)|f1(λ)g1(λ), 另一方面, , 可令 d(λ)= f(λ)g(λ),其中 f(λ)|f1(λ),g(λ)|g1(λ). , , 由于 (f1(λ), g2(λ))=1,故 (f(λ), g2(λ))=1, , 由 f(λ)|f2(λ)g2(λ),又得 f(λ)|f2(λ),因而 f(λ)|d1(λ) . , , 同理 g(λ)|d2(λ). 所以 d(λ)|d1(λ)d2(λ). 证毕. 于是 d(λ)=d1(λ)d2(λ) . 证毕
返回
上页
下页
二、初等因子与不变因子的求法 上面的分析给了我们一个如何从初等因子和 上面的分析给了我们一个如何从初等因子和 如何从初等因子 矩阵的级数唯一地作出不变因子的方法 设一个n 矩阵的级数唯一地作出不变因子的方法. 设一个 唯一地作出不变因子的方法 级矩阵的全部初等因子为已知, 级矩阵的全部初等因子为已知,在全部初等因子 全部初等因子为已知 将同一个一次因式(λ中将同一个一次因式 -λj), (j=1,2, …,r)的方幂的那 的方幂的那 些初等因子按降幂排列,而且当这些初等因子的 些初等因子按降幂排列, 个数不足n时 就在后面补上适当个数的 , 个数不足 时,就在后面补上适当个数的1,使得 凑成n个 设所得排列 排列为 凑成 个. 设所得排列为
第八章第五节莫言苏童

• 他将目光锁定在广阔 的历史空间,始终坚 守着对待历史的民间 立场、个人立场。 • 莫言的小说以“高密 东北乡”为起点解读 历史,形成一种“文 学地理”。
• 民间的营养渗透在文本的各个方面: • 材料来源:家乡大地上流传的传说、故事, 或作者想象的故乡的历史; • 情节构成:人们为生存的奋斗过程和大胆恣 肆的男女性爱——一个富有生命活力的民间 世界; • 叙述语言:磅礴大气,自由流畅,充满民间 的野性美。 • 作者的立场:以“民间”身份叙述和关怀民 间乡土社会 。
《丰乳肥臀》
• 写高密东北乡的百年精神发展史,概括了民族精神 的百年屈辱和百年荒唐的历史。 • 通过母亲上官鲁氏及其儿女们的坎坷、曲折的人生 遭遇和命运的描写,重新审视了20世纪中国的历史 进程。 • 塑造了上官鲁氏和上官金童的形象,尤其是上官金 童的“恋乳症”的象征意味,更能引起人们的思索。
《檀香刑》
• 苏童小说的基本母题: 1、“逃离——回归”(还乡小说) • 乡村和城市是苏童小说两个并行的叙事空 间。“我的血脉在乡村这一侧,我的身体 却在城市那一侧。” (《世界两侧》 ) • 《一九三四年的逃亡》:陈宝年 • “几十年后我隐约听到那阵叛逆性的脚步 声穿透了历史,我茫然失神。老家的女人 们你们为什么无法留住男人同生同死呢? 女人不该像我祖母蒋氏一样沉浮在苦海深 处,枫杨树不该成为女性的村庄啊。 ”
• “一穗一穗被露水打得精湿的高粱在雾洞里忧悒地注视着 我父亲,父亲也虔诚地望着它们。父亲恍然大悟,明白了 它们都是活生生的灵物。它们扎根黑土,受日精月华,得 雨露滋润,上知天文下知地理。”
• “奶奶听到了宇宙的声音,那声音来自一株株红高粱…… 奶奶觉得天与地与人、与高粱交织在一起……所有的忧虑、 痛苦、紧张、沮丧都落在了高粱地里,都冰雹般打在高粱 梢头,在黑土上扎根开花,结出酸涩的果实,让下一代又 一代承受……”
第八章 第五节 直线、圆的位置关系

3.两圆公切线的条数 . (1)两圆内含时,公切线条数为0; 两圆内含时,公切线条数为 ; 两圆内含时 (2)两圆内切时,公切线条数为1; 两圆内切时,公切线条数为 ; 两圆内切时 (3)两圆相交时,公切线条数为2; 两圆相交时,公切线条数为 ; 两圆相交时 (4)两圆外切时,公切线条数为3; 两圆外切时,公切线条数为 ; 两圆外切时 (5)两圆相离时,公切线条数为4. 两圆相离时,公切线条数为 两圆相离时 因此求两圆的公切线条数主要是判断两圆的位置关系, 因此求两圆的公切线条数主要是判断两圆的位置关系, 反过来知道两圆公切线的条数, 反过来知道两圆公切线的条数,也可以判断出两圆的位 置关系. 置关系.
条公切线. ∴两圆相交,故有2条公切线. 两圆相交,故有 条公切线 答案: 答案:2
直线与圆的位置关系有相离(没有公共点 、相切(只 直线与圆的位置关系有相离 没有公共点)、相切 只 没有公共点 有一个公共点)、相交(有两个公共点 三种,判断直线与圆 有两个公共点)三种 有一个公共点 、相交 有两个公共点 三种, 的位置关系主要有两种方法: 的位置关系主要有两种方法:一是圆心到直线的距离与圆 的半径比较大小; 的半径比较大小;二是直线与圆的方程组成的方程组解的 个数. 个数.
3.已知0<r< .已知 < < 的位置关系是 A.外切 . C.相交 .
+1,则圆 2+y2=r2与(x-1)2+(y+1)2=2 ,则圆x - + ( B.内含 . D.相离 . )
解析:两圆连心线长|O1O2|= 解析:两圆连心线长 = r1+r2=r+ + 所以 <r+ + ,|r1-r2|=| = <2 +1,- ,-
5.两圆x2+y2-6x+6y-48=0与x2+y2+4x-8y-44=0 .两圆 + - = 与 - - = 公切线的条数是__________. 公切线的条数是 . 解析:两圆为 - 解析:两圆为(x-3)2+(y+3)2=66和 + 和 (x+2)2+(y-4)2=64, + - , 两圆圆心距离
高等数学第八章第5节

− 4 x + 2 y − 2z − 1 = 0 − 4 x + 2 y + 2z − 2 = 0
r n2 = {−4, 2,−2}
2 −1 1 , 两平面平行 ⇒ = = −4 2 −2 Q M (1,1,0) ∈ Π 1 M (1,1,0) ∉ Π 2
两平面平行但不重合. 两平面平行但不重合.
பைடு நூலகம்
2 −1 −1 , 两平面平行 ( 3) Q = = 2 −4 2
4 x − y + 2 z = 8 垂直,求此平面方程 垂直,求此平面方程.
解 设平面为 Ax + By + Cz + D = 0, 由平面过原点知 D = 0,
由平面过点( 6,−3, 2) 知 6 A − 3 B + 2C = 0
r Q n⊥{4,−1,2},
∴ 4 A − B + 2C = 0
2 ⇒ A = B = − C, 3 所求平面方程为 2 x + 2 y − 3 z = 0.
特别,当平面与三坐标轴的交点分别为 当平面与三坐标轴的交点分别为 时,平面方程为 x y z + + = 1 (a , b, c ≠ 0) a b c 此式称为平面的截距式方程 截距式方程. 截距式方程 分析:利用三点式
Ax + By + Cz + D = 0 ( A + B + C ≠ 0 )
2 2 2
平面一般式方程的几种特殊情形: • 当 D = 0 时, A x + B y + C z = 0 表示 通过原点 通过原点的平面; • 当 A = 0 时, B y + C z + D = 0 的法向量
高等数学_第八章_多元微分_第五节_隐函数求导
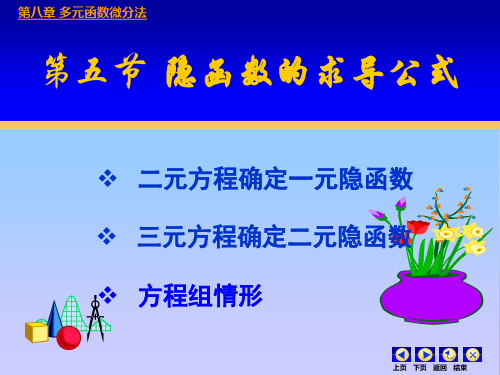
Fx F v Gx Gv
课本P34课本P34-P35 P34
Fy F v GyGv
F Fx u Gu Gx F u Gu
参见二元 线性方程 组的求解 公式
Fy Gy
上页 下页 返回 结束
例4. 设 x = e
u+v
, y =e
u+v
u−v
, z = uv , 求
u−v
解 现在 z = uv , 式中 u = u(x, y), v = v(x, y)由方程 由方程
z
z
F′⋅ 1 1 z
∂z =− y ∂y ′ F′⋅ (− x ) + F2 ⋅ (− 2 ) 1 2
z z
F′ ⋅ 1 2 z
′ z F2 = ′ x F′ + y F2 1
故
Fx ∂z ∂z ∂z z dz = dx + dy = =− (F′dx + F′dy) 1 2 ∂x ∂y x F′ + y F′ ∂x Fz 1 2
再对 x 求导
2+
∂z 2 1+ ( ) ∂x
∂2z −4 2 = 0 ∂x
上页
下页
返回
结束
解二 利用隐函数求导公式 设 则
F(x, y, z) = x2 + y2 + z2 − 4z
Fx = 2x,
Fz = 2z − 4
∴
x x Fx ∂z = =− =− z −2 2− z ∂x Fz
两边对 x 求偏导
上页 下页 返回 结束
微分法. 解二 微分法 对方程
两边求微分: 两边求微分
x y F′⋅ d( ) + F′ ⋅ d( ) = 0 2 1 z z zdx − xdz zdy − ydz F′⋅ ( ) + F′ ⋅( ) =0 1 2 z2 z2 ′ xF′+ yF2 F′dx +F′ dy 1 2 整理得 dz = 1 2 z z z dz = (F′dx + F′dy) 解得 1 2 x F′ + y F′ 1 2
毛概 第八章 第五节 建设社会主义生态文明

一、树立社会主义 生态文明新理念 二、坚持节约资源 和保护环境的基本 国策 三、完善生态文明 制度体系
公益-CCTV公益广 告《雾霾篇》[高清].mp4
By:饶章瀚
建设社会主义生态文明的总体要求
• 生态是指生物之间以及生物 与非生物环境之间的相互关 系和存在状态。 • 生态文明是指人类在改造客 观世界的同时,积极改善和 优化人与自然的关系,建设 有序的生态运行机制和良好 的生态环境所取得的物质、 精神、制度方面成果的总和。 • 生态文明是人与自然和谐共 生、全面协调、持续发展的 社会和自然状态。
我们应如何建设生态文明?
日本垃圾分类
•
在日本,你如果你不严格的执行垃 圾分类的话,将面临巨额的罚款, 在以住宅团地为单位的区域社会, 落下个“不履行垃圾分类”的名声, 那可是老丢人的事了。 • 日本的垃圾分类是母亲手把手教 下一代的。从出生开始就学起的。 有些学到老也分不对的也大有人在。 比如一个香烟盒,其间的纸盒、外 包的塑料薄膜、封口处的那圈铝箔。 这个香烟盒就要分三类:外包是塑 料,盒子是纸,铝箔是金属,所以 这件东西就要分三类丢弃。 • 日本几乎做到了垃圾百分之百回收, 依赖的不是先进的技术和发达的科 技,是全民对环境的敬畏、真挚的 感情和高度的民众的自觉性。
在我国各种污染日趋严重,包括大气污染、水污染、 光污染、噪音污染、土壤污染、固体废弃物污染等 等。其中水污染和大气污染尤为严重。 光污染 空气污染
噪音污染 水污染
固体废弃物 污染
土壤污染
2009 年,一位海洋 摄影师在北极地区偶然 拍摄到冰盖融化形成的 天然雕塑——一张哭泣 的脸。气候变化已成为 当今国际社会面临的最 大挑战之一。正如学者 所言,“金融危机要钱, 气候变化要命”。
第八章 第五节.电功率和安全用电(教案)

彩田学校物理学案第八章电功率第5节.电功率和安全用电班级:姓名:五、电功率和安全用电【学习目标】1、知道电功率和电路中电流的关系,理解电路中的总电流随用电器功率的增大而增大;2、知道电路中安装保险丝,为什么能够“保险”。
【课前检测】1.电功的计算公式:W=Pt 、W=UIt 、W=U2 t / R 、W= I 2 R t2.电功率的计算公式:P=W/t 、P= UI 、P=U 2 / R 、P = I 2 R3.电能(电功)的国际单位是焦耳简称焦,单位的符号 J ;另外还有“度”,学名叫做千瓦时,符号 kW·h 。
它们之间的换算关系是: 1kW·h=3.6×10 6J。
4.物理学中用“电功率”表示用电器消耗电能的快慢,该物理量的符号是P ,其单位有瓦特(单位符号W )、千瓦(单位符号kW ),单位间的换算1kW=1000W 。
5.焦耳定律:电流通过导体产生的热量跟电流的二次方成正比,跟导体的电阻成正比,跟通电时间成正比。
用公式表示为: Q =I2Rt 。
在纯电阻电路中,电流产生的热量Q等于消耗的电能W,即Q=W=P t = U I t = I 2 R t = U2 t / R 。
【课堂导学】【学点一】电功率和安全用电(阅读课本51页“电功率与安全用电”部分,回答下列问题)1.通过公式P=UI,你能推导出I= P/U 。
因为家庭电路中的电压为 220 V保持不变,所以用电器的功率越大,通过用电器的电流越大。
2.家庭电路中各用电器是并联的,如果多个用电器同时使用,总功率会比较大,那么总电流会比较大。
因此,一定注意不要让总电流超过家里供电线路和电能表所允许的最大值。
3.电路中同时使用的用电器不能太多,否则容易烧坏保险丝,甚至引起火灾。
4.讨论右图电路,用电流表测干路电流。
先连入一个灯泡,然后并联第二个、第三个灯泡……,观察电流表示数,可以看到,电流表示数变大,当连入的灯泡达到一定数目时,保险丝会熔断。
第八章 第五节 黄土高原的区域发展与居民生活

•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/42021/9/4Saturday, September 04, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/42021/9/42021/9/49/4/2021 3:06:58 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/42021/9/42021/9/4Sep-214-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/42021/9/42021/9/4Saturday, September 04, 2021
单项选择
【基础过关】
1.黄土高原位于( B )
A.大兴安岭以东 B.太行山以西 C.秦岭以南 D.乌鞘岭以北
2.黄土高原重要的生态问题是( B )
A.荒漠化 B.水土流失 C.全球变暖 D.酸雨
3.黄土高原的地貌特征是( B )
A.地面崎岖、峰岭众多 B.沟壑纵横、支离破碎 C.地势西高东低 D.石灰岩广布、多喀斯特地形
【名师点拨】 黄土高原水土流失的原因是什么? 自然原因:①地形方面:黄土高原平地少,斜坡多,地面破 碎。②土质方面:黄土结构疏松,多孔隙和垂直方向的裂隙;许 多物质易溶于水。③降水方面:黄土高原降水集中在 7、8 月份, 且多暴雨。④植被方面:植被严重破坏,大多数地区地表裸露。 人为原因:人类的过度开发(过度放牧、开矿、毁林开荒)。
9.在黄土高原生态环境建设中,不.可.取.的做法是( D )
A.植树种草、整修梯田 B.退耕还林、还草 C.减少放牧的牧畜数量 D.开垦陡坡,扩大耕地面积
同济版高等数学第六版课件第八章第五节曲面及其方程

曲面的应用领域
物理学:研究曲面形状对 物理现象的影响
计算机图形学:用于创建 三维模型和动画
地质学:用于描述地球表 面的形态
生物学:用于研究生物体 的表面结构
工程学:用于设计各种曲 面形状的物体,如汽车车 身、飞机机翼等
数学:用于研究曲面的性 质和结构,以及解决相关 的数学问题
06
曲面方程的解题技 巧与注意事项
同济版高等数学第 六版课件第八章第 五节曲面及其方程
单击此处添加副标题
汇报人:PPT
目录
添加目录项标题 曲面方程的求解方法 曲面方程的拓展知识
曲面及其方程的基本概念
曲面方程的应用实例 曲面方程的解题技巧与注 意事项
01
添加章节标题
02
曲面及其方程的基 本概念
曲面的定义和分类
曲面的定义:曲面是连续但不光滑的二维图形,由一条或多条曲线组成
04
曲面方程的应用实 例
球面方程的应用
定义:球面方程是描述球面形状的数学方程 应用实例1:计算球面上的点到球心的距离 应用实例2:确定球面上点的坐标 应用实例3:绘制球面图形
柱面方程的应用
定义:柱面方程是 平面与空间直线或 平面相交形成的曲 面
应用实例1:在计 算机图形学中,柱 面方程可以用来描 述三维图形的旋转 和扭曲
总结:通过对解题思路的总结,可以更好地掌握曲面方程的解题技巧 和注意事项,提高解题效率。
感谢观看
汇报人:PPT
解题技巧
熟练掌握曲面方 程的基本形式和 性质
灵活运用代数运 算技巧,简化方 程
掌握常见的曲面 方程的解题方法
注意方程的适用 范围和限制条件
注意事项
理解曲面方程的 基本概念和性质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
① ②
课 时 知 能 训 练
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
自 主 落 实 · 固 基 础
将①②两式相加,得|O1M|+|O2M|=12>|O1O2|, ∴动圆圆心M(x,y)到点O1(-3,0)和O2(3,0)的距离和是常数 12, 所以点M的轨迹是焦点为O1(-3,0)、O2(3,0), 长轴长等于12的椭圆. ∴2c=6,2a=12,∴c=3,a=6, ∴b2=36-9=27, x2 y2 ∴圆心轨迹方程为 + =1,轨迹为椭圆. 36 27
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能
自 主 落 实 · 固 基 础
1.解答本题时,易忽视点(-4,0)和(4,0)不合要求,致使 答案错误.
2.求轨迹方程时,若动点与定点、定线间的等量关系
满足圆、椭圆、双曲线、抛物线的定义,则可以直接根据定 义先定轨迹类型,再写出其方程,这种求轨迹方程的方法叫
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
已知A、B为两定点,动点M到A与到B的距离比为常数λ,求点 M的轨迹方程,并说明轨迹是什么曲线.
自 主 落 实 · 固 基 础
【解】 建立直角坐标系如图所 示,设|AB|=2a,则A(-a,0), B(a,0), 设M(x,y)是轨迹上任意一点, |MA| 则由题设,得 =λ(λ>0),坐 |MB| x+a2+y2 标代入,得 =λ,化简得 2 2 x-a +y (1-λ2)x2+(1-λ2)y2+2a(1+λ2)x+(1 -λ2)a2=0.
【尝试解答】 过点A、B、O分别作直线l的垂线,垂足分 别为A′、B′、O′. ∵|AO|=|BO|, ∴|AA′|+|BB′|=2|OO′|=8, 设抛物线的焦点为F,则|AF|+|BF|=|AA′|+|BB′|=8, 又|AB|=4, ∴点F的轨迹在以点A、B为焦点的椭圆上, x 2 y2 设所求椭圆方程为 2+ 2=1, a b 则a2=42=16,b2=42-22=12, x2 y2 ∴抛物线焦点的轨迹方程为 + =1(x≠± 4). 16 12
自 主 落 实 · 固 基 础
)
A.圆
C.双曲线
B.椭圆
D.抛物线
→ PN → 【解析】 ∵PM· =0, ∴PM⊥PN, ∴点P的轨迹是以线段MN为直径的圆.
【答案】 A
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
用定义法求轨迹方程 (2012· 佛山模拟)如图8-5-2,
自 主 落 实 · 固 基 础
圆O:x2+y2=16,A(-2,0),B(2,0)为
两个定点.直线l是圆O的一条动切线, 若经过A、B两点的抛物线以直线l为 准线,求抛物线焦点的轨迹方程.
自 主 落 实 · 固 基 础
1 1 4.(2012· 河源质检)已知点 F( ,0),直线 l:x=- ,点 B 是 4 4 l 上的动点.若过点 B 垂直于 y 轴的直线与线段 BF 的垂直平分线 交于点 M,则点 M 的轨迹是( )
A.双曲线 C.圆 【解析】 B.椭圆 D.抛物线 由已知:|MF|=|MB|,根据抛物线的定义知,
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
2.求曲线方程的一般步骤 有序实数对(x,y) (1)建立适当的坐标系,用______________________表示曲线 上任意一点的坐标;
自 主 落 实 · 固 基 础
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
用代入法(相关点法)求轨迹方程
自 主 落 实 · 固 基 础
x2 已知双曲线 -y2=1的左、右顶点分别为A1、A2,点 2 P、Q是双曲线上不同的两个关于x轴的对称点.求直线A1P与 A2Q交点M的轨迹E的方程.
y2 整理得 x - =4mn, 3 1 又 mn= , 4
2
y2 ∴P 点的轨迹方程为 x2- =1(x>0). 3 它表示以原点为中心,焦点在 x 轴上,实轴长为 2,焦距为 4 的双 y2 曲线 x - =1 的右支. 3
2
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
自 主 落 实 · 固 基 础
【解析】 【答案】
由xy<0知,曲线在第二、四象限,故选C. C
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
3.若M、N为两个定点,且|MN|=6,动点P满足·=0,则P点的 轨迹是(
自 主 落 实 · 固 基 础
在平面直角坐标系中,如果某曲线C上的点与一个二元方程f(x, y)=0的实数解建立了如下关系:
(1)曲线上点的坐标都是________________. 这个方程的解
(2)以这个方程的解为坐标的点都是_______________.那么这 曲线上的点 个方程叫做______________,这条曲线叫做____________. 曲线的方程 方程的曲线
点M的轨迹是以点F为焦点,直线l为准线的抛物线,故选D. 【答案】 D
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
用直接法求轨迹方程
自 主 落 实 · 固 基 础
如图8-5-1,A(m, 3 m)和 B(n,- 3n)两点分别在射线OS,OT 1 → OB → 上移动,且OA· =- ,O为坐标原 2 → → → 点,动点P满足OP=OA+OB. (1)求mn的值; (2)求动点P的轨迹方程,并说明 它表示什么曲线?
高 考 体 验 · 明 考 情
做定义法,其关键是准确应用解析几何中有关曲线的定义.
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
如图8-5-3所示,一动圆与圆x2+y2
+6x+5=0外切,同时与圆x2+y2-6x
【思路点拨】
设抛物线的焦点为F,利用抛物线的定义可得:
课 时 知 能 训 练
|AF|+|BF|=8,从而点F的轨迹是椭圆,又当点F与点A、B在一 条直线上时,不合题意,故应除去两点.
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
自 主 落 实 · 固 基 础
2.轨迹与轨迹方程相同吗?
【提示】 不同.前者为图形包括轨迹的形状、方程、图形等,
而后者仅指方程.
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
自 主 落 实 · 固 基 础
1.(教材改编题)若动点P到点O(0,0)的距离和到点A(c,0)的距 离的平方差为常数c(c≠0),则点P的轨迹方程是( ) A.x2+y2=c2 B.x2-y2=c2 c+1 c C.x= D.x= 2 2
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
1.解答本题(2)时,根据
自 主 落 实 · 固 基 础
利用第(1)问的
结论消去m,n得到轨迹方程是解题的关键.
2.如果动点满足的几何条件就是一些与定点、定直线
有关的几何量的等量关系,而该等量关系又易于表达成含x, y的等式,从而可直接得到轨迹方程,这种求轨迹方程的方法 称为直接法. 3.求点的轨迹时,要明确题设的隐含条件,以免增解, 如本例中动点P的轨迹只是双曲线的右支.
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
1.如果曲线与方程只满足第(2)个条件,会出现什么情况?
自 主 落 实 · 固 基 础
【提示】
若只满足“以这个方程的解为坐标的点都是曲线上
的点”,则这个方程可能只是部分曲线的方程,而非整个曲线 的方程,如分段函数的解析式.
【解析】 设P(x,y),由题意知(x2+y2)-[(x-c)2+y2]=c c+1 化简得x= . 2
【答案】 D
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
2.方程x2+y2=1(xy<0)的曲线形状是(
)
课 时 知 能 训 练
菜
单
一轮复习 ·新课标 ·数学(理)(广东专用)
典 例 探 究 · 提 知 能 高 考 体 验 · 明 考 情
→ → → (2)设 P(x,y)(x>0),由OP=OA+OB, 得(x,y)=(m, 3m)+(n,- 3n)=(m+n, 3m- 3n).
