三元系相图基础1
合集下载
三元系相图简介
析Sn+Bi：
Wl KM Ws OM
WSn KBi Ws WSn WBi , WBi SnK
三、三元水盐系相图
水+两种盐，且两盐有共同的一种离子
1.纯盐(B+C)与水(A)体系
A(H2O)
纯盐：不形成共溶盐
不形成化合物
F D E
不形成水合盐
D点：B盐在纯水中的
B
C
溶解度； F点：C盐在纯水中的溶解度； E点：共饱和点（三相点）
平行于底面
Bi
二次结晶面：二元共晶线到三元共晶线间的线 段，从一个组元温度轴，通过二次结晶线向另 一个组元温度轴滑动，在空间所留下的轨迹面。
T T T T T T T T T
e1
Bi
e2 e3
Bi Sn Pb Bi
e
Pb
e
Pb Sn Sn
e
液相(单相)区：液相面以上的空间区域； 两相区：3个
液相面以下，二次结晶面以上的空间区域；
c
b’
B P
A
a’
Aa’= cb’=Pc：
代表体系P中C物的含量；
A
b
c’
C
a
1. 等含量规则
一组体系点同在平行于三角形某一
b’
B P Q R
b
C
边的线上，该则组体系中平行线对
应的顶点组成含量相同。
2. 定比规则
凡位于通过顶点(A)的任一直线上的 体系，其中顶点代表的组元含量不 同，其余两组元(B和C)的含量比相 同，即： cB ( R ) cB ( P ) cB ( Q ) cC( R ) cC( P ) cC( Q ) 3. 杠杆规则 由两个三元体系(M和N)混合得到的
三元系统相图
第五节
三元系统相图
一、三元系统相图概述
三元凝聚系统相律： F＝C－P＋1＝4－P
1、三元系统组成表示方法
——浓度（组成）三角形 应用： 1）已知点 的位置， 确定其组成； 2）已知组成，确定 点的位置；
双线法：
2、浓度三角形规则
（1）等含量规则 等含量规则：平行于浓度 三角形一边的直线上的各点， 其第三组分的含量不变，即： MN线上C％相等。
在在mn外mpn二三元系统相图基本类型一具有一个低共熔点的简单三元系统相图二生成一个一致熔融二元化合物的三元系统相图三具有一个一致熔融三元化合物的三元系统相图四生成一个不一致熔融二元化合物的三元系统相图五具有一个不一致熔融三元化合物的三元系统相图六生成一个固相分解的二元化合物的三元系统相图七具有多晶转变的三元系统相图八形成一个二元连续固溶体的三元系统相图九具有液相分层的三元系统相图一具有一个低共熔点的简单三元系统相图1立体相图2平面投影图投影图上温度表示法
T转 > Te3 、 T转 < Te2——多晶转变点P
T转 < Te2 、Te3——多晶转变点P1、P2
（八）形成一个二元连续固溶体的三元系统相图
（九）具有液相分层的三元系统相图
总结：
分析实际三元系统（复杂三元系统）相图的步骤
一、判断化合物的性质；
二、划分副三角形； 三、判断界线上温度变化——连（结）线规则； 四、判断界线性质——切线规则； 五、确定三元无变量点的性质——重心原理；
（三） 具有一个一致熔融三元化合物的三元系统相图
（四） 生成一个不一致熔融二元化合物的三元系统相图 1、相图组成
（1）不一致熔融化合物S不在自己的相区内； （2）化合物S性质的改变，导致CS连线、无变 量点P、界线的性质改变。 （a）CS连线 （b）无变量点：P点
三元系统相图
一、三元系统相图概述
三元凝聚系统相律： F＝C－P＋1＝4－P
1、三元系统组成表示方法
——浓度（组成）三角形 应用： 1）已知点 的位置， 确定其组成； 2）已知组成，确定 点的位置；
双线法：
2、浓度三角形规则
（1）等含量规则 等含量规则：平行于浓度 三角形一边的直线上的各点， 其第三组分的含量不变，即： MN线上C％相等。
在在mn外mpn二三元系统相图基本类型一具有一个低共熔点的简单三元系统相图二生成一个一致熔融二元化合物的三元系统相图三具有一个一致熔融三元化合物的三元系统相图四生成一个不一致熔融二元化合物的三元系统相图五具有一个不一致熔融三元化合物的三元系统相图六生成一个固相分解的二元化合物的三元系统相图七具有多晶转变的三元系统相图八形成一个二元连续固溶体的三元系统相图九具有液相分层的三元系统相图一具有一个低共熔点的简单三元系统相图1立体相图2平面投影图投影图上温度表示法
T转 > Te3 、 T转 < Te2——多晶转变点P
T转 < Te2 、Te3——多晶转变点P1、P2
（八）形成一个二元连续固溶体的三元系统相图
（九）具有液相分层的三元系统相图
总结：
分析实际三元系统（复杂三元系统）相图的步骤
一、判断化合物的性质；
二、划分副三角形； 三、判断界线上温度变化——连（结）线规则； 四、判断界线性质——切线规则； 五、确定三元无变量点的性质——重心原理；
（三） 具有一个一致熔融三元化合物的三元系统相图
（四） 生成一个不一致熔融二元化合物的三元系统相图 1、相图组成
（1）不一致熔融化合物S不在自己的相区内； （2）化合物S性质的改变，导致CS连线、无变 量点P、界线的性质改变。 （a）CS连线 （b）无变量点：P点
三元系相图简介培训课件.ppt
T* f,B i
e1
e2
e3
则
l Pb Sn
l
Pb
l Pb
e3
l Bi
Sn
Bi
Pb
l Sn l Bi Sn
e
Pb
e3
M
Bi
N
Sn
Bi
精品课件
若 Te T Te3
T* f,Pb
T* f,Sn
T* f,B i
e1
e2
e3
则
l Pb Sn
代表体系P中A物的含量；
a’
ba’= Cc’=Pb：
代表体系P中B物的含量；
c
Aa’= cb’=Pc：
b’ P
b
代表体系P中C物的含量；
A
B a c’
C
1. 等含量规则
一组体系点同在平行于三角形某一
b’ P Q R
B
b 边的线上，该则组体系中平行线对
应的顶点组成含量相同。
C
精品课件
2. 定比规则
凡位于通过顶点(A)的任一直线上的
T
三相区：3+1个 二次结晶面以下，三元共晶 面以上——两个固相+液相 三元共晶面以下
——三个固相
精品课件
T
T
e1 e3
e2
Bi
e
Pb
Sn
(2) 冷却过程分析
x
T* f,Pb
x → x1：熔体冷却；
x1：开始析出固态Bi，
T* f,Sn
液相组成将沿x1 y变化； x1 → y： Bi不断析出，熔
e1 x1
Bi
精品课件
则
Sn
Sn
e1
e2
e3
则
l Pb Sn
l
Pb
l Pb
e3
l Bi
Sn
Bi
Pb
l Sn l Bi Sn
e
Pb
e3
M
Bi
N
Sn
Bi
精品课件
若 Te T Te3
T* f,Pb
T* f,Sn
T* f,B i
e1
e2
e3
则
l Pb Sn
代表体系P中A物的含量；
a’
ba’= Cc’=Pb：
代表体系P中B物的含量；
c
Aa’= cb’=Pc：
b’ P
b
代表体系P中C物的含量；
A
B a c’
C
1. 等含量规则
一组体系点同在平行于三角形某一
b’ P Q R
B
b 边的线上，该则组体系中平行线对
应的顶点组成含量相同。
C
精品课件
2. 定比规则
凡位于通过顶点(A)的任一直线上的
T
三相区：3+1个 二次结晶面以下，三元共晶 面以上——两个固相+液相 三元共晶面以下
——三个固相
精品课件
T
T
e1 e3
e2
Bi
e
Pb
Sn
(2) 冷却过程分析
x
T* f,Pb
x → x1：熔体冷却；
x1：开始析出固态Bi，
T* f,Sn
液相组成将沿x1 y变化； x1 → y： Bi不断析出，熔
e1 x1
Bi
精品课件
则
Sn
Sn
三元系统相图及其应用
S : a' k ' b' M a
L SS L SS L A SS L : a k b L A SS C d ( L消失)
液相到 C 点 ，相应 SS 为 C’ ， ΔC’CA, a 在其中，重心位置。 C （L）与a连线，交AC’上M，即为 固相组成点。
a1 a 2 a3 b1 b2 b3
u点在a2－b3连线上，析晶 过程固相组成点在l2u的连线上。 （与a-b的交点）
u
15
第三节 三元系统相图
6.在一个二元体系内生成转熔型有限固溶体的三元体 系相图
与前面一个不同的是，PP1在不混溶区的外面，在PP1线 上进行的是单变量的转熔过程，L+β →α m点的析晶过程： L：m →l1，液相沿P1P线变化，l1 → l2 → l3 S：b0 ' b1 固相. a1 a2 a3
4
第三节 三元系统相图
2. 只有一个二元系统生成连续固溶体的三元系统相 图
做等温截面，可以看出各稳定共存的相
5
第三节 三元系统相图
析晶过程分析（在A的初晶区）
当 液 相 到 达 P 点 ， SS 在 P’, ΔAPP’, M处于其中，重心位置， 固相总组成在G。 xA:xSS:xL=P’y:Ax:xy
右图是这类相图的立体图。注意： 连接 C-AmBn的垂直平面，交 P’E3’ 于 K ，把 P’E3’ 分成两段，这两段上界线 的 性 质 是 不 同 的 ， P’K’ 是 转 熔 线 ， L+A→SS, K’E3’ 是 共 熔 线 ， L→A+SS （ l1 与 A+SS1 共存，作 l1 的切线交 于 A-SS1 连 线 上 ， L→A+SS ， l2 与 A+SS2共存，作l2的切线交于A-SS2连 线上， L+A→SS）
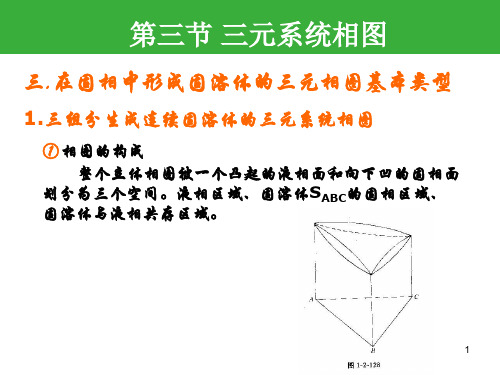
L SS L SS L A SS L : a k b L A SS C d ( L消失)
液相到 C 点 ，相应 SS 为 C’ ， ΔC’CA, a 在其中，重心位置。 C （L）与a连线，交AC’上M，即为 固相组成点。
a1 a 2 a3 b1 b2 b3
u点在a2－b3连线上，析晶 过程固相组成点在l2u的连线上。 （与a-b的交点）
u
15
第三节 三元系统相图
6.在一个二元体系内生成转熔型有限固溶体的三元体 系相图
与前面一个不同的是，PP1在不混溶区的外面，在PP1线 上进行的是单变量的转熔过程，L+β →α m点的析晶过程： L：m →l1，液相沿P1P线变化，l1 → l2 → l3 S：b0 ' b1 固相. a1 a2 a3
4
第三节 三元系统相图
2. 只有一个二元系统生成连续固溶体的三元系统相 图
做等温截面，可以看出各稳定共存的相
5
第三节 三元系统相图
析晶过程分析（在A的初晶区）
当 液 相 到 达 P 点 ， SS 在 P’, ΔAPP’, M处于其中，重心位置， 固相总组成在G。 xA:xSS:xL=P’y:Ax:xy
右图是这类相图的立体图。注意： 连接 C-AmBn的垂直平面，交 P’E3’ 于 K ，把 P’E3’ 分成两段，这两段上界线 的 性 质 是 不 同 的 ， P’K’ 是 转 熔 线 ， L+A→SS, K’E3’ 是 共 熔 线 ， L→A+SS （ l1 与 A+SS1 共存，作 l1 的切线交 于 A-SS1 连 线 上 ， L→A+SS ， l2 与 A+SS2共存，作l2的切线交于A-SS2连 线上， L+A→SS）
第六章 三元相图
来计算。
如右图中的合金o，其中的
A
C
相与 相的相对量分别为：
% mo 100%
mn
三元相图中的杠杆定律
% on 100%
mn
6-1 三元相图基础
3. 重心法则：当三元系合金
B
处于三相平衡时，研究它们之间
的成分和相对量的关系，则须用
重心法则。如右图中，O为合金
( )
的成分点，P、Q、S分别为三个
三条三相共晶转变线相交于 a
E点。成分为 E 的液相在该点温
l
度下发生四相平衡共晶转变： f
LE TE A B C
E点称为三元共晶点，其所对应 m
的温度成为四相共晶转变温度。 A
c
e3 k
j
e1
b
e2
p g Eh
C
三元共晶点 E与三个固相的 成分点m、n、p 组成的水平面称 为四相平衡共晶转变平面。
由于第三组元的加入，三个
二元共晶点在三元系中均演化成
为三相共晶转变线 e1E、e2E 和 e3E。当液相成分沿着这三条曲 线变化时，则分别发生三相共晶
转变： e1 E e2E e3E
L AB L BC L AC
a c
e3
l
k
f j
e1
b
e2
m
p
g
A
Eh C
n
B
固态互不溶解的三元共晶相图
6-2 固态互不溶解的三元共晶相图
6-1 三元相图基础
三、三元相图中的杠杆定律及重心法则
1. 直线法则：一定温度下，三元系材料处于两相平衡 时，材料的成分点和其两个平衡相的成分点必然位于同一条 直线上，该规律称为直线法则或三点共线原则。
三元相图-材料科学基础
3.成分的其它表示法
●直角成分三角形 当三元系中以某一组元 为主，某余两组元量很少 时，合金成分点靠近成分 三角形某一顶角附近区域 内，可采用直角成分三角 形。直角坐标原点代表含 量高的组元，两坐标轴代 表其它两组元的成分。 如P点合金： W（Mn）=0.8% W（si）=0.6%，余为Fe
二、三元相图中的法则(及定律)
一、立体图形
三元相图中A、B、C三个 组元，任意两个组元都可以 形成一个二元匀晶相图。三 元匀晶相图的侧面是由这三 个二元匀晶相图围成的。其 上的两个曲面分别为液相面 （liquidus surface）和固 相面（solidus surface）。 两个面把相图分为三个区： 液相区（L）、固相区（α）、 两相区（L+α）。
1.直线法则(共线法则)和杠杆定律
由直线法则和杠杆定律可得出 以下推论: (1) 当给定合金（ o 点）在一 定温度下处于两相（α、β） 平衡时，若其中一相（α）的 成分给定（a点），另一相 （β）的成分点必在两已知成 分点（ o、a）连线的延长线上。 (2)若两平衡相（α、β）的 成分点（ a、b）已知，合金的 成分点必然位于两已知成分点 （a、b）的连线上。
三.等温（水平）截面图
等温截面图确定了给定温度下的相平衡关系，利用系列等 温截面图可以分析给定合金的相变和在某一温度下的状态。 根据直线法则可确定液固两相的成分，根据杠杆定律可以计 算两平衡相的相对量。
如成分为 O 的合金， 在该温度下平衡时α 和L的含量：
Wα= no/mn×100% WL = mo/mn×100%
WA=sc=Ca WB=sa=Ab WC=sb=Bc 注： sa + sb + sc = 100%
注意：刻度与读数顺序 的一致性(同为顺时针 或逆时针)
三元系统相图
※3、无变量点性质的判断
方法一：根据无变量点与对应副△的位置 关系来判断。 —— 重心规则 方法二：根据无变量点周围三条界线的箭
头指向来判断。
4、结晶过程
配料点1：
配料点2：
配料点3：
几点讨论：
（1）P点是单转熔点，不一定是析晶结束点； 三元低共熔点
一定是析晶结束点；
P点：L＋B → S＋C，有三种析晶结果 1）L先消失，B有剩余，P为析晶结束点，组成点在 ▲BSC内； 2）B先消失，L剩余，转熔结束，组成点在▲PSC内； 3）L与B同时消失，P点结晶结束，产物为S、C两相， 组成点在SC连线上。 （2）转熔线上的穿相区现象，发生在界线转熔过程中，组成
ห้องสมุดไป่ตู้
（一）具有一个低共熔点的简单三元系统相图 （1）立体相图
（2）平面投影图
投影图上温度表示法：
1）等温线法； 2）特殊点温度直接标注或列表
表示；
3）箭头表示温度下降方向。
（3）结晶过程
小结： 1）初晶区规则： 判断最初析出晶相
最初析出晶相
2）杠杆规则：
原始组成点所在相区对应的晶相
相平衡的液相、固相、总组成点始终在一条杠杆上
3）三元低共熔点一定是析晶结束点
（4）加热过程
小结：
1）一种晶相析出时，液相在相区变化，固相组 成在投影图上的△顶点；
2）二种晶相析出时，液相在界线上变化，固相
组成在投影图上的△边上； 3）三种晶相析出时，液相在无变量点上变化， 固相组成进入△内与原始组成重合。
（5）各相量计算 —— 杠杆规则
第五节
三元系统相图
一、三元系统相图概述
三元凝聚系统相律： F＝C－P＋1＝4－P
物理化学三元相图详解
E(
L F
B 0,
S C L消失
）
（5）熔体M冷却析晶过程 固相：B B B B B BS w B SC M
4.液相到达低共 熔点E时，固相 组成到w点，液 相同时析出BSC， 固相由w逐渐靠 向M，到达M时，
液相消耗完毕， 析晶结束
3.到达在界线上v点后， 同时析出B β和S， F=1，液相组成沿着 界线变化，固相组成 离开B
液相消耗完毕， 析晶结束
当固相组成点达 到熔体原始组成 点时，冷却析晶
结束
v u x
w
液相在E点析晶时，固相 组成由w向M移动，刚离 开w时，L%=Mw/Ew。 到达x时，L%=Mx/Ex，
可见液相不断减少。达 到M点是L%=0
液相：M
L B F 2
u(B
L
B
)
L F
B 2
v L B S F 1
2.在多晶转变等温 线u上Bа全部转变 为Bβ后继续降温
v u
w
1.熔体M在初晶区 B内先析出Bа，液 相组成沿背向线 变化，固相组成
在B
（6）M结晶结束时各相的百分含量
结晶结束是晶相为B、S、C 利用双线法，过M做三角形 SC、SB两边的平行线Mb，
Md，可得 B:S:C=Cb:db:dB
b
d
（7）熔体N冷却析晶过程
(5)熔体1冷却析晶过程
1、由1点所在副三 角形判出1的冷却 析晶结束的无变量
点为E4
2、由1点所在初晶 区得出1首次析晶 为B，得到固相组 成点，应用背向线
规则知道液相组成 变化路径
a b
液相：1 L B a L B A E5( B L,A B ) L B A E4( L A B S1)
材料科学基础三元相图
材料科学基础三元相图
一．三元相图的成分表示法：等腰三角形
材料科学基础三元相图
一．三元相图的成分表示法：直角坐标系
材料科学基础三元相图
3．浓度三角形中特殊线： 3.1 平行浓度三角形任一边的直线
3.2 从浓度三角形的一个顶点到对边的任意直线
材料科学基础三元相图
二、杠杆定律及重心法则
单相平衡勿须计算，四相平衡无从计算 1．两相平衡：杠杆定律
2．合金的凝固过程和组织
各点合金的组织
如表4-3（表中nmp区需修正） 如合金I：L→A 剩余液相交np于n1：L+A→M 至n2点，A消失，L→M 液相沿e1E：L→M+B 液相成分在E点：L→M+B+C
材料科学基础三元相图
材料科学基础三元相图
3．等温截面
材料科学基础三元相图
4。变温截面
材料科学基础三元相图
2.三元相图分析 法 总 结 --- 三 相 平 衡 -- 三 相
反应的判定--：
投影图判断三 相反应
液相单变量线穿 过两旁固相成分点连 线的为二元共晶型， 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应，且靠近单变线 的为生成相
材料科学基础三元相图
3．三元相图分析法总结---四相平衡
x合金结晶：
L→A，L+A→M，L→M，L→M+C，L→M+B+C
y合金结晶： L→A，L+A→M，L+A→M+C，L→M+C，L→M+B+C 5．固相有固溶度时的包共晶 包共晶：Lα+P→Md1+γc1 包晶反应 LE→Md2+βb+γc2 d1d2，c2c1为M+γ二元共晶结 束面投影
一．三元相图的成分表示法：等腰三角形
材料科学基础三元相图
一．三元相图的成分表示法：直角坐标系
材料科学基础三元相图
3．浓度三角形中特殊线： 3.1 平行浓度三角形任一边的直线
3.2 从浓度三角形的一个顶点到对边的任意直线
材料科学基础三元相图
二、杠杆定律及重心法则
单相平衡勿须计算，四相平衡无从计算 1．两相平衡：杠杆定律
2．合金的凝固过程和组织
各点合金的组织
如表4-3（表中nmp区需修正） 如合金I：L→A 剩余液相交np于n1：L+A→M 至n2点，A消失，L→M 液相沿e1E：L→M+B 液相成分在E点：L→M+B+C
材料科学基础三元相图
材料科学基础三元相图
3．等温截面
材料科学基础三元相图
4。变温截面
材料科学基础三元相图
2.三元相图分析 法 总 结 --- 三 相 平 衡 -- 三 相
反应的判定--：
投影图判断三 相反应
液相单变量线穿 过两旁固相成分点连 线的为二元共晶型， 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应，且靠近单变线 的为生成相
材料科学基础三元相图
3．三元相图分析法总结---四相平衡
x合金结晶：
L→A，L+A→M，L→M，L→M+C，L→M+B+C
y合金结晶： L→A，L+A→M，L+A→M+C，L→M+C，L→M+B+C 5．固相有固溶度时的包共晶 包共晶：Lα+P→Md1+γc1 包晶反应 LE→Md2+βb+γc2 d1d2，c2c1为M+γ二元共晶结 束面投影
三元相图
三元系统相图一、相律及组成表示法根据吉布斯相律 f = c－p＋2p －相数c －独立组分数f －自由度数2 －温度和压力外界因素凝聚态系统不考虑压力的影响，相律为:f = c－p + 1（温度）（一）相律三元相图比二元相图多一个组元，根据相律，三元凝聚系统:f ＝c －p ＋1＝4 －p，当p=1 时，f max＝3 ( 即两个成分变量x1、x2和温度的变化)当f＝0时，体系具有做多的平衡相P=4 （四相共存）在硅酸盐系统中经常采用氧化物作为系统的组分。
一元系统如：SiO2Al2O3－SiO2二元系统CaO－Al2O3－SiO2三元系统注意区分：2CaO.SiO2(C2S) ;CaO－SiO2;K2O.Al2O3..4SiO2 －SiO2f ＝c －p ＋1＝4 －p•最大自由度f max＝3是指两个独立的浓度变量和一个温度变量•如何用相图表示？•一般用正三棱柱•三个顶点表示三个纯组分•纵坐标表示温度•三角形中表示各种配比的混合物•由于A+B+C为一恒定值，所以三者中只有两个是独立的变量三坐标的立体图平面投影图相图图1 三元匀晶相图图2 三元共晶相图（二）三元系统组成的表示方法浓度三角形:在三元系统中用等边三角形来表示组成。
（组成的百分含量可以是质量分数，亦可是摩尔分数）。
顶点：单元系统或纯组分；边：二元系统；内部：三元系统。
图3 浓度三角形909090808080707070606060505050404040303030202020101010cEM DaABCa图4 双线法确定三元组成CABMbc a一个三元组成点愈靠近某一角顶，该角顶所代表的组分含量必定愈高。
例题1：在浓度三角形中：•定出P 、R 、S 三点的成分。
•若有P 、R 、S 三点合金的质量分别为2，4，7Kg ，将其混合构成新合金，求混合后该合金的成分。
•定出Wc=0.80，W A /W B 等于S 中的W A /W B 时的合金成分。
2-三元系相图基础1
L 1 S1+S2+S3
E 2 3
•单转熔点（双升点） 特点：对应三组分的成分三角形之外， 交叉位置 L +S1 S2+S3
交叉
交叉
交叉
•双转熔点（双降点）
特点；处于相应成分三角形的共轭位置 S3 L+S1+S2
共轭
•双降点形式的过渡点
特点：共轭位置的极限情况 L+S1+S2 无对应的三角形，是一条线
（3）无论熔体M在三角形的何种位置，析 晶产物都是A、B、C 三种晶相，且都在三 元低共熔点上析晶结束，因此三元低共熔 点一定是析晶的结束点。
杠杆规则的应用 （1）当液相组成点刚刚到达D点:
CM L% = ×100% CD DM C% = ×100% CD
C F
Mt1
（2）当液相组成点刚刚到达E点:
单相区： 一个
L
TA A3 A2 A1 TB E1 E3 TC E C3 C2 C1 E2 B3 B2 B1
双相区： 三个
L + A、L + B、L + C
A
B
三相区： 四个
L + A + B、L + B +C、 L + A + C、 A + B + C
C
四相区： 一个
L+A+B+C
27
等温截面及其投影
e3
t2 A
t2 D E t2
e2
t1
.
B
e1
熔体的结晶路程： 液相点： →C →C + A M 1 ⎯L ⎯ ⎯→ D ⎯L ⎯ ⎯ ⎯→ E ( LE → C + A + B ) 固相点：
E 2 3
•单转熔点（双升点） 特点：对应三组分的成分三角形之外， 交叉位置 L +S1 S2+S3
交叉
交叉
交叉
•双转熔点（双降点）
特点；处于相应成分三角形的共轭位置 S3 L+S1+S2
共轭
•双降点形式的过渡点
特点：共轭位置的极限情况 L+S1+S2 无对应的三角形，是一条线
（3）无论熔体M在三角形的何种位置，析 晶产物都是A、B、C 三种晶相，且都在三 元低共熔点上析晶结束，因此三元低共熔 点一定是析晶的结束点。
杠杆规则的应用 （1）当液相组成点刚刚到达D点:
CM L% = ×100% CD DM C% = ×100% CD
C F
Mt1
（2）当液相组成点刚刚到达E点:
单相区： 一个
L
TA A3 A2 A1 TB E1 E3 TC E C3 C2 C1 E2 B3 B2 B1
双相区： 三个
L + A、L + B、L + C
A
B
三相区： 四个
L + A + B、L + B +C、 L + A + C、 A + B + C
C
四相区： 一个
L+A+B+C
27
等温截面及其投影
e3
t2 A
t2 D E t2
e2
t1
.
B
e1
熔体的结晶路程： 液相点： →C →C + A M 1 ⎯L ⎯ ⎯→ D ⎯L ⎯ ⎯ ⎯→ E ( LE → C + A + B ) 固相点：
(详细)NH3——CO2——H2O三元体系相图
NH3-CO2-H2O三元体系相图所谓的相图就是相平衡图，是物系在平衡时各组成条件（温度、浓度、压力）之间的关系图。
图2-22中的纵坐标代表CO2的质量分数，横坐标代表NH3的质量分数，坐标原点代表纯水。
纵轴100处代表纯CO2，横轴100处代表纯NH3。
图中每种化合物（或混合物）的总碳量均以CO2来表示，总氮量均以NH3表示。
在CO2 -NH3连线以下的区域中的化合物（或混合物）由CO2、NH3和H2O构成，把这类化合物称为亲水化合物。
在CO2-NH3连线以上的区域的化合物（或混合物），则是NH3和CO2及负水（脱水）构成的，把它称为憎水化合物。
在CO2-NH3连线上的化合物（或混合物）则是只由NH3和CO2构成的。
由此可知，凡在CO2-NH3连线以上区域的组成点，其CO2和NH3的质量分数之和均超过100%。
图中标有温度的组线是等温溶解度曲线，它代表一种盐与液相平衡。
该线经过转折后表示与液相呈平衡的是另外一种盐。
转折点代表同一温度下两条溶解曲线的交点，因此在该点与液相呈平衡的是两种盐。
图中的粗线就是这类转折点的连线，也就是多温图上的两种盐共饱和线。
将各条粗线描绘出来就将图2-22分成各个区域。
各区中的化合物就代表在该区内与液相呈平衡的盐。
右边有一分层区，在该区内，任何等温线上的一个组成点，都分为两个界线分明的液体层，它们的组成分别为该等温线与分层区域界线的两个交点所代表。
一、CO2 -NH3 -H2O体系（Ⅰ）恒温相图图2-23为20℃时CO2-NH3-H2O体系的恒温相图。
图中有四条溶解度曲线：E'E1是NH4HCO3(组成点为C)的溶解度曲线，E1E2是复盐2NH4HCO3•(NH4)2CO3•H2O（组成点为P）的溶解度曲线，E2E3是一水碳酸盐(NH4)2CO3•H2O(组成点为S)的溶解度曲线，E3F'是氨基甲酸铵（组成点为A）的溶解度曲线。
因为E'E1和E3 F'两条曲线未能在图上完全表示出来，因此E'和F'分别为两条曲线上的一个点。
§5-6 三元相图
典型合金的凝固过程
（4）投影图
e3
A α E β B
液相区投影
l
γ
e2 A
C
A l C
C
e1
l e3 m e1 n B
固相区投影
p B
e
2
各典型区域凝固过程和室温组织
五. 三元相图的一些规律
1. 单相区 自由度是3，其形状不受温度、成分对应关系的制约， 截面可以是多种形状的平面图形。 2. 双相区
分析合金在加热和冷却过程中的转变。
四. 三元共晶相图
1. 组元在固态完全不溶的三元共晶相图
（1）相图分析
A
B
A C
B C
点：熔点 tA，tB，tC 二元共晶点 E1，E2，E3 三元E2E，E3E
面：3个液相面
1个固相面
固相面
（三元共晶面）
6个二元共晶面
杠杆定律
由二种合金合成一种合金成分
由一种合金分解成二种合金成分
PR / RQ Wq / Wp
W / W R / R
2.重心法则
合金o分解为α 、β 和L三个平衡相，a、b、c 分别是 α 、β 和L的成分点。
则
oa ' w 100% aa ' ob' w 100% bb' oc ' wL 100% cc '
3 等温截面（水平截面）
T
共轭曲线及直线规则
共轭曲线
液、固相 等温线
两相区平衡两 相的成分连线
共轭连线
在等温截面的两相区内，根据相律 F=3-2=1， 说明两个相的成分只有一个是独立可变的。两个平 衡相的成分对应关系由直线法则决定。
水盐体系相图及其应用第三章三元水盐体系相图.
应用此类相图可判断怎样可得固体纯盐?
如有B和C固体盐的混合物, 问能否通过 加水使之部分溶解的方法从其中获取一 种纯盐固体, 能得到哪一种纯盐固体? 可 从相图加以讨论. (1) 稀释法分离提纯盐 设起始物系点为a, 向其中加水,体系的组 成沿aA线向A方向移动. 物系点在BFC区 时, 体系三相平衡共存. 到达b点时,C全部 溶完, 剩下B固体与溶液F共存, 过滤可得 纯B固体盐. 由图知, 混合盐的总组成在B
f =3-3+1=1
e2 e
e3
ABCe为ABC共晶区； f =34+1=0
B C
A
三、立体图中的冷却过程
m→m1：随温度下降，宏观无现象，各 盐浓度增加。 m1：与B盐饱和面相交，B盐开始饱和。 c m1→m2：B盐单独析出，固相为B点， 液相沿m1→l移动。 m2：液相与B、C盐共饱和线相交，C盐开
第三章
三元水盐体系相图
第一节 三元体系相图的组成表示方法及基本规则
简单三元水盐体系：由具有共同离子的两种盐和水构成的体系。 NaCl KCl H 2O
Na2 SO4 ( NH 4 ) 2 SO4 H 2O
复杂三元水盐体系： 不具有共同离子的两种盐和水构成的体系，或是盐和
水生成了结晶水复盐以及两种盐结合形成了新的复盐
的体系，情况较为复杂，我们称这样的体系为复杂三 元水盐体系。
特殊三元水盐体系： 构成体系的不是两种盐而是一种碱性物和一种酸性物，
如重过磷酸钙的生产，在不考虑磷石中的杂质时，可 表示为： 示为； 体系。 NH3 CO2 H 2O
CaO P2O5体系，碳酸氢铵体系可表 H 2O
一、三组分系统相图
b
T1
c
第8章三元相图
根据需要只把一部分相界面 的等温线投影下来。经常用 到的是液相面投影图或固相 面投影图。图为三元匀晶相
图的固相液相投影图。
6
8.1 三 元 相 图 基 础
8.1.4 三元相图的杠杆定律及重心定律
1. 直线法则：在一定温度下三组元材料两相平衡时， 材料的成分点和其两个平衡相的成分点必然位于成
分三角形内的一条直线上。
21
8.2 固 态 互 不 溶 解 的 三 元 共 晶 相 图
☆ 投影图应用举例（以合金o为例）
合金组织组成物的相对含量可以利用杠杆法
则进行计算。如合金o刚要发生两相共晶转变
时，液相成分为q，初晶A和液相L的质量分
数为：
22
8.2 固 态 互 不 溶 解 的 三 元 共 晶 相 图
☆ 投影图应用举例（以合金o为例） q成分的液体刚开始发生两相共晶转变时，液体含量几乎 占百分之百，而共晶体（A＋C）的含量近乎为零，所以这 时（A＋C）共晶的成分点应是过 q点所作的切线与AC边 的交点d。继续冷却时，液相和两相共晶（A＋C）的成分 都将不断变化，液相成分沿 qE线改变，而每瞬间析出的 （A＋C）共晶成分则可由 qE线上相应的液相成分点作切 线确定。在液相成分达到E点时，先后析出的两相共晶（A ＋C）的平均成分应为 f（Eq连线与AC边的交点）。因为 剩余液相E与所有的两相共晶（A＋C）的混合体应与开始 发生两相共晶转变时的液相成分q相等。因此合金o中两相 共晶（A＋C）和三相共晶（A＋B＋C）的质量分数应为
元
相 图
25
8.3 固 态 有 限 溶 解 的 三 元 共 晶 相 图
8.2 固态有限溶解的三元共晶相图
8.3.1 相图的空间模型 1.相图分析
三元系统相图
第四节 三元系统相图
三元系统：c
相律
=3
f c p 1 4 p
温度、浓度 不可能出现5相 或更多相平衡 1
pmin 1, f max 3 f min 0, pmax 4
一、 三元相图的组成表示方法
通常采用等边三角形表示三元系统的组成
—— 浓度三角形
三个顶点表示三个纯 组分A、B、C的一元 系统； 三条边表示三个二元 系统A-B、B-C、CA的组成； 三角形内任意一点表 示一个含有A、B、C 三个组分的三元系统 2 的组成。
界线上任一点的切线与 相应连线的交点实际上 表示了该点液相的瞬时 析晶组成
瞬时析晶组成是指液 相冷却到该点温度， 从该点组成的液相中 所析出的晶相组成
17
（3） 重心规则
判断无变量点的性质
• 如无变量点处于其相应的副三角形的重心位，则该无变 量点为低共熔点；如无变量点处于其相应的副三角形的 交叉位，则为单转熔点；如无变量点处于其相应的副三 角形的共轭位，则为双转熔点。
双线法确定三元组成—过M点引另两条边 的平行线
3
浓度三角形的两个性质：
（1） 等含量规则
平行于三角形某一边的直线上的各点，其第三组
分的含量不变。
4
（2） 定比例规则 从浓度三角形某角顶 引出之射线上各点，另外 二个组分含量的比例不变。 推论：
从三个组元的混合物中不 断取走C组元，那么这个系统 的组成点将沿CM延长线并沿
f=1
E (L C+A+B, f = 0) 固相点 C F M FLASH
12
杠杆规则计算液相量和固相量
液相到达D点时：
固相量 CM 液相量 MD
固相量 CM 固液总量(原始配料量) CD 液相量 MD 固液总量(原始配料量) CD
三元系统：c
相律
=3
f c p 1 4 p
温度、浓度 不可能出现5相 或更多相平衡 1
pmin 1, f max 3 f min 0, pmax 4
一、 三元相图的组成表示方法
通常采用等边三角形表示三元系统的组成
—— 浓度三角形
三个顶点表示三个纯 组分A、B、C的一元 系统； 三条边表示三个二元 系统A-B、B-C、CA的组成； 三角形内任意一点表 示一个含有A、B、C 三个组分的三元系统 2 的组成。
界线上任一点的切线与 相应连线的交点实际上 表示了该点液相的瞬时 析晶组成
瞬时析晶组成是指液 相冷却到该点温度， 从该点组成的液相中 所析出的晶相组成
17
（3） 重心规则
判断无变量点的性质
• 如无变量点处于其相应的副三角形的重心位，则该无变 量点为低共熔点；如无变量点处于其相应的副三角形的 交叉位，则为单转熔点；如无变量点处于其相应的副三 角形的共轭位，则为双转熔点。
双线法确定三元组成—过M点引另两条边 的平行线
3
浓度三角形的两个性质：
（1） 等含量规则
平行于三角形某一边的直线上的各点，其第三组
分的含量不变。
4
（2） 定比例规则 从浓度三角形某角顶 引出之射线上各点，另外 二个组分含量的比例不变。 推论：
从三个组元的混合物中不 断取走C组元，那么这个系统 的组成点将沿CM延长线并沿
f=1
E (L C+A+B, f = 0) 固相点 C F M FLASH
12
杠杆规则计算液相量和固相量
液相到达D点时：
固相量 CM 液相量 MD
固相量 CM 固液总量(原始配料量) CD 液相量 MD 固液总量(原始配料量) CD
三元系统相图分析及析晶规律
点、液相组成点和固相（或混合物）的组成点始终在一条直 线上。 （3）无论熔体M在三角形的何种位置，析晶产物都是A、 B、C 三种晶相，且都在三元低共熔点上析晶结束，因此三 元低共熔点一定是析晶的结束点。
2015物理与电子工程学院青年教师课堂教学比赛
4、杠杆规则的应用
（1）当液相组成点刚刚到达D点:
2015物理与电子工程学院青年教师课堂教学比赛
3、重心规则
用途：判断无变量点的性质 内容：无变量点处于其相应副三角形的重心位，则为共熔点； 无变量点处于其相应副三角形的交叉位，则为单转熔点； 无变量点处于其相应副三角形的共轭位，则为双转熔点； ## 副三角形：指与该无变量点液相平衡的三个晶相组成点连 接成的三角形。
2015物理与电子工程学院青年教师课堂教学比赛
2015物理与电子工程学院青年教师课堂教学比赛
2. 平面投影图
C
.
e2
t1
e3
t2
A
t2 E t2
.
B
.
t1
e1
2015物理与电子工程学院青年教师课堂教学比赛
说明：
（1）三棱边：A、B、C 的三个一元系统；
（2）三侧面：构成三个简单二元系统状态图，并具有相 应的二元 低共熔点；
（3）液相面: 液相面代表了一种二相平衡状态 f 个液相面以上的空间为 熔体的单相区 f
温度下降的方向
（3）对一些特殊的点 如各组分及化合物的、无变
量点等，将其温度直接标入图中或列表注明。
2015物理与电子工程学院青年教师课堂教学比赛
M
.
4、结晶路程
C
F
Mt1
. .
e2
t2
.
.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2、连结线规则（艾氏连线）
C
连接线之间可以 相交但不能交叉
E
F
A D B
3、切线规则
C
E A B
A
B
A
B
4、无变量点
低共熔点（三升点） 特点：三条低共熔线相交点，三曲面相 交的温度最低点，处于对应三组分的重 心位置
L
1
S1+S2+S3
E 2 3
•单转熔点（双升点） 特点：对应三组分的成分三角形之外，交叉 位置 L +S1 S2+S3
P，相反P要分解为N和M时，需要加入一定量 的Q，此时，P点的位置叫“交叉位置”。
新组成点P落在三角形MNQ的外边，并在 MQ和NM的延长线所包围的范围内，其组 成及量与M、N、Q的关系为Q+N+P=M， 故M-（Q+N）=P。
从混合物M中取出一定量的Q+N才能得到
P。反过来，P分解时，要加入相应量的Q ＋N才能得到M，P的这种位置叫“共轭位 置”。
C
C
A A
D
B
D
B
C
C
E1 E2
鞍形点
A A
D D
B B
C
原始成分点与结 晶终点
C
结晶结束的组分 为三角形顶点组分
A A
1
D
2
B B
D
3 生成一个同成分熔融三元化合物的三 元相图
体系特征：体系中含有三元稳定化合物， 组分间液相完全互溶，固相完全不互溶；
相图特征：四个初晶区，六条相区界限， 三个无变量点，三个副三角形。
相图特征： 三个初晶区， 三条相区界线， 一个无变量点。
C A E
B
B A
C
2 具有低共熔点的生成二元化合物的三 元相图
体系的特征：化合物为稳定化合物，每种 组分都有确定的熔点，组分间液相完全互 溶，固相完全不互溶；
相图的特征：多于一个无变量点，四个初 晶区，五个相区界限（均为低共熔线）， 两个无变量点（均为低共熔点），两个副 三角形。
如果新出现的混合物或化合物的组成点不 在原始已知的三个混合物所联成的三角形 内时，就不能用相加的方法求得。
新组成点P落在三角形MNQ的外边，并在 MQ和QN的延长线的范围内，则P的组成 及量与M、N、Q的关系由下式求得：因
M+N=t；Q+P=t；则可得到M+N=Q+P；
要从混合物M+N中取出一定量的Q才能得到
交叉
交叉
交叉
•双转熔点（双降点）
特点；处于相应成分三角形的共轭位置 L+S1+S2 S3
共轭
•双降点形式的过渡点
特点：共轭位置的极限情况 （L）+S1+S2 S3
无对应的三角形，是一条线
5、析出规则（背向规则）
A
B
C
二、在固相中完全不互溶的三元相图 基本类型
1、具有一个低共熔点的不生成化合物的三 元相图 体系特征：液相完全互溶，固相完全不互 溶
总组成点、液相组成点和固相组成点始终
在一条直线上，形成杠杠。此杠杠随着固、
液相组成的变化，以系统总组成点为支点
旋转。
液相组成点的变化途径一般是从系统的组
成点开始，经过相应的初晶区、界线，直
到三元低共熔点为止；
固相组成点的变化途径则一般是从三角形的某
一个顶点开始（只析出一种晶相），经过三角
形的一条边（同时析出两种晶相），进入三角
形内部（同时析出三种晶相），直到与系统的
总组成点重合（结晶结束）。固、液相的变化
途径形成一条首尾相接的曲线。
无论熔体 M在三角形ABC内的何种位置， 析晶产物都是 A、B、C三种晶相，而且都 在（A）、（B）、（C）三个初晶区所包 围的三元无变量的低共熔点上结晶结束。 因此三元低共熔点一定是结晶的结束点。
A
1、2、3均为三升点
A
1
S
S
2
B
C
3
B
C
小结
原始熔体M在哪个初晶区内，冷却时，从
液相中首先析出该初晶区所对应的那种晶 相，M熔体所处等温线温度表示析出初晶 相的温度。在初晶相的析出过程中，液相 组成点的变化路线遵守背向规则。
冷却过程中系统的总组成点即原始组成点 在投影图上的位置始终不变，而且系统的
1、组成表示法： 平面三角形
①等量规则：
A
C含量相等
A的含量相等
B
C
②等比规则
A
B与C的比恒定
B
C
③杠杆规则
A
c
a
b
B
C
④重心规则
A
两次使用杠杆规则
M O定在三角形 MNQ的几何重心上。反过来如果P点组成 分解，则可得到相当量的组成为M、N、Q 的三个混合物。