矩阵乘法的优化
矩阵乘法的优化

矩阵乘法的优化
矩阵乘法的优化指的是对矩阵乘法运算的改进,以提高其计算效率。
矩阵乘法的优化主要有以下几种方式:
1、使用缓存。
缓存可以提供更快的访问速度,并降低内存访问开销。
在矩阵乘法运算中,多次访问相同矩阵元素时,使用缓存可以有效提高计算效率。
2、采用分块算法。
分块算法将矩阵分割成若干小矩阵,每次计算一小块,从而减少了矩阵的大小,减少了计算量。
3、利用多核处理器。
多核处理器可以同时实现多个矩阵乘法计算,有效提高计算效率。
4、使用SIMD指令。
SIMD指令是单指令多数据指令,可以同时处理多个数据,有效提高计算效率。
5、利用GPU加速。
GPU拥有很高的计算性能,可以有效加速矩阵乘法运算,提高计算效率。
6、使用矩阵复用技术。
矩阵复用技术可以将原来需要执行的多次矩阵乘法运算合并为一次,有效降低计算量。
7、采用矩阵分解算法。
矩阵分解算法可以将大矩阵分解成若干小矩阵,进而减少计算量,提高计算效率。
综上所述,矩阵乘法的优化主要有使用缓存、采用分块算法、利用多核处理器、使用SIMD指令、利用GPU加
速、使用矩阵复用技术、采用矩阵分解算法等方式。
这些方法都可以有效提高矩阵乘法的计算效率,提高矩阵乘法的运行速度,减少计算量。
矩阵乘法优化算法

矩阵乘法优化算法矩阵乘法是一种常见的计算任务,它在许多科学、工程和计算机图形学领域都有广泛的应用。
由于矩阵乘法涉及大量的运算,所以提高矩阵乘法的效率对于提升整体算法的性能至关重要。
在本文中,我们将讨论一些矩阵乘法的优化算法,通过减少计算、提高并行性和利用硬件特性等方式来提高矩阵乘法的效率。
1. 基本优化技术:- 提前转置矩阵:通过将矩阵转置,可以改善缓存的命中率,从而提高计算效率。
- 随机化访问顺序:通过对输入矩阵的访问顺序进行随机化,可以减少缓存的碰撞,提高缓存的使用效率。
- 分块方法:将大矩阵分成小的子矩阵,利用局部性原理提高缓存的使用效率。
- SIMD指令集:利用单指令多数据流(SIMD)指令集执行并行计算,可以在不增加额外开销的情况下提高计算效率。
2. Strassen算法:Strassen算法是一种基于分治的矩阵乘法优化算法,通过将矩阵乘法划分为较小的子问题,减少了计算量。
该算法的关键思想是通过将乘法操作转化为更少次数的加法和减法运算,从而减少计算量。
3. 并行算法:- 多线程并行:利用多线程技术将矩阵乘法的计算任务划分为多个子任务,分别由不同的线程并行执行,提高计算效率。
- 分布式并行:将矩阵乘法的计算任务划分为多个子任务,分配给不同的处理节点并行执行,通过并行计算加快整体计算速度。
4. 混合算法:- 能量效率优化:通过降低电压、频率和运算精度等方式来降低功耗,提高矩阵乘法的能效。
- 多级优化:将矩阵乘法任务划分为多个阶段,在每个阶段采用不同的算法进行计算,从而综合考虑计算和传输开销的平衡。
除了以上具体的优化算法之外,还可以通过利用硬件特性来提高矩阵乘法的效率:- GPU加速:利用图形处理器的并行计算能力,通过GPU加速库(如CUDA、OpenCL)来并行执行矩阵乘法计算。
- FPGA加速:利用现场可编程门阵列(FPGA)的灵活性,通过定制化的硬件电路来进行矩阵乘法计算,提高计算效率。
矩阵运算中的矩阵乘法的性质及其运用

矩阵运算中的矩阵乘法的性质及其运用矩阵乘法是一种重要的矩阵运算,广泛应用于数学、物理、工程、计算机等领域。
在矩阵乘法中,两个矩阵相乘可以得到一个新的矩阵,这个新矩阵的每个元素是原矩阵的各行与各列乘积之和。
矩阵乘法具有许多重要的性质,这些性质为我们在矩阵运算中的应用提供了方便。
首先,矩阵乘法是结合律的,也就是说,对于任意的矩阵A、B和C,都有(A*B)*C=A*(B*C)。
这个性质使我们可以在不改变结果的前提下改变矩阵乘法的顺序,从而减少计算量。
其次,矩阵乘法不一定是交换律的,也就是说,对于任意的矩阵A和B,不一定有A*B=B*A。
这是因为矩阵的乘法顺序的改变将导致不同的相乘方式,从而得到的结果也会不同。
因此,在实际应用中,我们必须特别注意矩阵相乘的顺序。
第三,矩阵乘法具有分配律,也就是说,对于任意的矩阵A、B和C,都有A*(B+C)=A*B+A*C和(B+C)*A=B*A+C*A。
这个性质使矩阵乘法更方便,使复杂的计算变得简单。
最后,矩阵乘法还可以用来解决线性方程组。
对于一个n阶的线性方程组Ax=b,其中A是一个nXn的系数矩阵,b是一个n维的列向量,x是一个n维的未知向量,我们可以使用矩阵乘法将其表示为Ax=b。
在实际应用中,矩阵乘法被广泛应用于机器学习、计算机图形学、数字信号处理、优化问题等领域。
例如,在机器学习中,我们可以使用矩阵乘法快速计算训练数据的内积,从而得到更好的分类器。
在计算机图形学中,我们可以使用矩阵乘法来对三维图形进行旋转、缩放和平移等变换。
在数字信号处理中,我们可以使用矩阵乘法来实现数字滤波器,从而去除信号中的噪声和干扰。
在优化问题中,我们可以将目标函数表示为矩阵乘积的形式,从而更容易地进行求解。
总之,矩阵乘法作为一种重要的矩阵运算,具有许多重要的性质和广泛的应用。
我们需要深入学习矩阵乘法的原理和性质,以便更好地应用于实际问题中。
矩阵乘法加速python

矩阵乘法是线性代数中的一种常见操作,Python 中有多种方式可以用来加速矩阵乘法。
以下是一些常见的方法:1. 使用 NumPy 库:NumPy 是 Python 中用于科学计算的强大库,提供了高效的数组操作和数学函数。
NumPy 的 `dot()` 函数可以用来执行矩阵乘法,它的实现利用了优化的线性代数库(如LAPACK 和 BLAS),可以大大提高计算速度。
```pythonimport numpy as npA = np.array([[1, 2], [3, 4]])B = np.array([[5, 6], [7, 8]])C = np.dot(A, B)```2. 使用优化的线性代数库:NumPy 的实现依赖于优化的线性代数库,如 LAPACK 和 BLAS。
这些库使用优化的算法和底层代码,可以在许多情况下提供比纯 Python 代码更高的性能。
如果需要更高级的数学运算,可以考虑使用这些库。
3. 使用并行计算:对于大规模的矩阵乘法,可以使用并行计算来加速计算过程。
Python 中有许多并行计算库,如multiprocessing、joblib 等。
这些库可以将计算任务分配给多个处理器核心,从而提高计算速度。
4. 使用GPU:如果有一块支持CUDA 的GPU,可以使用PyCUDA 或 CuPy 等库将矩阵乘法任务转移到 GPU 上执行。
GPU 的并行处理能力可以大大提高计算速度,尤其是在处理大规模数据时。
5. 使用稀疏矩阵:如果矩阵 A 和 B 中的大多数元素都是零,则可以使用稀疏矩阵来表示它们。
稀疏矩阵可以大大减少存储空间和计算时间,因为它们只存储非零元素。
Python 中有许多稀疏矩阵库,如 SciPy、NetworkX 等。
矩阵乘法优化算法

矩阵乘法优化算法矩阵乘法是计算机科学中的重要算法之一,它在很多领域都有着广泛的应用,如图像处理、机器学习等。
然而,矩阵乘法的计算量非常大,尤其是在大规模数据处理时,会导致运行时间过长。
因此,为了提高矩阵乘法的效率,需要对其进行优化。
本文将介绍矩阵乘法的优化算法。
一、传统矩阵乘法在介绍优化算法之前,先来回顾一下传统的矩阵乘法算法。
假设有两个矩阵A和B,它们的大小分别为m×n和n×p,则它们相乘得到的结果C大小为m×p。
传统的矩阵乘法可以表示为以下代码:```pythondef matrix_multiply(A, B):m, n = A.shapen, p = B.shapeC = np.zeros((m, p))for i in range(m):for j in range(p):for k in range(n):C[i][j] += A[i][k] * B[k][j]return C```这段代码中使用了三重循环来实现矩阵相乘,在数据量较小的情况下可以得到正确的结果,但当数据量变大时运行速度会变得非常慢。
二、矩阵乘法的优化算法为了提高矩阵乘法的效率,可以采用以下几种优化算法:1.分块矩阵乘法分块矩阵乘法是将大矩阵划分成若干个小块,然后对每个小块进行计算。
这种方法可以减少计算量,提高计算效率。
具体实现如下:```pythondef block_matrix_multiply(A, B, block_size):m, n = A.shapen, p = B.shapeC = np.zeros((m, p))for i in range(0, m, block_size):for j in range(0, p, block_size):for k in range(0, n, block_size):C[i:i+block_size,j:j+block_size] +=np.dot(A[i:i+block_size,k:k+block_size],B[k:k+block_size,j:j+block_size])return C```在这段代码中,我们将大矩阵A和B划分成了若干个大小为block_size×block_size的小块,并对每个小块进行计算。
矩阵连乘问题方程

矩阵连乘问题方程
矩阵连乘问题是一个经典的优化问题,涉及到多个矩阵的乘法操作。
为了提高计算效率,我们需要找到一种最优的矩阵乘法顺序,使得计算成本最低。
假设我们有一组矩阵A1, A2, ..., An,它们需要进行连乘操作,即C = A1 * A2 * ... * An。
我们需要找到一种最优的乘法顺序,使得计算矩阵C 的成本最低。
根据矩阵乘法的性质,我们可以知道以下规律:
1. 矩阵的乘法满足结合律,即(A * B) * C = A * (B * C)。
2. 矩阵的乘法不满足交换律,即A * B 不一定等于B * A。
因此,我们不能简单地将矩阵按照任意顺序进行连乘,而是需要寻找一种最优的乘法顺序。
一种常见的解决方法是使用动态规划算法。
我们可以定义一个二维数组dp[i][j],表示前i 个矩阵进行连乘,最终得到矩阵j 的最小计算成本。
然后我们遍历所有可能的矩阵乘法顺序,更新dp 数组的值。
最终,dp[n][j] 的值就是我们要求的最小计算成本。
下面是具体的算法步骤:
1. 初始化dp 数组为一个n 行j 列的全零数组。
2. 遍历所有可能的矩阵乘法顺序,对于每个顺序,计算当前乘法操作的成本,并更新dp 数组的值。
3. 最后,dp[n][j] 的值就是我们要求的最小计算成本。
需要注意的是,由于矩阵的维度可能很大,导致可能的矩阵乘法顺序非常多,因此这个问题的计算复杂度是非常高的。
在实际应用中,我们通常会使用一些启发
式算法来近似最优解。
转载-CUDA矩阵向量乘的多种优化

转载-CUDA矩阵向量乘的多种优化写在前⾯本⽂转载⾃。
实验简介使⽤下⾯⼀种或多种优化⽅法完成 CUDA 的矩阵向量乘法\(A\times b=C\),其中 A 是\(2^{14}\times 2^{14}\)的⽅阵,\(b\)为\(2^{14}\)维向量。
假设矩阵\(A\)的元素为\(a_{i,j}=i-0.1\times j+1\),向量\(b\)的元素为\(b_i=\log\sqrt{i\times i-i+2}\)。
使⽤ global memory使⽤合并访存使⽤ constant memory 存放向量使⽤ shared memory 存放向量和矩阵实验环境实验在⽼师提供的计算集群的⼀个节点上进⾏。
单节点的显卡配置如下:$ nvdia-smiMon Dec 2 08:38:49 2019+-----------------------------------------------------------------------------+| NVIDIA-SMI 410.48 Driver Version: 410.48 ||-------------------------------+----------------------+----------------------+| GPU Name Persistence-M| Bus-Id Disp.A | Volatile Uncorr. ECC || Fan Temp Perf Pwr:Usage/Cap| Memory-Usage | GPU-Util Compute M. ||===============================+======================+======================|| 0 Tesla V100-PCIE... On | 00000000:3B:00.0 Off | 0 || N/A 30C P0 24W / 250W | 0MiB / 16130MiB | 0% Default |+-------------------------------+----------------------+----------------------++-----------------------------------------------------------------------------+| Processes: GPU Memory || GPU PID Type Process name Usage ||=============================================================================|| No running processes found |+-----------------------------------------------------------------------------+实验原理优化 CUDA 架构上的程序,⼀般从以下⼏个⽅⾯考虑:选择好的并⾏算法,发掘更多的数据并⾏性保持 SM 尽可能忙碌,尽量利⽤所有的 SM 参与计算加⼤数据量减⼩线程块⼤⼩优化存储器的使⽤全局存储器合并访问使⽤更快的 constant memory 或 shared memory实验过程由于都是 CUDA 架构上的核函数对⽐性能,下⾯的计时都只测了⽤于核函数计算的时间,⽽不包含数据拷贝的部分(否则运⾏时间都在 300ms 左右,基本上都是拷贝的时间⽽没有参考价值了)。
矩阵乘法优化之分块矩阵

矩阵乘法优化之分块矩阵当矩阵尺⼨过⼤时,数据的⼤⼩将超过缓存的⼤⼩,这是容易出现满不命中现象。
将矩阵进⾏分块可以解决这个问题,以下是完整的矩阵乘法代码:vord brck(array A, array B, array C, int n, int bsize){int r, c, k, kk, cc;double sum;int en = bsize * (n/bsize); /* Amount that frts evenly into blocks */for (r = 0; r < n; r++)for (c = 0; c < n; c++)C[r][c] = 0.0;for (kk = 0; kk < en; kk += bsize) {for (cc = 0; cc < en; cc += bsize) {for (r = 0; r < n; r++) {for (c = cc; c < cc + bsize; c++) {sum = C[r][c];for (k = kk; k < kk + bsize; k++) {sum += A[r][k]*B[k][c];}C[r][c] = sum;}}} 分析思路: 1. 矩阵分块前后的乘法计算总数恒定不变,分块前是n^3 。
2. 现将矩阵按mxm进⾏分块,整个矩阵被分成n^2/m^2 个⼦矩阵,乘法计算总是(n^2/m^2) x n x m^2 。
3. 由2可知,分块后,矩阵以mxm为单位进⾏乘法运算,它被嵌套在三层循环内。
ps: 本算法分块后的并不是正⽅形矩阵,⽽是在n⾏或者n列上的矩阵乘积和。
优点:每次都在相邻位置上进⾏读写,提⾼了访问性能。
矩阵乘法优化算法

矩阵乘法优化算法引言矩阵乘法是计算机科学和线性代数中的一个重要问题,它在很多领域都有广泛的应用。
随着矩阵规模的增大,传统的矩阵乘法算法的时间复杂度很高,因此需要寻求更高效的算法来解决这个问题。
本文将介绍一些优化矩阵乘法算法的方法,以及它们的原理和优势。
传统的矩阵乘法算法传统的矩阵乘法算法是通过对每个元素进行乘法和累加的方式来计算结果。
具体而言,对于两个矩阵A和B,它们的乘积C的第i行第j列的元素可以通过以下公式计算得到:C(i, j) = A(i, 1) * B(1, j) + A(i, 2) * B(2, j) + … + A(i, n) * B(n, j)其中,n是矩阵的大小。
这种算法的时间复杂度为O(n^3),对于大规模的矩阵运算来说,效率较低。
因此,我们需要寻找更高效的算法来优化矩阵乘法的计算过程。
分块矩阵乘法算法分块矩阵乘法算法是一种通过分块计算的方式来优化矩阵乘法的算法。
具体而言,将两个矩阵A和B分别分成若干个大小相等的小块,然后对每个小块进行乘法计算,最后将结果合并得到最终的乘积矩阵C。
分块矩阵乘法算法的优势在于它可以利用硬件的并行计算能力,提高矩阵乘法的计算效率。
此外,它还可以充分利用计算机的存储层次结构,减少数据的访问延迟,进一步提高计算效率。
下面是分块矩阵乘法算法的具体步骤:1.将矩阵A和B分别分成大小相等的小块,记作A(i,j)和B(i,j)。
2.对于每个小块A(i,j)和B(i,j),计算它们的乘积C(i,j)。
3.将所有的乘积小块C(i,j)合并得到最终的乘积矩阵C。
分块矩阵乘法算法的优化在实际应用中,可以对分块矩阵乘法算法进行一些优化,进一步提高计算效率。
下面介绍几种常见的优化方法:1. 优化块的大小选择合适的块大小可以显著影响计算性能。
一般来说,较大的块可以减少计算过程中的乘法次数,但会增加访存操作的次数。
因此,要根据具体的硬件和应用场景选择合适的块大小。
2. 填充技术填充技术是一种通过在分块矩阵中添加额外的元素来提高访存效率的方法。
c语言矩阵乘法函数

c语言矩阵乘法函数C语言矩阵乘法函数矩阵乘法是线性代数中的一个重要概念,在计算机科学和工程领域也经常会用到。
C语言作为一种高效的编程语言,提供了丰富的数据类型和操作符,非常适合实现矩阵乘法函数。
本文将介绍如何使用C语言实现矩阵乘法函数,并对其进行详细的解析和优化。
1. 矩阵乘法的定义矩阵乘法是指两个矩阵相乘的运算。
给定两个矩阵A和B,如果A 的列数等于B的行数,则可以将A乘以B得到一个新的矩阵C。
C 的行数等于A的行数,列数等于B的列数。
矩阵乘法的定义如下:C[i][j] = sum(A[i][k] * B[k][j]),其中k的取值范围为0到A的列数-1。
2. C语言矩阵乘法函数的实现下面是一个简单的C语言矩阵乘法函数的实现:```cvoid matrix_multiply(int A[][N], int B[][M], int C[][M]){for(int i=0; i<N; i++){for(int j=0; j<M; j++){C[i][j] = 0;for(int k=0; k<L; k++){C[i][j] += A[i][k] * B[k][j];}}}}```在上述代码中,函数`matrix_multiply`接受三个参数:矩阵A、矩阵B和结果矩阵C。
其中,矩阵A的维度是N×L,矩阵B的维度是L×M,结果矩阵C的维度是N×M。
函数通过三层循环遍历A、B矩阵的元素,并根据矩阵乘法的定义计算出结果矩阵C的每个元素。
3. 矩阵乘法函数的优化上述的矩阵乘法函数实现了矩阵乘法的基本功能,但在实际应用中可能会遇到大规模的矩阵乘法运算,效率的提升是非常重要的。
下面介绍两种常见的矩阵乘法优化方法。
3.1. 矩阵转置优化矩阵转置优化是指将矩阵B进行转置,使得内存访问更加连续,从而提高缓存的命中率。
优化后的代码如下:```cvoid matrix_multiply(int A[][N], int B[][M], int C[][M]){int BT[M][L]; // 转置后的矩阵Bfor(int i=0; i<M; i++){for(int j=0; j<L; j++){BT[i][j] = B[j][i];}}for(int i=0; i<N; i++){for(int j=0; j<M; j++){C[i][j] = 0;for(int k=0; k<L; k++){C[i][j] += A[i][k] * BT[j][k];}}}}```在优化后的代码中,我们首先定义了一个转置后的矩阵BT,然后将矩阵B的元素按列复制到BT中。
矩阵连乘最优结合问题(一)

矩阵连乘最优结合问题(一)
矩阵连乘最优结合问题
简介
矩阵连乘最优结合问题是一个经典的动态规划问题,它的目标是找到一种最优的方式来计算一系列矩阵的乘积。
在实际应用中,这个问题往往涉及到优化计算时间和空间的需求。
相关问题及解释
1.矩阵连乘的计算顺序问题:给定一系列矩阵的维度,如何确定它
们的乘积计算顺序,使得总的计算次数最少。
2.最优连乘加括号问题:在确定计算顺序的基础上,如何添加括号
来改变计算的顺序,使得计算的效率更高。
问题1:矩阵连乘的计算顺序问题
•当只有两个矩阵相乘时,它们的乘积计算次数是确定的,并且只有一种可能的计算顺序。
•然而,当矩阵的数量增加时,不同的计算顺序会导致不同的计算次数。
•因此,需要通过动态规划的方法来确定最优的计算顺序。
问题2:最优连乘加括号问题
•在确定了矩阵乘法的计算顺序后,可以通过添加括号来改变计算的顺序。
•这样做的目的是为了减少矩阵乘法的计算次数,从而提高计算效率。
•通过动态规划的方法,可以找到一种最优的添加括号方式。
总结
矩阵连乘最优结合问题是一个经典的动态规划问题,涉及到确定最优的矩阵乘法计算顺序和添加最优的括号方式。
通过动态规划的方法,可以高效地解决这些问题,优化计算时间和空间的利用。
在实际应用中,矩阵连乘最优结合问题具有广泛的应用领域,如计算机图形学、数据分析等。
矩阵乘法是一种高效的算法可以把一些一维递推优化到log
矩阵运算是属于线性代数里的一个重要内容,上学期学完后只觉得矩阵能解线性方程,不过高中的时候听说过矩阵能优化常系数递推以及将坐标上的点作线性变换,于是找了些资料研究了一下,并把许多经典题以及HDU shǎ崽大牛总结的矩阵乘法的题目[1]、[2]和开设的矩阵乘法DIY Contest给做完了,感觉收获颇丰。
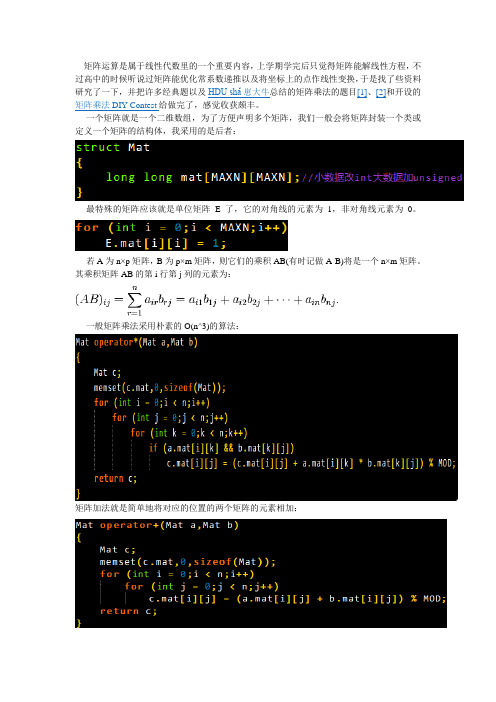
一个矩阵就是一个二维数组,为了方便声明多个矩阵,我们一般会将矩阵封装一个类或定义一个矩阵的结构体,我采用的是后者:最特殊的矩阵应该就是单位矩阵E了,它的对角线的元素为1,非对角线元素为0。
若A为n×p矩阵,B为p×m矩阵,则它们的乘积AB(有时记做A·B)将是一个n×m矩阵。
其乘积矩阵AB的第i行第j列的元素为:一般矩阵乘法采用朴素的O(n^3)的算法:矩阵加法就是简单地将对应的位置的两个矩阵的元素相加:在ACM的题目中,我们一般考虑的是n阶方阵之间的乘法以及n阶方阵与n维向量(把向量看成n×1的矩阵)的乘法。
矩阵乘法最重要的性质就是满足结合律,同时它另一个很重要的性质就是不满足交换率,这保证了矩阵的幂运算满足快速幂取模(A^k % MOD)算法:假设k = 27,则k的二进制表示为11011,所以按二进制展开,乘以相应的权值,可以看出:k的二进制的每一位矩阵A都要平方,在k二进制为1的位:末矩阵×平方后的A,在k二进制为0的位则末矩阵×E(单位矩阵),即不变。
代码如下:重载按位与(乘方)和加法时注意,加法的优先级高于按位与*->+->^许多题目还要求S = A + A2 + A3+ … + A k.。
其实再作一次二分即可:只需计算log(n)个A 的幂即可。
()()343251A6231=+++++将二分+⨯+AAAeA+AAAAA若A中=m表示从i到j有m条有向边,则kA中=n表示从i经过k条有向边到达j,这样的走法有n种矩阵在ACM 里用处最大的就是加速常系数递推方程的计算,最经典的例子就是Fibonacci 数列,如果普通的递推,计算第n 项复杂度为o(n),显然对于10^9左右的数据就力不从心了。
矩阵乘法优化算法

矩阵乘法优化算法矩阵乘法是一种常见的线性代数运算,它的计算复杂度较高,特别是在大规模矩阵相乘时。
为了提高矩阵乘法的性能,可以采用一些优化算法。
本文将介绍几种常见的矩阵乘法优化算法,并提供一些相关的参考内容。
一、基本的矩阵乘法算法首先,我们可以回顾一下基本的矩阵乘法算法。
假设我们有两个矩阵A和B,它们的维度分别为m×n和n×p,我们要计算它们的乘积C=A×B,结果矩阵C的维度为m×p。
具体的计算过程如下:```for i = 1 to mfor j = 1 to pc[i][j] = 0for k = 1 to nc[i][j] += a[i][k] * b[k][j]```这是一个简单的三重循环算法,时间复杂度为O(mnp)。
二、缓存友好的算法矩阵乘法算法的性能很大程度上取决于CPU缓存的使用效率。
缓存友好的算法能够合理地利用CPU缓存,减少缓存未命中的次数,从而提高计算性能。
一种缓存友好的算法是布洛克矩阵乘法算法。
它将矩阵划分成较小的子矩阵,并对子矩阵进行计算。
这样可以提高数据的局部性,减少缓存未命中的次数。
具体的实现方法和相关的优化技巧可以参考以下参考内容:- 参考书籍:《Computer Organization and Design: The Hardware/Software Interface》(第五版)作者:David A. Patterson, John L. Hennessy,该书第4.3.2节介绍了布洛克矩阵乘法的算法和优化原理。
三、并行计算算法另一种优化矩阵乘法的方法是利用并行计算的技术。
在多核CPU或者GPU上进行并行计算,可以将矩阵的计算任务分配给多个处理单元同时执行,从而提高计算性能。
目前,有很多并行计算工具和库可用于矩阵乘法的优化。
以下是一些相关的参考内容:- 参考文献:《High Performance Computing: Modern Systems and Practices》作者:Thomas Sterling,该书第11.4节介绍了在GPU上进行矩阵乘法的并行计算方法,包括CUDA和OpenCL的实现原理和优化技巧。
利用高速缓存(Cache)的局部性优化矩阵乘法

for ( si = 0; si < n; si += blocksize ) for ( sk = 0; sk < n; sk += blocksize )
-4-
do_block(n, blocksize, si, sj, sk, A, B, C); }
*B, double *C)
{
dgemm (n, blocksize, A+si*n+sk, B+sk*n+sj, C+si*n+sj);
//printf("\n");
//printf("%d %d %d\n", si, sj, sk);
//for(int i = 0; i < n; i++)
//{
}
-2-
分析: 计算机在实际计算上述普通矩阵乘法时,所计算矩阵 C 的每一个数据时,都要用到 矩阵 A 的某行和矩阵 B 中的某列,而矩阵 A、B 和 C 都是存储在内存中的,又由于 CPU 的速度远远大于访问内存的速度,如果是直接从内存读取和写回计算数据,那么计算效率 是非常低下的,由于访问内存会导致时延,CPU 的计算资源被浪费,即计算效率低。 为了提高计算速度,引入了 cache 机制,即先把存放在内存中的矩阵 A、B 的元素调 入 cache,这样寄存器可以先寻访 cache,访问 cache 的速度要比访问内存的速度快,如果 在 cache 中没有所需要的数据时,才需要访问内存。 但是,矩阵 A、B 在实际应用中都包含大量的元素,数据量非常分庞大,也即,上述 程序中 n 很大,而处理器中的 cache 往往很小,因此不能将整个矩阵全部放入 cache 中。 因此需要将这些大的矩阵按照某种方法进行分块,使得分块后的小矩阵可以放入到 cache 中,但是分块又不能随意分,需要有一定的原则去分块,如果分块子矩阵太大,那么子矩 阵还是不能全部放入 cache 中,如果分块子矩阵太小,那么为了计算一个大矩阵的数据, 需要调入 cache 的子矩阵的次数会增加,因此需要选择合适的分块方法。 2.分块实现矩阵乘法,利用 cache 的局部性,优化程序性能: a) 安装 Linux 系统: b) 查看 Linux 系统 cache 的大小:
反向传播算法中的矩阵计算优化(六)

反向传播算法是深度学习中最重要的算法之一。
它通过迭代计算损失函数对神经网络参数的梯度,从而实现参数的更新和优化。
在反向传播算法中,矩阵计算是一个非常关键的环节,对其进行优化可以大大提高算法的效率和速度。
本文将从反向传播算法的基本原理入手,探讨如何优化矩阵计算,以提高算法的性能。
反向传播算法的基本原理是通过链式法则,将损失函数对神经网络参数的梯度反向传播到每一层网络中,从而实现参数的更新。
在这个过程中,涉及到大量的矩阵计算,包括矩阵乘法、矩阵转置、矩阵求导等。
这些矩阵计算不仅在理论上具有复杂性,而且在实际计算中也往往需要大量的计算资源。
因此,如何优化这些矩阵计算成为了反向传播算法性能提升的关键。
首先,我们来看矩阵乘法的优化。
在反向传播算法中,矩阵乘法是最为常见的计算操作之一。
传统的矩阵乘法算法是通过三重循环实现的,这种算法的时间复杂度较高,尤其是在大规模矩阵计算时,计算时间会呈现出指数级增长。
为了解决这一问题,有学者提出了一种名为Strassen算法的矩阵乘法优化方法。
Strassen 算法通过将矩阵乘法分解成更小的子问题,并通过递归的方式进行计算,从而降低了时间复杂度。
此外,还有一些基于并行计算的矩阵乘法优化方法,如CUDA等,可以进一步提高计算效率。
其次,矩阵转置也是反向传播算法中的重要计算操作。
矩阵转置是指将矩阵的行列互换,这在神经网络中经常用到,如全连接层的权重矩阵初始化等。
传统的矩阵转置算法也是通过循环实现的,时间复杂度较高。
针对这一问题,可以采用分块转置的方法进行优化。
分块转置将大矩阵分成若干个小块,然后分别对每个小块进行转置操作,最后再将这些小块合并成一个大矩阵。
这样可以大大减小内存访问的开销,从而提高了转置操作的效率。
除了矩阵乘法和矩阵转置,矩阵求导也是反向传播算法中的关键计算操作。
在神经网络中,我们经常需要计算损失函数对参数的梯度,而这涉及到大量的矩阵求导。
传统的矩阵求导方法是通过数值计算的方式进行的,这种方法在计算精度和效率上都存在一定的问题。
矩阵乘法递推的优化

a2 0 1 0 . . . 0 0
a3 0 0 1 . . . 0 0
··· ··· ··· ··· .. . ··· ···
ak −1 0 0 0 . . . 1 0
ak 0 0 0 . . . 0 0
hk−1 hk−2 hk−3 . . X= . h2 h1 h0 1 (k+1)×1 a1 1 0 Y = MX = 0 . . . 0 0 a2 0 1 0 . . . 0 0 a3 0 0 1 . . . 0 0 ··· ··· ··· ··· .. . ··· ··· ak −1 0 0 0 . . . 1 0 ak 0 0 0 . . . 0 0 h h b n k −1 k hk−2 hk−1 0 hk−3 hk−2 0 . . . . 0 . = . h2 h3 . . . h2 h1 0 h0 h1 1 1 1
k ∑ i=1
ai · pn + bn
2 利用矩阵乘法计算递推数列的某一项
2.1 构造递推矩阵
设数列 {hn } 满足 k 阶常系数线性递推关系: hn = a1 hn−1 + a2 hn−2 + a3 hn−3 + · · · + ak hn−k 构造矩阵 a1 1 0 M=0 . . . 0 0 与初始值向量 a2 0 1 0 . . . 0 0 a3 0 0 1 . . . 0 0 ··· ··· ··· ··· .. . ··· ··· ak −2 0 0 0 . . . 1 0 ak −1 0 0 0 . . . 0 1 ak 0 0 0 . . . 0 0 k×k
矩阵乘法算法加速

矩阵乘法算法加速1. 引言矩阵乘法是计算机科学中常见的一种基本操作,广泛应用于科学计算、图形处理、机器学习等领域。
由于矩阵乘法的计算复杂度较高,如何提高矩阵乘法的计算效率成为一个重要的研究课题。
本文将探讨矩阵乘法算法的加速方法,包括优化算法、并行计算、硬件加速等方面。
2. 矩阵乘法算法矩阵乘法的定义是将两个矩阵相乘得到一个新的矩阵。
设有两个矩阵A和B,它们的乘积C的元素c[i][j]可以通过以下公式计算:c[i][j] = sum(a[i][k] * b[k][j]) for k in range(0, n)其中,n为矩阵的维度。
传统的矩阵乘法算法的时间复杂度为O(n^3),这意味着随着矩阵维度的增加,计算时间将呈指数级增长。
为了提高矩阵乘法的计算效率,需要寻找优化算法和加速方法。
3. 优化算法3.1. 基本优化方法矩阵乘法的基本优化方法包括:•基于行优先或列优先的存储方式:在计算矩阵乘法时,采用合适的存储方式可以减少内存访问的次数,提高计算效率。
•循环展开:将循环展开成多个独立的计算任务,使得计算任务可以并行执行,提高计算效率。
•寄存器变量:将一些常用的变量存储到寄存器中,减少内存访问的开销,提高计算效率。
3.2. 分块矩阵乘法分块矩阵乘法是一种常见的矩阵乘法优化方法。
将矩阵划分为若干个小块,通过对小块的乘法运算得到最终结果。
分块矩阵乘法可以提高计算效率,减少内存访问的次数。
分块矩阵乘法的关键是选择合适的分块策略。
常见的分块策略有:•传统分块:将矩阵划分为均匀的小块,适用于大规模矩阵的乘法计算。
•Strassen算法:将矩阵划分为4个小块,通过递归计算得到最终结果。
Strassen算法的时间复杂度为O(n^log2(7)),比传统的矩阵乘法算法更快。
•Cannon算法:将矩阵划分为若干个小块,通过循环移位和局部乘法得到最终结果。
Cannon算法适用于并行计算,可以提高计算效率。
4. 并行计算并行计算是提高矩阵乘法计算效率的重要方法之一。
gemm cpu矩阵乘法

gemm cpu矩阵乘法
GEMM是General Matrix Multiply的缩写,指的是矩阵乘法运算。
在CPU上执行矩阵乘法时,可以使用各种优化技术来提高计算性能。
在进行CPU矩阵乘法时,可以考虑以下几个方面的优化:
1. 数据布局优化:将矩阵数据按照连续的方式存储在内存中,可以提高访存效率。
例如,使用行主序(row-major order)或列主序(column-major order)存储方式,以便于CPU缓存的预取和利用。
2. 循环展开:通过展开内层循环,减少循环迭代次数,提高计算效率。
可以根据具体情况选择展开的程度,并结合编译器的优化选项进行调整。
3. 原位操作:如果矩阵C可以原地存储,即结果矩阵可以覆盖其中一个输入矩阵的内存空间,可以减少内存读写,提高性能。
4. 多线程并行:利用多线程技术,将矩阵乘法任务划分为多个子任务,并行计算。
可以使用线程池或OpenMP等工具来实现多线程并行。
5. SIMD指令优化:使用CPU支持的SIMD(Single Instruction, Multiple Data)指令集,如SSE、AVX等,进行向量化计算。
这些指令可以同时对多个数据元素执行相同的操作,提高计算效率。
6. 算法选择:根据具体需求和硬件平台的特点,选择合适的矩阵乘法算法。
常见的算法包括经典的三重循环算法、分块矩阵乘法(Blocked Matrix Multiply)以及基于Strassen算法的优化算法等。
以上是一些常见的CPU矩阵乘法的优化技巧,具体的实现方式和效果还需要根据具体情况进行调整和评估。
矩阵乘法分配律+bitset优化——hdu4920

矩阵乘法分配律+bitset优化——hdu4920因为是模3,所以把原矩阵拆成两个01矩阵,然后按分配律拆开分别进⾏矩阵乘法,⾏列⽤bitset来存进⾏优化即可注意int bitset<int>::count() 函数可以统计bitset⾥有多少1int bitset<int>::any() 函数可以统计bitset⾥是否有1/*(A+B)*(C+D)=A*C+A*D+B*C+B*D*/#include<bits/stdc++.h>using namespace std;#define maxn 805struct Matrix{int n;bitset<maxn>r[maxn];//按⾏表⽰bitset<maxn>c[maxn];//按列表⽰}A,B,C,D;int E[maxn][maxn],F[maxn][maxn],G[maxn][maxn],H[maxn][maxn];int n;void mul(Matrix A,Matrix B,int res[maxn][maxn]){bitset<maxn>tmp;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){tmp=A.r[i]&B.c[j];res[i][j]=tmp.count()%3;}}int main(){while(cin>>n){A.n=B.n=C.n=D.n=n;for(int i=1;i<=n;i++){A.c[i].reset();A.r[i].reset();B.c[i].reset();B.r[i].reset();C.c[i].reset();C.r[i].reset();D.c[i].reset();D.r[i].reset();}for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){int x;scanf("%d",&x);x%=3;if(x>=1){A.r[i][j]=1;A.c[j][i]=1;}if(x==2){B.r[i][j]=1;B.c[j][i]=1;}}for(int i=1;i<=n;i++)for(int j=1;j<=n;j++){int x;scanf("%d",&x);x%=3;if(x>=1){C.r[i][j]=1;C.c[j][i]=1;}if(x==2){D.r[i][j]=1;D.c[j][i]=1;}}mul(A,C,E);mul(A,D,F);mul(B,C,G);mul(B,D,H);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){int ans=E[i][j]+F[i][j]+G[i][j]+H[i][j];if(j!=1)printf("");printf("%d",ans%3); }puts("");}}}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
>才智
/207
分析方法,分别a/b、c/a、t/a、d/l、h/a 对最大翘曲应力精确度的影响。
限于文章篇幅有限,本文仅讨论h/a 对求最大翘曲应力精度的的影响。
h/a 的变化情况可以直接反映连梁的数量以及杆件有效高度Z 的变化情况。
取a/b=1.30,c/a=0.30,t/a=0.06,并固定三者数值不变。
然后分别取h/a=0.60、1.0、1.50、2.0、3.0。
即截面尺寸为:a=10.0cm,b=8.0cm,c=2.50cm,壁厚t=0.50cm,杆件材料的弹性模量E=2.50×105N/cm2,泊松比V= V=0.1667,杆件顶端所受到的几种扭矩大小M=2010N.cm。
对其最大翘曲应力进行计算,其中有限元计算结果同理论解的比较见表2。
表2有限元解同理论解的比较结果
从表2中可以看出,当h/a 的取值越小时,本文采用的连续法所得到的结果越接近理论值,随着h/a 比值的逐渐增大,有限元解同理论解之间的相对误差逐渐增大。
2 结语
本文以高层建筑筒体结构约束扭转为研究对象,较为详细的分析了连梁对开口薄壁筒体约束扭转的影响,最后,探讨了连续化方法求最大翘曲应力时对精确度的影响关系。
希望本文的提出能起到抛砖引玉的作用,其他研究人员继续这方面的研究,为取得更大的研究成果而不懈努力。
参考文献:
[1] 往荫长. 高层建筑筒体结构的计算,科学出版社,1988.
[2] 鲍永方. 薄壁结构的约束扭转分析[D]. 北京农业工程大学学报,北京,1996.
矩阵乘法的优化
谢林川 武警警官学院电子技术系 610041
在科学与工程计算的许多问题中经常需要进行矩阵计算。
矩阵乘、求解线性方程组和矩阵特征值问题是矩阵计算最基本的内核。
许多先进的计算机上都配有高效的串行程序库。
为了在并行计算环境上实现矩阵乘积,研究并行算法是非常必要的。
本文主要讲述了如何在多核处理器上对矩阵乘法进行优化。
1. 矩阵乘法串行算法
矩阵乘法在实现上比较简单,可以通过3层循环得到。
例如我们求C=Beta*C+Alpha*A*B,其中A,B,C,Alpha,Beta 都是双精度浮点数据。
串行算法的实现原理是:矩阵A 中的一行和矩阵B 中的一列对应元素进行乘加得到矩阵C 中的对应元素。
假设A 是一个m*k 的矩阵,B 是一个k*n 矩阵,因此C 是一个m*n 矩阵,我们可以得到串行算法程序如下:
for i=1, m for j=1, n
C(i,j)=C(i,j)*Beta for L=1, k
C(i,j)= C(i,j)+Alpha*A(i,L)*B(L,j) endfor endfor endfor
2.矩阵乘法分块算法
上面我们对矩阵乘法的串行算法做了分析,我们在计算矩阵C 的每一个数据时,都要用到矩阵A 的某行和矩阵B 的某列的数据,在实际计算过程中,A、B 的元素是存放在内存中的,所以为了提高计算速度,我们把存放在内存中的矩阵A、B 的元素调入Cache 中,这样寄存器可以首先寻访Cache,如果没有需要的数据才会访问内存。
但是矩阵A、B 在实际应用中都包含大量的元素,数据量非常庞大,而处理器的Cache 往往很小,因此不可能将整个矩阵全部放入Cache。
因此我们需要把这些大的矩阵按照某种方法进行分块,使得分块后的小矩阵可以放入Cache。
但是分块不是随意分,有一定的分块原则,如果分块子矩阵太大,造成子矩阵不能放入Cache;如果分块子矩阵太小,那么为了计算一个大矩阵的数据,需要调入Cache 的子矩阵的次数会增多,会大大加剧处理器的负荷。
因此,如何对矩阵进行分块,既能使得每次参与计算的矩阵块都能放入Cache,也不存在多次从内存中拷贝矩阵块到Cache 中增加处理器的负载,也是本文需要分析的地方。
同样假设A 是一个m*k 的矩阵,B 是一个k*n 矩阵,因此C 是一个m*n 矩阵,矩阵A 的分块大小为m*k,矩阵B 的分块大小为k*n,下面是分块算法:
for i=1, m ,M for j=1,n,N for p=I,min(i+M,m) for q=j,min(j+N,n) C(p,q)=C(p,q)*Beta Endfor endfor
for L=1,k,K
for p=i,min(i+M,m) for q=j,min(j+N,n) for r=l,min(L+K,k)
C(p,q)=C(p,q)+Alpha*A(p,r)*B(r,q) endfor endfor endfor endfor 3.分层技术
因为处理器L1cache 和L2cache 到寄存器的带宽大致相同,L2cacahe 的大小明显大于L1cache,这样能够存放更多的数据,基于这种情况,提出把分块A 存放在L2cache 中,使得B 矩阵的运算访存比得到了提高。
此外,对矩阵乘法划分方法进行了总结,通过分析得出:对矩阵A 和B 都进行划分,得到的性能是最优的。
可以对 GEBP 算法的实现做了进一步的优化:在寄存器中预取A 和B,隐藏访存时间;增大分块参数kc,降低读写 C 子矩阵的平均开销;把 A 分块存放在L2cache 中,增大A 分块的参数,提高矩阵的运算访存比。
4.对矩阵乘法进行多线程(OPENMP)优化
在进行矩阵乘法的运算时候,考虑到在实际的工作中,矩阵都是相当大的,这就需要我们对矩阵进行分块,每个线程执行块A 和块B 的乘加运算。
多核处理器一般又多个线程,这样就可以同时在多个线程中进行并行运算,可以大大的提高处理器的运算效率。
因此,在实际编程过程中,我们可以采用OPENMP 多线程来对矩阵乘法进行优化。
5.封装技术
矩阵A、B 进行分块后,在存储空间有可能不是连续存放的,这也就意味着对这些不连续的分块进行映射需要更多条目的TLB。
解决的方法就是将这些分块存放在连续的数组中,之后计算的数据直接从数组中读取,以保证这些数据的地址可以在TLB 中找到。
这样做不会引入额外的开销,因为这些子矩阵被复制以后,其地址就已经保存在了TLB 中,而其数据则保存在cache 中。
这样的过程称为Packing。
在计算的时候,将矩阵A 、B 分别存放进连续的内存空间 和 中,计算C=C+ 。
矩阵乘法的优化
作者:谢林川
作者单位:武警警官学院电子技术系 610041
刊名:
才智
英文刊名:caizhi
年,卷(期):2013(16)
本文链接:/Periodical_caiz201316191.aspx。
