常用均匀设计表
应用统计方法课件 5.2 均匀试验设计
No
1
2
3
4
5
6
1
1
2
4
5
7
8
2
2
4
8
1
5
7
3
3
6
3
6
3
6
4
4
8
7
2
1
5
5
5
1
2
7
8
4
6
6
3
6
3
6
3
7
7
5
1
8
4
2
8
8
7
5
4
2
1
9
9
9
9
9
9
9
用上述步骤生成的均匀设计表记作U n (nm ) ,向量 h 称为该表的生成向量,有时为了强调 h 的作用,可将 U n (nm ) 记成 U n (h) 。给定 n ,相应的 h 可以象上例那 样方便地求得,从而 m 也就确定。所以 m 是 n 的一个函
u42 = 6 + 2 = 8 ,u52 = 8 + 2 = 10 = 1(mod 9) ,
u62 = 1 + 2 = 3 , u72 = 3 + 2 = 5 ,
u82 = 5 + 2 = 7 , u92 = 7 + 2 = 9 ,
其结果列于表 5-29 的第二列。
表 5-29 U 9 (96 )
5
3
1
2
6
6
5
4
1
7
7
7
7
7
( ) 表 5-24
U
* 7
74
No
均匀设计与均匀设计表

第一章试验设计和均匀设计1.1试验设计在工农业生产和科学研究中,经常需要做试验,以求达到预期的目的。
例如在工农业生产中希望通过试验达到高质、优产、低消耗,特别是新产品试验,未知的东西很多,要通过试验来摸索工艺条件或配方。
如何做试验,其中大有学问。
试验设计得好,会事半功倍,反之会事倍功半,甚至劳而无功。
本世纪30年代,由于农业试验的需要,费歇尔(R.A.Fisher)在试验设计和统计分析方面做出了一系列先驱工作,从此试验设计成为统计科学的一个分支。
随后,F.Yates,R.C.Bose,O.Kempthome,W.G.Cochran,D.R.Cox和G.E.P.Box对试验设计都作出了杰出的贡献,使该分支在理论上日趋完善,在应用上日趋广泛。
60年代,日本统计学家田口玄一将试验设计中应用最广的正交设计表格化,在方法解说方面深入浅出为试验设计的更广泛使用作出了众所周知的贡献。
田口玄一的方法对我国试验设计的普及和广泛应用有巨大的影响,70年代我国许多统计学家深入工厂、科研单位,用通俗的方法介绍正交试验设计,帮助工程技术人员进行试验的安排和数据分析,获得了一大批优秀成果,出版了许多成果汇编,举办了不少成果展览会。
在广泛使用试验设计方法的洪流中,必然会出现一些新的问题,这些总是用原有的各种试验设计方法不能圆满地解决,特别是当试验的范围较大,试验因素需要考察较多等级(在试验设计中这些等级称之为水平)时,用正交试验及其它流行的试验方法要求做较多的试验,常使得试验者望而生畏。
许多实际问题要求一种新的试验方法,它能有效地处理多水平的试验,于是王元和方开泰于1978年提出了均匀设计(见文献「1-3」),该设计考虑如何将设计点均匀地散布在试验范围内,使得能用较少的试验点获得最多的信息。
10多年来,均匀设计在国内得到了广泛应用,并获得不少好的成果。
试验设计在工业生产和工程设计中能发挥重要的作用,例如:1)提高产量;2)减少质量的波动,提高产品质量水准;3)大大缩短新产品试验周期;4)降低成本;5)延长产品寿命。
2012均匀试验

均匀设计的灵活应用
1.混合水平的均匀设计 采用拟水平法,每个水平重复使用。 如在一个试验中考察三个因素,因素A、B为3水平, 因素C为2水平,选用均匀设计表U6 *(64),按 使用表的推荐用1,2,3前3列。若将A 和B 放 在前两列,C 放在第3列,并将前两列的水平合并: {1,2}1,{3,4}2,{5,6}3, 同时将第3列水平合并为2水平:{1,2,3} 1,{4,5,6}2,于是得设计表7。这是一 个混合水平的设计表U6(32×21)。
例题1: 在淀粉接枝丙烯酸制备高吸水性树脂的试 验中,为了提高树脂吸盐水的能力,考察了丙 烯酸用量 (x1),引发剂用量 (x2), 丙烯酸中和度 (x3)和甲醛用量 (x4) 四个因素,每个因素取9个水平,因素水平如 表所示
解:根据因素和水平,可以选取均匀设计表 U9 (94)或 U9*(95)。 均匀表 U9 *(94)最多只能安排3个因素, 所以选用 U9(95)表来安排该试验。
四、均匀设计基本步骤
(5)进行表头设计。 根据试验的因素数和该均匀表对应的使用表,将各 因素安排在均匀表相应的列中,如果是混合水平的均匀 表,则可省去表头设计这一步。 (6)列出试验方案表,进行试验。 (7)对实验数据进行分析。 采用直观分析与回归分析相结合方式。 均匀表中的空白列,既不能安排交互作用,也不能用来 估计试验误差,所以在分析试验结果时不用列出。
由方差分析知,所求得的回归方程非常显著,该回 归方程是可信的。
由回归方程可知: x1、x3 的系数为正,表明试验指标随因素x1、 x3 的增加而增加;x2、x4 的系数为负值,则 表示试验指标随因素x2、x4 的增加而减少。 所以,在确定优方案时,因素x1、x3 的取值 应偏上限,即丙烯酸用量取32mL,丙烯酸中和 度取92%;同理,因素x2、x4 的取值应偏下限, 即引发剂用量取0.3%,甲醛用量取0.2mL。 将以上各值代入上述回归方程,得到y=76.3, 这一结果好于表中的9个试验结果,但是否可行, 还应进行验证试验。
均匀设计与均匀设计表

第一章试验设计和均匀设计1.1试验设计在工农业生产和科学研究中,经常需要做试验,以求达到预期的目的。
例如在工农业生产中希望通过试验达到高质、优产、低消耗,特别是新产品试验,未知的东西很多,要通过试验来摸索工艺条件或配方。
如何做试验,其中大有学问。
试验设计得好,会事半功倍,反之会事倍功半,甚至劳而无功。
本世纪30年代,由于农业试验的需要,费歇尔(R.A.Fisher)在试验设计和统计分析方面做出了一系列先驱工作,从此试验设计成为统计科学的一个分支。
随后,F.Yates,R.C.Bose,O.Kempthome,W.G.Cochran,D.R.Cox和G.E.P.Box对试验设计都作出了杰出的贡献,使该分支在理论上日趋完善,在应用上日趋广泛。
60年代,日本统计学家田口玄一将试验设计中应用最广的正交设计表格化,在方法解说方面深入浅出为试验设计的更广泛使用作出了众所周知的贡献。
田口玄一的方法对我国试验设计的普及和广泛应用有巨大的影响,70年代我国许多统计学家深入工厂、科研单位,用通俗的方法介绍正交试验设计,帮助工程技术人员进行试验的安排和数据分析,获得了一大批优秀成果,出版了许多成果汇编,举办了不少成果展览会。
在广泛使用试验设计方法的洪流中,必然会出现一些新的问题,这些总是用原有的各种试验设计方法不能圆满地解决,特别是当试验的范围较大,试验因素需要考察较多等级(在试验设计中这些等级称之为水平)时,用正交试验及其它流行的试验方法要求做较多的试验,常使得试验者望而生畏。
许多实际问题要求一种新的试验方法,它能有效地处理多水平的试验,于是王元和方开泰于1978年提出了均匀设计(见文献「1-3」),该设计考虑如何将设计点均匀地散布在试验范围内,使得能用较少的试验点获得最多的信息。
10多年来,均匀设计在国内得到了广泛应用,并获得不少好的成果。
试验设计在工业生产和工程设计中能发挥重要的作用,例如:1)提高产量;2)减少质量的波动,提高产品质量水准;3)大大缩短新产品试验周期;4)降低成本;5)延长产品寿命。
常用均匀设计表

常用(校园交达电脑最新版)均匀设计表表1)5(35U试验号 1 2 3 1 1 2 4 2 2 4 3 3 3 1 2 4 4 3 1 55 5 5表2)5(35U 的使用表因素个数列号 D2 1 2 0、3100 31230、4570表3 )6(4*6U 试验号 1 2 3 4 1 1 2 3 6 2 2 4 6 5 3 3 6 2 4 4 4 1 5 3 5 5 3 1 2 66 541表4)6(4*6U 的使用表因素个数列 号D 2 1 3 0、1875 3 1 2 3 0、2656 412340、2990表5 )7(47U试验号12341 123 6 2 24 65 3 36 2 4 4 4 1 5 3 5 5 3 1 2 6 6 5 4 1 77777表6 )7(47U 的使用表因素个数列号D 2 1 3 0、2398 3 1 2 3 0、3721 412340、4760表7 )7(4*7U 试验号 1 2 3 4 1 1 3 5 7 2 2 6 2 6 3 3 1 7 5 4 4 4 4 4 5 5 7 1 3 6 6 2 6 2 77531表8 )7(4*7U 的使用表 因素个数列号 D2 13 0、1582 32340、2132表9 )8(5*8U 试验号 1 2 3 4 5 1124782 2 4 8 5 73 3 6 3 3 64 4 8 7 15 5 5 1 2 8 46 6 3 6 6 37 7 5 1 4 2 887521表10 )8(5*8U 的使用表 因素个数列号D 2 1 3 0、1445 3 1 3 4 0、2000 412350、2709表11 )9(59U试验号 1 2 3 4 5 1 1 2 4 7 8 2 2 4 8 5 7 3 3 6 3 3 6 4 4 8 7 1 5 5 5 1 2 8 4 6 6 3 6 6 3 7 7 5 1 4 2 8 8 7 5 2 1 999999表12 )9(59U 的使用表因素个数列号D 2 1 3 0、1944 3 1 3 4 0、3102 412350、4066表13 )9(4*9U 试验号 1 2 3 4 1 1 3 7 9 2 2 6 4 8 3 3 9 1 7 4 4 2 8 6 5 5 5 5 5 6 6 8 2 4 7 7 1 9 3 8 8 4 6 2 99731表14 )9(4*9U 的使用表 因素个数列号 D2 1 2 0、1574 32340、1980表15 )10(8*10U 试验号 1 2 3 4 5 6 7 8 1 1 2 3 4 5 7 9 10 2 2 4 6 8 10 3 7 9 3 3 6 9 1 4 10 5 8 4 4 8 1 5 9 6 3 7 5 5 10 4 9 3 2 1 6 6 6 1 7 2 8 9 10 5 7 7 3 10 6 2 5 8 4 8 8 5 2 10 7 1 6 3 9 9 7 5 3 1 8 4 2 10109876421表16 )10(8*10U 的使用表因素个数列号D 2 1 6 0、1125 3 1 5 6 0、1681 4 1 3 4 5 0、2236 5 1 3 4 5 7 0、2414 6123 5680、2994表17 )11(611U试验号 1 2 3 4 5 8 1 1 2 3 5 7 10 2 2 4 6 10 3 9 3 3 6 9 4 10 8 4 4 8 1 9 6 7 5 5 10 4 3 2 6 6 6 1 7 8 9 5 7 7 3 10 2 5 4 8 8 5 2 7 1 3 9 9 7 5 1 8 2 10 10 9 8 6 4 1 11111111111111表18 )11(611U 的使用表因素个数列号D 2 1 5 0、1632 3 1 4 5 0、2649 4 1 3 4 5 0、3528 5 1 2 3 4 5 0、4286 6123 4560、4942表19 )11(4*11U 试验号 1 2 3 41 1 5 7 112 2 10 2 103 3 3 9 94 4 8 4 85 5 1 11 76 6 6 6 67 7 11 1 58 8 4 8 49 9 9 3 3 10 10 2 10 2 1111751表20 )11(4*11U 的使用表 因素个数列号 D 2 1 2 0、1136 32340、2307表21 )12(10*12U 试验号 1 2 3 4 5 6 7 8 9 10 1 1 2 3 4 5 6 8 9 10 12 2 2 4 6 8 10 12 3 5 7 11 3 3 6 9 12 2 5 11 1 4 10 4 4 8 12 3 7 11 6 10 1 9 5 5 1 6 6 12 5 11 4 10 9 2 8 7 7 7 1 8 2 9 3 4 11 5 6 8 8 3 11 6 1 9 12 7 2 5 9 9 5 1 10 6 2 7 3 12 4 1 2 9 3 11 11 9 7 5 3 1 10 8 6 2 121211109875431表22 )12(10*12U 的使用表 因素个数列号 D 2 1 5 0、1163 3 1 6 9 0、1838 4 1 6 7 9 0、2233 5 1 3 4 8 10 0、2272 6 1 2 6 7 8 9 0、2670 7126789100、2768表23 )13(813U试验号 1 2 3 4 5 6 7 8 1 1 2 5 6 8 9 10 12 2 2 4 10 12 3 5 7 11 3 3 6 2 5 11 1 4 10 4 4 8 7 11 6 10 1 9 5 5 10 12 4 1 6 11 8 6 6 12 4 10 9 2 8 7 7 7 1 9 3 4 11 5 6 8 8 3 1 9 12 7 2 5 9 9 5 6 2 7 3 12 4 1 3 11 11 9 3 1 10 8 6 2 12 12 11 8 7 5 4 3 13131313表24 )13(813U 的使用表因素个数列号 D 2 1 3 0、1405 3 1 4 7 0、2308 414570、31075 1 4 567 0、38146 1 2 4 5 67 0、44397 1 2 4 5 6 7 8 0、4992 Uniform Design tables 网站地址Uniform Design tables:均匀设计表factor:因素level:水平run:试验次数。
第7章_均匀设计

Page 23
第7章 均匀设计
Uniform Design 用Excel“规划求解”工具寻求例7-2的最优方案
目标单元格输入回归方程: “=275.85-9.16*C3-21.90*C4 -21.14*C5+1.40*C6+ 1.16*C3*C4+0.73*C5^2”
Page 24
例如:某试验有A,B,C三个因素;A,B为3水平;C为2水平。 若用正交设计:可用L18(21×37)或拟水平选L9(34)。 用均匀设计:可将U6*(64)改造成U6(32×21)。 改造方法:将A和B放在前两列,C放在第3列。然后将前两列 的水平合并为3水平,第3列的水平合并为2水平。即 前两列:{1,2}合并为1,{3,4}合并为2,{5,6}合并为3。 第3列:{1,2,3}合并为1,{4,5,6}合并为2。 于是可得一个混合水平的设计表:U6(32×21)。
0.986 0.973 0.964 2.047 9
由于x3,x4不显著,去掉x3,x4再进行回归分析,得回归方 程为: y=20.393+1.72x1-10.33x2 x1对应的P-value<0.01,非常显著; x2对应的0.01<P-value<0.05,显著。 (3)优方案确定 据第一个回归方程,系数为正取上限 ,系数为负取下 限 ,故优方案为: A9B5C9D8
Page 5
第7章 均匀设计
Uniform Design
U 6 (32 21 )
试验号 1 2 3 4 5 6
列号 1
(1)1 (2)1 (3)2 (4)2 (5)3 (6)3
2
(2)1 (4)2 (6)3 (1)1 (3)2 (5)3
3
(3)1 (6)2 (2)1 (5)2 (1)1 (3)2
混合水平的均匀设计表共90页文档

8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——德谟耶克斯
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
均匀设计与均匀设计表

第一章试验设计和均匀设计1.1试验设计在工农业生产和科学研究中,经常需要做试验,以求达到预期的目的。
例如在工农业生产中希望通过试验达到高质、优产、低消耗,特别是新产品试验,未知的东西很多,要通过试验来摸索工艺条件或配方。
如何做试验,其中大有学问。
试验设计得好,会事半功倍,反之会事倍功半,甚至劳而无功。
本世纪30年代,由于农业试验的需要,费歇尔(R.A.Fisher)在试验设计和统计分析方面做出了一系列先驱工作,从此试验设计成为统计科学的一个分支。
随后,F.Yates,R.C.Bose,O.Kempthome,W.G.Cochran,D.R.Cox和G.E.P.Box对试验设计都作出了杰出的贡献,使该分支在理论上日趋完善,在应用上日趋广泛。
60年代,日本统计学家田口玄一将试验设计中应用最广的正交设计表格化,在方法解说方面深入浅出为试验设计的更广泛使用作出了众所周知的贡献。
田口玄一的方法对我国试验设计的普及和广泛应用有巨大的影响,70年代我国许多统计学家深入工厂、科研单位,用通俗的方法介绍正交试验设计,帮助工程技术人员进行试验的安排和数据分析,获得了一大批优秀成果,出版了许多成果汇编,举办了不少成果展览会。
在广泛使用试验设计方法的洪流中,必然会出现一些新的问题,这些总是用原有的各种试验设计方法不能圆满地解决,特别是当试验的范围较大,试验因素需要考察较多等级(在试验设计中这些等级称之为水平)时,用正交试验及其它流行的试验方法要求做较多的试验,常使得试验者望而生畏。
许多实际问题要求一种新的试验方法,它能有效地处理多水平的试验,于是王元和方开泰于1978年提出了均匀设计(见文献「1-3」),该设计考虑如何将设计点均匀地散布在试验范围内,使得能用较少的试验点获得最多的信息。
10多年来,均匀设计在国内得到了广泛应用,并获得不少好的成果。
试验设计在工业生产和工程设计中能发挥重要的作用,例如:1)提高产量;2)减少质量的波动,提高产品质量水准;3)大大缩短新产品试验周期;4)降低成本;5)延长产品寿命。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表1 U s(53)
试验号 1 2 3
1 1
2 4
2 2 4 3
3 3 1 2
4 4 3 1
5 5 5 5
表2 U s (53) 的使用表
因素个数列号 D
2 1 2 0.3100
3 1 2 3 0.4570
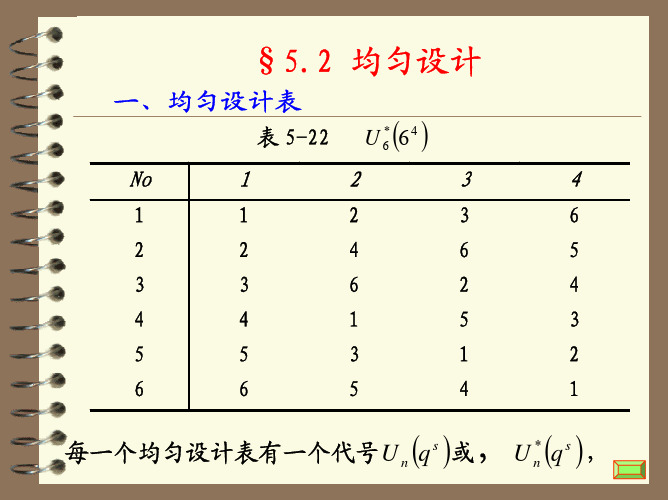
表3 U;(64)
试验号 1 2 3 4
1 1
2
3 6
2 2 4 6 5
3 3 6 2 4
4 4 1
5 3
5 5 3 1 2
6 6 5 4 1
表4 U6(64) 的使用表
因素个数列号 D
2 1
3 0.1875
3 1 2 3 0.2656
4 1 2 3 4 0.2990
表5 U7(74)
试验号 1 2 3 4
1 1
2
3 6
2 2 4 6 5
3 3 6 2 4
4 4 1
5 3
5 5 3 1 2
6 6 5 4 1
7 7 7 7 7
表6 U7 (74)的使用表
因素个数列号 D
2 1
3 0.2398
3 1 2 3 0.3721
4 1 2 3 4 0.4760
表7 U;(74)
试验号 1 2 3 4
1 1 3 5 7
2 2 6 2 6
3 3 1 7 5
4 4 4 4 4
5 5 7 1 3
6 6 2 6 2
7 7 5 3 1
表8 U;(74)的使用表
表9 U;(85)
试验号 1 2 3 4 5
1 1
2 4 7 8
2 2 4 8 5 7
3 3 6 3 3 6
4 4 8 7 1 5
5 5 1 2 8 4
6 6 3 6 6 3
7 7 5 1 4 2
8 8 7 5 2 1
表10 U;(85)的使用表
因素个数列号 D
2 1
3 0.1445
3 1 3
4 0.2000
4 1 2 3
5 0.2709
表11 U9(95)
试验号 1 2 3 4 5
1 1
2 4 7 8
2 2 4 8 5 7
3 3 6 3 3 6
4 4 8 7 1 5
表12 U 9(95)的使用表
表 13 U ;(94)
试验号
1 2 3 4 1 1 3 7 9 2 2 6 4 8 3 3 9 1 7 4 4 2 8 6 5 5 5 5 5 6 6 8 2 4 7 7 1 9 3 8 8 4 6 2 9
9
7
3
1
表14
U 9
(94)
的使用表
因素个数
列号
D 2
1
2
0.1574
3 2
3
4
0.1980
5
6 7 8 9
5 6 7 8 9
6 4 2 9
3 2 1 9
表15 U;(108)
试验号 1 2 3 4 5 6 7 8
1 1
2
3
4
5 7 9 10
2 2 4 6 8 10
3 7 9
3 3 6 9 1
4 10
5 8
4 4 8 1
5 9
6 3 7
5 5 10 4 9 3 2 1 6
6 6 1
7 2
8
9 10 5
7 7 3 10 6 2 5 8 4
8 8 5 2 10 7 1 6 3
9 9 7 5 3 1 8 4 2
10 10 9 8 7 6 4 2 1
表16 U;0(108)的使用表
因素个数列号 D
2 1 6 0.1125
3 1 5 6 0.1681
4 1 3 4
5 0.2236
5 1 3 4 5 7 0.2414
6 1 2 3 5 6 8 0.2994
表17 Un(116)
试验号 1 2 3 4 5 8
1 1
2
3 5 7 10
2 2 4 6 10
3 9
3 3 6 9
4 10 8
4 4 8 1 9 6 7
6 6 17
7 7 3 10
8 8 5 2
9 9 7 5
10 10 9 8 8
2
7
1
6
9
5
1
8
4
5
4
3
2
1
1
1
11 11 11 11 11 11
表18 Un(116)的使用表
因素个数列号 D
2 1 5 0.1632
3 1
4
5 0.2649
4 1 3 4
5 0.3528
5 1 2 3 4 5 0.4286
6 1 2 3 4 5 6 0.4942
表19 U;1 (114)
试验号 1 2 3 4
1 1 5 7 11
2 2 10 2 10
3 3 3 9 9
4 4 8 4 8
5 5 1 11 7
6 6 6 6 6
7 7 11 1 5
8 8 4 8 4
9 9 9 3 3
10 10 2 10 2
11 11 7 5 1
表20 U i*i(114)的使用表
表21 U I*2(1210)
试验号 1 2 3 4 5 6 7 8 9 10
1 1
2
3
4
5
6 8 9 10 12
2 2 4 6 8 10 12
3 5 7 11
3 3 6 9 12 2 5 11 1
4 10
4 4 8 12 3 7 11 6 10 1 9
5 5 10 2 7 12 4 1
6 11 8
6 6 12 5 11 4 10 9 2 8 7
7 7 1 8 2 9 3 4 11 5 6
8 8 3 11 6 1 9 12 7 2 5
9 9 5 1 10 6 2 7 3 12 4
10 10 7 4 1 11 8 2 12 9 3
11 11 9 7 5 3 1 10 8 6 2
12 12 11 10 9 8 7 5 4 3 1
表22 U;2(1210)的使用表
因素个数列号 D
2 1 5 0.1163
3 1 6 9 0.1838
4 1 6 7 9 0.2233
5 1 3 4 8 10 0.2272
6 1 2 6
7
8
9 0.2670
7 1 2 6 7 8 9 10 0.2768
表23 几(138)
试验号 1 2 3 4 5 6 7 8
1 1
2 5 6 8 9 10 12
2 2 4 10 12
3 5 7 11
3 3 6 2 5 11 1
4 10
4 4 8 7 11 6 10 1 9
5 5 10 12 4 1
6 11 8
6 6 12 4 10 9 2 8 7
7 7 1 9 3 4 11 5 6
8 8 3 1 9 12 7 2 5
9 9 5 6 2 7 3 12 4
10 10 7 11 8 2 12 9 3
11 11 9 3 1 10 8 6 2
12 12 11 8 7 5 4 3 1
13 13 13 13 13 13 13 13 13
表24 U13( (138)的使用表
因素个数列号 D
2 1
3 0.1405
3 1
4 7 0.2308
4 1 4
5 7 0.3107
5 1 4 5
6
7 0.3814
6 1 2 4 5 6
7 0.4439
7 1 2 4 5 6 7 8 0.4992 Uniform Desig n tables 网站地址
http://www.math.hkbu.
edu.hk/UniformDesign/
:均匀设计表
Uniform Design tables factor :因素level :水平run :试验次数。
