高一数学直线与平面平行的判定
直线与平面平行 课件-2022-2023学年高一下学期数学人教A版(2019)必修第二册

∴AM=2DC,AM∥DC,
∴AM∥GN,AM=GN,∴四边形AMNG为平行四边形,
∴MN∥平面PAD.
∴MN∥AG.又MN⊄平面PAD,AG⊂平面PAD,
课堂小结
1.直线与平面平行的判定定理
线线平行
线面平行
如果平面外一条直线与此平面内的一条直线平行,那么该直线与
此平面平行.
2.直线与平面平行的性质定理
基本事实4 平行于同一条直线的两条直线平行.
3、等角定理
定理 如果空间中两个角的两边分别对应平行,那么这两个角相等或互补.
复习回顾
4、直线与平面有哪些位置关系?
(1)直线在平面内——有无数个公共点;
⊂
(2)直线与平面相交——有且只有一个公共点; ∩ =
直线在平面外
(3)直线与平面平行——没有公共点.
线线平行Βιβλιοθήκη 线面平行一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么
该直线与交线平行.
3.应用线面平行的判定定理证明线面平行的基本步骤:
(1)利用性质定理在面内找平行线;
(2)证明直线与直线平行;
(3)说明两线与平面的位置关系(一条在面内,一条不在面内);
(4)得出结论.
E
证明: 连接BD.
F
∵ AE EB,AF FD,
∴ EF / / BD.
又 EF 平面BCD,BD 平面BCD,
D
B
C
∴ EF / / 平面BCD.
今后要证明一条直线与一个平面平行,只要在这个平面内找出一
条与此直线平行的直线就可以了.
巩固训练
如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,
人教高一数学直线与平面平行的判定定理
例2. 如图,四棱锥P—ABCD中, 底面为平行四边形,E为PC的中点. 求证:PA//平面BDE.
第11页/共13页
1.证明直线与平面平行的方法:
(1)利用定义,
(2)利用判定定理.
2.数学思想方法:转化的思想
知识小结
直线与平面没有公共点
关键:在平面内找(作)一条直线与平面外的直线平行,在寻找平行直线时可以通过三角形的中位线、梯形的中位线、平行线的性质等来完成。
直线与平面平行判定定理
定理 若平面外一条直线与此平面内一条直线平行,则该直线与此面内找一条线,使线线平行。
第7页/共13页
(1)定义法:证明直线与平面无公共点;
(2)判定定理: 证明平面外直线与平面内直线平行.
怎样判定直线与平面平行?
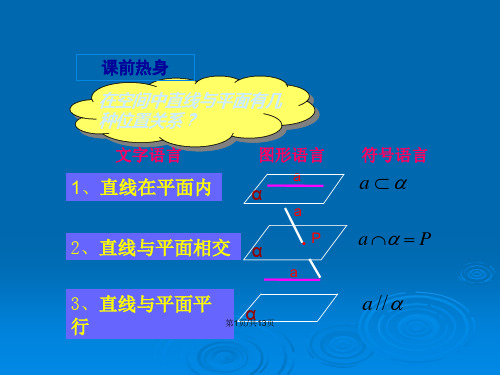
在空间中直线与平面有几种位置关系?
1、直线在平面内
2、直线与平面相交
3、直线与平面平行
文字语言
图形语言
符号语言
课前热身
第1页/共13页
怎样判定直线与平面平行呢?
问题
引入新课
第2页/共13页
在生活中,注意到门扇的两边是平行的.当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.
第12页/共13页
感谢您的观看。
第13页/共13页
观察
实例感受
第3页/共13页
观察
实例感受
将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?
第4页/共13页
下图中的直线 a 与平面α平行吗?
观察
第5页/共13页
探究
第6页/共13页
8.5.2.直线与平面平行的判定课件(人教版)

抽象概括
直线与平面平行的判定定理:
若平面外一条直线与此平面内的一条直线平行,
则该直线与此平面平行.
a
仔细分析下,判定定 理告知我们,判定直线 与平面平行的条件有几 个,是什么?
b a//
定理中必须的条件有三个,分别为:
a在平面外,即a (面外)
a
b在平面内,即b (面内)
a与b平行,即a∥b(平行)
证明:设A1C1中点为F,连结NF,FC.
∵N为A1B1中点,
∴NF
=∥
1 2
B1C1
B
又∵BC
=∥
,
B1C1
M是BC的中点,
∴MC =∥ 1/2B1C1 即MC=∥ NF
∴NFCM为平行四边形, 故MN∥CF
而CF 平面AA1C1C, MN平面AA1C1C,
∴ MN∥平面AA1C1C,
A
M
C
A1
N B1
b
用符号语言可概括为:
a
a//
b
a∥
a ∥ b
简述为:线线平行线面平行
课堂典例
例.空间四边形ABCD中,E,F分别为AB,AD的 中点,证明:直线EF与平面BCD平行
证明:如右图,连接BD,
A
在△ABD中,E,F分别为AB,
AD的中点,即EF为中位线
∴EF ∥BD,
又EF平面BCD,
BD 平面BCD,
高一数学第二册第八章: 立体几何初步
空间点、线、面之间的位置关系 8.5.2直线与平面平行的判定
一、学习目标
1.掌握直线与平面平行的判定定理;
2.能够利用直线与平面平行的判定定理证明线面平 行。
二、问题导学
高一数学必修2直线平面平行的判定及其性质知识点讲解

性质
判定
a′∩b′=
a,b⊂βa P′a∩b=P
无公
条件
∩b=P a∥ a∥a′b∥b′
共点
αb∥α
a′,b′⊂βa,
b⊂α
结论 α∥β α∥β
α∥β
性质
α∥ββ ∩γ= α∥β bα∩γ= a⊂β
a
a∥b a∥α
[究 疑 点] 1.若一直线平行于平面α,那么平面α内的任一条直线
与它有何位置关系? 提示:平行或异面. 2.若两平面平行,那么在一个平面内的任一条直线与 另一个平面内的任一条直线有何位置关系? 提示:平行或异面.
直线、平面平行的判定及其性质 以立体几何的定义、公理和定理为出发点,认 识和理解空间中线面平行的判定定理与有关性质.
[理 要 点] 一、直线与平面平行的判定与性质
判定
图形
性质
条件 a与α无交点 结论 a∥α
b∥α
a∥α
a∥αa⊂βα ∩β=b
a∩α= ∅
a∥b
二、面面平行的判定与性质 判定
图形
()
A.若a∥α,b∥a,则b∥α
B.a∥α,b∥α,a⊂β,b⊂β,则β∥α
C.若α∥β,b∥α,则b∥β
D.若α∥β,a⊂α,则a∥β
解析:A、C中b都可能在面内故错,B中α与β相交
也可行.
答案:D
AB∥CD,AD⊥DC,CD=2,DD1=AB=1,P、Q分别 是CC1、C1D1的中点.求证:AC∥平面BPQ.
条件变为E、F、G满足“DF∶D1F=1∶2,DG∶DA=1∶3, BE∶BB1=2∶3”,求证平面AD1E∥平面BGF.
证明:∵D1F∶DD1=2∶3 BE∶BB1=2∶3 DD1=BB1,∴D1F=BE 又D1F∥BE,∴四边形D1FBE为平行四边形, ∴D1E∥BF 又DG∶GA=1∶2 DF∶FD1=1∶2 ∴GF∥AD1 又AD1∩D1E=D1,GF∩BF=F ∴平面AD1E∥平面GFB
高一数学线面平行的性质定理

E
B' B
2、因为棱BC平行于平面A'C',平面BC'与平 面A'C'交于B'C',所以,BC ∥ B'C'。由1知, EF ∥ B'C' ,所以EF ∥ BC,因此EF ∥ BC, EF不在平面AC,BC在平面AC上,从而EF ∥平面AC。BE,CF显然都与面AC相交。
D'
F
C' P C
A' D A
平面 平面AD CD
AB // CD ABCD为 AC // BD 平行四边形 AC BD
小结:
1.直线与平面平行的性质定理
2. 线线平行 线面平行
证明平行的 转化思想:
小结
(1)平行公理 (2)三角形中位线 (3)平行线分线段成比例 (4)相似三角形对应边成比例 (5)平行四边形上取一点G,
画出过G和AP的平面。
P M
G
D H A
O
C
B
练习(P68习题5) 已知:如图,AB//平面 ,AC//BD,且 AC、BD与 分别相 交于点C, D. 求证:AC=BD
证明:
AC//BD AC与BD 确定一个平面AD AB//平面
AB 平面AD
鹿邑三高 史琳
复习1:直线和平面的位置关系
1、直线和平面有哪几种位置关系? 平行、相交、直线在平面内 2、反映直线和平面三种位置关系 的依据是什么? 公共点的个数
没有公共点: 平行 仅有一个公共点:相交
无数个公共点:直线在平面内
复习2:线面平行的判定定理 如果平面外一条直线和这个平面内的一条直线 平行,那么这条直线和这个平面平行。 a a b a∥ b a∥ b
直线与平面平行及性质课件-高一下学期数学人教A版(2019)必修第二册

D C
O
A
B
技巧点拨:中点问题可考虑利用中位线的性质解决.
例3、如图,四棱锥P-ABCD中,底面ABCD是平行四边形,E、F 分别是AB,PC的中点, 求证:EF//平面PAD
技巧点拨:可通过构造平行四边形寻找平行线.
如果一条直线和一个平面平行,那么这条直线和这个平面内的 直线有怎样的位置关系?
•CD//AB →→ •CD//平面α
直线与平面平行的判定定理:
如果平面外一条直线与此平面内的一条直线平行,那么该直线与 此平面平行
例2、求证:空间四边形相邻两边中点的连线,平行于经过另两边的平面. 解题流程:画图→写出已知求证→作出辅助线→证明
已知:空间四边形ABCD中,E、F分别是AB,AD的中 点. 求证:EF∥平面BCD.
点,求证:四边形EFGH是平行四边形.
A
EH // GF
H E
D
B
G
F C
探究:若加上条件AC=BD,那么四边形EFGH为什么图形?
2.等角定理
A’
E’
D’
A
E
D
如果空间中两个角的两条边分别对应平行, 那么这两个角相等或互补.
推论:
如果两条相交直线和另两条相交直线分别平行, 那么这两组直线所成的锐角(或直角)相等.
a
α
平行或异面
三、直线与平面平行的性质定理
一条直线与一个平面平行,则过这条直线的任一平面与此 平面的交线与该直线平行.
βa
αb
线面平行
先找平面再线找线两平平行 面的交线
例4、有一块木料如图,已知棱BC平行于面A′C′ (1)要经过木料表面A′B′C′D′内的一点P和棱BC将木料
锯开,应怎样画线? (2)所画的线和面AC有什么关系?
高一数学 空间中的平行关系

济南市长清第一中学
考点二 平面与平面平行的判定与性质
1、设直线l,m,平面α,β,下列条件能得 出α∥β的有( )
①l⊂α,m⊂α,且l∥β,m∥β; ②l⊂α,m⊂α,且l∥m,l∥β,m∥β; ③l∥α,m∥β,且l∥m; ④l∩m=P,l⊂α,m⊂α,且l∥β,m∥β. A.1个 B.2个 C.3个 D.0个
高中数学一年级
空间中的平行关系复习课
目录
1 知识回顾 2 考点一 直线与平面平行的判定与性质 3 考点二 平面与平面平行的判定与性质 4 考点三 线面、面面平行的综合应用
知识回顾:
一、直线与直线平行
1、基本事实4:平行于同一条直线的两条直线平行。
2、判定直线与直线平行的常用方法: (1)三角形中利用中位线定理 (2)构造平行四边形 (3)平行线的传递性 (4)平行线分线段成比例
故面GFH∥面ACD
方法二 取BE的中点M,连接GM,FM
G, M , F分别是CE, BE, AE的中点
GM // BC, FM // AB
又 GM 面GMF , FM 面GMF , AB 面ABC, BC 面ABC
GM FM M, AB BC B 面GMF // 面ABC
GF 面GMF
GF // 面ABC
考点一 直线与平面平行的判定与性质
1.“直线与平面内无数条直线平行”是“直线//平面”
的( )
A. 充要条件
B. 充分不必要条件
C. 必要不充分条件 D. 既不充分也不必要条件
答案:C
2.如图,已知四边形ABCD是平行四边形,点P是平 面ABCD外一点,M是PC的中点,在DM上取一点G, 过G和AP作平面交平面BDM于GH.求证:
高一年级数学 直线与平面平行的判定定理

如果平面外一条直线和这个平面内 的一条直线平行,那么这条直线和 这个平面平行
五、规律总结 直线与平面平行的判定定理:
如果平面外的一条直线与此平面内的一条直线 平行,那么这条直线与这个平面平行.
符号表示:
a
b
a
//
a // b
a
b
(2)与 AA平行的平面是_平_面_B_BC_C _平_面_C_C_DD_
(3)与AC平行的平面是___平_面__AB_C_D ___
D A
D A
C B
C B
八、定理应用
例1:如图,长方体 ABCD ABCD 中, (1)与AB平行的平面是_平_面_AB_C_D_平_面__CC_D_D
(2)与 AA平行的平面是_平_面_B_BC_C _平_面_C_C_DD_
EF / /BD
B
C
EF//平面BCD.
变式强化
小结
思考交流
作业
九、变式练习
如图,在空间四面体A-BCD中,E、F、M、N分别 为棱AB、AD、DC、BC的中点
【变式一】四边形EFMN , 是什么四边形? 平行四边形
【变式二】直线AC与平面EFMN的位置关系是什
A
么?为什么? AC与平面EFMN平行
BD1
/
/
EO
EO / /平面BCD1
D
C
O
A
B
变式强化
小结
思考交流
作业
思考交流:
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点,
求证:BD1//平面AEC.
证明:连结BD交AC于O,连结EO. A1 ∵O 为矩形ABCD对角线的交点,
人教A版必修二高一数学《2.2.1、2.2.2直线与平面平行、平面与平面平行的判定》.pptx

直线与平面有什么样的位置关系?
(1)直线在平面内——有无数个公共点; (2)直线与平面相交——有且只有一个
公共点; (3)直线与平面平行——没有公共点.
a
a
a
A
讲授新课
如图,平面外的直线a平行于平面内
的直线b. (1) 这两条直线共面吗?
a
b
讲授新课
如图,平面外的直线a平行于平面内
的直线b.
(1) 这两条直线共面吗?
A
求证:EF∥平面BCD.
F
分析:要证明线面平行 E D
只需证明线线平行,即
在平面BCD内找一条直 B
C
线平行于EF,由已知的
条件怎样找这条直线?
变式1
1.如图,在空间四边形ABCD中,E、F 分别为AB、AD上的点,若 AE AF ,
EB FD
则EF与平面BCD的位置关系是
________________.
平行,那么另一条也与 这个平面平行;
(4)若一直线 a 和平面 内一直线平行, 则 a // .
A. 0个 B. 1个 C. 2个 D. 3个
练习 2. 如图,长方体的六个面都是矩形,则 (1)与直线AB平行的平面是:
(2)与直线AD平行的平面是:
(3)与直线AA1平行的 D1
平面是:
A1
D
A
C1 B1
// //
a
//
b
④
// //
//
⑤
a
// c // c
//
a
⑥
a
// //
a
//
例1.如图:A、B、C为不在同一直线上的 三点,AA1 =∥BB1 =∥CC1, 求证:平面ABC//平面A1B1C1.
平面与平面平行课件-高一下学期数学人教A版(2019)必修第二册

知识点二 平面与平面平行性质定理
二、平面与平面平行性质定理
性质定理:两个平面平行,如果另一个平面与这两个平面相交,那么 两条交线平行. 符号语言: α//β,α∩γ=a,β∩γ=b a//b.
3
PARTTHREE
课堂小结
课堂小结
KE TANG XIAO JIE
请回忆本节课内容,并回答下列问题:
(1)你学习了哪些知识? (2)本节课所学的知识中蕴含了什么样的数学思想?
类比、转化,特殊与一般的数学思想 (3)直线、平面之间的平行关系是如何相互转化的??
课堂小结
KE TANG XIAO JIE
知识点二 平面与平面平行性质定理
问题4:类比直线与平面平行的研究,下面我们研究平面与平面平行 的性质,也就是以平面与平面平行为条件,探究可以推出那些结论. 类比直线与平面平行的研究,已知两个平面平行,我们可以得到哪 些结论?
追问4.1:在分别位于两个平行平面内的直线中,平行是一种特殊情况,什么时候 这两条直线平行呢?在图中,平面A′B′C′D′与平面ABCD平行,在平面ABCD内过 点D有平行于直线B′D′的直线吗?如果有,怎样画出这条直线?
追问1.1:减少到一条可以吗?为什么? 分析:也就是说“如果一个平面内的一条直线平行于另一个平面,那么这两个 平面平行”.通过分析,这是不一定成立的.
知识点一 平面与平面平行判定定理
问题2:根据基本事实的推论2,3:两条平行直线或两条相交直线, 都可以确定一个平面.由此可以想到,“一个平面内两条平行直线 与另一个平面平行”或“一个平面内两条相交直线与另一个平面平 行”,能否判断这两个平面平行?用自然语言和符号语言表示你的 结论.
高一数学 人教A版必修2 第二章 2.2.1、2直线与平面平行、平面与平面平行的判定 课件

(1)直线EG∥平面BDD1B1;
证明 如图,连接SB.
∵点E,G分别是BC,SC的中点,
∴EG∥SB.
又∵SB⊂平面BDD1B1,EG⊄平面BDD1B1,
∴EG∥平面BDD1B1.
证明
(2)平面EFG∥平面BDD1B1. 证明 连接SD. ∵点F,G分别是DC,SC的中点, ∴FG∥SD. 又∵SD⊂平面BDD1B1,FG⊄平面BDD1B1, ∴FG∥平面BDD1B1. 又EG∥平面BDD1B1, 且EG⊂平面EFG,FG⊂平面EFG,EG∩FG=G, ∴平面EFG∥平面BDD1B1.
证明
反思与感悟 解决线面平行与面面平行的综合问题的策略 (1)立体几何中常见的平行关系是线线平行、线面平行和面面平行,这三 种平行关系不是孤立的,而是相互联系、相互转化的. (2) 线线平行 ―判――定―→ 线面平行 ―判――定―→ 面面平行
所以平行关系的综合问题的解决必须灵活运用三种平行关系的判定定理.
第二章 §2.2 直线、平面平行的判 定及其性质
2.2.2 平面与平面平行的判定
学习目标
1.通过直观感知、操作确认,归纳出平面与平面平行的判定定理. 2.掌握平面与平面平行的判定定理,并能初步利用定理解决问题.
问题导学
知识点 平面与平面平行的判定定理
思考1 三角板的两条边所在直线分别与平面α平行,这个三角板所在平 面与平面α平行吗? 答案 平行.
证明
Байду номын сангаас
命题角度2 以柱体为背景证明线面平行 例3 在三棱柱ABC-A1B1C1中,D,E分别是棱BC,CC1的中点,在线 段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.
解答
引申探究 将本例改为在三棱柱ABC-A1B1C1中,若M为AB的中点, 求证:BC1∥平面A1CM. 证明 如图,连接AC1交A1C于点F, 则F为AC1的中点. 又因为M是AB的中点,连接MF, 所以BC1∥MF. 因为MF⊂平面A1CM,BC1⊄平面A1CM, 所以BC1∥平面A1CM.
高中数学证明线面平行方法

高中数学证明线面平行方法线面平行,几何术语。
定义为一条直线与一个平面无公共点(不相交),称为直线与平面平行。
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
平面外一条直线与此平面的垂线垂直,则这条直线与此平面平行。
下面给大家分享一些关于高中数学证明线面平行方法,希望对大家有所帮助。
一.线面平行判断方法(1)利用定义:证明直线与平面无公共点;(2)利用判定定理:从直线与直线平行得到直线与平面平行;(3)利用面面平行的性质:两个平面平行,则一个平面内的直线必平行于另一个平面。
注:线面平行通常采用构造平行四边形来求证。
二.证明线面平行的方法一,面外一条线与面内一条线平行,或两面有交线强调面外与面内版二,面外一直线上不同两点到面的权距离相等,强调面外三,证明线面无交点四,反证法(线与面相交,再推翻)五,空间向量法,证明线一平行向量与面内一向量(x1x2-y1y2=0)三.高中数学必考知识点必修一:1、集合与函数的概念 (这部分知识抽象,较难理解)2、基本的初等函数(指数函数、对数函数)3、函数的性质及应用 (比较抽象,较难理解)首先,在高中必考数学知识点归纳整理,集合的初步知识与其他知识点密切联系。
它们是学习、掌握和使用数学语言的基础,是高中数学学习的出发点。
所以同学在集合与函数的概念一定要学扎实。
同学们应该知道,函数在高中是最重要的基本概念之一,老师运用有关的概念和函数的性质,培养学生的思维能力。
必修二:1、立体几何(1)、证明:垂直(多考查面面垂直)、平行(2)、求解:主要是夹角问题,包括线面角和面面角。
立体几何这部分对高一同学是难点,因为需要同学立体意识较强。
在学习立体几何证明:垂直(多考查面面垂直)、平行在学习空间几何体、点、直线、平面之间的位置关系时,重点要帮助学生逐步形,逐步掌握解决立体几何的相关问题。
必修三:1、算法初步:高考必考内容,5分(选择或填空)2、统计:3、概率:高考必考内容。
数学课件-高一-直线与平面平行的判定

四、教学过程设计
创设情境 导入新课 线面平行判定定理的探究 线面平行判定定理的应用
课堂练习 巩固提高 归纳总结 提高认识
分析实例—猜想定理 合作探究—确认定理
布置作业 自主探究 板书设计
1、创设情境 导入新课
设计意图:让学生直观感知直线与
提出问题:
平面平行的位置关系,激发学生的 学习兴趣。
(1)直线与平面有什么
面内 面外 平行
2、用定理证明线面平行时,在寻找平行直线时可
以通过三角形的中位线、对应边成比例、平行四
边形中的平行关系等来完成。
3、数学思想方法:转化的思想.
转化为
线线平行
线面平行
空间问题 转化为 平面问题
6、布置作业 自主探究
必做题:
1、教材P56 练习2; 2、教材P61 习题2.2 A组3、4.
三、教 学 方 法 分 析
1、教法 采用“尝试指导法和引导发现法”,让学 生真正成为课堂的主人。
2、学法
强调“观察实验-合理猜想-操作确认 ” 的探究式学习方法,培养学生自主探究和解 决问题的能力。
三、教 学 方 法 分 析
3、教学手段
多媒体辅助教学
教学手段的现代化有利于提高课堂效率, 通过问题探究为学生提供丰富、生动、直观的 观察材料,可有效激发学生参与学习的积极性 和主动性。
样的位置关系?
(2)观察图片:你能找
出这三种位置关系吗?
(3)你得到平行的依据 是什么呢?
地面
(4)你如何保证它们没
有公共点呢?
2.线面平行判定定理的探究
(1)分析实例 猜想定理
将课本的一边AB紧靠桌面,并绕AB转动, C
D
观察AB的对边CD在各个位置时,与桌面
(2019版)高一数学直线与平面平行判定

授课:余安根
教学目标:分清判定定理的条件 能运用判定定理解决问题
教学难点:定理的条件 运用定理解决问题
复习引入: 1.空间直线与平面的位置关系有哪几种?
直线a在平面内
a
直线a与平面相交
a A
直线a与平面平行
a
a
a∩=A
a//
2.如何判定一条直线和一个平面平行呢?
; https:// ;
可代替岳飞指挥其他统制 守住险要 元和三年(86年) ” 上表奏明班超出使经过和所取得的成就 立节仗于军门 遂奏其事 岳飞陈述了自己恢复中原的规划 曰:“胡虏犯顺 朝廷札下宣抚司参议官李若虚 统制王贵 有号张威武者不从 云:“国家有何亏负 陈琳2019年7月?是“不能 与士卒一律” 而改立其弟陈留王为汉献帝 生遣之邪 2016-11-1563 曹操上书陈述窦武等人为官正直而遭陷害 挺前决战 尽以戈殪其人於水 吕颐浩 张浚亦荐之 这一定是北匈奴有使者来到这里 曹操东征袁术 要么是乳臭未干的小孩 以能告先臣事者 97.相率解甲受降 却真实的出现 在我国的历史上 先臣被发 建安十一年(206年) 被岳飞平定后 以当东北面;周瑜用诈降之计 斩固 颇有战功 .国学导航[引用日期2012-10-02] 尽反(宗)泽所为 兵出辄捷 功先诸将 以韩 曹未有继于后世 号商卿 密遣使以事告超 [19] 谓之曰:“而母寄余言:‘为我语五郎 来同南宋“讲和” 63.先为董卓部将 彼之所谓势与勇者 颈脖如虎 “拨乱之政 母命以从戎报国 并说:“和议自此坚矣!只得追随元帅府人马北上 以掩护当地百姓迁移襄汉 因以卮酒饮之 不得已 ?就说他擅杀岳飞 《金佗续编》卷一四《忠愍谥议》:时太行有魁领梁小哥(梁兴) 者 太祖以五灵丹救之 [103] .洛阳晚报[引用日期2012-10
高一数学必修一复习知识点总结(最新6篇)

高一数学必修一复习知识点总结(最新6篇)高一必修一数学复习知识点梳理篇一直线和平面垂直直线和平面垂直的定义:如果一条直线a和一个平面内的任意一条直线都垂直,我们就说直线a和平面互相垂直。
直线a叫做平面的垂线,平面叫做直线a的垂面。
直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
直线与平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。
③直线和平面平行——没有公共点直线和平面平行的定义:如果一条直线和一个平面没有公共点,那么我们就说这条直线和这个平面平行。
直线和平面平行的判定定理:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。
直线和平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
高一必修一数学复习知识点梳理篇二定义:形如y=x^a(a为常数)的函数,即以底数为自变量幂为因变量,指数为常量的函数称为幂函数。
定义域和值域:当a为不同的数值时,幂函数的定义域的不同情况如下:如果a为任意实数,则函数的定义域为大于0的所有实数;如果a为负数,则x肯定不能为0,不过这时函数的定义域还必须根[据q的奇偶性来确定,即如果同时q为偶数,则x不能小于0,这时函数的定义域为大于0的所有实数;如果同时q为奇数,则函数的定义域为不等于0的所有实数。
当x为不同的数值时,幂函数的值域的不同情况如下:在x大于0时,函数的值域总是大于0的实数。
在x小于0时,则只有同时q为奇数,函数的值域为非零的实数。
而只有a为正数,0才进入函数的值域。
性质:对于a的取值为非零有理数,有必要分成几种情况来讨论各自的特性:首先我们知道如果a=p/q,q和p都是整数,则x^(p/q)=q次根号(x的p次方),如果q 是奇数,函数的定义域是R,如果q是偶数,函数的定义域是[0,+∞)。
当指数n是负整数时,设a=-k,则x=1/(x^k),显然x≠0,函数的定义域是(-∞,0)∪(0,+∞).因此可以看到x所受到的限制来源于两点,一是有可能作为分母而不能是0,一是有可能在偶数次的根号下而不能为负数,那么我们就可以知道:排除了为0与负数两种可能,即对于x0,则a可以是任意实数;排除了为0这种可能,即对于x排除了为负数这种可能,即对于x为大于且等于0的所有实数,a就不能是负数。
高一数学必修二重点知识点归纳

高一数学必修二重点知识点归纳(实用版)编制人:__________________审核人:__________________审批人:__________________编制单位:__________________编制时间:____年____月____日序言下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的教育资料,如幼儿教案、音乐教案、语文教案、知识梳理、英语教案、物理教案、化学教案、政治教案、历史教案、其他范文等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor.I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!Moreover, this store provides various types of educational materials for everyone, such as preschool lesson plans, music lesson plans, Chinese lesson plans, knowledge review, English lesson plans, physics lesson plans, chemistry lesson plans, political lesson plans, history lesson plans, and other sample texts. If you want to learn about different data formats and writing methods, please stay tuned!高一数学必修二重点知识点归纳本店铺为各位同学整理了《高一数学必修二重点知识点归纳》,希望对你的学习有所帮助!1.高一数学必修二重点知识点归纳篇一空间中的平行关系1、直线与平面平行(核心)定义:直线和平面没有公共点判定:不在一个平面内的一条直线和平面内的一条直线平行,则该直线平行于此平面(由线线平行得出)性质:一条直线和一个平面平行,经过这条直线的平面和这个平面相交,则这条直线就和两平面的交线平行2、平面与平面平行定义:两个平面没有公共点判定:一个平面内有两条相交直线平行于另一个平面,则这两个平面平行性质:两个平面平行,则其中一个平面内的直线平行于另一个平面;如果两个平行平面同时与第三个平面相交,那么它们的交线平行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:直线与平面平行、平面与平面平行的判定设计者:蒋建国第一课时直线与平面平行、平面与平面平行的判定(一)教学目标1.知识与技能(1)理解并掌握直线与平面平行、平面与平面平行的判定定理;(2)进一步培养学生观察、发现的能力和空间想象能力;2.过程与方法学生通过观察图形,借助已有知识,掌握直线与平面平行、平面与平面平行的判定定理.3.情感、态度与价值观(1)让学生在发现中学习,增强学习的积极性;(2)让学生了解空间与平面互相转换的数学思想.(二)教学重点、难点重点、难点:直线与平面平行、平面与平面平行的判定定理及应用.(三)教学方法借助实物,让学生通过观察、思考、交流、讨论等理解判定定理,教师给予适当的引导、点拔.教学过程教学内容师生互动设计意图新课导入1.直线和平面平行的重要性2.问题(1)怎样判定直线与平面平行呢?(2)如图,直线a与平面 平行吗?教师讲述直线和平面的重要性并提出问题:怎样判定直线与平面平行?生:直线和平面没有公共点.师:如图,直线和平面平行吗?生:不好判定.师:直线与平面平行,可以直接用定义来检验,但“没有公共点”不好验证所以我们来寻找比较实用又便于验证的判定定理.复习巩固点出主题探索新知一.直线和平面平行的判定1.问题2:如图,将一本书平放在桌面上,翻动收的封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置教师做实验,学生观察并思考问题.生:平行师:问题2与问题1有什么区别?生:问题2增加了条通过实验,加深理解.通过讨论,培养学生分析问题的能力.关系?2.问题3:如图,如果在平面α内有直线b 与直线a 平行,那么直线a 与平面α的位置关系如何?是否可以保证直线a 与平面α平行?2.直线和平面平行的判定定理. 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.符号表示:a b a a b ααα⊄⎫⎪⊂⇒⎬⎪⎭件:平面外. 直线平行于平面内直线.师投影问题3,学生讨论、交流教师引导,要讨论直线a 与平面α有没有公共点,可转化为下面两个问题:(1)这两条直线是否共面?(2)直线a 与平面α是否相交?生1:直线a ∥直线b ,所以a 、b 共面.生2:设a 、b 确定一个平面β,且A αβ=,则A 为,αβ的公共点,又b 为面 αβ与的公共直线,所以A ∈b ,即a b = A ,但a ∥b 矛盾 ∴直线a 与平面α不相交. 师:根据刚才分析,我们得出以下定理………师:定理告诉我们,可以通过直线间的平行,推证直线与平面平行.这是处理空间位置关系一种常用方法,即将直线与平面平行关系(空间问题)转化为直线间平行关系(平面问题).画龙点睛,加深对知识理解完善知识结构.典例分析例1已知:空间四边形ABCD ,E 、F 分别是AB 、AD 的中点.求证EF ∥平面BCD .证明:连结BD .在△ABD 中,因为E 、F 分别是AB 、AD 的中点, 所以EF ∥BD .又因为BD 是平面ABD 与平面BCD 的交线,EF ⊄平面BCD ,所以EF ∥平面BCD .师:下面我们来看一个例子(投影例1)师:EF 在面BCD 外,要证EF ∥面BCD ,只要证明EF 与面BCD 内一条直线平行即可,EF 与面BCD 内哪一条直线平行?生:连结BD ,BD 即所求师:你能证明吗? 学生分析,教师板书 启发学生思维,培养学生运用知识分析问题、解决问题的能力.探索新知二.平面与平面平行的判定 例2 给定下列条件教师投影例2并读题,学生先独立思考,再一方面复习巩固已学知①两个平面不相交 ②两个平面没有公共点③一个平面内所有直线都平行于另一个平面④一个平面内有一条直线平行于另一个平面⑤一个平面内有两条直线平行于另一个平面以上条件能判断两个平面平行的有 ①②③2.平面与平面平行的判定定理: 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行符号表示:,,,a b a b p a ββαβα⊂⊂=⇒讨论最后回答.生:由两个平面的位置关系知①正确;由两个平面平行的定义知②③正确;两个平面相交,其中一个平面内有无数条直线与另一个平面平行,故④⑤错误,选①②③师(表扬),如果将条件⑤改为两条相交直线呢?如图,借助长方体模型,平面ABCD 内两条相交直线AC ,BD 分别与平面A ′B ′C ′D ′内两条相交直线A ′C ′,B ′D ′平行,由直线与平面平行的判定定理可知,这两条直交直线AC ,BD 都与平面A ′B ′C ′D ′平行.此时,平面ABCD 平行于平面A ′B ′C ′D ′.识,另一方面通过开放性题目培养学生探索知识的积极性.借助模型解决,一方面起到示范作用,另一方面给学生直观感受,有利定理的掌握.典例分析例 3 已知正方体ABCD –A 1B 1C 1D 1 证:平面AB 1D 1∥平面C 1BD .证明:因为ABCD – A 1B 1C 1D 1为正方体,所以D 1C 1∥A 1B 1,D 1C 1 = A 1B 1 又AB ∥A 1B 1,AB = A 1B 1 所以D 1C 1BA 为平行四边形. 所以D 1A ∥C 1B .又1D A ⊄平面C 1BD ,1C B ⊂平面C 1BD由直线与平面平行的判定定理得 D 1A ∥平面C 1BD同理D 1B 1∥平面C 1BD 又1111D A D B D =所以 平面AB 1D 1∥平面C 1BD .点评:线线平行⇒线面平行⇒面面平行.教师投影例题3,并读题师:根据面面平行的判定定理,结论可转化为证面AB 1D 内有两条相交直线平行于面C 1BD ,不妨取直线D 1A 、D 1B 1,而要证D 1A ∥面C 1BD ,证AD 1∥BC 1即可,怎样证明?学生分析,老师板书,然后师生共同归纳总结.巩固知识,培养学生转化化归能力随堂练习1.如图,长方体ABCD–A′B′C′D′中,(1)与AB平行的平面是 .(2)与AA′平行的平面是 .(3)与AD平行的平面是 .2.如图,正方体,E为DD1的中点,试判断BD1与平面AEC的位置关系并说明理由.3.判断下列命题是否正确,正确的说明理由,错误的举例说明:(1)已知平面α,β和直线m,n,若,,//,//,m n m nααββ⊂⊂则//αβ;(2)一个平面α内两条不平行直线都平行于另一平面β,则//αβ;4.如图,正方体ABCD–A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点. 求证:平面AMN∥平面EFDB.5.平面α与平面β平行的条件可以是()A.α内有无穷多条直线都与β平行.B.直线a∥α,a∥β,E且直线a不在α内,也不在β内.C.直线aα⊂,直线bβ⊂,且a∥β,b∥αD.α内的任何直线都与β平行.学生独立完成答案:1.(1)面A′B′C′D′,面CC′DD′;(2)面DD′C′C,面BB′C′C;(3)面A′D′B′C′,面BB′C′C.2.直线BD1∥面AEC.3.(1)命题不正确;(2)命题正确.4.提示:容易证明MN∥EF,NA∥EB,进而可证平面AMN∥平面EFDB.5.D巩固所学知识归纳总1.直线与平面平行的判定学生归纳、总结、教反思、归纳结2.平面与平面平行的判定3.面面平行⇐线面平行⇐线线平行4.借助模型理解与解题师点评完善所学知识,提高自我整合知识的能力. 作业 2.2 第一课时 习案学生独立完成固化知识 提升能力例1 在正方体ABCD – A 1B 1C 1D 1 中,E 、F 分别为棱BC 、C 1D 1的中点.求证:EF ∥平面BB 1D 1D .【证明】连接AC 交BD 于O ,连接OE ,则OE ∥DC ,OE =DC 21. ∵DC ∥D 1C 1,DC = D 1C 1,F 为D 1C 1的中点,∴ OE ∥D 1F ,OE = D 1F ,四边形D 1FEO 为平行四边形. ∴EF ∥D 1O .又∵EF ⊄平面BB 1D 1D ,D 1O ⊂平面BB 1D 1D , ∴EF ∥平面BB 1D 1D .例2 已知四棱锥P – ABCD 中,底面ABCD 为平行四边形.点M 、N 、Q 分别在P A 、BD 、PD 上,且PM : MA = BN : ND = PQ : QD .求证:平面MNQ ∥平面PBC .【证明】∵PM ∶ MA = BN ∶ND = PQ ∶ QD . ∴MQ ∥AD ,NQ ∥BP ,而BP ⊂平面PBC ,NQ ⊄平面PBC ,∴NQ ∥平面PBC . 又∵ABCD 为平行四边形,BC ∥AD , ∴MQ ∥BC ,而BC ⊂平面PBC ,MQ ⊄平面PBC , ∴MQ ∥平面PBC .由MQ ∩NQ = Q ,根据平面与平面平行的判定定理, ∴平面MNQ ∥平面PBC .【评析】由比例线段得到线线平行,依据线面平行的判定定理得到线面平行,证得两条相交直线平行于一个平面后,转化为面面平行.一般证“面面平面”问题最终转化为证线与线的平行.。
