立体几何基础训练

立体几何基础训练：

一、框架

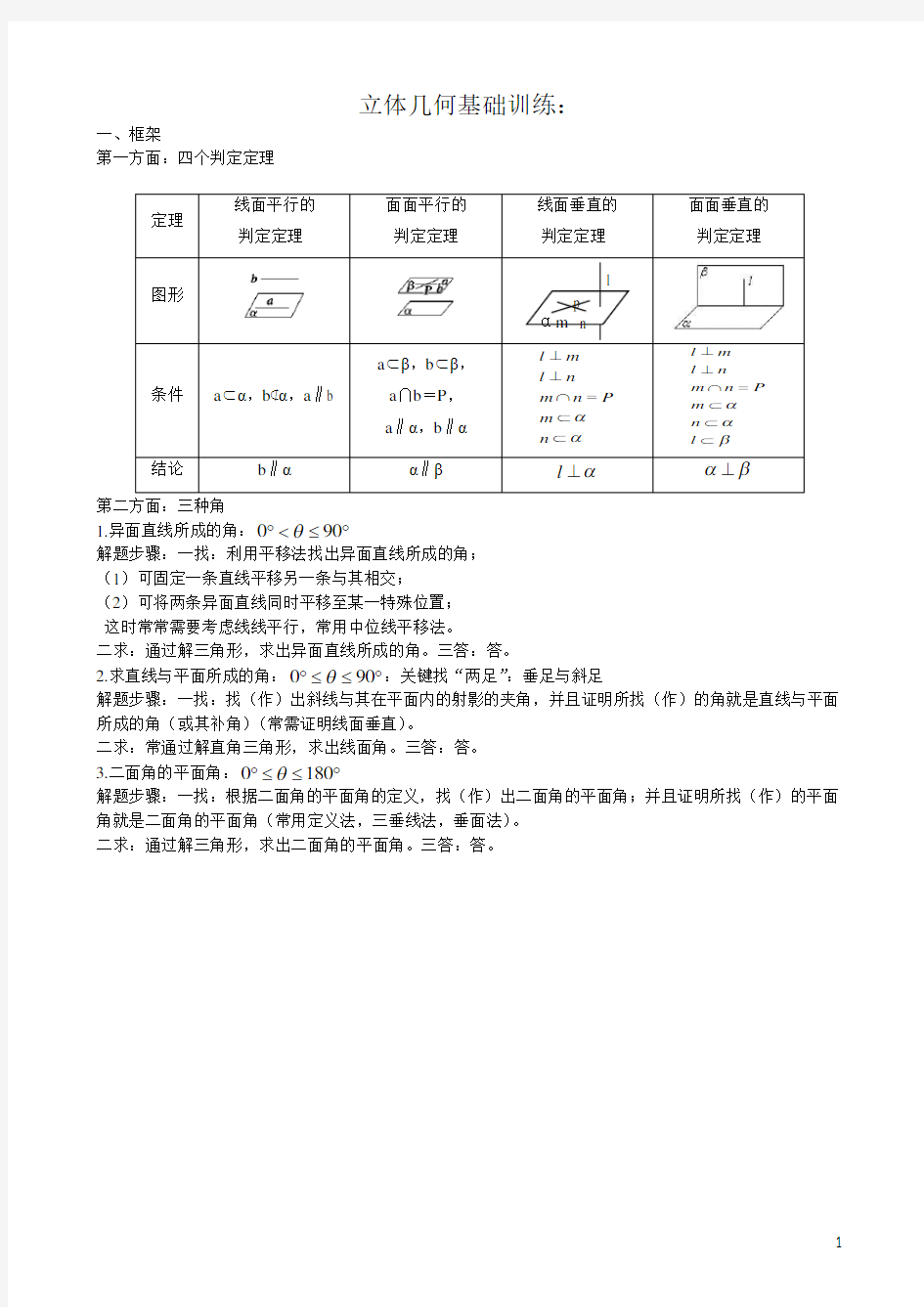
第一方面：四个判定定理

定理

线面平行的 判定定理[来源

面面平行的 判定定理

线面垂直的 判定定理[来源

面面垂直的 判定定理

图形

条件

a ?α，

b ?α，a ∥b

a ?β，

b ?β，

a ∩

b ＝P ， a ∥α，b ∥α

l m l n m n P m n αα

⊥⊥?=?? l m l n m n P m n l ααβ

⊥⊥?=???

结论

b ∥α

α∥β

l α⊥

αβ⊥

第二方面：三种角

1.异面直线所成的角：090θ?<≤?

解题步骤：一找：利用平移法找出异面直线所成的角； （1）可固定一条直线平移另一条与其相交；

（2）可将两条异面直线同时平移至某一特殊位置； 这时常常需要考虑线线平行，常用中位线平移法。

二求：通过解三角形，求出异面直线所成的角。三答：答。 2.求直线与平面所成的角：090θ?≤≤?：关键找“两足”：垂足与斜足

解题步骤：一找：找（作）出斜线与其在平面内的射影的夹角，并且证明所找（作）的角就是直线与平面所成的角（或其补角）（常需证明线面垂直）。

二求：常通过解直角三角形，求出线面角。三答：答。 3.二面角的平面角：0180θ?≤≤?

解题步骤：一找：根据二面角的平面角的定义，找（作）出二面角的平面角；并且证明所找（作）的平面角就是二面角的平面角（常用定义法，三垂线法，垂面法）。 二求：通过解三角形，求出二面角的平面角。三答：答。 l

α m n

p

二、方法诠释

第一方面：简单的证明问题

例1：如图，在三棱柱ABC﹣A1B1C1中，AA1⊥底面ABC，且△ABC为正三角形，AA1=AB=6，D为AC 的中点．

（1）求证：直线AB1∥平面BC1D；

（2）求证：平面BC1D⊥平面ACC1A；

（3）求三棱锥C﹣BC1D的体积．

解：（1）证明：连接B1C交BC1于点O，连接OD，则点O为B1C的中点．

∵D为AC中点，得DO为△AB1C中位线，

∴A1B∥OD．

∵OD?平面AB1C，A1B?平面AB1C，

∴直线AB1∥平面BC1D；

（2）证明：∵AA1⊥底面ABC，

∴AA1⊥BD，

∵底面ABC正三角形，D是AC的中点

∴BD⊥AC

∵AA1∩AC=A，∴BD⊥平面ACC1A1，

∵BD?平面BC1D，∴平面BC1D⊥平面ACC1A；

（3）解：由（2）知，△ABC中，BD⊥AC，BD=BCsin60°=3，

∴S△BCD==，

∴V C﹣BC1D=V C1﹣BCD=??6=9．

例2：如图，直三棱柱ABC －A

1B 1C 1中，D ，E 分别是AB ，BB 1的中点． (1)证明：BC 1∥平面A 1CD ；

(2)设AA 1＝AC ＝CB ＝2，AB ＝22，求三棱锥C －A 1DE 的体积． 【审题视点】

(1)运用直线与平面平行的判定定理进行求解；

(2) 求三棱锥的体积，应先找出三棱锥的高及底面积并求出，然后运用体积公式求解． 【思维流程】

由中点想中位线，找平行线．

列举线面平行条件，得结论．

由垂直关系，确定CD ⊥面ABB 1A 1，即三棱锥C －A 1DE 的高．

计算，求S △ADE 和CD.

计算体积(代入公式)．

【解答过程】 (1)证明：连接AC 1交A 1C 于点F ，则F 为AC 1中点．

又D 是AB 中点，连接DF ，则BC 1∥DF.3分

因为DF ?平面A 1CD ，BC 1?平面A 1CD ，所以BC 1∥平面A 1CD.6分

(2)因为ABC －A 1B 1C 1是直三棱柱，所以AA 1⊥CD. 由已知AC ＝CB ，D 为AB 的中点，所以CD ⊥AB.

又AA 1∩AB ＝A ，于是CD ⊥平面ABB 1A 1.8分

由AA 1＝AC ＝CB ＝2，AB ＝22得

∠ACB ＝90°，CD ＝2，A 1D ＝6，DE ＝3，A 1E ＝3，

故A 1D 2＋DE 2＝A 1E 2，即DE ⊥A 1D.10分

所以V 三棱锥C －A 1DE ＝13×1

2×6×3×2＝1.12分

【规范建议】

(1)证明BC 1∥面A 1CD 的条件有：①BC 1∥DF ，②DF ?面A 1CD ，③BC 1?面A 1CD 缺一不可，应写全面． (2)CD 是三棱锥C －A 1DE 的高，要有证明过程，不能任空想象．

(3)为计算△A 1DE 的面积，需要说明其特征，不能缺少“A 1D 2＋DE 2＝A 1E 2，DE ⊥A 1D ”的内容．

例3.如图，在棱长为1的正方体

1111

ABCD A BC D

-中，E是CD的中点．

（1）求证：

1

AC平面

1

AD E；

（2）在对角线

1

AC上是否存在点P，使得DP⊥平面

1

AD E？

若存在，求出CP的长；若不存在，请说明理由．

解：（1）证明：连结

1

A D，交

1

AD于

点F，连结EF．………………1分

因为四边形

11

ADD A是正方形，所以F是

1

A D的中点，

又E是CD的中点，

所以

1

EF AC．……………………………………………3分

因为EF?平面

1

AD E，

1

AC?平面

1

AD E，……………5分

所以

1

AC平面

1

AD E．………………………………………6分

所以当

3

3

CP=时，DP⊥平面

1

AD E．………………………14分

A B

C

D E

1

A

A

1

B

1

C

A

1

D

A

D

G

F

E

A B C

三、练习巩固 1.如图，在三棱柱ABC EFG -中，侧棱垂直于底面，3=AC ，4=BC ，5=AB ，4=AE ，点D 是AB 的中点．

(1) 求证：BFGC AE 平面//；

(2) 求证：AC BG ⊥；

(3) 求三棱锥DBF C -的体积.

2．如图在四棱锥P ABCD -中，底面ABCD 是菱形，O 是AC ，BD 的交点，PA=PC ，PB=PD ，E 是PC 上一点． 求证：（1）PO ⊥AB ；（2）．平面PAC ⊥平面BDE ．

C 1

B 1

A 1

D

B

A

C

3.如图，长方体ABCD ﹣A 1B 1C 1D 1中，AB=AD=1，AA 1=2，点P 为DD 1的中点． （1）求证：直线BD 1∥平面PAC ；

（2）求证：平面PAC ⊥平面BDD 1B 1； （3）求CP 与平面BDD 1B 1所成的角大小．

4.如图，三棱柱111ABC A B C -中，侧棱垂直底面，∠ACB=90°，

11

2

AC BC AA ==，D 是棱1AA 的中点

（1）证明：平面1BDC ⊥平面BDC ；

（2）平面1BDC 分此棱柱为两部分，求这两部分体积的比

.

5.已知直三棱柱111C B A ABC -的所有棱长都相等，且F E D ,,分别为11,,AA BB BC 的中点. (1) 求证：平面//1FC B 平面EAD ； （2）求证：⊥1BC 平面EAD .

6. 如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，45ADC ∠=?，1AD AC ==，

O 为AC 的中点，PO ⊥平面ABCD ，2PO =，M 为PD 的中点．

（1）证明：//PB 平面ACM ； （2）证明： AD ⊥平面PAC ；

（3）求直线AM 与平面ABCD 所成角的正切值．

D

1

C F

E

B

A

C

1

A 1

B

7.如图，P A ⊥平面ABCD ，ABCD 是矩形，P A ＝AB ＝1，AD ＝3，点F 是PB 的中点，点E 在边BC 上移动．

(1)求三棱锥E —P AD 的体积；

(2)当点E 为BC 的中点时，试判断EF 与平面P AC 的位置关系，并说明理由； (3)证明：无论点E 在边BC 的何处，都有PE ⊥AF .

8.如图，在四棱锥P ABCD -中，PB ⊥底面ABCD ， 底面ABCD 为梯形，BC AD //，AD AB ⊥， 且3,1PB AB AD BC ====． （1）若点F 为PD 上一点且1

3

PF PD =

， 求证：//CF 平面PAB ；

（2）在线段PD 上是否存在一点M ，使得CM PA ⊥? 若存在，求出PM 的长；若不存在，说明理由．

F

A

D

C

B

P

立体几何基础训练答案：

1.（1）证明：∵CG AE //，BFGC CG 平面?BFGC AE 平面?， ∴BFGC AE 平面//

（2）证明：在直三棱柱ABC EFG -中 AC CG ⊥

22291625AC BC AB +=+==

.AC BC ∴⊥G ,C BC C ?=又

.AC GBC ∴⊥面

,GB GBC ?面.AC BG ∴⊥

134324CDB ABC S S ???=

==134 4.33

C DBF F CDB CDB V V S FB --??∴==?== 2.证明：(1)∵PA=PC,PB=P

D ∴PO ⊥AC,PO ⊥BD 又AC ∩BD=O ∴PO ⊥平面ABCD 又AB ?平面ABCD ∴PO ⊥AB （2）∵底面ABCD 是菱形 ∴AC ⊥ BD 又∵PO ⊥BD

AC ∩PO=O ∴BD ⊥平面PAC 又∵BD ?平面BDE ∴平面PAC ⊥平面BDE

3.解：

（2）

长方体ABCD ﹣A 1B 1C 1D 1中，AB=AD=1，底面ABCD 是正方形，则AC ⊥BD ，又DD 1⊥面ABCD ，则DD 1⊥AC ．

∵BD ?平面BDD 1B 1，D 1D ?平面BDD 1B 1，BD ∩D 1D=D ，∴AC ⊥面BDD 1B 1．∵AC ?平面PAC ，∴平面PAC ⊥平面BDD 1B 1 ． （3）由（2）已证：AC ⊥面BDD 1B 1，∴CP 在平面BDD 1B 1内的射影为OP ，∴∠CPO 是CP 与平面BDD 1B 1所成的角． 依题意得

，

，在Rt △CPO 中，

，∴∠CPO=30°

∴CP 与平面BDD 1B 1所成的角为30°． D

G F

E

A

B

C

4.(1) 证明：由题知BC ⊥CC 1，BC ⊥AC ，CC 1∩AC=C ， 所以BC ⊥平面AC C 1A 1，

又DC 1?平面AC C 1A 1，所以DC 1⊥BC. …………（3分）

由题知∠A 1 DC 1=∠A DC=45o ，所以∠CDC 1=90 o ，即DC 1⊥DC ，……………（5分）

又DC∩BC=C ，DC 、BC ?平面BDC ，所以DC 1⊥平面BDC ， 又DC 1?平面BDC 1，故平面BDC 1⊥平面BDC. ………6分 （2）解：设棱锥B —DACC 1的体积为V 1，AC=1，由题意得 V 1 =2

1

1122131=??+?

…9分 又三棱柱ABC —A 1B 1C 1的体积为V=1，所以（V-V 1）:V 1=1:1，

故平面BDC 1分此棱柱为两部分体积的比为1:1. …………………12分 5.【证明】（1）由已知可得1//AF B E ，1AF B E =，

∴四边形E AFB 1是平行四边形，∴1//FB AE ，

AE ?平面FC B 1，1FB ?平面FC B 1， //AE ∴平面FC B 1；

又 E D ,分别是1,BB BC 的中点，∴C B DE 1//， ED ?平面FC B 1，1B C ?平面FC B 1，

//ED ∴平面FC B 1； ,A E D E

E A E =?平面EAD ，ED ?平面EAD ， ∴平面FC B 1∥平面EAD .

(2) 三棱柱111C B A ABC -是直三棱柱，

∴ ⊥C C 1面ABC ，又?AD 面ABC ，∴⊥C C 1AD . 又直三棱柱111C B A ABC -的所有棱长都相等，D 是BC 边中点，

∴ABC ?是正三角形，∴BC AD ⊥， 而1C C BC C =， 1CC ?面11B BCC ，BC ?面11B BCC ，⊥∴AD 面11B BCC ， 故 1AD BC ⊥ . 四边形11BCC B 是菱形，∴C B BC 11⊥， 而C B DE 1//，

故 1DE BC ⊥ , 由D DE AD = AD ?，面EAD ，ED ?面EAD ，得 ⊥1BC 面EAD . 6.解 (1)证明：如图，因为三棱柱111ABC A B C -是直三棱柱，

所以1AE BB ⊥又E 是正三角形ABC 的边BC 的中点，所以AE BC ⊥,因此AE ⊥平面11B BCC .

而AE ?平面AEF ，所以平面AEF ⊥平面11B BCC .

(2)设AB 的中点为D ，连接1A D ，CD .因为ABC 是正三角形，所以CD AB ⊥.又三棱柱111

ABC A B C -是直三棱柱，所以1CD AA ⊥. 因此CD ⊥平面11A ABB ，

于是1CA D ∠为直线1AC 与平面11A ABB 所成的角． 由题设，145CA D ∠=， 所以13

32

A D CD A

B ==

=. 在1Rt AA D 中，2211312A A A D AD =-=-=，

所以11222FC AA ==.故三棱锥F AEC -的体积1

1326

332212

AEC

V S FC =?=??=.

7.解：(1)∵V E —PAD ＝V P —ADE ，又PA ＝1，S △ADE ＝12AD·AB ＝3

2，

∴V E －PAB ＝13PA·S △ADE ＝13×1×32＝3

6

.

(2)当点E 为BC 的中点时，EF 与平面PAC 平行．

∵在△PBC 中，E 、F 分别为BC 、PB 的中点，∴EF ∥PC ， 又EF ?平面PAC ，PC ?平面PAC ，∴EF ∥平面PAC.

(3)证明 ∵PA ⊥平面ABCD ，BC ?平面ABCD ，∴BC ⊥PA ，又BC ⊥AB ，AB ∩PA ＝A ， ∴BC ⊥平面PAB.又AF ?平面PAB ，∴AF ⊥BC. 又PA ＝AB ＝1，点F 是PB 的中点，∴PB ⊥AF ，

又∵PB ∩BC ＝B ，∴AF ⊥平面PBC. 又∵PE ?平面PBC ，∴AF ⊥PE.

8.证明：（1）过点F 作AD FH //，交PA 于H ,连接BH ,…1分

∵13PF PD =， ∴13HF AD BC

==．

又∵AD FH //，AD BC //，∴BC HF //． …2分

∴BCFH 为平行四边形, ∴BH CF //． ……3分 又∵BH ?平面PAB ，CF ?平面PAB , ……4分 ∴//CF 平面PAD ． ………5分 （2）存在点M 为线段PD 的中点，使得PA ⊥CM . …6分 取PA 的中点G ，连接BG ，GM.

∵BP=BA ，G 是PA 的中点，∴PA ⊥BG ，………7分 ∵PB ⊥底面ABCD ，ABCD BC 面?，

∴BC ⊥PB ，又BC AD //，AD AB ⊥，……8分

∴BC ⊥AB ，B PB = AB ，∴PAB 面⊥BC ，PAB 面PA ?，………9分 ∴BC PA ⊥，又PA ⊥BG ，B BG BC = ，

∴BCMG 面PA ⊥，PAB 面MG ?，∴PA ⊥CM ， ……10分 由计算可知，BD=23，PD=33，∴PM=

2

3

3. …12分