SVM习题集

SVM

1.判断题

(1) 在SVM训练好后，我们可以抛弃非支持向量的样本点，仍然可以对新样本进行分类。(T)

(2) SVM对噪声（如来自其他分布的噪声样本）鲁棒。(F)

2．简答题

现有一个点能被正确分类且远离决策边界。如果将该点加入到训练集，为什么SVM的决策边界不受其影响，而已经学好的logistic回归会受影响？

答：因为SVM采用的是hinge loss，当样本点被正确分类且远离决策边界时，SVM给该样本的权重为0，所以加入该样本决策边界不受影响。而logistic回归采用的是log损失，还是会给该样本一个小小的权重。

3．产生式模型和判别式模型。（30分，每小题10分）

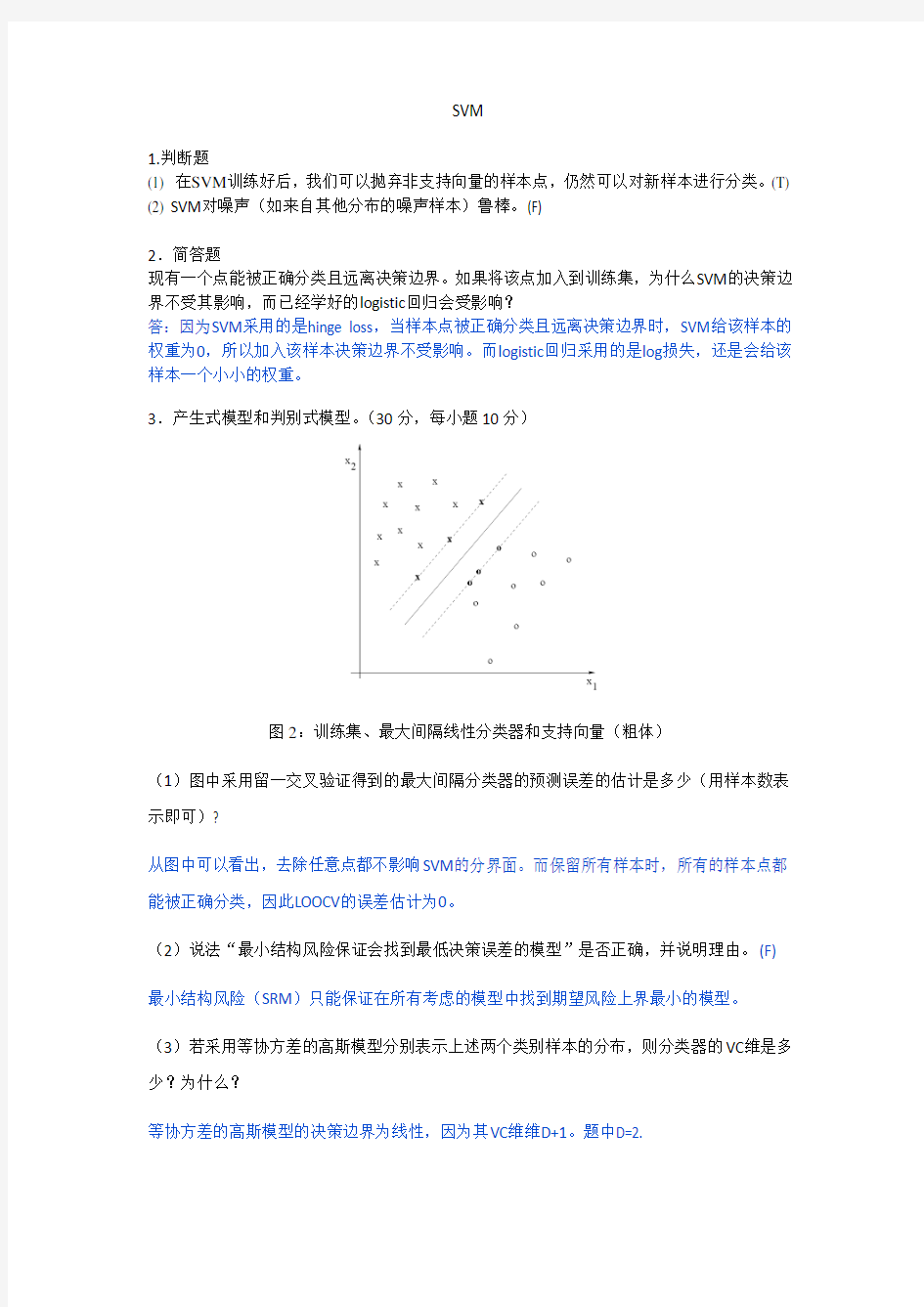
图2：训练集、最大间隔线性分类器和支持向量（粗体）

（1）图中采用留一交叉验证得到的最大间隔分类器的预测误差的估计是多少（用样本数表示即可）?

从图中可以看出，去除任意点都不影响SVM的分界面。而保留所有样本时，所有的样本点都能被正确分类，因此LOOCV的误差估计为0。

（2）说法“最小结构风险保证会找到最低决策误差的模型”是否正确，并说明理由。(F)

最小结构风险（SRM）只能保证在所有考虑的模型中找到期望风险上界最小的模型。

（3）若采用等协方差的高斯模型分别表示上述两个类别样本的分布，则分类器的VC维是多少？为什么？

等协方差的高斯模型的决策边界为线性，因为其VC维维D+1。题中D=2.

4、SVM 分类。（第1~5题各4分，第6题5分，共25分）

下图为采用不同核函数或不同的松弛因子得到的SVM 决策边界。但粗心的实验者忘记记录每个图形对应的模型和参数了。请你帮忙给下面每个模型标出正确的图形。

(1)、211min , s.t.2N

i i C ξ=??+ ?

??

∑w

()00, 1, 1,....,, T i i i y w i N ξξ≥+≥-=w x

其中0.1C =。 线性分类面，C 较小，

正则较大，||w||较小，Margin 较大, 支持向量较多（c ）

(2)、211min , s.t.2N

i i C ξ=??+ ?

??

∑w

()00, 1, 1,....,, T i i i y w i N ξξ≥+≥-=w x

其中1C =。

线性分类面，C 较大，

正则较小，||w||较大，Margin 较小 支持向量的数目少（b ）

(3)、()111

1max ,2N N N

i i j i j i j i i j y y k ααα===??- ???

∑∑∑x x

1

s.t. 0, 1,....,, 0N

i i i i C i N y αα=≤<==∑

其中()()2

,T T k '''=+x x x x x x 。

二次多项式核函数，决策边界为二次曲线 (d)

(4)、()1111max ,2N N N

i i j i j i j i i j y y k ααα===??- ?

??

∑∑∑x x 1

s.t. 0, 1,....,, 0N

i i i i C i N y αα=≤<==∑

其中()21,exp 2k ??''=-- ???

x x x x 。

RBF 核函数，决策边界为曲线, σ=1较大，曲线更平滑 (a)

(5)、()111

1max ,2N N N i i j i j i j i i j y y k ααα===??- ???

∑∑∑x x 1

s.t. 0, 1,....,, 0N

i i i i C i N y αα=≤<==∑

其中()()

2,exp k ''=--x x x x 。 RBF 核函数，决策边界为曲线, σ=sqrt(1/2)较小，曲线更弯曲 (e)

(6)考虑带松弛因子的线性

SVM

分类器：211min , s.t.

2N

i i C ξ=??+ ?

??

∑w ()00, 1, 1,....,, T i i i y w i N ξξ≥+≥-=w x 下面有一些关于某些变量随参数C 的增大而变化的表

述。如果表述总是成立，标示“是”；如果表述总是不成立，标示“否”；如果表述的正确性取决于C 增大的具体情况，标示“不一定”。

(1) 0w 不会增大 （不一定）

(2) ?w 增大

（不一定）

(3) ?w 不会减小

（是）

(4) 会有更多的训练样本被分错（否）

(5) 间隔(Margin)不会增大（是）

5、考虑带松弛因子的线性SVM 分类器：()2

T 011min , s.t. 1, 2N

i i i i i C y w i ξξ=??++≥-? ???

∑w w x 。

在下图中，0.1, 1, 10, 100C =，并且已经标出分界面和支持向量。请给每幅图标出最可能的C 的取值，并分析原因（20分）。

答：

()2

T 01, subject to 1, 2

i i i i i

C y w i ξξ+

+≥-?∑w w x 等价于

()2

T 01, subject to 1, 2i i i i i

y w i C

ξξ+

+≥-?∑w w x 所以2

2

1, ,

C ↑↑↓w w

，即margin 减小(当C 增大到一定程度时，Margin 不再变化)，不

允许错分太多样本（对错分样本的惩罚大），支持向量（落在Margin 内的样本和错分的样本）的数目减少。

6. SVM

(1) 下面的情况，适合用原SVM 求解还是用对偶SVM 求解。 1) 特征变换将特征从D 维变换到无穷维。(对偶)

2) 特征变换将特征从D 维变换到2D 维，训练数据有上亿个并且线性可分。(原)

(2) 在线性可分情况下，在原问题形式化中怎样确定一个样本为支持向量？

在原问题中，给出了w ,w 0，支持向量满足：()

**01T

i i y w x +=w 。

7．SVM 和松弛因子。

考虑如图给出的训练样本，我们采用二次多项式做为核函数，松弛因子为C 。请对下列问题做出定性分析，并用一两句话给出原因。

(1) 当C →∞时，决策边界会变成什么样？

答：当C 很大时，错分样本的惩罚会非常大，因此模型会尽可能将样本分对。（记住这里决策边界为二次曲面）

C →∞ C →0

(2) 当C →0时，决策边界会变成什么样？ 可以错分少量样本，但Margin 大

(3) 你认为上述两种情况，哪个在实际测试时效果会好些？

我们不能过于相信某个特定的样本，因此C →0的效果会好些，因为它最大化样本云团之间的Margin.

(4) 在图中增加一个点，使得当C →∞时，决策边界会不变。

能被原来的分类器正确分类，不会是支持向量。

(5) 在图中增加一个点，使得当C ∞时，该点会显著影响决策边界。

能被原来的分类器正确分类，不会是支持向量。

当C 很大时，错分样本的惩罚会非常大，因此增加一个不能被原来分类器正确分类的样本会影响决策边界。

8．对outlier 的敏感性。

我们知道在SVM 用于回归时，等价于采用ε不敏感的损失函数（如下图所示），即SVM 的目标为：

()()()2,,1

1?min ,2..0,0

N

i i

i i i i i i i i i C s t

y f y f ξξεξεξξξ+-+-

=+-

+-=++≤++≥--≥≥∑w ξξw w x x 。

课堂已经讨论L2损失对outliers 比较敏感，而L1损失和huber 损失相对不敏感些。 (1) 请说明为什么L2损失比较L1损失对outliers 更敏感。

Outlier 为离群点，因此其预测残差r 会比较大。L2损失为残差r 的平方r 2，L1损失为残差r 的绝对值|r|。当r>1时，r 2>|r|，从而L2损失在outliter 样本点的值会非常大，对结果影响更大。

(2) 请给出一个outlier 影响预测子的例子。

(3) 相比于L2损失和L1损失，分析SVM 的ε不敏感的损失函数对outliers 敏感性。

ε不敏感的损失函数对outliers 的敏感性更接近于L1损失，因此比L2损失更不敏感。初看起来，ε不敏感的损失函数在区间[-ε,ε]不施加惩罚，似乎比L1对outliers 更不敏感。但实际上outliers 对应的残差通常很大，所以不会落在区间[-ε,ε]，所以ε不敏感的损失函数对outliers 的敏感性和L1损失相似。

(4) SVM 也等价于MAP 估计，则该MAP 估计对应的先验和似然是什么？

同岭回归类似，先验为0均值得高斯分布，但方差为2C ，同时各维独立，即

()()0,2j

p C =∏w N ，

似然函数在区间[-ε,ε]为常数，其他地方为Laplace 分布：

()()

10

22|,1exp 22T T y p y y otherwise

εεε?

-≤??+=?

?---?+?

w x w x w x

9. 多个数据源的SVM

假设你在两天内用两个不同的仪器收集了两批数据，你觉得数据集1标签的可信度为数据集2的两倍。 我们分别用(){}

1

11

,N i

i

i y ==

x D 表示数据集1，(){}

2

21

,N i

i

i v ==

u D 表示数据集2，数据集1的松弛

因子表示为ξ，数据集2的松弛因子表示ζ，二者的Lagrange 乘子分别表示为α和β。 关于怎样处理这两批数据，你的朋友们给出了不同的建议。 张三：将数据集1的松弛惩罚乘以2，因此优化问题为：

(){}(){}{}{}11

2

,,11

T 01T 02121min 22subject to

1, 1,2.,,,,, 1, 1,2.,,,,,

0, 1,2.,,,,, 0, 1,2.,,,,,

N N i j i j i i i j j j i j C C y w i N v w j N i N j N ξ?ξ?ξ?ξ?==+++≥-?∈+≥-?∈≥?∈≥?∈∑∑w w w x w u

李四：将数据集1的Lagrange 乘子乘以2，因此优化问题为：

{}{}121112

22

1

2

1

1

11

11

11

121

1

1max 22αα,2α,,2subject to

20, 1,2.,,,,, 0, 1,2.,,,,,

20

N N N N N N N N i j i j i j i j i j i j i j

i j i j i j i j i j i j i j i j N N i i

j

j

i j C C y y y v v v c i N c j N y v

αββββαβαβ==========+---≥≥?∈≥≥?∈+=∑∑∑∑∑∑∑∑∑∑α,β

x x x u u u

王五：将数据集1的数据点复制一份（即数据集1中的每个样本点变成2个），然后照常处理。

问题：请说明上述处理是否等价（得到的分界面相同）。

解：我们从张三的建议的对偶表示开始，即

()()()

()()

{}{}12

1

2

12

2

011

T

T

001

1

1

1

121,,,,22 11subject to

1,2.,,,,, 1,2.,,,,,

0, 0, 0N N i j

i j N N N N i i i i i i i i i i i i

i i i i i j i L w C C y w v w e f i N j N e ξ?αξβ?ξ?αβ=======++-+-+-+-+---?∈?∈≥≥≥∑∑∑∑∑∑αβe,f w w w x w u (){}(){}()()T 01T 02T

0T 0, 0

1, 1,2.,,,,, 1, 1,2.,,,,, 0, 0

10,10

j i i i j j j i i j j i i i i j j j j f y w i N v w j N e f y w v w ξ?ξ?αξβ?≥+≥-?∈+≥-?∈==??+-+=????+-+=??w x w u w x w u

优化0,,w e,f w ，目标函数对0,,w e,f w 求导等于0，

12

110N N i i i i i i i i L y v αβ*

==?=?=+?∑∑w x u w ，(1) 1211

000N N i i i i i i L

y v w αβ==?=?+=?∑∑， (2) 02i i i

L

C e αξ?=?=-?， (3) 0i i i

L

C f β??=?=-?， (4) 由于有约束0, 0, 0, 0 i j i j e f αβ≥≥≥≥，公式(3)(4)变成 20, 0,

i j c c αβ≥≥≥≥。

将上述公式代入L ，消除0,,,i j w ξ?w ，得到对偶表示：

(

){}{}1

2

1112

22

1

2

111111

11121

111,αα,α,,22subject to

20, 1,2.,,,,, 0, 1,2.,,,,,

20

N N N N N N N N i j i j i j i j i j i j i j i j i j i j

i j i j i j i j i j N N i i

j

j

i j L C C y y y v v v c i N c j N y v

αββββαβαβ===========+---≥≥?∈≥≥?∈+=∑∑∑∑∑∑∑∑∑∑αβx x x u u u 可以看出，这和下面李四的建议不同。

{}{}1

2

1

1

1

2

22

1

2

1

1

11

11

11

121

1

1max 22αα,2α,,2subject to

20, 1,2.,,,,, 0, 1,2.,,,,,

20

N N N N N N N N i j i j i j i j i j i j i j

i j i j i j i j i j i j i j i j N N i i

j

j

i j C C y y y v v v c i N c j N y v

αββββαβαβ==========+---≥≥?∈≥≥?∈+=∑∑∑∑∑∑∑∑∑∑α,β

x x x u u u 。

王五的建议如下，

111

2

,,111

1min 2N N N i i j i i j C C C ξ?ξξ?===+++∑∑∑w w ，

和张三的建议相同，即张三= 王五。