高等数学 简明二阶微分方程讲义

高等数学简明二阶微分方程讲义
作者:齐睿添
————微分方程的理论帮助了很多工程学,物理学中实际
问题的解决
讨论0. 欧拉公式
欧拉公式在二阶线性齐次常系数方程通解的推导和其非齐次方程的自由项为三角函数时的求解过程中有重要的应用.
讨论1. 二阶常系数线性齐次微分方程
实际问题1.
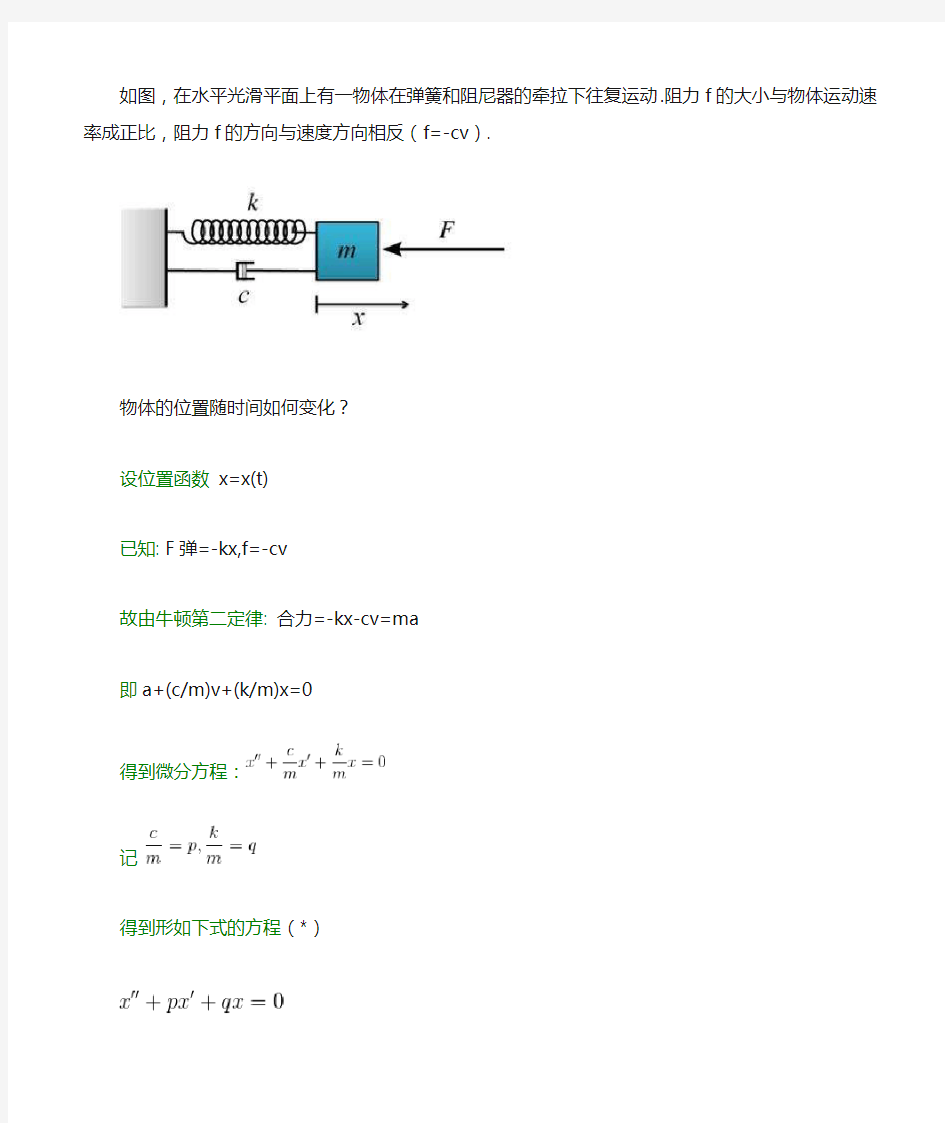
如图,在水平光滑平面上有一物体在弹簧和阻尼器的牵拉下往复运动.阻力f的大小与物体运动速率成正比,阻力f的方向与速度方向相反(f=-cv).
物体的位置随时间如何变化?
设位置函数x=x(t)
已知: F弹=-kx,f=-cv
故由牛顿第二定律: 合力=-kx-cv=ma
即a+(c/m)v+(k/m)x=0
得到微分方程:
记
得到形如下式的方程(*)
这便是一个二阶常系数线性齐次微分方程. 其通解如下表所示:
特征方程
(上表的具体推导与证明详见教材P174-177)
可以发现其通解形式是符合物块运动的直观直觉的.
1)如果阻力很大,弹簧弹性弱,那么物块晃动两下很快就会停止. 这种情况下,列出方程的通解应是表中第一条或者第二条.
例如:取m=1kg, k=3, c=4, 一开始物块位置在+0.5m处, 给予它一个初速度-5 m/s.
我们依照数学习惯将时间(自变量)记为x, 将位置(因变量)记为y. 那么方程为: .
特征方程为,有两个不相等实根
通解为
把初值条件带入
求得
故该例的解为
图像
2)如果阻力很小,弹簧的弹性很强,那么物块将反复往返震荡,幅度随时间越来越小.这种情况下方程通解应是上表第三条.
例如: 取m=1kg,c=3,k=4,一开始物块位置在+0.5m处, 给予它一个初速度-5 m/s.
即为
带入初值条件
C_1=1/2, C_2=-17根号7/14
图像为
讨论2. 更高阶的常系数线性齐次微分方程
(上图出自教材P178)
问题1.
求解
(该问题出自教材P181练习)
问题2.
求解
实系数代数方程的虚根成对(共轭复数根)出现,上面的因式分解说明特征方程有一对2重复根.
通解为
讨论3. 高阶线性微分方程通解的结构
1.二阶微分方程的通解包含2个任意常数C,n阶微分方程的通解包含n个任意常数C.
2.线性相关则是指方程的几个解之间是否满足线性关系,即
ay1+by2+...=0当系数a,b...不全为零时等式可以成立,就称这些解为线性相关.必须全为零时才满足则称为线性无关.对于二阶方程而言,y1/y2或者y2/y1为零就是线性相关;y1/y2或者y2/y1是不为零的某一函数就是线性无关.
3.对于n阶线性齐次方程,如果能够找到n个线性无关的特解,那么
方程通解就是C_1y_1(x)+C_2y_2(x)+...+C_ny_n(x)
4.对于n阶线性非齐次方程,如果能找到它的一个特解y*(x) ,且能够找到其对应的齐次方程的通解Y(x),那么原方程通解就是
Y(x)+y*(x).
5.y1,y2是二阶线性非齐次方程的两个不同的解,那么y1-y2就是其对应二阶线性齐次方程的一个解.
(上述定理的具体证明详见教材P162-166)
线性微分方程的通解结构与其微分算子的线性性有很大关系,有兴趣的同学可以参考《常微分方程(第三版)》(王高雄,朱思铭等著)和其配套的《学习辅导》.
讨论4. 常数变易法解二阶线性微分方程
具体推导公式详见教材P168-171
讨论5. 比较系数法解二阶线性常系数非齐次微分方程根据讨论3的第4条.
对于n阶线性非齐次方程,如果能找到它的一个特解y*(x) ,且能够找到其对应的齐次方程的通解Y(x),那么原方程通解就是
Y(x)+y*(x).
实际问题1.
问题2.
问题3.
问题4.
问题5.
对于二阶线性常系数非齐次微分方程的求解,算子法和拉普拉斯变换法有时也是一种清晰简明的方法,但教材中并未提及,有兴趣的同学可以参考《常微分方程(第三版)》(王高雄,朱思铭等著)和其配套的《学习辅导》.
讨论6. 欧拉方程
讨论7. 可降阶的二阶微分方程问题1.
缺y型
问题2.
缺x型
(完整版)高等数学微分方程试题
第十二章 微分方程 §12-1 微分方程的基本概念 一、判断题 1.y=ce x 2(c 的任意常数)是y '=2x 的特解。 ( ) 2.y=(y '')3是二阶微分方程。 ( ) 3.微分方程的通解包含了所有特解。 ( ) 4.若微分方程的解中含有任意常数,则这个解称为通解。 ( ) 5.微分方程的通解中任意常数的个数等于微分方程的阶数。 ( ) 二、填空题 1. 微分方程.(7x-6y)dx+dy=0的阶数是 。 2. 函数y=3sinx-4cosx 微分方程的解。 3. 积分曲线y=(c 1+c 2x)e x 2中满足y x=0=0, y ' x=0=1的曲线是 。 三、选择题 1.下列方程中 是常微分方程 (A )、x 2+y 2=a 2 (B)、 y+0)(arctan =x e dx d (C)、22x a ??+22y a ??=0 (D ) 、y ''=x 2+y 2 2.下列方程中 是二阶微分方程 (A )(y '')+x 2y '+x 2=0 (B) (y ') 2+3x 2y=x 3 (C) y '''+3y ''+y=0 (D)y '-y 2=sinx 3.微分方程2 2dx y d +w 2 y=0的通解是 其中c.c 1.c 2均为任意常数 (A )y=ccoswx (B)y=c sinwx (C)y=c 1coswx+c 2sinwx (D)y=c coswx+c sinwx 4. C 是任意常数,则微分方程y '=3 23y 的一个特解是 (A )y-=(x+2)3 (B)y=x 3+1 (C) y=(x+c)3 (D)y=c(x+1)3 四、试求以下述函数为通解的微分方程。 1.2 2 C Cx y +=(其中C 为任意常数) 2.x x e C e C y 3221+=(其中21,C C 为任意常数) 五、质量为m 的物体自液面上方高为h 处由静止开始自由落下,已知物体在液体中受的阻力与运动的速度成正比。用微分方程表示物体,在液体中运动速度与时间的关系并写出初始条件。
高数公式大全(全)
高数公式大全 1.基本积分表: 三角函数的有理式积分: 2 22212211cos 12sin u du dx x tg u u u x u u x += =+-=+=, , , 一些初等函数: 两个重要极限: ? ?????????+±+=±+=+=+=+-=?+=?+-==+==C a x x a x dx C shx chxdx C chx shxdx C a a dx a C x ctgxdx x C x dx tgx x C ctgx xdx x dx C tgx xdx x dx x x )ln(ln csc csc sec sec csc sin sec cos 222 22 22 2C a x x a dx C x a x a a x a dx C a x a x a a x dx C a x arctg a x a dx C ctgx x xdx C tgx x xdx C x ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=????????arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 2 2222222? ????++-=-+-+--=-+++++=+-= ==-C a x a x a x dx x a C a x x a a x x dx a x C a x x a a x x dx a x I n n xdx xdx I n n n n arcsin 22ln 22)ln(221 cos sin 22 2222222 2222222 22 2 22 2 ππx x arthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x x x x x x x -+=-+±=++=+-==+= -=----11ln 21)1ln(1ln(:2 :2:22)双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim 0==+=∞→→e x x x x x x
高数下要点含微分方程自己的完整版
高数下要点含微分方程 自己的 HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】
第六章 微分方程 一、一阶微分方程 1、一阶线性方程 )()(x Q y x P dx dy =+ 2、伯努利方程 )1,0()()(d d ≠=+n y x Q y x P x y n ).()(d d 1111x Q y x P x y n n n =+?---令.1n y z -= 二、可降阶的高阶方程 1.)() (x f y n = n 次积分 2.)',("y x f y = 不显含 y 令)('x p y =,化为一阶方程 ),('p x f p =。 3.)',("y y f y = 不显含自变量 令)('y p y =,dy dp p dx y d =22,化为一阶方程。 三、线性微分方程 )()()()(1)1(1)(x f y x a y x a y x a y n n n n =+'+++-- , 0)(≡x f 时称为齐次的,0)(≡/x f 称为非齐次的。
1.二阶线性齐次线性方程 0)()(=+'+''y x Q y x P y (1) 如果函数 )(1x y 与)(2x y 是方程(1)的两个解, 则)()(2211x y C x y C y += 也是(1)的解,其中21,C C 是任意常数。 如果 )(1x y 与)(2x y 是方程(1)的两个线性无关的特解, 则 )()(2211x y C x y C y += (21,C C 是任意常数)是(1)的通解. 两个函数 )(1x y 与)(2x y 线性无关的充要条件为 C x y x y ≡/) () (21(常数) 2.二阶线性非齐次线性方程 设 )(*x y 是二阶线性非齐次线性方程 )()()(x f y x Q y x P y =+'+'' 的一个特解,)(x Y 是它对应的齐次方程(1)的通解,则 )()(*x y x Y y += 是该方程的 通解. 设 )(* 1x y 与)(*2 x y 分别是二阶线性非齐次方程 )()()(1x f y x Q y x P y =+'+'' 与 )()()(2x f y x Q y x P y =+'+'' 的两个特解。则 +)(*1x y )(*2x y 是 的特解。(叠加原理)
高等数学 微分方程
第十二章 微分方程 § 1 微分方程的基本概念 1、由方程x 2-xy+y 2=C 所确定的函数是方程( )的解。 A. (x-2y)y '=2-xy '=2x-y C.(x-2)dx=(2-xy)dy D.(x-2y)dx=(2x-y)dy 2、曲线族y=Cx+C 2 (C 为任意常数) 所满足的微分方程 ( ) 4.微分方程y '=y x 21-写成以 y 为自变量,x 为函数的形式为( ) A.y x 21dx dy -= B.y x 21dy dx -= '=2x-y D. y '=2x-y §2 可分离变量的微分方程 1.方程P(x,y)dx+Q(x,y)dy=0是( ) A.可分离变量的微分方程 一阶微分方程的对称形式, C.不是微分方程 D.不能变成 ) y ,x (P ) y ,x (Q dy dx -= 2、方程xy '-ylny=0的通解为( ) A y=e x B. y=Ce x cx D.y=e x +C 3、方程满足初始条件:y '=e 2x-y , y|x=0=0的特解为( ) A. e y =e 2x +1 2 1 e ln x 2+= C. y=lne 2x +1-ln2 D. e y =21e 2x +C 4、已知y=y(x)在任一点x 处的增量α+?+=?x x 1y y 2 ,且当?x →0时,α是?x 高阶无穷小,y(0)=π,则y(1)=( ) A. 2π B. π C. 4 e π 4e ππ 5、求特解 cosx sinydy=cosy sinxdx , y|x=0=4 π 解:分离变量为tanydy=tanxdx ,即-ln(cosy)=-ln(cosx)-lnC ,cosy=ccosx 代入初始条件:y|x=0= 4π 得:2 2C =特解为:2cosy=cosx 6、求微分方程()2 y x cos y x 2 1cos dx dy +=-+满足y(0)=π的特解。
高等数学微分方程练习题
(一)微分方程的基本概念 微分方程:含未知函数的导数或微分的方程,称为微分方程、 微分方程的阶:微分方程所含未知函数的最高阶导数或微分的阶数称为微分方程的阶数、 1、不就是一阶微分方程. A、正确 B、不正确 2、不就是一阶微分方程. A、正确 B、不正确 一阶线性微分方程:未知函数及其导数都就是一次的微分方程d ()() d y P x y Q x x +=称为一阶 线性微分方程、 微分方程的解:如果一个函数代入微分方程后,方程两边恒等,则称此函数为微分方程的解、通解:如果微分方程的解中所含独立任意常数C的个数等于微分方程的阶数,则此解称为微分方程的通解、 特解:在通解中根据附加条件确定任意常数C的值而得到的解,称为特解、 1、就是微分方程的解. A、正确 B、不正确 2、就是微分方程的解. A、正确 B、不正确 3、就是微分方程的通解. A、正确 B、不正确 4、微分方程的通解就是( ). A、 B、 C、 D、
(二)变量可分离的微分方程:()()dy f x g y dx = 一阶变量可分离的微分方程的解法就是: (1)分离变量:1221()()()()g y f x dy dx g y f x =;(2)两边积分:1221()()()()g y f x dy dx g y f x =?? 左边对y 积分,右边对x 积分,即可得微分方程通解、 1、微分方程 的通解就是( ). A 、 B 、 C 、 D 、 2、微分方程的通解就是( ). A 、 B 、 C 、 D 、 3、微分方程的通解就是( ). A 、 B 、 C 、 D 、 4、微分方程 的通解就是( ). A 、 B 、 C 、 D 、 5、微分方程 的通解就是( ). A 、 B 、 C 、 D 、 6、微分方程的通解( ). A 、 B 、 C 、 D 、 7、微分方程 的通解就是( ). A 、 B 、 C 、 D 、 8、 x y dy e dx -=就是可分离变量的微分方程. A 、正确 B 、不正确
高等数学第九章微分方程试题及答案
第九章 常微分方程 一.变量可分离方程及其推广 1.变量可分离的方程 (1)方程形式: ()()()()0≠=y Q y Q x P dx dy 通解() ()? ?+=C dx x P y Q dy (注:在微分方程求解中,习惯地把不定积分只求出它的一个原函数,而任意 常数另外再加) (2)方程形式:()()()()02211=+dy y N x M dx y N x M 通解()()()() C dy y N y N dx x M x M =+??1221 ()()()0,012≠≠y N x M 2.变量可分离方程的推广形式 (1)齐次方程 ?? ? ??=x y f dx dy 令 u x y =, 则()u f dx du x u dx dy =+= ()c x c x dx u u f du +=+=-?? ||ln 二.一阶线性方程及其推广 1.一阶线性齐次方程 ()0=+y x P dx dy 它也是变量可分离方程,通解()?-=dx x P Ce y ,(c 为任意常数) 2.一阶线性非齐次方程 ()()x Q y x P dx dy =+ 用常数变易法可求出通解公式 令()()?-=dx x P e x C y 代入方程求出()x C 则得 ()()()[] ?+=??-C dx e x Q e y dx x P dx x P 3.伯努利方程 ()()()1,0≠=+ααy x Q y x P dx dy 令α-=1y z 把原方程化为()()()()x Q z x P dx dz αα-=-+11 再按照一阶线性非齐次方程求解。 4.方程: ()()x y P y Q dx dy -=1可化为()()y Q x y P dy dx =+ 以y 为自变量,x 为未知函数 再按照一阶线性非齐次方程求解。 三、可降阶的高阶微分方程
第五章 高等数学(理专) 微分方程试题库1
第五章 微分方程 试题库一 1.填空题 (1) 微分方程0),,,()4(='y y y x F 是 阶微分方程. (2)通过点)1,1(处,且在任意一点),(y x P 处的切线斜率为x 的曲线方程为 . (3) 微分方程054=-'-''y y y 的特征方程为 . (4) 微分方程03='-''y y 的通解为 . (5) 微分方程09=-''y y 的通解为 . (6) 微分方程y x x y -=e d d 的通解为 . (7) 微分方程054=-'+''y y y 的通解为 . (8) 微分方程20yy x '+=的通解为 . (9)微分方程560y y y '''-+=的特征方程为 . (10) 微分方程440y y y '''-+=的通解为 . 2.选择题 (1) 微分方程0))(,,,(24='''y y y x F 的通解中含有的相互独立的任意常数的个数是( ). A.1; B.2; C.3; D.4. (2) 下列微分方程中是可分离变量的微分方程的是( ). A.y xy x y +=d d ; B. y x y xy sin e d d =; C. 2d d y xy x y +=; D. 22d d y x x y +=. (3) 下列微分方程中是一阶线性非齐次微分方程的是( ). A. 2d d y xy x y +=; B.x xy y =+''; C.x xy y =+'; D. 02=+'xy y . (4) 微分方程x y e =''的通解为( ). A. x y e =; B. C y x +=e ; C. Cx y x +=e ; D. 21e C x C y x ++=.
(完整版)高等数学第七章微分方程试题及答案
第七章 常微分方程 一.变量可分离方程及其推广 1.变量可分离的方程 (1)方程形式: ()()()()0≠=y Q y Q x P dx dy 通解() ()? ?+=C dx x P y Q dy (注:在微分方程求解中,习惯地把不定积分只求出它的一个原函数,而任意常数另外再加) (2)方程形式:()()()()02211=+dy y N x M dx y N x M 通解()()()() C dy y N y N dx x M x M =+??1221 ()()()0,012≠≠y N x M 2.变量可分离方程的推广形式 (1)齐次方程 ?? ? ??=x y f dx dy 令 u x y =, 则()u f dx du x u dx dy =+= ()c x c x dx u u f du +=+=-?? ||ln 二.一阶线性方程及其推广 1.一阶线性齐次方程 ()0=+y x P dx dy 它也是变量可分离方程, 通解()?-=dx x P Ce y ,(c 为任意常数) 2.一阶线性非齐次方程 ()()x Q y x P dx dy =+ 用常数变易法可求出通解公式 令()()?-=dx x P e x C y 代入方程求出()x C 则得 ()()()[] ?+=??-C dx e x Q e y dx x P dx x P 3.伯努利方程 ()()()1,0≠=+ααy x Q y x P dx dy 令α -=1y z 把原方程化为()()()()x Q z x P dx dz αα-=-+11 再按照一阶线性 非齐次方程求解。 4.方程: ()()x y P y Q dx dy -=1可化为()()y Q x y P dy dx =+ 以y 为自变量,x 为未知函数 再按照一阶线性非齐次方程求解。
高数(下)要点(含微分方程)——自己整理的
第六章 微分方程 一、一阶微分方程 1、一阶线性方程 )()(x Q y x P dx dy =+ ])([)()(C dx e x Q e y dx x P dx x P +?? =?-通解 2、伯努利方程 )1,0()()(d d ≠=+n y x Q y x P x y n ).()(d d 1111x Q y x P x y n n n =+?---令.1n y z -= 二、可降阶的高阶方程 1.)()(x f y n = n 次积分 2. )',("y x f y = 不显含y 令)('x p y =,化为一阶方程 ),('p x f p =。 3. )',("y y f y = 不显含自变量 令)('y p y =,dy dp p dx y d =22,化为一阶方程。 三、线性微分方程 )()()()(1)1(1)(x f y x a y x a y x a y n n n n =+'+++-- , 0)(≡x f 时称为齐次的,0)(≡/x f 称为非齐次的。 1.二阶线性齐次线性方程 0)()(=+'+''y x Q y x P y (1) 如果函数)(1x y 与)(2x y 是方程(1)的两个解, 则 )()(2211x y C x y C y += 也是(1)的解,其中21,C C 是任意常数。 如果)(1x y 与)(2x y 是方程(1)的两个线性无关的特解, 则 )()(2211x y C x y C y += (21,C C 是任意常数)是(1)的通解. 两个函数)(1x y 与)(2x y 线性无关的充要条件为
C x y x y ≡/) () (21(常数) 2.二阶线性非齐次线性方程 设 )(*x y 是二阶线性非齐次线性方程 )()()(x f y x Q y x P y =+'+'' 的一个特解,)(x Y 是它对应的齐次方程(1)的通解,则 )()(*x y x Y y += 是该方程 的通解. 设)(* 1x y 与 )(*2x y 分别是二阶线性非齐次方程 )()()(1x f y x Q y x P y =+'+'' 与 )()()(2x f y x Q y x P y =+'+'' 的两个特解。则+ )(* 1x y )(* 2x y 是 )()()()(21x f x f y x Q y x P y +=+'+'' 的特解。(叠加原理) 3.二阶线性常系数齐次方程 0'"=++qy py y 特征方程02 =++q pr r ,特征根 ,r r 4.二阶线性常系数非齐次方程 i) 如果 x m e x P x f λ)()(=, 则二阶线性常系数非齐次方程具有形如 x m k e x Q x y λ)(*= 的特解。 其中,)(x P m 是 m 次多项式, )(x Q m 也是系数待定的m 次多项式; 2,1,0=k 依照λ为特征根的重数而取值. i) 如果 []x x P x x P e x f n l x ωωλsin )(cos )()(+=, 则二阶线性常系数非齐次方程的特解可设为 [] x x R x x R e x y m m x k ωωλsin )(cos )() 2()1(*+=
高等数学——微分方程
第八章 常微分方程 一、本章学习要求与内容提要 (一)基本要求 1.了解微分方程和微分方程的阶、解、通解、初始条件与特解等概念. 2.掌握可分离变量的微分方程和一阶线性微分方程的解法. 3.了解二阶线性微分方程解的结构. 4.掌握二阶常系数齐次线性微分方程的解法. 5.会求自由项为x m x P λe )(或x x P x m βαcos e )(,x x P x m βαsin e )(时的二阶常系数非 齐次线性微分方程的解. 6. 知道特殊的高阶微分方程()()(x f y n =,),(y x f y '='',),(y y f y '='')的降阶法. 7.会用微分方程解决一些简单的实际问题. 重点 微分方程的通解与特解等概念,一阶微分方程的分离变量法,一阶线性微分方程的常数变易法,二阶线性微分方程的解的结构,二阶常系数非齐次线性微分方程的待定系数法。 难点 一阶微分方程的分离变量法,一阶线性微分方程的常数变易法,二阶常系数非齐次线性微分方程的待定系数法,高阶微分方程的降阶法,用微分方程解决一些简单的实际问题. (二)内容提要 ⒈ 微分方程的基本概念 ⑴ 微分方程的定义 ①凡是含有未知函数的导数(或微分)的方程,称为微分方程. ②未知函数是一元函数的微分方程称为常微分方程,未知函数是多元函数的微分方程称为偏微分方程.本书只讨论常微分方程,简称微分方程. ⑵ 微分方程的阶、解与通解 微分方程中出现的未知函数最高阶导数的阶数,称为微分方程的阶.如果把函数 )(x f y =代入微分方程后,能使方程成为恒等式,则称该函数为该微分方程的解.若微分方 程的解中含有任意常数,且独立的任意常数的个数与方程的阶数相同,则称这样的解为微分方程的通解. ⑶ 初始条件与特解 用未知函数及其各阶导数在某个特定点的值作为确定通解中任意常数的条件,称为初始条件.满足初始条件的微分方程的解称为该微分方程的特解. ⑷ 独立的任意常数 ①线性相关与线性无关 设)(),(21x y x y 是定义在区间),(b a 内的函数,若存在两个不全为零的数21,k k ,使得对于区间),(b a 内的任一x ,恒有 0)()(2211=+x y k x y k
微分方程总结
第七章 微分方程 1.一阶微分方程 (1)微分方程的基本概念: ①、微分方程:含有未知函数、未知函数的导数即自变量的等式叫做微分方程。未知函数是一元函数,叫做常微分方程;未知函数是多元函数,叫做偏微分方程。 ②、微分方程的阶:微分方程中所出现的未知函数导数的最高阶数,叫做微分方程的阶。 ③、微分方程的解:若某个函数代入微分方程能使该方程成为恒等式,这个函数就叫做该微分方程的解。 ④、微分方程的通解:若微分方程的解中所含相互独立的任意常数的个数与微分方程的阶数相同,这样的解叫做微分方程的通解。 ⑤、微分方程的初始条件、特解:用来确定微分方程通解中任意常数的条件叫做初始条件。确定了通解中任意常数的解称为微分方程的特解。 (2)可分离变量方程:形如)()(dx dy x g x f =的方程称为可分离变量微分方程。设g(y)≠0,则可将方程化为dx )() (dy x f y g ,其特点是方程的一端只含有y 的函数dy ,另一端只含有x 的函数dx ,即将两个变量分离在等式两端,其接法是分离变量后两边积分得到通解。 (3)齐次方程:形如)(y x y f ='的方程称为齐次方程。其解法是做变换x y u =,则y=ux,dx du dx dy x u +=,代入方程化为可分离变量的微分方程。 (4)一阶线性微分方程:形如)()(dx dy x Q y x P =+的方程称为一阶线性微分呢方程,其特点是方程中的未知函数及其导数为一次的。如果0)(≡x Q ,则称为一阶线性齐次微分方程;如果Q(x)不恒等于零 ,则称为一阶线性非齐次微分方程,其通解为 C dx e x Q e y dx x P dx x P +?=??-)()()((。 (5)伯努利方程:形如)1,0()()('≠=+n y x Q y x P y n 的方程称为伯努利方程。次方程的特点是未知函数的导数仍是一次的,但未知函数出现n 次方幂。其解法是做变量替换n y z -=1,则: ,dx dz 11dx dy ,dx dy )1(dx dz 11n y y n n n -=-=--即 代入原方程,得: ),()1()()1(dx dz x Q n z x P n -=-+ 这是一个线性非齐次微分方程,再按线性非齐次微分方程的解法求出通解;最后以n y z -=1换回原变量,即为所求。 2、高阶微分方程,常系数线性微分方程: (1)可降价的高阶微分方程: ①、)()(x f y n =:其特点是右端仅含有自变量x ,通过连续积分n 次得到通解。 ②、)',(''y x f y =:其特点是方程不显含未知函数y 。令'''),('p y x p y ==则,代入原方程化为一阶微分
高等数学微分方程试题汇编
第十二章微分方程 §2-1 微分方程的基本概念 一、 判断题 1. y=ce 2x (c 的任意常数)是y ' =2x 的特解。 ( ) 2. y=( y )3是二阶微分方程。 ( ) 3. 微分方程的通解包含了所有特解。 ( ) 4. 若微分方程的解中含有任意常数,则这个解称为通解。 ( ) 5. 微分方程的通解中任意常数的个数等于微分方程的阶数。 ( ) 二、 填空题 微分方程.(7x-6y)dx+dy=0的阶数是 _______________ 。 2. 函数y=3sinx-4cosx ___________ 微分方程的解。 3. 积分曲线y=(c 1 +c 2x)e 2x 中满足 y x=o =O, y" x=o =1的曲线是 _________________ 。 三、选择题 1. _________________ 下列方程中 是常微分方程 _2 _2 2 2 2 d arctan x 3 '3 2 2 (A )、x+y =a (B)、 y+——(e ) = 0 (C)、—2 +— =0 ( D )、y =x +y dx ex cy 2. _______________ 下列方程中 是二阶微分方程 2 y 2 i-2 2 3 2 (A ) ( y ) +x +x =0 (B) ( y ) +3x y=x (C) y +3 y +y=0 (D) y -y =sinx (A ) y=ccoswx (B)y=c sinwx (C)y=c i coswx+c 2sinwx (D)y=c coswx+c sinwx 2 4. C 是任意常数,则微分方程 y =3y 3的一个特解是 ______________ 3 3 3 3 (A ) y-=(x+2) (B)y=x +1 (C) y=(x+c) (D)y=c(x+1) 四、试求以下述函数为通解的微分方程。 2 2 2x 3x 1. y =Cx C (其中C 为任意常数) 2.y =C i e C 2e (其中C-C ?为任意常数) 五、质量为 m 的物体自液面上方高为 h 处由静止开始自由落下,已知物体在液体中受的阻 力与运 3.微分方程 穿+w2y =0的通解是 ______ 中c.c i.c 2均为任意常数
高等数学基础班常微分方程
第六章 常微分方程 常微分方程是高等数学中理论性和应用性都较强的一部分,是描述客观规律的一种重要方法,是处理物理、力学、几何等应用问题的一个重要工具,微分和积分的知识是研究微分方程的基础。微分方程作为考试的重点内容,每年研究生考试均会考到。特别是微分方程的应用问题,既是重点,也是难点,在复习时必须有所突破。 【大纲内容】常微分方程的基本概念;变量可分离的方程;齐次方程;一阶线性方程;伯努利(Bernoulli )方程;全微分方程;可用简单的变量代换求解的某些微分方程;可降阶的高阶微分方程;线性微分方程解的性质及解的结构定理;二阶常系数齐次线性微分方程;高于二阶的某些常系数齐次线性微分方程;简单的二阶常系数非齐次线性微分方程;欧拉(Euler )方程;微分方程的简单应用。 【大纲要求】要理解微分方程的有关概念,如阶、解、通解、特解、定解条件等,掌握几类方程的解法:如变量可分离方程,齐次方程,一阶线性微分方程,伯努利方程,可降阶方程等。理解线性微分方程解的性质和解的结构,掌握求解常系数齐次线性方程的方法,掌握求解某些自由项的常系数非齐次线性方程的待定系数法。了解欧拉方程的概念,会求简单的欧拉方程。会用微分方程处理物理、力学、几何中的简单问题。 【考点分析】本章包括三个重点内容: 1.常见的一阶、二阶微分方程求通解或特解。求解常微分方程重要的是判断方程为哪种类型,并记住解法的推导过程。 2.微分方程的应用问题,这是一个难点,也是重点。利用微分方程解决实际问题时,若是几何问题,要根据问题的几何特性建立微分方程。若是物理问题,要根据某些物理定律建立微分方程,也有些问题要利用微元法建立微分方程。 3.数学三要求掌握一阶常系数线性差分方程的求解方法,了解差分与差分方程及其通解与特解等概念,会用差分方程求解简单的经济应用问题。 【考点一】形如()()y f x g y '=的一阶微分方程称为变量可分离微分方程。可分离变量的微分方程的解题程序: 当()0,()()()() dy g y y f x g y f x dx g y '≠=?=时,然后左、右两端积分 (),()dy f x dx C g y =+? ?上式即为变量可分离微分方程的通解。其中,C 为任意常数,1()() dy g y g y ?表示函数的一个原函数,()f x dx ?表示函数()f x 的一个原函数. 【例1】若连续函数()f x 满足关系式()20ln 22x t f x f dt ??=+ ????,则()f x 等于 ( ) (A )ln 2.x e (B )2ln 2.x e (C )ln 2.x e +(D )2ln 2.x e + 【例2】已知曲线()()10,,,2y f x x y ? ?=- ??? 过点且其上任一点处的切线斜率为
高等数学题库第06章(常微分方程)
第6章 常微分方程 习题一 一、填空题: 1、 微分方程1sin 2=+''-'''x y y 的阶数为__________。 2、 设某微分方程的通解为()x e x c c y 221+=,且00==x y ,10='=x y 则 ___________1=c ,_____________2=c 。 3、 通解为x ce y =(c 为任意常数)的微分方程是___________。 4、 满足条件()()=+?dx x f x f x 02的微分方程是__________。 5、 y y x 4='得通解为__________。 6、 1+=y dx dy 的满足初始条件()10=y 的特解为__________。 7、 设()n c c c x y y ???=,,,21是微分方程12=+'-'''y y x y 的通解,则任意常数的个数__________=n 。 8、 设曲线()x y y =上任意一点()y x ,的切线垂直于该点与原点的连线,则曲线所满足的微 分方程为___________ 。 二、求下列微分方程满足初始条件的特解: 1、y y x y ln sin =',e y x ==2π 2、()0sin 1cos =-+-ydy e ydx x ,40π==x y 3、y x e y -='2,00==x y 4、xdx y xdy y sin cos cos sin =,40π ==x y 三、求下列微分方程得通解: 1、122 2+='y y y x 2、2211y y x -='- 3、0ln =-'y y y x 4、 by ax e dx dy += 5、022=---'x y y y x 6、x y y dx dy x ln = 四、验证函数x e c x c y 21+=是微分方程()01=-'+''-y y x y x 的通解,并求满足初始条件1,100='-===x x y y 的特解。 五、验证函数2 2x x y -=是微分方程x y y x =-''22的解。
高数知识汇总之微分方程.docx
第六章微分方程 6.1 微分方程的基本概念 微分方程: 含有未知函数的导数(或微分)的等式称为微分方程。 微分方程的阶: 微分方程中,所含未知函数的导数的最高阶数称为微分方程的阶。 微分方程的通解: 如果微分方程的解这中含有任意常数,且任意个不相关的常数的个数与微分方程的阶数相同,这样的解称为微分方程的通解。 微分方程的特解: 在通解中给予任意常数以确定的值而得到的解,称为特解。 初始条件: 用于确定通解中的任意常数而得到特解的条件称为初始条件。 积分曲线: 微分方程的特解的图形是一条曲线,叫做微分方程的积分曲线。 6.2 一阶微分方程的求解方法 6.2.1分离变量法 可分离变量的微分方程: 形如dy f ( x) g ( y) 的微分方程,称为可分离变量的微分方程。dx 特点: 等式右边可以分解成两个函数之积,其中一个是只含有x 的函数,另一个是只含有y 的函数.解法: 当 g( y)0 时,把dy f ( x) g( y) 分离变量为dy f ( x)dx, ( g ( y) 0) 对上式两边积dx g( y) 分,得通解为 dy f ( x)dx C g( y) (这里我们把积分常数 C 明确写出来,而把dy , f ( x)dx 分别理解为 1 和f (x)的g( y)g( y) 一个确定的原函数。) 6.2.2齐次方程和可化为齐次方程的一阶方程不考。 6.2.3一阶线性微分方程 一阶线性微分方程: 如果一阶微分方程 F (x, y, y ) 0 可以写为 y p( x) y q( x) 则称之为一阶线性微分方程,
其中 p(x) 、 q(x) 为连续函数.当q( x)0 时,此方程为dy 0 ,称它为对应于 p(x) y dx 非齐次线性方程的齐次线性微分方程;当 q(x)0 时,称为非齐次线性微分方程。 解法: 用常数变易法可得其通解为: p( x) dx p( x) dx c) y e( q(x)e dx (注:其中每个积分,不再加任意常数C。)6.4可降阶的二阶微分方程 6.4.1不显含未知函数y 的二阶方程:y f ( x, y ) 解法: 令 y p p( x) ,则 y dp dp ,方程变为 dx dx yp( x)dx ,即得通解。 6.4.2不显含自变量 x 的二阶方程 : y f ( y, y )解法: 令 y= p = p( y) ,则y dp p ,方程变为p dp dy dy 解。f ( x, p) f ( y, p) ,解之得p ,再积分得 ,解之得p ,再积分得通 6.5二阶线性微分方程 6.5.1二阶线性微分方程的解的结构 二阶线性微分方程: 形如y p(x) y q( x) y f(x) 的方程,称为二阶线性微分方程。若 f ( x) 0,称之为二阶齐次线性微分方程;若 f ( x)0 ,称之为二阶非齐次线性微分方程。 齐次线性方程解的叠加原理: 如果函数 y1, y2是齐次方程y p( x) y q(x) y 0 的两个解,则y C1 y1C2 y2也是方程 y p(x) y q( x) y0的解 ,其中C ,C均为任意常数。 12 齐次线性方程的通解结构: 如果函数 y1 ( x) , y2 (x) 是齐次方程y p(x) y q(x)y 0的两个线性无关解 ,则函数y C y C y C C y p( x) y q(x) y0
高等数学微分方程试题及答案
第九章 常微分方程 一.变量可分离方程及其推广 1.变量可分离的方程 (1)方程形式: ()()()()0≠=y Q y Q x P dx dy 通解() ()? ?+=C dx x P y Q dy (注:在微分方程求解中,习惯地把不定积分只求出它的一个原函数,而任意 常数另外再加) (2)方程形式:()()()()02211=+dy y N x M dx y N x M 通解()()()() C dy y N y N dx x M x M =+??1221 ()()()0,012≠≠y N x M 2.变量可分离方程的推广形式 (1)齐次方程 ?? ? ??=x y f dx dy 令 u x y =, 则()u f dx du x u dx dy =+= ()c x c x dx u u f du +=+=-?? ||ln 二.一阶线性方程及其推广 1.一阶线性齐次方程 ()0=+y x P dx dy 它也是变量可分离方程,通解()?-=dx x P Ce y ,(c 为任意常数) 2.一阶线性非齐次方程 ()()x Q y x P dx dy =+ 用常数变易法可求出通解公式 令()()?-=dx x P e x C y 代入方程求出()x C 则得 ()()()[] ?+=??-C dx e x Q e y dx x P dx x P 3.伯努利方程 ()()()1,0≠=+ααy x Q y x P dx dy 令α-=1y z 把原方程化为()()()()x Q z x P dx dz αα-=-+11 再按照一阶线性非齐次方程求解。 4.方程: ()()x y P y Q dx dy -=1可化为()()y Q x y P dy dx =+ 以y 为自变量,x 为未知函数 再按照一阶线性非齐次方程求解。 三、可降阶的高阶微分方程
(完整版)高等数学微分方程试题.doc
专业班级学号姓名成绩时间174 第十二章微分方程 §12-1 微分方程的基本概念 一、判断题 1.y=ce 2 x (c 的任意常数 )是y =2x 的特解。( ) 2.y=( y ) 3是二阶微分方程。( ) 3.微分方程的通解包含了所有特解。( ) 4.若微分方程的解中含有任意常数,则这个解称为通解。() 5.微分方程的通解中任意常数的个数等于微分方程的阶数。() 二、填空题 1. 微分方程 .(7x-6y)dx+dy=0 的阶数是。 2. 函数 y=3sinx-4cosx 微分方程的解。 3. 积分曲线 y=(c 1 +c 2 x)e 2 x 中满足 y x=0=0, y x=0=1的曲线是。 三、选择题 1.下列方程中是常微分方程 ( A )、 x2+y 2=a2 d (e arctan x ) 0 (C)、 2 a 2 a =0 ( D)、y =x 2+y 2 (B) 、 y+ 2 + 2 dx x y 2.下列方程中是二阶微分方程 ( A )(y)+x 2 y +x 2=0(B) ( y ) 2+3x 2y=x 3 (C) y +3 y +y=0 (D) y -y2=sinx d 2 y 2 1. 2 3.微分方程 dx2 +w y=0 的通解是其中 c.c c 均为任意常数 ( A )y=ccoswx (B)y=c sinwx (C)y=c 1coswx+c 2sinwx (D)y=c coswx+c sinwx 2 4. C 是任意常数,则微分方程y = 3y3 的一个特解是 ( A )y-=(x+2) 3 (B)y=x 3+1 (C) y=(x+c) 3 (D)y=c(x+1) 3 四、试求以下述函数为通解的微分方程。 1.y Cx2 C 2 (其中 C 为任意常数) 2. y C1e2 x C 2e3x (其中 C1 ,C2 为任意常数) 五、质量为m 的物体自液面上方高为h 处由静止开始自由落下,已知物体在液体中受的阻力与 运动的速度成正比。用微分方程表示物体,在液体中运动速度与时间的关系并写出初始条件。
同济大学(高等数学)-第三篇-常微分方程
第三篇 常微分方程 第六章 常微分方程 函数是研究客观事物运动规律的重要工具,找出函数关系,在实践中有重要意义.但是在许多问题中,常常不能直接找出这种函数关系,但却能根据问题所处的环境,建立起这些变量和它们的导数(或微分)之间的方程,这样的方程称为微分方程. 在本章中,主要介绍常微分方程的基本概念和几种常用的常微分方程的解法. 第一节 微分方程的概念 下面我们通过两个例子来说明常微分方程的基本概念. 1.1 引例 引例1 一曲线通过点(1,2),且在该曲线上任一点),(y x P 处的切线斜率为x 2,求这条曲线方程. 解 设所求曲线方程为()y f x =,且曲线上任意一点的坐标为),(y x .根据题意以及导数的几何意义得 x dx dy 2=. 两边同时积分得 2y x c =+ (c 为任意常数). 又因为曲线通过(1,2)点,把1x =,2y =代入上式,得1=c .故所求曲线方程为 21y x =+. 引例2 将温度为C ο100的物体放入温度为C ο0的介质中冷却,依照冷却定律,冷却的速度与温度T 成正比,求物体的温度T 与时间t 之间的函数关系. 解 依照冷却定律,冷却方程为 kt dt dT -= (k 为比例常数), 所求函数关系满足0t =,100T =. 以上我们仅以几何、物理上引出关于变量之间微分方程的关系. 下面我们介绍有关微分方程基本概念. 1.2 微分方程的基本概念
定义1 含有未知函数以及未知函数的导数(或微分)的方程称为微分方程.在微分方程中,若未知函数为一元函数的微分方程称为常微分方程.若未知函数为多元函数的微分方程称为偏微分方程. 例如 下列微分方程中, (1) 13=-'x y ; (2)sin 0dy y xdx +=; (3)21 ()20y y x '''+ += (4)22221u u x y ??+=??; (5)cos 3dy y x dx +=. 都是微分方程,其中(1)、(2)、(3)、(5)是常微分方程,(4)是偏微分方程. 本课程只讨论常微分方程. 定义2 微分方程中含未知函数的导数的最高阶数称为微分方程的阶. 在上例中,(1)、(2)、(5)是一阶常微分方程,(3)是二阶常微分方程. 一般地,n 阶微分方程记为: 0) , , , ,()(='n y y y x F . 定义3 若将()y f x =代入微分方程中使之恒成立,则称()y f x =是微分方程的解(也称显式解);若将0),(=y x ?代入微分方程中使之恒成立,则称关系式0),(=y x ?是微分方程的隐式解. 定义4 微分方程的解中含有任意常数,并且任意常数的个数与微分方程的阶数相同,这样的解称为微分方程的通解. 引例1中,积分后得到C x y +=2为微分方程的通解,由于通解中含有任意常数,所以它不能完全确定地反映客观事物的规律性,必须确定这些常数,为此,要根据实际问题,提出确定通解中的常数的条件. 设微分方程中未知函数)(x y y =,如果微分方程是一阶的,确定任意常数的条件是 00 y y x x ==;如果微分方程是二阶的确定任意常数的条件是00 y y x x ==,10 y y x x ='=,上述 这些条件叫做初始条件. 定义 5 求解微分方程),(y x f y ='满足初始条件00 y y x x ==的特解问题称为一阶微分 方程的初值问题.记作 ?????=='=00 ) ,(y y y x f y x x . 例1 验证at c at c x sin cos 21+=是微分方程 02=+''x a x 的解.
专插本高等数学例题和习题ch5常微分方程
第五章 常微分方程(简记ODE ) 本章主要知识点 ● 可分离变量的ODE ● 一阶线性非齐次常微分方程及推广 ● 二阶常系数线性齐次与非齐次常微分方程 ● 一些特殊类方程 一、可分离变量的ODE 1.基本型的解法 基本型: ()()dy G x H y dx = 基本解法: ()() dy G x dx H y = ()()dy G x dx H y =?? 例5.1.1)0(,==-y e dx dy y x 解:dx e dy e x y = ??=dx e dy e x y 通解为:c e e x y += 将1,0==y x 得: 1-=e c 得 1-+=e e e x y 例5.2.(1)ln y y y xdx '+= 解:(1)ln y dy xdx y += 1(1)ln dy xdx y +=??, 得:ln ||ln y y x x x C +=-+ 例5.3.dx y x dy y x )1()1(122+=+-
解:dx x x y dy y 2211)1(-=++ ,2(1)1y dy y +=+? 得:( )21arctan ln 12 y y C ++= 例5.4.已知()f x 满足 0()(1)()1x f t dt x f x +-=?,求()f x 。 解:由0()(1)()1x f t dt x f x +-=?知(0)1f =-。方程两边对x 求导得 ()()(1)()0f x f x x f x '++-=,分离变量求得2()(1)c f x x = -, 将(0)1f =-代入得1c =-,21()(1) f x x =- -。 2.可转化的可分离变量的齐次方程 ()x y f y '= 方法:令()y p y p x x y p xp x ''= ?=?=+ x dx p p f dp p f dx dp x p =-?=+?)()(。 例5.5.y x y x dx dy +-= 解:x y x y dx dy +- =11 令p p dx dp x p xp p y px y x y p +-=+?+=?=?=11'', p p p p p p dx dp x +--=-+-=?121112 x dx p p dp p =--+? 221)1( x dx p dp p =+-+??2)1(2)1( C x p p +=---?ln 21ln 2 12, 将x y p =代入即可。 例5.6.dx y x dy x )(2 22+=
