勾股定理有着悠久的历史
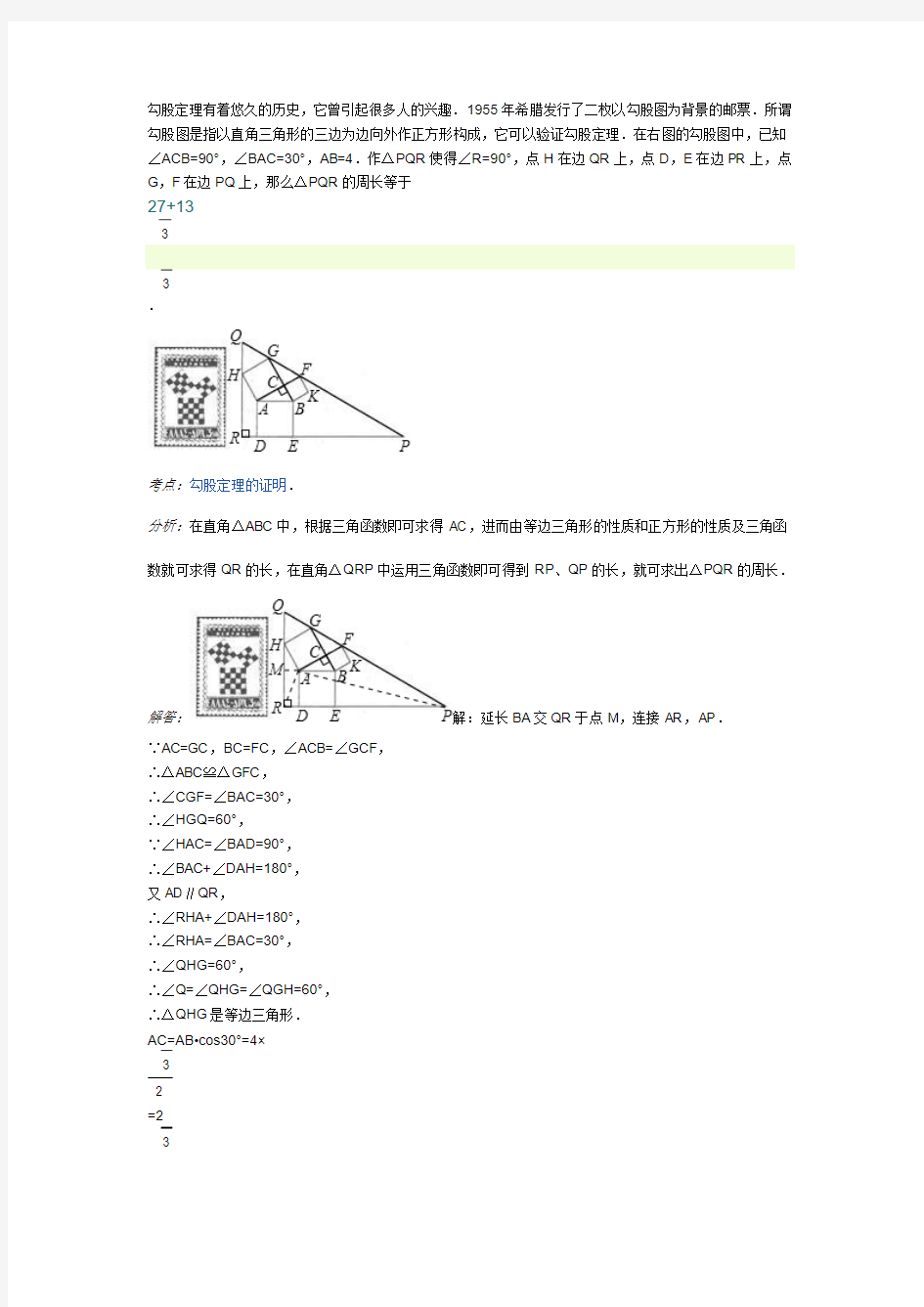

勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在右图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR使得∠R=90°,点H在边QR上,点D,E在边PR上,点G,F在边PQ上,那么△PQR的周长等于
27+13
3
.
考点:勾股定理的证明.
分析:在直角△ABC中,根据三角函数即可求得AC,进而由等边三角形的性质和正方形的性质及三角函数就可求得QR的长,在直角△QRP中运用三角函数即可得到RP、QP的长,就可求出△PQR的周长.
解答:解:延长BA交QR于点M,连接AR,AP.
∵AC=GC,BC=FC,∠ACB=∠GCF,
∴△ABC≌△GFC,
∴∠CGF=∠BAC=30°,
∴∠HGQ=60°,
∵∠HAC=∠BAD=90°,
∴∠BAC+∠DAH=180°,
又AD∥QR,
∴∠RHA+∠DAH=180°,
∴∠RHA=∠BAC=30°,
∴∠QHG=60°,
∴∠Q=∠QHG=∠QGH=60°,
∴△QHG是等边三角形.
AC=AB?cos30°=4×
3
2
3
.
则QH=HA=HG=AC=2
3
.
在直角△HMA中,HM=AH?sin60°=2
3
3
2
3
.
在直角△AMR中,MR=AD=AB=4.
∴QR=2
3
3
.
∴QP=2QR=14+4
3
.
PR=QR?
3
+6.
∴△PQR的周长等于RP+QP+QR=27+13
3
.
故答案为:27+13
3
.
点评:正确运用三角函数以及勾股定理是解决本题的关键.
(完整word版)中国悠久的相机发展历史
中国悠久的相机发展历史 相机,那肯定是个好东西,自从有了相机,我们的快乐、悲伤就能随时随地地定格在张张小纸片上,甚至在电脑上,在网络上。我国的照相机有过一段灿烂的历史。传统照相机工业在我国的发展,至今已经有60年的历史。让我们回到那一段历史中去,一起感受我国相机60年的足迹。 一、诞生:1955年-1960年 关键词:大跃进 严格来说,我国的照相机技术可以追溯到遥远的宋代或者更遥远的春秋战国时期,因为早在公元前四百多年,我国的《墨经》一书就详细记载了光的直线前进、光的反射,以及平面镜、凹面镜、凸面镜的成像现象。到了宋代,在沈括所著的《梦溪笔谈》一书中,还详细叙述了“小孔成像匣”的原理。中华民国时期虽然曾有“仙乐”的昙花一现,可是真正的起步却到了二十世纪五十年代中期。 产品搜索一:仙乐(SELO)牌照相机 说到仙乐,不能不提中国照相机工业第一人——郑崇兰先生,同时还有他的一句话“我开照相馆以后,发觉所用器材都是从外国进口,我想这些东西我们自己也可以做,何必要买外国货。”正是他的人,他的话,为我国照相机工业的建立奠定了信念上的基础——国货当自强
(郑崇兰和仙乐)
(至今国内仅存的一台“仙乐”,正面视图)
(“仙乐”俯视图) 产品搜索二:大来(也有称“大莱”)牌照相机 “大来”照相机是新中国第二台由照相机生产企业生产的相机,据说效果不错,在当年惹来了《工人曰报》与《北京曰报》的长篇报道。 (当年《工人曰报》对“大来”生产的报道)
(“大来”的“后代”——“天坛”) 产品搜索三:七一牌照相机(幸福I型) “七一” 牌照相机是我国第一台自己制造的折叠式照相机,也就是业内称的120照相机,于1956年7月1曰作为党庆礼物试制成功,但是没有对外发售,是一台标准小型折叠式相机。除了镜头用的光学玻璃以外,所有四百八十多个零件,都是用国产原料做的。 (“七一”的后身——“幸福I型”) 产品搜索四:上海58-I型照相机、上海58-II型相机
勾股定理的发现和证明-
勾股定理的发现和证明 中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话: 周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地得到数据呢?” 商高回答说:“数的产生来源于对方和圆这些形体饿认识。其中有一条原理:当直角三角形‘矩’得到的一条直角边‘勾’等于3,另一条直角边‘股’等于4的时候,那么它的斜边‘弦’就必定是5。这个原理是大禹在治水的时候就总结出来的呵。” 从上面所引的这段对话中,我们可以清楚地看到,我国古代的人民早在几千年以前就已经发现并应用勾股定理这一重要懂得数学原理了。稍懂平面几何饿读者都知道,所谓勾股定理,就是指在直角三角形中,两条直角边的平方和等于斜边的平方。如图所示,我们 图1 直角三角形 用勾(a)和股(b)分别表示直角三角形得到两条直角边,用弦(c)来表示斜边,则可得: 勾2+股2=弦2 亦即: a2+b2=c2
勾股定理在西方被称为毕达哥拉斯定理,相传是古希腊数学家兼哲学家毕达哥拉斯于公元前550年首先发现的。其实,我国古代得到人民对这一数学定理的发现和应用,远比毕达哥拉斯早得多。如果说大禹治水因年代久远而无法确切考证的话,那么周公与商高的对话则可以确定在公元前1100年左右的西周时期,比毕达哥拉斯要早了五百多年。其中所说的勾3股4弦5,正是勾股定理的一个应用特例(32+42=52)。所以现在数学界把它称为勾股定理,应该是非常恰当的。 在稍后一点的《九章算术一书》中,勾股定理得到了更加规范的一般性表达。书中的《勾股章》说;“把勾和股分别自乘,然后把它们的积加起来,再进行开方,便可以得到弦。”把这段话列成算式,即为: 弦=(勾2+股2)(1/2) 亦即: c=(a2+b2)(1/2) 中国古代的数学家们不仅很早就发现并应用勾股定理,而且很早就尝试对勾股定理作理论的证明。最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽。赵爽创制了一幅“勾股圆方图”,用形数结合得到方法,给出了勾股定理的详细证明。在这幅“勾股圆方图”中,以弦为边长得到正方形ABDE是由4个相等的直角三角形再加上中间的那个小正方形组成的。每个直角三角形的面积为ab/2;中间懂得小正方形边长为b-a,则面积为(b-a)2。于是便可得如下的式子: 4×(ab/2)+(b-a)2=c2 化简后便可得: a2+b2=c2 亦即: c=(a2+b2)(1/2)
《勾股定理》典型例题
《勾股定理》典型例题 例1 在两千多年前我国古算术上记载有“勾三股四弦五”.你知道它的意思吗? 它的意思是说:如果一个直角三角形的两条直角边长分别为3和4个长度单位,那么它的斜边的长一定是5个长度单位,而且3、4、5这三个数有这样的关系:32+42=52. (1)请你动动脑筋,能否验证这个事实呢?该如何考虑呢? (2)请你观察下列图形,直角三角形ABC 的两条直角边的长分别为AC =7,BC =4,请你研究这个直角三角形的斜边AB 的长的平方是否等于42+72? 解: (1)边长的平方即以此边长为边的正方 形的面积,故可通过面积验证.分别以这个直 角三角形的三边为边向外做正方形,如右 图:AC =4,BC =3, S 正方形ABED =S 正方形FCGH -4S Rt △ABC =(3+4)2-4×2 1×3×4=72-24=25 即AB 2=25,又AC =4,BC =3, AC 2+BC 2=42+32=25 ∴AB 2=AC 2+BC 2 (2)如图(图见题干中图)
S 正方形ABED =S 正方形KLCJ -4S Rt △ABC =(4+7)2-4×2 1×4×7=121-56=65=42+72 例2 下图甲是任意一个直角三角形ABC ,它的两条直角边的边长分别为a 、b ,斜边长为c .如图乙、丙那样分别取四个与直角三角形ABC 全等的三角形,放在边长为a +b 的正方形内. ①图乙和图丙中(1)(2)(3)是否为正方形?为什么? ②图中(1)(2)(3)的面积分别是多少? ③图中(1)(2)的面积之和是多少? ④图中(1)(2)的面积之和与正方形(3)的面积有什么关系?为什么? 由此你能得到关于直角三角形三边长的关系吗? 解: ①图乙、图丙中(1)(2)(3)都是正方形.易得(1)是以a 为边长的正方形, (2)是以b 为边长的正方形,(3)的四条边长都是c ,且每个角都是直角,所以(3)是以c 为边长的正方形. ②图中(1)的面积为a 2,(2)的面积为b 2,(3)的面积为c 2. ③图中(1)(2)面积之和为a 2+b 2. ④图中(1)(2)面积之和等于(3)的面积. 因为图乙、图丙都是以a +b 为边长的正方形,它们面积相等,(1)(2)的面
中国是一个具有悠久历史和灿烂文化的文明古国
中国是一个具有悠久历史和灿烂文化的文明古国。中国画的历史源远流长,为世界创造了举世公认的辉煌艺术成就。从现存的原始社会的岩画和彩陶上已经充分地证明了这一点。中国画成熟于秦汉时期,隋唐时期发展成为具有多种门类的综合性绘画,宋元时期达到鼎盛。中国画概括明确追求内在的精神气韵,具有诗、书、画、印四位一体的美,追求以黑白为主的色彩方法,以线造型的笔墨观,以及打破时空局限的透视方法等特征,体现出中国绘画有别于西方绘画的独特风格。中国画的艺术特征在世界上是独一无二的,它集中体现出东方美学思想。其中,儒、道、释哲学思想是形成和孕育其艺术特征的精神家园。 一、儒家“天人合一”思想在中国画中的体现。 在中西绘画中都强调绘画的风格特点和独特个性,它是作品的艺术生命力。我们认为,一切优秀的艺术作品都是内容和形式的完美、和谐的统一。然而当前西方在现代文化思潮的影响下,艺术作品片面追求形式,强调极端的个性解放,许多荒诞离奇、标新立异的作品充斥于艺术创作中,完全背离了西方传统绘画的传统,给社会带来诸多负面的影响。在如何对待传统与创新的问题上,中西绘画有着不同的状况。中国画虽然经历了数千年的历史变迁,仍然日新月异、枝繁叶茂,不断稳步发展,并没有出现“无度”的发展变化,主要原因在于受到儒家思想的影响和规范。自汉代董仲舒提倡“罢黜百家,独尊儒术”以来,儒家哲学一直是统治阶层治国安邦的正统哲学思想。在汉代,中国画开始走向成熟,它自然地受到儒家思想的深刻影响。儒家思想是一种注重仁学,主张爱人,强调“修身、齐家、治国、平天下”的伦理政治学思想,是一种能使分裂混乱的社会环境有效地秩序化与和谐化的思想。孔子讲:“志于道,据于德,依于仁,游于艺。” 实践证明,在中国一切艺术创作都无不受到伦理道德规范的影响,中国画所表现的内容和形式同样要具有“成教化、助人伦”的教化功能。首先,中国画强调画家后天的学识修养,主张“读万卷书,行万里路”,通过学习、体验来弥补先天的不足,以使在有效继承传统文化的基础上更好地发展,这是一种蕴含着社会使命感和责任感的理想要求。具体表现在,旧文人画家的作品虽然也有消极避世的成分,但内容大都是健康向上催人奋进的。比如,文人常画“四君子”,竹象征虚心劲节,梅象征凌寒傲雪,兰象征虚怀若谷,菊象征岁寒不凋,表现出文人的审美理想,借以自喻和启迪人们的高尚情操。在创作中,由于受到儒家“质胜文则野,文胜质则史。文质彬彬,然后君子” 的影响从而有效地把内容和形式有机统一起来,形成完美的整体。在中国画中,画家通过描写对象来达到“缘物寄情”的目的,把对象之形神与画家之性情内在地结合起来,从而达到“天人合一”的理想境界。另外,中国画还特别提出了人品的重要性,认为“人品不高,画品亦不高”,“人品第一,画品第二”,就是说,只有品德高尚的人才能画出高雅纯正的作品来,才能受到后人的喜爱,相反,人品低劣的人纵有高超的技艺也为人唾弃,如蔡京、秦桧、张瑞图等人的作品就为仁人志士所不齿,而颜真卿、岳飞、八大山人、梅兰芳、齐白石等因其德艺双馨而被广为传颂。同时,历代画家中也不乏热爱生活、关注民生的大家,如郑板桥在其画竹石轴上题诗云:“衙斋卧听萧萧竹,疑是民间疾苦声,些小吾曹州县吏,一枝一叶总关情”。便表现出一个旧文人对劳动人民的深切关注!而八大山人画中冷眼看清天的个性化的“鸟”,也是他仇视统治者的自我写照。由此可见,内蕴着德行、学识、修养的中国画,
常见的勾股数及公式
常见的勾股数及公式 武安市黄冈实验学校 翟升华搜集整理 我们知道,如果∠C=90°,a 、b 、c 是直角三角形的三边,则由勾股定理,得a 2+b 2=c 2;反之,若三角形的三边 a 、 b 、 c 满足a 2+b 2=c 2,则该三角形是直角三角形,c 为斜边.与此相类似,如果三个正整数a 、b 、c 满足a 2+b 2=c 2,则称a 、b 、c 为勾股数,记为(a ,b ,c ).勾股数有无数多组,下面向同学们介绍几种: 一、三数为连续整数的勾股数 (3,4, 5)是我们所熟悉的一组三数为连续整数的勾股数,除此之外是否还有第二组或更多组呢? 设三数为连续整数的勾股数组为(x -1,x ,x +1),则由勾股数的定义,得(x+1)2+x 2=(x+1)2,解得x = 4或x =0(舍去),故三数为连续整数的勾股数只有一组(3,4,5);类似有3n,4n,5n (n 是正整数)都是勾股数 。 二、后两数为连续整数的勾股数 易知:(5,12,13),(9,40,41),(113,6338,6385),…,都是勾股数,如此许许多多的后两数为连续整数的勾股数,它的一般形式究竟是什么呢? a=2n+1,b=2n 2+2n,c=2n 2+2n+1(其特点是斜边与其中一股的差为1). 分别取n =1,2,3,…就得勾股数组(3,4,5),(5,12,13),(7,24,25),… 三、前两数为连续整数的勾股数 你知道(20,21,29),(119,120,169),(4059,4060,5741)…,这些都是前两数为连续整数的勾股数组。其公式为:(x ,x +1,1222++x x )(x 为正整数)。 设前两数为连续整数的勾股数组为(x ,x +1,y ),y=1222++x x 则()22 21y x x =++(*) 整理,得1222++x x =2y ,化为()121222-=-+y x ,即()y x 212++() y x 212-+=-1, 又()()2121-+=-1,∴()122 1++n ()1221+-n =-1(n∈N), 故取()y x 212++=()1221++n ,()y x 212-+=()1 221+-n , 解之,得x =41〔()1221++n +()1221+-n -2〕,y =42〔()1221++n -()1221+-n 〕, 故前两数为连续整数的勾股数组是(4 1〔()1221++n +()1221+-n -2〕,41〔()1221++n +()1221+-n -2〕+1,42〔()1221++n -()1221+-n 〕). 四、后两数为连续奇数的勾股数 如(8,15,17), (12,35,37) …其公式为:4(n+1),4(n+1)2-1,4(n+1)2+1(n 是正整数) . 五、其它的勾股数组公式: 1.a=2m,b=m 2-1,c=m 2+1(m 大于1的整数). 2.a=21(m 2-n 2),b=mn,c= 21(m 2+n 2 )(其中m>n 且是互质的奇数). 3.a=2m,b=m 2-n 2,c=m 2+n 2(m>n,互质且一奇一偶的任意正整数). 下面我们把100以内的勾股数组列出来,供同学们参考: 3 4 5;5 12 13;6 8 10;7 24 25;8 15 17;9 12 15;9 40 41;10 24 26;11 60 61;12 16 20; 12 35 37;13 84 85;14 48 50;15 20 25;15 36 39;15 112 113;16 30 34;16 63 65 17 144 145;18 24 30;18 80 82;19 180 181;20 21 29;20 48 52;20 99 101;21 28 35 21 72 75;21 220 221;22 120 122;23 264 265;24 32 40;24 45 51;24 70 74;24 143 145
勾股定理和历史
勾股定理的历史 勾股定理是“人类最伟大的十个科学发现之一”,是初等几何中的一个基本定理。那么大家知道多少勾股定理的别称呢?我可以告诉大家,有:毕达哥拉斯定理, 商高定理,百牛定理,驴桥定理和埃及三角形等。所谓勾股定理,就是 指“在直角三角形中,两条直角边的平方和等于斜边的平方。”这个 定理有十分悠久的历史,几乎所有文明古国(希腊、中国、埃及、巴比 伦、印度等)对此定理都有所研究。勾股定理在西方被称为毕达哥拉斯 定理,相传是古希腊数学家兼哲学家毕达哥拉斯(Pythagoras,公元前 572?~公元前497?)于公元前550年首先发现的。但毕达哥拉斯对勾 股定理的证明方法已经失传。著名的希腊数学家欧几里得(Euclid,公元前330~公元前275)在巨著《几何原本》(第Ⅰ卷,命题47)中给出一个很好的证明。(右图为欧几里得和他的证明图) 中国古代对这一数学定理的发现和应用,远比毕达哥拉斯早得多。中国最早的一部数学著作——《周髀算经》的开头,记载着一段周公向商高请教数学知识的对话:周公问:“我听说您对数学非常精通,我想请教一下:天没有梯子可以上去,地也没法用尺子去一段一段丈量,那么怎样才能得到关于天地得到数据呢?”商高回答说:“数的产生来源于对方和圆这些形体的认识。其中有一条原理:当直角三角形‘矩'得到的一条直角边‘勾'等于3,另一条直角边’股'等于4的时候,那么它的斜边'弦'就必定是5。这个原理是大禹在治水的时候就总 结出来的呵。”如果说大禹治水因年代久远而无法确切考证的话,那么周 公与商高的对话则可以确定在公元前1100年左右的西周时期,比毕达哥拉 斯要早了五百多年。其中所说的勾3股4弦5,正是勾股定理的一个应用特 例。所以现在数学界把它称为“勾股定理”是非常恰当的。
(完整版)勾股定理典型例题详解及练习(附答案)
典型例题 知识点一、直接应用勾股定理或勾股定理逆定理 例1:如图,在单位正方形组成的网格图中标有AB CD EF、GH四条线段, 其中能构成一个直角三角形三边的线段是() A.CD、EF、 GH C. AB、CD GH B.AB、EF、GH D. AB、CD EF 愿路分乐屮 1)題意分析’本题考查幻股定理及勾股定理的逆定理.亠 2)解題思器;可利用勾脸定理直接求出各边长,再试行判断?』 解答过整屮 在取DEAF中,Af=l, AE=2,根据勾股定理,得昇 EF = Q抡於十£尸° = Q +F二艮 同理HE = 2百* QH. = 1 CD = 2^5 计算发现W十◎血尸=(鸥31即血+曲=GH2,根据勾股定理的逆宦理得到UAAE、EF\ GH为辺的三角形是直毎三角形.故选B. * 縮題后KJ思专:* 1.勾股定理只适用于直角三角形,而不适用于说角三角形和钝角三角形? 因此」辭题时一宦妾认真分析题目所蛤■条件■,看是否可用勾股定理来解口* 2.在运用勾股左理时,要正确分析题目所给的条件,不要习惯性地认为就是斜 迫而“固执”地运用公式川二/十就其实,同样是S6
"不一罡就等于餌,疋不一罡就昱斜辺,KABC不一定就是直角三祐
3.直角三第形的判定条件与勾股定理是互逆的.区别在于勾股定理的运用是一个从 卅形s—个三角形是直角三角形)到懺 y =沖十沪)的过程,而直角三角形的判定是一 ①从嗦(一个三角形的三辺满足X二护+酹的条件)到偲个三角形是直角三角形)的过 程.a 4?在应用勾股定理解题叭聲全面地琴虑间题.注意m题中存在的多种可能性,遊免漏辭.初 例玉如圏,有一块直角三角形?椀屈U,两直角迫4CM5沁丸m?现将直角边AC沿直绘AD折蠡便它落在斜边AB上.且点C落到点E处, 则切等于(、* C/) "禎 B. 3cm G-Icni n題童分析,本题着查勾股定理的应用刎 :)解龜思路;車题若直接在△MQ中运用勾股定理是无法求得仞的长的,因为貝知遒一条边卫0的长,由题意可知,AACD和心迓门关于直线KQ对称.因而^ACD^hAED ?进一歩则有应RUm CZAED ED 丄AB,设UD=E2>黄泱,则在Rt A ABO中,由勾股定 理可得^=^(^+^=^83=100,得AB=10cm,在松迟DE 中,W ClO-fl)2= d驚解得尸 九4 解龜后的思琴尸 勾股定理说到底是一个等式,而含有未知数的等式就是方程。所以,在利用勾股定理求线段的长时常通过解方程来解决。勾股定理表达式中有三个量,如果条件中只有一个已知量,必须设法求出另一个量或求出另外两个量之间的关系,这一点是利用勾股定理求线段长时需要明确的思路。 方程的思想:通过列方程(组)解决问题,如:运用勾股定理及其逆定理求线段的长度或解决实际问题时,经常利用勾股定理中的等量关系列出方程来解 决问题等。 例3:一场罕见的大风过后,学校那棵老杨树折断在地,此刻,张老师正和占 明、清华、绣亚、冠华在楼上凭栏远眺。 清华开口说道:“老师,那棵树看起来挺高的。” “是啊,有10米高呢,现在被风拦腰刮断,可惜呀!” “但站立的一段似乎也不矮,有四五米高吧。”冠华兴致勃勃地说。 张老师心有所动,他说:“刚才我跑过时用脚步量了一下,发现树尖距离树根恰好3米,你们能求出杨树站立的那一段的高度吗?” 占明想了想说:“树根、树尖、折断处三点依次相连后构成一个直角三角
勾股定理
尊敬的各位评委、老师,您们好。今天我说课的内容是人教版《数学》八年级下册第十八章第一节《勾股定理》第一课时,我将从教材、教法与学法、教学过程、教学评价以及设计说明五个方面来阐述对本节课的理解与设计。 一、教材分析: (一)教材的地位与作用 从知识结构上看,勾股定理揭示了直角三角形三条边之间的数量关系,为后续学习解直角三角形提供重要的理论依据,在现实生活中有着广泛的应用。 从学生认知结构上看,它把形的特征转化成数量关系,架起了几何与代数之间的桥梁; 勾股定理又是对学生进行爱国主义教育的良好素材,因此具有相当重要的地位和作用。 根据数学新课程标准以及八年级学生的认知水平我确定如下学习目标:知识技能、数学思考、问题解决、情感态度。其中【情感态度】方面,以我国数学文化为主线,激发学生热爱祖国悠久文化的情感。 (二)重点与难点 为变被动接受为主动探究,我确定本节课的重点为:勾股定理的探索过程。限于八年级学生的思维水平,我将面积法发现勾股定理确定为本节课的难点,我将引导学生动手实验突
出重点,合作交流突破难点。 二、教法与学法分析 教学方法叶圣陶说过“教师之为教,不在全盘授予,而在相机诱导。”因此教师利用几何直观提出问题,引导学生由浅入深的探索,设计实验让学生进行验证,感悟其中所蕴涵的思想方法。 学法指导为把学习的主动权还给学生,教师鼓励学生采用动手实践,自主探索、合作交流的学习方法,让学生亲自感知体验知识的形成过程。 三、教学过程 我国数学文化源远流长、博大精深,为了使学生感受其传承的魅力,我将本节课设计为以下五个环节。 首先,情境导入 给出《七巧八分图》中的一组图片,让学生利用两组七巧板进行合作拼图。(请看视频)让学生观察并思考三个正方形面积之间的关系?它们围成了什么三角形?反映在三边上,又蕴含着什么数学奥秘呢?寓教于乐,激发学生好奇、探究的欲望。 第二步追溯历史解密真相 勾股定理的探索过程是本节课的重点,依照数学知识的循序渐进、螺旋上升的原则,我设计如下三个活动。 从上面低起点的问题入手,有利于学生参与探索。学生很容
勾股定理证明评鉴
勾股定理证明评鉴 勾股定理(又叫「勾股定理」)说:「在一个直角三角形中,斜边边长的平方等于两条直角边边长平方之和。」据考证,人类对这条定理的认识,少说也超过4000 年!又据记载,现时世上一共有超过300 个对这定理的证明! 我觉得,证明多,固然是表示这个定理十分重要,因而有很多人对它作出研究;但证明多,同时令人眼花缭乱,亦未能够一针见血地反映出定理本身和证明中的数学意义。故此,我在这篇文章中,为大家选出了7 个我认为重要的证明,和大家一起分析和欣赏这些证明的特色,与及认识它们的历史背境。 证明一 图一 在图一中,D ABC为一直角三角形,其中D A为直角。我们在边AB、BC和AC之上分别画上三个正方形ABFG、BCED和ACKH。过A点画一直线AL使其垂直于DE并交DE于L,交BC于M。不难证明,D FBC全等于D ABD(S.A.S.)。所以正方形ABFG 的面积= 2 ′ D FBC的面积= 2 ′ D ABD的面积= 长方形BMLD的面积。类似地,正方
形ACKH的面积= 长方形MCEL的面积。即正方形BCED的面积= 正方形ABFG的面积+ 正方形ACKH的面积,亦即是AB2 + AC2 = BC2。由此证实了勾股定理。 这个证明巧妙地运用了全等三角形和三角形面积与长方形面积的关系来进行。不单如此,它更具体地解释了,「两条直角边边长平方之和」的几何意义,这就是以ML将正方形分成BMLD和MCEL的两个部分! 这个证明的另一个重要意义,是在于它的出处。这个证明是出自古希腊大数学欧几里得之手。 欧几里得(Euclid of Alexandria)约生于公元前325 年,卒于约公元前265 年。他曾经在古希腊的文化中心亚历山大城工作,并完成了著作《几何原本》。《几何原本》是一部划时代的著作,它收集了过去人类对数学的知识,并利用公理法建立起演绎体系,对后世数学发展产生深远的影响。而书中的第一卷命题47,就记载着以上的一个对勾股定理的证明。 证明二 图二 图二中,我们将4个大小相同的直角三角形放在一个大正方形之内,留意大正方形中间的浅黄色部分,亦都是一个正方形。设直角三角形的斜边长度为c,其余两边的长度为a和b,则由于大正方形的面积应该等于4 个直角三角形和中间浅黄色正方形的面积之和,所以我们有
勾股定理经典例题(含答案)
类型一:勾股定理的直接用法 1、在Rt△ABC中,∠C=90° (1)已知a=6,c=10,求b,(2)已知a=40,b=9,求c;(3)已知c=25,b=15,求a. 思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。 解析:(1) 在△ABC中,∠C=90°,a=6,c=10,b= (2) 在△ABC中,∠C=90°,a=40,b=9,c= (3) 在△ABC中,∠C=90°,c=25,b=15,a= 举一反三 【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少? 【答案】∵∠ACD=90° AD=13, CD=12 ∴AC2 =AD2-CD2 =132-122 =25 ∴AC=5 又∵∠ABC=90°且BC=3 ∴由勾股定理可得 AB2=AC2-BC2 =52-32 =16 ∴AB= 4 ∴AB的长是4. 类型二:勾股定理的构造应用 2、如图,已知:在中,,,. 求:BC的长. 思路点拨:由条件,想到构造含角的直角三角形,为此作于D,则有 ,,再由勾股定理计算出AD、DC的长,进而求出BC的 长. 解析:作于D,则因, ∴(的两个锐角互余) ∴(在中,如果一个锐角等于, 那么它所对的直角边等于斜边的一半). 根据勾股定理,在中, . 根据勾股定理,在中,
. ∴. 举一反三【变式1】如图,已知:,,于P. 求证:. 解析:连结BM,根据勾股定理,在中, . 而在中,则根据勾股定理有 . ∴ 又∵(已知), ∴. 在中,根据勾股定理有 , ∴. 【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。 分析:如何构造直角三角形是解本题的关键,可以连结AC,或延长AB、DC交于F,或延长AD、BC交于点E,根据本题给定的角应选后两种,进一步根据本题给定的边选第三种较为简单。 解析:延长AD、BC交于E。 ∵∠A=∠60°,∠B=90°,∴∠E=30°。 ∴AE=2AB=8,CE=2CD=4, ∴BE2=AE2-AB2=82-42=48,BE==。 ∵DE2= CE2-CD2=42-22=12,∴DE==。 ∴S四边形ABCD=S△ABE-S△CDE=AB2BE-CD2DE= 类型三:勾股定理的实际应用(一) 用勾股定理求两点之间的距离问题3、如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了 到达B点,然后再沿北偏西30°方向走了500m到达目的地C点。(1)
勾股定理(基础)
勾股定理(基础) 一、目标与策略 明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数! 学习目标: ● 掌握勾股定理的内容,了解勾股定理的多种证明方法,体验数形结合的思想; ● 能够运用勾股定理求解三角形中相关的边长(只限于常用的数); ● 通过对勾股定理的探索解决简单的实际问题,进一步运用方程思想解决问题. 学习策略: ● 体验勾股定理的探索过程,掌握方程思想; ● 牢记直角三角形中两条直角边的平方和等于斜边的平方. 二、学习与应用 1. 正数的平方根有 ,它们互为 ,其中正的那个叫它的____;负数 ,0的平方根是 . 2. 324的算术平方根是 , 256的平方根是 . 3.196= ,144 = . 要点一、勾股定理 直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长 分别为a b ,,斜边长为c ,那么 . 要点诠释:(1)勾股定理揭示了一个直角三角形三边之间的数量关系. (2)利用勾股定理,当设定一条直角边长为未知数后,根据题目已知的 线段长可以建立方程求解,这样就将数与形有机地结合起来,达到了解决问题的目 的. (3)理解勾股定理的一些变式: “凡事预则立,不预则废”.科学地预习才能使我们上课听讲更有目的性和针对性.我们要在预习的基础上,认真听讲,做到眼睛看、耳朵听、心里想、手上记. 要点梳理——预习和课堂学习 认真阅读、理解教材,尝试把下列知识要点内容补充完整,带着自己预习的疑惑认真听 课学习.课堂笔记或者其它补充填在右栏. 知识回顾——复习 学习新知识之前,看看你的知识贮备过关了吗?
2______ a=,2______ b=,()2 2____ c a b =+- 要点二、勾股定理的证明 方法一:将四个全等的直角三角形拼成如图(1)所示的正方形. 图(1)中,所以. 方法二:将四个全等的直角三角形拼成如图(2)所示的正方形. 图(2)中,所以. 方法三:如图(3)所示,将两个直角三角形拼成直角梯形. ,所以. 要点三、勾股定理的作用 1.已知直角三角形的任意两条边长,求第三边; 2.用于解决带有平方关系的证明问题; 3. 与勾股定理有关的面积计算; 4. 勾股定理在实际生活中的应用. 类型一、勾股定理的直接应用 例1、在△ABC中,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.(1)若a=5,b=12,求c; (2)若c=26,b=24,求a. 典型例题——自主学习 认真分析、解答下列例题,尝试总结提升各类型题目的规律和技巧,然后完成举一反三.课堂笔记或者其它补充填在右栏.
运用勾股定理证明与计算
勾股定理 学习目标 掌握勾股定理,会用面积法证明勾股定理。 导学过程 一、 忆一忆 1、直角△ABC 的主要性质是:∠C=90°(用几何语言表示) (1)两锐角之间的关系: (2)若D 为斜边中点,则斜边中线是 (3)若∠B=30°,则∠B 二、学一学 1、(1)、画一个直角边为3cm 和4cm 的直角△ABC (2)、再画一个两直角边为5和12的直角△ABC 问题:你是否发现23+24与25,25+212和213 命题1:如果直角三角形的两直角边分 么 。 三、合作探究: 方法1、已知:在△ABC 中,∠C=90°,∠A 、∠B 求证: 222a b c += 证明:4S △+S 小正=S 大正 根据的等量关系:由此我们得出勾股定理 的内容是 b b
方法2、已知:在△ABC 中,∠C=90°,∠A 、∠B 、 ∠C 的对边为a 、b 、c 。 求证:a 2+b 2=c 2。 根据如图所示,利用面积法证明勾 股定理 四、练一练: 1、在Rt △ABC ,∠C=90° (1)已知a=b=5,求c 。(2)已知a=1,c=2, 求b 。(3)已知c=17,b=8, 求a 。 ⑷已知a :b=1:2,c=5, 求a 。⑸已知b=15,∠A=30°,求a ,c 2、一个直角三角形的两边长分别为3cm 和4cm,则第三边的长为 。 3.如图,三个正方形中的两个的面积S 1=25,S 2=144,则另一个的面积S 3为________. 4.直角三角形两直角边长分别为5和12,则它斜边上的高为__________。 5.等腰三角形底边上的高为8,周长为32,则三角形的面积为( ) A 、56 B 、48 C 、40 D 、32 6、已知,如图在ΔABC 中,AB=BC=CA=2cm ,AD 是边BC 上的高. 求 ①AD 的长;②ΔABC 的面积. 7.如图,小李准备建一个蔬菜大棚,棚宽4m ,高3m ,长20m ,棚的斜面用塑料薄膜遮盖,不计墙的厚度,请计算阳光透过的最大面积. b c c a A E B 3m 4m 20m
勾股定理典型题总结(较难)
勾股定理 一.勾股定理证明与拓展 模型一 . 图中三个正方形面积关系 思考:如下图,以直角三角形a 、b 、c 为边,向外作等边三角形、半圆、等腰直角三角形和正方形,上述四种情况的面积有和关系? 例1、有一个面积为1的正方形,经过一次“生长”后,在他的左右肩上上生出两个小正方形(如图1),其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,生出了4个正方形(如图2),如果按此规律继续“生长”下去,它将变得“枝繁叶茂”;在“生长”了2017次后形成的图形中所有正方形的面积和是 . 变式1:在直线l 上依次摆放着七个正方形(如图1所示).已知斜放置的三个正方形的面积分别是1,1. 21,1. 44,正放置的四个正方形的面积依次是1234S S S S ,,,,则41S S =______.
变式2:如图,四边形ABCD 中,AD ∥BC ,∠ABC +∠DCB =90°,且BC =2AD ,以AB 、BC 、DC 为边向外作正方形,其面积分别为S 1、S 2、S 3,若S 1=3,S 3=9,求S 2. (变式2) (变式3) 变式3:如图,Rt △ABC 的面积为10cm 2 ,在AB 的同侧,分别以AB ,BC ,AC 为直径作三个半圆,则阴影部分的面积为 . (难题)如图,是小明为学校举办的数学文化节设计的标志,在△ABC 中,∠ACB = 90°,以△ABC 的各边为边作三个正方形,点 G 落在 HI 上,若 AC +BC =6,空白部分面积为 10.5,则阴影部分面积 模型二 外弦图 D C B A 内弦图 G F E H 例题2.四年一度的国际数学大会于2002年8月20日在北京召开,大会会标如图所示,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积为 13,每个直角三角形两直角边的和是5。求中间小正方形的面积为__________;
中国是一个具有五千年悠久历史的国度
中国是一个具有五千年悠久历史的国度。在这片古老而神奇的土地上,聪明、勤劳、智慧的中华民族创造了辉煌的文明和灿烂的文化,其中,甲骨文就是中华文明和传统 文化中的一块瑰宝。 甲骨文,是指中国古代殷商时期刻在龟甲和兽骨上的文字,内容多与占卜有关,因此,又称“卜辞”或“龟甲”文字。甲骨文最早发现于河南安阳小屯村一带,是商王盘庚迁殷以后到纣王亡国时的遗物,距今已3000多年,目前出土的甲骨已达15万片之多。甲骨文是中国迄今为止发现的最早的可识读的文字,目前,共发现单字4500左右。可识者近2000字。甲骨文记载的内容极为丰富,不仅包括政治、经济、军事、文化等内容,而且涉及天文、历法、医药等科学技术,被称为中国古代最早的“档案库”。从文字结构看,甲骨文不仅具备现代汉字的方块字特点,符合汉字造字的“六书”理论,而且,由甲骨文、两周金文,到春秋战国的大篆、小篆,再到汉魏的隶书以及以后的行书、楷书,其嬗变轨迹清晰可见。甲骨文作为中国汉字的鼻祖,是中国传统文化的根,也是人类文化的瑰宝,在世界文化宝库中占据着非常重要的地位。 为促进中日两国间的文化交流,由中国人民对外友好协会、中国殷商文化学会和日本北枝篆会等联合主办的“中国古文字起源——中日甲骨文书法展”近日在北京中国国家博物馆 举行。 这次展览以汉字文化中的瑰宝甲骨文为主题,展出中日两国古文字专家、学者、书法家模拟甲骨文创作的书法、篆刻以及甲骨文考古挖掘图片等共计210余件。台湾省古文字学者也对此表达了极大兴趣,创作了多幅书法作品参加展览。其中有日本书法篆刻家北枝篆会会长北室南苑先生及其会员以甲骨文为主要题材创作的书法篆刻作品85件,中国(含台湾地区)甲骨文学者及书法家作品100件左右。 展览目的在于使更多的人了解甲骨文,了解中国古代悠久灿烂的文化,从而博得更多人士对甲骨文书法艺术的热爱和关心,进一步加强中日两国间的文化交流,促进两国人民世代友好交往。 现刊载此次展览的部分作品,以飨读者。
勾股定理经典例题(含答案)
勾股定理经典例题透析 类型一:勾股定理的直接用法 1、在Rt△ABC中,∠C=90° (1)已知a=6, c=10,求b, (2)已知a=40,b=9,求c; (3)已知c=25,b=15,求a. 思路点拨:写解的过程中,一定要先写上在哪个直角三角形中,注意勾股定理的变形使用。 解析:(1) 在△ABC中,∠C=90°,a=6,c=10,b= (2) 在△ABC中,∠C=90°,a=40,b=9,c= (3) 在△ABC中,∠C=90°,c=25,b=15,a= 举一反三 【变式】如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少? 【答案】∵∠ACD=90° AD=13, CD=12 ∴AC2 =AD2-CD2 =132-122 =25 ∴AC=5 又∵∠ABC=90°且BC=3 ∴由勾股定理可得 AB2=AC2-BC2 =52-32
=16 ∴AB= 4 ∴AB的长是4. 类型二:勾股定理的构造应用 2、如图,已知:在中,,,. 求BC的长. 思路点拨:由条件,想到构造含角的直角三角形,为此作于D,则有 ,,再由勾股定理计算出AD、DC的长,进而求出BC的长. 解析:作于D,则因, ∴(的两个锐角互余) ∴(在中,如果一个锐角等于 , 那么它所对的直角边等于斜边的一半). 根据勾股定理,在中, . 根据勾股定理,在中,
. ∴. 举一反三【变式1】如图,已知:,,于P. 求证:. 解析:连结BM,根据勾股定理,在中, . 而在中,则根据勾股定理有 . ∴ 又∵(已知), ∴. 在中,根据勾股定理有 , ∴. 【变式2】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。
关于写中国历史悠久的句子
关于写中国历史悠久的句子 本文是关于关于写中国历史悠久的句子,仅供参考,希望对您有所帮助,感谢阅读。 历史孕育了真理;它能和时间抗衡,把遗闻旧事保藏下来;它是往古的迹象,当代的鉴戒,后世的教训。 史者,所以明夫治天下之道也。 古之所谓良史者,其明必足以周万事之理,其道必足民适天下之用,其智必足以通难知之意,其文必足以发难显之情,然而其任可得而称也。 一代天骄,莫属于从蒙古大草原崛起的马上皇帝——元太祖成吉思汗了。这成吉思汗就是一代明君,他懂得爱民,他懂得每个人的生命都是非常宝贵的,所以他从不会随意错杀好人、平民。 究天人之际,通古今之变。 到学校报道后来到寝室,迫不及待打开电脑,结果是学校还没开通网线于是想到把上学期遗留下的历史问题给解决了先 历史有如悲剧,要没有情欲、罪恶、灾难,在其中掀风作浪,就会显得毫无生气,令人生厌。 历史给我们的最好的东西就是它所激起的热情。歌德 《中华上下五千年》讲的是五千年来中国——这个大国的改革和变迁,生动有趣地介绍了中国历史上重大的历史事件、重要的历史人物或历史现象。 路是脚踏出来的,历史是人写出来的,人的每一步行动都在书写自己的历史。 历史的第一页是从互相猜忌、搞阴谋和耍手腕开始的。米左琴科 正如哲学是研究他人误解的学问,历史是研究他人错误的学问。 人类的具体历史,如果有的话,那一定是所有人的历史,也必然是人类的一切希望、斗争和受难的历史。波普 历史家的任务在于区别真实的和虚假的,确定的和不确定的,以及可疑的和不能够接受的。 人事有代谢,往来成古今。江山留胜迹,我辈复登临。——《与诸子登岘山》作者:[唐]孟浩然
历史不过是追求着自己目的的人的活动而已。马克思和恩格斯 历史著作有开始也有结束,但它们描写的事件却并不如此。科林伍德 历史并没有真正的科学价值,它的唯一目的乃是教育别人。历史上最突出的偶然的机遇是赫赫名人、伟大人物的间歇出现。历史永远是陈旧的,新的生活不能把历史为根据,这正如一种新的爱情不能和旧的爱情一样。胡也频
勾股定理典型题型
新人教版八年级下册勾股定理典型例习题 一、经典例题精讲 题型一:直接考查勾股定理 例1.在ABC ?中,90C ∠=?. ⑴已知6AC =,8BC =.求AB 的长 ⑵已知17AB =,15AC =,求BC 的长分析:直接应用勾股定理 222a b c += 解:⑴2210AB AC BC =+= ⑵228BC AB AC =-= 题型二:利用勾股定理测量长度 例题1 如果梯子的底端离建筑物9米,那么15米长的梯子可以到达建筑物的高度是多少 米? 解析:这是一道大家熟知的典型的“知二求一”的题。把实物模型转化为数学模型后,. 已知斜边长和一条直角边长,求另外一条直角边的长度,可以直接利用勾股定理! 根据勾股定理AC 2+BC 2=AB 2, 即AC 2+92=152,所以AC 2 =144,所以AC=12. 例题2 如图(8),水池中离岸边D 点1.5米的C 处,直立长着一根芦苇,出水部分B C 的长是0.5米,把芦苇拉到岸边,它的顶端B 恰好落到 D 点,并求水池的深度AC. 解析:同例题1一样,先将实物模型转化为数学模型,如 图2. 由题意可知△ACD 中,∠ACD=90°,在Rt △ACD 中,只知道CD=1.5,这是典型的利用勾 股定理“知二求一”的类型。 标准解题步骤如下(仅供参考): 解:如图2,根据勾股定理,AC 2+CD 2=AD 2 设水深AC= x 米,那么AD=AB=AC+CB=x +0.5 x 2+1.52=( x +0.5)2 解之得x =2. 故水深为2米. 题型三:勾股定理和逆定理并用—— 例题3 如图3,正方形ABCD 中,E 是BC 边上的中点,F 是AB 上一点,且AB FB 4 1= 那么△DEF 是直角三角形吗?为什么? C B D A
勾股定理 例题详解
勾股定理经典例题详解 知识点一:勾股定理 如果直角三角形的两直角边长分别为:a,b,斜边长为c,那么a2+b2=c2.即直角三角形中两直角边的平方和等于斜边的平方. 要点诠释:(1)勾股定理揭示的是直角三角形平方关系的定理。 (2)勾股定理只适用于直角三角形,而不适用于锐角三角形和钝角三角。 (3)理解勾股定理的一些变式: c2=a2+b2, a2=c2-b2, b2=c2-a2,c2=(a+b)2-2ab 知识点二:用面积证明勾股定理 方法一:将四个全等的直角三角形拼成如图(1)所示的正方形。 图(1)中,所以。 方法二:将四个全等的直角三角形拼成如图(2)所示的正方形。 图(2)中,所以。 方法三:将四个全等的直角三角形分别拼成如图(3)—1和(3)—2所示的两个形状相同的正方形。
在(3)—1中,甲的面积=(大正方形面积)—(4个直角三角形面积), 在(3)—2中,乙和丙的面积和=(大正方形面积)—(4个直角三角形面积), 所以,甲的面积=乙和丙的面积和,即:. 方法四:如图(4)所示,将两个直角三角形拼成直角梯形。 ,所以。 知识点三:勾股定理的作用 1.已知直角三角形的两条边长求第三边;2.已知直角三角形的一条边,求另两边的关系; 3.用于证明平方关系的问题; 4.利用勾股定理,作出长为 的线段。 2. 在理解的基础上熟悉下列勾股数 满足不定方程x2+y2=z2的三个正整数,称为勾股数(又称为高数或毕达哥拉斯数),显然,以x,y,z为三边长的三角形一定是直角三角形。 熟悉下列勾股数,对解题是会有帮助的: ①3、4、5②5、12、13;③8、15、17;④7、24、25;⑤10、24、26;⑥9、 40、41.
勾股定理的证明方法
勾股定理的证明方法 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】
勾股定理的证明方法 勾股定理是初等几何中的一个基本定理。这个定理有十分悠久的历史,两千多年来,人们对勾股定理的证明颇感兴趣,因为这个定理太贴近人们的生活实际,以至于古往今来,下至平民百姓,上至帝王总统都愿意探讨和研究它的证明.下面结合几种图形来进行证明。 一、传说中毕达哥拉斯的证法(图1) 左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为、,斜边为的直角三角形拼成的。右边的正方形是由1个边长为的正方形和4个直角边分别为、,斜边为的直角三角形拼成的。因为这两个正方形的面积相等(边长都是),所以可以列出等式 ,化简得。 在西方,人们认为是毕达哥拉斯最早发现并证明这一定理的,但遗憾的是,他的证明方法已经失传,这是传说中的证明方法,这种证明方法简单、直观、易懂。 二、赵爽弦图的证法(图2) 第一种方法:边长为的正方形可以看作是由4个直角边分别为、,斜边为的直
角三角形围在外面形成的。因为边长为的正方形面积加上4个直角三角形的面积等于外围正方形的面积,所以可以列出等式,化简得。 第二种方法:边长为的正方形可以看作是由4个直角边分别为、,斜边为的 角三角形拼接形成的(虚线表示),不过中间缺出一个边长为的正方形“小洞”。 因为边长为的正方形面积等于4个直角三角形的面积加上正方形“小洞”的面积,所以可以列出等式,化简得。 这种证明方法很简明,很直观,它表现了我国古代数学家赵爽高超的证题思想和对数学的钻研精神,是我们中华民族的骄傲。 三、美国第20任总统茄菲尔德的证法(图3) 这个直角梯形是由2个直角边分别为、,斜边为的直角三角形和1个直角边为 的等腰直角三角形拼成的。因为3个直角三角形的面积之和等于梯形的面积,所以可以列出等式,化简得。
