t分布与t检验

t分布

从数理统计的理论上讲，并且上节的实例也已说明，在总体均数为μ，总体标准差为σ的正态总体中随机抽取n相等的许多样本，分别算出样本均数，这些样本均数呈正态分布。而当样本含量n不太小时，即使总体不呈正态分布，样本均数的分布也接近正态。在下式中，

由于μ与（样本均数的标准差）都是常量，又

X呈正态分布，所以u

也呈正态分布。但实际上总体标准差往往是不知道的，上式分母中的σ要由S替代，成为

，那么由于样本标

准差有抽样波动，SX也有抽样波动，于是，在用S代替σ

后上式等号右边的变量便不呈正态分布而呈t分布，其定义公式是

（6.5)

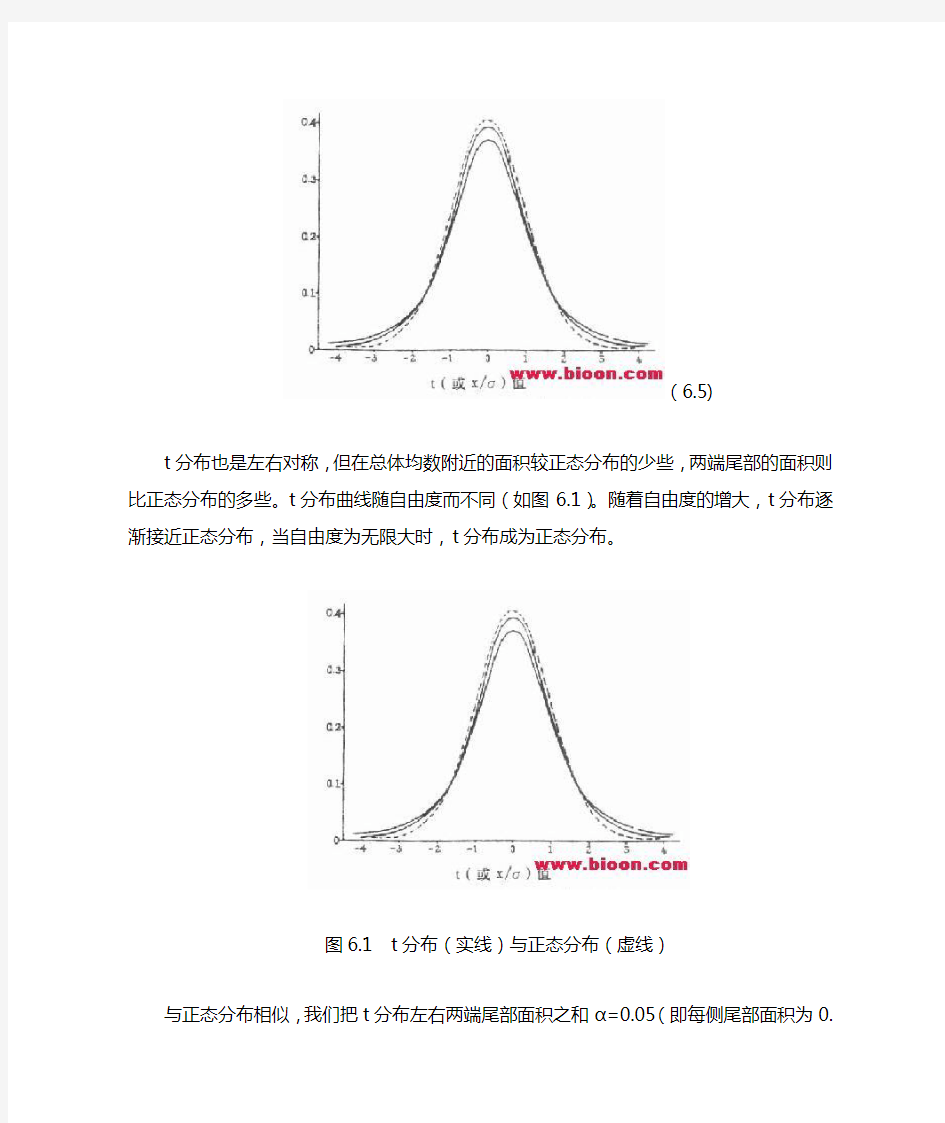
t分布也是左右对称，但在总体均数附近的面积较正态分布的少些，两端尾部的面积则比正态分布的多些。t分布曲线随自由度而不同（如图6.1）。随着自由度的增大，t分布逐渐接近正态分布，当自由度为无限大时，t分布成为正态分布。

图6.1t分布（实线）与正态分布（虚线）

与正态分布相似，我们把t分布左右两端尾部面积之和α=0.05（即每侧尾部面积为0.025）相应的t值称为5%界，符号为t0.05,,，这里ν是自由度。把左右两端尾部面积之和α为0.01相应的t值称为1%界，符号为t0.01,,。t的5%界与1%界可查附表3，t值表。例如当自由度为10-1=9时，t0.05,9=2.262，t0.01,9=3.250。

可信区间的估计

一、参数估计的意义

一组调查或实验数据，如果是计量资料可求得平均数，标准差等统计指标，如果是计数资料则求百分率藉以概括说明这群观察数据的特征，故称特征值。由于样本特征值是通过统计求得的，所以又称为统计量以区别于总体特征值。总体特征值一般称为参数（总体量）。我们进行科研所要探索的是总体特征值即总体参数，而我们得到的却是样本统计量，用样本统计量估计或推论总体参数的过程叫参数估计。

本章第一节例6.1通过检查110个健康成人的尿紫质算得阳性率为10%，这是样本率，可用它来估计总体率，说明健康成人的尿紫质阳性率水平，这样的估计叫“点估计”。但由于存在抽样误差，不同样本（如再检查110人）可能得到不同的估计值。因此我们常用“区间估计”总体率（或总体均数）大概在那一个范围内，这个范围就叫可信区间。区间小的一端叫下限，大的一端叫上限。常用的有95%可信区间与99%可信区间。根据同一资料所作95%可信区间比99%可信区间窄些（上、下限较靠近），但估计错误的概率后者为1%，前者为5%，进行总体参数的区间估计时可根据研究目的与标准误的大小选用95%、或99%。

二、总体均数的估计

http://127.0.0.1:11643/library/stats/html/Distributions.html

本文来自: 人大经济论坛R语言论坛版，详细出处参考：https://www.360docs.net/doc/0219204641.html,/forum.php?mod=viewt hread&tid=3615789&page=1

为了说明常用的总体均数之区间估计法，我们不妨回顾一下上节所叙的t分布。

由求t的基本公式

我们看到X与μ的距离等于t（SX），又根据X集中分布在μ周围的特点，若取t的5%

界即t0.05,,（或1%界）乘以SX作为X与μ的距离范围，就可用式（6.6）或式(6.7)求

出区间来估计总体均数μ所在范围，估错的概率仅有5%或1%，因此称95%或99%可信区间。下面用实例说明其求法。

95%可信区间X-t0.05,νSX<μ

99%可信区间X-t0.05,νSX<μ

例6.2上面抽样实验中第1号样本的均数为488.6，标准差为61.65，例数10，自由度ν=10-1=9，试求95%与99%可信区间。

1．求标准误

95%可信区间488.6-2.262(19.50)<μ<488.6+2.262(19.50),即有95%的把握估计μ是在444.49～532.71区间内

99%可信区间488.6-3.250(19.50)<μ<488.6+3.250(19.50),可有99%的把握估计μ是在425.22～551.98区间内

这里两个可信区间都包含μ=500在内，所以这次估计是估计对了。

抽样实验共抽了100个样本，除1号样本外其余99个样本均数也对μ作了区间估计，这些95%可信区间列在表6.4中。我们看到，只有5个95%可信区间（右上角标有星号）不包含总体均数μ=500在内，它们是：

样本号X 95%可信区间 6 546.7 515.78～577.62 7 524.5 500.45～548.55 28 476.1 454.91～497.29 72 4 65.3 447.02～483.58 75 526.6 503.10～550.10

平时我们并不重复抽取许多样本来一次次估计总体均数而仅是一次，至于算出的均数会类似一百个样本均数中的那一个就很难说了。如果不遇到类似上列那些均数过大或过小的样本，求出可信区间后总体均数真是在该区间内，那么便是一次成功的估计：但是极少数情况下我们也会遇到极端的样本，以至总体均数并不在我们提出的区间内。不过，我们具体所作的这次估计到底属于前种情况还是后一种，这是无法知道的，因为我们不知道μ是多少（若已知μ便不必估计它了）。然而象后种情况那样作出错估的概率终究很小，只5%或1%，所以用这样的方法估计总体均数还是可行的。

三、总体率的估计

上面已经提到，计数资料可以计算相对数（率）。我们若由样本统计量P估计总体参数π，同样要考虑率的抽样误差，据数理统计研究结果，样本率的分布也近似正态分布，尤其当π比较靠近50%且样本较大时。于是对样本，百分率的可信区间可利用正态分布规律估计，公式是：

95%可信区间P-1.96Sp<π< p>

99%可信区间P-2.58Sp<π< p>

（按正态分布，双侧尾部面积α=0.05时的u值为1.96，α=0.01时的u值为2.58，故用这两式求可信区间时不必查表找临界u值，记住这两数即可。）

例6.3某医院收治200例急性菌痢患者，其中粪便细菌培养阳性者共80例，试估计菌痢细菌培养的总体阳性率95%与99%可信区间。

1.求阳性率P＝80／200×100％＝40％（或0.40）

2.

3．求可信区间

95%可信区间40%-1.96(3.46%)<π<40%+1.96(3.46%)，即估计π在33.22%～46.78%之间

99%可信区间40%-2.58(3.46%)<π<40%+2.58(3.46%)，即估计π在31.07%～48.93%之间

如果是小样本的百分率，求可信区间可通过查表获得，附表4是n为10、15、20、30时查95%与99%可信区间的一个简表。此外，统计学专著中还有更详细的表可查

t检验与u检验

抽样研究包含参数估计与通过假设检验作统计推断这样一些重要内容。前者在第六章最后一节中已经涉及，后者如X2检验，我们亦已有过接触。本章将介绍两均数相比时的假设检验。

第一节t检验

一、样本均数与总体均数的比较

为了判断观察到的一组计量数据是否与其总体均数接近，两者的相差系同一总体中样本与总体之间的误差，相差不大；还是已超出抽样误差的一般允许范围而存在显著差别？应进行假设检验，下面通过实例介绍t检验的方法步骤。

例7.1根据大量调查得知，健康成年男子脉搏均数为72次/分，某医生在某山区随机抽查健康成年男子25人，其脉搏均数为74.2次/分，标准差为6.5次/分。根据这个资料能否认为某山区健康成年男子的脉搏数与一般健康成年男子的不同？

在医学领域中有一些公认的生理常数如本例提到的健康成人平均脉搏次数72次/分，一般可看作为总体均数μ。已知在总体均数μ和总体标准差σ已知的情况下可以予测样本均数分布情况，现缺总体标准差，则需用样本标准差来估计它，那么样本均数围绕总体均数散布的情况服从t分布（尤其当样本含量n较小时，）。t分布的基本公式即6.5。

从式中可知，t是样本均数与总体均数之差（以标准误为单位），t的绝对值越大也即X距μ越远。在t分布中距μ越远的样本均数分布得越少（所占百分比小，P值小），后面附表3右上角的示意图中展示了这种关系，如欲知各自由度下t值与其相应的P值可查附表3。

下面回答本例提出的问题而进行假设检验。按一般步骤：

（1）提出检验假设H0与备择假设H1。本例H0为某山区成年男子的脉搏均数与一般成年男子的相等，μ=μ0=72次/分；H1为两者不相等μ≠μ0，即μ大于或小于μ0（这是双侧检验，如果事先已肯定山区人的脉搏不可能低于一般人，只检验它是否高于一般人，则应用单侧检验，H1必为μ>μ）。

（2）定显著性水准α，并查出临界t值。α是：若检验假设为真但被错误地拒绝的概率。现令α=0.05，本例自由度ν=n-1=25-1=24、查附表3得t0.05,24=2.064。若从观察资料中求出的∣t∣值小于此数，我们就接受H0；若等于或大于此值则在α=0.05水准处拒绝H0而接受H1。

（3）求样本均数X、标准差S及标准误Sχ并进而算出检验统计量t。现已知X=74.2次/分，S=6.5次/分，只要求出Sχ及t值即可。

（4）下结论：因∣t∣t0.05,24=2.064，所以检验假设H0得以接受，从而认为就本资料看，尚不能得出山区健康成年人的脉搏数不同于一般人而具有显著差别的结论。

二、成对资料样本均数的比较

上面介绍了已知总体均数时的显著性检验方法，但有时我们并不知道总体均数，且医学数据资料中更为常见的是成对资料，若一批某病病人治疗前有某项测定记录，治疗后再次测定以观察疗效，这样，观察n例就有n对数据，这即是成对资料（也可对动物做成病理模型进行治疗实验以收集类似的成对资料）；如果有两种处理要比较，将每一份标本分成两份各接受一种处理，这样观察到的一批数据也是成对资料，医学科研中有时无法对同一批对象进行前后或对应观察，而只得将病人（或实验动物）配成对子，尽量使同对中的两者在性别、年龄或其它可能会影响处理效果的各种条件方面极为相似，然后分别给以一种不同的处理后观察反应，这样获得的许多对不可拆散的数据同样是成对资料。由于成对资料可控制个体差异使之较小，故检验效率是较高的。

关于成对资料，每对数据始终相联这是它的特点，我们可以先初步观察每对数据的差别情况，进一步算出平均相差作为样本均数，再与假设的总体均数比较看相差是否显著，下面举实例说明检验过程。

表7.1豚鼠注入上腺素前后每分钟灌流滴数

豚鼠号每分钟灌流滴数用药前用药后增加数d 1 30 46 16 2 38 50 12 3 48 52 4 4 48 52 4 5 60 5 8 -2 6 46 64 18 7 26 56 30 8 58 54 -4 9 46 54 8 10 48 58 10 11 44 36 -8 12 46 54 8 总计——96

例7.2为了验证肾上腺素有无降低呼吸道阻力的作用，以豚鼠12只，进行支气管灌流实验，在注入定量肾上腺素前后，测定每分钟灌流滴数，结果见表7.1，问用药后灌流速度有无显著增加？

（1）假设用药前后灌流滴数相同，则相差的总体均数μ为0；即H0：μ=μ0；H1：μ≠μ0。

（2）令显著性水准α=0.05，由本例ν=12-1=11查得临界值t0.05,11=2.201。

（3）求样本统计量平均相差数d、差数的标准差S d、标准误Sd及检验统计量t值。

（4）下结论。今∣t∣t0.05,11，p <0.05，故认为检验假设μ=μ0难以接受，在α=0.05水准外拒绝H O而接受H1，相差显著，注入肾上腺素后每分钟灌流滴数比注射前要多。

例7.3从以往资料发现，慢性支气管炎病人血中胆碱酯酶活性常常偏高。某校药理教研室将同性别同年龄的病人与健康人配成8对，测量该值加以比较，资料如下。问可否通过这一资料得出较为明确的结论？

表7.2慢性气管炎病人与健康人血液胆碱酯酶活性测定（μM/ml）

对子序号病人组，X1健康人组，X2差数

D=X1-X21 3．28 2．36 0．92 2 2．60 2．40 0．20 3 3．32 2．40 0．92 4 2．72 2．52 0．20 5 2．3 8 3．04 -0.66 6 3．64 2．64 1．00 7 2．98 2．56 0．42 8 4．40 2．40 2．00

（1）检验假设H0：μ=μ0；H1：μ>μ0

（2）令α=0.05，得t0.05,7=1.895(单侧)

（3）用差数求统计量

（4）结论∣t∣=2.264>t0.05,7=1.895,P<0.05,在α=0.05水准处拒绝H0，接受备择假设，认为慢性气管炎病人血中胆碱酯酶高于正常人。

上例用了单侧检验是因为事先并不认为该类病人血中胆碱酯含量会出现低于健康人的情况。

三、两组资料样本均数的比较

在日常工作中，我们经常要比较某两组计量资料的均数间有无显著差别，如研究不同疗法的降压效果或两种不同制剂对杀灭鼠体内钩虫的效果（条数）等。这时假若事先难以找到年龄、性别等条件完全一样的人（或动物）作配对比较，那么不能求每对的差数只能先算出各组的均数，然后进行比较。两组例数可以相等也可稍有出入。检验的方法同样是先假定两组相应的总体均数相等，看两组均数实际相差与此假设是否靠近，近则把相差看成抽样误差表现，远到一定界限则认为由抽样误差造成这样大的相差的可能性实在太小，拒绝假设而接受H1,作出两总体不相等的结论。

例7.4为观察中成药青黛明矾片对急性黄疸肝炎的退黄效果，以单用输液保肝的病人作为对照进行了观察，两组患者均为成人，黄疸指数在30-50之间，各人退黄天数如下，试比较用药组（1组）与对照组（2组）退黄天数有无显著差别。

表7.3急性黄疸性肝炎病人的退黄天数

中药组，X15 10 14 21 17 ∑X1=67 对照组，X218 21 30 23 22 22 ∑X2=136

（1）检验假设设该药对缩短退黄天数无效，两组的总体均数相等，即H0=μ1=μ2；H1：μ1≠μ2。

（2）求自由度ν

ν=n1+n2-2

=5+6-2=9 (7.1)

定α=0.05，ν=9时的t值为t0.05,9=2.262

（3）计算各组均数，合并方差S2c及两均数相差的标准误Sχ1-χ2，然后求t值。

合并方差：(7.2)

代入得

两均数相差的标准误：

(7.3)

代入得

求t：

(7.4)

（4）下结论因│t┃>t0.05,9,P<0.02，所以我们在α=0.05水准处拒绝H0而接受H1，两者平均退黄天数和有显著差别，服青黛明矾片药的病人退黄天数较短。如果检验假设属实，这样的结论也还可能下错，但概率在2%以下。

上例为两组资料均数间的比较，与前面成对资料的t检验有些区别。前者每对中两数据不能分离，后者任一组中的各数据可以在组内前后互换位置；前者只有一个样本平均差数d对应于一个假设的总体平均差数μ0，后者，认为X1为第一个总体的随机样本均数，X2则来自μ2，所以后者要计算两组合并的方差S2 c(方差是标准差的平方)。再者，与前者相比标准误、自由度的计算方法也不相同。

例7.5某人测定半岁至1岁小儿、7至8岁儿童各9人的免疫球蛋白IgG（国际单位/ml），算得平均数与标准差前者（第1组）为55.1±11.5,后者（第2组）为95.5 ±17.8，试检验这两种不同年龄的人免疫球蛋白IgG有无显著差别。

（1）检验假设H0：μ1=μ2；H1：μ1≠μ2。

（2）令α=0.01,查自由度ν=9+9-2=16时的临界值，得t0.01,16=2.921

（3）求统计量已知X1=55.1,X2=95.5,至于求t值时作为分母的标准误，在暂缺原始数据时由已知的两个标准差先推算出合并方差S c2进而求出Sχ1-χ2即可，方法如下；

①一般方法；根据标准差算式

则

于是

由式(7.2)

由式（7.3）

②在两组例数相等时也可直接用S1、S2代入下式求Sχ1-χ2，结果一样。

现已有了均数及标准误可由X1、X2、Sχ1-χ2求出t值。

（4）结论│t│>=5.719>t0.01,16=2.921,P<0.001，在α=0.01水准处拒绝H0，接受H1，两年龄组的人免疫球蛋白IgG的均数相差显著，7-8岁组的高于小几组。

关于检验水准α定在0.05还是0.01或其它处，要看检验者事先对结论的可靠性要求之高低而定。本例定α=0.01，要求是较高的，最后查出P值小于0.001就更说明X1-X2=-40.4随机来自μ1-μ2=0的假设总体的可能性是很小的。