to_char函数
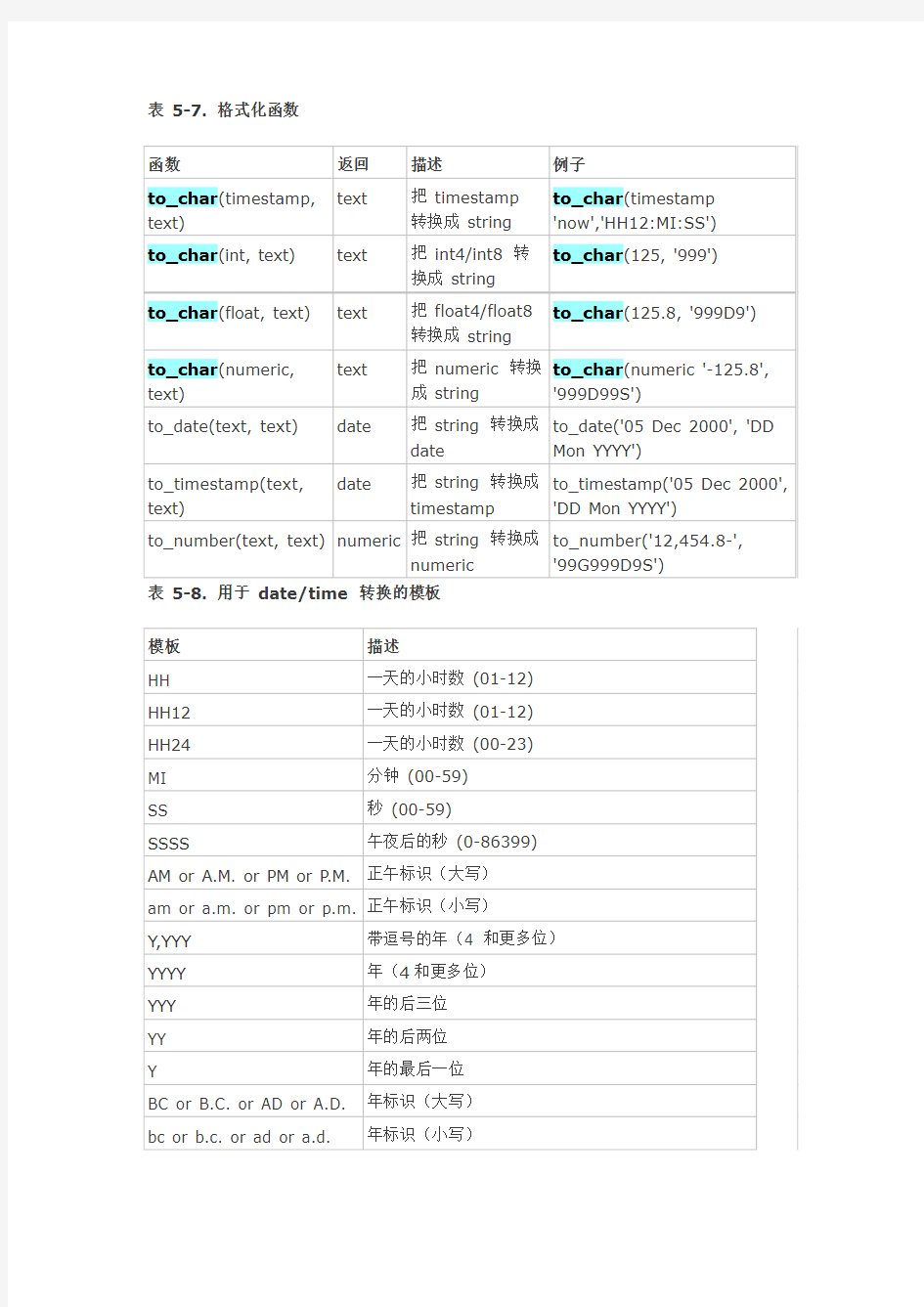

表5-7. 格式化函数
函数返回描述例子
to_char(timestamp, text) text 把timestamp
转换成string
to_char(timestamp
'now','HH12:MI:SS')
to_char(int, text) text 把int4/int8 转
换成string
to_char(125, '999')
to_char(float, text) text 把float4/float8
转换成string
to_char(125.8, '999D9')
to_char(numeric, text) text 把numeric 转换
成string
to_char(numeric '-125.8',
'999D99S')
to_date(text, text) date 把string 转换成
date to_date('05 Dec 2000', 'DD Mon YYYY')
to_timestamp(text, text) date 把string 转换成
timestamp
to_timestamp('05 Dec 2000',
'DD Mon YYYY')
to_number(text, text) numeric 把string 转换成
numeric to_number('12,454.8-', '99G999D9S')
表5-8. 用于date/time 转换的模板
模板描述
HH 一天的小时数(01-12) HH12 一天的小时数(01-12) HH24 一天的小时数(00-23) MI 分钟(00-59)
SS 秒(00-59)
SSSS 午夜后的秒(0-86399) AM or A.M. or PM or P.M. 正午标识(大写)
am or a.m. or pm or p.m. 正午标识(小写)
Y,YYY 带逗号的年(4 和更多位)YYYY 年(4和更多位)
YYY 年的后三位
YY 年的后两位
Y 年的最后一位
BC or B.C. or AD or A.D. 年标识(大写)
bc or b.c. or ad or a.d. 年标识(小写)
用法须知:
?如果没有使用FX选项,to_timestamp和to_date忽略空白。FX必须做为模板里的第一个条目声明。
?反斜杠("\")必须用做双反斜杠("\\"),例如'\\HH\\MI\\SS'。
?双引号('"')之间的字串被忽略并且不被分析。如果你想向输出写双引号,你必须在双引号前面放置一个双反斜杠('\\'),例如'\\"YYYY Month\\"'。
?to_char支持不带前导双引号('"')的文本,但是在双引号之间的任何字串会被迅速处理并且还保证不会被当作模板关键字解释(例如:'"Hello Year: "YYYY')。表5-10. 用于to_char(numeric) 的模板
模板描述
9 带有指定位数的值
0 前导零的值
. (句点)小数点
, (逗号)分组(千)分隔符
PR 尖括号内负值
S 带负号的负值(使用本地化)
L 货币符号(使用本地化)
D 小数点(使用本地化)
G 分组分隔符(使用本地化)
MI 在指明的位置的负号(如果数字< 0)
PL 在指明的位置的正号(如果数字> 0)
SG 在指明的位置的正/负号
RN 罗马数字(输入在1 和3999 之间)
TH or th 转换成序数
V 移动n位(小数)(参阅注解)
EEEE 科学记数。现在不支持。
用法须知:
?使用'SG','PL' 或'MI' 的带符号字并不附着在数字上面;例如,to_char(-12, ' S9999') 生成' -12',而to_char(-12, 'MI9999') 生成'- 12'。Oracle里的实现不允许在9前面使用MI,而是要求9在MI前面。
?PL,SG,和TH是 Postgres 扩展。
?9表明一个与在9字串里面的一样的数字位数。如果没有可用的数字,那么使用一个空白(空格)。
?TH不转换小于零的值,也不转换小数。TH是一个 Postgres 扩展。
?V方便地把输入值乘以10^n,这里n是跟在V后面的数字。to_char不支持把V与一个小数点绑在一起使用(例如. "99.9V99" 是不允许的)。
表5-11. to_char例子
输入输出
to_char(now(),'Day, HH12:MI:SS') 'Tuesday , 05:39:18' to_char(now(),'FMDay, HH12:MI:SS') 'Tuesday, 05:39:18' to_char(-0.1,'99.99') ' -.10'
to_char(-0.1,'FM9.99') '-.1'
to_char(0.1,'0.9') ' 0.1'
to_char(12,'9990999.9') ' 0012.0'
to_char(12,'FM9990999.9') '0012'
to_char(485,'999') ' 485'
to_char(-485,'999') '-485'
to_char(485,'9 9 9') ' 4 8 5'
to_char(1485,'9,999') ' 1,485'
to_char(1485,'9G999') ' 1 485'
to_char(148.5,'999.999') ' 148.500'
to_char(148.5,'999D999') ' 148,500'
to_char(3148.5,'9G999D999') ' 3 148,500'
to_char(-485,'999S') '485-'
to_char(-485,'999MI') '485-'
to_char(485,'999MI') '485'
to_char(485,'PL999') '+485'
to_char(485,'SG999') '+485'
to_char(-485,'SG999') '-485'
to_char(-485,'9SG99') '4-85'
to_char(-485,'999PR') '<485>'
to_char(485,'L999') 'DM 485
to_char(485,'RN') ' CDLXXXV'
to_char(485,'FMRN') 'CDLXXXV'
to_char(5.2,'FMRN') V
to_char(482,'999th') ' 482nd'
to_char(485, '"Good number:"999') 'Good number: 485' to_char(485.8,'"Pre-decimal:"999" 'Pre-decimal: 485
几种特殊性质的函数的周期
几种特殊性质的函数的周期: ①y=f(x)对x ∈R 时,f(x +a)=f(x -a) 或f(x -2a )=f(x) (a>0)恒成立,则y=f(x)是周期为2a 的周期函数; ②y=f(x)对x ∈R 时,f(x+a)=-f(x)(或f(x+a)= ) (1x f -,则y=f(x)是周期为2a 的周期函数; ③若y=f(x)关于点(a,0),(b,0)对称,则f(x)是周期为2b a -的周期函数; ④y=f(x)的图象关于直线x=a,x=b(a ≠b)对称,则函数 y=f(x)是周期为2b a -的周期函数;如:正弦函数 sin y x = ⑤若y=f(x)是偶函数,其图像又关于直线x=a 对称,则 f(x)是周期为2︱a ︱的周期函数; ⑦正(余)弦型函数定义域为R ,周期为T ,那么,对于任意R m ∈,区间[)T m m +,内有且只有两个量21,x x ,满足()()21x f x f =。正切型函数则只有一个。 ⑧0)()(=+=a x f x f , 或)0)(() (1)(≠= +x f x f a x f , 或1()()f x a f x +=-(()0)f x ≠, 例1.若函数)(x f 在R 上是奇函数,且在()01, -上是增函数,且)()2(x f x f -=+,则 ①)(x f 关于 对称; ②)(x f 的周期为 ; ③)(x f 在(1,2)是 函数(增、减); ④)时,,(若10∈ x )(x f =x 2,则=)(log 18 21f 。 例2.设)(x f 是定义在),(+∞-∞上,以2为周期的周期函数,且)(x f 为偶函数,在区间 [2,3]上 )(x f =4)3(22+--x ,则时,]2,0[∈x )(x f = 。 4.函数(图象)的对称性 1)证明一个函数图象自身的对称问题及证明两个函数图象的对称关系问题
构造辅助函数证明微分中值定理及应用
构造辅助函数证明微分中值定理及应用 摘要:构造辅助函数是证明中值命题的一种重要途径。本文给出了几种辅助函数的构造方法:微分方程法,常数K值法,几何直观法,原函数法,行列式法;并且举出具体例子加以说明。 关键字:辅助函数,微分方程,微分中值定理 Constructing auxiliary function to prove differential median theorem and its copplications
Abstract: Constructing auxiliary function is the important method to prove median theorem. This paper gives several ways of constructing auxiliary function:Differential equation, Constant K, Geometry law, Primary function law, Determinant law;and Gives some specific examples to illustrate how to constructing. Key words: Auxiliary function; Differential equation; Differential median theorem 目录 一:引言 (4) 二:数学分析中三个中值定理 (4) 三:五种方法构造辅助函数 (6) 1:几何直观法 (6)
2:行列式法…………………………………………………………………… .第7页 3:原函数法 (8) 4:微分方程法 (10) 5:常数k值法 (13) 四:结论 (15) 参考文献 (15) 致谢 (16) 一:引言 微分中值定理是应用导数的局部性质研究函数在区间上的整体性质的基本工具,在高等数学课程中占有十分重要的地位,是微分学的理论基础,这部分内容理论性强,抽象程度高,所谓中值命题是指涉及函数(包括函数的一阶导数,二阶导数等)定义区间中值一些命
常见的几个函数不等式及其应用
常见的几个函数不等式及其应用
利用上述类似构造函数方法,还可以得到以下一些重要不等式: (6)贝努尼不等式:当1->x 时, )0,1(1)1(<≥+≥+αααα 或x x , ? )10(1)1(<<+≤+ααα x x ? (7))0(2 1)1ln(2 ≥-≥+x x x x ? 二、常见的函数不等的作用 利用上述介绍的函数不等式,无论是去研究函数性质,还是去证明函数不等式或证明数列不等式都会带来许多便利.下面分别联系近几年高考的命题进行说明。 (1)求函数的单调区间或研究函数的单调性,求函数的极值或最值 例 1 (2008年湖南卷,理21)已知函数 x x x x f +- +=1)1(ln )(2 2 . (Ⅰ)求函数)(x f 的单调区间; (Ⅱ)若不等式e )11(≤++α n n 对任意的* ∈N n 都成立,求α的最大值. 解:(Ⅰ)对)(x f 求导数,得 2 2) 1()1(211)1ln(2)(x x x x x x x f +-+-+?+=' )]11 1(21)1[ln(12x x x x +-+-++= . 由不等式④)1)(1(21ln ≥-≤x x x x ,⑤)10)(1 (21ln ≤<-≥x x x x 可知: 当0≥x 时,11≥+x ,有)111(21)1ln(x x x +-+≤+,0)(≤'x f ; 当01≤<-x 时,110≤+ 为增函数. (Ⅱ)由e ) 11(≤++α n n 可知,1)11ln()(≤+?+n n α,所以n n -+≤) 1 1ln(1 α. 记]1,0(1∈=t n ,则t t 1 )1ln(1-+≤ α,]1,0(∈t . 由不等式⑨ )10(2 11)1ln(112ln 1≤<<-+≤-x x x ,可知 1 2 ln 1 1)1ln(1-≥-+t t , 12 ln 1 -≤ ∴α. 所以,α的最大值为12ln 1-. (2)利用常用不等式求参数的取值范围 例2 (2010年全国卷,理22)设x x f --=e 1)(. (Ⅰ)证明:1->x 时,1 )(+≥x x x f ; (Ⅱ)设0≥x 时,1)(+≤ax x x f ,求a 的取值范围. 解:(Ⅰ)利用分析法,结合①式) 1()1ln(1->≤+≤+x x x x x 可以证明. (Ⅱ)因为1e 110+≤- 求函数解析式的几种常 用方法 -CAL-FENGHAI.-(YICAI)-Company One1 求函数解析式的几种常用方法 一、高考要求: 求解函数解析式是高考重点考查内容之一,需引起重视.本节主要帮助考生在深刻理解函数定义的基础上,掌握求函数解析式的几种方法,并形成能力,并培养考生的创新能力和解决实际问题的能力. 重难点归纳: 求解函数解析式的几种常用方法主要有: 1.待定系数法,如果已知函数解析式的构造时,用待定系数法; 2.换元法或配凑法,已知复合函数f [g (x )]的表达式可用换元法,当表达式较简单时也可用配凑法; 3.消参法,若已知抽象的函数表达式,则用解方程组消参的方法求解f (x ); 另外,在解题过程中经常用到分类讨论、等价转化等数学思想方法. 二、题例讲解: 例1.(1)已知函数f (x )满足f (log a x )= )1 (1 2x x a a --.(其中a >0,a ≠1,x >0),求f (x )的表达式. (2)已知二次函数f (x )=ax 2+bx +c 满足|f (1)|=|f (-1)|=|f (0)|=1,求f (x )的表达式. 命题意图:本题主要考查函数概念中的三要素:定义域、值域和对应法则,以及计算能力和综合运用知识的能力. 知识依托:利用函数基础知识,特别是对“f ”的理解,用好等价转化,注意定义域. 错解分析:本题对思维能力要求较高,对定义域的考查、等价转化易出错. 技巧与方法:(1)用换元法;(2)用待定系数法. 解:(1)令t=log a x (a >1,t >0;01,x >0;0 几种构造辅助函数的方法及应用 许生虎 (西北师范大学数学系,甘肃 兰州 730070) 摘 要:在对数学命题的观察和分析基础上给出了构造辅助函数的方法,举例说明了寻求 辅助函数的几种方法及在解题中的作用。 关键词:辅助函数 弧弦差法 原函数法 几何直观法 微分方程法 1. 引言 在解题过程中,根据问题的条件与结论的特点,通过逆向分析、综合运用数学的基本概念和原理,经过深入思考、缜密的观察和广泛的联想,构造出一个与问题有关的辅助函数,通过对函数特征的考查达到解决问题的目的,这种解决问题的方法叫做构造辅助函数法。 构造函数方法在许多命题证明中的应用,使问题得以解决,如在微分中值定理、泰勒公式、中值点存在性、不等式等证明。但构造辅助函数方法的内涵十分丰富没有固定的模式和方法,构造过程充分体现了数学的发现、类比、逆向思维及归纳、猜想、分析与化归思想。但如何通过构造,构造怎样的辅助函数给出命题的证明,是很难理解的问题之一,本文通过一些典型例题归纳、分析和总结常见的构造辅助函数方法及应用。 2. 构造辅助函数的七中方法 2.1“逆向思维法” 例1: 设()x f 在[]1,0 上可微,且满足 ()()?=2 1 21dx x xf f ,证明在][1,0内至少有一点θ, 使()() θθθf f -='. 证明:由所证明的结论出发,结合已知条件,探寻恰当的辅助函数. 将()() θθθf f '变为()()0='?+θθθf f ,联想到()[]()()θθθθf f x xf x '?+='=,可考虑 辅助函数 ()()[].1,0,∈=x x xf x F 因为()()ξξf f =1 , 而对于()x F ,有()()ξξξf F =,()().11f F = 所以,()()1F F =ξ ,由罗尔定理知,至少存在一点()1,ξθ∈,使得()0='θF 即:()() θθθf f -='. 证毕 2.2 原函数法 在微分中值定理(尤其是罗尔定理)求解介值(或零点)问题时要证明的结论往往是某一个函数的导函数的零点,因此可通过不定积分反求出原函数作为辅助函数,用此法构造辅助函数的具体步骤如下: (1)将要证的结论中的;)(0x x 换或ξ (2)通过恒等变换,将结论化为易积分(或易消除导数符号)的形式; (3)用观察法或凑微分法求出原函数(必要时可在等式两端同乘以非零的积分因子),为简便起见,可将积分常数取为零; 集合不等式函数测试试卷 (: 120 分分:120分) 班姓名分 一.(本大共10 小;每小 4 分,共 40 分. 在每小出的四个中,只有 一是符合目要求的) 1.集合 {1,2, 3}的真子集共有() A、 5 个 B、 6 个 C、 7 个 D、 8 个 2.中的阴影表示的集合是() A .A C u B B.B C u A A B C.C u( A B) D.C u( A B) U 3. 以下五个写法中:①{0}∈{ 0,1,2};②{1,2};③{ 0,1,2 }={ 2,0,1 };④0 ; ⑤ A A ,正确的个数有() A .1 个B. 2 个C.3 个D. 4 个 4.已知y f x 是定义在 R 上的奇函数,则下列函数中为奇函数的是( ) ① y f x ② y f x ③ y xf x ④ y f x x A.①③B.②③C.①④D.②④ 5.函数y x 4 )| x | 的定域( 5 A.{ x | x 5} B.{ x | x 4} C.{ x | 4 x 5} D. x x 4且x 5 6.若函数f (x) x 1, ( x 0) , f ( 3) 的()f ( x 2), ( x 0) A .5 B.- 1 C.- 7 D .2 7.已知函数y f x , x a,b ,那么集合 x, y y f x , x a,b x, y x 2 中元素的个数?() A . 1B. 0C. 1 或 0D. 1 或 2 8.已知函数 f (x) 的定域 [ a, b] ,函数 y f (x) 的象如甲所示,函数y f ( x ) 的象是乙中的() 函数、不等式恒成立问题解法(老师用) 恒成立问题的基本类型: 类型1:设)0()(2 ≠++=a c bx ax x f ,(对于任意实数R 上恒成立) (1)R x x f ∈>在0)(上恒成立00?且a ; (2)R x x f ∈<在0)(上恒成立00a 时,],[0)(βα∈>x x f 在上恒成立?????>>-?????<- ?0 )(2020)(2βββαααf a b a b f a b 或或, ],[0)(βα∈ 1 集合不等式知识点整理 一. 集合及其表示法 1、我们把_能确切指定的一些对象的全体_叫做集合。集合中各个对象叫做__元素_,他们的特征是:①__确定性__②__互异性__③__无序性__. 2、数的集合简称数集,我们把常用的数集用特定的字母表示: 全体自然数的集合,记作_N _,不包括零的自然数组成的集合,记作_* N _; 全体整数组成的集合,记作_Z _; 全体有理数组成的集合,记作_Q _; 全体实数组成的集合,记作_R _. 正整数集,负整数集,正有理数集,负有理数集,正实数集,负实数集分别表示为_,,,,,Z Z Q Q R R +-+-+-_ 3、我们把含有有限个数的集合叫做__有限集_,含有无限个元素的集合叫做_无限集_. 我们引进空集,规定空集_不含有任何元素_,记作__ φ __. 4、集合的表示方法有:_列举法、描述法、文氏图_. 5、元素与集合之间应用__,∈?_ 二. 集合之间的关系 1、对于两个集合A 和B ,如果__A 中的任意元素也都是B 中的元素___,那么集合A 叫做集合B 的子集,记作_A B ?_,数学的表达式是_,x A x B ?∈∈__. 2、如果__A 是B 的子集,B 也是A 的子集__,那么叫做集合A 和集合B 相等,记作__A B =_ 【用来证明两个集合相等的方法】 3、对于两个集合,如果__A 是B 的子集且B 中至少有一个元素不属于A _,那么集合A 叫做集合B 的真子集,记作 A B ? ,数学的表达式是_,x A x B ?∈∈且,b B b A ?∈?_. 4、 数集*,,,,N N R Q Z 之间的关系是_*N N Z Q R ????_. 5、空集是任何集合的_子集__,是任何非空集合的_真子集__.【任何涉及到子集和真子集问题,要考虑空集!】 6、若集合是有限集,元素有n 个,则这个集合的子集有___2n _个,真子集有__21n -___ 高考题汇编 一.集合 1、已知集合A={x|x <1},B={x|3x <1},则( ) A 、A∩B={x|x <0} B 、A ∪B=R C 、A ∪B={x|x >1} D 、A∩B=? 2、设集合A={1,2,4},B={x|x 2﹣4x+m=0}.若A∩B={1},则B=( ) A 、{1,﹣3}B 、{1,0}C 、{1,3}D 、{1,5} 3、已知集合A={(x ,y )|x 2+y 2=1},B={(x ,y )|y=x},则A∩B 中元素的个数为( ) A 、3 B 、2 C 、1 D 、0 4.设集合A={1,2,6},B={2,4},C={x ∈R|﹣1≤x≤5},则(A ∪B )∩C=( ) A 、{2} B 、{1,2,4} C 、{1,2,4,5} D 、{x ∈R|﹣1≤x≤5} 5.已知集合P={x|﹣1<x <1},Q={x|0<x <2},那么P ∪Q=( ) A 、(﹣1,2)B 、(0,1)C 、(﹣1,0)D 、(1,2) 二.充分必要条件 1.设函数f (x )=cos x +b sin x (b 为常数),则“b =0”是“f (x )为偶函数”的 A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件 2.若0,0a b >>,则“4a b +≤”是 “4ab ≤”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 3.已知R a ∈,则“1a >”是“ 1 1a <”的( ) A .充分非必要条件B .必要非充分条件C .充要条件 D .既非充分又非必要条件 4.设 , ,则“ ”是“ ”的 A .充要条件 B .充分而不必要条件 C .必要而不充分条件 D .既不充分也不必要条件 5.已知函数f(x)=x 2+bx ,则“b <0”是“f(f(x))的最小值与f(x)的最小值相等”的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 6.设,都是不等于的正数,则“ ”是“ ”的( ) A .充要条件 B .充分不必要条件 C .必要不充分条件 D .既不充分也不必要条件 三.求函数值,计算 7.设()(),0121,1x x f x x x ?< 集合、不等式、函数练习题 1.已知集合}1,1{-=A ,}1|{==mx x B ,且A B A =?,则m 的值为 ( ) A .1 B .—1 C .1或—1 D .1或—1或0 2..已知集合A ={x |x 2-3x -10≤0}集合B ={x |m +1≤x ≤2m -1},若B ?A ,则实数m 的取 A .(-∞,3] B .(0,3] C .[3,+∞) D .(-3,0) 3.如图,U 是全集,M 、P 、S 是U 的3个子集,则阴影部分所表示的集合是 ( ) A 、 ()M P S B 、 ()M P S C 、 ()u M P C S D 、 ()u M P C S 4.设{}022=+-=q px x x A ,{}05)2(62=++++=q x p x x B ,若? ?? ???=21B A ,则=B A ( ) (A )??????-4,31 ,21 (B )??????-4,21 (C )??????31,21 (D)? ?????21 5.函数2x y -=的定义域为( ) A 、(],2-∞ B 、(],1-∞ C 、11,,222????-∞ ? ????? D 、11,,222????-∞ ? ?? ??? 6.不等式3≤|5-2x |<9的解集是 A .(-∞, -2)∪(7, +∞) B .[1, 4] C .[-2, 1]∪[4, 7] D .(-2, 1]∪[4, 7) 7.若不等式x >ax +2 3的解集为(4, b ),则a , b 的值分别为 A .36, 81 B .81, 36 C .41, 9 D .9, 4 1 8.设? ??<+≥-=)10()],6([)10(,2)(x x f f x x x f 则)5(f 的值为( ) A .10 B .11 C .12 D .13 9.设2 2 (1)() (12)2 (2)x x f x x x x x +≤-??=-< 很多学生在学习中把函数、方程和不等式看作三个独立的知识点。实际上,他们之间的联系非常紧密。如果能熟练地掌握三者之间的联系,并在做题时灵活运用,将会有事半功倍的收效。 ★函数与方程之间的关系。 先看函数解析式:(0)y ax b a =+≠,这是一个一次函数,图像是一条直线。对于这个函数而言,x 是自变量,对应的是图像上任意点的横坐标;y 是因变量,也就是函数值,对应的是图像上任意点的纵坐标。如果令0y =,上面的解析式也就变成了0ax b +=,也就是一个一元一次方程了。我们知道,一般在求一个函数图像与x 轴交点的时候,令0y =(同理求一个函数图像与y 轴交点的时候,令0x =)。所以上面的意义可以这样表达:将函数解析式中的y 变为0,那么就得到相应的方程。这个方程的解也就是原先的函数图像与x 轴交点的横坐标。这就是函数解析式与方程之间的关系,它适用于所有的函数解析式。举例说明如下: 例如函数23y x =-的图像如右所示: 该函数与x 轴的交点坐标为3 (,0)2 ,也就是在函数 解析式23y x =-中,令0y =即可。令0y =也 就意味着将一元一次函数23y x =-变成了一元 一次方程230x -=,其解和一次函数与x 轴的交 点的横坐标是相同的。接下来推广到二次函数: 例如函数2 252y x x =-+的图像如右图所示: 很容易验证,该函数图象与x 轴的交点的横坐标 正是方程2 2520x x -+=的解。 如果右边的函数图象是通过列表、描点、连线 的方式作出来的,虽然比较精确,但过程十分繁琐。 在实际中,很多时候并不要求我们把函数图象作得 很精准。有时候只需要作出大致图像即可。 既然上面讲述了函数图象与对应的方程之间 的关系,我们可不可以通过利用方程的根来绘制 对应的函数图象呢 函数2 252y x x =-+对应的方程是2 2520x x -+=,先求出这个方程的两个解。很容 易根据十字相乘法(21)(2)0x x --=得出该方程的两个解分别为 1 2 和2。这样,根据函数 微分中值定理证明中辅助函数的构造 1 原函数法 此法是将结论变形并向罗尔定理的结论靠拢,凑出适当的原函数作为辅助函数,主要思想分为四点:(1)将要证的结论中的ξ换成x ;(2)通过恒等变形将结论化为易消除导数符号的形式;(3)用观察法或积分法求出原函数(等式中不含导数符号),并取积分常数为零;(4)移项使等式一边为零,另一边即为所求辅助函数()F x . 例1:证明柯西中值定理. 分析:在柯西中值定理的结论 ()()'()()()'()f b f a f g b g a g ξξ-=-中令x ξ=,得()()'()()()'()f b f a f x g b g a g x -=-,先变形为()()'()'()()()f b f a g x f x g b g a -=-再两边同时积分得 ()()()()()() f b f a g x f x C g b g a -=+-,令0C =,有() ()()()0()()f b f a f x g x g b g a --=-故()()()()()()() f b f a F x f x g x g b g a -=--为所求辅助函数. 例2:若0a ,1a ,2a ,…,n a 是使得1200231 n a a a a n ++++=+…的实数.证明方程20120n n a a x a x a x ++++=…在(0,1)内至少有一实根. 证:由于2231120120()231n n n n a a a a a x a x a x dx a x x x x C n +++++=++++++?…… 并且这一积分结果与题设条件和要证明的结论有联系,所以设 231120()231 n n a a a F x a x x x x n +=+++++…(取0C =),则 1)()F x 在[0,1]上连续 2)()F x 在(0,1)内可导 3)(0)F =0, 120(1)0231 n a a a F a n =++++=+… 故()F x 满足罗尔定理的条件,由罗尔定理,存在(0,1)ξ∈使'()0F ξ=,即231120()'0231 n n x a a a a x x x x n ξ+=++++=+…亦即20120n n a a a a ξξξ++++=…. 高职单招数学集合不等式函数试 ————————————————————————————————作者:————————————————————————————————日期: 数学周末练习《集合》 刘素卿 2015.6.13 1.,{|32}.{|32}.{|32}.{|32}.{|32} U U R A x x C A A x x x B x x x x x x D x x x ==-≤<= ≤-≥≤-><-><-≥设全集集合,则 或 或 C 或 或 2.已知集合{1,1}M =-,{1,2}N =,则M N U 等于 (A){1} (B){1,1}- (C){1,2} (D){1,1,2}- 3.己知全集U={}8,7,6,5,4,3,2,1 ,{}5,4,3=A ,{}6,3,1=B ,则集合{}8,7,2是( ) A. B A ? B. B A ? C . B C A C U U ? D. B C A C U U ? D 4.设集合A ={}x|-2<x <3,B ={}x|x >1,则集合A ∩B 等于 A.{}x|x >-2 B. {}x|-2<x <3 C.{}x|x >1 C. {}x|1<x <3 5.集合A ={} 3|≤x x ,则下面式子正确的是 ( ) A .2∈A B .2?A C .2?A D .{}?2 A 6.设2:3,:230p x q x x =--=,则下面表述正确的是 ( ) A .p 是q 的充分条件,但p 不是q 的必要条件 B .p 是q 的必要条件,但p 不是q 的充分条件 C .p 是q 的充要条件 D .p 既不是q 的充分条件也不是q 的必要条件 7.若集合{}{}|13,|2A x x B x x =<≤=>,则A B I 等于 (A) {}|1x x > (B) {}|3x x ≤ (C) {}|23x x <≤ (D){}|12x x << (A)0 (B) 1 (C)2 (D)3 8.集合{1,2,3}的子集共有 个 9.满足条件{1,2}{1,2,3}M ??的集合M 的个数为 2011年中考复习二轮材料 函数、方程、不等式综合应用专题 一、专题诠释 函数思想就是用联系和变化的观点看待或提出数学对象之间的数量关系。函数是贯穿在中学数学中的一条主线;函数思想方法主要包括建立函数模型解决问题的意识,函数概念、性质、图象的灵活应用等。函数、方程、不等式的结合,是函数某一变量值一定或在某一范围下的方程或不等式,体现了一般到特殊的观念。也体现了函数图像与方程、不等式的内在联系,在初中阶段,应该深刻认识函数、方程、不等式三部分之间的内在联系,并把这种内在联系作为学生学习的基本指导思想,这也是初中阶段数学最为重要的内容之一。而新课程标准中把这个联系提到了十分明朗、鲜明的程度。因此,第二轮中考复习,对这部分内容应予以重视。 这一专题,往往以计算为主线,侧重决策问题,或综合各种几何知识命题,近年全国各地中考试卷中占有相当的分量。这类问题的主要特点是包含知识点多、覆盖面广、逻辑关系复杂、解法灵活。考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力,要求学生熟练掌握三角形、四边形、三角函数、圆等几何知识,较熟练地应用转化思想、方程思想、分类讨论思想、数形结合思想等常见的数学思想。解题时必须在充分利用几何图形的性质及题设的基础上挖掘几何图形中隐含的数量关系和位置关系,在复杂的“背景”下辨认、分解基本图形,或通过添加辅助线补全或构造基本图形,并善于联想所学知识,突破思维障碍,合理运用方程等各种数学思想才能解决。 二、解题策略和解法精讲 函数与方程、函数与不等式密不可分,紧密联系。 利用kx+b=0或ax2+bx+c=0可以求函数与x轴的交点坐标问题,利用Δ与0的关系可以判定二次函数与x轴的交点个数等。等式与不等式是两种不同的数量关系,但在一定条件下又是可以转化的,如一元二次方程有实数根,可得不等式Δ≥0等。 一次函数及其图像与一元一次方程及一元一次不等式有着密切的关系,函数y=ax+b(a≠0,a,b为常数)中,函数的值等于0时自变量x的值就是一元一次方程ax+b=0(a≠0)的解,所对应的坐标(-b/a,0)是直线y=ax+b与x轴的交点坐标,反过来也成立;?直线y=ax+b在x轴的上方,也就是函数的值大于零,x的值是不等式ax+b>0(a≠0)的解;在x轴的下方也就是函数的值小于零,x的值是不等式ax+b<0(a≠0)的解. 一般地,每个二元一次方程组,都对应着两个一次函数,于是也就是对应着两条直线,从“数”的角度看,解方程相当于考虑自变量为何值时两个函数的值相等,以及这两函数值是何值;从形的角度考虑,解方程组相当于确定两条直线的交点坐标。 两条直线的位置关系与二元一次方程组的解: (1)二元一次方程组有唯一的解直线y=k1x+b1不平行于直线y=k2x+b2 k1≠k2.(2)二元一次方程组无解直线y=k1x+b1∥直线y=k2x+b2 k1=k2,b1≠b2. (3)二元一次方程组有无数多个解直线y=k1x+b1与y=k2x+b2重合k1=k2,b1=b2.在复习中,本专题应抓好两个要点:第一个要点是各个内容之间相关概念之间的联系、第二个要点是各个内容之间相关性质之间的联系,以期在综合运用中灵活把握。 三、考点精讲 考点一:函数与方程(组)综合应用 例1.(2010广西梧州)直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b =0的解是x=______ 【分析】∵直线y=2x+b与x轴的交点坐标是(2,0),则x=2时,y=0,∴关于x的方程2x+b=0的解是x=2。 高中数学常用公式及常用结论(集合&不等式&函数) 1. 元素与集合的关系 U x A x C A ∈??,U x C A x A ∈??. 2.德摩根公式 ();()U U U U U U C A B C A C B C A B C A C B == . 3.包含关系 A B A A B B =?= U U A B C B C A ???? U A C B ?=Φ U C A B R ?= 4.容斥原理 ()()card A B cardA cardB card A B =+- ()()card A B C cardA cardB cardC card A B =++- ()()()()card A B card B C card C A card A B C ---+ . 5.集合12{,,,}n a a a 的子集个数共有2n 个;真子集有2n –1个;非空子集有2n –1个;非空的真子集有2n –2个. 6.二次函数的解析式的三种形式 (1)一般式2 ()(0)f x ax bx c a =++≠; (2)顶点式2 ()()(0)f x a x h k a =-+≠; (3)零点式12()()()(0)f x a x x x x a =--≠. 7.解连不等式()N f x M <<常有以下转化形式 ()N f x M <- ? 11 ()f x N M N >--. 8.方程0)(=x f 在),(21k k 上有且只有一个实根,与0)()(21 中值定理构造辅助函数 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】 微分中值定理证明中辅助函数的构造 1 原函数法 此法是将结论变形并向罗尔定理的结论靠拢,凑出适当的原函数作为辅助函数,主要思想分为四点:(1)将要证的结论中的ξ换成x ;(2)通过恒等变形将结论化为易消除导数符号的形式;(3)用观察法或积分法求出原函数(等式中不含导数符号),并取积分常数为零;(4)移项使等式一边为零,另一边即为所求辅助函数()F x . 例1:证明柯西中值定理. 分析:在柯西中值定理的结论()()'()()()'() f b f a f g b g a g ξξ-=-中令x ξ=,得()()'()()()'()f b f a f x g b g a g x -=-,先变形为()()'()'()()() f b f a g x f x g b g a -=-再两边同时积分得()()()()()()f b f a g x f x C g b g a -=+-,令0C =,有()()()()0()() f b f a f x g x g b g a --=-故()()()()()()() f b f a F x f x g x g b g a -=--为所求辅助函数. 例2:若0a ,1a ,2a ,…,n a 是使得1200231 n a a a a n ++++=+…的实数.证明方程20120n n a a x a x a x ++++=…在(0,1)内至少有一实根. 证:由于2231120120()231 n n n n a a a a a x a x a x dx a x x x x C n +++++=++++++?…… 并且这一积分结果与题设条件和要证明的结论有联系,所以设 231120()231 n n a a a F x a x x x x n +=+++++…(取0C =),则 1)()F x 在[0,1]上连续 2)()F x 在(0,1)内可导 3)(0)F =0, 120(1)0231 n a a a F a n =++++=+… 集合不等式函数测试试卷 (时间:120分钟 总分:120分) 班级 姓名 评分 一.选择题(本大题共10小题;每小题4分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的) 1.集合{1,2,3}的真子集共有( ) A 、5个 B 、6个 C 、7个 D 、8个 2.图中的阴影表示的集合是( ) A .B C A u ? B .A C B u ? C .)(B A C u ? D .)(B A C u ? 3. 以下五个写法中:①{0}∈{0,1,2};②??{1,2};③{0,1,2}={2,0,1};④?∈0;⑤A A =??, 正确的个数有( ) A .1个 B .2个 C .3个 D .4个 4.已知()x f y =是定义在R 上的奇函数,则下列函数中为奇函数的是( ) ①()x f y = ②()x f y -= ③()x xf y = ④()x x f y += A .①③ B .②③ C .①④ D .②④ 5.函数5 ||4 --= x x y 的定义域为( ) A .}5|{±≠x x B .}4|{≥x x C .}54|{< 学年论文 题目凹凸函数及其在证明不等式中的应用学院数学与计算机科学学院 专业数学与应用数学 级别10级 姓名洪玉茹 学号101301040 摘 要 首先给出了凸函数的定义,.接着给出了凸函数的一个判定定理 以及Jesen 不等式.通过例题展示了凸函数在不等式证明中的应用.凸函数具有重要的理论研究价值和实际广泛应用,利用凸函数的性质证明不等式;很容易证明不等式的正确性.因此,正确理解凸函数的定义、性质及应用,更对有关学术问题进行推广研究起着举足轻重的作用. 关键词 凸函数,凸函数判定定理Jensen 不等式。 下面我们主要研究凸函数,凹函数由读者自行探索。 一、 凸函数的等价定义 定义1 若函数()f x 对于区间(,)a b 内的任意12,x x 以及(0,1)λ∈,恒有 []1212(1)()(1)()f x x f x f x λλλλ+-≤+-, 则称()f x 为区间(,)a b 上的凸函数. 其几何意义为:凸函数曲线()y f x =上任意两点1122(,()),(,())x f x x f x 间的 线总在曲线之上. 定义2 若函数()f x 在区间(,)a b 内连续,对于区间(,)a b 内的任意12,x x ,恒有 []12121 ( )()()22 x x f f x f x +≤+, 则称()f x 为区间(,)a b 上的凸函数. 其几何意义为:凸函数曲线()y f x =上任意两点1122(,()),(,())x f x x f x 间割线的中点总在曲线上相应点(具有相同横坐标)之上. 定义3 若函数()f x 在区间(,)a b 内可微,且对于区间(,)a b 内的任意x 及0x , 恒有 000()()()()f x f x f x x x '≥+-, 则称()f x 为区间(,)a b 上的凸函数.求函数解析式的几种常用方法
几种构造辅助函数的方法及应用
集合不等式函数测试试卷.doc
函数不等式恒成立问题经典总结
集合不等式知识点整理(答案)
高考数学题汇编(集合函数不等式充分必要条件)
集合、不等式、函数练习题
函数、方程、不等式之间的关系
中值定理构造辅助函数
高职单招数学集合不等式函数试
函数方程不等式综合应用专题
数学公式(集合&不等式&函数)
中值定理构造辅助函数
集合不等式函数测试试卷
函数的凹凸性在不等式证明中的应用
