最优化实验报告(单纯形法的matlab程序,lingo程序)

实验一:线性规划单纯形算法
一、实验目的
通过实验熟悉单纯形法的原理,掌握Matlab 循环语句的应用,提高编程的能力和技巧。
二、实验用仪器设备、器材或软件环境
Windows Xp 操作系统 ,Matlab6.5,计算机
三、算法
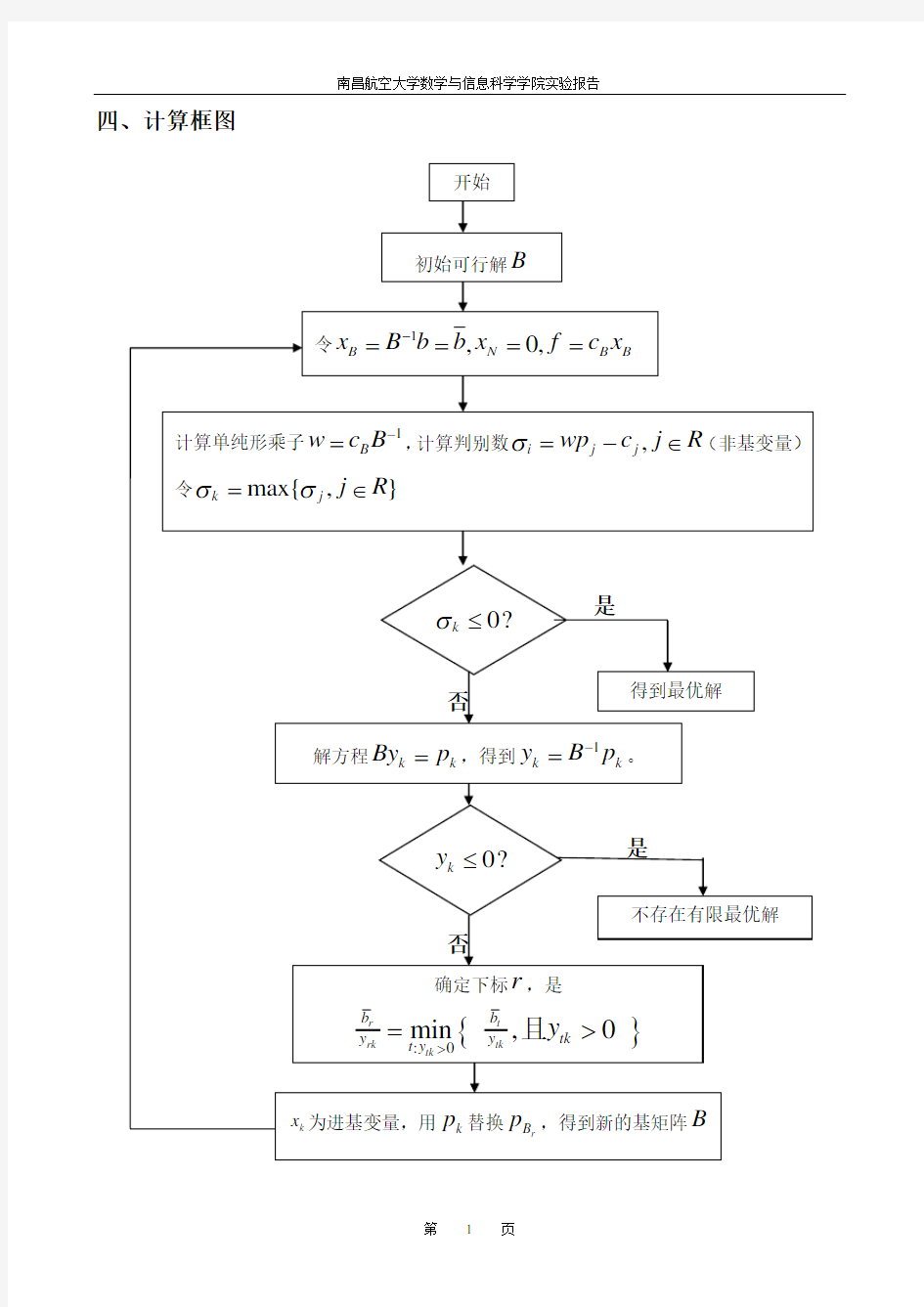
对于一般的标准形式线性规划问题(求极小问题),首先给定一个初始
基本可行解。设初始基为B,然后执行如下步骤:
(1).解B Bx b =,求得1
B
x B b -=,0,N B B x f c x ==令计算目标函数值 1(1,2,...,)i m B b i -=i 以b 记的第个分量
(2).计算单纯形乘子w
, B wB C =,得到1
B w
C B -=,对于非基变量,计算判别数
1i i i B i i z c c B p c σ-=-=-,令 max{}k i i i R
z c σ∈=-,R 为非基变量集合
若判别数0k σ≤ ,则得到一个最优基本可行解,运算结束;否则,转到下一步
(3).解k k By p =,得到
1
k k y B p -=;若0k y ≤,即k y 的每个分量均非正数,则停止计算,问题不存在有限最优解,否则,进行步骤(4). (4).确定下标r,使
{
}
:0
min ,0
t r
rk
tk
tk b b tk y y t y y >=>且r B x 为离基变量。
k x 为进基变量,用k p 替换r B p ,得到新的基矩阵B ,返回步骤(1)。
对于极大化问题,可以给出完全类似的步骤,只是确定进基变量的准则不同。对于极大化问题,应令
min{}k k j j z c z c -=-
四、计算框图 是
否
是
否
开始
初始可行解B
令1,0,B
N B B x B b b x f c x -====
计算单纯形乘子1
B w c B -=,计算判别数,i j j wp c j R σ=-∈(非基变量)
令max{,}k
j j R σσ=∈
0?k σ≤
得到最优解
解方程k
k By p =,得到1k k y B p -=。
0?k y ≤
不存在有限最优解
确定下标r ,是
{
}:0
min ,0
t r
rk
tk
tk b b tk y y t y y >=>且
k x 为进基变量,用
k p 替换r B p ,得到新的基矩阵B
五、计算程序
function [x,f]=zuiyouhua(A,b,c)
size(A)=[m,n];
i=n+1:n+m;%基变量集合,后面m个松弛变量为初始基变量; N=1:n;%初始非基变量;
B=eye(m,m);
xb=b';
xn=zeros(m,1);
f1=0;
w=zeros(1,m);
z=-c;%初始判别数;
flag=1;
while(1)
[a,k]=max(z);%x(k)为进基变量;
if a<=0
flag=0;
break
else
y=inv(B)*A(:,k)
if y<=0
flag=0;
fprintf('不存在最优解')
break
end
t=find(y>0);
[a,r1]=min(b1(t)./y(t))
r=t(r1); %基变量中第r 个变量为退基变量; i(:,r)=k
B(:,r)=A(:,k);%换基,即将原基中第r个变量换成第k个变量; cb=c(:,i);%新的价值系数; xb=inv(B)*b; b0=xb; x=zeros(1,n+m) x(:,i)=xb' f=cb*xb
z=cb*inv(B)*A-c;%可用z=cb*(B\A)-c,判别数. end end
六、数值实验及结果分析
求解线性规划问题:
???????=≥≤-=+-=++--4
,3,2,1,012216443033..3min 21421
3212
1i x x x x x x x x x t s x x i
在工作区输入:
A=[3,3,1,0;-4,-4,0,1;2,-1,0,0];
b=[30,16,12]';
c=[-3,1,0,0];
[x,f]=zuiyouhua(A,b,c)
x =
7.3333 2.6667 0 0 0 56.0000 0
f =
-19.3333
检验结果正确
七、心得体会
通过这次试验,使我对单纯形法的计算有了更进一步的了解。但是在编程过程中由于对matlab不是很熟悉还是遇到了很多麻烦,所以我觉得老师在让我们编程的时候不能只
是简单的介绍一下算法,更要着重说明一下软件的使用方法。这样我们在编程的时候就能
更加的得心应手。本次完全仿照老师给的程序,没有能够形成自己的东西。自己编程的能
力还是很差的,对于这种已经给出算法的程序也不能正确的编写出来。所以在今后要加强
这方面的学习。
实验二:Lingo求解动态规划问题
一、实验目的
通过本实验熟悉动态规划的原理,了解动态规划的应用,并能利用数学软件(Lingo )求解动态规划模型。
二、问题重述
某公司打算向他的营业区增设4个销售点,各区赚取的利润与增设的销售点个数有关,其数据为: 销售店增加数
第一区利润(万元)
第二区利润(万元)
第三区利润(万元)
第四区利润(万元)
0 160 190 200 250 1 310 225 298 308 2 541 445 399 487 3 600 517 601 655 4
705
632
721
674
试求各区应分配几个增设的销售书店,才能使利润最大?其值是多少?
三、数学模型
设(1,2,3,4)i x i =为第i 区增设销售点的个数,()(1,2,3,4)i i g x i =为增设第i 个点所
得到的盈利。故问题模型为:
112233441234max ()()()()..40,1,2,3,4
i z g x g x g x g x s t x x x x x i =++++++=≥=
四、计算编程 model :
sets :
quyu/1..4/; zl/0..4/;
lirun(quyu,zl):g,c;
endsets
data:
g=160 310 541 600 705,
190 225 445 517 632,
200 298 399 601 721,
250 308 487 655 674;
enddata
max=@sum(lirun(i,j):g(i,j)*c(i,j));
@for(quyu(i):@sum(lirun(i,j):c(i,j))<=1);
@for(lirun:@bin(c));
@sum(lirun(i,j):(j-1)*c(i,j))=4;
End
五、计算结果
Global optimal solution found.
Objective value: 1436.000
Objective bound: 1436.000
Infeasibilities: 0.000000
Extended solver steps: 0
Total solver iterations: 0
Variable Value Reduced Cost G( 1, 1) 160.0000 0.000000 G( 1, 2) 310.0000 0.000000 G( 1, 3) 541.0000 0.000000 G( 1, 4) 600.0000 0.000000 G( 1, 5) 705.0000 0.000000 G( 2, 1) 190.0000 0.000000 G( 2, 2) 225.0000 0.000000 G( 2, 3) 445.0000 0.000000 G( 2, 4) 517.0000 0.000000 G( 2, 5) 632.0000 0.000000 G( 3, 1) 200.0000 0.000000 G( 3, 2) 298.0000 0.000000 G( 3, 3) 399.0000 0.000000 G( 3, 4) 601.0000 0.000000 G( 3, 5) 721.0000 0.000000 G( 4, 1) 250.0000 0.000000 G( 4, 2) 308.0000 0.000000 G( 4, 3) 487.0000 0.000000 G( 4, 4) 655.0000 0.000000
G( 4, 5) 674.0000 0.000000 C( 1, 1) 0.000000 -160.0000 C( 1, 2) 0.000000 -310.0000 C( 1, 3) 1.000000 -541.0000 C( 1, 4) 0.000000 -600.0000 C( 1, 5) 0.000000 -705.0000 C( 2, 1) 0.000000 -190.0000 C( 2, 2) 0.000000 -225.0000 C( 2, 3) 1.000000 -445.0000 C( 2, 4) 0.000000 -517.0000 C( 2, 5) 0.000000 -632.0000 C( 3, 1) 1.000000 -200.0000 C( 3, 2) 0.000000 -298.0000
六、分析、检验和结论
结果中Variable 列对应的(,)C i j ,i 表示第i 区,j 表示增加1j -个销售点,Value
列对应的0.000000表示不增加销售点,1.000000表示增加销售点。例如 C( 1, 3) 1.000000表示第一区增加两个销售点。(,
)G i j 表示第i 行第j 列对应的值。从结果中我们
知道最优解是第一区和第二区分别增加2个销售点,第三区和第四区增加0个销售点此时盈利z =1436为最优值。经过检验结果正确。
七、心得体会
通过实验我熟悉了Lingo 的使用方法,学会了用Lingo 编写计算程序。同时也掌握了分配问题的算法。由于之前没有接触过Lingo 软件,老师也没有系统的讲述Lingo 的使用规则,所以我通过老师给的例题,依葫芦画瓢的写出了本问题的程序。但是对实质性的东西还不是很了解,没有达到举一反三的地步。仅仅只会分配法这一类问题的算法和程序,对程序中函数的具体应用还不了解。
所以我希望老师能在上实验课之前给我们讲述一下这种题型编程的注意事项,和涉及函数的具体意思,这样更有利于我们对问题的理解。同时我也体会到自己没有主动的去学习而是被动的等待老师来讲解,从而造成了实验过程中出现了一些问题。所以,以后要主动学习。
最优化实验报告(单纯形法的matlab程序,lingo程序)
实验一:线性规划单纯形算法 一、实验目的 通过实验熟悉单纯形法的原理,掌握Matlab 循环语句的应用,提高编程的能力和技巧。 二、实验用仪器设备、器材或软件环境 Windows Xp 操作系统 ,Matlab6.5,计算机 三、算法 对于一般的标准形式线性规划问题(求极小问题),首先给定一个初始 基本可行解。设初始基为B,然后执行如下步骤: (1).解B Bx b =,求得1 B x B b -=,0,N B B x f c x ==令计算目标函数值 1(1,2,...,)i m B b i -=i 以b 记的第个分量 (2).计算单纯形乘子w , B wB C =,得到1 B w C B -=,对于非基变量,计算判别数 1i i i B i i z c c B p c σ-=-=-,令 max{}k i i i R z c σ∈=-,R 为非基变量集合 若判别数0k σ≤ ,则得到一个最优基本可行解,运算结束;否则,转到下一步 (3).解k k By p =,得到 1 k k y B p -=;若0k y ≤,即k y 的每个分量均非正数,则停止计算,问题不存在有限最优解,否则,进行步骤(4). (4).确定下标r,使 { } :0 min ,0 t r rk tk tk b b tk y y t y y >=>且r B x 为离基变量。 k x 为进基变量,用k p 替换r B p ,得到新的基矩阵B ,返回步骤(1)。 对于极大化问题,可以给出完全类似的步骤,只是确定进基变量的准则不同。对于极大化问题,应令 min{}k k j j z c z c -=-
四、计算框图 是 否 是 否 开始 初始可行解B 令1,0,B N B B x B b b x f c x -==== 计算单纯形乘子1 B w c B -=,计算判别数,i j j wp c j R σ=-∈(非基变量) 令max{,}k j j R σσ=∈ 0?k σ≤ 得到最优解 解方程k k By p =,得到1k k y B p -=。 0?k y ≤ 不存在有限最优解 确定下标r ,是 { }:0 min ,0 t r rk tk tk b b tk y y t y y >=>且 k x 为进基变量,用 k p 替换r B p ,得到新的基矩阵B
单纯形法matlab
数 学 软 件 与 实 验 数学与信息科学学院 信息与计算科学
单纯形法的Matlab程序如下:function [xx,fm]=myprgmh(m,n,A,b,c) B0=A(:,1:m); cb=c(:,1:m); xx=1:n; sgm=c-cb*B0^-1*A; h=-1; sta=ones(m,1); for i=m+1:n if sgm(i)>0 h=1; end end while h>0 [msg,mk]=max(sgm); for i=1:m sta(i)=b(i)/A(i,mk); end [mst,mr]=min(sta); zy=A(mr,mk); for i=1:m
if i==mr for j=1:n A(i,j)=A(i,j)/zy; end b(i)=b(i)/zy; end end for i=1:m if i~=mr for j=1:n A(i,j)=A(i,j)-A(i,mk)*A(mr,j); end b(i)=b(i)-A(i,mk)*b(mr); end end B1=A(:,1:m); cb(mr)=c(mk); xx(mr)=mk; sgm=c-cb*B1*A; for i=m+1:n if sgm(i)>0 h=1;
end end end fm=c*xx; 例题: 编写下列求解如下线性规划问题的单纯形法函数min f'x s.t ax<=b(其中b>=0) 函数形式function [x,fval,it,op]=singl(f,a,b) 输出中x为最优解 fval为最优值 it为迭代次数 无最优解op=0 有最优解op=1 编写程序如下: function [x,fval,it,op]=singl(f,a,b) [m,n]=size(a); c=[a eye(m) b;f' zeros(1,m+1)]; fval=0; x=zeros(m+n,1); op=1; it=0; e=zeros(1,m); lie=find(f<0); l=length(lie); while(l>0) for j=1:l d=find(c(:,lie(j)));
Matlab频谱分析程序
Matlab频谱分析程序
Matlab 信号处理工具箱 谱估计专题 频谱分析 Spectral estimation (谱估计)的目标是基于一个有限的数据集合描述一个信号的功率(在频率上的)分布。功率谱估计在很多场合下都是有用的,包括对宽带噪声湮没下的信号的检测。 从数学上看,一个平稳随机过程n x 的power spectrum (功率谱)和correlation sequence (相关序列)通过discrete-time Fourier transform (离散时间傅立叶变换)构成联系。从normalized frequency (归一化角频率)角度看,有下式 ()()j m xx xx m S R m e ωω∞ -=-∞ = ∑ 注:()() 2 xx S X ωω=,其中 ()/2 /2 lim N j n n N N X x e N ωω=-=∑ πωπ -<≤。 其matlab 近似为X=fft(x,N)/sqrt(N),在下文中()L X f 就是指matlab fft 函数的计算结果了 使用关系2/s f f ωπ=可以写成物理频率f 的函数,
其中s f 是采样频率 ()()2/s jfm f xx xx m S f R m e π∞ -=-∞ = ∑ 相关序列可以从功率谱用IDFT 变换求得: ()()()/2 2//2 2s s s f jfm f j m xx xx xx s f S e S f e R m d df f πωππ ωωπ- -= =?? 序列n x 在整个Nyquist 间隔上的平均功率可以 表示为 ()()() /2 /2 02s s f xx xx xx s f S S f R d df f ππ ωωπ- -= =?? 上式中的 ()()2xx xx S P ωωπ = 以及()()xx xx s S f P f f = 被定义为平稳随机信号n x 的power spectral density (PSD)(功率谱密度) 一个信号在频带[]1 2 1 2 ,,0ωωωω π ≤<≤上的平均功率 可以通过对PSD 在频带上积分求出 []()()2 1 121 2 ,xx xx P P d P d ωωωωωω ωωωω-- = +?? 从上式中可以看出()xx P ω是一个信号在一个无 穷小频带上的功率浓度,这也是为什么它叫做功率谱密度。
matlab单纯形法
%求解标准型线性规划:max c*x;s.t. A*x=b;x>=0 %本函数中的A是单纯初始表,包括:最后一行是初始的检验数,最后一列是资源向量b %N是初始的基变量的下标 %输出变量sol是最优解 %输出变量val是最优值,kk是迭代次数 function [sol,val,kk]=ssimplex(A,N) [mA,nA]=size(A); kk=0; %迭代次数 flag=1; while flag kk=kk+1; if A(mA,:)<=0 %已找到最优解 flag=0; sol=zeros(1,nA-1);%给每个变量赋初值0 for i=1:mA-1 sol(N(i))=A(i,nA);%给基变量赋新值(替换0) end %给出最优解 val=-A(mA,nA); else for i=1:nA-1 if A(mA,i)>0&A(1:mA-1,i)<=0 %问题有无界解 disp('have infinite solution!'); flag=0; break; end end if flag %还不是最优表,进行转轴运算 temp=0; for i=1:nA-1 if A(mA,i)>temp temp=A(mA,i); inb=i; % 进基变量的下标 end end %选择最大检验数纵向对应的变量为进基变量 sita=zeros(1,mA-1); for i=1:mA-1 if A(i,inb)>0 sita(i)=A(i,nA)/A(i,inb); end end temp=inf; for i=1:mA-1 if sita(i)>0&sita(i) 信号检测与估值 仿真报告 题目信号检测与估值的MATLAB仿真学院通信工程学院 专业通信与信息系统 学生姓名 学号 导师姓名 作业1 试编写程序,画出相干移频键控、非相干移频键控(无衰落)和瑞利衰落信道下非相干移频键控的性能曲线。 (1)根据理论分析公式画性能曲线; (2)信噪比范围(0dB-10dB),间隔是1dB; (3)信噪比计算SNR=10lg(Es/N0) 一、脚本文件 1、主程序 %******************************************************** %二元移频信号检测性能曲线(理论分析) %FSK_theo.m %******************************************************** clear all; clc; SNRindB=0:1:20; Pe_CFSK=zeros(1,length(SNRindB)); Pe_NCFSK=zeros(1,length(SNRindB)); Pe_NCFSK_Rayleigh=zeros(1,length(SNRindB)); for i=1:length(SNRindB) EsN0=exp(SNRindB(i)*log(10)/10); Es_aveN0=exp(SNRindB(i)*log(10)/10); Pe_CFSK(i)=Qfunct(sqrt(EsN0));%相干移频键控系统 Pe_NCFSK(i)=0.5*exp(-EsN0/2);%非相干移频键控系统(无衰落) Pe_NCFSK_Rayleigh(i)=1/(2+Es_aveN0);%非相干移频键控系统(瑞利衰落)end semilogy(SNRindB,Pe_CFSK,'-o',SNRindB,Pe_NCFSK,'-*',SNRindB,Pe_NCFSK_Rayleigh ,'-'); xlabel('Es/No或平均Es/No(dB)'); ylabel('最小平均错误概率Pe'); legend('相干移频','非相干移频(无衰落)','非相干移频(瑞利衰落)'); title('二元移频信号检测性能曲线'); axis([0 20 10^-7 1]); grid on; 2、调用子函数 %******************************************************** %Q函数 %Qfunct.m %******************************************************** 算法实现与分析 算法1.单纯形法 具体算例: 标准化后: 用单纯形法求解,程序如下: clear clc M=1000000; A=[3,2,-3,1,0;1,-2,1,0,1];%系数矩阵 C=[-3,1,2,M,M,0];%价值矩阵 B=[6;4]; Xt=[4 5]; for i=1:length(C)-1 D=0; for j=1:length(Xt) D=D+A(j,i)*C(Xt(j)); end xi(i)=C(i)-D; end s=[]; for i=1:length(xi) if xi(i)<0 s=[s,i]; end end f=length(s); h=1; while(f) for k=1:length(s) j=1; A x=[]; for i=1:length(Xt) if A(i,s(k))>0 x(j)=i; j=j+1; end end x if(length(x)+1==1) break; end y=1 x for i=1:length(x) if B(x(i))/A(x(i),s(k)) 实验报告三 实验目的: 实现常规波束形成及基于MUSIC 方法的方位估计。 实验内容: 1)若干阵元的接收阵,信号频率为10KHz ,波束主轴12度,仿真给出常规波束形成的波束图。 2)16个阵元的均匀线列阵,信号频率为10KHz ,信号方位为12度,用MUSIC 方法完成目标定向,信噪比-5dB ,0dB ,5dB 。 i) 波束形成时的阵型设计为两种,一种是均匀线列阵,阵元16个;一种是均匀圆阵,阵元数为16个,比较这两种阵型的波束图。 ii )比较不同信噪比下MUSIC 方法估计的性能(统计100次)。 实验原理: i)常规波束形成: 如图所示,基阵的输出),(θt v 。 ∑∑=*=* ==M m i i M m i i w t x t x w t v 1 1 ) ()()()(),(θθθ 采用向量符号则有, )()()()(),(H H θθθw x x w t t t v == 式中,x(t)和w(q )分别为观测数据向量和加权系数向量, ) ,(θt v 图 1 波束形成器基本原理图 T M 21])()()([)(t x t x t x t Λ=x T M 21])()()([)(θθθθw w w Λ =w 基阵输出端的空间功率谱表示为: ) ()( )()]()([)( )]()()()([ )],(),([ ] ),([)(H H H H H *2 θθθθθθθθθθRw w w x x w w x x w =====t t E t t E t v t v E t v E P 式中,R 为观测数据的协方差矩阵。 ii )基于MUSIC 方法的方位估计: )()()()(1 t n t s a t x i d i +=∑=θ T M 21])()()([)(t x t x t x t Λ =x )()()()(t n t s A t x +=θ 假设: (1 ) 信号源的数目d 是已知的, 且d < M ; (2 ) 各信号的方向矢量是相互独立的, 即)(θA 是一个列满秩矩阵; (3 ) 噪声)(t n 是空间平稳随机过程, 为具有各态历经性的均值为零、方差为σ2n 的高斯过程; (4 ) 噪声各取样间是统计独立的。 在上述假设条件下, 基阵输出的协方差矩阵可表示为: I A AR t x t x E R H s H 2])()([α+== 其中, R s 为信号的协方差矩阵;I 为单位矩阵。对R 进行特征分解, 并以特 征值降值排列可得 H m m M d m m H m m d m m e e e e R ∑∑+==+ =1 1λ λ 信号子空间与噪声子空间正交。 若噪声子空间记为E N , 即 ∑+== M d m H m m N e e E 1 单纯形法(Matlab 程序) %%单纯形法( Matlab 程序) a=input('input the major matrix A '); b=input('input the matrix b '); n=input('input the judgement '); %%为计数器(确定循环次数) g=0; while g<40 %%确定非负 alength=max(size(n)); blength=max(size(b)); m=0; for i=1:alength if n(i)>=0 m=m+1; end end; if m==alength x=b; break end; %%找 K s=min(n); for i=1:alength if n(i)==s k=i; break end; end; %%a[i,k] 的非负性 m=0; for i=1:blength if a(i,k)<0 m=m+1; end; end; if m==blength disp('x does not exit'); judge=1; break end; %%找 L 确定主元 cc=100000; for i=1:blength if a(i,k)>0 if (b(i)/a(i,k))< cc cc=b(i)/a(i,k); end end end; for i=1:blength if a(i,k)~=0 if (b(i)/a(i,k))==cc l=i; break end end end; %%计算 ,a 标准化 zu=a(l,k); aa=a; for i=1:l-1 for j=1:alength aa(i,j)=a(i,j)- a(l,j)*a(i,k)/a(l,k); end end; for i=l+1:blength for j=1:alength aa(i,j)=a(i,j)- a(l,j)*a(i,k)/a(l,k); end end; for j=1:alength aa(l,j)=a(l,j)/zu; end; %%b勺判别 bb=b; bb(l)=b(l)/zu; for i=1:l-1 bb(i)=b(i)- b(l)*a(i,k)/a(l,k); end; for i=l+1:blength bb(i)=b(i)- b(l)*a(i,k)/a(l,k); end; b=bb; %%确定判别数 线性规划 线性规划是处理线性目标函数和线性约束的一种较为成熟的方法,目前已经广泛应用于军事、经济、工业、农业、教育、商业和社会科学等许多方面。 8.2.1 基本数学原理 线性规划问题的标准形式是: ????? ??????≥=+++=+++=++++++=0,,,min 21221122222121112 121112211n m n mn m m n n n n n n x x x b x a x a x a b x a x a x a b x a x a x a x c x c x c z 或 ???? ?????=≥===∑∑==n j x m i b x a x c z j n j i j ij n j j j ,,2,1,0,,2,1,min 1 1 写成矩阵形式为: ?? ???≥==O X b AX CX z min 线性规划的标准形式要求使目标函数最小化,约束条件取等式,变量b 非负。不符合这几个条件的线性模型可以转化成标准形式。 MATLAB 采用投影法求解线性规划问题,该方法是单纯形法的变种。 8.2.2 有关函数介绍 在MATLAB 工具箱中,可用linprog 函数求解线性规划问题。 linprog 函数的调用格式如下: ●x=linprog(f,A,b):求解问题minf'*x ,约束条件为A*x<=b 。 ●x=linprog(f,A,b,Aeq,beq):求解上面的问题,但增加等式约束,即Aeq*x=beq 。若没有不等式约束,则令A=[ ],b=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub):定义设计x 的下界lb 和上界ub ,使得x 始终在该范围内。若没有等式约束,令Aeq=[ ],beq=[ ]。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0):设置初值为x0。该选项只适用于中型问题,默认时大型算法将忽略初值。 ●x=linprog(f,A,b,Aeq,beq,lb,ub,x0,options):用options 指定的优化参数进行最小化。 ●[x,fval]=linprog(…):返回解x 处的目标函数值fval 。 ●[x,lambda,exitflag]=linprog(…):返回exitflag 值,描述函数计算的退出条件。 ●[x,lambda,exitflag,output]=linprog(…):返回包含优化信息的输出参数output 。 ●[x,fval,exitflag,output,lambda]=linprog(…):将解x 处的拉格朗日乘子返回到lambda 参数中。 Matlab 信号处理工具箱 谱估计专题 频谱分析 Spectral estimation (谱估计)的目标是基于一个有限的数据集合描述一个信号的功率(在频率上的)分布。功率谱估计在很多场合下都是有用的,包括对宽带噪声湮没下的信号的检测。 从数学上看,一个平稳随机过程n x 的power spectrum (功率谱)和correlation sequence (相关序列)通过discrete-time Fourier transform (离散时间傅立叶变换)构成联系。从normalized frequency (归一化角频率)角度看,有下式 ()()j m xx xx m S R m e ωω∞ -=-∞ = ∑ 注:()() 2 xx S X ωω=,其中( )/2 /2 lim N j n n N n N X x e ωω=-=∑ πωπ-<≤。其matlab 近似为X=fft(x,N)/sqrt(N),在下文中()L X f 就是指matlab fft 函数的计算结果了 使用关系2/s f f ωπ=可以写成物理频率f 的函数,其中s f 是采样频率 ()()2/s jfm f xx xx m S f R m e π∞ -=-∞ = ∑ 相关序列可以从功率谱用IDFT 变换求得: ()()()/2 2//2 2s s s f jfm f j m xx xx xx s f S e S f e R m d df f πωπ π ωωπ--= =? ? 序列n x 在整个Nyquist 间隔上的平均功率可以表示为 ()()() /2 /2 02s s f xx xx xx s f S S f R d df f π π ωωπ--= =? ? 多目标线性规划的若干解法及MATLAB 实现 一.多目标线性规划模型 多目标线性规划有着两个和两个以上的目标函数,且目标函数和约束条件全是线性函 数,其数学模型表示为: 11111221221122221122max n n n n r r r rn n z c x c x c x z c x c x c x z c x c x c x =+++??=+++?? ??=+++? (1) 约束条件为: 1111221121122222112212,,,0 n n n n m m mn n m n a x a x a x b a x a x a x b a x a x a x b x x x +++≤??+++≤?? ??+++≤?≥?? (2) 若(1)式中只有一个1122i i i in n z c x c x c x =+++ ,则该问题为典型的单目标线性规划。我们记:()ij m n A a ?=,()ij r n C c ?=,12(,,,)T m b b b b = ,12(,,,)T n x x x x = , 12(,,,)T r Z Z Z Z = . 则上述多目标线性规划可用矩阵形式表示为: max Z Cx = 约束条件:0 Ax b x ≤?? ≥? (3) 二.MATLAB 优化工具箱常用函数[3] 在MA TLAB 软件中,有几个专门求解最优化问题的函数,如求线性规划问题的linprog 、求有约束非线性函数的fmincon 、求最大最小化问题的fminimax 、求多目标达到问题的fgoalattain 等,它们的调用形式分别为: ①.[x,fval]=linprog(f,A,b,Aeq,beq,lb,ub) f 为目标函数系数,A,b 为不等式约束的系数, Aeq,beq 为等式约束系数, lb,ub 为x 的下 限和上限, fval 求解的x 所对应的值。 算法原理:单纯形法的改进方法投影法 ②.[x,fval ]=fmincon(fun,x0,A,b,Aeq,beq,lb,ub ) fun 为目标函数的M 函数, x0为初值,A,b 为不等式约束的系数, Aeq,beq 为等式约束 %模拟2ASK % Pe=zeros(1,26); jishu=1; for snr=-10:0.5:15 max = 10000; s=round(rand(1,max));%长度为max的随机二进制序列 f=100;%载波频率 nsamp = 1000;每个载波的取样点数 tc=0:2*pi/999:2*pi;tc的个数应与nsamp相同 cm=zeros(1,nsamp*max); cp=zeros(1,nsamp*max); mod=zeros(1,nsamp*max); for n=1:max; if s(n)==0; m=zeros(1,nsamp); b=zeros(1,nsamp); else if s(n)==1; m=ones(1,nsamp); b=ones(1,nsamp); end end c = sin(f*tc); cm((n-1)*nsamp+1:n*nsamp)=m; cp((n-1)*nsamp+1:n*nsamp)=b; mod((n-1)*nsamp+1:n*nsamp)=c; end tiaoz=cm.*mod;%2ASK调制 t = linspace(0,length(s),length(s)*nsamp); tz=awgn(tiaoz,snr);%信号tiaoz中加入白噪声,信噪比为SNR=10dB jiet = 2*mod.*tz; %相干解调 [N,Wn]=buttord(0.2,0.3,1,15); [b,a]=butter(N,Wn); dpsk=filter(b,a,jiet);%低通滤波 % 抽样判决,判决门限为0.5 depsk = zeros(1,nsamp*max); for m = nsamp/2:nsamp:nsamp*max; if dpsk(m) < 0.5; for i = 1:nsamp depsk((m-500)+i) = 0; end 北京联合大学 实验报告 项目名称:运筹学专题实验报告 学院:自动化专业:物流工程 班级: 1201B 学号:2012100358081 姓名:管水城成绩: 2015 年 5 月 6 日 实验二:MATLAB 编程单纯形法求解 一、实验目的: (1)使学生在程序设计方面得到进一步的训练;,掌握Matlab (C 或VB)语言进行程序设计中一些常用方法。 (2)使学生对线性规划的单纯形法有更深的理解. 二、实验用仪器设备、器材或软件环境 计算机, Matlab R2006 三、算法步骤、计算框图、计算程序等 本实验主要编写如下线性规划问题的计算程序: ?? ?≥≥≤0 ,0..min b x b Ax t s cx 其中初始可行基为松弛变量对应的列组成. 对于一般标准线性规划问题: ?? ?≥≥=0 ,0..min b x b Ax t s cx 1.求解上述一般标准线性规划的单纯形算法(修正)步骤如下: 对于一般的标准形式线性规划问题(求极小问题),首先给定一个初始基本可行解。设初始基为B,然后执行如下步骤: (1).解B Bx b =,求得 1 B x B b -=,0,N B B x f c x ==令计算目标函数值 1(1,2,...,)i m B b i -=i 以b 记的第个分量 (2).计算单纯形乘子w, B wB C =,得到1 B w C B -=,对于非基变量,计算判别 数1i i i B i i z c c B p c σ-=-=-,可直接计算 σ =1 B A c c B --令 max{}k i R σσ∈=,R 为非基变量集合 若判别数0k σ≤ ,则得到一个最优基本可行解,运算结束;否则,转到下一 步 (3).解k k By p =,得到 1 k k y B p -=;若0k y ≤,即k y 的每个分量均非正数, 则停止计算,问题不存在有限最优解,否则,进行步骤(4).确定下标r,使 { }:0 min ,0 t r rk tk tk b b tk y y t y y >=>且r B x 为离基变量, ,r k B x p k 为进基变量,用p 替换得到新的基矩阵B,还回步骤(1) ; 大连民族学院 数学实验报告 课程:____________________ 最优化方法______________________ 实验题目: ___________ 单纯形法的matlab实现 ___________________ 系别:______________________ 理学院________________________ 专业:__________________ 信息与计算科学____________________ 姓名:__________________________________________________ 班级:_____________________ 信息102班 ____________________ 指导教师:___________________ 葛仁东_______________________ 完成学期:2013 年__9 ___________ 月_2________ 日 实验目的: 实验方法和步骤(包括数值公式、算法步骤、程序) : 考察标准形式的线性规划问题: min f(x) C T x s.t Ax b, x 0 设x(k)F为一个基本可行解,单纯形方法首先检验它的最优性。如果它不是最优的,确定与该顶点相连的一条使目标函数下降的边;接下来确定沿这个边移 动多远可以到达另一个更优的相邻点,也就是得出一个新的基本可行解 算法步骤: 步骤1给定一个初始基本可行解,记迭代次数 k 1 ; 步骤2 :计算单纯形乘子y k B k T c B k)和简约价值系数向量C N k) c N k) N T y k ; 步骤3 :最优性检验,计算C?k) min{C (k)|j 2},如果C?k) 0,则x (k)为最优解, 停止迭代;否则有x p 0,选x p 为入基变量; 步骤4:确定出基变量,计算g k) B k 1a p ,如果对所有j B k ,有器)0,则问题 无有界的最优解,停止迭代;否则确定出基变量指标 步骤5:交换B k 的列a q 与N k 的列a p 得到新的基矩阵 盼和山+1,计算新的基本可 行解 x (k1),置k:k 1后转步骤 2; 在上述算法中,当存在不止一个简约价值系数 C j k) 0时,选取最负的?“的 指标为p ,并以X p 作为入基变量。 Matlab 计算程序: Function] x,f]=zuiyouhua(A,b,c) Size(A)=[m, n]; i=n+1: n+m; N=1: n; B=eye(m,m); xb=b '; xn=zeros(m,1); f1=0; w=zeros(1,m); z=-c; flag=1; while(1) [a,k]=max(z); If a<=0 flag=0; break else y=i nv(B)*A(:,k) b (k) B k }; min{ _(k )殆 0, j function Z=dcxf(c,A,N) %定义函数名称为dcxf。 l=length(N); CB=c(N(1):N(l)) [m,n]=size(A); b=A(:,n); A=A(:,1:n-1); %参数包括目标函数系数(C),约束条件的系数矩阵(A), %其中A的最后一列为约束条件的右端值b,初始基向量的位置(N)。 sigma=c-CB*A;%计算检验数sigma。 display('初始单纯形表为:');%输出初始的单纯形表table=[nan,nan,nan,c;CB',N',b,A;nan,nan,nan,si gma] opt=1;step=0; while opt step=step+1;%定义循环,直到第“step”步找到最优解(opt=0)。 if sum(sigma>0)==0 %利用检验数判断是否得到最优解,并给出提示。 display('没有得到最优解,继续迭代.'); opt=0; else inb=find(sigma==max(sigma)); %利用单纯形方法找到入基变量的位置 num=length(inb); Inb=inb(num) flag=0; for i=1:m %利用单纯形方法找出出基变量的位置 if A(i,inb)>0 theta(i)=b(i)/A(i,inb); else theta(i)=inf; end end outb=find(theta==min(theta)); num=length(outb); %判断足否出现退化现象,如出现退化,给il{语言提示,并取最后出现的符合出基条件的变量为出基变量。 if num~=1 display('出现退化情况.'); end outb=outb(num); 单纯形法(Mat lab程序) %%单纯形法(Mat lab程序)a= input (' input the major matrix A '); b=input (' input the matrix b '); n=input C input the judgement '); %%为计数器(确定循环次数) 萨0; while g<40 %%确定非负 alength=max(size(n)); blength二max(size(b)); m=0; for i=l:alength 辻n(i)〉=0 m二m+1; end end; if m==alength x=b; break end; %%找K s二min(n); for i=l:alength if n(i) ==s k二i; break end; end; %%a[i,k]的非负性 m=0; for i=l:blength if a(i, k)<0 m二m+1; end; end; if m==blength disp('x does not exit'); judge二1; break end; %%找L确定主元cc=100000; for i=l:blength if a (i, k) >0 if (b(i)/a(i, k))< cc cc=b(i)/a(i, k); end end end; for i=l:blength if a(i, k)~=0 if (b(i)/a(i, k))==cc 1二i; break end end end; %%计算,a 标准化zu=a(l, k); aa=a; for i=l:1-1 for j=l:alength aa(i, j)=a(i, j)- a(l, j)*a(i, k)/a(l, k); end end; for i=l+l:blength for j=l :alength aa(i, j)=a(i, j)- a(l, j)*a(i, k)/a(l, k); end end; for j=l:alength aa(l, j)=a(l, j)/zu; end; %%b 勺判别bb=b; bb(l)=b(l)/zu; for i=l: 1~1 bb(i)=b(i)~ b⑴*a(i, k)/a(l, k); end; for i=l+l:blength bb(i)二b(i)- b(l)*a(i, k)/a(l, k); end; b二bb; %%确定判别数 -20-15-10-50510152000.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 Kalman滤波器在matlab仿真程序下的不同信噪比时的误码率: %multiuser_dectect.m clc; clear all; hold on BER_sum=zeros(1,13);%设定求和误码率的零矩阵; BER_ave=zeros(1,13); %设定平均误码率的零矩阵; for m=1:10;%m的长度为1到10 间隔为1; snr_in_db=-20:3:16;%定义信噪比的长度为-20到16 间隔为3;snr_in_db是信噪比用db表示 for i=1:length(snr_in_db);%i的长度为1到信噪比的长度 BER(i)= Kalman_S1(snr_in_db(i));%卡尔曼的误码率函数; end BER_sum=BER_sum+BER;%误码率求和的算法 end; BER_ave=0.1* BER_sum ; %误码率平均值的算法 semilogy( snr_in_db,BER_ave,'rd-');%y轴维数坐标图定义横坐标为信噪比,纵坐标为误码率; %Kalman_S1.m %Kalman algorithm %synchronous CDMA同步cdma %channel: White Gaussis Noise function [p] = Kalman_S1(snr_in_dB) SNR=10^(snr_in_dB/10); %信噪比由dB形式转化 sgma=1; % noise standard deviation is fixed 定义方差 Eb=sgma^2*SNR; A=[sqrt(Eb),sqrt(Eb),sqrt(Eb),sqrt(Eb),sqrt(Eb),sqrt(Eb),sqrt(Eb),sqrt(Eb),sqrt(Eb),sqr t(Eb),sqrt(Eb),sqrt(Eb),sqrt(Eb),sqrt(Eb),sqrt(Eb)]; K=length(A); 实验报告 实验题目: 单纯形法的matlab实现学生: 学号: 实验时间: 2013-4-15 一.实验名称: 单纯形法的MATLAB 实现 二.实验目的及要求: 1. 了解单纯形算法的原理及其matlab 实现. 2. 运用MATLAB 编辑单纯形法程序解决线性规划的极小化问题, 求出最优解及目标函数值. 三.实验容: 1. 单纯形方法原理: 单纯形方法的基本思想, 是从一个基本可行解出发, 求一个使目标函数值有所改善的基本可行解; 通过不断改进基本可行解, 力图达到最优基本可行解. 对问题 . 0 ,A s.t. def min ≥=x b x cx f 其中A 是一个m ×n 矩阵, 且秩为m, c 为n 维行向量, x 为n 维列向量, b 为m 维非负列向量. 符号“”表示右端的表达式是左端的定义式, 即目标函数f 的具体形式就是cx . 记 ),...,,(n 21p p p A = 令A =(B,N), B 为基矩阵, N 为非基矩阵, 设 ?? ? ???=0B 1-) 0(b x 是基本可行解, 在) 0(x 处的目标函数值 b c b c c cx f 1 -B 1-N B ) 0(0B 0B ),(=?? ????==, 其中B c 是c 中与基变量对应的分量组成的m 维行向量; N c 是c 中与非基变量对应的分量组成的n-m 维行向量. 现由基本可行解) 0(x 出发求解一个改进的基本可行解. 设?? ? ? ??=N B x x x 是任一可行解, 则由b Ax =得到 N 1-1-B N B B x b x -=, 在点x 处的目标函数值 ∑∈--=?? ? ???==R j j j j f x x c c cx f x )c z (),(0N B N B , 其中R 是非基变量下标集, j j p c 1-B B z =. 2. 单纯形方法计算步骤: 首先给定一个初始基本可行解, 设初始基为B, 然后执行下列主要步骤: (1)解b x B =B , 求得_ 1 b b B x B ==-, 令0=N x , 计算目标函数值B B x c f =. (2)求单纯形乘子w , 解B c wB =, 得到1 -=B c w B . 对于所有非基变量, 计算判别数 j j j j j c c -z -=p w . 令 } c -{z max c -z j j R j k k ∈=. 若0c -z k k ≤, 则对于所有非基变量0c -z j j ≤, 对应基变量的判别数总是为零, 因此停止计算, 现行基本可行解是最优解. 否则, 进行下一步. (3)解k k p By =, 得到k 1 k p B y -=, 若0k ≤y , 即k y 的每个分量均非正数, 则停止计算, 问题不存在有限最优解. 否则进行步骤(4). (4)确定下标r, 使 功率谱密度估计方法的MATLAB实现 在应用数学和物理学中,谱密度、功率谱密度和能量谱密度是一个用于信号的通用概念,它表示每赫兹的功率、每赫兹的能量这样的物理量纲。在物理学中,信号通常是波的形式,例如电磁波、随机振动或者声波。当波的频谱密度乘以一个适当的系数后将得到每单位频率波携带的功率,这被称为信号的功率谱密度(power spectral density, PSD)或者谱功率分布(spectral power distribution, SPD)。功率谱密度的单位通常用每赫兹的瓦特数(W/Hz)表示,或者使用波长而不是频率,即每纳米的瓦特数(W/nm)来表示。信号的功率谱密度当且仅当信号是广义的平稳过程的时候才存在。如果信号不是平稳过程,那么自相关函数一定是两个变量的函数,这样就不存在功率谱密度,但是可以使用类似的技术估计时变谱密度。信号功率谱的概念和应用是电子工程的基础,尤其是在电子通信系统中,例如无线电和微波通信、雷达以及相关系统。因此学习如何进行功率谱密度估计十分重要,借助于Matlab工具可以实现各种谱估计方法的模拟仿真并输出结果。下面对周期图法、修正周期图法、最大熵法、Levinson递推法和Burg法的功率谱密度估计方法进行程序设计及仿真并给出仿真结果。 以下程序运行平台:Matlab R2015a(8.5.0.197613) 一、周期图法谱估计程序 1、源程序 Fs=100000; %采样频率100kHz N=1024; %数据长度N=1024 n=0:N-1; t=n/Fs; xn=sin(2000*2*pi*t); %正弦波,f=2000Hz Y=awgn(xn,10); %加入信噪比为10db的高斯白噪声 subplot(2,1,1); plot(n,Y) title('信号') xlabel('时间');ylabel('幅度');信号检测与估值matlab仿真报告
单纯形法matlab程序
music 方位估计 实验报告三 MATLAB 代码
单纯形法MATLAB程序
运用Matlab进行线性规划求解(实例)
Matlab频谱分析程序
多目标线性规划的若干解法及MATLAB实现
(完整版)MATLAB模拟2ASK调制误码率与信噪比关系曲线的程序
实验二:MATLAB编程单纯形法求解
单纯形法的matlab实现(20200814192014)
单纯形法matlab程序
单纯形法MATLAB程序
kalman滤波在不同信噪比时的误码率matlab仿真程序
单纯形法的matlab实现(极小化问题)
功率谱密度估计方法的MATLAB实现
