计算方法-数值积分实验

实验二数值积分实验
一. 实验目的
(1)熟悉数值积分与数值微分方法的基本思想,加深对数值积分与数值微分方法的理解。
(2)熟悉Matlab编程环境,利用Matlab实现具体的数值积分与数值微分方法。
二. 实验要求
用Matlab软件实现复化梯形方法、复化辛甫生方法、龙贝格方法和高斯公式的相应算法,并用实例在计算机上计算。
三.实验内容
1. 实验题目
已知x
e
x
f x4
sin
1
)
(-
+
=的数据表
分别编写用复化梯形法、复化辛甫生公法、龙贝格法、三点高斯法求积分?=1
) (dx x
f
I 近似值的计算机程序。
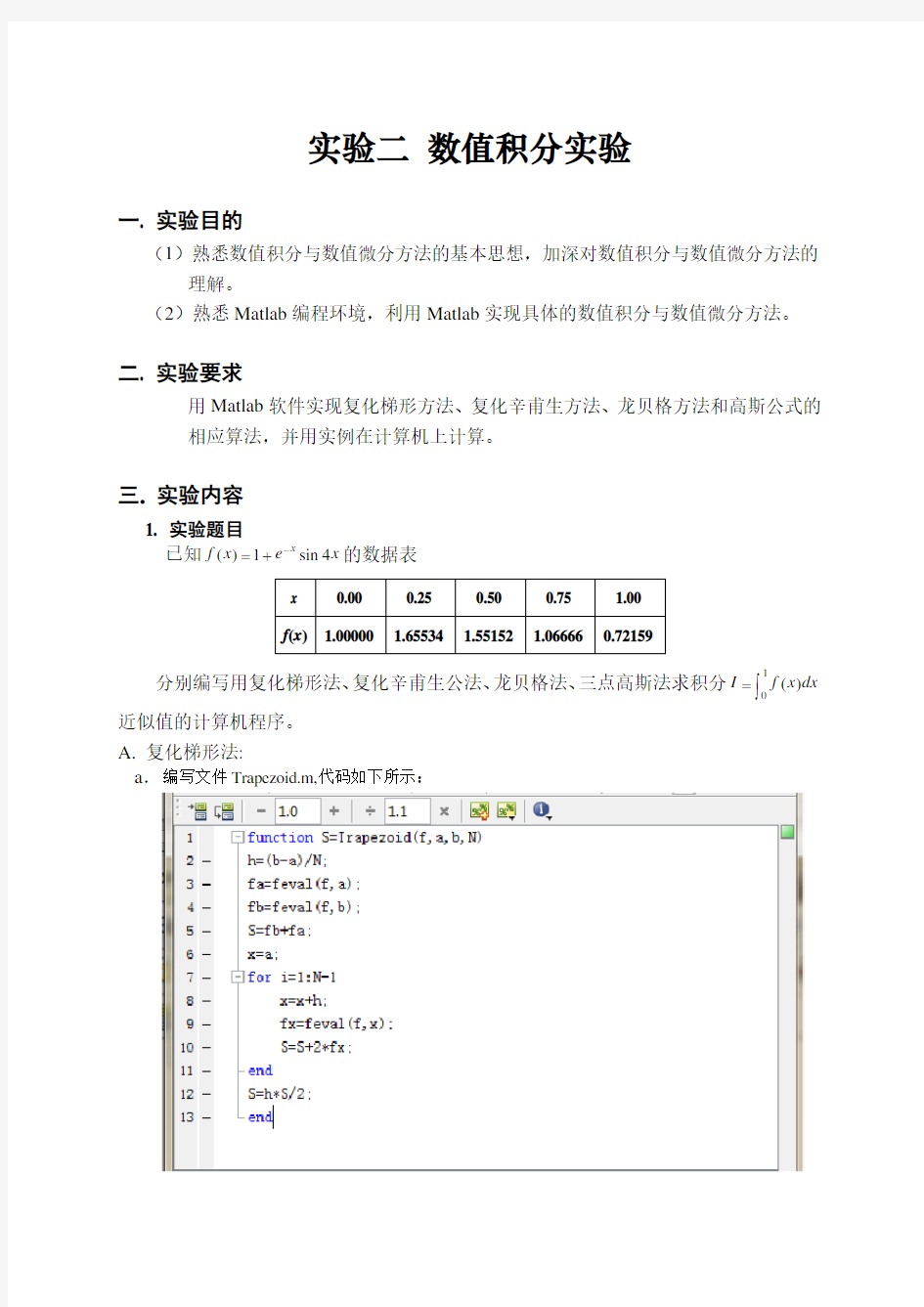
A.复化梯形法:
a.编写文件Trapezoid.m,代码如下所示:
b.编写文件f2.m:
c.运行:
B.复化辛甫生公法
a.编写文件FSimpson.m,代码如下所示:
b.编写文件f2.m: function f=f2(x)
f=1+exp(-x).*sin(4*x);
c.运行:
C.龙贝格法
a.编写文件Romberg.m,代码如下所示:
b.运行:
D.三点高斯法
a.编写文件TGauss.m文件,如下所示:
b.运行:
2. 设计思想
要求针对上述题目,详细分析每种算法的设计思想。
总体的思想是化复杂为简单的重复
A.复化梯形法使用直接法,通过递归,缩减规模;
B.复化辛甫生也是使用直接法,根据公式直接进行编程,通过递归缩减规模;
C.龙贝格算法应该在做了的几个中最体现了“化复杂为简单的重复”的思想,多个循环通过变量的适当递增,和一个for循环语句来实现,循环主体只有一句话,但确是整个程序中的亮点和难点;
D.三点高斯法直接通过一条简单的公式来编写程序,难度不大;
四.实验体会
对实验过程进行分析总结,对比不同方法的精度,指出每种算法的设计要点及应注意的事项,以及自己通过实验所获得的对数值积分方法的理解。
数值计算实验课题目
数值实验课试题 本次数值实验课结课作业,请按题目要求内容写一篇文章。按题目要求 人数自由组合,每组所选题目不得相同(有特别注明的题目除外)。试题如下: 1)解线性方程组的Gauss 消去法和列主元Gauss 消去法(2人)/*张思珍,巩艳华*/ 用C 语言将不选主元和列主元Gauss 消去法编写成通用的子程序,然后用你编写的程序求解下列84阶的方程组 ???? ?????? ? ??=??????????? ????????????? ? ?1415151515768 168 168 168 1681684 8382321 x x x x x x 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值线性代数》,徐树方、高立、张平文编 3.《数值分析简明教程》,王能超编 2)解线性方程组的平方根法(4人)/*朱春成、黄锐奇、张重威、章杰*/ 用C 语言将平方根法和改进的平方根法编写成通用的子程序,然后用你编写的程序求解对称正定方程组b Ax =,其中 (1)b 随机的选取,系数矩阵为100阶矩阵 ?????? ???? ? ? ?101 1101 1101 1101 1101110 ; (2)系数矩阵为40阶的Hilbert 矩阵,即系数矩阵A 的第i 行第j 列元素为 1 1-+= j i a ij ,向量b 的第i 个分量为∑=-+ = n j i j i b 1 1 1. 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值线性代数》,徐树方、高立、张平文编
3.《数值分析简明教程》,王能超编 3)三对角线方程组的追赶法(3人)/*黄佳礼、唐伟、韦锡倍*/ 用C 语言将三对角线方程组的追赶法法编写成通用的子程序,然后用你编写的程序求解如下84阶三对角线方程组 ???? ?????? ? ??=??????????? ????????????? ? ?1415151515768 168 168 168 16816 84 8382321 x x x x x x 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值分析简明教程》,王能超编 4)线性方程组的Jacobi 迭代法(3人)/*周桂宇、杨飞、李文军*/ 用C 语言将Jacobi 迭代法编写成独立的子程序,并用此求解下列方程组, 精确到小数点后5位 ???? ? ??=????? ??????? ? ?-149012 2111221 3 2 1 x x x 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值线性代数》,徐树方、高立、张平文编 3.《数值分析简明教程》,王能超编 5)线性方程组的Gauss-Seidel 迭代法(3人)/*张玉超、范守平、周红春*/ 用C 语言将Gauss-Seidel 迭代法编写成独立的子程序,并用此求解下列方程组,精确到小数点后5位 ???? ? ??=????? ??????? ? ?--39721 1111112 3 2 1 x x x 参考书目: 1.《计算机数值方法》,施吉林、刘淑珍、陈桂芝编 2.《数值线性代数》,徐树方、高立、张平文编 3.《数值分析简明教程》,王能超编 6)解线性方程组的最速下降法法(2人)/*赵育辉、阿热孜古丽*/ 用C 语言将最速下降法编写成通用的子程序,然后用你编写的程序求解对称
数值分析实验报告1
实验一误差分析 实验1.1(病态问题) 实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。通过本实验可获得一个初步体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 问题提出:考虑一个高次的代数多项式 显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。现考虑该多项式的一个扰动 其中ε(1.1)和(1.221,,,a a 的输出b ”和“poly ε。 (1(2 (3)写成展 关于α solve 来提高解的精确度,这需要用到将多项式转换为符号多项式的函数poly2sym,函数的具体使用方法可参考Matlab 的帮助。 实验过程: 程序: a=poly(1:20); rr=roots(a); forn=2:21 n form=1:9 ess=10^(-6-m);
ve=zeros(1,21); ve(n)=ess; r=roots(a+ve); -6-m s=max(abs(r-rr)) end end 利用符号函数:(思考题一)a=poly(1:20); y=poly2sym(a); rr=solve(y) n
很容易的得出对一个多次的代数多项式的其中某一项进行很小的扰动,对其多项式的根会有一定的扰动的,所以对于这类病态问题可以借助于MATLAB来进行问题的分析。 学号:06450210 姓名:万轩 实验二插值法
(精选)实验二 数值方法计算积分
实验二数值方法计算积分 学号:姓名:指导教师:实验目的 1、了解并掌握matlab软件的基本编程、操作方法; 2、初步了解matlab中的部分函数,熟悉循环语句的使用; 3、通过上机进一步领悟用复合梯形、复合辛普森公式,以及用龙贝格求积 方法计算积分的原理。 一、用不同数值方法计算积分 10x ln xdx=-94. (1)取不同的步长h.分别用复合梯形及辛普森求积计算积分,给出误差中关 于h的函数,并与积分精确值比较两个公式的精度,是否存在一个最小 的h,使得精度不能再被改善? (2)用龙贝格求积计算完成问题(1)。 二、实现实验 1、流程图: 下图是龙贝格算法框图:
2、 算法: (1) 复合梯形公式:Tn=++)()([2b f a f h 2∑-=1 1 )](n k xk f ; (2) 复合辛普森公式:Sn=6h [f(a)+f(b)+2∑-=11)](n k xk f +4∑-=+1 )2/1(n k x f ]; 以上两种算法都是将a-b 之间分成多个小区间(n ),则h=(b-a)/n,x k =a+kh, x k+1/2=a+(k+1/2)h,利用梯形求积根据两公式便可。 (3) 龙贝格算法:在指定区间内将步长依次二分的过程中运用如下公式 1、Sn= 34T2n-31 Tn 2、 Cn=1516S2n-151 Sn 3、 Rn=6364C2n-631 Cn 从而实现算法。 3、 程序设计 (1)、复合梯形法: function t=natrapz(fname,a,b,n) h=(b-a)/n; fa=feval(fname,a);fb=feval(fname,b);f=feval(fname,a+h:h:b-h+0. 001*h); t=h*(0.5*(fa+fb)+sum(f)); (2)、复合辛普森法: function t=natrapz(fname,a,b,n) h=(b-a)/n; fa=feval(fname,a);fb=feval(fname,b);f1=feval(fname,a+h:h:b-h+0 .001*h); f2=feval(fname,a+h/2:h:b-h+0.001*h); t=h/6*(fa+fb+2*sum(f1)+4*sum(f2)); (3)龙贝格法: function [I,step]=Roberg(f,a,b,eps) if(nargin==3) eps=1.0e-4; end; M=1; tol=10; k=0; T=zeros(1,1); h=b-a; T(1,1)=(h/2)*(subs(sym(f),findsym(sym(f)),a)+subs(sym(f),findsym(sym(f)),
曲线拟合的数值计算方法实验
曲线拟合的数值计算方法实验 【摘要】实际工作中,变量间未必都有线性关系,如服药后血药浓度与时间的关系;疾病疗效与疗程长短的关系;毒物剂量与致死率的关系等常呈曲线关系。曲线拟合(curve fitting)是指选择适当的曲线类型来拟合观测数据,并用拟合的曲线方程分析两变量间的关系。曲线直线化是曲线拟合的重要手段之一。对于某些非线性的资料可以通过简单的变量变换使之直线化,这样就可以按最小二乘法原理求出变换后变量的直线方程,在实际工作中常利用此直线方程绘制资料的标准工作曲线,同时根据需要可将此直线方程还原为曲线方程,实现对资料的曲线拟合。常用的曲线拟合有最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束。 关键词曲线拟合、最小二乘法拟合、幂函数拟合、对数函数拟合、线性插值、三次样条插值、端点约束 一、实验目的 1.掌握曲线拟合方式及其常用函数指数函数、幂函数、对数函数的拟合。 2.掌握最小二乘法、线性插值、三次样条插值、端点约束等。 3.掌握实现曲线拟合的编程技巧。 二、实验原理 1.曲线拟合 曲线拟合是平面上离散点组所表示的坐标之间的函数关系的一种数据处理方法。用解析表达式逼近离散数据的一种方法。在科学实验或社会活动中,通过 实验或观测得到量x与y的一组数据对(X i ,Y i )(i=1,2,...m),其中各X i 是彼此不同的。人们希望用一类与数据的背景材料规律相适应的解析表达式,y=f(x,c)来反映量x与y之间的依赖关系,即在一定意义下“最佳”地逼近或 拟合已知数据。f(x,c)常称作拟合模型,式中c=(c 1,c 2 ,…c n )是一些待定参 数。当c在f中线性出现时,称为线性模型,否则称为非线性模型。有许多衡量拟合优度的标准,最常用的一种做法是选择参数c使得拟合模型与实际观测值在
几种定积分的数值计算方法
几种定积分的数值计算方法 摘要:本文归纳了定积分近似计算中的几种常用方法,并着重分析了各种数值方法的计 算思想,结合实例,对其优劣性作了简要说明. 关键词:数值方法;矩形法;梯形法;抛物线法;类矩形;类梯形 Several Numerical Methods for Solving Definite Integrals Abstract:Several common methods for solving definite integrals are summarized in this paper. Meantime, the idea for each method is emphatically analyzed. Afterwards, a numerical example is illustrated to show that the advantages and disadvantages of these methods. Keywords:Numerical methods, Rectangle method, Trapezoidal method, Parabolic method, Class rectangle, Class trapezoid
1. 引言 在科学研究和实际生产中,经常遇到求积分的计算问题,由积分学知识可知,若函数 )(x f 在区间],[b a 连续且原函数为)(x F ,则可用牛顿-莱布尼茨公式 ?-=b a a F b F x f ) ()()( 求得积分.这个公式不论在理论上还是在解决实际问题中都起到了很大的作用. 在科学研究和实际生产中,经常遇到求积分的计算问题,由积分学知识可知,若函数)(x f 在区间],[b a 连续且原函数为)(x F ,则可用牛顿-莱布尼茨公式 ?-=b a a F b F x f ) ()()( 求得积分.这个公式不论在理论上还是在解决实际问题中都起到了很大的作用.另外,对于求导数也有一系列的求导公式和求导法则.但是,在实际问题中遇到求积分的计算,经常会有这样的情况: (1)函数)(x f 的原函数无法用初等函数给出.例如积分 dx e x ?-1 02 , ? 1 sin dx x x 等,从而无法用牛顿-莱布尼茨公式计算出积分。 (2)函数)(x f 使用表格形式或图形给出,因而无法直接用积分公式或导数公式。 (3)函数)(x f 的原函数或导数值虽然能够求出,但形式过于复杂,不便使用. 由此可见,利用原函数求积分或利用求导法则求导数有它的局限性,所以就有了求解数值积分的很多方法,目前有牛顿—柯特斯公式法,矩形法,梯形法,抛物线法,随机投点法,平均值法,高斯型求积法,龙贝格积分法,李查逊外推算法等等,本文对其中部分方法作一个比较. 2.几何意义上的数值算法 s 在几何上表示以],[b a 为底,以曲线)(x f y =为曲边的曲边梯形的面积A ,因此,计 算s 的近似值也就是A 的近似值,如图1所示.沿着积分区间],[b a ,可以把大的曲边梯形分割成许多小的曲边梯形面积之和.常采用均匀分割,假设],[b a 上等分n 的小区间 ,x 1-i h x i +=b x a x n ==,0,其中n a b h -= 表示小区间的长度. 2.1矩形法
太原理工大学数值计算方法实验报告
本科实验报告 课程名称:计算机数值方法 实验项目:方程求根、线性方程组的直接解 法、线性方程组的迭代解法、代数插值和最 小二乘拟合多项式 实验地点:行勉楼 专业班级: ******** 学号: ********* 学生姓名: ******** 指导教师:李誌,崔冬华 2016年 4 月 8 日
y = x*x*x + 4 * x*x - 10; return y; } float Calculate(float a,float b) { c = (a + b) / 2; n++; if (GetY(c) == 0 || ((b - a) / 2) < 0.000005) { cout << c <<"为方程的解"<< endl; return 0; } if (GetY(a)*GetY(c) < 0) { return Calculate(a,c); } if (GetY(c)*GetY(b)< 0) { return Calculate(c,b); } } }; int main() { cout << "方程组为:f(x)=x^3+4x^2-10=0" << endl; float a, b; Text text; text.Getab(); a = text.a; b = text.b; text.Calculate(a, b); return 0; } 2.割线法: // 方程求根(割线法).cpp : 定义控制台应用程序的入口点。// #include "stdafx.h" #include"iostream"
心得体会 使用不同的方法,可以不同程度的求得方程的解,通过二分法计算的程序实现更加了解二分法的特点,二分法过程简单,程序容易实现,但该方法收敛比较慢一般用于求根的初始近似值,不同的方法速度不同。面对一个复杂的问题,要学会简化处理步骤,分步骤一点一点的循序处理,只有这样,才能高效的解决一个复杂问题。
数值计算实验报告
(此文档为word格式,下载后您可任意编辑修改!) 2012级6班###(学号)计算机数值方法 实验报告成绩册 姓名:宋元台 学号: 成绩:
数值计算方法与算法实验报告 学期: 2014 至 2015 第 1 学期 2014年 12月1日课程名称: 数值计算方法与算法专业:信息与计算科学班级 12级5班 实验编号: 1实验项目Neton插值多项式指导教师:孙峪怀 姓名:宋元台学号:实验成绩: 一、实验目的及要求 实验目的: 掌握Newton插值多项式的算法,理解Newton插值多项式构造过程中基函数的继承特点,掌握差商表的计算特点。 实验要求: 1. 给出Newton插值算法 2. 用C语言实现算法 二、实验内容 三、实验步骤(该部分不够填写.请填写附页)
1.算法分析: 下面用伪码描述Newton插值多项式的算法: Step1 输入插值节点数n,插值点序列{x(i),f(i)},i=1,2,……,n,要计算的插值点x. Step2 形成差商表 for i=0 to n for j=n to i f(j)=((f(j)-f(j-1)(x(j)-x(j-1-i)); Step3 置初始值temp=1,newton=f(0) Step4 for i=1 to n temp=(x-x(i-1))*temp*由temp(k)=(x-x(k-1))*temp(k-1)形成 (x-x(0).....(x-x(i-1)* Newton=newton+temp*f(i); Step5 输出f(x)的近似数值newton(x)=newton. 2.用C语言实现算法的程序代码 #include
数值分析实验指导 - 7 积分
数值分析实验指导 潘志斌 2014年3月
实验七 数值积分 数值实验综述:通过数值积分实验掌握数值积分的实现,理解各种数值积分公式的特性,并能用数值积分求解积分方程和微分方程。 基础实验 7.1 Newton-cotes 型求积公式 实验目的:学会Newton-cotes 型求积公式,并应用该算法于实际问题. 实验内容:求定积分 ? π cos xdx e x 实验要求:选择等分份数n ,用复化Simpson 求积公式求上述定积分的误差不超过810-的近似值,用MATLAB 中的内部函数int 求此定积分的准确值,与利用复化Simpson 求积公式计算的近似值进行比较。 7.2 Romberg 算法 实验目的:学会数值求积的Romberg 算法,并应用该算法于实际问题. 实验内容:求定积分 ? 1 5 .0dx x 实验要求: (1)要求程序不断加密对积分区间的等分,自动地控制Romberg 算法中的加速收敛过程,直到定积分近似值的误差不超过610-为止,输出求得的定积分近似值。 (2)可用MATLAB 中的内部函数int 求得此定积分的准确值与Romberg 算法计算的近似值进行比较。 7.3 Gauss 型求积公式 实验目的:学会Gauss 型求积公式,并应用该算法于实际问题. 实验内容:求定积分 ? -+4 42 1x dx 实验要求: (1)把Gauss 点的表格存入计算机,以Gauss-Legendre 求积公式作为本实验的例子,要求程序可以根据不同的阶数n ,自动地用n 阶Gauss-Legendre 求积
公式计算上述定积分的近似值.体会Gauss型求积公式是具有尽可能高的代数精度的数值求积公式。 (2)可用MATLAB中的内部函数int求得此定积分的准确值与Gauss型求积公式求得的值进行比较。
数值分析实验报告1
实验一 误差分析 实验(病态问题) 实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。通过本实验可获得一个初步体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 问题提出:考虑一个高次的代数多项式 )1.1() ()20()2)(1()(20 1∏=-=---=k k x x x x x p 显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。现考虑该多项式的一个扰动 )2.1(0 )(19=+x x p ε 其中ε是一个非常小的数。这相当于是对()中19x 的系数作一个小的扰动。我们希望比较()和()根的差别,从而分析方程()的解对扰动的敏感性。 实验内容:为了实现方便,我们先介绍两个Matlab 函数:“roots ”和“poly ”。 roots(a)u = 其中若变量a 存储n+1维的向量,则该函数的输出u 为一个n 维的向量。设a 的元素依次为121,,,+n a a a ,则输出u 的各分量是多项式方程 01121=+++++-n n n n a x a x a x a 的全部根;而函数 poly(v)b =
的输出b 是一个n+1维变量,它是以n 维变量v 的各分量为根的多项式的系数。可见“roots ”和“poly ”是两个互逆的运算函数。 ;000000001.0=ess );21,1(zeros ve = ;)2(ess ve = ))20:1((ve poly roots + 上述简单的Matlab 程序便得到()的全部根,程序中的“ess ”即是()中的ε。 实验要求: (1)选择充分小的ess ,反复进行上述实验,记录结果的变化并分析它们。 如果扰动项的系数ε很小,我们自然感觉()和()的解应当相差很小。计算中你有什么出乎意料的发现表明有些解关于如此的扰动敏感性如何 (2)将方程()中的扰动项改成18x ε或其它形式,实验中又有怎样的现象 出现 (3)(选作部分)请从理论上分析产生这一问题的根源。注意我们可以将 方程()写成展开的形式, ) 3.1(0 ),(1920=+-= x x x p αα 同时将方程的解x 看成是系数α的函数,考察方程的某个解关于α的扰动是否敏感,与研究它关于α的导数的大小有何关系为什么你发现了什么现象,哪些根关于α的变化更敏感 思考题一:(上述实验的改进) 在上述实验中我们会发现用roots 函数求解多项式方程的精度不高,为此你可以考虑用符号函数solve 来提高解的精确度,这需要用到将多项式转换为符号多项式的函数poly2sym,函数的具体使用方法可参考Matlab 的帮助。
数值计算方法实验5
实验报告 学院(系)名称: 主程序部分列选主元部分
实验结果: 一.列主元消去法 输入各个数据,最终使用列选主元法,得到结果为:x1=x2=x3=1二.高斯-赛德尔迭代法 输入各个数据,输出每一步迭代数据,最终结果为:x1=0.285716,附录(源程序及运行结果) 一.列主元高斯消去法 #include 目录 第一章数值积分计算的重述 (1) 1.1引言 (1) 1.2问题重述 (2) 第二章复化梯形公式 (3) 2.1 复化梯形公式的算法描述 (3) 2.2 复化梯形公式在C语言中的实现 (3) 2.3 测试结果 (4) 第三章复化simpson公式 (6) 3.1 复化simpson公式的算法描述 (6) 3.2 复化simpson公式在C语言中的实现 (6) 3.3 测试结果 (7) 第四章复化cotes公式 (8) 4.1 复化cotes公式的算法描述 (8) 4.2 复化cotes公式在C语言中的实现 (9) 4.3 测试结果 (10) 第五章Romberg积分法 (11) 5.1 Romberg积分法的算法描述 (11) 5.2 Romberg积分法在C中的实现 (12) 5.3 测试结果 (13) 第六章结果对比分析和体会 (144) 参考文献 (16) 附录 (16) 数值积分?-10 2 dx e x (一) 第一章 数值积分计算的重述 1.1引言 数值积分是积分计算的重要方法,是数值逼近的重要内容,是函数插值的最直接应用,也是工程技术计算中常常遇到的一个问题。在应用上,人们常要求算出具体数值,因此数值积分就成了数值分析的一个重要内容。在更为复杂的计算问题中,数值积分也常常是一个基本组成部分。 在微积分理论中,我们知道了牛顿-莱布尼茨(Newton-Leibniz)公式 ()() () b a f x d x F b F a =-? 其中()F x 是被积函数()f x 的某个原函数。但是随着学习的深入,我们发现一个问题: 对很多实际问题,上述公式却无能为力。这主要是因为:它们或是被积函数没有解析形式的原函数,或是只知道被积函数在一些点上的值,而不知道函数的形式,对此,牛顿—莱布尼茨(Newton-Leibniz)公式就无能为力了。此外,即使被积函数存在原函数,但因找原函数很复杂,人们也不愿花费太多的时间在求原函数上,这些都促使人们寻找定积分近似计算方法的研究,特别是有了计算机后,人们希望这种定积分近似计算方法能在计算机上实现,并保证计算结果的精度,具有这种特性的定积分近似计算方法称为数值积分。由定积分知识,定积分只与被积函数和积分区间有关,而在对被积函数做插值逼近时,多项式的次数越高,对被积函数的光滑程度要求也越高,且会出现Runge 现象。如7n >时,Newton-Cotes 公式就是不稳定的。因而,人们把目标转向积分区间,类似分段插值,把积分区间分割成若干小区间,在每个小区间上使用次数较低的Newton-Cotes 公式,然后把每个小区间上的结果加起来作为函数在整个区间上积分的近似,这就是复化的基本思想。本文主要 1. 设?+=1 05dx x x I n n , (1) 由递推公式n I I n n 1 51+-=-,从0I 的几个近似值出发,计算20I ; 解:易得:0I =ln6-ln5=0.1823, 程序为: I=0.182; for n=1:20 I=(-5)*I+1/n; end I 输出结果为:20I = -3.0666e+010 (2) 粗糙估计20I ,用n I I n n 51 5111+- =--,计算0I ; 因为 0095.05 6 0079.01020 201 020 ≈<<≈??dx x I dx x 所以取0087.0)0095.00079.0(2 1 20=+= I 程序为:I=0.0087; for n=1:20 I=(-1/5)*I+1/(5*n); end I 0I = 0.0083 (3) 分析结果的可靠性及产生此现象的原因(重点分析原因)。 首先分析两种递推式的误差;设第一递推式中开始时的误差为000I I E '-=,递推过程的舍入误差不计。并记n n n I I E '-=,则有01)5(5E E E n n n -==-=-Λ。因为=20E 20020)5(I E >>-,所此递推式不可靠。而在第二种递推式中n n E E E )5 1(5110-==-=Λ,误差在缩小, 所以此递推式是可靠的。出现以上运行结果的主要原因是在构造递推式过程中,考虑误差是否得到控制, 即算法是否数值稳定。 2. 求方程0210=-+x e x 的近似根,要求4 1105-+?<-k k x x ,并比较计算量。 (1) 在[0,1]上用二分法; 程序:a=0;b=1.0; while abs(b-a)>5*1e-4 c=(b+a)/2; 实验报告一 题目:非线性方程求解 摘要:非线性方程的解析解通常很难给出,因此线性方程的数值解法就尤为重要。本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。 前言:(目的和意义) 掌握二分法与Newton法的基本原理和应用。 数学原理: 对于一个非线性方程的数值解法很多。在此介绍两种最常见的方法:二分法和Newton法。 对于二分法,其数学实质就是说对于给定的待求解的方程f(x),其在[a,b]上连续,f(a)f(b)<0,且f(x)在[a,b]内仅有一个实根x*,取区间中点c,若,则c恰为其根,否则根据f(a)f(c)<0是否成立判断根在区间[a,c]和[c,b]中的哪一个,从而得出新区间,仍称为[a,b]。重复运行计算,直至满足精度为止。这就是二分法的计算思想。 Newton法通常预先要给出一个猜测初值x0,然后根据其迭代公式 产生逼近解x*的迭代数列{x k},这就是Newton法的思想。当x0接近x*时收敛很快,但是当x0选择不好时,可能会发散,因此初值的选取很重要。另外,若将该迭代公式改进为 其中r为要求的方程的根的重数,这就是改进的Newton法,当求解已知重数的方程的根时,在同种条件下其收敛速度要比Newton法快的多。 程序设计: 本实验采用Matlab的M文件编写。其中待求解的方程写成function的方式,如下 function y=f(x); y=-x*x-sin(x); 写成如上形式即可,下面给出主程序。 二分法源程序: clear %%%给定求解区间 b=1.5; a=0; %%%误差 R=1; k=0;%迭代次数初值 while (R>5e-6) ; c=(a+b)/2; if f12(a)*f12(c)>0; a=c; else b=c; end R=b-a;%求出误差 k=k+1; end x=c%给出解 Newton法及改进的Newton法源程序:clear %%%% 输入函数 f=input('请输入需要求解函数>>','s') %%%求解f(x)的导数 df=diff(f); 数值分析实验报告总结 随着电子计算机的普及与发展,科学计算已成为现代科 学的重要组成部分,因而数值计算方法的内容也愈来愈广泛和丰富。通过本学期的学习,主要掌握了一些数值方法的基本原理、具体算法,并通过编程在计算机上来实现这些算法。 算法算法是指由基本算术运算及运算顺序的规定构成的完 整的解题步骤。算法可以使用框图、算法语言、数学语言、自然语言来进行描述。具有的特征:正确性、有穷性、适用范围广、运算工作量少、使用资源少、逻辑结构简单、便于实现、计算结果可靠。 误差 计算机的计算结果通常是近似的,因此算法必有误差, 并且应能估计误差。误差是指近似值与真正值之差。绝对误差是指近似值与真正值之差或差的绝对值;相对误差:是指近似值与真正值之比或比的绝对值。误差来源见表 第三章泛函分析泛函分析概要 泛函分析是研究“函数的函数”、函数空间和它们之间 变换的一门较新的数学分支,隶属分析数学。它以各种学科 如果 a 是相容范数,且任何满足 为具体背景,在集合的基础上,把客观世界中的研究对象抽 范数 范数,是具有“长度”概念的函数。在线性代数、泛函 分析及相关的数学领域,泛函是一个函数,其为矢量空间内 的所有矢量赋予非零的正长度或大小。这里以 Cn 空间为例, Rn 空间类似。最常用的范数就是 P-范数。那么 当P 取1, 2 ,s 的时候分别是以下几种最简单的情形: 其中2-范数就是通常意义下的距离。 对于这些范数有以下不等式: 1 < n1/2 另外,若p 和q 是赫德尔共轭指标,即 1/p+1/q=1 么有赫德尔不等式: II = ||xH*y| 当p=q=2时就是柯西-许瓦兹不等式 般来讲矩阵范数除了正定性,齐次性和三角不等式之 矩阵范数通常也称为相容范数。 象为元素和空间。女口:距离空间,赋范线性空间, 内积空间。 1-范数: 1= x1 + x2 +?+ xn 2-范数: x 2=1/2 8 -范数: 8 =max oo ,那 外,还规定其必须满足相容性: 所以 基础实验二 定积分数值计算 一、实验目的 学习定积分的数值计算方法,理解定积分的定义,掌握牛顿-莱布尼兹公式。 二、实验材料 2.1定积分的数值计算 计算定积分?b a dx x f )(的近似值,可将积分区间n 等分而得矩形公式 n a b n a b i a f dx x f n i b a ---+≈∑?=]) 1([)(1 或 n a b n a b i a f dx x f n i b a --+≈∑?=][)(1 也可用梯形公式近似计算 n a b b f a f n a b i a f dx x f n i b a -++-+≈∑?-=]2)()()([)(11 如果要准确些,可用辛普森公式 n a b b f a f a b i a f n a b i a f dx x f n i n i b a 6)]()()2)21((4)(2[)(111-++--++-+≈∑∑?=-= 对于?1 0sin xdx ,矩形公式、梯形公式、辛普森公式的Mathematica 程序为 a=0;b=1;k=10; f[x_]:=Sin[x]; d=N[Integrate[f[x],{x,a,b}],k];(计算精确值) s1[m_]:=N[Sum[f[a+i*(b-a)/m]*(b-a)/m,{i,0,m-1}],k];(取小区间左端点的矩形公式) s2[m_]:=N[Sum[f[a+(i+1/2)*(b-a)/m]*(b-a)/m,{i,0,m-1}],k]; (取小区间中点的矩形公式) s3[m_]:=N[Sum[f[a+i*(b-a)/m]*(b-a)/m,{i,1,m}],k]; (取小区间右端点的矩形公式) s4[m_]:=N[Sum[(f[a+i*(b-a)/m]+f[a+(i+1)*(b-a)/m])/2*(b-a)/m,{i,0,m-1}],k]; (梯形公式) s5[m_]:=N[(b-a)/m/6*((f[a]+f[b])+2*Sum[f[a+i*(b-a)/m],{i,1,m-1}] 实验一 误差分析 实验1.1(病态问题) 实验目的:算法有“优”与“劣”之分,问题也有“好”与“坏”之别。对数值方法的研究而言,所谓坏问题就是问题本身对扰动敏感者,反之属于好问题。通过本实验可获得一个初步体会。 数值分析的大部分研究课题中,如线性代数方程组、矩阵特征值问题、非线性方程及方程组等都存在病态的问题。病态问题要通过研究和构造特殊的算法来解决,当然一般要付出一些代价(如耗用更多的机器时间、占用更多的存储空间等)。 问题提出:考虑一个高次的代数多项式 )1.1() ()20()2)(1()(20 1∏=-=---=k k x x x x x p 显然该多项式的全部根为1,2,…,20共计20个,且每个根都是单重的。现考虑该多项式的一个扰动 )2.1(0 )(19=+x x p ε 其中ε是一个非常小的数。这相当于是对(1.1)中19x 的系数作一个小的扰动。我们希望比较(1.1)和(1.2)根的差别,从而分析方程(1.1)的解对扰动的敏感性。 实验内容:为了实现方便,我们先介绍两个Matlab 函数:“roots ”和“poly ”。 roots(a)u = 其中若变量a 存储n+1维的向量,则该函数的输出u 为一个n 维的向量。设a 的元素依次为121,,,+n a a a ,则输出u 的各分量是多项式方程 01121=+++++-n n n n a x a x a x a 的全部根;而函数 poly(v)b = 的输出b 是一个n+1维变量,它是以n 维变量v 的各分量为根的多项式的系数。可见“roots ”和“poly ”是两个互逆的运算函数。 ;000000001.0=ess );21,1(zeros ve = ;)2(ess ve = 实验五 解线性方程组的直接方法 实验5.1 (主元的选取与算法的稳定性) 问题提出:Gauss 消去法是我们在线性代数中已经熟悉的。但由于计算机的数值运算是在一个有限的浮点数集合上进行的,如何才能确保Gauss 消去法作为数值算法的稳定性呢?Gauss 消去法从理论算法到数值算法,其关键是主元的选择。主元的选择从数学理论上看起来平凡,它却是数值分析中十分典型的问题。 实验内容:考虑线性方程组 编制一个能自动选取主元,又能手动选取主元的求解线性方程组的Gauss 消去过程。 实验要求: (1)取矩阵?? ? ?? ?? ?????????=????????????????=1415157,6816816816 b A ,则方程有解T x )1,,1,1(* =。取n=10计算矩阵的 条件数。让程序自动选取主元,结果如何? (2)现选择程序中手动选取主元的功能。每步消去过程总选取按模最小或按模尽可能小的元素作为主元,观察并记录计算结果。若每步消去过程总选取按模最大的元素作为主元,结果又如何?分析实验的结果。 (3)取矩阵阶数n=20或者更大,重复上述实验过程,观察记录并分析不同的问题及消去过程中选择不同的主元时计算结果的差异,说明主元素的选取在消去过程中的作用。 (4)选取其他你感兴趣的问题或者随机生成矩阵,计算其条件数。重复上述实验,观察记录并分析实验结果。 思考题一:(Vadermonde 矩阵)设 ?? ??????????????????????=? ? ? ?????????????=∑∑∑∑====n i i n n i i n i i n i i n n n n n n n x x x x b x x x x x x x x x x x x A 0020 10022222121102001111 ,, 其中,n k k x k ,,1,0,1.01 =+=, (1)对n=2,5,8,计算A 的条件数;随n 增大,矩阵性态如何变化? (2)对n=5,解方程组Ax=b ;设A 的最后一个元素有扰动10-4,再求解Ax=b (3)计算(2)扰动相对误差与解的相对偏差,分析它们与条件数的关系。 (4)你能由此解释为什么不用插值函数存在定理直接求插值函数而要用拉格朗日或牛顿插值法的原因吗? 相关MATLAB 函数提示: zeros(m,n) 生成m 行,n 列的零矩阵 ones(m,n) 生成m 行,n 列的元素全为1的矩阵 eye(n) 生成n 阶单位矩阵 rand(m,n) 生成m 行,n 列(0,1)上均匀分布的随机矩阵 diag(x) 返回由向量x 的元素构成的对角矩阵 tril(A) 提取矩阵A 的下三角部分生成下三角矩阵 数值分析实验报告 一、 实验目的 1、会使用Sor 法求解一个线性方程组 2、熟悉matlab 语言并结合原理编程求方程组 3、改变ω的值观察实验结果 4、会分析实验结果 二、实验题目 编制Sor 迭代格式程序进行求解一个线性方程组的迭代计算情况,运行中要选用不同的松弛因子ω进行尝试 三、 实验原理 Jacobi 迭代和seidel 迭代对具体的线性方程组来说,逼近*x 的速度是固定不变的,遇到收敛很慢的情况时就显得很不实用。 Sor 法是一seidel 迭代为基础,并在迭代中引入参数ω以增加迭代选择的灵活性,具体为: ! 用seidel 迭代算出的,)()1()()1(k k J k k J x x x x x -=?++相减得到差向量与再用参数ω乘之再加上 )1()()()1()1()()()1(++++-=?+=k J k k k k k k x x x x x x x x ωωω,即的下一步迭代作为,由seidel 迭代的公式可以得到Sor 法的迭代格式为 n i x a x a b a x x k j n i j ij k j i j ij i ii k i k i ,2,1),()1()(1)1(11)()1( =--+-=∑∑+=+-=+ω ω 式中ω称为松弛因子。 四、 实验内容 用matlab 编程得到Sor 法求线性方程组的算法为: function [x,n]=SOR(A,b,x0,w,eps,M) if nargin==4 eps= ; M = 200; elseif nargin<4 error return : elseif nargin ==5 M = 200; end if(w<=0 || w>=2) error; return; end D=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵( U=-triu(A,1); %求A的上三角阵B=inv(D-L*w)*((1-w)*D+w*U); f=w*inv((D-L*w))*b; x=B*x0+f; n=1; %迭代次数 while norm(x-x0)>=eps x0=x; x =B*x0+f; n=n+1; if(n>=M) ( 差值法实验日志 实验题目:插值法 实验目的: 1.掌握拉格朗日插值、牛顿插值、分段低次插值和样条插值的方法。 2.对四种插值结果进行初步分析。 实验要求: (1)写出算法设计思想; (2)程序清单; (3)运行的结果; (4)所得图形; (5)四种插值的比较; (6)对运行情况所作的分析以及本次调试程序所取的经验。如果程序未通过,应分析其原因。 实验主要步骤: 1.已知函数) f满足: (x x0.0 0.1 0.195 0.3 0.401 0.5 f(0.39894 0.39695 0.39142 0.38138 0.36812 x ) 0.35206 (1)用分段线性插值; 打开MATLAB,按以下程序输入: x0=-5:5; y0=1./(1+x0.^2); x=-5:0.1:5; y=1./(1+x.^2); y1=lagr(x0,y0,x); y2=interp1(x0,y0,x); y3=spline(x0,y0,x); for k=1:11 xx(k)=x(46+5*k); yy(k)=y(46+5*k); yy1(k)=y1(46+5*k); yy2(k)=y2(46+5*k); yy3(k)=y3(46+5*k); end [xx;yy;yy2;yy3]' z=0*x; plot(x,z,x,y,'k--',x,y2,'r') plot(x,z,x,y,'k--',x,y1,'r') pause plot(x,z,x,y,'k--',x,y3,'r') 回车得以下图形: (2) 拉格朗日插值。 创建M 文件,建立lagr 函数: function y=lagr1(x0,y0,x) n=length(x0);m=length(x); for i=1:m z=x(i); s=0.0; for k=1:n p=1.0; for j=1:n if j~=k p=p*(z-x0(j))/(x0(k)-x0(j)); end end s=p*y0(k)+s; end y(i)=s; end 新建一个M 文件,输入: x0=[0.0 0.1 0.195 0.3 0.401 0.5]; y0=[0.39894 0.39695 0.39142 0.38138 0.36812 0.35206]; x=0.0:0.01:0.5; y1=lagr1(x0,y0,x); 00.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1数值积分 (论文)
(完整版)数值计算方法上机实习题答案
(完整版)哈工大-数值分析上机实验报告
数值分析实验报告总结
基础实验二 定积分数值计算
数值分析实验报告1
数值分析实验报告
数值分析实验报告-Sor法分析
数值计算方法实验报告
